等效电路分析.

什么是等效电路？等效电路是指在电路中，把一部分电路装置（包括电源、负载等）简化为一个与之等效的电路，该电路具有相同的输入输出特性。

等效电路是电路分析中的重要概念，对于电路的设计和分析具有重要的指导意义。

本文将介绍等效电路的基本概念、分类、应用和具体实例。

一、等效电路的基本概念1. 等效电路的定义所谓等效电路，是指将一个复杂的电路简化为一个与之等效的简单电路，该简单电路具有相同的输入输出特性。

等效电路是为了方便电路的设计和分析，使用较简单的元件或电路把复杂的电路剖分出来，从而使电路的分析、计算和实现变得更加简单。

2. 等效电路的基本原理等效电路的基本原理是利用各种电学定律和电路分析方法，将一个复杂的电路转化为一个与之等效的简单电路。

常见的等效电路包括电阻、电容、电感等元件等效电路，以及放大器、滤波器等电路装置等效电路。

二、等效电路的分类1. 元件等效电路元件等效电路主要是把复杂的元件（例如电阻、电容、电感等）用一个简单的等效电路来代替。

这样做的好处是使电路分析和计算更加简单，方便设计和理解电路的工作原理。

常用的元件等效电路有串联等效电路、并联等效电路等。

2. 电路装置等效电路电路装置等效电路是将电路中的某个特定的装置（例如放大器、滤波器等）用一个简单的等效电路来代替。

这样做的好处是能够更加精确地预测电路的性能和工作特性，便于电路的设计和分析。

常见的电路装置等效电路有放大器等效电路、滤波器等效电路等。

三、等效电路的应用1. 电路分析与计算等效电路在电路分析与计算中具有重要的作用。

通过将复杂的电路转化为等效电路，可以简化电路的分析与计算过程，从而降低分析的难度。

利用等效电路，可以方便地计算电流、电压、功率等电路参数。

2. 电路设计与优化在电路设计与优化中，等效电路可以帮助工程师更好地理解电路的工作原理，从而选择合适的元件和电路装置。

通过对等效电路的分析和优化，可以提高电路的性能和效率，实现电路的设计目标。

等效电路详细讲解
等效电路是指将电路中的某一部分比较复杂的结构用一比较简单的结构替代，替代之后的电路与原电路对未变换的部分（或称外部电路）保持相同的作用效果。

等效电路的主要目的是简化电路分析，其等效的条件是对外部电路或端口而言的，对内部电路可以不同。

等效电路只适用于线性网络，不适用于非线性网络。

等效电路又称“等值电路”，它通过电阻等效、电容等效、电源等效等方法，化简成具有与原电路功能相同的简单电路。

画等效电路图的步骤包括认真审题，在草稿纸上画出原图，并把开关的状态、滑动变阻器的滑片所处的位置依题意画下；根据电流路径的优先走法，把没有电流经过的元件用橡皮擦擦掉，同时将断开的开关及与其串联的元件与擦掉，闭合的开关用导线代替；正确分析电路的连接方式，明确电流表测哪部分电路的电流，电压表测谁的电压，再将电路图整理，即画出了等效电路图；把已知条件尽可能标注在等效电路图上；找出所求的物理量与哪个等效图对应，然后根据串、并联电路的特点，特别注意电源电压不变，定值电阻的阻值不变，正确运用电学公式来分析解答。

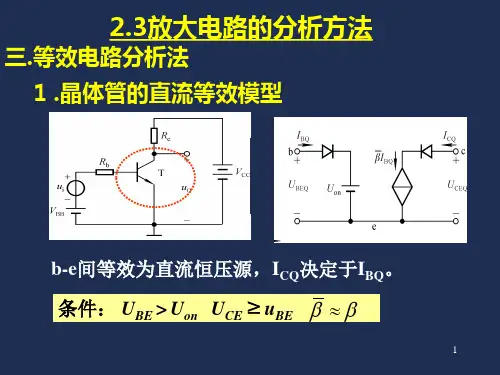
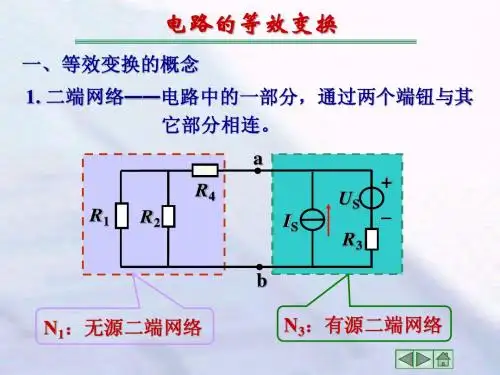
电阻网络的等效电路分析电阻网络是电路中常见的一种电路元件组合形式，在电子电路设计和分析中扮演着重要角色。

通过等效电路分析，我们可以将复杂的电阻网络简化为一个等效电路，便于电路的计算和设计。

本文将详细介绍电阻网络的等效电路分析方法及应用。

一、电阻网络的基本概念电阻网络由多个电阻器按照一定的连接方式组成。

电阻器是一种被动元件，具有阻抗特性。

在电阻网络中，电阻器的连接方式可以是串联或并联。

1. 串联连接：当多个电阻器相互连接，电流依次经过每个电阻器后流入负载，称为串联连接。

图1为三个电阻器R1、R2和R3串联连接的电阻网络示意图。

```plaintext图1：串联连接示意图```2. 并联连接：当多个电阻器的一端或两端直接相连，电流在各个电阻器中分流，称为并联连接。

图2为三个电阻器R1、R2和R3并联连接的电阻网络示意图。

```plaintext图2：并联连接示意图```二、电阻网络的等效电路分析方法等效电路分析是指将复杂的电阻网络转化为简化的等效电路，以方便电路的计算和分析。

下面将介绍两种常用的等效电路分析方法：串并联电阻法和特殊电阻组合法。

1. 串并联电阻法串并联电阻法是将复杂的电阻网络通过串联和并联电阻的等效性，转化为简化的电阻网络。

具体步骤如下：步骤一：将电阻网络中的串联电阻进行合并。

若电阻网络中存在多个串联电阻，将其合并为一个等效电阻。

例如，图3为一个含有多个串联电阻的电阻网络。

```plaintext图3：含有多个串联电阻的电阻网络示意图```可以将R1和R2合并为一个等效电阻Req1，R3和R4合并为一个等效电阻Req2，得到简化的电阻网络。

```plaintext图4：等效电阻合并后的简化电阻网络示意图```步骤二：将电阻网络中的并联电阻进行合并。

若电阻网络中存在多个并联电阻，将其合并为一个等效电阻。

例如，图4中的电阻网络可以将Req1和Req2合并为一个等效电阻Req。

步骤三：根据需要，继续进行串并联电阻的合并，直到最终得到等效电路。

了解电路的分析方法有几种
电路的分析方法主要有以下几种：
1. 等效电路分析法：将复杂的电路简化为等效电路进行分析。

常见的方法有等效电路的串、并联、星、三角转换，以及戴维南定理、叠加原理等。

2. 特征方程法：通过求解电路的特征方程，得到系统的频率响应和稳定性信息，用于分析电路的动态特性。

3. 网络定理法：包括基尔霍夫定律、戴维南和肖特定理、超定方程组法等，通过建立电路的节点或回路方程，求解未知电流和电压。

4. 拉普拉斯变换法：将时域中的微分或积分方程转换为复频域中的代数方程，利用代数方法求解电路中的电流和电压。

5. 瞬态响应分析法：分析电路在初始时刻和临近时刻的瞬态响应，包括过渡过程和保持过程的分析方法。

6. 直流分析法：分析直流电路中的电流和电压分布，包括欧姆定律、电压分压定律、电流分流定律等。

7. 交流分析法：分析交流电路中的电流和电压分布，包括复数表示法、阻抗、
导纳和功率分析等。

以上是常见的电路分析方法，根据电路的性质和问题的要求选择相应的方法进行分析。

电动势与电阻的串联与并联等效电路分析电动势（EMF）和电阻是电路中两个重要的元素。

在电路中，电动势提供电能，而电阻则阻碍电流的流动。

电动势与电阻可以通过串联和并联的方式连接在一起，形成不同的电路结构，从而产生不同的电路特性。

本文将讨论电动势与电阻的串联和并联等效电路的分析和应用。

一、串联等效电路分析1.1 串联电动势与电阻的特性串联电路是将电动势和电阻依次连接在一起，电流通过它们按顺序流过。

在串联电路中，电流大小相同，但电压分布不同。

电动势和电阻的总电压等于它们各自电压之和。

根据基尔霍夫电压定律，可以得到串联电路中的电压关系式：总电压=电动势1 + 电动势2 +…+ 电阻1 *电流 + 电阻2 *电流+…1.2 串联电动势与电阻的等效电路计算在某些情况下，我们需要将串联电动势和电阻简化为一个等效电路，以方便分析和计算。

串联电动势的等效电动势等于各个电动势之和，而串联电阻的等效电阻等于各个电阻之和。

这种简化可以使电路的分析更加方便和直观。

1.3 串联电动势与电阻的应用举例串联电动势和电阻的等效电路在实际应用中具有广泛的用途。

例如，串联电池中的多个电池通过串联连接起来，可以提供更高的电动势，从而满足某些特定设备的需求。

此外，在直流电源中，连接在一起的电阻可以增加电路的总电阻，控制电流的大小。

二、并联等效电路分析2.1 并联电动势与电阻的特性并联电路是将电动势和电阻并列连接在一起，电流同时通过它们。

在并联电路中，电压大小相同，但电流分布不同。

电动势和电阻的总电流等于它们各自电流之和。

根据基尔霍夫电流定律，可以得到并联电路中的电流关系式：总电流=电动势1 / 电阻1 + 电动势2 / 电阻2 +…2.2 并联电动势与电阻的等效电路计算与串联电路类似，我们也可以将并联电动势和电阻简化为一个等效电路，以方便分析和计算。

并联电动势的等效电动势等于各个电动势之和，而并联电阻的等效电阻等于它们的乘积除以它们的总电阻。

等效电路法等效电路法是电路分析中常用的一种方法，通过将复杂的电路替换为等效简化的电路，从而简化电路分析的过程。

本文将介绍等效电路法的基本原理、应用场景以及具体步骤。

一、基本原理等效电路法的基本原理是将原始电路替换为具有相同电流电压特性的简化电路，以便更方便地进行电路分析和计算。

在等效电路中，电路元件的参数可以根据实际情况进行调整，以满足分析需要。

二、应用场景等效电路法在电路分析中有广泛的应用场景，特别适用于以下几种情况：1. 复杂电路的简化：当电路非常复杂时，可以使用等效电路将其简化为更易于分析的形式，从而提高计算效率。

2. 近似计算：在某些情况下，为了简化计算，可以使用等效电路来近似代替原始电路，以便更方便地进行分析。

3. 参数调整：等效电路法可以根据实际情况调整电路元件的参数，以满足分析的需要。

三、具体步骤等效电路法的具体步骤如下：1. 根据实际情况选择适当的等效电路模型：根据电路特性和分析需求，选择适当的等效电路模型，比如理想电流源、理想电压源、电阻等。

2. 确定等效电路元件的参数：根据实际情况，确定等效电路元件的参数，如电流源的电流值、电压源的电压值、电阻的阻值等。

3. 确定等效电路连接方式：根据电路的拓扑结构，确定等效电路元件之间的连接方式，如串联、并联等。

4. 进行电路分析：使用等效电路进行电路分析，可以直接应用电路分析方法进行计算，如欧姆定律、基尔霍夫定律等。

5. 检验等效电路的准确性：在完成电路分析后，需对等效电路的准确性进行检验，比较等效电路计算结果与原始电路的实际测量结果是否一致。

四、注意事项在使用等效电路法进行电路分析时，需要注意以下几点：1. 确保等效电路能准确地描述原始电路的电流电压特性，避免引入误差。

2. 在选择等效电路模型和确定参数时，需要根据实际情况进行合理的假设和近似，以满足分析的精度要求。

3. 对于复杂电路，可以采用分层逐步简化的方法，先对子电路进行等效，然后再将简化后的子电路组合为整体等效电路。

戴维南等效电路详细讲解戴维南等效电路是电子电路中常用的一种简化方法，它可以将复杂的电路简化为一个等效电路，从而更方便地进行分析和计算。

本文将详细讲解戴维南等效电路的原理、应用以及计算方法。

戴维南等效电路是一种将多个电阻、电源和其他元件简化为一个等效电路的方法。

通过等效电路，我们可以用更简单的方式来描述电路的行为和特性。

戴维南等效电路主要基于两个原则：Thevenin定理和Norton定理。

我们来讲解Thevenin定理。

Thevenin定理指出，任何线性电路都可以用一个电压源和一个电阻串联起来来等效表示。

具体来说，我们可以将电路中的电源和电阻替换为一个电压源和一个电阻，并且这个等效电路与原电路在输出端口上的电压和电流完全一致。

接下来，我们来讲解Norton定理。

Norton定理与Thevenin定理类似，它也是一种将复杂电路简化为一个等效电路的方法。

不同的是，Norton定理是将电源和电阻替换为一个电流源和一个电阻，并且这个等效电路与原电路在输出端口上的电流和电压完全一致。

以上就是戴维南等效电路的基本原理。

接下来，我们将通过一个具体的例子来说明戴维南等效电路的应用和计算方法。

假设我们有一个复杂的电路，其中包含多个电阻和电源。

我们希望将这个电路简化为一个等效电路，以便更方便地进行分析。

首先，我们可以使用Thevenin定理将电路简化为一个电压源和一个电阻。

具体步骤如下：1. 找到我们感兴趣的输出端口，并将其他部分从电路中移除。

2. 计算输出端口上的开路电压，即在输出端口上不连接任何负载时的电压。

3. 计算输出端口上的短路电流，即在输出端口上短路时的电流。

4. 根据Thevenin定理，将电路简化为一个与原电路在输出端口上的电压和电流完全一致的电压源和电阻。

接下来，我们来看一个具体的例子。

假设我们有一个电路，其中包含一个电阻R1和一个电源V1，我们希望将这个电路简化为一个等效电路。

具体步骤如下：1. 我们感兴趣的输出端口是电阻R1的两端。

10种复杂电路的分析方法1.基本电路分析法：基本电路分析法是最常见和最简单的分析电路方法之一、它通过应用欧姆定律、基尔霍夫定律和电流分流法等基本电路定理，对电路进行分析和计算。

2.等效电路分析法：等效电路分析法通过将复杂的电路简化为等效电路，以便更好地理解和分析。

这种方法通常包括电位器等效电路和戴维南定理等。

3.直流戴维南定理：直流戴维南定理是分析含直流电源的复杂电路的一种有效方法。

它通过将电源和负载电阻分别简化为等效电路，从而降低了分析电路的复杂度。

4.交流戴维南定理：交流戴维南定理是分析含交流电源的复杂电路的一种方法。

它类似于直流戴维南定理，但还包括复数和矢量运算等。

5.电压和电流分布法：该方法通过分析电路中的电压和电流分布来推导电路的整体性能。

它依赖于电路中的节点和网孔等概念，通常用于分析高频电路和复杂电路。

6.参数扫描法：参数扫描法是一种通过调节电路中的一些参数并分析其影响来理解和优化电路的方法。

它通常用于分析射频电路和混频器等。

7.稳态响应分析法：稳态响应分析法用于分析电路的稳态行为，即电路在稳定工作条件下的性能。

它通常涉及使用复数技术、矩阵分析和频域分析等方法。

8.传递函数法：传递函数法是分析电路的频率响应的一种方法。

它通过将输入输出关系表示为传递函数的形式，以便分析和设计滤波器、放大器和控制系统等。

9.相位平面分析法：相位平面分析法用于分析电路的相位响应特性。

它通过绘制相位频率响应曲线和利用极点和零点等概念来分析电路。

10.二端口网络分析法：二端口网络是指具有两个输入端口和两个输出端口的网络。

该方法通过线性系统理论和矩阵方法来分析和设计二端口网络。

四种常用的电路分析法
常用分析电路的方法有以下几种：
1、直流等效电路分析法
在分析电路原理时，要搞清楚电路中的直流通路和交流通路。

直流通路是指在没有输入信号时，各半导体三极管、集成电路的静态偏置，也就是它们的静态工作点。

交流电路是指交流信号传送的途径，即交流信号的来龙去脉。

在实际电路中，交流电路与直流电路共存于同一电路中，它们既相互联系，又互相区别。

直流等效分析法，就是对被分析的电路的直流系统进行单独分析的一种方法，在进行直流等效分析时，完全不考虑电路对输入交流信号的处理功能，只考虑由电源直流电压直接引起的静态直流电流、电压以及它们之间的相互关系。

电路等效原理及应用分析电路等效原理是电气工程中非常重要的理论之一，它为电路设计与分析提供了一种便捷有效的方法。

在本文中，我们将对电路等效原理进行详细的探讨，并结合实际应用进行分析。

一、等效原理的概念及原理电路等效原理是指通过一定的变换，将一个复杂的电路模型简化为与之等效的简单电路模型，在等效电路中，原电路与等效电路具有相同的输入输出特性，即二者之间的电流、电压关系相同。

通过电路等效原理，我们可以简化电路结构，减少计算复杂度，提高电路分析的效率。

电路等效原理的核心思想在于，将电路中的元件根据其电性质与连接方式进行适当的抽象和简化。

常见的等效方法包括戴维南等效电路和泰勒等效电路。

戴维南等效电路是将一个复杂电路模型简化为一个等效电源与等效电阻串联的简单电路。

它基于原电路的两个重要性质：1. 两个点之间的电压是固定的，2. 两个点之间的电流流向是固定的。

这样，我们可以通过测量原电路两点之间的开路电压和短路电流来确定等效电源和等效电阻的值。

泰勒等效电路是将一个非线性电路模型在某一工作点上线性化为等效线性电路。

它基于泰勒级数展开的原理，将原电路的非线性特性通过线性元件进行近似表示。

通过选择合适的工作点和一阶导数，可以得到与原电路在该点附近非常接近的等效线性电路。

二、电路等效原理的应用电路等效原理在实际工程中有广泛的应用，主要包括以下几个方面：1. 电路设计与优化在电路设计过程中，通过等效原理可以将复杂的电路模型转化为简单的等效电路，从而更好地评估不同设计方案的性能指标。

例如，在放大电路设计中，我们可以通过等效原理将复杂的放大电路模型简化为简单的等效电路，从而更好地估计放大器的增益、频率响应等性能。

2. 电路分析与计算对于复杂电路的分析与计算往往会耗费大量的时间与计算资源。

而通过等效原理，我们可以将复杂电路转化为简单等效电路进行分析，大大简化了分析的过程。

例如，在交流电路分析中，通过泰勒等效电路的方法，我们可以将非线性负载电路模型线性化为等效电阻，从而方便地进行交流特性计算。