一阶RC低通滤波和信号调制解调实验

实验二十一一阶线性电路过滤过程的观测
一、实验目的
1、测定RC一阶电路的零输入响应,零状态响应及完全响应;
2、学习电路时间常数的测量方法;
3、掌握有关微分电路和积分电路的概念;
4、学会用示波器测绘图形;
二、实验内容
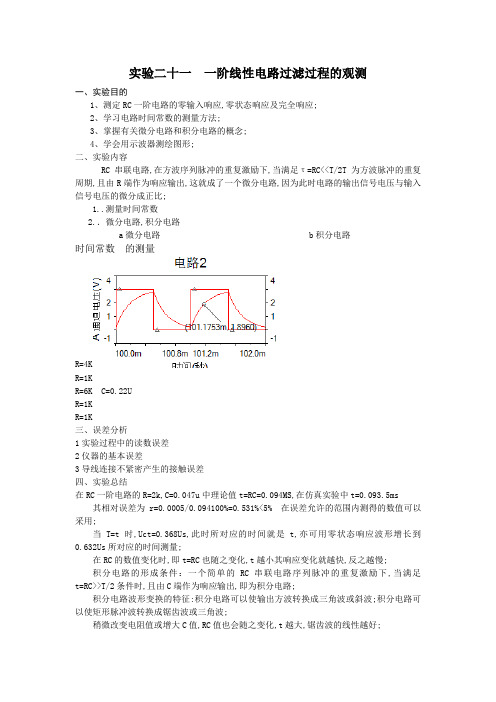
RC串联电路,在方波序列脉冲的重复激励下,当满足τ=RC<<T/2T为方波脉冲的重复周期,且由R端作为响应输出,这就成了一个微分电路,因为此时电路的输出信号电压与输入信号电压的微分成正比;
1..测量时间常数
2.．微分电路,积分电路
a微分电路 b积分电路
时间常数的测量
R=4K
R=1K
R=6K C=0.22U
R=1K
R=1K
三、误差分析
1实验过程中的读数误差
2仪器的基本误差
3导线连接不紧密产生的接触误差
四、实验总结
在RC一阶电路的R=2k,C=0.047u中理论值t=RC=0.094MS,在仿真实验中t=0.093.5ms 其相对误差为r=0.0005/0.094100%=0.531%<5% 在误差允许的范围内测得的数值可以采用;
当T=t时,Uct=0.368Us,此时所对应的时间就是t,亦可用零状态响应波形增长到0.632Us所对应的时间测量;
在RC的数值变化时,即t=RC也随之变化,t越小其响应变化就越快,反之越慢;
积分电路的形成条件：一个简单的RC串联电路序列脉冲的重复激励下,当满足t=RC>>T/2条件时,且由C端作为响应输出,即为积分电路;
积分电路波形变换的特征:积分电路可以使输出方波转换成三角波或斜波;积分电路可以使矩形脉冲波转换成锯齿波或三角波;
稍微改变电阻值或增大C值,RC值也会随之变化,t越大,锯齿波的线性越好;。

自适应信号处理姓名：战飞学号：2013021314专业：通信与信息系统班级：2013级13班2014年8月15日RC 低通滤波和信号调制解调 利用Simulink 生成系统及波形仿真一、实验目的：1、学习使用MATLAB 附带的Simulink 软件做系统仿真实验。

2、研究矩形脉冲通过RC 低通网络的波形变化。

3、验证调制解调的过程。

二、实验原理：1、RC 低通网络如下图所示其模型可用微分方程1c ic dv v v dt CRCR += 表示 系统函数为 RCj RC j H 11)(+=ωω这里的时间常数为RC=0.1s ，这个数值不同，输出波形会随之变化。

u iRC﹢﹢﹣﹣u c令wc=1/RC ，得到：ωωωωj j H c c +=)(其幅频特性为:(j )H ω=带宽可由输出电压从最大值下降到0.707倍时的频率来定义其相频特性为: c ()arctan ωϕωω⎛⎫=-⎪⎝⎭我们采用的激励信号)2()(ττ-=t Eg t v i 激励信号vi(t)的傅里叶变换式为2)2()(ωτωττωj i eSa E j V -=得到响应)(t V c 的傅里叶变换为：)(2|)(|)2()()()(ωϕωτωωωωωττωωωj c c c j i c e j V j eSa E j H j V j V =+=⋅=--(ϕ-(jH ωc响应)()]()()[1()(00τετεεωω-+---=--t Ee t t e E t v tt c 2、调制只是频谱搬移，不改变带宽。

载波信号为cos(w0t),将调制信号g(t)与cos(w0t)进行时域相乘，得到f(t)=g(t)cos(w0t) 所以f(t)的傅里叶变换为)]]([)]([[21)]()([*)(21)(0000ωωωωωωπδωωπδωπω-++=-++=j G j G j G j F 可见信号调制只是将信号左右平移w0，系数同时乘以0.5，得到的已调信号的频谱为F （jw ）。

rc一阶电路的响应测试实验报告实验目的，通过实验，了解RC一阶电路对直流电压和交流电压的响应特性，掌握RC一阶电路的响应测试方法及实验步骤。

实验仪器与设备，示波器、信号发生器、电阻箱、电容器、万用表、直流稳压电源、导线等。

实验原理，RC一阶电路是由电阻和电容串联而成的电路。

在实验中，我们将通过对RC电路施加不同的输入信号，观察电路的响应情况，了解电路的频率特性和相位特性。

实验步骤：1. 搭建RC一阶电路。

将电阻和电容串联连接，接入示波器和信号发生器。

调节信号发生器的频率和幅值，使其输出正弦波信号。

2. 测量直流电压响应。

将信号发生器输出直流电压信号，通过示波器观察电路的响应情况。

记录电路的电压响应曲线，并测量电路的时间常数。

3. 测量交流电压响应。

将信号发生器输出交流电压信号，通过示波器观察电路的响应情况。

记录电路的电压响应曲线，并测量电路的频率特性和相位特性。

实验数据与分析：1. 直流电压响应曲线如图所示。

根据实验数据，我们可以得到电路的时间常数τ=RC，其中R为电阻值，C为电容值。

时间常数τ描述了电路对直流信号的响应速度，τ越小，电路的响应速度越快。

2. 交流电压响应曲线如图所示。

根据实验数据，我们可以得到电路的频率特性和相位特性。

当输入信号的频率接近电路的截止频率时，电路的响应幅值将下降，相位延迟将增加。

这表明电路对高频信号的响应能力较弱。

实验结论，通过本次实验，我们深入了解了RC一阶电路对直流电压和交流电压的响应特性。

我们掌握了RC一阶电路的响应测试方法，并通过实验数据分析了电路的时间常数、频率特性和相位特性。

这些知识对于我们理解电路的响应特性，设计滤波器和信号处理器等具有重要的意义。

实验注意事项：1. 在搭建电路时，务必注意电路连接的正确性，避免出现短路或断路等情况。

2. 在测量电路响应时，要注意调节信号发生器的频率和幅值，确保输出信号符合实验要求。

3. 实验过程中要注意安全，避免触电和短路等危险情况的发生。

一阶RC电路的实验研究一、实验目的1.理解一阶RC电路的基本原理和特性。

2.熟悉一阶RC电路的实验测量方法。

3.观察和分析一阶RC电路的时间响应特性。

二、实验器材1.信号发生器2.示波器3.电阻箱4.电容器5.万用表6.连线电缆7.电源三、实验步骤1.搭建一阶RC电路，将信号发生器、电阻箱、电容器和示波器依次连接在一起。

注意保持正确的电路连接。

2.设置信号发生器输出一个方波信号，并通过示波器观察输出波形。

3.调节信号发生器的频率和幅度，观察RC电路的响应，并记录实验数据。

4.通过示波器的测量功能，测量电阻和电容的值，并记录实验数据。

5.根据测量数据，计算RC电路的时间常数（τ=R×C）。

6.重复实验步骤2-5，分别改变电阻和电容的值，观察RC电路的响应特性，并记录实验数据。

四、实验结果1.绘制RC电路的幅频特性图，研究电路的频率响应特性。

2.绘制RC电路的相频特性图，研究电路的相位响应特性。

3.绘制RC电路的阶跃响应曲线，研究电路的时间响应特性。

4.分析和讨论实验结果，比较不同参数下RC电路的性能差异。

五、实验分析1.从幅频特性图可以观察到RC电路的频率响应特性。

随着频率的增加，对输入信号的衰减程度逐渐增大。

2.从相频特性图可以观察到RC电路的相位响应特性。

随着频率的增加，输出信号的相位逐渐滞后于输入信号。

3.从阶跃响应曲线可以观察到RC电路的时间响应特性。

在电容充电过程中，电压会逐渐上升，且上升的速度随着电阻和电容的增大而减小。

4.实验数据和结果的分析需要结合理论知识进行，可以对不同参数下的RC电路性能进行比较和评估。

六、实验注意事项1.搭建电路时注意正确连接和保持连接可靠。

2.使用示波器时，选择适当的触发模式和合适的触发电平。

3.测量电阻和电容时，注意接线正确且稳定，避免误差。

4.保持实验环境稳定，减少干扰对实验结果的影响。

七、实验总结通过实验研究一阶RC电路，我们可以更加深入地理解电路的基本原理和特性。

自适应信号处理姓名：战飞学号：2013021314专业：通信与信息系统班级：2013级13班2014年8月15日RC 低通滤波和信号调制解调 利用Simulink 生成系统及波形仿真一、实验目的：1、学习使用MATLAB 附带的Simulink 软件做系统仿真实验。

2、研究矩形脉冲通过RC 低通网络的波形变化。

3、验证调制解调的过程。

二、实验原理：1、RC 低通网络如下图所示其模型可用微分方程1c ic dv v v dt CRCR += 表示 系统函数为 RCj RC j H 11)(+=ωω这里的时间常数为RC=0.1s ，这个数值不同，输出波形会随之变化。

u iRC﹢﹢﹣﹣u c令wc=1/RC ，得到：ωωωωj j H c c +=)(其幅频特性为:(j )H ω=带宽可由输出电压从最大值下降到0.707倍时的频率来定义其相频特性为: c ()arctan ωϕωω⎛⎫=-⎪⎝⎭我们采用的激励信号)2()(ττ-=t Eg t v i 激励信号vi(t)的傅里叶变换式为2)2()(ωτωττωj i eSa E j V -=得到响应)(t V c 的傅里叶变换为：)(2|)(|)2()()()(ωϕωτωωωωωττωωωj c c c j i c e j V j eSa E j H j V j V =+=⋅=--(ϕ-(jH ωc响应)()]()()[1()(00τετεεωω-+---=--t Ee t t e E t v t t c2、调制只是频谱搬移，不改变带宽。

载波信号为cos(w0t),将调制信号g(t)与cos(w0t)进行时域相乘，得到f(t)=g(t)cos(w0t) 所以f(t)的傅里叶变换为)]]([)]([[21)]()([*)(21)(0000ωωωωωωπδωωπδωπω-++=-++=j G j G j G j F 可见信号调制只是将信号左右平移w0，系数同时乘以0.5，得到的已调信号的频谱为F （jw ）。

电路原理实验RC一阶电路的响应测试RC一阶电路是由电阻R和电容C组成的电路。

它是一种常见的滤波电路，可以用于对信号进行滤波和延时等处理。

本实验将对RC一阶电路的响应进行测试，包括频率响应和时间响应两个方面。

一、频率响应测试频率响应测试可以了解RC一阶电路对不同频率信号的响应情况，即电路的频率特性。

我们可以通过改变输入信号的频率，测量输出信号的幅值和相位，从而绘制出RC电路的幅频特性曲线和相频特性曲线。

实验步骤如下：1.搭建RC一阶电路实验电路。

将电容C和电阻R按照串联的方式连接，接入信号发生器的输出端，然后将电路的输出端连接到示波器上。

确保电路接线正确，电容C和电阻R的数值符合实验要求。

2.打开信号发生器和示波器，将信号发生器的频率调节到最低，幅值调节到合适的范围内。

3.逐步增加信号发生器的频率，同时观察示波器上输出信号的幅值和相位。

记录下不同频率下的输出幅值和相位数据。

4.根据记录的数据，绘制RC电路的幅频特性曲线和相频特性曲线。

可以选择使用半对数坐标系或对数坐标系进行绘制，以更清晰地展示电路的频率特性。

二、时间响应测试时间响应测试可以了解RC一阶电路对输入信号的响应速度和衰减情况。

我们可以通过输入一个脉冲信号或方波信号，观察输出信号的波形，从而了解RC电路的时间特性。

实验步骤如下：1.搭建RC一阶电路实验电路。

将电容C和电阻R按照串联的方式连接，接入信号发生器的输出端，然后将电路的输出端连接到示波器上。

确保电路接线正确，电容C和电阻R的数值符合实验要求。

2.打开信号发生器和示波器，将信号发生器的频率调节到适当的范围内，幅值调节到合适的范围内。

3.输入一个脉冲信号或方波信号，观察示波器上输出信号的波形。

记录下输出信号的上升时间、下降时间和衰减时间等数据。

4.根据记录的数据，分析RC电路的时间特性。

可以计算RC电路的时间常数，即RC的乘积，进一步了解电路的响应速度和衰减情况。

总结：通过频率响应测试和时间响应测试，我们可以全面了解RC一阶电路的响应特性。

一阶rc电路的过渡过程实验报告实验一：一阶RC电路的理论分析一阶RC电路是一种常见的模拟电路。

它由一个电阻器和一个电容器组成。

在这个电路中，电容器表现出一种电学性质，称为电容。

当电容的电压发生变化时，它可以在电路中存储或释放电荷。

我们可以通过理论分析来研究一阶RC电路的特性。

在这个过程中，我们需要了解电阻、电容和电压的基本知识，以及欧姆定律、电流定律、基尔霍夫电压定律和基尔霍夫电流定律等电路理论方面的基本知识。

我们可以使用一些基本电路方程来描述一阶RC电路的行为。

这些方程包括欧姆定律、电容电压关系和基尔霍夫电压定律。

我们可以通过这些方程来解决电路中的电压和电流，进而得到一阶RC电路的特性。

欧姆定律(V = IR)是电路中最基本的方程之一。

它描述了电路中的电压、电流和电阻之间的关系。

如果我们知道电路中的电压和电阻，我们可以使用欧姆定律来计算电流。

对于一阶RC电路，我们可以使用欧姆定律来计算电阻的电流。

在这个电路中，电流的值是由电压和电阻的值决定的。

我们可以使用公式I = V/R来计算电流。

另一个重要的方程是电容电压关系(Q = CV)。

这个方程描述了电容器在电路中储存和释放电荷的能力。

如果我们知道电容的容量和电荷的电压，我们就可以通过电容电压关系来计算电荷的数量。

在一阶RC电路中，电容的电压随时间的变化可以使用基尔霍夫电压定律来描述。

基尔霍夫电压定律表示，在一个电路中，电压沿电路中的任何路径保持总和等于零。

这个定律是基于电压的守恒原理。

实验二：一阶RC电路的电路图一阶RC电路的电路图如下所示：电路图中包括一个电容、一个电阻和一个电源。

在这个电路中，电源提供一个不变的电压，而电容器和电阻器被连接在一起。

实验三：一阶RC电路的过渡过程实验步骤1. 准备实验设备和材料，并将电路连接起来。

2. 将一个始末电容器连接到电路中。

3. 调整电容器的值，以便于实验。

4. 开始实验。

将电源连接到电路上，并进行实验过渡过程。

一阶rc电路实验报告标题：一阶RC电路实验报告概述：本实验旨在通过搭建一阶RC电路并对其进行实验，深入了解电路的基本原理和特性。

通过实验，观察和分析电路中电流、电压的变化规律，探究RC电路的时域和频域特性。

实验器材和材料：1. 电压源：稳压直流电源2. 电阻：1kΩ3. 电容：100nF4. 示波器：万用表5. 连接线等实验流程：1. 搭建电路：按照电路图连接电源、电阻和电容，注意正负极的连接。

2. 测量电压：使用示波器，依次测量并记录电压源电压、电容两端电压以及电阻两端电压。

3. 测量电流：使用万用表，测量并记录电路中的电流值。

4. 观察数据：将实测数据整理成表格或图像，通过观察和分析，得出电流和电压随时间变化的规律。

5. 测试频率响应：改变电源频率，分别测量并记录不同频率下的电压值，研究电路的频域特性。

实验结果：1. 时域特性：通过示波器观察得到的电压波形图，可以清晰地看到电容两端的电压随时间的指数下降，形成充放电过程。

2. 频域特性：通过改变电源频率并测量电压值，得到电压-频率的响应曲线。

观察到，在低频时，电容器对交流信号的阻抗较大，限制了电流的流动；而在高频时，电容器对交流信号的阻抗较小，电流更容易通过。

实验分析：1. 时域特性分析：由电容的电压随时间指数下降的特性可知，当电容开始充电时，电流经过电阻的阻塞，电压上升较慢，而当电容器充满电后，电阻将充分放行，电流几乎流过电容而不经过电阻，电压迅速下降至零。

这反映了电容在电路中的存储和释放电荷的特性。

2. 频域特性分析：电容器的阻抗随频率变化而变化，频率越高，电阻越小，电容的影响越小。

这是因为在高频下，电容器内部的电导效应变得更加显著，电流更容易通过。

这一特性广泛应用于滤波、耦合和频率选择电路等领域。

实验应用：1. 一阶RC电路在滤波中的应用：利用电容器对高频信号的阻隔特性，可以设计出低通RC滤波电路，将高频信号滤除，保留低频信号。

相应地，高通RC滤波电路则可将低频信号滤除，保留高频信号。