昆一中西山学校20172018学年下学期期末考试答案

2017-2018学年云南省昆明一中西山学校八年级（下）期末物理试卷一、单选题（本大题共8小题，每小题3分，共24分）．下列各题的答案中只有一个是正确的，请考生用2B铅笔把答题卡上对应题目的答案标号涂黑．1．（3分）下列四种物态变化相同的一组是（）①夏天，草叶上的露珠；②冬天，窗户上的冰花；③深秋，树上的白霜；④初春，冰雪消融。

A．①③B．①④C．②③D．②④2．（3分）下列关于力和运动的说法正确的是（）A．人推墙的力和墙对人的力是一对平衡力B．物体在平衡力的作用下一定保持匀速直线运动C．给正在运动的物体再施加一个力，物体就会比原来运动得更快D．在平直轨道上匀速行驶的火车车厢里，竖直向上跳起的人仍然落回原地（不计空气阻力）3．（3分）一个铁锭（如图甲所示）放置在水平地面上时，对地面产生的压力和压强分别是F1和p1；当如图乙所示放置在水平地面上时，对地面产生的压力和压强分别是F2和p2，那么（）A．F1＝F2，p1＝p2B．F1＝F2，p1＜p2C．F1＞F2，p1＝p2D．F1＜F2，p1＞p24．（3分）游乐场中的翻滚过山车是一种惊险、刺激的游戏，如图是翻滚过山车的简化模型，图中B点为最低点，C点为轨道弧形部分的最高点。

翻滚过山车在运动过程中。

下列说法正确的是（）A．运动到B 点时，动能最大B．运动到C 点时，重力势能最大C．从B 点到C 点，重力势能减小，动能增大D．从A 点到B 点，重力势能增大，动能减小5．（3分）用相同的滑轮和绳子分别组成如图所示的甲、乙两个滑轮组，把相同重物匀速提升相同的高度，若不计绳重及摩擦，下列说法正确的是（）A．绳子受的拉力F1和F2的大小不相等，滑轮组的机械效率不同B．绳子自由端移动的距离不相等，拉力对滑轮组所做的功相等C．绳子受的拉力F1和F2的大小相等，滑轮组的机械效率相同D．绳子自由端移动的距离不相等，拉力对滑轮组所做的功不相等6．（3分）小吴同学为探究力之间的关系做了如图所示的实验。

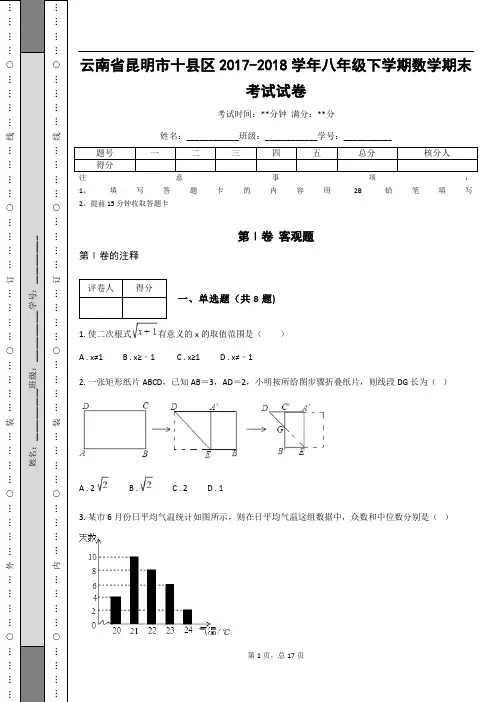
…………外…………○…………装…………○…………订…………○…………线…………○…………姓名：____________班级：____________学号：___________…………内…………○…………装…………○…………订…………○…………线…………○…………云南省昆明市十县区2017-2018学年八年级下学期数学期末考试试卷考试时间：**分钟 满分：**分姓名：____________班级：____________学号：___________题号 一 二 三 四 五 总分 核分人得分注意事项：1、填写答题卡的内容用2B铅笔填写2、提前 15 分钟收取答题卡第Ⅰ卷 客观题第Ⅰ卷的注释评卷人 得分一、单选题（共8题)1. 使二次根式有意义的x 的取值范围是（ ）A . x≠1B . x≥﹣1C . x≥1D . x≠﹣12. 一张矩形纸片ABCD ，已知AB ＝3，AD ＝2，小明按所给图步骤折叠纸片，则线段DG 长为（ ）A . 2B .C . 2D . 13. 某市6月份日平均气温统计如图所示，则在日平均气温这组数据中，众数和中位数分别是（ ）答案第2页，总17页…○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※…○…………内…………○…………装…………○…………订…………○…………线…………○…………A . 21，21B . 21，21.5C . 21，22D . 22，224. 下列根式是最简二次根式的是（ ）A .B .C .D .5. 下列各组线段能构成直角三角形的一组是（ ）A . 3，4，6B . 5，9，12C . 30，40，50D . 7，12，136. 一木杆在离地面5m 处析断，木杆顶端落在木杆底端12m 处，则木杆析断前高为（ ）A . 18mB . 13mC . 17mD . 12m7. 已知函数y ＝2x+k ﹣1的图象不经过第二象限，则（ ） A . k ＜1 B . k ＞1 C . k≥1 D . k≤18. 如图，在菱形ABCD 中，点A 在x 轴上，点B 的坐标为（8，2），点D 的坐标为（0，2），则菱形ABCD 面积为（ ）A . 8B . 16C . 24D . 32第Ⅱ卷 主观题第Ⅱ卷的注释评卷人得分一、填空题（共7题)…………外…………○…………装…………○…………订…………○…………线…………○…………姓名：____________班级：____________学号：___________…………内…………○…………装…………○…………订…………○…………线…………○…………1. = ．2. 若点A （2，﹣12）在正比例函数y ＝kx （k≠0）的图象上，则正比例函数的解析式为 .3. 如图，A ，B 两点被池塘隔开，不能直接测量其距离.于是，小明在岸边选一点C ，连接CA ，CB ，分别延长到点M ，N ，使AM ＝AC ，BN ＝BC ，测得MN ＝200m ，则A ，B 间的距离为 m.4. 学校准备从甲、乙、丙、丁四个科创小组中选出一组代表学校参加青少年科技创新大赛，各组的平时成绩的平均数 （单位：分）及方差s 2如表所示： 甲 乙 丙 丁 7 8 8 7s 2 1 1.2 1 1.8如果要选出一个成绩较好且状态稳定的组去参赛，那么应选的组是 . 5. 如图，在Rt△ABC 中，△ABC=90°，AC=10cm ，点D 为AC 的中点，则BD=cm.6. 在矩形ABCD 中，AB ＝2，AD ＝3，点P 是BC 上的一个动点，连接AP 、DP ，则AP+DP 的最小值为 .7. 如图,在△ABCD 中,△D=100°,△DAB 的平分线AE 交DC 于点E,连接BE.若AE=AB,则△EBC 的度数为 .评卷人得分二、计算题（共1题)答案第4页，总17页…○…………外…………○…………装…………○…………订…………○…………线…………○…………※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※…○…………内…………○…………装…………○…………订…………○…………线…………○…………8. 计算：（1）2 ﹣6 +2（2）（ + ） ﹣3 ÷评卷人 得分三、解答题（共2题)9. 如图，隔湖有两点A ，B ，为了测A ，B 两点间的距离，从与AB 方向成直角的BC 方向取一点C ，若测得CB ＝150m ，△ACB ＝30°，求A ，B 两点间的距离.10. 如图，矩形ABCD 的对角线AC ，BD 相交于点O ，点E ，F 在BD 上，BE ＝DF.求证：AE ＝CF.评卷人 得分四、综合题（共5题)11. 为了了解我县中学生参加“科普知识”竞赛成绩的情况，随机抽查了部分参赛学生的成绩，整理并制作.组别 分数段（分） 频数 百分率（%）A 组 60≤x ＜7030 10 B 组 70≤x ＜8090 n…………外…………○…………装…………○…………订…………○…………线…………○…………姓名：____________班级：____________学号：___________…………内…………○…………装…………○…………订…………○…………线…………○…………C 组 80≤x ＜90 m 40D 组 90≤x ＜10060 20（1）样本容量a ＝ ，表中m ＝ ，n ＝ ；（2）补全频数分布直方图；（3）若成绩在80分以上（包括80分）为“优”等，请你估计我县参加“科普知识”竞赛的1.5万名学生中成绩是“优”等的约有多少人？12. 某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准.该市的用户每月应交水费y(元)是用水量x(立方米)的函数，其图象如图所示.（1）若每月用水量为18立方米，则应交水费多少元？（2）求当x>18时，y 关于x 的函数解析式.若小敏家某月交水费81元，则这个月用水量为多少立方米？ 13. 如图，在平行四边形ABCD 中，边AB 的垂直平分线交AD 于点E ，交CB 的延长线于点F ，连接AF ，BE.。

云南省昆明市2017-2018学年八年级下期末试卷解析和答案2017-2018学年云南省昆明市官渡区八年级（下）期末考试数学试卷一、填空题（每小题3分，共24分）1.当x为正实数时，在实数范围内有意义。

2.在▱ABCD中，∠A=70°，则∠C=110度。

3.正比例函数y=kx（k≠0）的图象经过点A（-1，5），则k=5.4.如图，分别以Rt△ABC的三边为边长，在三角形外作三个正方形，若正方形P的面积等于89，Q的面积等于25，则正方形R的边长是6.5.如图，在平行四边形ABCD中，点E、F分别在边BC、AD上，使得EF平行于AB，则四边形AECF是平行四边形。

6.有两名学员___和___练射击，第一轮10枪打完后两人打靶的环数如图所示，通常新手的成绩不太稳定，那么根据图中的信息，估计___和___两人中新手是___。

7.如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，若AB=6cm，BC=8cm，则△AEF的周长=10cm。

8.一次函数y1=kx+b与y2=x+a的图象如图所示，则不等式kx+ba-k。

二、选择题（每小题3分，共24分）9.下列二次根式中，最简二次根式是（C）。

10.下列计算正确的是（B）。

11.如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，CD是AB边上的中线，则CD的长是（D）10.12.一次函数y=kx+b的图象如图所示，则k、b的符号（C）k<0，b<0.13.下列命题中，为真命题的是（D）对角线互相垂直平分的四边形是正方形。

14.为了调查某小区居民的用水情况，随机抽查了若干户家庭的月用水量，结果如下表：月用水量（吨）户数2 33 44 55 8则关于这若干户家庭的月用水量，下列说法错误的是（A）平均数是4.6吨。

1.解方程36x=33.6x+84，得到x=35；2.当y1>y2时，解不等式36x>33.6x+84，得到x>35；3.当y1<y2时，解不等式36x<33.6x+84，得到x<35；4.由x>10得到10<x<35；5.如果购买35个书包，则选A、B品牌都一样；如果购买35个以上书包，则选B品牌更划算；如果购买书包个数超过10个但小于35个，则选A品牌更划算。

2017-2018学年云南省昆明市十县区七年级（下）期末数学试卷一、填空题（每小题3分，满分18分）1．如果x2＝3，则x＝．2．如图，直线l与直线AB、CD分别相交于E、F，∠1＝120°，当∠2＝时，AB∥CD．3．由3x﹣2y﹣4＝0，得到用x表示y的式子为y＝．4．如图，点P在直线l外，PB⊥l于B，A为l上任意一点，则PA与PB的大小关系是PA PB．5．不等式组无解，则a的取值范围是．6．线段CD是由线段AB平移得到的．点A（﹣2，5）的对应点为C（3，7），则点B（﹣3，0）的对应点D的坐标为．二、选择题（本大题共8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的，每小题选出答案后，用2B铅笔将答题卡上对应题目的答案标号的小框涂黑)7．下列调查方式，你认为最合适的是（）A．日光灯管厂要检测一批灯管的使用寿命，采用全面调查方式B．旅客上飞机前的安检，采用抽样调查方式C．了解北京市居民日平均用水量，采用全面调查方式D．了解北京市每天的流动人口数，采用抽样调查方式8．用加减法将方程组中的未知数x消去后，得到的方程是（）A．2y＝6B．8y＝16C．﹣2y＝6D．﹣8y＝169．如图，点E在AC的延长线上，下列条件中能判断AB∥CD的是（）A ．∠3＝∠4B ．∠D +∠ACD ＝180°C ．∠D ＝∠DCED ．∠1＝∠210．不等式组的解集在数轴上表示正确的是（ ）A ．B ．C ．D ． 11．永川到成都路程全长288km ，一辆小汽车和一辆客车同时从永川、成都两地相向而行，经过1小时50分钟相遇，相遇时小汽车比客车多行驶40km ．设小汽车和客车的平均速度为x km /h 和y km /h ，则下列方程组正确的是（ ）A ．B ．C ．D ．12．点P （x ，y ）在第四象限，且|x |＝3，|y |＝2，则P 点的坐标是（ ）A ．（3，2）B ．（3，﹣2）C ．（﹣2，3）D ．（2，﹣3）13．9的算术平方根是（ ）A ．±3B ．3C ．﹣3D ．14．若关于x 的不等式mx +1＞0的解集是x ＜，则关于x 的不等式（m ﹣1）x ＞﹣1﹣m 的解集是（ ）A ．xB ．xC ．xD ．x三、解答题（本大题共9小题，共70分。

云南省昆明市2017-2018学年高一下学期期末考试数学试卷注意事项：1. 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2．选择题必须使用2B铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。

3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。

4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题（每个小题5分，共12个题）1.已知集合，则的子集个数为（）A. 2B. 4C. 7D. 8【答案】D【解析】【分析】根据集合交集的定义和集合中子集的个数的计算公式，即可求解答案．【详解】由题意集合，∴，∴的子集个数为．故选D．【点睛】本题主要考查了集合的交集运算及子集个数的判定，其中熟记集合交集的运算和集合中子集个数的计算公式是解答的关键，着重考查了推理与计算能力，属于基础题．2.函数的定义域是( )A. (－1，＋∞)B. [－1，＋∞)C. (－1,1)∪(1，＋∞)D. [－1,1)∪(1，＋∞)【答案】C【解析】由题意得，∴，故选C.3.一个直角三角形绕其最长边旋转一周所形成的空间几何体是（）A. 一个棱锥B. 一个圆锥C. 两个圆锥的组合体D. 无法确定【答案】C【解析】一个直角三角形绕其最长边AC旋转一周所形成的空间几何体是以斜边的高BD为半径的底面圆，以斜边被垂足D分得的两段长AD，CD为高的两个倒扣的圆锥的组合体故选C4.已知一个几何体的三视图如图所示，则这个几何体的体积是（）A. B. C. D.【答案】B【解析】【分析】根据几何体的三视图，得到该几何体为一个圆柱去掉一个内接圆锥，利用圆柱和圆锥的体积公式，即可求解．【详解】由题意，根据给定的三视图可知，该几何体为一个圆柱去掉一个内接圆锥，所以体积为，故选B.【点睛】在由三视图还原为空间几何体的实际形状时，要从三个视图综合考虑，根据三视图的规则，空间几何体的可见轮廓线在三视图中为实线，不可见轮廓线在三视图中为虚线．在还原空间几何体实际形状时，一般是以正视图和俯视图为主，结合侧视图进行综合考虑．求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解．5.为了得到函数的图像，可以将函数的图像（）A. 向左平移个单位长度B. 向右平移个单位长度C. 向左平移个单位长度D. 向右平移个单位长度【答案】B【解析】【分析】先化简函数，再根据三角函数的图象变换，即可求解．【详解】由题意，函数，所以为了得到函数的图象，可以将函数的图象向右平移个单位长度，故选B．【点睛】本题考查三角函数的图象的平移与伸缩变换，注意先伸缩后平移时的系数是解题的关键，着重考查了分析问题和解答问题的能力，属于基础题.6.若直线过点（1，2），（4，2+）则此直线的倾斜角是（）A. B. C. D.【答案】A【解析】【分析】设直线的倾斜角为，根据直线的斜率和倾斜角的关系，即可求解．【详解】设直线的倾斜角为，则，又∵，所以，故选A.【点睛】本题主要考查直线的斜率与倾斜角，属于简单题. 求直线的倾斜角往往先求出直线的斜率，求直线斜率的常见方法有一以下三种，（1）已知直线上两点的坐标求斜率：利用；（2）已知直线方程求斜率：化成点斜式即可；（2）利用导数的几何意义求曲线切点处的切线斜率.7.圆的圆心坐标和半径分别是A. B. C. D.【答案】D【解析】【分析】把圆的一般方程化简为圆的标准方程，即可求解圆的圆心坐标和半径，得到答案．【详解】依题意可得：∴圆的圆心坐标和半径分别是，，故选：D【点睛】本题主要考查了圆的方程的应用，其中熟记圆的标准方程和圆的一般的形式和互化是解答的关键，着重考查了推理与运算能力，属于基础题．8.直线截圆所得的弦长为A. B.C. D.【答案】D【解析】【分析】由题意，求得圆的圆心坐标和半径，利用圆的弦长公式，即可求解．【详解】由题意圆的方程，可知圆心，半径，则圆心到直线的距离为，所以弦长为，故选D．【点睛】本题主要考查了圆的弦长公式应用，其中解答中熟记直线与圆的位置关系和直线与圆的弦长公式是解答的关键，着重考查了推理与运算能力，属于基础题．9.中，角的对边分别为，已知，，，则（）A. B. C. D.【答案】C【解析】【分析】在三角形中，利用正弦定理，即可求解．【详解】在△ABC中，，∴则，∴由正弦定理可得：故选C【点睛】本题主要考查了正弦定理、余弦定理的应用，其中利用正弦、余弦定理可以很好地解决三角形的边角关系，熟练掌握定理、合理运用是解本题的关键．在中，通常涉及三边三角，知三（除已知三角外）求三，可解出三角形，当涉及两边及其中一边的对角或两角及其中一角对边时，运用正弦定理求解；当涉及三边或两边及其夹角时，运用余弦定理求解.10.在中，角的对边分别为，若，则( )A. 60°B. 120°C. 45°D. 30°【答案】B【解析】【分析】根据题意，由余弦定理求得，即可求解答案．【详解】因为，由余弦定理得，又∵，所以，故选B．【点睛】本题主要考查了正弦定理、余弦定理的应用，其中利用正弦、余弦定理可以很好地解决三角形的边角关系，熟练掌握定理、合理运用是解本题的关键．在中，通常涉及三边三角，知三（除已知三角外）求三，可解出三角形，当涉及两边及其中一边的对角或两角及其中一角对边时，运用正弦定理求解；当涉及三边或两边及其夹角时，运用余弦定理求解.11.已知等差数列{a n}中，a3=9，a9=3，则公差d的值为（）A. B. 1 C. - D. -1【答案】D【解析】【分析】利用等差数列的通项公式，列出方程组，求得的值，得到答案．【详解】等差数列中，，由等差数列的通项公式，可得解得，即等差数列的公差d=﹣1．故选D．【点睛】本题主要考查等差数列的通项公式、等差数列的前项和公式，属于中档题. 等差数列基本量的运算是等差数列的一类基本题型，数列中的五个基本量，一般可以“知二求三”，通过列方程组所求问题可以迎刃而解，另外，解等差数列问题要注意应用等差数列的性质与前项和的关系，利用整体代换思想解答.12.数列的前项和为，若，则等于（）A. 1B.C.D.【答案】C【解析】试题分析：由题意得，数列的通项公式，所以，故选B.考点：数列的求和.【方法点晴】本题主要考查了数列的求和问题，其中解答中涉及到数列通项公式的列项、数列的列项相消求和，着重考查了学生分析问题和解答问题的能力，以及退了与运算能力，试题比较基础，属于基础题，本题解答中吧数列的通项公式化简为是解答的关键，平时注意总结和积累.第II卷（非选择题共90分）二、填空题（共20分）13.已知，且是第二象限角，则___________．【答案】【解析】【分析】根据角为第二象限角，得，再由三角函数的基本关系式，即可求解．【详解】因为是第二象限角，∴，又，由三角函数的基本关系式可得．【点睛】本题主要考查了同角三角函数的基本关系的化简求值问题，其中根据角的象限，判定三角函数的符号是解答的一个易错点，同时熟记三角函数的基本关系式是解答的关键，着重考查了推理与运算能力．14.已知点与点，则的中点坐标为__________．【答案】【解析】【分析】根据题意与点，根据中点的坐标公式，即可求解．【详解】由题意点与点，根据中点坐标公式可得的中点坐标为，即的中点坐标为.【点睛】本题主要考查了空间向量的坐标表示及中点中点坐标公式的应用，其中解答中熟记空间向量的坐标表示和中点的坐标公式是解答的关键，着重考查了推理与运算能力，属于基础题．15.函数，则的值为__________.【答案】1【解析】【分析】根据分段函数的解析式，代入即可求解．【详解】当时，，，当时，，.【点睛】本题主要考查了分段函数的求函数值问题，其中把握分段函数的分段条件，准确运算是解答的关键，着重考查了推理与运算能力，属于基础题．16.直线与直线互相垂直，则实数等于________．【答案】2【解析】【分析】利用两条直线互相垂直，列出方程，即求解．【详解】直线与直线互相垂直，则，∴，故答案为2【点睛】本题主要考查了两条直线的位置关系的应用，其中熟记两条直线的位置关系，列出方程求解是解答的关键，着重考查了推理与运算能力，属于基础题．三、解答题（共70分，17题10分其各题每题12分，要求写出必要的解题步骤）17.在等差数列{a n}中，a12=23，a42=143，a n=239，求n及公差d．【答案】n=66，d=4【解析】试题分析：由题意结合等差数列的定义可先求公差，再列关于n的方程，解方程可得试题解析：由题意可得，d==4，∴a1=﹣21∵a n=a1+（n﹣1）d=﹣21+4（n﹣1）=239，解得n=66综上，n=66，d=4.点睛：本题主要考查等差数列的通项公式、等差数列的前项和公式，属于中档题. 等差数列基本量的运算是等差数列的一类基本题型，数列中的五个基本量，一般可以“知二求三”，通过列方程组所求问题可以迎刃而解，另外，解等差数列问题要注意应用等差数列的性质（）与前项和的关系，利用整体代换思想解答.18.已知等比数列{a n}满足记其前n项和为(1)求数列{a n}的通项公式a n；(2)若，求n.【答案】(1)；(2)5.【解析】【分析】（1）设出等比数列的公比，由条件得到关于的方程组，求得便可得到数列的通项公式；（2）根据前n项和得到关于n的方程，解方程可得解．【详解】(1)设等比数列{a n}的公比为，由条件得,解得，∴ an=a1q n−1=.即数列{a n}的通项公式为．(2)由题意得，解得：.【点睛】本题主要考查了等比数列的通项公式及等比数列的前项和公式的应用，其中熟记等比数列的通项公式和前项和公式，准确计算是解答的关键，着重考查了推理与运算能力，属于基础题．19.如图，在中，，是边上一点，且.（1）求的长；（2）若，求的长及的面积.【答案】(1) (2)【解析】【分析】（1）在中由正弦定理可求得AD的长；（2）在中，由余弦定理可得，利用可得所求面积．【详解】（1）在中，由正弦定理得，即，∴（2）∵，∴在中，由余弦定理得∴∴.综上，的面积为．【点睛】本题主要考查了利用正弦定理和余弦定理、三角形的面积公式求解三角形问题，对于解三角形问题，通常利用正弦定理进行“边转角”寻求角的关系，利用“角转边”寻求边的关系，利用余弦定理借助三边关系求角，利用两角和差公式及二倍角公式求三角函数值. 利用正、余弦定理解三角形问题是高考高频考点，经常利用三角形内角和定理，三角形面积公式，结合正、余弦定理解题.20.在中，内角的对边分别为，且.（Ⅰ）求；（Ⅱ）若，求.【答案】（Ⅰ）;（Ⅱ）.【解析】【分析】（Ⅰ）利用正弦定理可对进行化简，即可得到的值；（Ⅱ）利用正弦定理对进行化简，可得到，再利用的余弦定理，可求出的值.【详解】（Ⅰ）由及正弦定理，得.在中，..（Ⅱ）由及正弦定理，得，①由余弦定理得，，即，②由①②，解得.【点睛】本题主要考查了正弦定理、余弦定理的应用，其中利用正弦、余弦定理可以很好地解决三角形的边角关系，熟练掌握定理、合理运用是解本题的关键．在中，通常涉及三边三角，知三（除已知三角外）求三，可解出三角形，当涉及两边及其中一边的对角或两角及其中一角对边时，运用正弦定理求解；当涉及三边或两边及其夹角时，运用余弦定理求解.21.已知直线经过点，且斜率为．（1）求直线的方程．（2）求与直线平行，且过点的直线方程．（3）求与直线垂直，且过点的直线方程．【答案】(1) (2) (3)【解析】【分析】（1）写出直线的点斜式方程，整理成一般方程即可．（2）可设直线的一般方程为，代入点求出的值，即可答案．（3）可设所求直线的方程为，代入点，求得的值，即可求解直线的方程；所求直线的斜率为，写出直线的点斜式方程，整理成一般方程即可．【详解】（1）由题设，根据直线的点斜式方程可得，整理得．（2）由题意，所以求直线与平行，设所求直线方程为，代入点，解得，所以直线方程为．（3）由题意，所以求直线与垂直，设所求直线的方程为，代入点，解得，所以直线方程为．【点睛】本题主要考查了直线方程的求解，其中熟记直线的点斜式方程、直线的一般式方程等形式，合理应用和准确计算是解答的关键，着重考查了推理与运算能力，属于基础题．22.如图，在五面体中，已知平面，，，，．（1）求证：；（2）求三棱锥的体积．【答案】（1）详见解析，（2）【解析】【分析】（1）由题意，利用线面平行的性质定理与判定定理进行转化，可作出证明；（2）由平面，所以有面平面，则作就可得平面，确定是三棱锥的高，利用三棱锥的体积公式，可求解．【详解】（1）因为，平面，平面，所以平面，又平面，平面平面，所以．（2）在平面内作于点，因为平面，平面，所以，又，平面，，所以平面，所以是三棱锥的高．在直角三角形中，，，所以，因为平面，平面，所以，又由（1）知，，且，所以，所以，所以三棱锥的体积．【点睛】本题主要考查了线面平行判定定理与性质定理，线面垂直判定定理与性质定理及三棱锥体积，熟练掌握空间中线面位置关系的定义、判定、几何特征是解答的关键，其中垂直、平行关系证明中应用转化与化归思想的常见类型：(1)证明线面、面面平行，需转化为证明线线平行；(2)证明线面垂直，需转化为证明线线垂直；(3)证明线线垂直，需转化为证明线面垂直．2018-2019学年高一数学下学期期末模拟试卷注意事项：1. 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。

2017-2018学年云南省昆明一中西山学校八年级（下）期末物理试卷一、单选题（本大题共8小题，每小题3分，共24分）．下列各题的答案中只有一个是正确的，请考生用2B铅笔把答题卡上对应题目的答案标号涂黑．1．下列四种物态变化相同的一组是（）①夏天，草叶上的露珠；②冬天，窗户上的冰花；③深秋，树上的白霜；④初春，冰雪消融。

A．①③B．①④C．②③D．②④2．下列关于力和运动的说法正确的是（）A．人推墙的力和墙对人的力是一对平衡力B．物体在平衡力的作用下一定保持匀速直线运动C．给正在运动的物体再施加一个力，物体就会比原来运动得更快D．在平直轨道上匀速行驶的火车车厢里，竖直向上跳起的人仍然落回原地（不计空气阻力）3．一个铁锭（如图甲所示）放置在水平地面上时，对地面产生的压力和压强分别是F1和p1；当如图乙所示放置在水平地面上时，对地面产生的压力和压强分别是F2和p2，那么（）A．F1＝F2，p1＝p2B．F1＝F2，p1＜p2C．F1＞F2，p1＝p2D．F1＜F2，p1＞p24．游乐场中的翻滚过山车是一种惊险、刺激的游戏，如图是翻滚过山车的简化模型，图中B点为最低点，C点为轨道弧形部分的最高点。

翻滚过山车在运动过程中。

下列说法正确的是（）A．运动到B 点时，动能最大B．运动到C 点时，重力势能最大C．从B 点到C 点，重力势能减小，动能增大D．从A 点到B 点，重力势能增大，动能减小5．用相同的滑轮和绳子分别组成如图所示的甲、乙两个滑轮组，把相同重物匀速提升相同的高度，若不计绳重及摩擦，下列说法正确的是（）A．绳子受的拉力F1和F2的大小不相等，滑轮组的机械效率不同B．绳子自由端移动的距离不相等，拉力对滑轮组所做的功相等C．绳子受的拉力F1和F2的大小相等，滑轮组的机械效率相同D．绳子自由端移动的距离不相等，拉力对滑轮组所做的功不相等6．小吴同学为探究力之间的关系做了如图所示的实验。

将弹簧测力计下端吊着的铝块逐渐浸入台秤上盛有水的烧杯中，直至刚没入水中（不接触容器，无水溢出）。

云南省昆明市重点名校2017-2018学年高一下学期期末达标检测地理试题一、单选题（本题包括30个小题，每小题2分，共60分）1．以工业机器人和互联网为代表的智能自动化生产，发展潜力巨大。

据此完成下面小题。

1．工业机器人正在大规模地走进珠江三角洲企业，有人说，该现象会给珠三角经济发展带来“阵痛”。

你认为带来的“阵痛”最可能是A．就业机会减少B．环境污染加剧C．产业结构的转型D．土地价格下降2．企业使用机器人，可以①增加产品的销量②提高产品的合格率③降低生产成本④增加产品的种类⑤提高安全系数A．①②⑤B．②③⑤C．③④⑤D．①③④【答案】1．A2．B【解析】1．珠三角劳动密集型产业密集，机器人的使用会导致工人就业机会减少，失业人口增加。

故A项正确。

工业机器人不会让环境污染加剧，B错；工业机器人还是在劳动力密集型产业中使用，没有变成其它产业，C错；不会影响到土地价格，D错。

2．产品的销量与产品的种类和市场需求有关，并不是依靠机器人能够解决的，①④错；根据材料的“智能”等信息可判断使用机器人相对于人工可提高产品的合格率；降低生产的成本；采用机器人操作，精确度更高，稳定性更高，安全性更强，可以保障人员安全。

故B项正确。

2．下图为我国某农村人口年龄结构金字塔图, 该村人口现状可能给当地带来的问题有①养老服务难以保障②加重就业困难③劳动力短缺④土地养老杯水车薪⑤使环境人口容量降低A．①②③B．①③④C．②③④D．③④⑤【答案】B【解析】【分析】本题考查人口年龄结构。

【详解】由图中可以看出该村少年儿童以及老年人口的比重大,劳动力较少,所以该村人口现状可能给当地带来的问题主要是养老服务难以保障,大量的人员外出务工,说明土地产值较少,土地养老杯水车薪。

环境人口容量受人口年龄结构影响小。

故本题选B。

3．读“某城市用地变化示意”图，据此完成下面小题。

1．老城区选址主要考虑的区位因素是A．气候B．铁路运输C．河流D．矿产资源2．由图中信息可知，该城市形态发展变化的主要原因是A．矿产资源的开发B．铁路运输的发展C．人口分布的改变D．环境污染的影响【答案】1．C2．B【解析】【分析】本题考查城市区位。

2017-2018 学年云南省昆明市盘龙区八年级（下）期末数学试卷一、填空题（本大题共 6 小题，每题 3 分，满分 18 分）1．若二次根式2－ x 存心义，则x的取值范围是．2．在数轴上表示实数 a 的点以下图，化简+| a﹣2| 的结果为．3．某中学随机抽查了50 名学生，认识他们一周的课外阅读时间，结果以下表所示：时间（小时）4567人数1020155则这 50 名学生一周的均匀课外阅读时间是小时．4．如图，已知四边形 ABCD是平行四边形，对角线 AC、BD 交于点 O，E 是 BC的中点，若 AB=6，则 OE=．5．如图，一只蚂蚁从棱长为 1 的正方体纸箱的 A 点沿纸箱表面爬到 B 点，那么它所爬行的最短路线的长是．6．以下图，四边形 ABCD为矩形，点 O 为对角线的交点，∠BOC=120°，AE⊥BO 交 BO 于点 E，AB=4，则 BE等于．二、选择题（本大题共8 个小题，每题只有一个正确选项，每题 4 分，满分 32 分）7．以下二次根式化简后，能与归并的是（）A．B．C．D．8．以下计算错误的选项是（）A．÷=3B．=5 C． 2 + =2D．2 ? =29．以下各组数中，不可以作为直角三角形的三边长的是（）A．，2，3 B．6，8，10 C．5，12，13D． 15，20，2510．以下说法正确的选项是（）A．为认识昆明市中学生的睡眠状况，应当采纳普查的方式B．数据 2，1，0，3，4 的均匀数是 3C．一组数据 1，5， 3， 2，3，4，8 的众数是 3D．在连续 5 次数学周考测试中，两名同学的均匀分同样，方差较大的同学数学成绩更稳固11．如图，已知一次函数y=kx+b 的图象经过点 A（5，0）与 B（0，﹣ 4），那么对于 x 的不等式kx+b＜0 的解集是（）A．x＜5B．x＞ 5C．x＜﹣ 4D．x＞﹣ 412．对于一次函数y=﹣2x+4，以下结论错误的选项是（）A．函数的图象不经过第三象限B．函数的图象与 x 轴的交点坐标是（ 2， 0）C．函数的图象向下平移 4 个单位长度得 y=﹣ 2x 的图象D．若两点 A（x1， y1）， B（ x2，y2）在该函数图象上，且x1＜x2，则 y1＜y213．如图，菱形 ABCD中，对角线 AC、BD 订交于点 O，H 为 AD 边中点， AC=12，菱形 ABCD的面积为 96，则 OH 的长等于（）A．6 B． 5 C．4D．314．如图 1 反应的过程是：矩形ABCD中，动点 P 从点 A 出发，挨次沿对角线AC、边 CD、边DA 运动至点 A 停止，设点 P 的运动行程为 x，S△ABP=y．则矩形 ABCD的周长是（）三、解答题（本大题共9 个小题，满分 70 分 .解答时一定写出必需的计算过程、推理步骤或文字说明 .）15．（5分）计算： 2﹣ 6 ﹣（﹣）16．（5分）计算：（7+）（7﹣） +（48﹣）÷17．（7分）重庆出租车计费的方法以下图，x（km）表示行驶里程， y（元）表示车资，请根据图象解答以下问题：（1）该地出租车起步价是元；（2）当 x＞ 2 时，求 y 与 x 之间的关系式；（3）若某乘客一次乘出租车的里程为18km，则这位乘客需付出租车车资多少元？18．（8 分）已知等腰三角形ABC的底边 BC=20cm，D 是腰 AB 上一点，且 CD=16cm，BD=12cm．（1）求证： CD⊥AB；（2）求该三角形的腰的长度．19．（8 分）如图，已知点E，C 在线段 BF上， BE=EC=CF，AB∥DE，∠ ACB=∠F．（1）求证：△ ABC≌△ DEF；（2）求证：四边形ACFD为平行四边形．20．（7 分）学生小明、小华为认识本校八年级学生每周上网的时间，各自进行了抽样检查．小间为；小华从全体 320 名八年级学生名单中随机抽取了40 名学生，检查了他们每周上网的时间，算得这些学生均匀每周上网时间为．小明与小华整理各自样本数据，如表所示．时间段（ h/ 周）小明抽样人数小华抽样人数0～16221～210102～31663～482（每组可含最低值，不含最高值）请依据上述信息，回答以下问题：（1）你以为哪位学生抽取的样本拥有代表性？．预计该校全体八年级学生均匀每周上网时间为h；（2）在拥有代表性的样本中，中位数所在的时间段是h/ 周；（3）专家建议每周上网2h 以上（含 2h）的同学应适合减少上网的时间，依据拥有代表性的样本预计，该校全体八年级学生中有多少名学生应适合减少上网的时间？21．（9 分）已知，如图，点D 是△ ABC的边 AB 的中点，四边形BCED是平行四边形．（1）求证：四边形ADCE是平行四边形；（2）在△ ABC中，若 AC=BC，则四边形 ADCE是；（只写结论，不需证明）（3）在（ 2）的条件下，当AC⊥BC时，求证：四边形ADCE是正方形．22．（9 分）学校需要采买一批演出服饰，A、B 两家制衣企业都愿成为这批服饰的供给商．经了解：两家企业生产的这款演出服饰的质量和单价都同样，即男装每套 120 元，女装每套 100 元．经洽商磋商： A 企业给出的优惠条件是，所有服饰按单价打七折，但校方需肩负2200 元的运费；B 企业的优惠条件是男女装均按每套100 元打八折，企业肩负运费．此外依据大会组委会要求，参加演出的女生人数应是男生人数的 2 倍少 100 人，假如设参加演出的男生有x 人．（1）分别写出学校购置A、B 两企业服饰所付的总花费y1（元）和 y2（元）与参演男生人数x之间的函数关系式；（2）问：该学校购置哪家制衣企业的服饰比较合算？请说明原因．平行四边形 ABCD．（1）求直线 AC的函数分析式；（2）设点 B（0，m），记平行四边形ABCD的面积为 S，请写出 S 与 m 的函数关系式，并求当BD 获得最小值时，函数S 的值；（3）当点 B 在 y 轴上运动，可否使得平行四边形ABCD是菱形？若能，求出点 B 的坐标；若不能，说明原因．2017-2018 学年云南省昆明市盘龙区八年级（下）期末数学试卷参照答案一、填空题（本大题共 6 小题，每题 3 分，满分 18 分）1．x≤2．2．3．3．4．35．6．2．二、选择题（本大题共8 个小题，每题只有一个正确选项，每题 4 分，满分 32 分）7-10:CCAC11-14：ADBC三、解答题（本大题共9 个小题，满分 70 分 .解答时一定写出必需的计算过程、推理步骤或文字说明 .）15．解：原式 =4﹣2﹣3+3 = +．16．解：原式 =49﹣5+16﹣2=42+16．17．解：（1）由函数图象知，出租车的起步价为10 元，故答案为： 10；（2）当 x＞ 2 时，每公里的单价为（ 14﹣ 10）÷（ 4﹣ 2） =2，∴当 x＞ 2 时， y=10+2（ x﹣2）=2x+6；（3）当 x=18 时， t=2×18+6=42 元，答：这位乘客需付出租车车资42 元．18．解：（1）∵ BC=20cm，CD=16cm，BD=12cm，222∴知足 BD +CD =BC，∴依据勾股定理逆定理可知，∠BDC=90°，即CD⊥AB；（2）设腰长为 x，则 AD=x﹣12，由（ 1）可知 AD2 +CD2=AC2，即：（x﹣12）2+162=x2，解得 x=，19．（1）证明：∵ AB∥DE，∴∠ B=∠DEF，∵BE=EC=CF，∴BC=EF，在△ ABC和△ DEF中∴△ ABC≌△ DEF（ ASA）．（2）证明：∵△ ABC≌△ DEF∴AC=DF，∵∠ ACB=∠ F，∴AC∥DF，∴四边形 ACFD是平行四边形．20．解：（1）小明抽取的样本太片面，信息技术兴趣小组的学生上网时间相对许多，因此不具代表性，而小华抽取的样本是随机抽取拥有代表性．故答案为：小华；．（2）由图表可知第20 和第 21 名同学所在的上网时间段为：0～ 1h/ 周，因此中位数为： 0～1h/ 周．故答案为： 0～1．（3）随机检查的 40 名学生中应当减少上网时间的学生的频次为：，故该校全体八年级学生中应当减少上网时间的人数为：320× 0.2=64（人）．答：该校全体八年级学生中应当减少上网时间的人数为64 人．21．证明：（1）∵四边形 ADCE是平行四边形∴BD∥CE， BD=CE∵D 是 AB 的中点∴AD=BD∴AD=CE又∵ BD∥CE∴四边形 ADCE是平行四边形（2）在△ ABC中，若 AC=BC，则四边形 ADCE是矩形，故答案为：矩形；（3）∵ AC⊥BC∴∠ ACB=90°∵在 Rt△ABC中， D 是 AB 的中点∴CD=AD= AB∵在△ ABC中， AC=BC，D 是 AB 的中点∴CD⊥AB∴∠ ADC=90°∴平行四边形 ADCE是正方形22．解：（1）总花费 y1（元）和 y2（元）与参演男生人数x 之间的函数关系式分别是：y1=0.7[ 120x+100（ 2x﹣100）]+ 2200=224x﹣4800，（x≥50），y2=0.8[ 100（3x﹣ 100）] =240x﹣8000，（x≥ 50）；（2）由题意，得当y1＞y2时，即 224x﹣4800＞240x﹣8000，解得： x＜200当y1=y2时，即 224x﹣ 4800=240x﹣8000，解得： x=200当y1＜y2时，即 224x﹣4800＜240x﹣8000，解得： x＞200答：当参演男生少于200 人时，购置 B 企业的服饰比较合算；当参演男生等于200 人时，购置两家企业的服饰总花费同样，可任一家企业购置；当参演男生多于200 人时，购置 A 企业的服饰比较合算．23．解：（1）∵ OA=3，OC=4，∴A（﹣ 3， 0）、C（0，4）．设直线 AC的函数分析式为y=kx+b，将点 A（﹣ 3，0）、C（0，4）代入 y=kx+b 中，得：，解得：，∴直线 AC的函数分析式为y=x+4．（2）∵点 B（0，m），四边形 ABCD为以 AC为对角线的平行四边形，∴m＜ 4， BC=4﹣ m，∴S=BC?OA=﹣3m+12（m＜ 4）．∵四边形 ABCD为平行四边形，∴AD∥BC，∴当 BD⊥ y 轴时， BD最小（如图 1）．∵AD∥OB，AO⊥OB，DA⊥ OB，∴四边形 AOBD为矩形，∴AD=OB=BC，∴点 B 为 OC的中点，即 m==2，此时 S=﹣3×2+12=6．∴S 与 m 的函数关式为 S=﹣3m+12（m＜4），当 BD获得最小值时的S的值为 6．（3）∵平行四边形ABCD是菱形，∴AB=BC．∵AB==，BC=4﹣m，∴=4﹣m，解得： m= ，∴B（0，）．。

昆明市重点名校2017-2018学年高一下学期期末质量跟踪监视数学试题一、选择题：本题共12小题，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．某赛季甲、乙两名篮球运动员5场比赛得分的茎叶图如图所示，已知甲得分的极差为32，乙得分的平均值为24，则下列结论错误的是（ ）A ．8x =B ．甲得分的方差是736C ．乙得分的中位数和众数都为26D ．乙得分的方差小于甲得分的方差 【答案】B 【解析】 【分析】根据题意，依次分析选项，综合即可得答案． 【详解】根据题意，依次分析选项：对于A ，甲得分的极差为32，30+x ﹣6=32，解得：x=8，A 正确， 对于B ，甲得分的平均值为142834386245++++=，其方差为()()()()()22222624142428243424382473655-+-+-+-+-=，B 错误；对于C ，乙的数据为：12、25、26、26、31，其中位数、众数都是26，C 正确， 对于D ，乙得分比较集中，则乙得分的方差小于甲得分的方差，D 正确； 故选：B ． 【点睛】本题考查茎叶图的应用，涉及数据极差、平均数、中位数、众数、方差的计算，属于基础题． 2．若偶函数()af x x =在(),0-∞上是增函数，则（ ）A ．0a >B ．0a <C ．0a =D ．不能确定【答案】B 【解析】 【分析】根据偶函数性质与幂函数性质可得． 【详解】偶函数()af x x =在(),0-∞上是增函数，则它在(0,)+∞上是减函数，所以0a <．故选：B ． 【点睛】本题考查幂函数的性质，考查偶函数性质，属于基础题．3．设,m n 是两条不同的直线,,αβ是两个不同的平面,下列命题中正确的是（ ） A ．若//m α,//m β,则//αβ B ．若m α⊥，m n ⊥,则n α⊥ C ．若m α⊥,//m n ,则n α⊥ D ．若αβ⊥,m α⊥,则//m β【答案】C 【解析】 【分析】在A 中，α与β相交或平行；在B 中，//n α或n ⊂α；在C 中，由线面垂直的判定定理得n α⊥；在D 中，m 与β平行或m β⊂． 【详解】设,m n 是两条不同的直线，,αβ是两个不同的平面，则： 在A 中，若//m α，//m β，则α与β相交或平行，故A 错误； 在B 中，若m α⊥，m n ⊥，则//n α或n ⊂α，故B 错误；在C 中，若m α⊥，//m n ，则由线面垂直的判定定理得n α⊥，故C 正确； 在D 中，若αβ⊥，m α⊥，则m 与β平行或m β⊂，故D 错误． 故选C ． 【点睛】本题考查命题真假的判断，考查空间中线线、线面、面面间的位置关系等基础知识，是中档题．4．若02πα<<，02πβ-<<，1cos 43πα⎛⎫+= ⎪⎝⎭，cos 42πβ⎛⎫-= ⎪⎝⎭cos 2βα⎛⎫+ ⎪⎝⎭等于（ ）A ．3 B ．3-C ．9D ．9-【答案】C 【解析】 【分析】利用同角三角函数的基本关系求出sin 4πα⎛⎫+⎪⎝⎭与sin 42πβ⎛⎫-⎪⎝⎭，然后利用两角差的余弦公式求出cos cos 2442βππβαα⎡⎤⎛⎫⎛⎫⎛⎫+=+-- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦值．【详解】02πα<<，3444πππα∴<+<，则sin 43πα⎛⎫+== ⎪⎝⎭，02πβ-<<，则4422ππβπ<-<，所以，sin 42πβ⎛⎫-==⎪⎝⎭， 因此，cos cos 2442βππβαα⎡⎤⎛⎫⎛⎫⎛⎫+=+-- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦1cos cos sin sin 44244233339ππβππβαα⎛⎫⎛⎫⎛⎫⎛⎫=+-++-=+⋅=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭， 故选C ． 【点睛】本题考查利用两角和的余弦公式求值，解决这类求值问题需要注意以下两点： ①利用同角三角平方关系求值时，要求对象角的范围，确定所求值的正负； ②利用已知角来配凑未知角，然后利用合适的公式求解．5．在ABC ∆中，内角,,A B C 所对的边分别为,,a b c ，且()cos 4cos a B c b A =-，则cos2A =（ ） A ．78B ．18C ．78-D ．18-【答案】C 【解析】 【分析】根据题目条件结合三角形的正弦定理以及三角形内角和定理可得sinA ，进而利用二倍角余弦公式得到结果. 【详解】∵()cos 4cos a B c b A =-． ∴sinAcosB ＝4sinCcosA ﹣sinBcosA 即sinAcosB+sinBcosA ＝4cosAsinC ∴sinC ＝4cosAsinC ∵1＜C ＜π，sinC≠1． ∴1＝4cosA ，即cosA 14=，那么27cos2218A cos A =-=-． 故选C 【点睛】本题考查了正弦定理及二倍角余弦公式的灵活运用，考查计算能力，属于基础题．6．如图，AB 是圆O 的直径，OC AB ⊥，假设你往圆内随机撒一粒黄豆，则它落到阴影部分的概率为（ ）A ．12πB ．1πC ．13πD ．1π【答案】B 【解析】 【分析】先根据条件计算出阴影部分的面积，然后计算出整个圆的面积，利用几何概型中的面积模型即可计算出对应的概率. 【详解】设圆的半径为R ，因为OC AB ⊥，所以2122ABCS R R R =⋅⋅=， 又因为2=OSR π，所以落到阴影部分的概率为221ABC O S R P S R ππ===. 故选：B. 【点睛】本题考查几何概型中的面积模型的简单应用，难度较易.注意几何概型的常见概率公式：P =目标事件的区域长度（面积、体积）试验的全部结果所构成的区域长度（面积、体积）.7．要得到函数2sin 25y x π⎛⎫=+ ⎪⎝⎭的图像，只需要将函数2sin 25y x π⎛⎫=-⎪⎝⎭的图像（ ） A ．向右平移25π个长度单位 B ．向左平移25π个长度单位 C ．向右平移5π个长度单位 D ．向左平移5π个长度单位【解析】 【分析】根据()sin y A x ωϕ=+的图像变换规律求解即可 【详解】设平移量为θ，则由2sin 22sin 22sin 22sin 25101010y x x y x x ππππθ⎛⎫⎛⎫⎛⎫⎛⎫=-=-→=-+=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，满足：10105x x πππθθ-+=+⇒=，故由2sin 25y x π⎛⎫=-⎪⎝⎭向左平移5π个长度单位可得到2sin 25y x π⎛⎫=+ ⎪⎝⎭故选：D 【点睛】本题考查函数()sin y A x ωϕ=+的图像变换规律，属于基础题8．如图，设、两点在河的两岸，一测量者在的同侧，在所在河岸边选定一点，测出的距离为，，后，就可以计算、两点的距离为（ ）A ．B ．C ．D ．【答案】A 【解析】 【分析】 计算出三个角的值，然后利用正弦定理可计算出的值.【详解】 在中，，，，即，由正弦定理得，，解得，故选A.本题考查正弦定理解三角形，要熟悉正弦定理解三角形对三角形已知元素类型的要求，考查运算求解能力，属于基础题.9．已知函数1()sin 123f x x π⎛⎫=-+ ⎪⎝⎭，那么下列式子：①(2)(2)f x f x ππ+=-；②10()3f x f x π⎛⎫-=⎪⎝⎭；③(2)(2)f x f x ππ+=-；④2()3f x f x π⎛⎫-=- ⎪⎝⎭；其中恒成立的是（ ） A ．①② B ．②③C ．①②④D ．②③④【答案】A 【解析】 【分析】根据正弦函数的周期性及对称性，逐项判断，即可得到本题答案. 【详解】由1()sin 123f x x π⎛⎫=-+ ⎪⎝⎭，得2412T ππ==，所以()f x 的最小正周期为4π，即(2)(2)f x f x ππ+=-，故①正确；由1()sin 123f x x π⎛⎫=-+ ⎪⎝⎭，令1,232x k k Z πππ-=+∈，得()f x 的对称轴为52,3x k k Z ππ=+∈，所以53x π=是()f x 的对称轴，2x π=不是()f x 的对称轴，故②正确，③不正确； 由1()sin 123f x x π⎛⎫=-+⎪⎝⎭，令1,23x k k Z ππ-=∈，得()f x 的对称中心为22,0,3k k Z ππ⎛⎫+∈ ⎪⎝⎭，所以,03π⎛⎫⎪⎝⎭不是()f x 的对称中心，故④不正确. 故选：A 【点睛】本题主要考查正弦函数的周期性以及对称性.10．△ABC 中，已知a x =，2b =，60B =，如果△ABC 有两组解，则x 的取值范围（ ） A ．2x > B ．2x <C．2x <≤D．2x <<【答案】D 【解析】由正弦定理得,sin sina ba AA B====A+C=180°-60°=120°，由题意得：A有两个值，且这两个值之和为180°，∴利用正弦函数的图象可得：60°＜A＜120°，若A=90，这样补角也是90°，一解，不合题意，2∴＜sinA＜1，∵x=3sinA，则2＜x＜3故选D11．设等差数列{}n a的前n项和为n S，首项10a>，公差0d<，10210a S⋅<，则nS最大时，n的值为( ) A．11 B．10 C．9 D．8【答案】B【解析】【分析】由等差数列前n项和公式得出21S1121a，结合数列{}n a为递减数列确定10110,0a a，从而得到nS 最大时，n的值为10.【详解】由题意可得2111112120212110212S a d a d a1021a S1011a a等差数列{}n a的首项10a>，公差0d <则数列{}n a为递减数列10110,0a a即当10n=时，nS最大故选B。

2017---2018学年度第二学期期末考试七年级数学试卷一、选择题（共10道小题，每小题3分，共30分） 下列各题均有四个选项，其中只有一个．．是符合题意的． 1．PM2.5也称为可入肺颗粒物,是指大气中直径小于或等于2.5微米的颗粒物.2.5微米等于 0.000 002 5米，把0.000 002 5用科学记数法表示为 A ．2.5×106 B ．0.25×10-5 C. 25×10-7 D ．2.5×10-6 2. 已知a b <，则下列不等式一定成立的是 A ．b a 2121<B ．22a b -<-C ．33->-b aD ．44a b +>+3．下列计算正确的是A ．2a +3a =6a B. a 2+a 3=a 5 C. a 8÷a 2=a 6 D. (a 3)4= a 74．⎩⎨⎧==3,1y x 是二元一次方程52=+ay x 的一个解，则a 的值为A. 1B.31C. 3D. －1 5．若把不等式x +2≤0的解集在数轴上表示出来，则正确的是A ．B ．C ．D ．6．下列因式分解正确的是A ．4)2)(2(2-=-+x x x B ．22)1(12x -=+-x x C ．()222211a a a -+=-+D ．()248224a a a a -=-7．小文统计了本班同学一周的体育锻练情况，并绘制了直方图①小文同学一共统计了60人;②这个班同学一周参加体育锻炼时间的众数是8; ③这个班同学一周参加体育锻炼时间的中位数是9; ④这个班同学一周参加体育锻炼时间的平均值为8.根据图中信息，上述说法中正确的是A. ①②B. ②③C.③④D. ①④8．将直尺和直角三角板按如图所示方式摆放，已知∠1=30°，则∠2的大小是A．30°B．45°C．60°D．65°9．某市居民用电的电价实行阶梯收费，收费标准如下表：一户居民每月用电量x（单位：度）电费价格（单位：元/度）0≤< 0.48x200<0.53200≤x400x>0.78400七月份是用电高峰期，李叔计划七月份电费支出不超过200元，直接写出李叔家七月份最多可用电的度数是A．100 B．396 C．397 D．40010用小棋子摆出如下图形，则第n个图形中小棋子的个数为A. nB. 2n Ｃ. n2Ｄ.n2+1二、填空题：（共6道小题，每小题3分，共18分） 11．因式分解：=__________________. 12．计算ab ab b a 44822÷-)(结果为_____________.13．一个角的补角等于这个角的3倍，则这个角的度数为_____________．14.已知x ，y 是有理数，且0106222=+-++y y x x ， 则y x = ．15.两个同样的直角三角板如图所示摆放，使点F ，B ，E ，C 在一条直线上，则有DF ∥AC ，理由是__________________．16．《九章算术》是中国古代的数学专著，下面这道题是《九章算术》中第七章的一道题：“今有共买物，人出八，盈三；人出七，不足四，问人数、物价各几何？”译文：“几个人一起去购买某物品，如果每人出8钱，则多了3钱；如果每人出7钱，则少了4钱．问有多少人，物品的价格是多少？”设有x 人，物品价格为y 钱，可列方程组为__________________．三、解答题（共10道小题，共52分,其中第17—24每小题5分，25，26每小题6分）17．计算：22-020173-）21（）14.3-（）1-（++π18．化简求值：已知250x x +-=，求代数式2(1)(3)(2)(2)x x x x x ---++-的值．19．完成下面的证明:2218x -如图，已知DE ∥BC ，∠DEB =∠GFC ，试说明BE ∥FG ． 解：∵DE ∥BC∴∠DEB =______（ ）. ∵∠DEB =∠GFC∴______=∠GFC （ ）.∴BE ∥FG （ ）.20.解方程组⎩⎨⎧=-=+133232y x y x21．解不等式组()315112 4.2x x x x -+⎧⎪⎨--⎪⎩＜，≥并求出它的非负整数解．22.某单位有职工200人，其中青年职工(20-35岁)，中年职工(35-50岁)，老年职工(50岁及以上)所占比例如扇形统计图所示.为了解该单位职工的健康情况，小张、小王和小李各自对单位职工进行了抽样调查，将收集的数据进行了整理，绘制的统计表分别为表1、表2和表3.表1：小张抽样调查单位3名职工的健康指数年龄 26 42 57 健康指数977972表2：小王抽样调查单位10名职工的健康指数年龄 23 25 26 32 33 37 39 42 48 52 健康指数 93899083797580696860表3：小李抽样调查单位10名职工的健康指数年龄 22 29 31 36 39 40 43 46 51 55 健康指数94908885827872766260根据上述材料回答问题：(1)扇形统计图中老年职工所占部分的圆心角度数为(2)小张、小王和小李三人中， 的抽样调查的数据能够较好地反映出该单位职工健康情况，并简要说明其他两位同学抽样调查的不足之处.23.已知：如图，DE 平分∠BDF .， ∠A =21∠BDF ，DE ⊥BF ，求证：AC ⊥BF24.列方程组解应用题新年联欢会上，同学们组织了猜谜活动，并采取每答对一题得分，每答错一题扣分记分方法。

2017—2018学年度第二学期期末考试七年级数学试题温馨提示：1.本试卷分第Ⅰ卷和第Ⅱ卷两部分，共4页.满分150分，考试用时120分钟.考试结束后，只收交答题卡.2.答卷前，考生务必用0.5毫米黑色签字笔将自己的学校、班级、姓名、考试号、座号填写在答题卡规定的位置上.3.第Ⅰ卷每小题选出答案后，必须用0.5毫米黑色签字笔将该答案选项的字母代号填入答题卡的相应表格中，不能答在试题卷上.4.第Ⅱ卷必须用0.5毫米黑色签字笔作答，答案必须写在答题卡各题目指定区域内相应的位置，不能写在试题卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.第Ⅰ卷（选择题 共36分）一、选择题：本大题共12个小题,在每小题的四个选项中只有一个是正确的,请把正确的选项选出来,并将该选项的字母代号填入答题卡的相应表格中.每小题涂对得3分,满分36分. 1.下列叙述中，正确的是 A ．相等的两个角是对顶角 B ．一条直线有且只有一条垂线C ．连接直线外一点与这条直线上各点的所有线段中，垂线段最短D ．同旁内角互补2.如图所示，直线a ，b 被直线c 所截，∠1与∠2是A ．同位角B ．内错角C ．同旁内角D ．邻补角3.如图，若△DEF 是由△ABC 经过平移后得到的，则平移的距离是A ．线段BC 的长度B ．线段BE 的长度C ．线段EC 的长度D ．线段EF 的长度 4.下列语言是命题的是A ．画两条相等的线段B ．等于同一个角的两个角相等吗？C ．延长线段AO 到C ，使OC =OAD ．两直线平行，内错角相等（第2题图） （第3题图）A ．9B ．±9C ．3D ．±36.下列计算结果正确的是A6± B3.6- CD ．7.如果12x y =⎧⎨=-⎩和14x y =-⎧⎨=-⎩都是某个二元一次方程的解，则这个二元一次方程是A ．x +2y =－3B ．2x －y =2C ．x －y =3D ．y =3x －58.用加减法解方程组时，若要消去y ，则应A ．①×3+②×2B ．①×3－②×2C ．①×5+②×3D ．①×5－②×3 9.如果x ≤y ，那么下列结论中正确的是 A ．4x ≥4y B ．－2x +1≥－2y +1 C ．x －2≥y +2D ．2－x ≤2－y10.利用数轴求不等式组103x x -≤⎧⎨>-⎩的解集时，下列画图表示正确的是A ．B ．C ．D ．11.在调查收集数据时，下列做法正确的是A ．电视台为了了解电视节目的收视率，调查方式选择在火车站调查50人B ．在医院里调查老年人的健康状况C ．抽样调查选取样本时，所选样本可按自己的喜好选取D ．检测某城市的空气质量，适宜采用抽样调查的方式12.小宁同学根据全班同学的血型情况绘制了如图所示的扇形统计图，已知该班血型为A 型的有20人，那么该班血型为AB 型的人数为A ．2人B ．5人C ．8人D ．10人第Ⅱ卷（非选择题 共114分）二、填空题：本大题共10个小题，每小题4分，满分40分. 13.命题“对顶角相等”的题设是 ．14.为了解某山区金丝猴的数量，科研人员在该山区不同的地方捕获了15只金丝猴，并在它们的身上做标记后放回该山区．过段时间后，在该山区不同的地方又捕获了32只金丝猴，其中4只身上有上次做的标记，由此可估计该山区金丝猴的数量约有 只． 15.一个容量为89的样本中，最大值是153，最小值是60，取组距为10，则可分成 组．16.-1.4144，2220.373π-g，，， 2.12112.其中 是无理数．（第12题图）17.如图，∠1=∠2=40°，MN 平分∠EMB ，则∠3= °．18．如图，若棋盘的“将”位于点（0，0），“车”位于点（－4，0），则“马”位于点 ．19.甲、乙两人相距42千米，若两人同时相向而行，可在6小时后相遇；而若两人同时同向而行，乙可在14小时后追上甲.设甲的速度为x 千米/时，乙的速度为y 千米/时，列出的二元一次方程组为 ．20.某花店设计了若干个甲、乙两种造型的花篮，一个甲种花篮由15朵红花、25朵黄花和20朵紫花搭配而成；一个乙种花篮由10朵红花、20朵黄花和15朵紫花搭配而成．若这些花篮一共用了2900朵红花，4000朵紫花，则黄花一共用了 朵．21.不等式组10324x x x ->⎧⎨>-⎩的非负整数解是 ．22.船在静水中的速度是24千米/小时，水流速度是2千米/小时，如果从一个码头逆流而上后，再顺流而下，那么这船最多开出 千米就应返回才能在6小时内回到码头. 三、解答题：本大题共6个小题，满分74分. 解答时请写出必要的演推过程. 23.请先阅读以下内容：，即23， ∴11＜2，1的整数部分为1，12． 根据以上材料的学习，解决以下问题：已知a3的整数部分，b3的小数部分，求32()(4)a b -++的平方根. 24.解下列方程组（不等式组）： （1）4(1)3(1)2,2;23x y y x y --=--⎧⎪⎨+=⎪⎩ （2）12(1)5;32122x x x --≤⎧⎪⎨-<+⎪⎩．25.某学校为加强学生的安全意识，组织了全校1500名学生参加安全知识竞赛，从中抽取了部分学生成绩（得分取正整数，满分为100分）进行统计．请根据尚未完成的频率分布表和频数分布直方图（如图），解答下列问题：（1）这次抽取了 名学生的竞赛成绩进行统计，其中m = ，n = ； （2）补全频数分布直方图；（3）若成绩在70分以下（含70分）的学生为安全意识不强，有待进一步加强安全教育，则该校安全意识不强的学生约有多少人？（第17题图）（第18题图）26.某商场销售国外、国内两种品牌的智能手机，这两种手机的进价和售价如下表所示：该商场计划购进两种手机若干部，共需14.8万元，预计全部销售后可获毛利润共2.7万元.[注：毛利润=（售价－进价）×销售量]（1）该商场计划购进国外品牌、国内品牌两种手机各多少部？（2）通过市场调研，该商场决定在原计划的基础上，减少国外品牌手机的购进数量，增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少数量的3倍，而且用于购进这两种手机的总资金不超过15.6万元，问该商场最多减少购进多少部国外品牌手机？27.如图，在长方形OABC 中，O 为平面直角坐标系的原点，点A 坐标为（a ，0），点C 的坐标为（0，b ），且a 、b 60b -=，点B 在第一象限内，点P 从原点出发，以每秒2个单位长度的速度沿着O →C →B →A →O 的线路移动． （1）a = ，b = ，点B 的坐标为 ； （2）求移动4秒时点P 的坐标；（3）在移动过程中，当点P 到x 轴的距离为5个单位长度时，求点P 移动的时间．28.如图，已知直线AB∥CD ，∠A =∠C =100°，点E ，F 在CD 上，且满足∠DBF =∠ABD ，BE 平分∠CBF ． （1）求证：AD ∥BC ； （2）求∠DBE 的度数；（3）若平移AD 使得∠ADB =∠BEC ，请直接写出此时∠ADB 的度数是 .（第28题图）（第27题图）2017—2018学年第二学期七年级数学试题参考答案及评分标准二、填空题：（每题4分，共40分）13. 两个角是对顶角；14．120；15． 10；16．23π-，；17．110；18. （3,3）；19．6642,141442x yy x+=⎧⎨-=⎩；20.5100 ；21．0；22．71.5.三、解答题：（共74分）23. 解：∵＜＜，……………………………………………………1分∴4＜＜5，…………………………………………………………………2分∴1＜﹣3＜2，…………………………………………………………………3分∴a=1，…………………………………………………………………………4分b=﹣4，………………………………………………………………………6分∴（﹣a）3+（b+4）2=（﹣1）3+（﹣4+4）2=﹣1+17 …………………………………………………………………………8分=16，…………………………………………………………………………9分∴（﹣a）3+（b+4）2的平方根是±4．………………………………………10分24. （1）解：化简，得………………………………………2分①×2+②得1122,x=③………………………………………3分2x=，………………………………………4分②①把2x =代入③，得3.y = ……………………………………5分所以这个方程组的解是23.x y =⎧⎨=⎩，……………………………………6分 （2）解：由①得：1﹣2x +2≤5 ………………………………………7分∴2x ≥﹣2即x ≥﹣1 ………………………………………8分 由②得：3x ﹣2＜2x +1 ………………………………………9分∴x ＜3． ………………………………………10分∴原不等式组的解集为：﹣1≤x ＜3． ……………………………………12分25. 解：（1）200， ………………………………………3分70；0.12； ………………………………………7分（2）如图，…………………………………9分（3）1500×（0.08+0.2）=420， ……………………………………11分 所以该校安全意识不强的学生约有420人． …………………………………12分 26. 解：（1）设商场计划购进国外品牌手机x 部，国内品牌手机y 部，由题意得 0.440.214.8,0.060.05 2.7,x y x y +=⎧⎨+=⎩…………………………………4分解得 20,30.x y =⎧⎨=⎩…………………………………6分答：商场计划购进国外品牌手机20部，国内品牌手机30部. ………7分（2）设国外品牌手机减少a部，由题意得-++≤15.6 …………………………………10分a a0.44(20)0.2(303)解得a≤5 …………………………………12分答：该商场最多减少购进5部国外品牌手机. ……………………………13分27. （1）a= 4 ，b= 6 ，点B的坐标为（4，6）；………………6分（2）∵P从原点出发以每秒2个单位长度的速度沿O→C→B→A→O的线路移动，∴2×4=8，……………………………………7分∵OA=4，OC=6，∴当点P移动4秒时，在线段CB上，离点C的距离是8﹣6=2，…………8分∴点P的坐标是（2，6）；……………………………………9分（3）由题意可知存在两种情况：第一种情况，当点P在OC上时，点P移动的时间是：5÷2=2.5秒，……………………………………11分第二种情况，当点P在BA上时．点P移动的时间是：（6+4+1）÷2=5.5秒，……………………………………12分故在移动过程中，当点P到x轴的距离为5个单位长度时，点P移动的时间是2.5秒或5.5秒．……………………………………13分28. 证明：（1）∵AB∥CD，∴∠A+∠ADC=180°，……………………………………2分又∵∠A=∠C∴∠ADC+∠C=180°，……………………………………4分∴AD∥BC；……………………………………6分（2）∵AB∥CD，∴∠ABC+∠C=180°………………………………8分又∠C=100°，∴∠ABC=180°﹣100°=80°，………………………………9分∵∠DBF=∠ABD，BE平分∠CBF，∴∠DBF=∠ABF，∠EBF=∠CBF，…………………10分∴∠DBE=∠ABF+∠CBF=∠ABC=40°；……………12分（3）∠ADB=60°．……………………………………14分。

2017—2018学年下学期期末检测八年级物理试题卷（全卷四个大题，共24个小题，共6页；满分100分，考试用时90分钟）注意事项：1．本卷为试题卷。

考生必须在答题卡上解题作答。

答案应书写在答题卡的相应位置上，在试题卷、草稿纸上作答无效。

2．考试结束后，请将试题卷和答题卡一并交回。

第Ⅰ卷一、单项选择题（本大题共8个小题，每小题的四个选项中只有一个符合题意，每小题3分，满分24分）1．为了预防感冒，有人常在屋里放一碟醋，不久整个房间就会充满醋味，这一现象说明: A．分子在永不停息地做无规则运动B．分子之间有相互作用的引力和斥力C．醋分子在不停地做无规则运动，空气分子没有运动D．物质是由分子组成的2．要剪开较硬的白铁皮，图1中哪种剪刀最合适A B C D3．在如图2所示的四幅图中，说明人对物体做了功的是A．踢出去的足球向 B．学生背着书包在 C．女孩把一箱书从 D．司机推汽车前运动一段距离水平路面上行走地面上搬起来但未推动4．一位同学在结冰的湖面上行走时，突然发现脚下的冰即将破裂，她应采取的措施是A．立即改为单脚站立 B．赶快跑向岸边C．站着不动，等待救援 D．就地趴伏在冰面上慢慢向岸边爬行5．在托里拆利实验中，以下哪种情况会对测量结果产生影响A．玻璃管内尚留有少许空气 B．换口径较粗的玻璃管做实验C．换口径较细的玻璃管做实验 D．将玻璃管向上提但管口不离开汞面6．图3是家用煤气灶灶头的示意图，使用时打开煤气阀门，拧动点火装置，煤气和空气在进口处混合后被点燃，而煤气不会从进口处泄露到空气中，其原因是A．进口处煤气流速小，压强大于大气压强B．进口处煤气流速小，压强小于大气压强C．进口处煤气流速大，压强小于大气压强D．进口处煤气流速大，压强大于大气压强7．连通器在日常生活、生产中有着广泛的应用，如图4所示的事例中没有利用连通器原理的是图1图2图3煤气空气空气混合气图4船闸拦河大坝洗手间下水管过路涵洞A B C D 8．将同一个小球分别放到三种密度不同的液体中， 小球静止时的情况如图5所示，那么 A ．图A 液体的密度最小B ．图B 液体的密度最小C ．图C 液体的密度最小D ．图A 跟图C 的液体密度一样大 二、填空题（每空１分，共21分）9．原子核由带正电的 和不带电的 组成。

昆明第一中学2018-2018学年度下学期期末考试高二年级物理试题试卷总分：100分考试时间：100分钟一．选择题（本题共12小题，每题4分，共48分。

每题最少有一个正确的答案，全部选对的得4分，选对不全给2分，有选错或不选的得0分）1．以下说法正确的选项是（）A．牛顿总结出了万有引力定律并测出了万有引力常量．法拉第发现了电磁感觉现象C．光电效应现象说明光拥有粒子性D．太阳辐射的能量主要来自太阳内部的核裂变反应2．有一理想变压器的原线圈连接一只交流电流表，副线圈接入电路的匝数能够经过滑动触头Q调治，如图所示，在副线圈两输出端连接了定值电阻R0和滑动变阻器R，在原线圈上加一电压为U的交流电，则（）A．保持Q的地址不动，将P向上滑动时，电流表的读数变大B．保持Q的地址不动，将P向上滑动时，电流表的读数变小C．保持P的地址不动，将Q向上滑动时，电流表的读数变大D．保持P的地址不动，将Q向上滑动时．电流表的读数变小3．关于天然放射现象，表达正确的选项是（）A．若使放射性物质的温度高升，其半衰期将减少B．β衰变所释放的电子是原子核外的电子电离形成的C．在α、β、γ这三种射线中，γ射线的穿透能力最强，α射线的电离能力最强D．铀核（23892U）衰变为铅核（20682Pb）的过程中，要经过8次α衰变和10次β衰变4．光照射到金属表面上能够发生光电效应，以下关于光电效应的表达中，正确的选项是（）A.金属电子逸出功与入射光的频率成正比B.单位时间内逸出的光电子数与入射光强度没关C.用绿光照射金属比用紫光照射同种金属产生的光电子的最大初动能大D.对某一种金属，入射光的波长必定小于极限波长才能产生光电效应5．以下列图，从点光源S发出的一细束白光以必然的角度入射到三棱镜的表面，经过三棱镜的折射后发生色散现象，在光屏的ab间形成一条彩色光带。

下面的说法中正确的选项是（）A．a侧是红色光，b侧是紫色光B．在真空中a侧光的波长大于b侧光的波长C．三棱镜对a侧光的折射率大于对b侧光的折射率D．在三棱镜中a侧光的流传速率大于b侧光的流传速率6．以下列图，在口字形闭合铁芯上绕有一组线圈，与滑动变阻器、电池构成闭合回路。

昆明市重点名校2017-2018学年高一下学期期末质量跟踪监视物理试题一、单项选择题：本题共6小题，每小题5分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的1．(本题9分)甲、乙两小球都在水平面上做匀速圆周运动，它们的线速度大小之比为1∶2，角速度大小之比为3∶2，则两球的向心加速度大小之比为（）A．1:2 B．2:1 C．3:4 D．3:2【答案】C【解析】【详解】根据a=vω，则两球的向心加速度大小之比为3：4，故ABD错误，C正确.2．做平抛运动的物体，在水平方向通过的最大距离取决于（）A．物体所受的重力和抛出点的高度B．物体的初速度和抛出点的高度C．物体所受的重力和初速度D．物体所受的重力、高度和初速度【答案】B【解析】【详解】对于做平抛运动的物体，水平方向上：x=v0t ；竖直方向上：h=12gt2；所以水平位移为2hx vg，所以水平方向通过的最大距离取决于物体的高度和初速度。

A. 物体所受的重力和抛出点的高度，与结论不相符，选项A错误；B. 物体的初速度和抛出点的高度，与结论相符，选项B正确；C. 物体所受的重力和初速度，与结论不相符，选项C错误；D. 物体所受的重力、高度和初速度，与结论不相符，选项D错误；3．(本题9分)如图所示，两小球从斜面的顶点先后以不同的初速度向右水平抛出，在斜面上的落点分别是a和b，不计空气阻力。

关于两小球的判断正确的是( )A．落在b点的小球飞行过程中速度变化快B．落在a点的小球飞行过程中速度变化大C．小球落在a点和b点时的速度方向不同D．两小球的飞行时间均与初速度0v成正比【答案】D【解析】【分析】两个小球做的都是平抛运动，平抛运动可以分解为水平方向上的匀速直线运动和竖直方向上的自由落体运动，物体的运动的时间是由竖直方向上下落的高度决定的．落地速度由高度和初速度共同决定，可列式进行分析．【详解】AB 、平抛运动是加速度为g 的匀变速曲线运动，速度变化一样快，b 球运动时间长所以速度变化大，故AB 错误C 、落在a 点和b 点的小球，由2012tan gt y x v tα==，而速度偏转角θ 应有0tan 2tan y x v gt v v θα===，由于θα一定所以确定 ，所以他们速度方向相同，故C 错误．D 、落在a 点和b 点的小球，由2012tan gt y x v tα==，得02tan v t g α=，所以运动时间t 与v 0成正比，D 正确4．已知一质量为m 的物体静止在北极与赤道对地面的压力差为ΔN ，假设地球是质量分布均匀的球体，半径为R ．则地球的自转周期为( )A．2T = B．2T = C．2T = D．2T = 【答案】A【解析】 试题分析：在赤道上物体所受的万有引力与支持力提供向心力可求得支持力，在南极支持力等于万有引力．在北极12 N Mm F G R =①，在赤道22224N Mm G F m R R Tπ-=②，根据题意，有12 N N F F N -=∆③，联立解得2T π=，A 正确． 5． (本题9分)如图所示,地球绕OO′轴自转,则下列正确的是（ ）A ．A 、B 两点线速度相等B ．A 、B 两点的角速度相等C ．A 、B 两点的转动半径相同D ．A 、B 两点的转动周期不同【答案】B【解析】A 、B 两点都绕地轴做匀速圆周运动，B 转动的半径大于A 转动的半径，两点共轴转动，角速度相同．根据v=rω，角速度相同，B 的半径大，则B 的线速度大；根据T=2π/ω，角速度相同，则周期相同．故B 正确，ACD 错误．故选B ．点睛：解决本题的关键掌握共轴转动，角速度相同，再结合v=rω、T=2π/ω，等公式即可判断． 6． (本题9分)如图是一汽车在平直路面上启动的速度—时间图象，从t 1时刻起汽车的功率保持不变，由图象可知( )①0～t 1时间内，汽车的牵引力增大，加速度增大，功率不变②0～t 1时间内，汽车的牵引力不变，加速度不变，功率增大③t 1～t 2时间内，汽车的牵引力减小，加速度减小④t 1～t 2时间内，汽车的牵引力不变，加速度不变A ．①③B ．①④C ．②③D ．②④【答案】C【解析】①、10t ～时间内，汽车的速度是均匀增加的，是匀加速运动，所以汽车的牵引力不变，加速度不变，功率增大，所以①错误，②正确；③、12t t ～时间内，汽车的功率已经达到最大值，功率不能再增加，所以汽车的牵引力在减小，加速度也要减小，所以③正确，④错误，故选项C 正确。

云南省2017—2018学年高一数学下学期期末考试试卷（一）（考试时间120分钟满分150分）一、单项选择题（共12小题，每小题5分，满分60分）1．点（1，1）到直线x﹣y+1=0的距离是（）A．B．C．D．2．已知直线l的方程为y=x+1，则该直线l的倾斜角为（）A．30°B．45°C．60°D．135°3．空间中，两条直线若没有交点，则这两条直线的位置关系是（）A．相交 B．平行 C．异面 D．平行或异面4．若直线a与平面α不垂直，那么在平面α内与直线a垂直的直线（）A．只有一条 B．无数条C．是平面α内的所有直线 D．不存在5．下列直线中与直线2x+y+1=0垂直的一条是（）A．2x﹣y﹣1=0 B．x﹣2y+1=0 C．x+2y+1=0 D．x+y﹣1=06．直线l在平面直角坐标系中的位置如图，已知l∥x轴，则直线l的方程不可以用下面哪种形式写出（）A．点斜式B．斜截式C．截距式D．一般式7．如图（1）、（2）、（3）、（4）为四个几何体的三视图，根据三视图可以判断这四个几何体依次分别为（）A．三棱台、三棱柱、圆锥、圆台B．三棱台、三棱锥、圆锥、圆台C．三棱柱、正四棱锥、圆锥、圆台D．三棱柱、三棱台、圆锥、圆台8．圆A：x2+y2+4x+2y+1=0与圆B：x2+y2﹣2x﹣6y+1=0的位置关系是（）A．相交 B．相离 C．相切 D．内含9．若直线mx+2ny﹣4=0始终平分圆x2+y2﹣4x+2y﹣4=0的周长，则m、n的关系是（）A．m﹣n﹣2=0 B．m+n﹣2=0 C．m+n﹣4=0 D．m﹣n+4=010．P是圆（x﹣5）2+（y﹣3）2=9上点，则点P到直线3x+4y﹣2=0的最大距离是（）A．2 B．5 C．8 D．911．已知圆C：（x﹣1）2+（y﹣2）2=5，直线l：x﹣y=0，则C关于l的对称圆C′的方程为（）A．（x+1）2+（y+2）2=5 B．（x﹣2）2+（y﹣1）2=5 C．（x﹣2）2+（y+1）2=5 D．（x﹣1）2+（y+2）2=512．如图，长方体ABCD﹣A1B1C1D1中，AA1=AB=2，AD=1，点E、F、G分别是DD1、AB、CC1的中点，则异面直线A1E与GF所成角的余弦值是（）A．B．C．D．0二、填空题（本题共4小题，每题5分，共20分．）13．若直线x﹣y=0与直线2x+ay﹣1=0平行，则实数a的值为．14．已知△P1P2P3的三顶点坐标分别为P1（1，2），P2（4，3）和P3（3，﹣1），则这个三角形的最大边边长是，最小边边长是．15．若球O内切于棱长为2的正方体，则球O的表面积为．16．若圆C：x2+y2﹣4x+2y+m=0与y轴交于A，B两点，且∠ACB=90°，则实数m的值为．三、解答题（共6小题，满分70分）17．如图，在平行四边形OABC中，点C（1，3）．（1）求OC所在直线的斜率；（2）过点C做CD⊥AB于点D，求CD所在直线的方程．18．已知圆C同时满足下列三个条件：①与y轴相切；②半径为4；③圆心在直线x﹣3y=0上．求圆C的方程．19．如图，已知正四棱锥V﹣ABCD中，AC与BD交于点M，VM是棱锥的高，若AC=6cm，VC=5cm．（1）求正四棱锥V﹣ABCD的体积；（2）求直线VD与底面ABCD所成角的正弦值．20．如图，在正方体ABCD﹣A1B1C1D1中，E、F分别为AD，AB的中点．（1）求证：EF∥平面CB1D1；（2）求证：平面CAA1C1⊥平面CB1D1．21．已知直线l在y轴上的截距为﹣2，且垂直于直线x﹣2y﹣1=0．（1）求直线l的方程；（2）设直线l与两坐标轴分别交于A、B两点，△OAB内接于圆C，求圆C的一般方程．22．已知圆O：x2+y2=1和定点A（2，1），由圆O外一点P（a，b）向圆O引切线PQ，切点为Q，且满足|PQ|=|PA|．（1）求实数a、b间满足的等量关系；（2）求线段PQ长的最小值．参考答案一、单项选择题1．C．2．B．3．D．4．B．5．B 6．C．7．C．8．C．．9．A 10．C．11．B．12．D二、填空题13．答案为﹣2．14．答案为：，．15．答案为4π．16．答案为：﹣3．三、解答题17．解：（1）∵点O（0，0），点C（1，3），∴OC所在直线的斜率为．（2）在平行四边形OABC中，AB∥OC，∵CD⊥AB，∴CD⊥OC．∴CD所在直线的斜率为．∴CD所在直线方程为，即x+3y﹣10=0．18．解：∵圆C同时满足下列三个条件：①与y轴相切；②半径为4；③圆心在直线x﹣3y=0上，设圆的圆心为（3b，b），则|3b|=4，∴b=±，故要求的圆的方程为（x﹣4）2+=16，或（x+4）2+=16．19．解：（1）∵正四棱锥V﹣ABCD中，ABCD是正方形，∴MC=AC=BD=3（cm）．=AC×BD=18（cm2）．且S正方形ABCDRt△VMC中，VM==4（cm）．∴正四棱锥的体积为V==（cm3）．（2）∵VM⊥平面ABCD，∴∠VDM是直线VD与底面ABCD所成角，∵VD=VC=5，在RT△VDM中，sin∠VDM=．所以直线VD与底面ABCD所成角的正弦值为．20．（1）证明：连结BD，在△ABD中，E、F分别为棱AD、AB的中点，故EF∥BD，又BD∥B1D1，所以EF∥B1D1，…又B1D1⊂平面CB1D1，EF不包含于平面CB1D1，所以直线EF∥平面CB1D1．…（2）证明：在正方体ABCD﹣A1B1C1D1中，底面A1B1C1D1是正方形，则A1C1⊥B1D1…又CC1⊥平面A1B1C1D1，B1D1⊂平面A1B1C1D1，则CC1⊥B1D1，…又A1C1∩CC1=C1，A1C1⊂平面CAA1C1，CC1⊂平面CAA1C1，所以B1D1⊥平面CAA1C1，又B1D1⊂平面CB1D1，所以平面CAA1C1⊥平面CB1D1．…21．解：（1）设直线l的方程为y=kx﹣2．直线x﹣2y﹣1=0的斜率为，所以k=﹣2．直线l的方程为y=﹣2x﹣2．（2）设圆C的一般方程为x2+y2+Dx+Ey+F=0．由于△OAB是直角三角形，所以圆C的圆心C是线段AB的中点，半径为；由A（﹣1，0），B（0，﹣2）得C（﹣，﹣1），|AB|=；故，解得D=1，E=2，F=0．圆C的一般方程为：x2+y2+x+2y=0．22．解：（1）连OP，∵Q为切点，PQ⊥OQ，由勾股定理有|PQ|2=|OP|2﹣|OQ|2又由已知|PQ|=|PA|，故：（a2+b2）﹣12=（a﹣2）2+（b﹣1）2化简得实数a、b间满足的等量关系为：2a+b﹣3=0．（2）由（1）知，点P在直线l：2x+y﹣3=0 上．∴|PQ|min=|PA|min ，即求点A 到直线l 的距离．∴|PQ|min═=。