东北大学模糊数学试题2010A

八、高等数学试题 2005/1/10一、填空题（本题20分，每小题4分）1．已知==⎪⎭⎫⎝⎛-+∞→a a x a x xx ，则9lim2．设函数⎪⎩⎪⎨⎧>+≤+=1112)(2x b ax x x x f ，，，当a = ,b = 时，f (x )在x =1处可导。

3．方程017=-+x x 共有 个正根。

4．当=x 时，曲线c bx ax y ++=2的曲率最大。

5．⎰=20sin πxdx x 。

二、选择题（本大题24分，共有6小题，每小题4分） 1．下列结论中，正确的是（ ）（A ）若a x n n =∞→2lim ，a x n n =+∞→12lim ，则a x n n =∞→lim ；（B ）发散数列必然无界；（C ）若a x n n =-∞→13lim ，a x n n =+∞→13lim ，则a x n n =∞→lim ；（D ）有界数列必然收敛。

2．函数)(x f 在0x x =处取得极大值，则必有（ ）。

（A ）0)(0='x f ； （B ）0)(0<''x f ；（C ）0)(0='x f 或)(0x f '不存在； （D ）0)(0='x f 且0)(0<''x f 。

3．函数⎰=xa dt t f x F )()(在][b a ，上可导的充分条件是：)(x f 在][b a ，上（ ）（A ）有界； （B ）连续； （C ）有定义； （D ）仅有有限个间断点。

4．设⎰-+=2242cos 1sin ππxdx x x M ，⎰-+=2243)cos (sin ππdx x x N ，⎰--=22432)cos sin (ππdx x x x P ，则必有关系式（ ）（A ） M P N <<；（B ）P M N <<；（C ）N P M <<；（D ）N M P <<。

2008~2009学年第二学期试题一、单项选择题（本题共4小题，每小题4分，共计16分）1.设函数(,)f x y 在点(0,0)的某邻域内有定义，且(0,0)3x f =，(0,0)1y f =-，则[ ] (A)(0,0)3dzdx dy =-；(B) 曲面(,)z f x y =在点(0,0,(0,0))f 的一个法向量为(3,1,1)-；(C)曲线(,)0z f x y y =⎧⎨=⎩在点(0,0,(0,0))f 的一个切向量为(1,0,3)；(D) 曲线(,)0z f x y y =⎧⎨=⎩在点(0,0,(0,0))f 的一个切向量为(3,0,1)2. 设10 (1,2,)n u n n≤<= ，则下列级数中必收敛的是[ ](A)1n n u ∞=∑； (B)1(1)nnn u∞=-∑； (C)n ∞=； (D)21(1)nnn u∞=-∑.3. 如果81lim1=+∞→nn n a a ，则幂级数∑∞=03n n n x a [ ] (A) 当8<x 时收敛； (B) 当2<x 时收敛； (C) 当81>x 时发散； (D) 当21>x 时发散.4. 设Ω是由球面2222x y z a ++=所围成的闭区域，则222x y z dv Ω++⎰⎰⎰= [ ] .(A) 545a π； (B) 44a π； (C) 543a π； (D) 525a π.二、填空题（本题共6小题，每小题4分，共计24分）1. 曲面2222321x y z ++=在点(1,2,2)-处的法线方程为 .2. 函数),(y x f 22y xy x +-=在点)1,1(处的全微分为 .3. 已知曲线L 为连接(1,0)和(0,1)两点的直线段，则曲线积分()Lx y ds +⎰= .4. 由曲面2243()z x y =-+与曲面22z x y =+所围立体的体积为 .5. 设∑为平面1234x y z++=在第一卦限中的部分，则曲面积分()234x y z dS ∑++⎰⎰= . 6. 设()f x 是周期为4的周期函数，它在[2,2)-上的表达式为0, 20()3, 022x f x x -≤<⎧⎪=⎨≤<⎪⎩，()f x 的Fourier 级数的和函数为()s x ，则(4)s = .三、计算下列各题 （本题共5小题，每小题6分，共计30分） 1. 求过点1(1,1,1)M 和2(0,1,1)M -且与平面0x y z ++=垂直的平面方程.2. 设z = f (e xsin y , x 2+ y 2), 其中f 具有二阶连续偏导数，求2zx y∂∂∂.3. 设(,,)F x y z 具有连续偏导数，且对任意实数t 有(,,)F tx ty tz (,,)k t F x y z =(k 为自然数)，试证:曲面(,,)0F x y z =上任意一点的切平面相交于一定点(设在任意点处2220x y z F F F ++≠).4. 计算二重积分Dxydxdy ⎰⎰，其中D 是由两条抛物线y x =，2y x =所围成的闭区域.5. 将函数()arctan f x x =展开成关于x 的幂级数，并求展开式成立的区间. 四、 (8分) 设曲线积分[]⎰-+BA x dy x f ydx x f e )()(与路径无关，且21)0(=f ，求)(x f ，并求当A ，B 分别为（0，0），（1，1）时的曲线积分值.五、(8分) 计算积分222(I x dydz y dzdx z dxdy ∑=++⎰⎰，其中∑是抛物面22z x y =+被平面4z =截下的有限部分的下侧.六、(8分) 3．(10分)平面通过球面x 2 + y 2 +z 2 = 4(x - 2y - 2z )的中心, 且垂直于直线L : 00x y z =⎧⎨+=⎩, 求平面与球面的交线在xOy 平面上的投影, 并求投影与(1, -4,1)点的最短和最长距离.七、(6分) )判断级数111ln n n n n ∞=+⎛⎫- ⎪⎝⎭∑的敛散性.解答一、1. 【解】应选择C.),(),,(0000y x f y x f y x 存在只是全微分存在的必要条件，故A 是错误的。

东北大学考试试卷（A B 卷） 2007 — 2008学年 第2学期课程名称：模糊数学┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄ 2分 共计10分） 1. 设论域12345{,,,,}U u u u u u =，F 模糊集(0.5,0.1,0,1,0.8)A =，(0.1,0.4,0.9,0.7,0.2)B =，(0.8,0.2,1,0.4,0.3)C =。

则_________A B ⋃=___________A B ⋂= ()____________A B C ⋃⋂=_________c A = 2. 设论 域{,,,,}U a b c d e =， 有{}0.70.8{,}0.50.7{,,}0.30.5{,,,}0.10.3{,,,,}00.1d c d A c d e b c d e a b c d e λλλλλλ<≤⎧⎪<≤⎪⎪=<≤⎨⎪<≤⎪≤≤⎪⎩ F 集A ＝_________________ 二、 计算题（共5小题，每题12分） 1. 设[0,10]U =为论域，对[0,1]λ∈，若F 集A 的λ截集分别为 [0,10]0[3,10]00.6[5,10]0.61[5,10]1A λλλλλλ=⎧⎪<≤⎪=⎨<<⎪⎪=⎩，求出：（1）(),[0,10]A x x ∈；（2）SuppA ；（3）KerA2． 设F 集112340.20.40.50.1A x x x x =+++，212340.20.50.30.1A x x x x =+++，312340.20.30.40.1A x x x x =+++， 12340.60.30.1B x x x =++，21230.20.30.5B x x x =++，试用格贴近度判断12,i B B A 与哪个最接近。

3．设120.100.80.70.20.40.90.50,0.30.10.600.40.310.50.2R R ⎛⎫⎛⎫ ⎪ ⎪== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，求12121,,cR R R R R ⋃⋂4．设12345{,,,,}U u u u u u =，在U 上存在F 关系，使10.800.10.20.810.400.900.41000.10010.50.20.900.51R ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦，求ˆR，并由此进行聚类分析，画出聚类分析图。

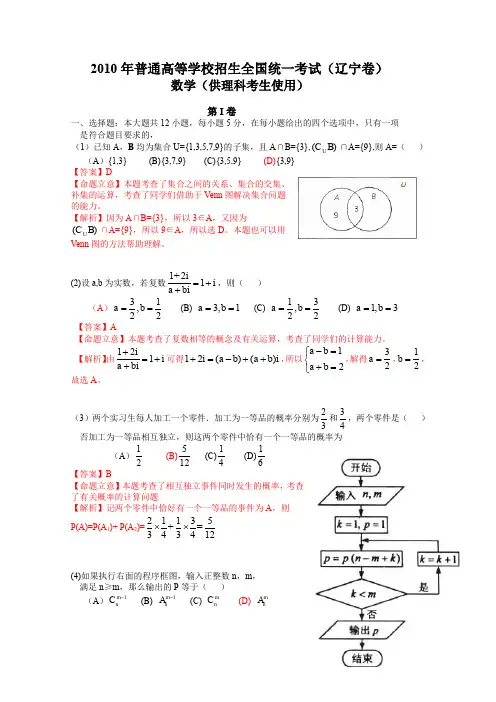
2010年普通高等学校招生全国统一考试（辽宁卷）数学（供理科考生使用）第I 卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项 是符合题目要求的，（1）已知A ，B 均为集合U={1,3,5,7,9}的子集，且A ∩B={3},B)(C U ∩A={9},则A=（ ） （A ）{1,3} (B){3,7,9} (C){3,5,9} (D){3,9} 【答案】D【命题立意】本题考查了集合之间的关系、集合的交集、补集的运算，考查了同学们借助于Venn 图解决集合问题的能力。

【解析】因为A ∩B={3}，所以3∈A ，又因为B)(C U ∩A={9}，所以9∈A ，所以选D 。

本题也可以用Venn 图的方法帮助理解。

(2)设a,b 为实数，若复数11+2ii a bi=++，则（ ） （A ）31,22a b == (B) 3,1a b == (C) 13,22a b == (D) 1,3a b == 【答案】A【命题立意】本题考查了复数相等的概念及有关运算，考查了同学们的计算能力。

【解析】由121i i a bi +=++可得12()()i a b a b i +=-++，所以12a b a b -=⎧⎨+=⎩，解得32a =，12b =，故选A 。

（3）两个实习生每人加工一个零件．加工为一等品的概率分别为23和34，两个零件是（ ） 否加工为一等品相互独立，则这两个零件中恰有一个一等品的概率为（A ）12 (B)512 (C)14 (D)16【答案】B【命题立意】本题考查了相互独立事件同时发生的概率，考查了有关概率的计算问题【解析】记两个零件中恰好有一个一等品的事件为A ，则 P(A)=P(A 1)+ P(A 2)=211335+=43412⨯⨯(4)如果执行右面的程序框图，输入正整数n ，m ， 满足n ≥m ，那么输出的P 等于（ ） （A ）1m n C - (B) 1m n A - (C) m n C (D) mn A【答案】D【命题立意】本题考查了循环结构的程序框图、排列公式，考查了学生的视图能力以及观察、推理的能力【解析】第一次循环：k =1,p =1,p =n -m +1;第二次循环：k =2,p =(n -m +1)(n -m +2)；第三次循环：k =3，p =(n -m +1) (n -m +2) (n -m +3) ……第m 次循环：k =3，p =(n -m +1) (n -m +2) (n -m +3)…(n -1)n此时结束循环，输出p =(n -m +1) (n -m +2) (n -m +3)…(n -1)n =mn A（5）设ω>0,函数y=sin(ωx+3π)+2的图像向右平移34π个单位后与原图像重合，则ω的最小值是（ ） （A ）23 (B)43 (C)32(D)3【答案】C【命题立意】本题考查了三角函数图像的平移变换与三角函数的周期性，考查了同学们对知识灵活掌握的程度。

2010年东北大学数学建模培训模拟竞赛试题问题-A海潮和泄洪近年来世界范围的气候情况发生了巨大的变化，极端气候出现频率大大增加，百年未遇的自然灾害每年都有极大可能发生。

其原因可能是由于：全球气候变暖、温室气体排放增多以及人类生产活动破坏了地表植被等原因造成的。

据国家减灾委、民政部的统计，截至8月6日，今年洪涝灾害造成全国2亿人(次)受灾，1454人死亡，669人失踪，1214.8万人(次)紧急转移安置，1347.1万公顷农作物受灾，其中209万公顷绝收，136.4万间房屋倒塌，358.1万间房屋损坏,因灾直接经济损失2751.6亿元。

给人民生命和财产造成了巨大损失。

2010年8月7日夜22点左右舟曲发生的特大洪水泥石流损失更是令人触目惊心！我国已经建立的一些水利设施在防洪减灾方面起到了很大作用。

三峡工程的作用主要有：发电、防洪、灌溉，首要任务是防洪。

连日来，三峡大坝及时挡水控泄，发挥重要的防洪作用。

截至14日，三峡已接受长江防总发出的11次调度令，或增大出库流量以腾出库容应对上游来水，或减少出库流量以缓解下游防汛压力。

长江下游的中心城市上海是我国重要的经济中心，其防洪任务非常艰巨和重要。

现在主要考虑海水和长江对上海的影响。

海水主要有由天体引潮力所引起的潮汐的天文潮和由于风暴的强风作用而引起港湾水面急速异常升高的风暴潮。

长江主要是上游洪水引起的。

当三种情况出现叠加(或两种叠加)就有可能造成上海的洪水施虐。

建立数学模型：(1)分析上海是否会出现被洪水淹没的可能性；(2)调控三峡大坝的泄洪量可以使得上海防洪压力减轻，设计一个算法，在大坝设施安全的前提下，根据海水的影响调整三峡大坝的泄洪量以确保上海市的安全并且不影响生产和生活。

问题-B车间打磨机的效率问题某个单位的车间工人上班时间为早8:00-16:00，中间没有休息时间。

此车间前一段时间花费了1万元购置了一台工具打磨机，工人的生产工具出现问题，必须中断生产前来打磨工具。

辽宁2010年高考数学(文)试题及参考答案(估分)总分：150分及格：90分考试时间：120分一、选择题：本卷共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

(1)<A href="javascript:;"></A>(2)<A href="javascript:;"></A>(3)<Ahref="javascript:;"></A>(4)<Ahref="javascript:;"></A>(5)<Ahref="javascript:;"></A>(6)<Ahref="javascript:;"></A>(7)<Ahref="javascript:;"></A>(8)<Ahref="javascript:;"></A>(9)<Ahref="javascript:;"></A>(10)<A href="javascript:;"></A>(11)<Ahref="javascript:;"></A>(12)<Ahref="javascript:;"></ A>二、填空题：本大题共4小题，每小题5分，共20分。

把答案填在题中横线上。

(1)三张卡片上分别写上字母E，E，B，将三张卡片随机地排成一行，恰好排成英文单词BEE 的概率为<U></U>。

东北大学考试试卷（A卷）2010—2011 学年第 2 学期课程名称：图论与代数结构┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄┄总分一二三四五六七八九学院班级学号姓名……………○……………密……………○……………封……………○…………线………………得分一．(15分) 填空1.设A={2, 4, 6, 8}，A上的二元运算*定义为：a*b=max{a, b}，则在独异点<A,*>中，单位元是 2 ，零元是8 。

2.设a是12阶群的生成元，则a2是 6 阶元素，a5是12 阶元素。

3.设〈G, *〉是一个群，G中的幂等元是 e 。

若G={a,b,c}，a*x=b，则x=a-1*b ；设a是幺元，则b*c= a 。

4.小于5个元素的格都是有补分配（布尔）格。

5.有n个结点的树，其结点度数之和是2(n-1)。

6.一个无向图有生成树的充分必要条件是该图是连通图__。

7.n阶无向完全图Kn 的边数是n(n-1)/2 ，每个结点的度数是n-1 。

若Kn为欧拉图，则n的取值为奇数。

8.具有6 个顶点，12条边的连通简单平面图中，每个面都是由 3 条边围成。

9.无向树T有8片树叶，2个3度分支结点，其余的分支结点都是4度顶点，则 2 个4度分支结点。

得分二． (26分)判断题4.（6分）判断下列集合和运算能否构成半群、独异点和群。

如果不能，简单说明理由。

（1）a是正整数，G={a n|n∈Z，Z为整数集}, 运算是普通乘法。

是半群、独异点和群。

（2分）（2）Q+是正有理数集，运算为普通加法。

（2分）是半群，不是独异点和群。

满足封闭、结合，但没有幺元。

（3）设Z为整数集，∀ x,y∈Z, 运算x*y=x+y-2。

是半群、群和独异点。

（2分）1.（6分）设V1=<Z,+>, V2=<Z, •>，其中Z为整数集合，+和•分别代表普通加法和乘法。

判断下述集合S能否构成V1和V2的子半群和子独异点。

东北大学高等数学（下册）试卷答案及评分标准2006．7．12一、选择题 (本大题6小题, 每小题4分, 共24分)1．)(B ； 2．)(A ； 3．)(C ；4．)(B ；5． )(D ；6. )(A 。

二．填空题（本大题5小题, 每小题4分, 共20分）1. 154221--=-=-z y x ；2．22-；3.44a π；4． λ=３；x x e C e C 321*.4+-；5．８． 三、（8分) 求过点M(3, 1, -2)且通过直线12354z y x =+=-的平面方程 所求平面的法线向量与直线12354z y x =+=-的方向向量s 1=(5, 2, 1)垂直. 因为点(3, 1, -2)和(4, -3, 0)都在所求的平面上, 所以所求平面的法线向量与向量s 2=(4, -3, 0)-(3, 1, -2)=(1, -4, 2)也是垂直的. 因此所求平面的法线向量可取为-------------2分k j i k j i s s n 229824112521--=-=⨯=. ------------6分 所求平面的方程为8(x -3)-9(y -1)-22(z +2)=0, 即8x -9y -22z -59=0.------------8分三、（8分) 求微分方程x y y x sin 2=+'的通解 解：把方程改写为x x y x y sin 2=+', 则------------2分 )sin (22C dx e xx e y dx x dx x +⎰⋅⎰=⎰- )s i n (12C x d x x x+=⎰-----------6分 )cos (sin 12C x x x x+-=------------8分四．（8分) 设方程0>a ，a z a 2≤<，az z y x 2222=++，求全微分与dz 及y x z ∂∂∂2． 解：dy za y dx z a x dz -+-= 于是z a x x z -=∂∂，za y y z -=∂∂------------4分()()22z a y z x z a z a x y y x z -∂∂+-=⎪⎭⎫ ⎝⎛-∂∂=∂∂∂()()()()322z a xy z a z a z a y xz a -+-=--+-=------------8分 五．（8分)计算σd y x y D ⎰⎰-22, 其中D 是由直线y =x 、x =1及y =0围成的闭区域.解 画出区域D , 可把D 看成是X --型区域: 0≤x ≤1, 0≤y ≤ x 于是⎰⎰⎰⎰-=-xD dy y x y dx d y x y 0221022σ ------------4分 ⎰⎰=-⋅-=103100232231)(3221dx x dx y x x 121=.------------8分 六．（8分) 设,0>a ,L 为圆ax y x 222=+逆时针方向一周，求⎰-L ydx x xdy y 22．解 y x P xy Q 22==, 22x y y P x Q +=∂∂-∂∂, ------------2分 由Green 公式有⎰-L y d x x x d y y22=dy dx x y D⎰⎰+)(22 =dr r d a ⎰⎰θπθcos 203202------------6分=⎰2044cos 4πθθπd a=443a π------------8分七．（８分）将函数xx f 431)(+=，展开为)2(+x 的幂级数并给出收敛域． 解：5)2(41151)2(451431+-⋅-=++-=+x x x ------------2分 ∑∞=⎥⎦⎤⎢⎣⎡+-=05)2(451n nx∑∞=++-=01)2(54n n n nx ------------6分收敛域满足 15)2(4<+x 解出得 43413-<<-x ------------8分 八．（8分)设0>a ，物体占有空间Ω是由yoz 坐标面上曲线az z y 222=+绕z 轴旋一周所形成的曲面所围成的闭区域，体密度函数为常数0ρ，求该物体对于坐标原点的转动惯量． 解：所求转动惯量为⎰⎰⎰Ω++=dv z y x I )(22200ρ，:Ωaz z y x 2222≤++------------2分利用球坐标替换，有dr r r d d I a ⎰⎰⎰=ππθϕϕθρ2020cos 202200sin ⎰=20550sin cos )2(512πϕϕϕπρd a ------------6分 2065506cos 522πϕπρ⎥⎦⎤⎢⎣⎡=a 501532a πρ=------------8分 九．（８分）设曲面为抛物面)10(122≤≤--=z y x z ，取上侧 计算dxdy dzdx y dydz x 22233++⎰⎰∑．解：补充平面)1(0:220≤+=∑y x z 取下侧，则0∑与∑围成空间区域Ω 于是 ⎰⎰⎰⎰∑∑+∑-=00I ------------2分π2)(622++=⎰⎰⎰Ωdv y x πθπ2621031020+=⎰⎰⎰-dz r dr d r ------------6分ππ2)(121053+-=⎰dr r r πππ32=+=------------8分。

模糊数学考试习题第一篇：模糊数学考试习题一、填空（每空3分）1.经典集合是论域U到集合的映射.2.模糊集合是论域U到集合的映射.3.经典集合的关系矩阵是.4.模糊集合的模糊关系矩阵是.5.模糊的不确定性即使时间过去了（或者实际作了一次试验）仍然是6.模糊数学把数学的应用范围从精确现象扩大到领域.7．模糊矩阵运算关于交的分配律.8.模糊集的隶属函数是专家给出的.9.模糊集强调的是集合边界的定义.10.模糊聚类方法给出的分类结果不是说事物绝对的属于或绝对的不属于类.11.集合U、V的直积U⨯V的子集R称为U到V的关系.12.U⨯V的一个模糊子集R称为U到V的关系.~13.经典集合的值域是.14.模糊集合的值域是.15.经典集合YI c的排中（互补）律.16.模糊集合YI c的排中（互补）律.17.模糊集的隶属函数是存在.18.模糊聚类方法给出的分类结果.19.模糊模式识别的最大隶属原则有个.20.模糊集的λ截集将模糊集的隶属函数转化为普通集合的二、简述题（每小题15分）1.简述模糊集的一种表示方法，并进行说明.2.简述模糊聚类的编网法.3.写出三种模糊分布函数.4.简述模糊集的一种运算，并进行说明.5.简述模糊聚类的最大树法.6.简述分解定理与扩张原理。

三、举一应用模糊数学方法解决实际问题的例子（25分）第二篇：数学考试一、聪明的你来填一填：（每空0.5分，共12分）1．在（）里填上合适的单位:一块玻璃的厚度大约是3（）骑自行车每小时行驶15（）李明体重35()一辆汽车载重5()2、在（）里填上合适的数：5厘米＝()毫米2千米＝()米()米＝50分米4000千克＝()吨6千克＝()克8吨＝()千克1600千克－600千克=（）吨14厘米 + 26厘米 =（）分米3、在○里填上“＞、＜或＝”:70厘米○90毫米5千米○4500米990克○1千克1500千克○2吨4、把序号填在下面的括号内：5、括号里最大能填几？（）×6＜498×（）＜63（）×5＜446、用0、1、2组成最大的三位数是（），最小的三位数是（），他们的差是（）。

2010年普通高等学校招生全国统一考试（辽宁卷）数学(文科)第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。

（1）已知集合{}1,3,5,7,9U =，{}1,5,7A =，则U C A =（A ）{}1,3（B ）{}3,7,9 （C ）{}3,5,9（D ）{}3,9（2）设,a b 为实数，若复数121ii a bi+=++，则 （A ）31,22a b == （B ）3,1a b ==（C ）13,22a b == （D ）1,3a b == （3）设n S 为等比数列{}n a 的前n 项和，已知3432s a =-，2332S a =-，则公比q =（A ）3（B ）4（C ）5（D ）6（4）已知0a >，函数2()f x ax bx c =++，若0x 满足关于x 的方程20ax b +=，则下列选项的命题中为假命题的是（A ）0,()()x R f x f x ∃∈≤ （B ）0,()()x R f x f x ∃∈≥ （C ） 0,()()x R f x f x ∀∈≤ （D ）0,()()x R f x f x ∀∈≥ （5）如果执行右图的程序框图，输入6,4n m ==，那么输出的p 等于（A ）720 （B ） 360 （C ） 240 （D ） 120（6）设0w >,函数sin()23y wx π=++的图像向右平移43π个单位后与原图像重合，则w 的最小值是 （A ）23 （B ） 43 （C ） 32（D ） 3 （7）设抛物线28y x =的焦点为F ，准线为l ，p 为抛物线上一点，PA l ⊥，A 为垂足，如果直线AF 斜率为PF =（A ）（B ） 8 （C ） （D ） 16（8）平面上,,O A B 三点不共线，设,OA a OB b ==,则OAB 的面积等于（A （B（C （D （9）设双曲的一个焦点为F ，虚轴的一个端点为B ,如果直线FB 与该双曲线的一条渐近线垂直，那么此双曲线的离心率为（A （B （C ）12 （D ）12（10）设525bm ==，且112a b+=，则m =（A （B ）10 （C ）20 （D ）100（11）已知,,,S A B C 是球O 表面上的点，SA ABC ⊥平面，AB BC ⊥，1SA AB ==，BC O 表面积等于（A ）4π （B ）3π （C ）2π （D ）π （12）已知点p 在曲线41x y e =+上，α为曲线在点p 处的切线的倾斜角，则α的取值范围是 (A) [0,)4π(B)[,)42ππ (C) 3(,]24ππ (D) 3[,)4ππ第Ⅱ卷本试卷包括必考题和选考题两部分。

2010年普通高等学校招生全国统一考试（辽宁卷）数学(文科)解析第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}1,3,5,7,9U =，{}1,5,7A =，则U A =ð （ ）A.{}1,3B.{}3,7,9C.{}3,5,9D.{}3,9【测量目标】集合的补集运算.【考查方式】集合的表示（列举法），求集合的补集. 【参考答案】D【试题解析】在集合U 中，去掉1,5,7，剩下的元素构成{}3,9U A =ð 2.设,a b 为实数，若复数12i1i ia b +=++，则 （ ） A.31,22a b == B.3,1a b == C.13,22a b == D.1,3a b ==【测量目标】复数代数形式的四则运算，复数相等.【考查方式】给出复数的除法形式，考查复数的代数四则运算. 【参考答案】A 【试题解析】12i 31i i 1i 22a b ++==++，因此31,22a b ==.3.设n S 为等比数列{}n a 的前n 项和，已知3432S a =-，2332S a =-，则公比q =（ ）A.3B.4C.5D.6【测量目标】等比数列的通项公式，等比数列的前n 项和. 【考查方式】给出等比数列前n 项和与其中一项的关系，求公比. 【参考答案】B【试题解析】 两式相减得，3433a a a =-，44334,4a a a q a =∴==. 4.已知0a >，函数2()f x ax bx c =++，若0x 满足关于x 的方程20ax b +=，则下列选项的命题中为假命题的是 （ ） A.0,()()x f x f x ∃∈R … B.0,()()x f x f x ∃∈R … C. 0,()()x f x f x ∀∈R … D.0,()()x f x f x ∀∈R … 【测量目标】全称量词与存在量词.【考查方式】将未知数设在方程里，与给定的0()f x 比较大小，判断命题的真假. 【参考答案】C【试题解析】函数()f x 的最小值是0()()2bf f x a-=等价于0,()()x f x f x ∀∈R …，所以命题C 错误.5.如果执行右面的程序框图，输入6,4n m ==，那么输出的p 等于 （ ）A.720B.360C. 240D. 120 【测量目标】循环结构的程序框图.【考查方式】考查循环结构的流程图，注意循环条件的设置，以及循环体的构成，特别是注意最后一次循环的k 值,输出p【参考答案】B【试题解析】当1,3k p ==，当2,12k p ==，当3,60k p ==，当4,360k p ==输出p .6.设0ω>,函数πsin()23y x ω=++的图像向右平移4π3个单位后与原图像重合，则ω的最小值是 （ ） A.23 B. 43 C. 32D. 3 【测量目标】函数sin()y A x ωϕ=+的图像和性质.【考查方式】给定函数式进行移动一定单位与原图像重合，求ω的最小值. 【参考答案】C【试题解析】由已知，周期2π4π3,.32T ωω==∴= 7.设抛物线28y x =的焦点为F ，准线为l ，P 为抛物线上一点，PA l ⊥，A 为垂足，如果直线AF 斜率为3-，那么PF = （ ） A.43 B. 8 C. 83 D. 16 【测量目标】抛物线的简单几何意义.【考查方式】给出抛物线的准线及准线上交点与焦点的斜率，图形结合求直线最小值. 【参考答案】B【试题解析】利用抛物线定义，易证PAF △为正三角形，则48sin30PF ︒== 8.平面上,,O A B 三点不共线，设,OA OB ==a b ,则OAB △的面积等于 （ ）A.222()- a b a bB.222()+ a b a bC.2221()2- a b a b D.2221()2+ a b a b【测量目标】平面向量的应用.【考查方式】给出平面向量的向量值，求三不共线向量围成的三角形面积. 【参考答案】C 【试题解析】2222111()sin ,1cos ,1222OABS =<>=-<>=- △a b a b a b a b a b a b a b2221()2=- a b a b9.设双曲线的一个焦点为F ，虚轴的一个端点为B ,如果直线FB 与该双曲线的一条渐近线垂直，那么此双曲线的离心率为 （ ） A.2 B.3 C.312+ D.512+ 【测量目标】双曲线的简单几何性质.【考查方式】给出双曲线方程，给出直线与渐近线的位置关系，求双曲线离心率. 【参考答案】D【试题解析】不妨设双曲线的焦点在x 轴上，设其方程为：22221(0,0)x y a b a b-=>>，则一个焦点为(,0),(0,)F c B b （步骤1） 一条渐近线斜率为：b a ，直线FB 的斜率为：bc -，()1b ba c∴-=- ，2b ac ∴=220c a ac --=，解得512c e a +==.（步骤2） 10.设25abm ==，且112a b+=，则m = （ ） A.10 B.10 C.20 D.100 【测量目标】对数运算.【考查方式】给出指数函数的方程式，用对数的方式求解. 【参考答案】A 【试题解析】211log 2log 5log 102,10,m m m m a b+=+==∴=又0,10.m m >∴= 11.已知,,,S A B C 是球O 表面上的点，SA ABC ⊥平面，AB BC ⊥，1SA AB ==，2BC =，则球O 的表面积等于 （ ）A.4πB.3πC.2πD.π 【测量目标】球的表面积公式.【考查方式】给出球面上线线的位置与数量关系，线面关系，求圆的表面积. 【参考答案】A【试题解析】由已知，球O 的直径为22R SC ==，∴表面积为24π4π.R = 12.已知点P 在曲线4e 1x y =+上，α为曲线在点P 处的切线的倾斜角，则α的取值范围是 （ ） A.π0,4⎡⎫⎪⎢⎣⎭ B.ππ,42⎡⎫⎪⎢⎣⎭ C.π3π,24⎛⎤ ⎥⎝⎦ D. 3π,π4⎡⎫⎪⎢⎣⎭【测量目标】导数的应用，基本不等式.【考查方式】给出曲线方程，利用导数求曲线上动点的切线倾斜角范围. 【参考答案】D 【试题解析】24e 41e 2e 1e 2e x x x x xy '=-=-++++，1e 2,10e xx y '+∴-< 厔，即1tan 0α-< (3)[,π)4α∴∈第Ⅱ卷本试卷包括必考题和选考题两部分.第（13）题～第（21）题为必考题，每个试题考生都必须作答.第（22）题～第（24）题为选考题，考生根据要求作答. 二、填空题：本大题共4小题，每小题5分.13.三张卡片上分别写上字母,,E E B ，将三张卡片随机地排成一行，恰好排成英文单词BEE的概率为 . 【测量目标】随机事件与概率.【考查方式】直接给出数字，求一定条件下的概率. 【参考答案】13【试题解析】题中三张卡片随机地排成一行，共有三种情况：,,BEE EBE EEB ，∴概率为：1.314.设n S 为等差数列{}n a 的前n 项和，若36324S S ==，，则9a = .【测量目标】等差数列的通项公式，等差数列的前n 项和.【考查方式】给出n S 中的数值，求n a 中的数值，求出通项公式进行求解. 【参考答案】15 【试题解析】316132332656242S a d S a d ⨯⎧=+=⎪⎪⎨⨯⎪=+=⎪⎩,解得112a d =-⎧⎨=⎩，（步骤1）91815.a a d ∴=+=（步骤2）15.已知14x y -<+<且23x y <-<，则23z x y =-的取值范围是 . （答案用区间表示）【测量目标】二元线性规划求目标函数的取值范围.【考查方式】给出两不等式，求z 的取值范围，将不等式化简后画图求解.【参考答案】（3,8） 【试题解析】利用线性规划，画出不等式组1423x y x y x y x y +>-⎧⎪+<⎪⎨->⎪⎪-<⎩表示的平面区域，即可求解.16.如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的 长为 .【测量目标】由三视图求几何体的棱长.【考查方式】给出图形的三视图，求几何体最长的棱长. 【参考答案】23【试题解析】画出直观图：图中四棱锥P ABCD -即是，22PA =,23,2,22PB PD PC ===,所以最长的一条棱的长为2 3.PB =三、解答题：解答应写出文字说明、证明过程或演算步骤. 17.（本小题满分12分）在ABC △中，a b c 、、分别为内角A B C 、、的对边，且2sin (2)sin (2)sin a A b c B c b C =+++ （Ⅰ）求A 的大小；（Ⅱ）若sin sin 1B C +=，试判断ABC △的形状.【测量目标】正弦定理余弦定理，利用正余弦定理判断三角形的形状.【考查方式】给出三角形边与角的等式，利用正、余弦定理求其中一角值；根据两角的关系判断ABC △的形状.【试题解析】解：（Ⅰ）由已知，根据正弦定理得c b c b c b a )2()2(22+++= 即bc c b a ++=222（步骤1） 由余弦定理得A bc c b a cos 2222-+=故1cos ,1202A A =-= （步骤2） （Ⅱ）由（Ⅰ）得.sin sin sin sin sin 222C B C B A ++=（步骤3）又1sin sin =+C B ，得21sin sin ==C B （步骤4）因为090,090B C <<<< ，故B C =（步骤5） 所以ABC △是等腰的钝角三角形.（步骤6）18.（本小题满分12分）为了比较注射,A B 两种药物后产生的皮肤疱疹的面积，选200只家兔做实验，将这200只家兔随机地分成两组.每组100只，其中一组注射药物A ，另一组注射药物B .表1和表2分别是注射药物A 药物B 后的实验结果.（疱疹面积单位：2mm ）（Ⅰ）完成下面频率分布直方图，并比较注射两种药物后疱疹面积的中位数大小；（Ⅱ）完成下面22⨯列联表，并回答能否有99.9％的把握认为“注射药物A 后的疱疹面积与注射药物B 的疱疹面积有差异”.附：22()()()()()n ad bc K a b c d a c b d -=++++【测量目标】频率分布直方图，独立性检验.【考查方式】给出图示，完成频率分布直方图，检验独立性. 【试题解析】 （Ⅰ）可以看出注射药物A 后的疱疹面积的中位数在65至70之间，而注射药物B 后的疱疹面积的中位数在70至75之间，所以注射药物A 后疱疹面积的中位数小于注射药物B 后疱疹面积的中位数.（步骤1） （Ⅱ）表3疱疹面积小于270mm疱疹面积不小于270mm 合计 注射药物A 70a = 30b = 100 注射药物B35c = 65d = 100 合计10595200n =56.2495105100100)30356570(20022≈⨯⨯⨯⨯-⨯⨯=K由于828.102>K ，所以有99.9%的把握认为“注射药物A 后的疱疹面积与注射药物B后的疱疹面积有差异”.（步骤2）19.（本小题满分12分）如图，棱柱111ABC A B C -的侧面11BCC B 是菱形，11B C A B ⊥（Ⅰ）证明：平面1ABC ⊥平面11A BC ； （Ⅱ）设D 是11AC 上的点，且1//A B 平面1B CD ，求11:A D DC 的值.【测量目标】线面垂直的判定，面面垂直的判定，平行与垂直关系的综合问题.【考查方式】线线垂直推出面面垂直；给出直线与面的位置关系，求两直线长度的比值. 【试题解析】解：（Ⅰ）因为侧面11BCC B 是菱形，所以11BC C B ⊥（步骤1） 又已知11,B C A B ⊥且11AB BC B =所又⊥C B 1平面11A BC ，又⊂C B 1平面1ABC ，（步骤2） 所以平面⊥C AB 1平面11A BC .（步骤3）（Ⅱ）设1BC 交1B C 于点E ，连结DE ， 则DE 是平面11A BC 与平面1B CD 的交线，（步骤4） 因为1A B 平面1B CD ，所以1A B DE .（步骤5） 又E 是1BC 的中点，所以D 为11AC 的中点.即11:1A D DC =.（步骤6） 20.（本小题满分12分）设1F ，2F 分别为椭圆2222:1x y C a b +=(0)a b >>的左、右焦点，过2F 的直线l 与椭圆C 相交于A ,B 两点，直线l 的倾斜角为60 ，1F 到直线l 的距离为23.（Ⅰ）求椭圆C 的焦距；（Ⅱ）如果222AF F B =,求椭圆C 的方程.【测量目标】椭圆与直线的位置关系，椭圆的简单几何性质.【考查方式】给出椭圆与直线的位置关系，直线的倾斜角，求椭圆的焦距；给出交点与焦距连线的两直线的数量关系，求椭圆方程.【试题解析】解：（Ⅰ）设焦距为2c ，由已知可得1F 到直线l 的距离323, 2.c c ==故 所以椭圆C 的焦距为4.（步骤1）（Ⅱ）设1122(,),(,),A x y B x y 由题意知120,0,y y <>直线l 的方程为3(2).y x =-联立2222422223(2),(3)4330.1y x a b y b y b x y ab ⎧=-⎪⇒++-=⎨+=⎪⎩解得221222223(22)3(22),.33b a b a y y a b a b -+--==++（步骤2）因为22122,2.AF F B y y =∴-=即2222223(22)3(22)2.33b a b a a b a b +--=++ （步骤3）得223.4, 5.a a b b =-=∴= （步骤4）故椭圆C 的方程为221.95x y +=（步骤5） 21.（本小题满分12分）已知函数2()(1)ln 1f x a x ax =+++. （Ⅰ）讨论函数()f x 的单调性；（Ⅱ）设2a -…，证明：对任意12,(0,)x x ∈+∞，1212|()()|4||f x f x x x --…. 【测量目标】利用导数判断函数的单调性，利用导数解决不等式问题.【考查方式】（1）给出函数式，求分类讨论其单调性；确定未知数的范围，证明不等式，需要间接转化为证明单调性.【试题解析】解：(Ⅰ)()f x 的定义域为(0,+∞)，2121()2a ax a f x ax x x+++'=+=.（步骤1） 当0a …时，()f x '＞0，故f (x )在(0,+∞)单调增加；（步骤2） 当1a -…时，()f x '＜0, 故f (x )在(0,+∞)单调减少；（步骤3）当1-＜a ＜0时，令()f x '＝0,解得x =12a a+-.当x ∈(0, 12a a+-)时, ()f x '＞0； x ∈(12a a +-，+∞)时，()f x '＜0, 故()f x 在（0, 12a a+-）单调增加，在（12a a+-，+∞）单调减少.（步骤4） (Ⅱ)不妨假设12x x ….由于2a -…,故f (x )在（0，+∞）单调减少.（步骤5） 所以1212()()4f x f x x x --…等价于12()()f x f x -…4x 1－4x 2,即f (x 2)+ 4x 2…f (x 1)+ 4x 1.（步骤6）令()()4g x f x x =+,则1()2a g x ax x+'=++4 ＝2241ax x a x+++.（步骤7） 于是()g x '…2441x x x -+-＝2(21)x x--…0.（步骤8） 从而()g x 在（0，+∞）单调减少，故g (x 1) …g (x 2)，即f (x 1)+ 4x 1…f (x 2)+ 4x 2，故对任意x 1,x 2∈(0,+∞) ，1212()()4f x f x x x --….（步骤9） 请考生在第（22）、（23）、（24）三题中任选一题做答，如果多做，则按所做的第一题记分.做答时用2B 铅笔在答题卡上把所选题目对应题号下方的方框涂黑.22.（本小题满分10分）选修4－1：几何证明选讲如图，ABC △的角平分线AD 的延长线交它的外接圆于点.E（Ⅰ）证明：ABE △∽ADC △;（Ⅱ）若ABC △的面积12S AD AE = ，求BAC ∠的大小. 【测量目标】圆的性质的应用.【考查方式】给出图示，求圆内接三角形的相似，给出三角形的表达式，求一角值.【试题解析】证明：（Ⅰ）由已知条件，可得∠BAE ＝∠CAD .（步骤1）因为∠AEB 与∠ACB 是同弧上的圆周角，所以∠AEB ＝∠ACD .故△ABE ∽△ADC .（步骤2）（Ⅱ）因为△ABE ∽△ADC ，所以AB AD AE AC=，即AB AC ＝AD AE .（步骤3） 又S ＝12AB AC sin BAC ∠，且12S AD AE = ，故sin AB AC BAC AD AE ∠= .（步骤4）则sin 1BAC ∠=，又∠BAC 为三角形内角，所以∠BAC ＝90 .（步骤5）23.（本小题满分10分）选修4－4：坐标系与参数方程已知P 为半圆C ：cos sin x y θθ=⎧⎨=⎩（θ为参数，0πθ剟）上的点，点A 的坐标为（1，0），O 为坐标原点，点M 在射线OP 上，线段OM 与C 的弧 AP 的长度均为π3. （Ⅰ）以O 为极点，x 轴的正半轴为极轴建立极坐标系，求点M 的极坐标; （Ⅱ）求直线AM 的参数方程.【测量目标】极坐标，圆的极坐标表示.【考查方式】给出圆的极坐标方程，给出部分坐标与位置关系，求一点的极坐标，及直线的参数方程.【试题解析】解：(Ⅰ)由已知，M 点的极角为π3，且M 点的极径等于π3， 故点M 的极坐标为(π3,π3) （步骤1） (Ⅱ)M 点的直角坐标为(π3π,66),A (l,0)，故直线AM 的参数方程为 π1(1).63π.6x t y t ⎧=+-⎪⎪⎨⎪=⎪⎩(t 为参数). （步骤2）24.（本小题满分10分）选修4-5:不等式选讲 已知,,a b c 均为正数，证明：a 2+b 2+c 2+2111a b c ⎛⎫++ ⎪⎝⎭…63，并确定,,a b c 为何值时， 等号成立.【测量目标】平均值不等式，基本不等式.【考查方式】给出未知数，求解不等式，解出当未知数为何值时，不等式等号成立. 【试题解析】证明：(证法一)因为,,a b c 均为正数，由平均值不等式得222233()a b c abc ++…, ① 111a b c ++…133()abc -, 所以2111a b c ⎛⎫++ ⎪⎝⎭…239()abc -. （步骤1） ②故a 2+b 2+c 2+2111a b c ⎛⎫++ ⎪⎝⎭…233()abc 239()abc -+.（步骤2） 又233()abc 239()abc -+…22763=， ③所以原不等式成立.（步骤3）当且仅当a =b =c 时,①式和②式等号成立.当且仅当22333()9()abc abc -=时, ③式等号成立.即当且仅当a =b =c =143时,原式等号成立.（步骤4）(证法二)因为,,a b c 均为正数,由基本不等式222a b ab +…222b c bc +…222c a ac +…所以a 2+b 2+c 2…ab bc ac ++ （步骤5） ① 同理222111a b c ++…111ab bc ac ++ ②故a 2+b 2+c 2+2111()a b c ++…ab bc ac +++31ab +31bc +31ac63…. ③所以原不等式成立（步骤6）当且仅当a =b =c 时,①式和②式等号成立,当且仅当a =b =c ,(ab )2=(bc )2=(ac )2=3时,③式等号成立.即当且仅当a =b =c =143时,原式等号成立. （步骤7）。

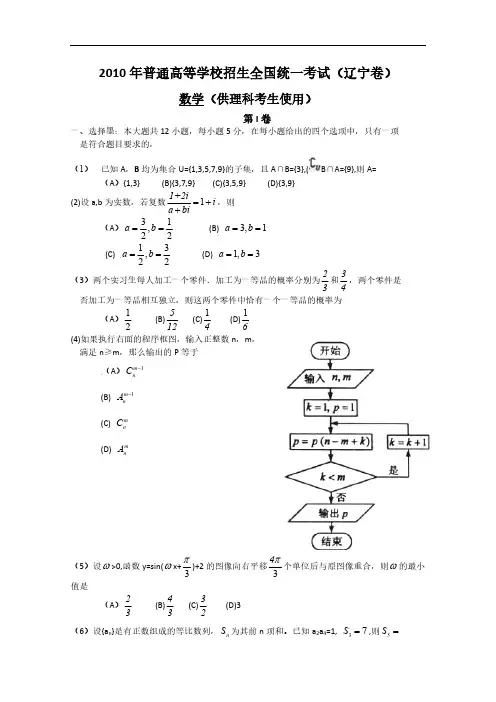
2010年高考辽宁卷理科数学试题及答案*************第I 卷一、选择墨：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项分，在每小题给出的四个选项中，只有一项 是符合题目要求的，是符合题目要求的，（1） 已知A ，B 均为集合U={1,3,5,7,9}的子集，且A ∩B={3},u ðB ∩A={9},则A= （A ）{1,3} (B){3,7,9} (C){3,5,9} (D){3,9} (2)设a,b 为实数，若复数11+2ii a bi =++，则，则（A ）31,22a b ==(B) 3,1a b == (C) 13,22a b ==(D) 1,3a b ==（3）两个实习生每人加工一个零件．加工为一等品的概率分别为23和34，两个零件是，两个零件是否加工为一等品相互独立，则这两个零件中恰有一个一等品的概率为否加工为一等品相互独立，则这两个零件中恰有一个一等品的概率为（A ）12(B)512(C)14(D)16(4)如果执行右面的程序框图，输入正整数n ，m ，满足n ≥m ，那么输出的P 等于等于（A ）1m n C -(B) 1m n A -(C) m nC (D) mn A（5）设w >0,函数y=sin(w x+3p)+2的图像向右平移34p 个单位后与原图像重合，个单位后与原图像重合，则则w 的最小值是小值是（A ）23 (B)43 (C)32 (D)3 （6）设{a n }是由正数组成的等比数列，n S 为其前n 项和。

已知a 2a 4=1, 37S =,则5S =（A ）152 (B)314 (C)334 (D)172-3383OA OA=a =a OB 222|||()|a b a b -222|||()|a b a b + 2221|||()2|a b a b -2221|||()2|a b a b + 233+5+4p )p p ,p p p 6222(C) (626222)x三、解答题：解答应写出文字说明，证明过程或演算步骤。

河南理工大学 2006-2007 学年第 1 学期《模糊数学》试卷（B 卷）考试方式 闭卷 本试卷考试分数占学生总评成绩的 80 %复查总分 总复查人一、填空题（本题共5小题，每小题4分，共20分）1、模糊数学和模糊控制的概念是由美国加利福尼亚大学著名控制论专家 ,首先提出，并被誉为2、设},,,{21n x x x U =,且∑==ni ii x x A A 1~~)(, ∑==ni ii x x B B 1~~)(, 则=~~B A ,=~~B A , =CA ~。

3、设,5.01.06.005~⎥⎦⎤⎢⎣⎡=A ,9.04.02.08.0~⎥⎦⎤⎢⎣⎡=B 则=~~B A , =~~B A , =CA ~。

4、设⎥⎦⎤⎢⎣⎡=5.08.0107.04.0A , ⎥⎥⎦⎤⎢⎢⎣⎡=3.006.04.07.01B , 则=B A 。

5、模糊矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=7.09.01.06.08.014.06.04.05.06.00A ，则=5.0A 。

二、计算题（本题共5小题，共60分）1． （本题12分）设6种商品的集合为{}654321,,,,,u u u u u u U =， U上的滞销商品模糊集为654321~4.05.06.001.01u u u u u u A +++++=， 脱销商品模糊集为654321~05.0006.01.00u u u u u u B +++++=， 畅销商品模糊集为 654321~5.04.04.018.00u u u u u u C +++++=.（1）求不滞销商品模糊集~D ；（2）求~D 与~C 的关系；（3）求既脱销又畅销的商品模糊集。

2．（本题9分）设论域{}54321,,,x x u u u U =，且54321~3.05.018.07.0u u u u u A ++++=，54321~7.08.09.06.05.0u u u u u B ++++=，试求~A 和~B 的内积和外积。