当前位置：文档之家 › 高中数学概率复习课件

高中数学概率复习课件

  • 格式：ppt
  • 大小：2.29 MB
  • 文档页数：29

下载文档原格式

  / 29

合集下载

高中数学概率知识点全面解析PPT

高中数学概率知识点全面解析PPT

乘法公式和全概率公式
乘法公式的应用 乘法公式在概率论中的应用广泛，例如计算两个事件同时发生的概 率，其计算公式为P(A并B)=P(A)*P(B)。根据统计数据，这种方法 的准确率高达90%以上。 全概率公式的价值 全概率公式可以解决复杂问题中的概率计算问题，如在多个互斥事 件中寻找某个事件发生的原因。根据一项研究，使用全概率公式解 决问题的效率比传统方法提高了约30%。
连续型随机变量
连续型随机变量定义 连续型随机变量是一个可能取无限多个值的随机变量。 概率密度函数 连续型随机变量的概率密度函数用于描述该随机变量在某一区 间内取值的概率。 期望与方差 连续型随机变量的期望和方差是其重要特性，它们描述了该随 机变量的平均水平和离散程度。 实际应用 连续型随机变量广泛应用于金融、工程等实际问题中，如期权 定价模型。
Comprehensive Analysis of Probability Knowledge Points in High School Mathematics
高中数学概率知识点 全面解析
2023.11.03
目录
Content
01 概率的基本概念 02 条件概率与独立性 03 随机变量及其分布 04 多维随机变量及其联合分布 05 大数定律与中心极限定理
THANK YOU
2023.11.03
中心极限定理的内容和应用
中心极限定理概念 中心极限定理是概率论中的一个重要定理，描述了大量随机变量和的分布趋近于正态分布的现象 大数定律与中心极限定理 大数定律揭示了样本数量增加时，样本平均值趋近于期望值，而中心极限定理则描述了这一过程的概率分布 正态分布在实际应用中的重要性 由于中心极限定理的作用，许多实际问题中的随机变量都可以近似为正态分布，方便进行统计分析 中心极限定理在高中数学教学中的地位 作为概率论的核心内容之一，中心极限定理对于培养学生的数学思维、解决实际问题具有重要意义

高中数学概率复习课件新人教版必修

高中数学概率复习课件新人教版必修
02
有一人在打靶中，连续射击2次，事件“至少有1次中靶”的对立事件是（ ） A.至多有1次中靶 B.2次都中靶 C.2次都不中靶 D.只有1次中靶
甲、乙两人下棋，两人下和棋的概率为 ，乙获胜的概率为 ，则甲获胜的概率为_______________
1、两事件对立，必定互斥，但互斥未必对立
互斥事件与对立事件的联系与区别：
2、互斥的概念适用于多个事件，但对立概念只适用于两个事件
Ⅱ.和事件A +B :
表示事件A、B中至少有一个发生的事件.
(1)当A、B是互斥事件时：
(2)当A、B是对立事件时：
求法：
(1)直接法：化成求一些彼此互斥事件的概率的和；
从10件产品（其中次品3件）中，一件一件地不放回地任意取出4件，求4件中恰有1件次品的概率
某公务员去开会，他乘火车 轮船 汽车 飞机去的概率分别为0.3 0.2 0.1 0.4 求他乘火车或乘飞机去的概率; 求他不乘轮船去的概率； 如果他去的概率为0.5，请问他有可能是乘何交通工具去的？
(2)间接法：求对立事件的概率.
Ⅲ.积事件A B :
表示事件A、B中同时发生的事件.
对事件A，B，如果A(B)发生的概率与B(A)是否发生没有关系，则称A，B互相独立. 若A，B互相独立，则P(AB)=P(A)·P(B)，反之亦然.
01
02
03
会把事件分成等可能基本事件
理解古典概型的特点，
掌握等可能事件的计算方法
理解等可能事件的意义
课堂练习
抛掷一枚质地均匀的硬币，如果连续抛掷1000次，那么第999次出现正面朝上的概率是（ ）
01
03
02
某种彩票中奖几率为0.1％，某人连续买1000张彩票，下列说法正确的是：（ ）

高中数学复习课第7课时概率课件

高中数学复习课第7课时概率课件
(1)将所求事件转化为几个彼此互斥的事件的和事件;
(2)将一个较复杂的事件转化为几个互斥事件的和事件,需要
分类较多,而其对立面的分类较少时,可考虑利用对立事件的
概率公式,即“正难则反”.它常用来求“至少……”或“至多……”
型事件的概率.
【变式训练4】 某商场进行有奖销售,购满100元商品得1张奖
券,多购多得.1 000张奖券为一个开奖单位,每个开奖单位设特
等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等
奖、二等奖的事件分别为A,B,C,求:
(1)P(A),P(B),P(C);
(2)1张奖券中奖的概率;
(3)1张奖券不中特等奖且不中一等奖的概率.


解:(1)P(A)= ,P(B)=
故事件


= ,P(C)=
的个数是有限的,那么称样本空间Ω为有限样本空间.
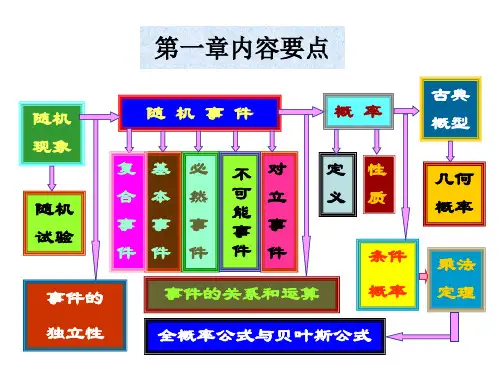
3.什么是随机事件,必然事件,不可能事件?
提示:一般地,把试验E的样本空间Ω的子集称为E的随机事件,
简称事件,常用A,B,C等表示.样本空间Ω是其自身的子集,因
此Ω也是一个事件;又因为它包含所有的样本点,每次试验无
论哪个样本点ω出现,Ω都必然发生,因此称Ω为必然事件.空
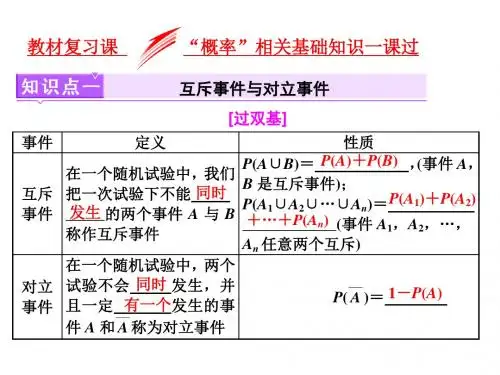
互斥事件与对立事件的判断方法:
(1)利用基本概念:①互斥事件不可能同时发生;②对立事件首
先是互斥事件,且必有一个发生.
(2)利用集合的观点:设事件A,B所包含的样本点组成的集合
表示分别是A,B.
①事件A与B互斥,即A∩B=⌀;
②事件A与B对立,即A∩B=⌀,且A∪B=Ω(Ω为样本空间),也即
A=∁ΩB或B=∁ΩA.
)
A.① B.②④ C.③ D.①③

高中数学第3章概率阶段复习课课件苏教版必修3

高中数学第3章概率阶段复习课课件苏教版必修3

产品编号
A6 A7 A8 A9 A10质量指标(x，y，z) (1,2,2) (2,1,1) (2,2,1) (1,1,1) (2,1,2)
(1)利用上表提供的样本数据估计该批产品的一等品率； (2)在该样本的一等品中，随机抽取2件产品， ①用产品编号列出所有可能的结果； ②设事件B为“在取出的2件产品中，每件产品的综合指标S都等于 4”，求事件B发生的概率.
[解析] (1)根据频数除以总数＝频率，分别求出即可； (2)根据(1)中所求即可得出任取 1 个 U 盘是次品的概率； (3)利用不等式得出 x(1－0.02)≥2 000，求出即可．
[解] (1)表中次品频率从左到右依次为0.06,0.04，0.025， 0.017,0.02,0.018.
(2)当抽取件数a越来越大时，出现次品的频率在0.02附近摆动，所以从 这批U盘中任意抽取一个是次品的概率约是0.02.
发达地区 参加测试的人数 30 50 100 200 500 800
得 60 分以上的人数 17 29 56 111 276 440 得 60 分以上的频率 0.567 0.580 0.560 0.555 0.552 0.550 (2)估计贫困地区和发达地区参加测试的儿童得 60 分以上的概率分别为 0.503 和 0.550.
(1)利用计算器计算两地区参加测试的儿童中得60分以上的频率(结果保 留到小数点后三位)；
(2)估计两个地区参加测试的儿童得60分以上的概率． [解析] 由频数求出频率，再由频率估计概率． [解] (1)贫因地区
参加测试的人数 30 50 100 200 500 800 得60分以上的人数 16 27 52 104 256 402 得60分以上的频率 0.533 0.540 0.520 0.520 0.512 0.503

高考数学总复习教材复习课“概率”相关基础知识课件理

高考数学总复习教材复习课“概率”相关基础知识课件理

比赛场馆服务的大学生志愿者中，有 2 名来自莫斯科国立大学，有
4 名来自圣彼得堡国立大学，现从这 6 名志愿者中随机抽取 2 人，
则至少有 1 名志愿者来自莫斯科国立大学的概率是
()
A.1145
B.115
C.35
D.25
解析：从 6 人中抽取 2 人的基本事件个数为 15，“至少有 1 名志愿
者来自莫斯科国立大学”的对立事件为“两名志愿者都来自圣彼得
示的韦恩图表示，由图可知，任何一个事件与其余
3 个事件的和事件必然是对立事件，任何两个事件的和事件与其
余两个事件的和事件也是对立事件．答案：D
古典概型
[过双基]
1．特点：
(1)试验中所有可能出现的基本事件只有 有限 个，即 有限性 ．
(2)每个基本事件发生的可能性 相等 ，即 等可能性 ．
2．古典概型概率公式：
堡国立大学”，而事件“两名志愿者都来自圣彼得堡国立大学”包含
的基本事件个数为 6，∴所求概率为 P＝1－165＝35. 答案：C
2．从一副混合后的扑克牌(52 张)中，随机抽取 1 张．事件 A 为“抽 到红桃 K”，事件 B 为“抽到黑桃”，则 P(A∪B)＝________(结 果用最简分数表示)． 解析：∵P(A)＝512，P(B)＝1532， ∴P(A∪B)＝P(A)＋P(B) ＝512＋1532＝1542＝276. 答案：276
一个兴趣小组的概率 P＝39＝13.
答案：A
2．(2017·唐山统考)抛掷两枚质地均匀的骰子，向上的点数之差的绝
对值为 3 的概率是
()
A.19
B.16
C.118
D.112
解析：抛掷两枚骰子，向上的点数情况共有 36 种等可能的结

高中数学第三章概率模块复习课课件新人教B版必修

高中数学第三章概率模块复习课课件新人教B版必修

1
3
= .
专题归纳
高考体验
专题三 几何概型
【例4】 如图所示,在圆心角为直角的扇形OAB中,分别以OA,OB
为直径作两个半圆.在扇形OAB内随机取一点,则此点取自阴影部
分的概率是 (
)
2
1
1
A.1-π
B.2 − π
C.
D.
2
π
1
π
专题归纳
高考体验
解析:如图所示:
不妨设扇形的半径为2a,记两块白色区域的面积分别为S1,S2,两块
1
1
看起来,一枚骰子赌“1”点可能性是6;那么两枚骰子就有3的可
1
2
能性,三枚就有 的可能性.即使是 1 元对 1 元的奖励,机会也是均等的,
专题四 概率在现实中的应用
【例6】 我们来看一种在国外颇为盛行的赌博——“碰运气游
戏”.它的规则如下:每个参加者每次先付赌金1元,然后将三枚骰子
一起掷出.他可以猜某一个点数,譬如赌“1”点.如果三枚骰子中出现
一个“1”点,庄家除把赌金1元返还外,再奖1元;如果出现两个“1”点,
除返还赌金外,再奖2元;如果全是“1”点,那么除返还赌金外,再奖3元.
区域的几何度量
知识网络
要点梳理
思考辨析
判断下列说法是否正确,正确的在后面的括号内画“√”,错误的画
“×”.
(1)随机事件和随机试验是一回事. (
)
(2)事件发生的频率与概率是相同的. (
)
(3)若A,B为互斥事件,则P(A)+P(B)=1. (
)
(4)掷一枚质地均匀的硬币两次,出现“两个正面”“一正一反”“两
第一张牌的数字
第二张牌的数字

高中数学概率论复习(全)PPT

高中数学概率论复习(全)PPT
（2）有界性：对任意实数 x ，有 0 F(x) 1，且
F() lim F(x) 0 x
F() lim F(x) 1 x
（3）右连续性：F(x) 是右连续的函数，即对任
意实数 x ，有 F(x 0) F(x) ． （4）对任意实数 x1, x2 (x1 x2 ) ，有 P{x1 X x2} P{X x2} P{X x1}
F (x2 ) F (x1)
【注】满足单调性、有界性和右连续性这三个性质的 函数，一定可以作为某个随机变量的分布函数.
离散型随机变量
离散型随机变量 X 的概率分布满足以下两个基本性质：
（1）非负性： pi 0 ， i 1, 2, ；
（2）规范性： pi 1 ． i 1
【注】满足非负性和规范性的数组 pi (i 1, 2, ) ，一 定是某个离散型随机变量的概率分布．
pij
( xi , y j )G
(4)
P{X xi} pij , i 1, 2, j 1
P{Y y j} pij , j 1, 2, i 1
二维连续型随机变量
（1）非负性 p(x, y) 0 ；
（2）规范性 p(x, y)dxdy F (, ) 1.
【注】若二元函数 p(x, y) 具有非负性和规范性，则 p(x, y) 一定是某个二维连续型随机变量的联合概率 密度函数．
定理 设随机变量 X 具有数学期望
E( X ) μ,方差 D( X ) σ 2,则对于任
（3）右连续性 F( x, y ) 分别对 x ， y 右连续，即
F(x 0, y) lim F(x , y) F(x, y) 0
F(x, y 0) lim F(x, y ) F(x, y) 0
（4）非负性 对于任意的实数 x1 x2 ， y1 y2 ，有

2025高考数学一轮复习课件 随机事件的概率

2025高考数学一轮复习课件 随机事件的概率

4. (2024·邢台市第二中学期末)如图所示，A，B，C 表示 3
个开关，若在某段时间内，它们正常工作的概率分别为 0.9，
0.8，0.8，则该系统的可靠性(3 个开关只要一个开关正常工作
即可靠)为( )
A．0.504
B．0.994
C．√0.996
D．0.964
解析 由题意知，所求概率为 1－(1－0.9)(1－0.8)(1－0.8)＝1－0.004＝ 0.996.故选 C.
C√．“恰有 1 个白球”和“恰有 2 个白球”
D．“至多有 1 个白球”和“都是红球”
【解析】 对于 A，“至少有 1 个白球”和“都是红球”是对立事件，不 符合题意；对于 B，“至少有 2 个白球”表示取出的 2 个球都是白色的，而“至 多有 1 个红球”表示取出的球 1 个是红球，1 个是白球，或者 2 个都是白球， 二者不是互斥事件，不符合题意；对于 C，“恰有 1 个白球”表示取出的 2 个 球 1 个是红球，1 个是白球，与“恰有 2 个白球”是互斥而不对立的两个事件， 符合题意；对于 D，“至多有 1 个白球”表示取出的 2 个球 1 个是红球，1 个 是白球，或者 2 个都是红球，与“都是红球”不是互斥事件，不符合题意．故 选 C.
并事件 (和事件)
若某事件发生当且仅当事件 A 发生或事件 B 发
生，称此事件为事件 A 与事件 B 的 __并__事__件__(或__和__事__件__)___
符号表示
___B_⊇__A___
(或 A⊆B)
_A__＝__B_
A∪B (或 A＋B)
交事件 (积事件) 互斥事件
对立事件
若某事件发生当且仅当 _事__件__A_发__生__ 且___事__件__B_发__生_____，则称此事件为

《高二数学概率复习》课件

《高二数学概率复习》课件
条件概率的公式
P(A|B) = P(A∩B) / P(B)。其中，P(A∩B)表示事件A和事件B同时发生的概率， P(B)表示事件B发生的概率。
条件概率的性质
非负性
P(A|B) ≥ 0。
规范性
当事件B是必然事件时，P(A|B) = P(A)。
条件概率的加法规则
如果两个事件B1和B2是互斥的，那么对于任一事件A，有 P(A|B1∪B2) = P(A|B1) + P(A|B2)。
04
概率的应用
概率在日常生活中的应用
天气预报
通过概率分析，预测未来天气变 化，为日常生活和出行提供参考
。
彩票
彩票中奖概率的计算，让人们理性 对待，避免盲目投入。
医学诊断
通过概率统计方法，提高疾病诊断 的准确率。
概率在科学实验中的应用
物理实验
在物理学中，概率被广泛应用于 粒子实验、量子力学等领域。
解析5
进阶题目5的答案是$frac{4}{8} times frac{3}{7} = frac{12}{56} = frac{3}{14}$，因为第一次摸出白球的概 率为$frac{4}{8}$，第二次摸出白球的概率为$frac{3}{7}$ 。
解析6
进阶题目6的答案是$frac{7}{10} times frac{3}{9} = frac{21}{90} = frac{7}{30}$，因为第一次摸出红球的概 率为$frac{7}{10}$，第二次摸出白球的概率为 $frac{3}{9}$。
《高二数学概率复习》ห้องสมุดไป่ตู้ppt课件
目 录
• 概率的基本概念 • 古典概型与几何概型 • 条件概率与独立性 • 概率的应用 • 复习题与答案解析

人教A版高中数学必修三课件概率复习课.pptx

人教A版高中数学必修三课件概率复习课.pptx
解：完成由甲地到乙地这件事有三类办法：
第一类办法坐火车，一天中有4种不同走法。 第二类办法坐汽车，一天中有2种不同走法。 第三类办法坐轮船，一天中有3种不同走法。 由加法原理得：4+2+3=9 答：有9种不同的走法。
作为练习：由数字1、2、3、4、5可以组成多
少个允许有重复数字的三位数？无重复数字的三位 数？
必然事件：在一定条件下，必然发生的事件
不可能事件：在一定条件下，不可能发生的事件 随机事件：在一定条件下，可能发生也可能不发生
的事件
做一件事，完成它有n类办法，其中第一类办法中 有m1种方法，第二类中有m2种方法……，第n类办 法中有mn种方法，那么完成这件事共有 N=m1+m2+…+mn种不同的方法。
：30内的任意时刻到达预定地点的机会是等可能的
。解 设甲乙二人到达预定地点
y
的时刻分别为 x 及 y（分钟）, 30
则
二人会面
10 10
x 30
Bertrant问题 已知半径为1的圆内接三角形的
边长为
在圆内随机取一条弦求弦长超过
的概率
ቤተ መጻሕፍቲ ባይዱ
B
A
D
B
O
A ① p = 1/3
A
B
D
② p = 1/2
③ p = 1/4
如果从A村经过B村到达C村可分为两个步骤完成： 第一步A村→B村，有3种不同的走法。 第二步B村→C村，有2种不同的走法。
由乘法原理，共有3×2=6种不同的走法。
分步计数原理也称为乘法原理。
问题：口袋里装有2个白球和2个黑球，这4个球除 颜色外完全相同，4个人按顺序依次从中摸 出一个球，试计算第二个人摸到白球的概率.

高中数学第13章概率章末复习提升课课件湘教版必修5

高中数学第13章概率章末复习提升课课件湘教版必修5

D．23
解析：选 C.EF 为△ABC 的中位线．当 点 P 位于四边形 BEFC 内时，S△PBC 的面 积小于S2， 又因为 S△AEF＝14S，SBEFC＝34S.
3 所以△PBC 的面积小于S2的概率为 P＝4SS＝34.
3．A 是平面上的不规则区域，作一个长 12 m，宽 8 m 的矩
事件的概率 解决实际问题时，要注意频率与概率的区别与联系： 概率是一个常数，频率是一个变数，它随着试验次数的变 化而变化，试验次数越多，频率就越接近于概率．
下列说法正确的有( ) ①频率反映事件发生的频繁程度，概率反映事件发生的可 能性的大小； ②做 n 次随机试验，事件 A 发生 m 次，则事件 A 发生的频 率mn 就是事件的概率； ③百分率是频率，但不是概率；
本部分内容讲授结束
按ESC键退出全屏播放
【解】 设 A＝{硬币落下后与格线没有
公共点}．
在等边三角形内作小等边三角形，使其
三边与原等边三角形三边距离都为 1，如
图所示，则小等边三角形的边长为 4 3－
2 3＝2 3，由几何概率公式得所求概率为
P(A)＝
43×（2 43×（4
33））22＝14.
【点评】 作出示意图是理解本题的最好手段．
1．从集合{1，3，6，8}中任取两个数相乘，积是偶数的概
3．古典概型 (1)基本特征：有限性、等可能性． (2)计算公式：P(A)＝mn (其中 n 为试验的基本事件总数，m 为事件 A 包含的基本事件数)．
4．几何概率 (1)几何概率的基本特征：基本事件的无限性、每个事件发 生的等可能性． (2)几何概率的概率计算公式： P(A)＝试验的构全成部事结件果A的构区成域的长区度域（长面度积（或面体积积或）体积）.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

5.概率的几个基本性质
（1）0≤P(A)≤1. （2）若事件A与B互斥，则
P（A∪B）＝P（A）＋P（B）.
（3）若事件A与B对立，则
P（A）互斥的； （2）任何事件（除不可能事件）都可以表示
成基本事件的和.
7.古典概型
一次试验中所有可能出现的基本事件只有有 限个（有限性），且每个基本事件出现的可能性
5、在相距5米的两根木杆上系一条绳子， 并在绳子上挂一盏灯，则灯与两端距 离都大于2米的概率为 1 ______________ 5
6．有一人在打靶中，连续射击2次，事 件“至少有1次中靶”的对立事件是（ C ） A.至多有1次中靶 B.2次都中靶 C.2次都不中靶 D.只有1次中靶
7.某公务员去开会，他乘火车 轮船 汽车 飞机去 的概率分别为0.3 0.2 0.1 0.4 （1）求他乘火车或乘飞机去的概率; （2）求他不乘轮船去的概率；
22 1 － 3 SG 5 P＝ S ＝ ＝ . 2 1 9 I
2
课堂练习
1. 抛掷一枚质地均匀的硬币，如果连续 抛掷1000次，那么第999次出现正面朝上 的概率是（D）
1 A. 999
B.
1 1000
C.
999 1000
1 D. 2
2、某种彩票中奖几率为0.1％，某 人连续买1000张彩票，下列说法 正确的是：（ C ） A、此人一定会中奖 B、此人一定不会中奖 C、每张彩票中奖的可能性都相等 D、最后买的几张彩票中奖的可能性 大些
(2)摸出的一个球为蓝球的概率．
解 记事件 A 为“摸到红球 ” ；事件 B 为 “ 摸到黄 球”，事件C为“摸到蓝球”． (1)A与B为互斥事件，故摸到红球或黄球的概率为 P(A∪B)＝P(A)＋P(B)＝0.45＋0.33＝0.78.
例2
口袋中有若干红球、黄球与蓝球，随机地从
中摸一个球，摸到红球的概率为0.45，摸到黄球的概率 为0.33，求：(1)摸出的一个球为红球或黄球的概率； (2)摸出的一个球为蓝球的概率． 解 记事件 A 为“摸到红球 ” ；事件 B 为 “ 摸到黄
例9 两人相约在0时到1时之间相遇，早到者应等 迟到者20分钟方可离去．如果两人出发是各自独立的 ，且在0时到1时之间的任何时刻是等概率的，问两人 相遇的可能性是多大？
解 假设两人分别在 x 时、y 时 1 到达，依题意：|x—y|≤ 才能相遇． 3 显然到达时间的全部可能结果均匀 分布在右面的单位正方形 I 内，而 相遇现象，则发生在图中阴影区域 G 中，由几何概率的定义：
5 1 (2)P = 1 = 6 6
例4
三个人玩传球游戏，每个人都等可能地传给
另两人(不自传)，若从A发球算起，经3次传球后又回 到A手中的概率是多少？
解 记三人为 A、B、C，则 3 次传球的所有可能可用树状图 方式列出：如右图．
每一个分支为一种传球 方案，则基本事件的总数为 8，而又回到 A 手中的事件 个数为 2 个，根据古典概型 概率公式得 P＝2/8=1/4.
球”，事件C为“摸到蓝球”． (2)事件C与A∪B为对立事件，故摸到蓝球的概率为 P(C)＝1－P(A∪B)＝1－0.78＝0.22.
例3.甲、乙两人下中国象棋，已知下成和棋的概
1 1 率是 ，乙获胜的概率是 ，求： 3 2
（1）乙不输的概率；
（2）甲获胜的概率.
1 1 5 解(1)P = + = 2 3 6
例6 某三件产品中有两件正品和一件次品，每次 从中任取一件，连续取两次，分别在下列条件下，求 取出的两件产品中恰有一件次品的概率. （1）每次取出产品后不放回；
（2）每次取出产品后放回.
解 记正品为1, 2, 次品为 a 4 2 (1) (1,2),(1,a),(2,1),(2,a),(a,1),(a,2) P (A )
例 5 有两个袋中都装有写着数字0,1,2,3,4,5的6张
卡片，若从每个袋中任意各取一张卡片，求取出的两 张卡片上数字之和等于5的概率． 解 从每个袋中任意取一张卡片有 36 个基本事
件．其中 “ 和等于 5” 的结果有 (0,5) ， (1,4) ， (2,3) ， (3,2)，(4,1), (5,0)共6个基本事件， 所以P＝6/36＝1/6.
相等（等可能性）.
8.古典概型的概率公式 P(A)=
事件A所包含的基本事件的个数 基本事件的总数
9.几何概型
每个事件发生的概率只与构成该事件区域的 长度（面积或体积）成比例.
10.几何概型的概率公式
构成事件A的区域长度（面积或体积）
P(A)=
试验的全部结果所构成的区域长度（面积或体积）
11.随机数
必修3第三章 概率复习课
知识结构
随机事件 频率 概率的意义与性质 概 率 的 实 际 应 用
古典概型
几何概型
随机数与随机模拟
知识梳理
1.事件的有关概念
(1)必然事件： 在条件S下，一定会发生的事件. (2)不可能事件： 在条件S下，一定不会发生的事件. (3)随机事件： 在条件S下，可能发生也可能不发生的事件.
例8 以半径为1的圆内任一点为中点作弦，求弦 长超过圆内接等边三角形边长的概率． 解 记事件 A 为“弦长超过圆内接等边三角形的 边长”，如图所示，作等边三角形 BCD 的内切圆，当 以小圆上任意一点作弦时， 弦长都等于等边三角形的边 长， 所以当弦的中点在小圆内时， 弦长超过圆内接等边 1 三角形的边长， 小圆的半径为 ， 所以由几何概型公式， 2 12 π2 1 得 P(A)＝ 2＝ ， π× 1 4 1 即弦长超过圆内接等边三角形的边长的概率为 . 4
（1）整数随机数：对于某个指定范围内的整 数，每次从中有放回随机取出的一个数.
（2）均匀随机数：在区间[a，b]上等可能取
到的任意一个值.
12. 随机模拟方法
利用计算器或计算机产生随机数，从而获得 试验结果.
例题精讲
例1 某人捡到一个不规则形状的五面体石块，他在每 个面上作了记号，投掷了100次，并且记录了每个面朝上 的次数如下表，如果再投掷一次，请估计石块的第4面落 在桌面上的概率是多少？ 石块的面 频数 1 32 2 18 3 15 4 13 5 22
解 由于投掷100次，第4面落在桌面上13次，故 其频率为＝13/100=0.13. 因此，如果再掷一次，估 计石块的第4面落在桌面上的概率是0.13.
例2
口袋中有若干红球、黄球与蓝球，随机地从
中摸一个球，摸到红球的概率为0.45，摸到黄球的概率
为0.33，求：(1)摸出的一个球为红球或黄球的概率；
6 3
(2) (1,1),(1,2),(1,a),(2,1),(2,2),(2,a),(a,1),(a,2),(a,a)
4 P (B ) 9
例7 如图，在三角形AOB中,已知AOB=60°, OA=2，OB=5，在线段OB上任意选取一点C，求 △AOC为钝角三角形的概率.
A
O
D
E
C
B
OD + EB 2 解 P = = = 0.4 OB 5
0.7
0.8
8、从1，2，3，4，5五个数字中任意取 2个出来组成一个没有重复数字的两位 数，求 3 （1）这个两位数是奇数的概率。5 3 （2）这个两位数大于30的概率。 5 （3）求十位和个位上数字之和大于4两 位数的概率。 4
5
A=B.
（3）并事件(和事件):当且仅当事件A发生或
事件B发生时，事件C发生，则C=A∪B（或A+B）.
（4）交事件（积事件）：当且仅当事件A发生 且事件B发生时，事件C发生，则 C=A∩B（或AB）.
（5）互斥事件：事件A与事件B不同时发生，
即A∩B＝Ф . （6）对立事件：事件A与事件B有且只有一个 发生，即A∩B为不可能事件，A∪B为必然事件.
3． 一批产品中，有10件正品和5件次品 ，对产品逐个进行检测，如果已检测到 前 3次均为正品，则第4次检测的产品仍 为正品的概率是（ A） A.7/12 B. 4/15 C. 6/11 D. 1/3
4、在去掉大小王的52张扑克中 ，随机抽取一张牌，这张牌是 J 2 13 或Q的概率为_________
2.事件A出现的频率
在相同的条件S下重复n次试验，事件A出现的 次数为nA与n的比值，即
nA f A ( n) n
3.事件A发生的概率
通过大量重复试验得到事件A发生的频率的稳 定值.
4.事件的关系与运算
（1）包含事件：如果当事件A发生时，事件B
一定发生，则 A B （或 B A ）. （2）相等事件： 若 A B ，且 B A ， 则