四面体与八面体

四面体间隙和八面体间隙是固体物质中晶格间隙的一种特殊排列结构，它们在固体材料中起着非常重要的作用。

铁素体和奥氏体作为两种重要的金属组织结构，在材料学中也扮演着至关重要的角色。

本文将以四面体间隙和八面体间隙为切入点，深入探讨铁素体和奥氏体的组织结构、特性和应用，旨在帮助读者更全面地理解和理解这两种金属组织结构。

1. 四面体间隙与八面体间隙四面体间隙是指正方晶系和六方晶系中，离子晶体结构最密堆积的结构中央空隙处，其原子堆积密度为74，通常由钠氯型晶体构成。

而八面体间隙则是指正方晶系和六方晶系中，离子晶体结构中心空隙处，其原子堆积密度为68，通常由氧化物晶体构成。

四面体间隙和八面体间隙的存在对固体材料的性质和应用有着重要的影响。

2. 铁素体铁素体是铁碳合金中的一种组织结构，主要由α-Fe和少量的固溶碳构成。

其结构呈等轴晶体结构，具有良好的塑性和韧性，适用于低温、高强度的工程钢材。

铁素体中的四面体间隙和八面体间隙对其力学性能和热处理性能起着重要作用，通过调控间隙结构可以实现对铁素体组织结构的控制和改善。

3. 奥氏体奥氏体是铁碳合金中的另一种组织结构，主要由γ-Fe和一定量的固溶碳构成。

其结构呈面心立方结构，具有优异的强度和硬度，适用于高温、高强度的工程钢材。

奥氏体中的四面体间隙和八面体间隙对其耐热性、耐蚀性和强度起着重要作用，通过调控间隙结构可以实现对奥氏体组织结构的控制和改善。

总结回顾：通过本文的深入探讨，我们对四面体间隙和八面体间隙有了更深入的了解，并且对铁素体和奥氏体的组织结构、特性和应用也有了更全面的认识。

四面体间隙和八面体间隙作为固体材料中晶格间隙的特殊排列结构，在材料学中具有重要的意义，通过对其结构的深入了解和控制，可以实现对金属组织结构的优化和改进。

个人观点和理解：在实际工程应用中，对四面体间隙和八面体间隙的深入研究将有助于材料设计和制备工艺的优化，从而实现对金属材料性能的有效控制和提升。

08金属的结构和性质[8.1】半径为尺的岡球堆枳成正四面体空晾，试作图it 算该四面休的边长和高.中心到顶 点即离、中心距离地而的高度、中心到两顶点连县的夹角以及中心到球面的最短即离。

解：4个等径岡球作紧密堆枳的情形示于图9.1 (a)和(b),图9.1(c)示出堆枳所形应的 正呱面体空隙。

垓正呱面体的顶点OP 球心位置，血长为岡球半径的2倍。

H9.1由图和正四面体的立(t 几何知识可知: 边长AB=2RAM =(AE 2-EM 2]^= AB 1-BE 1- -DE 高i=AB 2——ABV2OA = -AM = —/?«1.2257? 中心到顶点的脳离： 4 2 OM =丄 AM = — R^ 0.4087? 中心到(Kill 的高度：46中心到两硕点连线的夹角为：ZA °B= cos _, (-1/3) = 109.47°中心到球面的量短距离=04/0.225/?本题的it 算结果很亜要。

由lit 结果可知，半径为R 的等径同球最密堆枳结构中四面体空 除所能容纳的小球的最大半径为0.225R 。

而0.225正是典塑的二元离子晶体中正离子的配位 多而体为正四面体时正、负离子半径比的卞限。

此题的结果也是了解hep 结构中晶胞参数的 基KS （见习 g 9.04）o[8.2] 半径力尺的岡球堆枳成正八面体空B, it 算中心绢頂虑的更离。

-I AE (3& = cos°OA 2+OB 2-AB 22(OA)(O3)2(極/2「-(2町 2(偸/2『D解：正八面体空隙由6个等径||球密堆枳而成，其頂点即同球的球心，貝校长即圆球的Igo空隙的实际体枳小于八面图9.2中三图分别示出球的堆枳侑况及所形成的正由图（c）知，八面体空隙中心到顶点的距离为：OC = -AC = -y/2AB =丄VJx2R =血2 2 2而八面体空隙中心到球面的最短距离为:OC-R = d-R".4\4R此即半径为R的等径岡球最密堆枳形成的正八面体空除所能容纳的爪球的最大半径。

体心立方的八面体空隙和四面体空隙英文回答：The octahedral void and tetrahedral void are two typesof voids found in a body-centered cubic (bcc) crystallattice structure. These voids play an important role in determining the properties and behavior of the crystal.The octahedral void is a void that is surrounded by six atoms arranged in an octahedral shape. It is located at the center of each face of the unit cell in a bcc crystal lattice. This void is often occupied by larger atoms orions that can fit into the void without disrupting the crystal structure. An example of this is in the crystal structure of sodium chloride (NaCl), where the sodium ions occupy the octahedral voids between the chloride ions.On the other hand, the tetrahedral void is a void thatis surrounded by four atoms arranged in a tetrahedral shape. It is located at the center of the unit cell in a bcccrystal lattice. This void is often occupied by smaller atoms or ions that can fit into the void without disrupting the crystal structure. An example of this is in the crystal structure of diamond, where each carbon atom occupies a tetrahedral void between four neighboring carbon atoms.The octahedral void and tetrahedral void have different sizes and geometries, which affect the types of atoms or ions that can occupy them. The octahedral void is largerand can accommodate larger atoms or ions, while the tetrahedral void is smaller and can accommodate smaller atoms or ions. This difference in size and geometry leadsto different properties and behavior of the crystal.For example, in a bcc crystal lattice, if theoctahedral voids are occupied by larger atoms or ions, it can lead to the formation of an interstitial solid solution. This can result in changes in the mechanical, electrical, and thermal properties of the crystal. On the other hand,if the tetrahedral voids are occupied by smaller atoms or ions, it can lead to the formation of a substitutionalsolid solution. This can also result in changes in theproperties and behavior of the crystal.In summary, the octahedral void and tetrahedral void are two types of voids found in a bcc crystal lattice. They have different sizes and geometries, and can accommodate different types of atoms or ions. The occupation of these voids can result in changes in the properties and behavior of the crystal.中文回答：体心立方晶体结构中存在着八面体空隙和四面体空隙。

正四面体是什么
正四面体是由四个全等正三角形围成的空间封闭图形，所有棱长都相等。

它有4个面，6条棱，4个顶点。

正四面体是最简单的正多面体。

正四面体是五种正多面体中的一种，有4个正三角形的面，4个顶点，6条棱。

正四面体不同于其它四种正多面体，它没有对称中心。

正四面体有六个对称面，其中每一个都通过其一条棱和与这条棱相对的棱的中点。

正四面体很容易由正方体得到，只要从正方体一个顶点A引三个面的对角线AB，AC，AD，并两点两点连结之即可。

正四面体和一般四面体一样，根据保利克-施瓦兹定理能够用空间四边形及其对角线表示。

正四面体的对偶是其自身。

正四面体的性质
1、正四面体的每一个面是正三角形，反之亦然。

2、正四面体是三组对棱都垂直的等面四面体。

3、正四面体是两组对棱垂直的等面四面体。

4、正四面体的各棱的中点是正八面体的六顶点。

5、正四面体的四个旁切球半径均相等，等于内切球半径的2倍，或等于四面体高线的一半。

1。

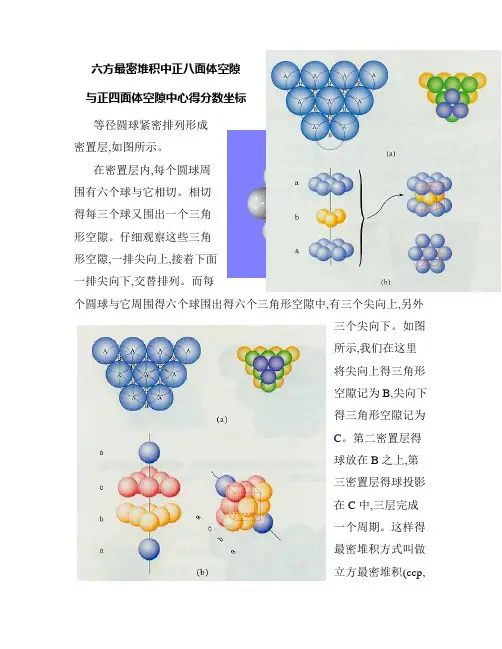
六方最密堆积中正八面体空隙与正四面体空隙中心得分数坐标等径圆球紧密排列形成密置层,如图所示。

在密置层内,每个圆球周围有六个球与它相切。

相切得每三个球又围出一个三角形空隙。

仔细观察这些三角形空隙,一排尖向上,接着下面一排尖向下,交替排列。

而每个圆球与它周围得六个球围出得六个三角形空隙中,有三个尖向上,另外三个尖向下。

如图所示,我们在这里将尖向上得三角形空隙记为B,尖向下得三角形空隙记为C。

第二密置层得球放在B之上,第三密置层得球投影在C中,三层完成一个周期。

这样得最密堆积方式叫做立方最密堆积(ccp,记为A1型),形成面心立方晶胞。

若第三密置层得球投影与第一密置层得球重合,两层完成一个周期。

这样得最密堆积方式叫做六方最密堆积(hcp,记为A3型),形成六方晶胞,如图所示。

在这两种堆积方式中,任何四个相切得球围成一个正四面体空隙;另外,相切得三个球如果与另一密置层相切得三个球空隙对应,它们六个球将围成一个正八面体空隙。

也就就是说,围成正八面体空隙得这六个球可以分为相邻得两层,每层得正三角形中心得连线垂直于正三角形所在得密置层,参瞧下图,黑色代表得不就是球而就是正八面体得中心。

在这两种最密堆积方式中,每个球与同一密置层得六个球相切,同时与上一层得三个球与下一层得三个球相切,即每个球与周围十二个球相切(配位数为12)。

中心这个球与周围得球围出八个正四面体空隙,平均分摊到每个正四面体空隙得就是八分之一个球。

这样,每个正四面体空隙分摊到得球数就是四个八分之一,即半个。

中心这个球周围还围出六个八面体空隙,它平均分摊到每个正八面体空隙得就是六分之一个球。

这样,每个正八面体空隙分摊到得球数就是六个六分之一,即一个。

总之,这两种最密堆积中,球数: 正八面体空隙数: 正四面体空隙数= 1:1:2 。

面心立方最密堆积(ccp, A1型)中正八面体空隙与正四面体空隙得问题比较简单、直观。

下面我们集中讨论六方最密堆积(hcp,A3型)中正八面体空隙与正四面体空隙中心得分数坐标。

高中化学晶胞的四面体空隙和八面体空隙的区别下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!而且本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!高中化学晶胞的四面体空隙和八面体空隙的区别。

八面体的体积计算公式
八面体是一种由八个等边三角形组成的多面体，具有八个面、12个边和6个顶点。

对于一个正八面体，其所在的立体角为4π/3，体积可通过以下公式进行计算：
V = (a^3 * √2) / 3
其中，a为八面体的边长。

这个公式的推导可以通过将八面体分解成六个正四面体来进行。

首先，画出八面体的立体图形，并连接其对边，将其分解成六个正四面体。

然后，计算一个正四面体的体积公式为：
V = (a^3) / 6√2
将六个正四面体的体积相加，得到八面体的体积公式为：
V = (a^3 * √2) / 3
通过这个公式，我们可以方便地计算出一个八面体的体积。

- 1 -。

08金属的结构和性质【8.1】半径为R 的圆球堆积成正四面体空隙，试作图计算该四面体的边长和高、中心到顶点距离、中心距离地面的高度、中心到两顶点连县的夹角以及中心到球面的最短距离。

解：4个等径圆球作紧密堆积的情形示于图9.1（a ）和(b)，图9.1(c)示出堆积所形成的正四面体空隙。

该正四面体的顶点即球心位置，边长为圆球半径的2倍。

图9.1由图和正四面体的立体几何知识可知： 边长AB=2R高()12122222213AM AE EMAB BE DE ⎡⎤⎛⎫=-=--⎢⎥⎪⎝⎭⎢⎥⎣⎦ ()11222222221132233AB AB AE R R R ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥=--=--⎢⎥ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎢⎥⎝⎭⎣⎦⎣⎦26 1.6333R R =≈中心到顶点的距离：36 1.22542OA AM R R==≈中心到底边的高度：160.4084OM AM R ==≈中心到两顶点连线的夹角为：AOB ∠()())()()2222211226/22cos cos 226/2R R OA OB AB OA OB R θ--⎡⎤-⎡⎤+-⎢⎥==⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦()1cos 1/3109.47-=-=︒中心到球面的最短距离0.225OA R R =-≈本题的计算结果很重要。

由此结果可知，半径为R 的等径圆球最密堆积结构中四面体空 隙所能容纳的小球的最大半径为0.225R 。

而0.225正是典型的二元离子晶体中正离子的配位多面体为正四面体时正、负离子半径比的下限。

此题的结果也是了解hcp 结构中晶胞参数的基础(见习题9.04)。

【8.2】半径为R 的圆球堆积成正八面体空隙，计算中心到顶点的距离。

解：正八面体空隙由6个等径圆球密堆积而成，其顶点即圆球的球心，其棱长即圆球的直径。

空隙的实际体积小于八面体体积。

图9.2中三图分别示出球的堆积情况及所形成的正八面体空隙。

图9.2由图（c ）知，八面体空隙中心到顶点的距离为：1112222222OC AC AB R R ===⨯=而八面体空隙中心到球面的最短距离为：20.414OC R R R R -=-≈此即半径为R 的等径圆球最密堆积形成的正八面体空隙所能容纳的小球的最大半径。