1.1.1集合的含义与表示

---------------------------------------------------------------最新资料推荐------------------------------------------------------1.1.1集合的含义与表示1. 1. 1 集合的含义与表示第 1 课时集合的含义与表示（一）教学目标 1．知识与技能（1）初步理解集合的含义，知道常用数集及其记法．（2）初步了解属于关系的意义．理解集合相等的含义. （3）初步了解有限集、无限集的意义，并能恰当地应用列举法或描述法表示集合. 2．过程与方法（1）通过实例，初步体会元素与集合的属于关系，从观察分析集合的元素入手，正确地理解集合．（2）观察关于集合的几组实例，并通过自己动手举出各种集合的例子，初步感受集合语言在描述客观现实和数学对象中的意义．（3）学会借助实例分析、探究数学问题（如集合中元素的确定性、互异性）．（4）通过实例体会有限集与无限集，理解列举法和描述法的含义，学会用恰当的形式表示给定集合掌握集合表示的方法. 3．情感、态度与价值观（1）了解集合的含义，体会元素与集合的属于关系．（2）在学习运用集合语言的过程中，增强学生认识事物的能力．初步培养学生实事求是、扎实严谨的科学态度．（二）教学重点、难点重点是集合的概念及集合的表示．难点是集合的特征性质和概念以及运用特征性质描述法正确地表示一些简单集合. （三）教学方法尝试指导与合作交流相结合．通过提出问题、观察实例，引导学生理解集合的概念，分析、讨论、探究集合中元素表达的基本要求，并能依照要求举出符合条件的例子，1 / 8加深对概用心爱心专心用心爱心专心用心爱心专心用心爱心专心例 1（1）利用列举法表法下列集合：①{15 的正约数} ；②不大于 10 的非负偶数集. （2）用描述法表示下列集合：①正偶数集；②{1， 3， 5， 7，， 39， 41} . 【分析】考查集合的两种表示方法的概念及其应用. 用心爱心专心【解析】（1）①{1， 3， 5，15} ②{0， 2， 4， 6， 8， 10} （2）①{x | x = 2n，nN*} ②{x | x = ( 1) n 1 (2n 1) ，n N*且 n21} . 【评析】（1）题需把集合中的元素一一列举出来，写在大括号内表示集合，多用于集合中的元素有有限个的情况. （2）题是将元素的公共属性描述出来，多用于集合中的元素有无限多个的无限集或元素个数较多的有限集. 例 2 用列举法把下列集合表示出来：（1） A = {xN | （2） B = {9N} ； 9 x9 N | xN } ；9 x （3） C = { y = y = x2 + 6， xN ， yN } ；（4）D = {(x， y) | y = x2 +6， xN } ；（5）E = {x | p= x，p + q = 5， pN ， qN*} . q 【分析】先看五个集合各自的特点：集合 A 的元素是自然数 x，它必须满足条件是自然数；集合 B 中的元素是自然数 9 也 9 x9，它必须满足条件 x 也是自然数；集合C 中的元 9 x 素是自然数 y，它实际上是二次函数 y= x2 + 6 (xN ) 的函数值；集合 D 中的元素是点，这些点必须---------------------------------------------------------------最新资料推荐------------------------------------------------------在二次函数 y = x2 + 6 (xN ) 的图象上；集合 E 中的元素是x，它必须满足的条件是 x =p，其中 p + q = 5，且 p N， qN*. q 【解析】（1）当 x = 0， 6， 8 这三个自然数时， 9=1， 3， 9 也是自然数. 9 x A = {0， 6， 9} （2）由（1）知， B = {1， 3， 9} . （3）由 y = x2 + 6， xN， yN 知 y6. x= 0， 1， 2 时， y = 6， 5， 2 符合题意. C = {2， 5， 6} . （4）点 {x， y} 满足条件 y = x2 + 6， xN， y N，则有：x 0, x 1, x 2, y 6, y 5, y 2.D = {(0， 6) (1， 5) (2， 2) } （5）依题意知 p + q = 5，p N， q N*，则p 0, p 1, p 2, p 3, p 4, q 5, q 4, q 3, q 2, q 1. Px 要满足条件 x =，q 132E = {0，，，， 4} . 423【评析】用描述法表示的集合，要特别注意这个集合中的元素是什么，它应该符合什么用心爱心专心条件，从而准确理解集合的意义. 例 3 已知 3A = {a 3， 2a 1， a2 + 1} ，求 a 的值及对应的集合 A. 3A，可知 3 是集合的一个元素，则可能 a 3 = 3，或 2a 1 = 3，求出a，再代入 A，求出集合 A. 【解析】由 3A，可知， a 3 = 3 或 2a 1 = 3，当 a 3 = 3，即 a = 0时， A = { 3，1， 1} 当 2a 1 = 3，即 a = 1 时， A = { 4， 3， 2} . 【评析】元素与集合的关系是确定的， 3 A，则必有一个式子的值为 3，以此展开讨论，便可求得 a. 用心爱心专心3 / 8HcQkYs) B5J dSm#u-D 7LfTn$w0E8N h Vp%y2GaOiXr* z3IcQkYt) B5J dSm#u-D7LfTo$w0E9NhVp%y2 GaOjXr *z4IcQ kYt) B5JeSm#u+D7LfTo$w0E9 NhVpy 2GaPjX r*z4IcQkZt) B5KeSm#u+D7Lf Uo$w0F9NhVp y2GaPjXr*A4IcQlZt) B5KeSm #v+D7L gUo$w0 F9NhVqy2GbPjXr*A4IcQlZt ) B6KeSm! v+D7 LgUo$w1F9NhWqy2GbPjXr(A 4IcRlZ t) B6Ke Sm!v+D7MgUo$x1F9NhWqy2H bPjXs( A4IcRl Zt) C6KeSn!v+D7MgUo$x1F9N iWqy3HbPjXs (A4IdRlZt-C6KeSn!v+D8MgU o%x1F9NiWqy 3HbPjYs(A4JdRlZt-C6KeTn! v+E8M gUo%x1F 9OiWqz3HbPjYs(A4JdRlZu- C6KfTn ! v+E8M gUp%x1FaOiWqz3HbPkYs(A5 JdRlZu-C6KfT n!v0E8 MgVp%x1FaOiWq*z3H bQkYs(A 5JdRl #u-C6LfTn!v0E8MgVp%x1GaO iWr*z3HbQkYs (B5JdRm#u-C6LfTn!w0E8MhV p%x1Ga OiWr*z 3HcQkYs) B5JdRm#u-C7LfTn$ w0E8Mh Vp%x2G aOiXr*z3HcQkYs) B5JdSm#u- D7LfTn$w0E8N hVp%y2GaOiXr * z3IcQkYt) B5 JdSm#u -D7LfT o$w0E9NhVp%y 2GaOjXr*z4Ic QkYt) B5JeSm# u+D7LfTo$w0E 9NhVpy2GaPj Xr*z4IcQkZt) B5KeSm#u+D7L f Uo$w0F9NhVp y2GaPjXr*A4 IcQlZt) B5KeSm#v+D7LgUo$w 0F9NhV qy2Gb PjXr*A4IcQlZt) B6KeSm!v+D 7LgUo$w1F9Nh Wqy2GbPjXr(A4IcRlZt) B6K eSm! v+ D7MgUo $x1F9NhWqy2HbPjXs(A4IcR lZt) C6KeSn!v +D7MgUo$x1F9NiWqy3HbPjX s(A4IdRlZt-C6KeSn!v+D8M g Uo%x1F9NiWq y3HbPjY s(A4 IdRlZt-C6KeT n !v+E8MgUo%x 1F9OiWq---------------------------------------------------------------最新资料推荐------------------------------------------------------z3Hb PjYs(A4JdRlZ u -C6KeTn! v+E 8MgUp%x 1FaOi Wqz3HbPkYs( A5JdRlZu-C6K fTn!v0E8MgUp %x1FaOiWq*z3 H bQkYs(A5JdR l#u-C6L fTn!v 0E8MgVp%x1Ga O iWq*z3HbQkY s(B5JdR m#u-C 6LfTn!w0E8Mh V p%x1GaOiWr* z3HcQkY s(B5J dRm#u-C7LfTn $w 0E8MhVp%x2 GaOiXr*z3HcQ kYs) B5JdSm#u - C7LfTn$w0E8 NhVp%y2GaOiX r*z3IcQkYt) B 5JdSm#u-D7Lf To$w0E8NhVp% y2GaOjXr*z4I cQkYt) B5JeSm #u+D7Lf To$w0 E9NhVpy2GaO jXr*z4IcQkZt ) B5KeSm #u+D7 LfUo$w0F9NhV py2GaPjXr*A 4IcQkZt)B5Ke Sm#vRdJ5A(sY k PbH3z qWiOaF1x%pUgM 8E+ v! nTeK6C-uZl Rd J4A(sYjPbH 3zqWiO9F 1x% oUgM8E+v!nTe K6C-tZlRdI4A (sYjPbH3y qW iN9F1x%oUgM8 D+v !nSeK6C-tZlRdI4A(sXjPbH2y qWiN9F1x$oUgM7D+v! nSeK6 C) tZlRcI4A(s XjPbH2yqWhN9F1w$oUgM7D+ v!mSeK6B) tZl RcI4A(rXjPbG 2yqWhN9F1w$ oUgL7D+v#mSe K6B) tZlQcI4 A *rXjPbG2yqV hN9F0w$oUgL7 D+v#mSeK5B)t ZkQcI4A*rXjP aG2y pVhN9F0 w$oUfL7D+u#m SeK5B) tZkQcI 4z*rX jOaG2y pVhN9E0w$oTfL7D+u#mSeJ5B ) tYkQ cI4z*rX jOaG2y%pVhN8E0w$oTfL7D-u #mSdJ 5B) tYkQ cI3z*rXiOaG2y%pVhN8E0w$n TfL7C -u#mSdJ 5B) sYkQcH3z*rXiOaG2x%pVh M8E0w$nTfL7C -u#mRdJ5B(sY kQcH3z*rWiOa G1x%p VhM8E0w !nTfL6C-u#m R dJ5B(sYkQbH3 z*qWiOaG1x%p5 / 8VgM8E0v!nTf L 6C-u#lRdJ5A( sYkQbH3z*qWi OaF1x% pUgM8E0v! nTfK6C-u ZlRdJ5A (sYkP bH3zqWiOaF1x%pUgM8E+v!n TeK6C- uZlRdJ 4A(sYjPbH3zqWiO9F1x%oUg M8E+v!nTeK6C -tZlRdI4A(sYjPbH3yqWiN9 F1x%oU gM8D+v !nSeK6C-tZlRdI4A(sXjPbH2 yqWiN9F1x$o UgM7D+v! nSeK6C) tZlRcI4A( sXjPbH 2yqWh N9F1w$oUgM7D+v!mSeK6B) tZ lRcI4A (rXjPb G2yqWhN9F1w$oUgL7D+v#mS eK6B) tZlQcI4 A*rXjPbG2yq V hN9F0w$oUgL 7D+v#mSeK5B) tZkQcHbPjXs( A 4IdRlZt) C6K eSn!v+D 8MgUo $x1F9NiWqy3 H bPjXs(A4IdR lZt-C6KeTn!v +D8MgUo%x1F9OiWqy3HbPjY s(A4Jd RlZtSe K6B) tZlQcI4A(rXjPbG2yqV hN9F1w $oUgL7 D+v#mSeK5B) tZlQcI4A*rXjP aG2yqVhN9F0w$oUfL7D+v# m SeK5B) tZkQc I4z*rXjPaG2y lZt) C6KeSn!v + D8MgUo%x1F9 NiWqy3HbPjY s(A4IdRlZt-C 6KeTn! v+D8Mg Uo%x1F9OiWq z3HbPjYs(A4J dRlZu-C6KeTn !v+E8MgU p%x1 F9OiWqz3HbP k Ys(A5JdRlZu -C6KfTn!v0E8 MgUp%x1FaOiW q* z3HbPkYs(A 5JdRl#u -C6Lf Tn!v0E8MgVp% x1GaOiWq*z3H bQkYs(B5JdRl #u-C6LfTn! w0 E 8MhVp%x1GaO iWr*z3HcQkYs (B5JdRm#u-C7 L f) tYkQcI3z* rXiOaG2y%pVh N8E0w$nTfL7D - u#mSdJ5B) sY kQcH3z* rXiOa G2x%pVhM8E0w $nTfL7C-u#mR dJ5B) sY kQcH3 z*rWiOaG1x%p V hM8E0w!nTfL 6C-u#mRd J5B( sYkQbH3z*rWi OaG1x%pVgM8E 0v! nTfL6C-u# lRdJ5A(sYkQb H 3z*qW iOaF1x%pVgM8E0v! n TfK6C-uZlRdG aOiXr*z3IcQk Ys) B5JdSm #u- D7LfTn$w0E8N hVp%y2GaOiXr *z3IcQkYt) B5 JeSm#u-D7LfTo$w0E---------------------------------------------------------------最新资料推荐------------------------------------------------------9NhVp%y 2GaOjXr*z4IcQkYt) B5JeSm# u+D7LfUo$w0E 9NhVpy2GaPjXr*z4IcQkZt) B5KeSm#u+D7L fUo$w0F9NhV q y2GaPjXr*A4 IcQlZ t) B5KeS m#v+D7r*z4Ic QkZt) B5KeSm# u+D7L fUo$w0F 9NhVqy2GaP j Xr*A4IcQlZt) B5KeSm#v+D7L gUo$w0F9NhVq y2GbPjXr(A4 IcQlZ t) B6KeS m!v+D7LgUo$w 1F9NhWqy2Gb PjXr( A4IcRlZ t) C6KeSm! v+ D 7MgUo$x1F9Nh Wqy2HbPjXs( A4IcRlZt) C6KeStZlRdI4A(s XjPbH 2yqWiN 9F1x$oUgM7D+v!mSeK6C) tZl RcI4A (rXjPbH 2yqWhN9F1w$oUgM7D+v! mSe K6B) tZlQcI4A (rXjPbG2yqVhN9F1w$oUgL7 D+v#m SeK6B) t ZlQcI4A*rXjPaG2yqVhN9F0 w$oUf L7D+v#m SeK5B) tZkQcI4PjXs(A4IdR lZt) C6KeSn!v +D8MgUo%x1F9NiWqy3HbPjY s(A4Id RlZt-C 6KeTn!v+D8MgUo%x1F9OiWq z3HbPjY s(A4J dRlZu-C6KeTn! v+E8MgUp%x1 F9OiWqz3HbP kYs(A4JdRlZu-C6KfTn! v0E8 MgUp%x1FaOiW q*z3Hb0w$oUfL7D+u#mSeK5B ) tZkQcI4z*rX jPaG2ypVhN9E0w$oTfL7D+u #mSeJ5B) tYkQ cI4z*rXjOaG2y%pVhN9E0w$o TfL7D- u#mSdJ 5B) tYkQcI3z*rXiOaG2y%pVh N8E0w$nTfL7D -u#mSdJ5B) sYkQcH3z*rXiOa G2RlZu -C6KfT n!v0E8MgVp%x 1FaOiWq*z3Hb QkYs(A5JdRl# u-C6LfTn!v0E8MgVp%x1GaOi Wr*z3H bQkYs( B5JdRm#u-C6LfTn!w0E8MhVp %x1GaO iWr*z3 HcQkYs) B5JdRm#u-C7LfTn$w 0E8MhVp%x2GaOiXpVhN8E0w $nTfL7C-u#mS dJ5B)7 / 8sY kQcH3 z*rXiOaG2x%p V hM8E0w!nTfL 7C-u#mRd J5B( sYkQcH3z*rWi O aG1x%pVhM8E 0w!nTfL 6C-u# lRdJ5B(sYkQb H3z*qWiOaG1x %pVgM8E0v!nT fL6C-u#lRdJ5 OiWr*z3HcQkY s) B5JdSm #u-C 7LfTn$w0E8Nh V p%x2GaOiXr* z3IcQkY s) B5J dSm#u-D7LfTo $w0E8NhVp%y2 GaOjXr*z3IcQ kYt) B5JeSm#u - D7LfTo$w0E9 NhVpy2GaOjX r*z4IcQkZt) B 5JeSm#u+D7Lf Uo$w0E9NhVp y2G#u-D7LfTo $w 0E9NhVpy2 GaOjXr*z4IcQ kZt) B5JeSm#u + D7LfUo$w0E9 NhVpy2G aPjX r*A4IcQkZt) B 5KeSm#v+D7Lf Uo$w0F9N hVq y2GaPjXr*A4I cQlZt) B6KeSm #v+D7LgU o$w1 F9NhVqWiO9F1 x %oUgM 8E+v!nTeK6C-tZlRd J4A(sYjPbH3y q WiO9F1x%oU gM8D+v!n SeK6 C-tZlRdI4A(sXjPbH3y qWiN9F1x$oUgM8D+v! nSeK6 C) tZlRcI4A(s XjPbH2yqWhN9F1x$oUgM7D+ v!mSeK 6C) tZl RcI4A(rXjA4IcQlZt) B6KeSm !v+D7L gUo$w1 F9NhWqy2GbPjXr(A4IcRlZt ) B6KeSm!v+D7 MgUo$x1F9NhWqy2HbPjXs(A 4IcRlZ t) C6Ke Sn!v+D7MgUo$ x1F9NiWqy3H bPjXs(A47D+v !nSeK6C) tZlR cI4A(rXjPbH2 yqWh N9F1w$o UgM7D+v!mSeK 6B) tZlRcI4A( rXjPbG2yqVh N9F1w$oUgL7D +。

§1.1.1 集合的含义及其表示一、教学目标（1）通过实例，了解集合的含义，体会元素与集合的理解集合“属于”关系；初步了解属于关系和集合相等的意义（2）能选择自然语言、图形语言、集合语言（列举法或描述法）描述不同的具体问题，感受集合语言的意义和作用；（3）熟记有关数集,培养学生认识事物的能力二、教学重点集合的基本概念与表示方法；三、教学难点运用集合的两种常用表示方法——列举法与描述法，正确表示一些简单的集合；四、教学过程1、创设情境，引入新课在小学和初中我们已经接触了一些集合，例如自然数的集合，有理数的集合，不等式x-7<3的解的集合，到一个定点的距离的定长的集合（即圆），到一条线段的两个端点距离相等的点的集合（即这条线段的垂直平分线）……那么集合的含义是什么呢？我们再来看看下面的一些例子：（1）1~20以内的所有质数（2）2010年4月1日之前与我国建立外交关系的所有国家（2）所有的正方形（3）高一<2>班的学生在上数学课（4）方程x2+3x-2=0的所有实数解上面这些例子有什么共同的特征？2、推进新课（1）元素与集合的概念：一般地，我们把研究对象统称为元素，把一些元素组成的总体叫做集合（简称为集）。

（2）集合的性质○1确定性：按照明确的判断标准给定一个元素或者在这个集合里，或者不在，不能模棱两可。

○2互异性：集合中的元素必须是互不相同的（即没有重复现象），相同的元素在集合中只能算作一个。

○3无序性：集合中的元素间是无次序关系的。

（3）集合相等：只要构成两个集合的元素是一样的，我们就称这两个集合是相等的。

练习：1.判断以下元素的全体是否组成集合（1）大于3小于11的偶数。

（2）我国的小河流。

2.说出集合A=｛a,b,c｝和集合B=｛b, a,c｝的关系。

（4）集合与元素的表示：集合通常用大括号或大写的拉丁字母表示,如{1，2，3，4，5}与{高一（2）班的所有学生}，又如A、B、C、P、Q……元素通常用小写的拉丁字母表示，如a、b、c、p、q……如果a是集合A的元素，就说a属于A，记作a∈A。

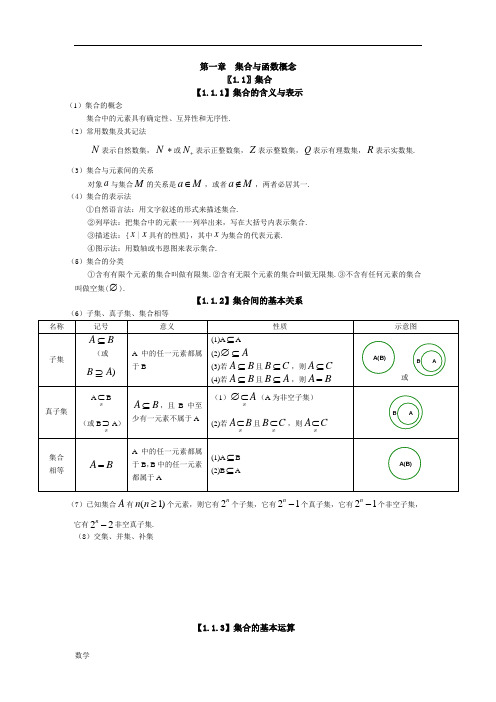
第一章 集合与函数概念〖1.1〗集合【1.1.1】集合的含义与表示（1）集合的概念集合中的元素具有确定性、互异性和无序性. （2）常用数集及其记法N 表示自然数集，N *或N +表示正整数集，Z 表示整数集，Q 表示有理数集，R 表示实数集.（3）集合与元素间的关系对象a 与集合M 的关系是a M ∈，或者a M ∉，两者必居其一. （4）集合的表示法①自然语言法：用文字叙述的形式来描述集合.②列举法：把集合中的元素一一列举出来，写在大括号内表示集合. ③描述法：{x |x 具有的性质}，其中x 为集合的代表元素. ④图示法：用数轴或韦恩图来表示集合. （5）集合的分类①含有有限个元素的集合叫做有限集.②含有无限个元素的集合叫做无限集.③不含有任何元素的集合叫做空集(∅).【1.1.2】集合间的基本关系（6）子集、真子集、集合相等（7）已知集合A 有(1)n n ≥个元素，则它有2n 个子集，它有21n -个真子集，它有21n -个非空子集，它有22n-非空真子集.（8）交集、并集、补集【1.1.3】集合的基本运算名称记号意义性质示意图交集A B{|,x x A∈且}x B∈（1）A A A=（2）A∅=∅（3）A B A⊆A B B⊆BA并集A B{|,x x A∈或}x B∈（1）A A A=（2）A A∅=（3）A B A⊇A B B⊇BA补集U A{|,}x x U x A∈∉且1()UA A=∅2()UA A U=【补充知识】含绝对值的不等式与一元二次不等式的解法（1）含绝对值的不等式的解法不等式解集||(0)x a a<>{|}x a x a-<<||(0)x a a>>|x x a<-或}x a>||,||(0)ax b c ax b c c+<+>>把ax b+看成一个整体，化成||x a<，||(0)x a a>>型不等式来求解（2）一元二次不等式的解法判别式24b ac∆=-∆>0∆=0∆<二次函数2(0)y ax bx c a=++>的图象O 一元二次方程20(0)ax bx c a++=>的根21,242b b acxa-±-=（其中12)x x<122bx xa==-无实根20(0)ax bx c a++>>的解集1{|x x x<或2}x x>{|x}2bxa≠-R()()()U U UA B A B=()()()U U UA B A B=〖1.2〗函数及其表示 【1.2.1】函数的概念（1）函数的概念①设A 、B 是两个非空的数集，如果按照某种对应法则f，对于集合A 中任何一个数x ，在集合B中都有唯一确定的数()f x 和它对应，那么这样的对应（包括集合A ，B 以及A 到B 的对应法则f ）叫做集合A 到B 的一个函数，记作:f A B →．②函数的三要素:定义域、值域和对应法则．③只有定义域相同，且对应法则也相同的两个函数才是同一函数． （2）区间的概念及表示法①设,a b 是两个实数，且a b <，满足a x b ≤≤的实数x 的集合叫做闭区间，记做[,]a b ；满足a xb <<的实数x 的集合叫做开区间，记做(,)a b ；满足a x b ≤<，或a x b <≤的实数x 的集合叫做半开半闭区间，分别记做[,)a b ，(,]a b ；满足,,,x a x a x b x b ≥>≤<的实数x 的集合分别记做[,),(,),(,],(,)a a b b +∞+∞-∞-∞． 注意：对于集合{|}x a x b <<与区间(,)a b ，前者a 可以大于或等于b ，而后者必须a b <．（3）求函数的定义域时，一般遵循以下原则：①()f x 是整式时，定义域是全体实数．②()f x 是分式函数时，定义域是使分母不为零的一切实数．③()f x 是偶次根式时，定义域是使被开方式为非负值时的实数的集合．④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1． ⑤tan y x =中，()2x k k Z ππ≠+∈．⑥零（负）指数幂的底数不能为零． ⑦若()f x 是由有限个基本初等函数的四则运算而合成的函数时，则其定义域一般是各基本初等函数的定义域的交集．⑧对于求复合函数定义域问题，一般步骤是：若已知()f x 的定义域为[,]a b ，其复合函数[()]f g x 的定义域应由不等式()a g x b ≤≤解出．⑨对于含字母参数的函数，求其定义域，根据问题具体情况需对字母参数进行分类讨论． ⑩由实际问题确定的函数，其定义域除使函数有意义外，还要符合问题的实际意义． （4）求函数的值域或最值求函数最值的常用方法和求函数值域的方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的，只是提问的角度不同．求函数值域与最值的常用方法：①观察法：对于比较简单的函数，我们可以通过观察直接得到值域或最值．②配方法：将函数解析式化成含有自变量的平方式与常数的和，然后根据变量的取值范围确定函数的值域或最值． ③判别式法：若函数()y f x =可以化成一个系数含有y 的关于x 的二次方程2()()()0a y x b y x c y ++=，则在()0a y ≠时，由于,x y 为实数，故必须有2()4()()0b y a y c y ∆=-⋅≥，从而确定函数的值域或最值．④不等式法：利用基本不等式确定函数的值域或最值．⑤换元法：通过变量代换达到化繁为简、化难为易的目的，三角代换可将代数函数的最值问题转化为三角函数的最值问题．⑥反函数法：利用函数和它的反函数的定义域与值域的互逆关系确定函数的值域或最值． ⑦数形结合法：利用函数图象或几何方法确定函数的值域或最值． ⑧函数的单调性法．【1.2.2】函数的表示法（5）函数的表示方法表示函数的方法，常用的有解析法、列表法、图象法三种．解析法：就是用数学表达式表示两个变量之间的对应关系．列表法：就是列出表格来表示两个变量之间的对应关系．图象法：就是用图象表示两个变量之间的对应关系． （6）映射的概念①设A 、B 是两个集合，如果按照某种对应法则f，对于集合A 中任何一个元素，在集合B 中都有唯一的元素和它对应，那么这样的对应（包括集合A ，B 以及A 到B 的对应法则f ）叫做集合A 到B 的映射，记作:f A B →．②给定一个集合A 到集合B 的映射，且,a A b B ∈∈．如果元素a 和元素b 对应，那么我们把元素b 叫做元素a 的象，元素a 叫做元素b 的原象．yxo〖1.3〗函数的基本性质 【1.3.1】单调性与最大（小）值（1）函数的单调性①定义及判定方法 函数的 性 质定义图象判定方法 函数的 单调性如果对于属于定义域I 内某个区间上的任意两个自变量的值x 1、x 2,当x ．1．< x ．．2．时，都有f(x ．．．1．)<f(x ．．．．．2．)．，那么就说f(x)在这个区间上是增函数．．．． x 1x 2y=f(X)xy f(x )1f(x )2o（1）利用定义（2）利用已知函数的单调性（3）利用函数图象（在某个区间图象上升为增） （4）利用复合函数 如果对于属于定义域I 内某个区间上的任意两个自变量的值x 1、x 2，当x ．1．< x ．．2．时，都有f(x ．．．1．)>f(x ．．．．．2．)．，那么就说f(x)在这个区间上是减函数．．．． y=f(X)yxox x 2f(x )f(x )211（1）利用定义（2）利用已知函数的单调性（3）利用函数图象（在某个区间图象下降为减） （4）利用复合函数②在公共定义域内，两个增函数的和是增函数，两个减函数的和是减函数，增函数减去一个减函数为增函数，减函数减去一个增函数为减函数． ③对于复合函数[()]y f g x =，令()u g x =，若()y f u =为增，()u g x =为增，则[()]y f g x =为增；若()y f u =为减，()u g x =为减，则[()]y f g x =为增；若()y f u =为增，()ug x =为减，则[()]y f g x =为减；若()y f u =为减，()u g x =为增，则[()]y f g x =为减．（2）打“√”函数()(0)af x x a x=+>的图象与性质()f x 分别在(,]a -∞-、,)a +∞上为增函数，分别在[,0)a 、]a 上为减函数．（3）最大（小）值定义 ①一般地，设函数()y f x =的定义域为I，如果存在实数M 满足：（1）对于任意的x I ∈，都有()f x M≤；（2）存在0x I ∈，使得0()f x M=．那么，我们称M 是函数()f x 的最大值，记作max ()f x M=．②一般地，设函数()y f x =的定义域为I ，如果存在实数m 满足：（1）对于任意的x I ∈，都有()f x m ≥；（2）存在0x I ∈，使得0()f x m =．那么，我们称m 是函数()f x 的最小值，记作max ()f x m =．【1.3.2】奇偶性（4）函数的奇偶性①定义及判定方法 函数的 性 质定义图象判定方法 函数的 奇偶性如果对于函数f(x)定义域内任意一个x ，都有f(．．－．x)=．．．－．f(x)．．．．,那么函数f(x)叫做奇函．．数．．（1）利用定义（要先判断定义域是否关于原点对称）（2）利用图象（图象关于原点对称）如果对于函数f(x)定义域内任意一个x ，都有f(．．－．x)=．．．f(x)．．．．,那么函数f(x)叫做偶函数．．．．（1）利用定义（要先判断定义域是否关于原点对称）（2）利用图象（图象关于y 轴对称） ②若函数()f x 为奇函数，且在0x =处有定义，则(0)0f =．③奇函数在y 轴两侧相对称的区间增减性相同，偶函数在y 轴两侧相对称的区间增减性相反．④在公共定义域内，两个偶函数（或奇函数）的和（或差）仍是偶函数（或奇函数），两个偶函数（或奇函数）的积（或商）是偶函数，一个偶函数与一个奇函数的积（或商）是奇函数．〖补充知识〗函数的图象（1）作图利用描点法作图：①确定函数的定义域； ②化解函数解析式； ③讨论函数的性质（奇偶性、单调性）； ④画出函数的图象． 利用基本函数图象的变换作图：要准确记忆一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、三角函数等各种基本初等函数的图象． ①平移变换0,0,|()()h h h h y f x y f x h ><=−−−−−−−→=+左移个单位右移|个单位0,0,|()()k k k k y f x y f x k ><=−−−−−−−→=+上移个单位下移|个单位②伸缩变换01,1,()()y f x y f x ωωω<<>=−−−−→=伸缩01,1,()()A A y f x y Af x <<>=−−−−→=缩伸③对称变换()()x y f x y f x =−−−→=-轴()()y y f x y f x =−−−→=-轴 ()()y f x y f x =−−−→=--原点1()()y x y f x y f x -==−−−−→=直线 ()(||)y y y y f x y f x =−−−−−−−−−−−−−−−→=去掉轴左边图象保留轴右边图象，并作其关于轴对称图象()|()|x x y f x y f x =−−−−−−−−−→=保留轴上方图象将轴下方图象翻折上去（2）识图对于给定函数的图象，要能从图象的左右、上下分别范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性，注意图象与函数解析式中参数的关系． （3）用图函数图象形象地显示了函数的性质，为研究数量关系问题提供了“形”的直观性，它是探求解题途径，获得问题结果的重要工具．要重视数形结合解题的思想方法．。