2020高考数学一轮复习第7章不等式第1讲一元二次不等式的解法分层演练文

§7.3一元二次不等式及其解法1.一元二次不等式的解集2.常用结论(x －a )(x －b )>0或(x －a )(x －b )<0型不等式的解法口诀：大于取两边，小于取中间． 概念方法微思考1．一元二次不等式ax 2＋bx ＋c >0(a >0)的解集与其对应的函数y ＝ax 2＋bx ＋c 的图象有什么关系？提示 ax 2＋bx ＋c >0(a >0)的解集就是其对应函数y ＝ax 2＋bx ＋c 的图象在x 轴上方的部分所对应的x 的取值范围．2．一元二次不等式ax 2＋bx ＋c >0(<0)恒成立的条件是什么？提示 显然a ≠0.ax 2＋bx ＋c >0恒成立的条件是⎩⎪⎨⎪⎧ a >0，Δ<0；ax 2＋bx ＋c <0恒成立的条件是⎩⎪⎨⎪⎧a <0，Δ<0.题组一 思考辨析1．判断下列结论是否正确(请在括号中打“√”或“×”) (1)若不等式ax 2＋bx ＋c <0的解集为(x 1，x 2)，则必有a >0.( √ )(2)若不等式ax 2＋bx ＋c >0的解集是(－∞，x 1)∪(x 2，＋∞)，则方程ax 2＋bx ＋c ＝0的两个根是x 1和x 2.( √ )(3)若方程ax 2＋bx ＋c ＝0(a ≠0)没有实数根，则不等式ax 2＋bx ＋c >0的解集为R .( × ) (4)不等式ax 2＋bx ＋c ≤0在R 上恒成立的条件是a <0且Δ＝b 2－4ac ≤0.( × )(5)若二次函数y ＝ax 2＋bx ＋c 的图象开口向下，则不等式ax 2＋bx ＋c <0的解集一定不是空集．( √ )题组二 教材改编2．已知集合A ＝{x |x 2－x －6>0}，则∁R A 等于( ) A ．{x |－2<x <3} B ．{x |－2≤x ≤3} C ．{x |x <－2}∪{x |x >3} D ．{x |x ≤－2}∪{x |x ≥3} 答案 B解析 ∵x 2－x －6>0，∴(x ＋2)(x －3)>0，∴x >3或x <－2，即A ＝{x |x >3或x <－2}．在数轴上表示出集合A ，如图所示．由图可得∁R A ＝{x |－2≤x ≤3}． 故选B.3．y ＝log 2(3x 2－2x －2)的定义域是________________． 答案 ⎝ ⎛⎭⎪⎫－∞，1－73∪⎝ ⎛⎭⎪⎫1＋73，＋∞ 解析 由题意，得3x 2－2x －2>0，令3x 2－2x －2＝0，得x 1＝1－73，x 2＝1＋73，∴3x 2－2x －2>0的解集为⎝ ⎛⎭⎪⎫－∞，1－73∪⎝ ⎛⎭⎪⎫1＋73，＋∞.题组三 易错自纠4．不等式－x 2－3x ＋4>0的解集为________．(用区间表示) 答案 (－4，1)解析 由－x 2－3x ＋4>0可知，(x ＋4)(x －1)<0， 得－4<x <1.5．若关于x 的不等式ax 2＋bx ＋2>0的解集是⎝⎛⎭⎫－12，13，则a ＋b ＝________.答案 －14解析 ∵x 1＝－12，x 2＝13是方程ax 2＋bx ＋2＝0的两个根，∴⎩⎨⎧a 4－b2＋2＝0，a 9＋b3＋2＝0，解得⎩⎪⎨⎪⎧a ＝－12，b ＝－2，∴a ＋b ＝－14.6．不等式(a －2)x 2＋2(a －2)x －4<0，对一切x ∈R 恒成立，则实数a 的取值范围是( ) A ．(－∞，2] B ．(－2，2] C ．(－2，2) D ．(－∞，2) 答案 B解析 ∵⎩⎪⎨⎪⎧a －2<0，Δ<0，∴－2<a <2，另a ＝2时，原式化为－4<0，不等式恒成立， ∴－2<a ≤2.故选B.题型一 一元二次不等式的求解命题点1 不含参的不等式例1 (2019·呼和浩特模拟)已知集合A ＝{x |x 2－x －2<0}，B ＝{y |y ＝2x }，则A ∩B 等于( ) A ．(－1，2) B ．(－2，1) C ．(0，1) D ．(0，2)答案 D解析 由题意得A ＝{x |x 2－x －2<0}＝{x |－1<x <2}，B ＝{y |y ＝2x }＝{y |y >0}， ∴ A ∩B ＝{x |0<x <2}＝(0，2)．故选D. 命题点2 含参不等式例2 解关于x 的不等式ax 2－(a ＋1)x ＋1<0(a >0)． 解 原不等式变为(ax －1)(x －1)<0，因为a >0，所以⎝⎛⎭⎫x －1a (x －1)<0. 所以当a >1时，解为1a <x <1；当a ＝1时，解集为∅； 当0<a <1时，解为1<x <1a.综上，当0<a <1时，不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪1<x <1a ； 当a ＝1时，不等式的解集为∅；当a >1时，不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪1a<x <1. 思维升华 对含参的不等式，应对参数进行分类讨论 (1)根据二次项系数为正、负及零进行分类． (2)根据判别式Δ判断根的个数．(3)有两个根时，有时还需根据两根的大小进行讨论． 跟踪训练1 解不等式12x 2－ax >a 2(a ∈R )． 解 原不等式可化为12x 2－ax －a 2>0， 即(4x ＋a )(3x －a )>0，令(4x ＋a )(3x －a )＝0， 解得x 1＝－a 4，x 2＝a3.当a >0时，不等式的解集为⎝⎛⎭⎫－∞，－a 4∪⎝⎛⎭⎫a3，＋∞； 当a ＝0时，不等式的解集为(－∞，0)∪(0，＋∞)； 当a <0时，不等式的解集为⎝⎛⎭⎫－∞，a 3∪⎝⎛⎭⎫－a4，＋∞.题型二 一元二次不等式恒成立问题命题点1 在R 上的恒成立问题例3 已知函数f (x )＝mx 2－mx －1.若对于x ∈R ，f (x )<0恒成立，求实数m 的取值范围． 解 当m ＝0时，f (x )＝－1<0恒成立．当m ≠0时，则⎩⎪⎨⎪⎧m <0，Δ＝m 2＋4m <0，即－4<m <0.综上，－4<m ≤0，故m 的取值范围是(－4，0]． 命题点2 在给定区间上的恒成立问题例4 已知函数f (x )＝mx 2－mx －1.若对于x ∈[1，3]，f (x )<5－m 恒成立，求实数m 的取值范围． 解 要使f (x )<－m ＋5在x ∈[1，3]上恒成立， 即m ⎝⎛⎭⎫x －122＋34m －6<0在x ∈[1，3]上恒成立． 有以下两种方法：方法一 令g (x )＝m ⎝⎛⎭⎫x －122＋34m －6，x ∈[1，3]． 当m >0时，g (x )在[1，3]上是增函数， 所以g (x )max ＝g (3)，即7m －6<0， 所以m <67，所以0<m <67；当m ＝0时，－6<0恒成立；当m <0时，g (x )在[1，3]上是减函数， 所以g (x )max ＝g (1)，即m －6<0， 所以m <6，所以m <0.综上所述，m 的取值范围是⎩⎨⎧⎭⎬⎫m ⎪⎪m <67. 方法二 因为x 2－x ＋1＝⎝⎛⎭⎫x －122＋34>0， 又因为m (x 2－x ＋1)－6<0，所以m <6x 2－x ＋1.因为函数y ＝6x 2－x ＋1＝6⎝⎛⎭⎫x －122＋34在[1，3]上的最小值为67，所以只需m <67即可．所以m 的取值范围是⎩⎨⎧⎭⎬⎫m ⎪⎪m <67. 引申探究1．若将“f (x )<5－m 恒成立”改为“f (x )<5－m 无解”，如何求m 的取值范围？ 解 若f (x )<5－m 无解，即f (x )≥5－m 恒成立， 即m ≥6x 2－x ＋1恒成立，又x ∈[1，3]，得m ≥6，即m 的取值范围为[6，＋∞)．2．若将“f (x )<5－m 恒成立”改为“存在x ，使f (x )<5－m 成立”，如何求m 的取值范围？ 解 由题意知f (x )<5－m 有解，即m <6x 2－x ＋1有解，则m <⎝ ⎛⎭⎪⎫6x 2－x ＋1max ， 又x ∈[1，3]，得m <6，即m 的取值范围为(－∞，6)． 命题点3 给定参数范围的恒成立问题例5 若mx 2－mx －1<0对于m ∈[1，2]恒成立，求实数x 的取值范围．解 设g (m )＝mx 2－mx －1＝(x 2－x )m －1，其图象是直线，当m ∈[1，2]时，图象为一条线段，则⎩⎪⎨⎪⎧ g (1)<0，g (2)<0，即⎩⎪⎨⎪⎧x 2－x －1<0，2x 2－2x －1<0，解得1－32<x <1＋32，故x 的取值范围为⎝⎛⎭⎪⎫1－32，1＋32.思维升华 解决恒成立问题一定要搞清谁是主元，谁是参数，一般地，知道谁的范围，谁就是主元，求谁的范围，谁就是参数． 跟踪训练2 函数f (x )＝x 2＋ax ＋3.(1)当x ∈R 时，f (x )≥a 恒成立，求实数a 的取值范围； (2)当x ∈[－2，2]时，f (x )≥a 恒成立，求实数a 的取值范围； (3)当a ∈[4，6]时，f (x )≥0恒成立，求实数x 的取值范围． 解 (1)∵当x ∈R 时，x 2＋ax ＋3－a ≥0恒成立，需Δ＝a 2－4(3－a )≤0，即a 2＋4a －12≤0， ∴实数a 的取值范围是[－6，2]．(2)当x ∈[－2，2]时，设g (x )＝x 2＋ax ＋3－a ≥0，分如下三种情况讨论(如图所示)： ①如图①，当g (x )的图象与x 轴不超过1个交点时， 有Δ＝a 2－4(3－a )≤0，即－6≤a ≤2. ②如图②，g (x )的图象与x 轴有2个交点， 但当x ∈[－2，＋∞)时，g (x )≥0，即⎩⎪⎨⎪⎧ Δ>0，x ＝－a2<－2，g (－2)≥0，即⎩⎪⎨⎪⎧a 2－4(3－a )>0，－a2<－2，4－2a ＋3－a ≥0，可得⎩⎪⎨⎪⎧a >2或a <－6，a >4，a ≤73，解得a ∈∅.③如图③，g (x )的图象与x 轴有2个交点， 但当x ∈(－∞，2]时，g (x )≥0.即⎩⎪⎨⎪⎧Δ>0，x ＝－a2>2，g (2)≥0，即⎩⎪⎨⎪⎧a 2－4(3－a )>0，－a2>2，7＋a ≥0，可得⎩⎪⎨⎪⎧a >2或a <－6，a <－4，a ≥－7.∴－7≤a <－6，综上，实数a 的取值范围是[－7，2]．(3)令h (a )＝xa ＋x 2＋3.当a ∈[4，6]时，h (a )≥0恒成立．只需⎩⎪⎨⎪⎧ h (4)≥0，h (6)≥0，即⎩⎪⎨⎪⎧x 2＋4x ＋3≥0，x 2＋6x ＋3≥0，解得x ≤－3－6或x ≥－3＋ 6. ∴实数x 的取值范围是(－∞，－3－6]∪[－3＋6，＋∞)．一、选择题1．已知集合A ＝{x |x ≥0}，B ＝{x |(x ＋1)(x －5)<0}，则A ∩B 等于( ) A ．[－1，4) B ．[0，5)C ．[1，4]D ．[－4，－1)∪ [4，5)答案 B解析 由题意得B ＝{x |－1<x <5}，故A ∩B ＝{x |x ≥0}∩{x |－1<x <5}＝[0，5)．故选B.2．(2018·沈阳二十中联考)若不等式ax 2＋bx ＋2>0的解集为{x |－1<x <2}，则不等式2x 2＋bx ＋a >0的解集为( )A.⎩⎨⎧⎭⎬⎫x ⎪⎪x <－1或x >12 B.⎩⎨⎧⎭⎬⎫x ⎪⎪－1<x <12 C ．{x |－2<x <1} D ．{x |x <－2或x >1}答案 A解析 ∵不等式ax 2＋bx ＋2>0的解集为{x |－1<x <2}，∴ax 2＋bx ＋2＝0的两根为－1，2，且a <0，即－1＋2＝－b a ，(－1)×2＝2a ，解得a ＝－1，b ＝1，则所求不等式可化为2x 2＋x －1>0，解得x <－1或x >12，故选A.3．若一元二次不等式2kx 2＋kx －38<0对一切实数x 都成立，则k 的取值范围为( )A ．(－3，0)B ．[－3，0]C ．[－3，0)D ．(－3，0] 答案 A解析 由题意可得⎩⎪⎨⎪⎧k <0，Δ＝k 2－4×2k ×⎝⎛⎭⎫－38<0，解得－3<k <0.4．若存在实数x ∈[2，4]，使x 2－2x ＋5－m <0成立，则m 的取值范围为( ) A ．(13，＋∞) B ．(5，＋∞) C ．(4，＋∞) D ．(－∞，13)答案 B解析 m >x 2－2x ＋5，设f (x )＝x 2－2x ＋5＝(x －1)2＋4，x ∈[2，4]，当x ＝2时f (x )min ＝5，∃x ∈[2，4] 使x 2－2x ＋5－m <0成立，即m >f (x )min ，∴m >5.故选B.5．若不等式x 2－(a ＋1)x ＋a ≤0的解集是[－4，3]的子集，则a 的取值范围是( ) A ．[－4，1] B ．[－4，3] C ．[1，3] D ．[－1，3] 答案 B解析 原不等式为(x －a )(x －1)≤0，当a <1时，不等式的解集为[a ，1]，此时只要a ≥－4即可，即－4≤a <1；当a ＝1时，不等式的解为x ＝1，此时符合要求；当a >1时，不等式的解集为[1，a ]，此时只要a ≤3即可，即1<a ≤3，综上可得－4≤a ≤3.6．若不等式x 2＋ax －2>0在区间[1，5]上有解，则a 的取值范围是( ) A.⎝⎛⎭⎫－235，＋∞ B.⎣⎡⎦⎤－235，1 C ．(1，＋∞)D.⎝⎛⎦⎤－∞，－235答案 A解析 由Δ＝a 2＋8>0知方程恒有两个不等实根，又因为x 1x 2＝－2<0，所以方程必有一正根，一负根，对应二次函数图象的示意图如图．所以不等式在区间[1，5]上有解的充要条件是f (5)>0，解得a >－235，故选A.7．在关于x 的不等式x 2－(a ＋1)x ＋a <0的解集中至多包含1个整数，则a 的取值范围是() A ．(－3，5) B ．(－2，4)C ．[－1，3]D ．[－2，4]答案 C解析 因为关于x 的不等式x 2－(a ＋1)x ＋a <0可化为(x －1)(x －a )<0，当a >1时，不等式的解集为{x |1<x <a }，当a <1时，不等式的解集为{x |a <x <1}，当a ＝1时，不等式的解集为∅，要使得解集中至多包含1个整数，则a ＝1或1<a ≤3或1>a ≥－1，所以实数a 的取值范围是a ∈[－1，3]，故选C.8．设a <0，(4x 2＋a )(2x ＋b )≥0在(a ，b )上恒成立，则b －a 的最大值为( )A.12B.13C.14D.22答案 C解析 当a <b <0时，∀x ∈(a ，b )，2x ＋b <0，所以(4x 2＋a )(2x ＋b )≥0在(a ，b )上恒成立，可转化为∀x ∈(a ，b )，a ≤－4x 2，所以a ≤－4a 2，所以－14≤a <0，所以0<b －a <14；当a <0<b 时，(4x 2＋a )(2x ＋b )≥0在(a ，b )上恒成立，当x ＝0时，(4x 2＋a )(2x ＋b )＝ab <0，不符合题意；当a <0＝b 时，由题意知x ∈(a ，0)，(4x 2＋a )2x ≥0恒成立，所以4x 2＋a ≤0，所以－14≤a <0，所以b －a ≤14. 综上所述，b －a 的最大值为14. 二、填空题9．(2018·全国名校大联考)不等式x 2－2ax －3a 2<0(a >0)的解集为________．答案 {x |－a <x <3a }解析 x 2－2ax －3a 2<0⇔(x －3a )(x ＋a )<0，∵a >0，∴－a <3a ，不等式的解集为{x |－a <x <3a }．10．(2018·烟台联考)不等式x >1x的解集为________． 答案 (－1，0)∪(1，＋∞)解析 当x >0时，原不等式等价于x 2>1，解得x >1；当x <0时，原不等式等价于x 2<1，解得－1<x <0.所以不等式x >1x的解集为(－1，0)∪(1，＋∞)． 11．若关于x 的不等式x 2－ax －a >0的解集为R ，则实数a 的取值范围是________． 答案 (－4，0)解析 因为x 2－ax －a >0的解集为R ，所以Δ＝(－a )2－4(－a )<0，解得－4<a <0，故实数a 的取值范围是(－4，0)．12．(2019·上海长宁、嘉定区模拟)不等式x x ＋1≤0的解集为________． 答案 (－1，0]解析 由x x ＋1≤0得x (x ＋1)≤0(x ≠－1)， 解得－1<x ≤0.13．若不等式x 2＋ax ＋4≥0对一切x ∈(0，1]恒成立，则a 的取值范围为________． 答案 [－5，＋∞)解析 由题意，分离参数后得，a ≥－⎝⎛⎭⎫x ＋4x . 设f (x )＝－⎝⎛⎭⎫x ＋4x ，x ∈(0，1]， 则只要a ≥[f (x )]max 即可．由于函数f (x )在区间(0，1]上单调递增，所以[f (x )]max ＝f (1)＝－5，故a ≥－5.三、解答题14．已知对于任意的x ∈(－∞，1)∪(5，＋∞)，都有x 2－2(a －2)x ＋a >0，求实数a 的取值范围．解 设f (x )＝x 2－2(a －2)x ＋a ，当Δ＝4(a －2)2－4a <0时，即1<a <4 时，f (x )>0 对x ∈R 恒成立；当a ＝1时，f (－1)＝0，不合题意；当a ＝4时，f (2)＝0 符合题意；当Δ>0 时，由⎩⎪⎨⎪⎧ Δ>0，1<a －2<5，f (1)≥0，f (5)≥0，即⎩⎪⎨⎪⎧ a <1或a >4，3<a <7，a ≤5，a ≤5，即4<a ≤5. 综上所述，实数a 的取值范围是(1,5]．15．已知f (x )＝－3x 2＋a (6－a )x ＋6.(1)解关于a 的不等式f (1)>0；(2)若不等式f (x )>b 的解集为(－1，3)，求实数a ，b 的值．解 (1)∵f (x )＝－3x 2＋a (6－a )x ＋6，∴f (1)＝－3＋a (6－a )＋6＝－a 2＋6a ＋3>0，即a 2－6a －3<0，解得3－23<a <3＋2 3.∴原不等式的解集为{a |3－23<a <3＋23}．(2)∵f (x )>b 的解集为(－1，3)，∴方程－3x 2＋a (6－a )x ＋6－b ＝0的两根为－1，3，∴⎩⎪⎨⎪⎧ －1＋3＝a (6－a )3，－1×3＝－6－b 3，解得⎩⎪⎨⎪⎧ a ＝3±3，b ＝－3.16．已知f (x )＝2x 2＋bx ＋c ，不等式f (x )<0的解集是(0，5)．(1)求f (x )的解析式；(2)若对于任意的x ∈[－1，1]，不等式f (x )＋t ≤2恒成立，求t 的取值范围． 解 (1)f (x )＝2x 2＋bx ＋c ，不等式f (x )<0的解集是(0，5)，即2x 2＋bx ＋c <0的解集是(0，5)，∴0和5是方程2x 2＋bx ＋c ＝0的两个根，由根与系数的关系知，－b 2＝5，c 2＝0， ∴b ＝－10，c ＝0，f (x )＝2x 2－10x .(2)f (x )＋t ≤2恒成立等价于2x 2－10x ＋t －2≤0恒成立，∴2x 2－10x ＋t －2在x ∈[－1，1]上的最大值小于或等于0.设g (x )＝2x 2－10x ＋t －2，x ∈[－1，1]，则由二次函数的图象可知g (x )＝2x 2－10x ＋t －2在区间[－1，1]上为减函数， ∴g (x )max ＝g (－1)＝10＋t ，∴10＋t ≤0，即t ≤－10.。

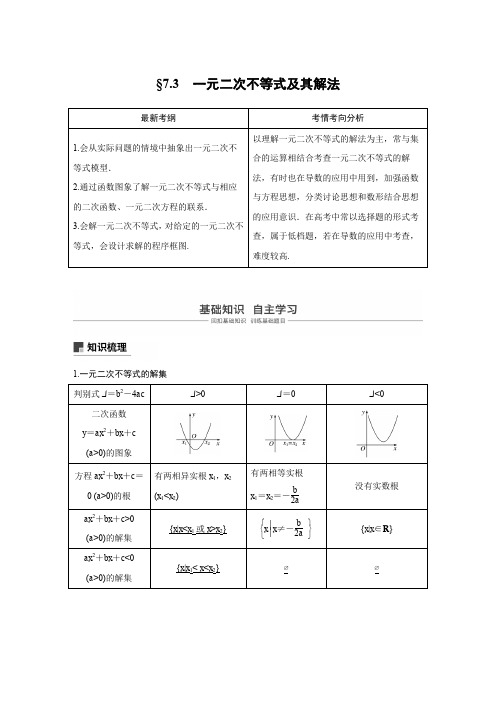
第一节一元二次不等式及其解法“三个二次”的关系一元二次不等式ax 2＋bx ＋c ＞0 (a ＞0)的解集 {x |x ＜x 1或x ＞x 2}⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x ≠－b 2a R一元二次不等式ax 2＋bx ＋c ＜0 (a ＞0)的解集{x |x 1＜x ＜x 2} ∅ ∅[小题体验]1．不等式3x 2－x －4≤0的解集是________．解析：由3x 2－x －4≤0，得(3x －4)(x ＋1)≤0，解得－1≤x ≤43.答案：⎩⎨⎧x ⎪⎪⎪⎭⎬⎫－1≤x ≤432．(2018·南京、盐城二模)已知函数f (x )＝⎩⎪⎨⎪⎧12x ＋1，x ≤0，－x －12，x ＞0，则不等式f (x )≥－1的解集是________．解析：不等式f (x )≥－1⇔⎩⎪⎨⎪⎧x ≤0，12x ＋1≥－1或⎩⎪⎨⎪⎧x ＞0，－x －12≥－1，解得－4≤x ≤0或0＜x ≤2，故不等式f (x )≥－1的解集是[－4,2]． 答案：[－4,2]3．已知不等式ax 2－bx －1≥0的解集是⎣⎢⎡⎦⎥⎤－12，－13，则不等式x 2－bx －a ＜0的解集是________．解析：由题意知－12，－13是方程ax 2－bx －1＝0的根，所以⎩⎪⎨⎪⎧－12＋⎝ ⎛⎭⎪⎫－13＝b a，⎝ ⎛⎭⎪⎫－12×⎝ ⎛⎭⎪⎫－13＝－1a ，解得⎩⎪⎨⎪⎧a ＝－6，b ＝5，不等式x 2－bx －a ＜0，即为x 2－5x ＋6＜0，解得2＜x ＜3.答案：{x |2＜x ＜3}1．对于不等式ax 2＋bx ＋c ＞0，求解时不要忘记讨论a ＝0时的情形． 2．当Δ＜0时，ax 2＋bx ＋c ＞0(a ≠0)的解集为R 还是∅，要注意区别． 3．含参数的不等式要注意选好分类标准，避免盲目讨论． [小题纠偏]1．已知不等式x 2－2x ＋k 2－3＞0的解集为R ，则实数k 的取值范围是________________． 解析：由Δ＝4－4(k 2－3)＜0，解得k ＞2或k ＜－2. 答案：(－∞，－2)∪(2，＋∞)2．若不等式(a －2)x 2＋2(a －2)x －4＜0对x ∈R 恒成立，则实数a 的取值范围是________．解析：当a －2＝0，即a ＝2时，原不等式为－4＜0，所以a ＝2时成立， 当a －2≠0，即a ≠2时，由题意得⎩⎪⎨⎪⎧a －2＜0，Δ＜0，即⎩⎪⎨⎪⎧a －2＜0，4a －22＋16a －2＜0，解得－2＜a ＜2. 综上所述，－2＜a ≤2. 答案：(－2,2]考点一 一元二次不等式的解法基础送分型考点——自主练透 [题组练透]1．(2018·南通中学检测)不等式－3x 2＋6x ＞2的解集为________．解析：将不等式－3x 2＋6x ＞2转化为3x 2－6x ＋2＜0，所以不等式的解集是⎩⎪⎨⎪⎧x ⎪⎪⎪⎭⎪⎬⎪⎫1－33＜x ＜1＋33.答案：⎩⎪⎨⎪⎧x ⎪⎪⎪⎭⎪⎬⎪⎫1－33＜x ＜1＋332．(2019·东湖中学检测)已知函数f (x )＝⎩⎪⎨⎪⎧－x 2，x ≥0，x 2＋2x ，x ＜0，则不等式f (f (x ))≤3的解集为________．解析：当x ≥0时，f (f (x ))＝f (－x 2)＝(－x 2)2－2x 2≤3，即(x 2－3)(x 2＋1)≤0，解得0≤x ≤3；当－2＜x ＜0时，f (f (x ))＝f (x 2＋2x )＝(x 2＋2x )2＋2(x 2＋2x )≤3，即(x 2＋2x －1)(x 2＋2x ＋3)≤0，即－2＜x ＜0；当x ≤－2时，f (f (x ))＝f (x 2＋2x )＝－(x 2＋2x )2≤3，解得x ≤ －2.综上，不等式的解集为{x |x ≤ 3}．答案：{x |x ≤3} 3．解下列不等式：(1)(易错题)－3x 2－2x ＋8≥0； (2)0＜x 2－x －2≤4.解：(1)原不等式可化为3x 2＋2x －8≤0， 即(3x －4)(x ＋2)≤0. 解得－2≤x ≤43，所以原不等式的解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫－2≤x ≤43.(2)原不等式等价于⎩⎪⎨⎪⎧x 2－x －2＞0，x 2－x －2≤4⇔⎩⎪⎨⎪⎧x 2－x －2＞0，x 2－x －6≤0⇔⎩⎪⎨⎪⎧x －2x ＋1＞0，x －3x ＋2≤0⇔⎩⎪⎨⎪⎧x ＞2或x ＜－1，－2≤x ≤3.借助于数轴，如图所示，所以原不等式的解集为{}x |－2≤x ＜－1或2＜x ≤3.[谨记通法]解一元二次不等式的4个步骤考点二 含参数的一元二次不等式的解法重点保分型考点——师生共研[典例引领](2019·天一中学检测)解关于x 的不等式：ax 2＋(a －2)x －2≥0. 解：①当a ＝0时，原不等式化为x ＋1≤0，解得x ≤－1.②当a ＞0时，原不等式化为⎝ ⎛⎭⎪⎫x －2a (x ＋1)≥0，解得x ≥2a或x ≤－1.③当a ＜0时，原不等式化为⎝⎛⎭⎪⎫x －2a (x ＋1)≤0.当2a ＞－1，即a ＜－2时，解得－1≤x ≤2a；当2a ＝－1，即a ＝－2时，解得x ＝－1； 当2a＜－1，即a ＞－2时，解得2a≤x ≤－1.综上所述，当a ＝0时，不等式的解集为{x |x ≤－1}；当a ＞0时，不等式的解集为⎩⎨⎧ x ⎪⎪⎪⎭⎬⎫x ≥2a或x ≤－1；当－2＜a ＜0时，不等式的解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫2a≤x ≤－1；当a ＝－2时，不等式的解集为{x |x ＝－1}；当a ＜－2时，不等式的解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫－1≤x ≤2a .[由题悟法]解含参数的一元二次不等式时分类讨论的依据(1)二次项中若含有参数应讨论是等于0，小于0，还是大于0，然后将不等式转化为一次不等式或二次项系数为正的形式．(2)当不等式对应方程的根的个数不确定时，讨论判别式Δ与0的关系．(3)确定无根时可直接写出解集，确定方程有两个根时，要讨论两根的大小关系，从而确定解集形式．[提醒] 当不等式中二次项的系数含有参数时，不要忘记讨论其等于0的情况．[即时应用]1．(2019·苏州实验中学检测)已知x 2＋px ＋q ＜0的解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫－12＜x ＜13，则不等式qx 2＋px ＋1＞0的解集为________．解析：∵x 2＋px ＋q ＜0的解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫－12＜x ＜13，∴－12，13是方程x 2＋px ＋q ＝0的两实数根，则⎩⎪⎨⎪⎧13－12＝－p ，13×⎝ ⎛⎭⎪⎫－12＝q ，解得⎩⎪⎨⎪⎧p ＝16，q ＝－16.∴不等式qx 2＋px ＋1＞0可化为－16x 2＋16x ＋1＞0，即x 2－x －6＜0，解得－2＜x ＜3，∴不等式qx 2＋px ＋1＞0的解集为{x |－2＜x ＜3}． 答案：{x |－2＜x ＜3}2．求不等式12x 2－ax ＞a 2(a ∈R)的解集． 解：原不等式可化为12x 2－ax －a 2＞0， 即(4x ＋a )(3x －a )＞0， 令(4x ＋a )(3x －a )＝0， 解得x 1＝－a 4，x 2＝a3.当a ＞0时，不等式的解集为⎝ ⎛⎭⎪⎫－∞，－a 4∪⎝ ⎛⎭⎪⎫a3，＋∞；当a ＝0时，不等式的解集为(－∞，0)∪(0，＋∞)； 当a ＜0时，不等式的解集为⎝ ⎛⎭⎪⎫－∞，a 3∪⎝ ⎛⎭⎪⎫－a4，＋∞. 考点三 一元二次不等式恒成立问题 题点多变型考点——多角探明[锁定考向]一元二次不等式与其对应的函数与方程之间存在着密切的联系．在解决具体的数学问题时，要注意三者之间的相互联系，并在一定条件下相互转换．对于一元二次不等式恒成立问题，常根据二次函数图象与x 轴的交点情况确定判别式的符号，进而求出参数的取值范围．常见的命题角度有：(1)形如f (x )≥0(f (x )≤0)(x ∈R)确定参数范围； (2)形如f (x )≥0(x ∈[a ，b ])确定参数范围；(3)形如f (x )≥0(参数m ∈[a ，b ])确定x 的范围．[题点全练]角度一：形如f (x )≥0(f (x )≤0)(x ∈R)确定参数范围1．(2019·南通中学测试)已知函数f (x )＝ax 2＋bx ＋c (a ，b ，c ∈R 且a ≠0)，若对任意实数x ，不等式2x ≤f (x )≤12(x ＋1)2恒成立．(1)求f (1)的值； (2)求a 的取值范围．解：(1)令x ＝1，由2x ≤f (x )≤12(x ＋1)2，可得2≤f (1)≤2，所以f (1)＝2.(2)由f (1)＝2，可得a ＋b ＋c ＝2，即b ＝2－(a ＋c )， 因为对一切实数x ，f (x )－2x ≥0恒成立，所以ax 2＋(b －2)x ＋c ≥0(a ≠0)对一切实数x 恒成立， 所以⎩⎪⎨⎪⎧a ＞0，Δ＝b －22－4ac ≤0，即⎩⎪⎨⎪⎧a ＞0，Δ＝a ＋c2－4ac ≤0.可得(a －c )2≤0，但(a －c )2≥0，即有a ＝c ＞0， 则f (x )＝ax 2＋bx ＋a ，f (x )≤12(x ＋1)2恒成立，即⎝⎛⎭⎪⎫a －12x 2＋(b －1)x ＋⎝⎛⎭⎪⎫a －12≤0恒成立，所以a －12＜0，且Δ＝(b －1)2－4⎝ ⎛⎭⎪⎫a －122≤0，由b －1＝1－2a ，即有Δ＝0成立．综上可得a 的取值范围是⎝ ⎛⎭⎪⎫0，12.角度二：形如f (x )≥0(x ∈[a ，b ])确定参数范围2．已知函数f (x )＝－x 2＋ax ＋b 2－b ＋1(a ∈R ，b ∈R)，对任意实数x 都有f (1－x )＝f (1＋x )成立，若当x ∈[－1,1]时，f (x )＞0恒成立，求b 的取值范围．解：由f (1－x )＝f (1＋x )知f (x )的图象关于直线x ＝1对称，即a2＝1，解得a ＝2.又因为f (x )开口向下，所以当x ∈[－1,1]时，f (x )为增函数， 所以f (x )min ＝f (－1)＝－1－2＋b 2－b ＋1 ＝b 2－b －2，f (x )＞0恒成立，即b 2－b －2＞0恒成立，解得b ＜－1或b ＞2.所以b 的取值范围为(－∞，－1)∪(2，＋∞)． 角度三：形如f (x )≥0(参数m ∈[a ，b ])确定x 的范围3．对任意m ∈[－1,1]，函数f (x )＝x 2＋(m －4)x ＋4－2m 的值恒大于零，求x 的取值 范围．解：由f (x )＝x 2＋(m －4)x ＋4－2m＝(x －2)m ＋x 2－4x ＋4， 令g (m )＝(x －2)m ＋x 2－4x ＋4.由题意知在[－1,1]上，g (m )的值恒大于零，所以⎩⎪⎨⎪⎧g －1＝x －2×－1＋x 2－4x ＋4＞0，g 1＝x －2＋x 2－4x ＋4＞0，解得x ＜1或x ＞3.故当x ∈(－∞，1)∪(3，＋∞)时，对任意的m ∈[－1,1]，函数f (x )的值恒大于零．[通法在握]一元二次型不等式恒成立问题的3大破解方法 方法解 读适合题型判别式法(1)ax 2＋bx ＋c ≥0对任意实数x 恒成立的条件是⎩⎪⎨⎪⎧a ＞0，Δ≤0；(2)ax 2＋bx ＋c ≤0对任意实数x 恒成立的条件是⎩⎪⎨⎪⎧a ＜0，Δ≤0二次不等式在R 上恒成立分离参数法如果不等式中的参数比较“孤单”，分离后其系数与0能比较大小，便可将参数分离出来，利用下面的结论求解：a ≥f (x )恒成立等价于a ≥f (x )max ；a ≤f (x )恒成立等价于a ≤f (x )min适合参数与变量能分离且f (x )的最值易求主参换位法把变元与参数交换位置，构造以参数为变量的函数，根据原变量的取值范围列式求解．常见的是转化为一次函数f (x )＝ax ＋b (a ≠0)在[m ，n ]恒成立问题，若f (x )＞0恒成立⇔⎩⎪⎨⎪⎧f m ＞0，f n ＞0，若f (x )＜0恒成立⇔⎩⎪⎨⎪⎧fm ＜0，f n ＜0若在分离参数时会遇到讨论参数与变量，使求函数的最值比较麻烦，或者即使能容易分离出却难以求出时[演练冲关]1．(2018·盱眙二模)若对于任意的a ，b ∈R ，存在λ∈R 使不等式a 2＋mb 2≥λb (a ＋b )成立，则实数m 的取值范围为________．解析：∵a 2＋mb 2≥λb (a ＋b )对于任意的a ，b ∈R 恒成立， ∴a 2＋mb 2－λb (a ＋b )≥0对于任意的a ，b ∈R 恒成立， 即a 2－(λb )a ＋(m －λ)b 2≥0恒成立，由二次不等式的性质可得，Δ＝λ2b 2＋4(λ－m )b 2≤0， 即λ2＋4λ－4m ≤0，又∵存在λ∈R 使得上述不等式恒成立， ∴Δ＝16＋16m ≥0，解得m ≥－1. 答案：[－1，＋∞)2．设函数f (x )＝mx 2－mx －1(m ≠0)，若对于x ∈[1,3]，f (x )＜－m ＋5恒成立，求m 的取值范围．解：要使f (x )＜－m ＋5在[1,3]上恒成立， 则mx 2－mx ＋m －6＜0，即m ⎝ ⎛⎭⎪⎫x －122＋34m －6＜0在x ∈[1,3]上恒成立．因为x 2－x ＋1＝⎝ ⎛⎭⎪⎫x －122＋34＞0，又因为m (x 2－x ＋1)－6＜0，所以m ＜6x 2－x ＋1.因为函数y ＝6x 2－x ＋1＝6⎝ ⎛⎭⎪⎫x －122＋34在[1,3]上的最小值为67，所以只需m ＜67即可． 因为m ≠0，所以m 的取值范围是(－∞，0)∪⎝ ⎛⎭⎪⎫0，67.一抓基础，多练小题做到眼疾手快1．(2019·扬州模拟)不等式2x 2－x －1＞0的解集为________．解析：不等式2x 2－x －1＞0可化为(2x ＋1)(x －1)＞0， 解得x ＞1或x ＜－12，则原不等式的解集为⎝ ⎛⎭⎪⎫－∞，－12∪(1，＋∞)． 答案：⎝⎛⎭⎪⎫－∞，－12∪(1，＋∞)2．(2018·靖江中学期末)若集合A ＝{x |ax 2－ax ＋1＜0}＝∅，则实数a 的取值范围是________．解析：由题意知a ＝0时，满足条件．a ≠0时，由⎩⎪⎨⎪⎧a ＞0，Δ＝a 2－4a ≤0，得0＜a ≤4，所以实数a 的取值范围是[0,4]．答案：[0,4]3．(2019·昆明模拟)不等式x 2－2x ＋5≥a 2－3a 对任意实数x 恒成立，则实数a 的取值范围为________．解析：x 2－2x ＋5＝(x －1)2＋4的最小值为4，所以x 2－2x ＋5≥a 2－3a 对任意实数x 恒成立，只需a 2－3a ≤4，解得－1≤a ≤4.答案：[－1,4]4．不等式|x (x －2)|＞x (x －2)的解集是________．解析：不等式|x (x －2)|＞x (x －2)的解集即x (x －2)＜0的解集，解得0＜x ＜2. 答案：(0,2)5．(2019·南通月考)关于x 的不等式x 2－⎝⎛⎭⎪⎫a ＋1a x ＋1＜0(a ＞1)的解集为________．解析：不等式x 2－⎝⎛⎭⎪⎫a ＋1a x ＋1＜0可化为(x －a )⎝ ⎛⎭⎪⎫x －1a ＜0，又a ＞1，∴a ＞1a，∴不等式的解集为⎝ ⎛⎭⎪⎫1a ，a .答案：⎝ ⎛⎭⎪⎫1a，a6．(2018·如东中学测试)已知函数f (x )＝⎩⎪⎨⎪⎧x ＋2，x ≤0，－x ＋2，x ＞0，则不等式f (x )≥x 2的解集为________．解析：当x ≤0时，x ＋2≥x 2，解得－1≤x ≤0；① 当x ＞0时，－x ＋2≥x 2，解得0＜x ≤1. ② 由①②得原不等式的解集为{x |－1≤x ≤1}． 答案：[－1,1]二保高考，全练题型做到高考达标1．(2019·常州检测)若关于x 的不等式x 2－3ax ＋2＞0的解集为{x |x ＜1或x ＞m }，则a ＋m ＝________.解析：关于x 的不等式x 2－3ax ＋2＞0的解集为{x |x ＜1或x ＞m }，则1与m 是对应方程x 2－3ax ＋2＝0的两个实数根，把x ＝1代入方程得1－3a ＋2＝0，解得a ＝1，∴不等式化为x 2－3x ＋2＞0，其解集为{x |x ＜1或x ＞2}，∴m ＝2，∴a ＋m ＝3. 答案：32．(2018·清河中学检测)不等式(x ＋2)x 2－9≤0的解集为________．解析：由题意⎩⎪⎨⎪⎧x ＋2≤0，x 2－9≥0或x2－9＝0，即⎩⎪⎨⎪⎧x ≤－2，x ≤－3或x ≥3或x ＝±3，即x ≤－3或x ＝3.答案：(－∞，－3]∪{3}3．(2019·郑州调研)规定记号“⊙”表示一种运算，定义a ⊙b ＝ab ＋a ＋b (a ，b 为正实数)，若1⊙k 2＜3，则k 的取值范围是________．解析：因为定义a ⊙b ＝ab ＋a ＋b (a ，b 为正实数)， 1⊙k 2＜3，所以k 2＋1＋k 2＜3，化为(|k |＋2)(|k |－1)＜0，所以|k |＜1， 所以－1＜k ＜1. 答案：(－1,1)4．如果关于x 的不等式5x 2－a ≤0的正整数解是1,2,3,4，那么实数a 的取值范围是________．解析：由5x 2－a ≤0，得－a5≤x ≤a5，而正整数解是1,2,3,4，则4≤ a5＜5，所以80≤a ＜125.答案：[80,125)5．(2019·南通调研)已知关于x 的一元二次不等式ax 2＋bx ＋c ＞0的解集为(－1,5)，其中a ，b ，c 为常数．则不等式cx 2＋bx ＋a ≤0的解集为________．解析：因为不等式ax 2＋bx ＋c ＞0的解集为(－1,5)，所以a (x ＋1)(x －5)＞0，且a ＜0，即ax 2－4ax －5a ＞0，则b ＝－4a ，c ＝－5a ，故cx 2＋bx ＋a ≤0，即为－5ax 2－4ax ＋a ≤0，从而5x 2＋4x －1≤0，故不等式cx 2＋bx ＋a ≤0的解集为⎣⎢⎡⎦⎥⎤－1，15.答案：⎣⎢⎡⎦⎥⎤－1，156．(2018·江阴期中)若关于x 的不等式mx 2－mx －1≥0的解集为∅，则实数m 的取值范围是________．解析：当m ＝0时，原不等式化为－1≥0，其解集是空集； 当m ≠0时，要使关于x 的不等式mx 2－mx －1≥0的解集为∅，则⎩⎪⎨⎪⎧m ＜0，－m 2－4m ·－1＜0，解得－4＜m ＜0.综上，实数m 的取值范围是(－4,0]． 答案：(－4,0]7．(2018·海门检测)已知一元二次不等式f (x )＜0的解集为⎩⎨⎧x ⎪⎪⎪⎭⎬⎫x ＜－1或x ＞13，则f (e x )＞0的解集为________．解析：由题意f (x )＞0的解集为⎣⎢⎡⎦⎥⎤－1，13，不等式f (e x )＞0可化为－1＜e x＜13，解得x＜－ln 3，即f (e x)＞0的解集为(－∞，－ln 3)．答案：(－∞，－ln 3)8．(2019·金陵中学检测)如果关于x 的不等式(1－m 2)x 2－(1＋m )x －1＜0的解集是R ，则实数m 的取值范围是________________．解析：令1－m 2＝0，解得m ＝±1；当m ＝1，不等式化为－2x －1＜0，不满足题意； 当m ＝－1时，不等式化为－1＜0，满足条件；当m ≠±1时，则有⎩⎪⎨⎪⎧1－m 2＜0，1＋m 2－41－m2×－1＜0，解得⎩⎪⎨⎪⎧m ＜－1或m ＞1，m ＜－1或m ＞53，即m ＜－1或m ＞53，综上，实数m 的取值范围是(－∞，－1]∪⎝ ⎛⎭⎪⎫53，＋∞. 答案：(－∞，－1]∪⎝ ⎛⎭⎪⎫53，＋∞9．已知f (x )＝－3x 2＋a (6－a )x ＋6. (1)解关于a 的不等式f (1)＞0；(2)若不等式f (x )＞b 的解集为(－1,3)，求实数a ，b 的值． 解：(1)因为f (x )＝－3x 2＋a (6－a )x ＋6， 所以f (1)＝－3＋a (6－a )＋6＝－a 2＋6a ＋3， 所以原不等式可化为a 2－6a －3＜0，解得3－23＜a ＜3＋2 3.所以原不等式的解集为{a |3－23＜a ＜3＋23}．(2)f (x )＞b 的解集为(－1,3)等价于方程－3x 2＋a (6－a )x ＋6－b ＝0的两根为－1,3，等价于⎩⎪⎨⎪⎧－1＋3＝a 6－a3，－1×3＝－6－b3，解得⎩⎨⎧a ＝3±3，b ＝－3.10．(2018·北京朝阳统一考试)已知函数f (x )＝x 2－2ax －1＋a ，a ∈R. (1)若a ＝2，试求函数y ＝f xx(x ＞0)的最小值； (2)对于任意的x ∈[0,2]，不等式f (x )≤a 成立，试求a 的取值范围．解：(1)依题意得y ＝f x x ＝x 2－4x ＋1x ＝x ＋1x－4.因为x ＞0，所以x ＋1x≥2.当且仅当x ＝1x时，即x ＝1时，等号成立．所以y ≥－2. 所以当x ＝1时，y ＝f xx的最小值为－2. (2)因为f (x )－a ＝x 2－2ax －1，所以要使得“∀x ∈[0,2]，不等式f (x )≤a 成立”， 只要“x 2－2ax －1≤0在[0,2]恒成立”． 不妨设g (x )＝x 2－2ax －1，则只要g (x )≤0在[0,2]上恒成立即可．所以⎩⎪⎨⎪⎧g 0≤0，g 2≤0，即⎩⎪⎨⎪⎧0－0－1≤0，4－4a －1≤0，解得a ≥34.则a 的取值范围为⎣⎢⎡⎭⎪⎫34，＋∞. 三上台阶，自主选做志在冲刺名校1．(2019·宿迁调研)若关于x 的不等式ax 2＋6x －a 2＜0的解集是(－∞，1)∪(m ，＋∞)，则实数m ＝________.解析：∵ax 2＋6x －a 2＜0的解集是(－∞，1)∪(m ，＋∞)， ∴a ＜0，且1和m 是方程ax 2＋6x －a 2＝0的两个根， ∴a ＋6－a 2＝0，即a 2－a －6＝0， 解得a ＝－2或a ＝3(舍去)．∴不等式化为－2x 2＋6x －4＜0，即x 2－3x ＋2＞0， 解得x ＜1或x ＞2，∴m ＝2. 答案：22．(2018·扬州中学检测)已知二次函数f (x )＝ax 2－(a ＋2)x ＋1(a ∈Z)，且函数f (x )在(－2，－1)上恰有一个零点，则不等式f (x )＞1的解集为________．解析：因为f (x )＝ax 2－(a ＋2)x ＋1(a ≠0)，Δ＝(a ＋2)2－4a ＝a 2＋4＞0，所以函数f (x )＝ax 2－(a ＋2)x ＋1必有两个不同的零点．因此f (－2)f (－1)＜0，所以(6a ＋5)(2a ＋3)＜0.解得－32＜ a ＜－56.又a ∈Z ，所以a ＝－1.不等式f (x )＞1，即为－x 2－x ＞0，解得－1＜x＜0.答案：(－1,0)3．已知函数f (x )＝ax 2＋2ax ＋1的定义域为R. (1)求a 的取值范围； (2)若函数f (x )的最小值为22，解关于x 的不等式x 2－x －a 2－a ＜0. 解：(1)因为函数f (x )＝ax 2＋2ax ＋1的定义域为R ， 所以 ax 2＋2ax ＋1≥0恒成立， 当a ＝0时，1≥0恒成立． 当a ≠0时，需满足题意，则需⎩⎪⎨⎪⎧a ＞0，Δ＝2a2－4a ≤0，解得0＜a ≤1，综上可知，a 的取值范围是[0,1]． (2)f (x )＝ax 2＋2ax ＋1＝a x ＋12＋1－a ，由题意及(1)可知0＜a ≤1， 所以当x ＝－1时，f (x )min ＝1－a ， 由题意得，1－a ＝22， 所以a ＝12，所以不等式x 2－x －a 2－a ＜0可化为x 2－x －34＜0.解得－12＜x ＜32，所以不等式的解集为⎝ ⎛⎭⎪⎫－12，32.。