圆柱表面积公式的推导.

圆柱表面积的公式
圆柱的表面积公式：s表=2πr²+2πrh。

圆柱的表面积=侧面积+两个底面积（s表=s侧+2s底）；圆柱的侧面积=底面的周长×高，也就是 s侧=2πrh；圆柱的底面积=圆的面积，也就是s底=πr²。

圆柱的底面都是圆，并且大小一样。

圆柱两个面之间的垂直距离叫做高，把圆柱的侧面打开，得到一个矩形，这个矩形的一条边就是圆柱的底面周长。

以矩形的一边所在直线为旋转轴，其余三边旋转形成的曲面所围成的几何体叫作圆柱(circularcylinder)，即矩形add'g 的一条边ag为轴，其余三边旋转一周所得的几何体。

其中ag 叫做圆柱的轴，ag叫做圆柱的高，无论旋转到什么位置不垂直于轴的边都叫做圆柱的母线。

da和d'g旋转形成的两个圆叫做圆柱的底面，dd'旋转形成的曲面叫做圆柱的侧面。

在同一个平面内有一条定直线和一条动线，当这个平面绕着这条定直线旋转一周时，这条动线所成的面叫做旋转面，这条定直线叫做旋转面的轴，这条动线叫做旋转面的母线。

如果母线是和轴平行的一条直线，那么所生成的旋转面叫做圆柱面。

如果用垂直于轴的两个平面去截圆柱面，那么两个截面和圆柱面所围成的几何体叫做直圆柱，简称圆柱。

圆柱表面积公式和体积公式转换
我们要探讨圆柱的表面积和体积公式之间的关系。

首先，我们需要知道圆柱的表面积和体积的公式是什么。

圆柱的表面积公式为：2πr(h + r)，其中 r 是圆柱的底面半径，h 是圆柱的高。

圆柱的体积公式为：πr^2h。

我们的目标是找到一个关系，使得我们可以从一个公式推导出另一个公式。

通过解方程，我们得到 h = 2r/(r - 2)。

这意味着，如果我们知道圆柱的底面半径 r 和体积 V，我们可以使用这个关系来找到高 h。

反之，如果我们知道 r 和 h，我们也可以使用这个关系来找到体积 V。

所以，我们可以说圆柱的表面积和体积公式之间存在以下关系：
表面积= 2πr(h + r)
体积= πr^2h
并且h = V/2πr^2 当体积给定时，或者V = πr^2h 当高给定时。

圆柱的表面积公式字母表示
一、圆柱的表面积的公式的英文字母表示：
S=2πrh+2πr2
其中，S表示圆柱的表面积；π表示圆周率（π≈3.14）；r为圆柱的半径；h表示圆柱的高度。

二、圆柱的表面积的公式的求解过程：
（1）先将圆柱分解成三部分：圆柱底面，侧面，和圆柱顶面。

（2）记圆柱底面平面的面积为A1，侧面平面的面积为A2，圆柱顶面
平面的面积为A3，则，圆柱的表面积S=A1+A2+A3。

（3）根据相关几何公式求解：
A1=πr2，表示圆柱底面的面积；
A2=2πrh，表示圆柱侧面的面积；
A3=πr2，表示圆柱顶面的面积。

（4）将求解出的A1、A2、A3代入圆柱的表面积公式中求解：S=A1+A2+A3=πr2+2πrh+πr2=2πr2+2πrh
最终，求得圆柱表面积的公式S=2πrh+2πr2。

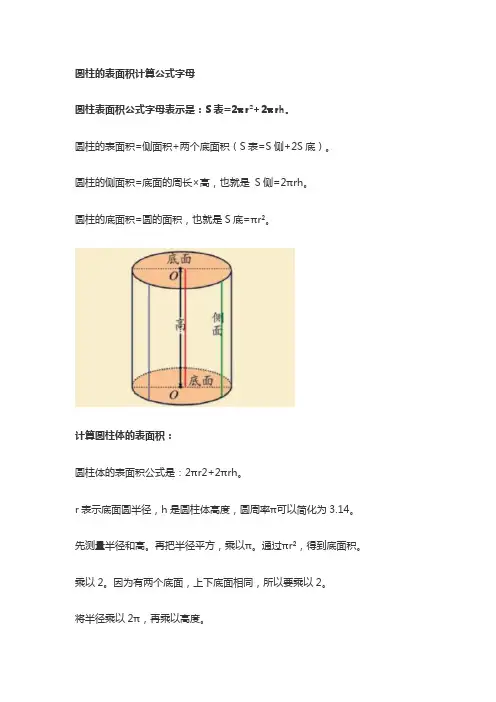
圆柱的表面积计算公式字母
圆柱表面积公式字母表示是：S表=2πr²+2πrh。

圆柱的表面积=侧面积+两个底面积（S表=S侧+2S底）。

圆柱的侧面积=底面的周长×高，也就是S侧=2πrh。

圆柱的底面积=圆的面积，也就是S底=πr²。

计算圆柱体的表面积：
圆柱体的表面积公式是：2πr2+2πrh。

r表示底面圆半径，h是圆柱体高度，圆周率π可以简化为3.14。

先测量半径和高。

再把半径平方，乘以π。

通过πr²，得到底面积。

乘以2。

因为有两个底面，上下底面相同，所以要乘以2。

将半径乘以2π，再乘以高度。

最后把上底和下底面积加上周长乘以高度的积，得到表面积。

圆柱的侧面积和表面积公式首先，让我们先介绍一下什么是圆柱。

圆柱是一个由两个平行相等的圆底面和它们之间的侧面组成的几何体。

其中，圆底面的直径称为圆柱的底面直径，它与底面上的圆心距离称为圆柱的高。

1.圆柱的侧面积公式：侧面积=底面周长×高侧面积=2πr×h其中，r是圆柱的底面半径，h是圆柱的高。

2.圆柱的表面积公式：圆柱的表面积等于两个底面加上侧面的总面积，即：表面积=2×底面积+侧面积表面积=2×πr²+2πr×h表面积=2πr×(r+h)其中，r是圆柱的底面半径，h是圆柱的高。

通过上述公式，我们可以计算出圆柱的侧面积和表面积。

下面我们将通过一些实际问题的应用案例来具体应用这些公式。

案例一：假设一个圆柱的底面半径为5cm，高为10cm，求该圆柱的侧面积和表面积。

根据圆柱的侧面积公式计算侧面积：侧面积=2πr×h侧面积=2π×5×10侧面积= 100π cm²根据圆柱的表面积公式计算表面积：表面积=2πr×(r+h)表面积=2π×5×(5+10)表面积=2π×5×15表面积= 150π cm²所以，该圆柱的侧面积为100π cm²，表面积为150π cm²。

案例二：一个铁管的内径为7cm，高度为30cm，如果该管的厚度为2cm，求这个铁管的侧面积和表面积。

首先，我们需要计算出铁管的外径。

由于铁管的厚度为2cm，所以外径等于内径加上2倍的厚度。

外径=内径+2×厚度外径=7+2×2外径 = 11cm根据圆柱的侧面积公式计算侧面积：侧面积=2πr×h侧面积=2π×11×30侧面积= 660π cm²根据圆柱的表面积公式计算表面积：表面积=2πr×(r+h)表面积=2π×11×(11+30)表面积=2π×11×41表面积= 902π cm²所以，这个铁管的侧面积为660π cm²，表面积为902π cm²。

圆柱的面积公式
圆柱的表面积公式=侧面积+两个底面积=2πrh+2πr²。

圆柱的体积=底面积×高=πr²×h。

圆柱的表面积指圆柱的底面积与侧面积之和。

圆柱表面积公式：圆柱的表面积=侧面积+两个底面积=2πrh+2πr²
底面积就是圆形面积公式：πR²
单位：平方厘米、平方米、平方分米。

圆柱是由以矩形的一条边所在直线为旋转轴，其余三边绕该旋转轴旋转一周而形成的几何体。

它有2个大小相同、相互平行的圆形底面和1个曲面侧面。

其侧面展开是矩形。

体积V=πr²h
π是圆周率，一般取3.14；
r是圆柱底面半径；
h为圆柱的高；
还可以是v=1/2ch×r；
侧面积的一半×半径。

圆柱表面积公式计算公式圆柱是一种常见的几何体，由一个圆和与该圆平行的两个相等的平行面组成。

圆柱的表面积是指圆柱的所有外部表面的总面积。

要计算圆柱的表面积，我们可以使用以下公式：S = 2πrh + 2πr²其中，S表示圆柱的表面积，r表示圆的半径，h表示圆柱的高。

我们来理解一下这个公式。

圆柱的外部表面由三部分组成：底面、侧面和顶面。

底面和顶面都是圆，面积为πr²。

侧面是一个长方形，其宽度等于圆的周长2πr，高度为h。

因此，侧面的面积为2πrh。

为了更好地理解这个公式，我们可以通过一个具体的例子来计算圆柱的表面积。

假设有一个半径为4cm，高度为6cm的圆柱。

首先，根据公式，我们可以计算侧面的面积：2π × 4cm × 6cm = 48π cm²。

接下来，我们计算底面和顶面的面积：2π × 4cm × 4cm = 32π cm²。

最后，我们将侧面和底面、顶面的面积相加：48π cm² + 32π cm² = 80π cm²。

这就是该圆柱的表面积。

除了使用公式计算圆柱的表面积，我们还可以通过其他方法来推导这个公式。

例如，我们可以将圆柱展开成一个矩形，然后计算矩形的面积。

假设圆柱的底面周长为C，高度为h。

由于矩形的长度等于底面周长C，宽度等于圆柱的高度h，所以矩形的面积为Ch。

由于圆柱的底面是一个圆，面积为πr²，所以矩形的面积也等于底面的面积。

因此，我们可以得出公式：Ch = 2πrh，即2πrh + 2πr²。

圆柱的表面积是一个重要的概念，在实际生活中有很多应用。

例如，在建筑设计中，计算圆柱的表面积可以帮助我们确定所需的材料数量。

另外，在工程领域中，计算圆柱的表面积可以帮助我们设计管道或容器的尺寸。

总结一下，圆柱的表面积可以通过公式S = 2πrh + 2πr²来计算。

圆柱的面积公式和表面积公式
圆柱的面积公式，表面积公式，体积公式分别如下所示：
1、圆柱表面积：S表=2πR(R+h)（其中R表示圆柱的底面半径，h表示圆柱的高）
2、圆柱体积：V=πR^2h（其中R表示圆柱的底面半径，h表示圆柱的高）
3、圆柱侧面积：S侧=2πRh（（其中R表示圆柱的底面半径，h表示圆柱的高）。

扩展资料：
圆柱的体积跟求长方体、正方体一样，都是底面积×高：设一个圆柱底面半径为r，高为h，则体积V：V＝πr^2·h 。

如S为底面积，高为h，体积为V：V=Sh。

圆柱体侧面积=底面周长×高（圆的周长（2πr）或（πd））
圆柱体的表面积=2个底面积+1个侧面积。

圆柱的表面积公式圆柱的表面积公式是指计算圆柱体表面积大小的公式，它是圆柱体重要的几何量之一，主要用于计算物体的表面积、涂料用量、热交换器的传热面积等等。

下面我将详细介绍圆柱的表面积公式的相关知识。

一、圆柱体的定义圆柱体是由两个同心圆及其二者的所有直线段相垂直投影形成的几何体，称为圆柱体(简称圆柱)，简称为圆柱体或圆柱。

它的侧面是一个矩形，两个底面是两个圆，以底面圆心连线(称为轴)为轴线。

二、圆柱的基本参数1. 圆柱的高(h)：圆柱的两个底面的圆心之间连线的长度。

2. 底面半径(r)：圆柱底面的半径。

3. 侧面长度(l)：圆柱的侧面长度，也就是圆柱的卷长。

三、圆柱的表面积圆柱体的表面积分为几个部分，分别是：1. 上底圆面积2. 下底圆面积3. 侧面矩形的面积四、圆柱表面积公式的推导为了求圆柱体的表面积公式，我们需要如何推导出上述三个部分的面积。

1. 上底圆面积公式上底圆面积就是圆的面积，半径为r，所以其面积公式为：S1=πr²2. 下底圆面积公式下底圆面积同样也是圆的面积，半径为r，所以其面积公式为：S2=πr²3. 侧面矩形的面积公式将圆柱体展开后，得到的是一个矩形，而矩形的面积公式是：S3=hl所以，圆柱的表面积公式为：S=S1+S2+S3=πr²+πr²+hlS=2πr²+hl五、计算实例举个例子，如果圆柱底面半径为2，高为5，那么它的表面积是多少呢？根据上述公式，我们可以将半径r和高h代入公式，得到：S=2π×2²+2×2×5=12π+20≈56.57所以圆柱的表面积约为56.57。

六、总结圆柱的表面积公式是2πr²+hl，其中r为圆柱的底面半径，h为圆柱的高度，l为圆柱的侧面长。

这个公式可以帮助我们方便地计算圆柱体的表面积，是物理和数学领域非常重要的一个公式。

球体分成圆柱表面积公式的推导
球体分成圆柱表面积是一个比较常见的数学问题，推导其公式也就成为了一项重要的数学实践。

先考虑球心位于圆柱体对称轴上的情况。

画一条沿着圆柱的母线，从一个端点开始，旋转一周，得到一个环形的圆，并将其剖成若干个菱形。

每个菱形的对角线分别是圆柱的直径和一个圆的弧。

而圆柱体的表面积等于所有菱形的总面积加上两个底面积，这可以通过化简得到公式：
S = 2πrh + 2πr^2
其中，r是圆柱的半径，h是圆柱的高度，2πrh表示侧面积，2πr^2表示顶底面积。

若球心不在圆柱体对称轴上，可以想象球体上面划去一小块区域，对应于圆柱上的一条带，周长为2πr sinθ，带长为2πr cosθ。

这个带的面积为2πr^2 sinθ cosθ。

将圆柱体剖成若干个高为2πr cosθ的平行截面，得到的每个截面都在球体表面上割去一部分，并且每个截面上割掉的部分的面积与上面带的面积相等。

因此，球体分成圆柱的表面积就等于所有截面的表面积之和。

化简可得：
S = 2πrh + 2πr^2 sinθ cosθ
这就是球体分成圆柱表面积的公式。

第 1 页共 1 页。