平面直角坐标系经典讲义

建立平面直角坐标系【知识点介绍】1、 在直线上规定了原点、正方向、单位长度就构成了数轴。

2、 在平面内画两条互相垂直的数轴，其中水平的数轴叫X 轴（或横轴）取向右为正方向，铅直 的数轴叫Y 轴（或纵轴），取向上为正方向，X 轴或Y 轴统称为坐标轴，它们的交点是原点，这 个平面叫坐标平面。

a>0?b>0------------------------------ >X 第四象限• Pgby3、 坐标系中的任意一点的坐标是有序实数对，用（a, b ）来表示。

4、 各象限中的坐标符号：第一象限（+ ,+ ）,第二象限（- ，+ ）,第三彖限（-，-）,第四象限（+，-） 横轴上的点的坐标为（X, 0）;纵轴上的点的坐标为（0, Y ）5、 当两点的横坐标相同，纵坐标互为相反数时，这两点关于X 轴对称；当两点的纵坐标相同，横坐标互为相反数时，这两点关于Y 轴对称； 当两点的横坐标、纵坐标互为相反数时，这两点关于原点对称； 【例题精讲】 知识一、坐标系的理解 例1、平面内点的坐标是()第二象限* Pgby第一象限第三象限A 一个点B 一个图形C 一个数D —个有序数对【同步练习】1. 在平面内要确定一个点的位置，一般需要______ 个数据；在空间内要确定一个点的位置，一般需要______ 个数据.2、在平面直角坐标系内，下列说法错误的是( )A、原点O不在任何象限内B、原点O的坐标是0C、原点O既在X轴上也在Y轴上D、原点O在坐标平面内知识二、已知坐标系中特殊位置上的点，求点的坐标点在x轴上，坐标为(x,0)在x轴的负半轴上时，x<0,在x轴的正半轴上时，x>0点在y轴上，坐标为(0,y)在y轴的负半轴上时，yvO,在y轴的正半轴上时，y>0 第一、三象限角平分线上的点的横纵坐标相同(即在y=x直线上)；坐标点(x, y) xy>0 第二、四象限角平分线上的点的横纵坐标相反(即在y二-x直线上)；坐标点(x, y) xy<0 例1点P在x轴上对应的实数是一馆，则点P的坐标是________________________________________ ,若点Q在 >'轴上对应的实数是*,则点Q的坐标是_____________ 。

七年级数学学案平面直角坐标系知识点概述1、定义：平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系，简称为直角坐标系2、已知点的坐标找出该点的方法：分别以点的横坐标、纵坐标在数轴上表示的点为垂足，作x轴y轴的的垂线，两垂线的交点即为要找的点。

3、已知点求出其坐标的方法: 由该点分别向x轴y轴作垂线，垂足在x轴上的坐标是改点的横坐标，垂足在y轴上的坐标是该点的纵坐标。

4、各个象限内点的特征第一象限：（+，+）点P (x,y )，则x>0,y >0;第二象限：（-，+）点P (x,y )，贝9 x v0,y >0;第三象限：（-，-）点P (x,y )，则x v 0,y v 0;第四象限：（+，-）点P (x,y )，贝9 x > 0,y v 0;5、坐标轴上点的坐标特征：x轴上的点，纵坐标为零；y轴上的点，横坐标为零;原点的坐标为（0,0 ）。

两坐标轴的点不属于任何象限6、点的对称特征：已知点P（m, n）.关于x轴的对称点坐标是（m,-n）, 横坐标相同，纵坐标反号关于y轴的对称点坐标是（-m, n）纵坐标相同，横坐标反号关于原点的对称点坐标是（-m,-n）横，纵坐标都反号7、平行于坐标轴的直线上的点的坐标特征:平行于x轴的直线上的任意两点：纵坐标相等;平行于y轴的直线上的任意两点：横坐标相等。

8、各象限角平分线上的点的坐标特征：第一、三象限角平分线上的点横、纵坐标相等。

点P（a,b）关于第一、三象限坐标轴夹角平分线的对称点坐标是（b, a）第二、四象限角平分线上的点横纵坐标互为相反数。

点P（a,b）关于第二、四象限坐标轴夹角平分线的对称点坐标是（-b,-a）9、点P（x,y ）的几何意义：点P（x,y ）到x轴的距离为|y| ，点P（x,y ）至9 y轴的距离为凶。

10、点的平移特征：在平面直角坐标系中,将点（x,y 向右平移a个单位长度，可以得到对应点（x-a , y);将点（x,y 向左平移a个单位长度，可以得到对应点（x+a , y);将点（x,y ）向上平移b个单位长度，可以得到对应点（x, y + b）;将点（x,y ）向下平移b个单位长度，可以得到对应点（x，y —b）。

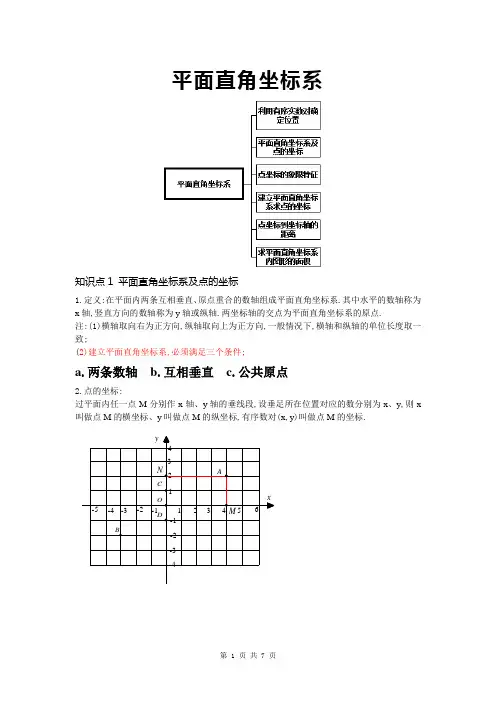
平面直角坐标系知识点1 平面直角坐标系及点的坐标1.定义:在平面内两条互相垂直、原点重合的数轴组成平面直角坐标系.其中水平的数轴称为x 轴,竖直方向的数轴称为y 轴或纵轴.两坐标轴的交点为平面直角坐标系的原点.注:(1)横轴取向右为正方向,纵轴取向上为正方向,一般情况下,横轴和纵轴的单位长度取一致;(2)建立平面直角坐标系,必须满足三个条件;a .两条数轴b .互相垂直c .公共原点2.点的坐标:过平面内任一点M 分别作x 轴、y 轴的垂线段,设垂足所在位置对应的数分别为x 、y ,则x 叫做点M 的横坐标、y 叫做点M 的纵坐标,有序数对(x ,y )叫做点M 的坐标.NM yx-1-2-3-41234-1-2-3-4-5654321O DCBA知识点2 点的坐标的象限特征3.探究活动.将任意点A放入直角坐标系中,由其所处的位置让学生确定点的坐标.在此过程中,学生将对由点确定坐标的方法不断深化,并逐渐理解并掌握点的坐标是一对有序的实数.并介绍象限的含义,同时,通过观察,让学生发现点在各个象限内以及点在坐标轴上的坐标特点.4.(1)各象限内点的坐标的符号的确定:P(a,b) 第一象限第二象限第三象限第四象限a,b与0的大小关系a>0,b>0 a<0,b>0 a<0,b<0 a>0,b<0 符号特征(+,+) (-,+) (-,-) (+,-)点P(a,b)在x轴上时记作P(a,0)点P(a,b)在y轴上时记作P(0,b)原点记作(0,0)(3)在平面直角坐标系中的点和有序数对是一一对应的关系.即:对于平面直内任意一点,都有唯一的有序数对与它对应.对于任意的有序数对,平面上都有唯一的一个点与它对应.知识点3 建立平面直角坐标系求点的坐标根据坐标描点的步骤:(1)找到该点的横坐标在x轴上对应的位置,过该位置作x轴的垂线;(2)找到该点的纵坐标在y轴上对应的位置,过该位置作y轴的垂线;(3)两线的交点即为要描出的点的位置.类型一利用有序实数对确定位置例1.如果约定街在前,巷在后,阳光花园在5街2巷的十字路口,用有序数对表示为（）（A）(2,5) （B）(5,2) （C）(5,5) （D）(2,2)例2.小明家的坐标为（1,2）,小丽家的坐标为（-1,-2）,如果规定向上为正北方向,则小丽家在小明家的（）（A）东南方向（B）东北方向（C）西南方向（D）西北方向类型二平面直角坐标系及点的坐标例1.有了平面直角坐标系,平面内的点就可以用一个来表示,点（3,-4）的横坐标是 ,纵坐标是 .类型三点坐标的象限特征例1.在平面直角坐标系中,点P（-2,5）在（）（A）第一象限（B）第二象限（C）第三象限（D）第四象限例2.若点P（a,b）在第四象限内,则a,b的取值范围是（）（A）a>0,b<0 （B）a>0,b>0 （C）a<0,b>0 （D）a<0,b<0类型四点坐标到坐标轴的距离例1.点P在第二象限,且到x轴的距离是2,到y轴的距离是3,则点P的坐标是______.类型五建立平面直角坐标系求点的坐标例1.如图是在方格纸上画出的小旗图案,若用(0,0)表示A点,(0,4)表示B点,那么C点的位置可表示为( )（A）(0,3) （B）(2,3)（C）(3,2) （D）(3,0)类型六求平面直角坐标系内图形的面积如图所示,在直角梯形OABC中,CB∥OA,CB＝8,OC＝8,∠OAB＝45°（1）求点A、B、C的坐标;（2）求△ABC的面积ABC练习题1.若点P （x ,y ）的坐标满足xy =0,则点P 必在（）（A ）原点 （B ）x 轴上 （C ）y 轴上 （D ）x 轴或y 轴上 2、已知()-++=230a b b ,则点P （-a ,-b ）的坐标为（ ）（A ）（2,3） （B ）（-3,3） （C ）（-2,3） （D ）（-2,-3） 3、若点A (2,m )在x 轴上,则点B (m -1,m +1)在 （ ）（A ）第一象限 （B ）第二象限 （C ）第三象限 （D ）第四象限 4.如图,△ABC 在直角坐标系中,（1）请写出△ABC 各点的坐标. （2）求出ABC S △（3）若把△ABC 向上平移2个单位,再向右平移2个单位得△A ′B ′C ′,在图中画出△A ′B ′C ′,并写出A ′、B ′、C ′的坐标.5.已知点A ()b a 2,3在x 轴上方,y 轴的左边,则点A 到x 轴、y 轴的距离分别为（ ） （A ）b a 2,3- （B ）b a 2,3- （C ）a b 3,2- （D ）a b 3,2-6.在平行四边形ACBO中,AO=5,则点B坐标为(-2,4)（1）写出点C坐标.（2）求出平行四边形ACBO面积.7.一个长方形在平面直角坐标系中三个顶点的坐标为（–1,– 1）、（– 1,2）、（3,– 1）,则第四个顶点的坐标为（）.（A）（2,2）（B）（3,2）（C）（3,3）（D）（2,3）8.已知点A(3a+5,a-3)在二、四象限的角平分线上,则a= .9.已知点P（2m-5,m-1 ）,当m为何值时,（1）点P在第二、四象限的平分线上？（2）点P在第一、三象限的平分线上？10.平行于x轴的直线上的任意两点的坐标之间的关系是( )（A）横坐标相等（B）纵坐标相等（C）横坐标的绝对值相等（D）纵坐标的绝对值相等11.如图所示,建立平面直角坐标系是点B、C的坐标分别为（0,0）,（4,0）,写出A、D、E、F、G的坐标,并写出所在象限.12.在平面直角坐标系中，若点P(x －2，x)在第二象限，则x 的取值范围为( ) A.0＜x ＜2 B.x ＜2 C.x ＞0 D.x ＞213.如果P （m+3，2m+4）在y 轴上，那么点P 的坐标是（ ） A ．（﹣2，0） B ．（0，﹣2） C ．（1，0） D ．（0，1）14.无论m 为何值，点A （m ，5﹣2m ）不可能在（ ）.A ．第一象限B ．第二象限C ．第三象限D ．第四象限15.在平面直角坐标系中，若m 为实数，则点（﹣2，m 2+1）在（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限16.若点A （﹣，﹣）在第三象限的角平分线上，则a 的值为（ ） A ． B ．﹣ C ．2 D ．﹣217.若点A （2，m ）在x 轴上，则点B （m ﹣1，m+1）在（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限18.点P 在四象限，且点P 到x 轴的距离为3，点P 到y 轴的距离为2，则点P 的坐标为（ ）A ．(3,2)--B ．(3,2)-C ．(2,3)D ．(2,3)-19.若点P （a ，a-2）在第四象限，则a 的取值范围是（ ） A ．-2＜a ＜0 B ．0＜a ＜2 C ．a ＞2 D ．a ＜020.下列两点中，关于y 轴对称的是（ ）A. (1,-3)和(-1,3)B. (3,-5)和(-5,3)C. (5,-4)和(5,4)D. (-2，4)和（2,4）21.在平面直角坐标系中，点 关于直线对称点的坐标是 ( ) A. B. C.D.22.△ABC在平面直角坐标系中的位置如图所示．(1)作出与△ABC关于x轴对称的△A1B1C1；(2)将△ABC向左平移4个单位长度，画出平移后的△A2B2C2.23.如图是丁丁画的一张脸的示意图，如果用（0，2）表示靠左边的眼睛，用（2，2）表示靠右边的眼睛，那么嘴的位置可以表示成（）A. （1，0）B. （﹣1，0）C. （﹣1，1）D. （1，﹣1）24如果将一张“8排3号”的电影票记为（8，3），那么电影票（3，8）表示的实际意义是________．25.如果将电影票上“6排3号”简记为(6，3)，那么“10排10号”可表示为_______；(7，1)表示的含义是___________．26.如下图，围棋盘的左下角呈现的是一局围棋比赛中的几手棋，为记录棋谱方便，横线用数字表示，纵线用英文字母表示，这样白棋②的位置可记为（E，3），则白棋⑥的位置应记为________．。

平面直角坐标系综合讲义一、【知识点拨】1.坐标平面内的点与有序实数对一一对应；2.点P （a ，b ）到x 轴的距离为│b │，• 到y 轴距离为│a │， 到原点距离为22a b +；3.各象限内点的坐标的符号特征：P （a ，b ）， P 在第一象限⇔a>0且b>0， P 在第二象限⇔a<0，b>0， P 在第三象限⇔a<0，b<0， P 在第四象限⇔a>0，b<0；4.点P （a ，b ）：若点P 在x 轴上⇔a 为任意实数，b=0；P 在y 轴上⇔a=0，b 为任意实数；P 在一，三象限坐标轴夹角平分线上⇔a=b ； P 在二，四象限坐标轴夹角平分线上⇔a=－b ； 5.点A （x 1，y 1），B （x 1，y 2）：A ，B 关于x 轴对称⇔x 1=x 2，y 1=－y 2； A 、B 关于的y 轴对称⇔x 1=－x 2，y 1=y 2； A ，B 关于原点对称⇔x 1=－x 2，y 1=－y 2； AB ∥x 轴⇔y 1=y 2且x 1≠x 2；AB ∥y 轴⇔x 1=x 2且y 1≠y 2（A ，B 表示两个不同的点）． 6点的平移：在平面直角坐标系中，教师寄语：对那些有自信心而不介意于暂时成败的人，没有所谓失败！对怀着百折不挠的坚定意志的人，没有所谓失败！对别人放手，而他仍然坚持；别人后退，而他仍然前冲的人，没有所谓失败！对每次跌倒，而立刻站起来；每次坠地，反会像皮球一样跳得更高的人，没有所谓失败！——雨果将点（x，y）向右平移a个单位长度，可以得到对应点（x＋a ，y）；将点（x，y）向左平移a个单位长度，可以得到对应点（x－a，y）将点（x，y）向上平移b个单位长度，可以得到对应点（x，y＋b）；将点（x，y）向下平移b个单位长度，可以得到对应点（x，y－b）。

二、【例题评析】例1（2011贵州贵阳，10分）【阅读】在平面直角坐标系中，以任意两点P（x1，y1）、Q（x2，y2）为端点的线段中点坐标为（x1+x22，y1+y22）．【运用】如图，矩形ONEF的对角线交于点M，ON、OF分别在x轴和y轴上，O为坐标原点，点E的坐标为（4，3），则点M的坐标为______；例2，在直角坐标系中，点A，B的坐标分别是（0，6），（－8，0），求Rt△ABO 的内心的坐标．三【综合能力训练】1.如图所示，在平面直角坐标系中，点A的坐标是（10，0），•点B的坐标为（8，0），点C，D在以OA为直径的半圆M上，且四边形OCDB是平行四边形，•求点C的坐标．2.如图所示，在直角坐标系中，矩形ABCD的边AD在x轴上，•点A在原点，AB=3，AD=5，矩形以每秒2个单位长度沿x轴正方向做匀速运动．同时点P从A点出发以每秒1个单位长度沿A─B─C─D的路线做匀速运动．当P点运动到D点时停止运动，矩形ABCD也随之停止运动．（1）求P点从A点运动到D点所需的时间；（2）设P点运动时间为t（s）；①当t=5时，求出点P的坐标；②若△DAP的面积为S，试求出S与t之间的函数关系式（并写出相应的自变量t•的取值范围）．3.将一矩形纸片OABC放在直角坐标系中，O为原点，C在x轴上，•OA=6，OC=10．（1）如图所示，在OA上取一点E，将△EOC沿EC折叠，使O点落在AB 边上的D点，求E点的坐标；（2）如图所示，将矩形变为矩形OA′B′C′，在OA′，OC′边上选择取适当的点E′，F′，将△E′OF沿E′F折叠，使O点落在A′B′边上的D′点，过D′作D′G•∥A′O交E′F于T点，交OC′于G点，求证：TG=A′E′．（3）在图的条件下，设T（x，y）：探求：y与x之间的函数关系式。

平面直角坐标系1．了解平面直角坐标系的产生过程；认识平面直角坐标系,理解横轴、纵轴、原点及象限；了解点与坐标的对应关系。

2．能够在给定的直角坐标系中，根据点的坐标指出点的位置，会由点的位置写出点的坐标。

3．了解平面直角坐标系中点之间的距离和平移的本质，充分利用数形结合解决平面直角坐标系相关应用。

1．在平面直角坐标系中表示点的坐标并能描点2．熟记概念及其特征，如平面直角坐标系、坐标轴、坐标原点、坐标平面、象限等等3．平面直角坐标系中两点间距离和平移的本质，掌握数形结合思想解决相关问题有序数对1、有序数对：用含有两个数的词表示一个确定的位置，其中各个数表示不同的含义，我们把这种有顺序的两个数a与b组成的数对，叫做有序数对,记作（a,b），如（2,3）（3,4）。

2、利用有序数对，可以很准确地表示出一个位置。

3、常见的确定平面上的点位置常用的方法（1）以某一点为原点（0，0）将平面分成若干个小正方形的方格，利用点所在的行和列的位置来确定点的位置。

（2）以某一点为观察点，用方位角、目标到这个点的距离这两个数来确定目标所在的位置。

例1.在奥运游泳馆“水魔方”一侧的座位席上，5排2号记为（5，2），则3排5号记为（）．练习1.根据下列条件，能确定位置的有哪些？①座位是2排4号；②某城市在东经118°，北纬39°；③家住前进路20号；④甲地距乙地20km；⑤沉船距A港50km练习2. 如图，是儿童乐园平面图．请建立适当的平面直角坐标系， 写出儿童乐园中各娱乐设施的坐标本类题考查了有序数对的具体表示形式，通过行和列具体确定平面中的具体位置。

平面直角坐标系1、平面内画两条互相垂直、原点重合的数轴，组成平面直角坐标系. 水平的数轴称为X轴或横轴，习惯上取向右为正方向；竖直的数轴为Y轴或纵轴，取向上为正方向；两个坐标轴的交点为平面直角坐标系的原点。

有了平面直角坐标系，平面内的点就可以用一个有序数对来表示了。

平面直角坐标系-位置认识1．小义同学给如图建立平面直角坐标系，使医院的坐标为（0，0），火车站的坐标为（2，2）．（1）写出体育场、文化馆、超市、宾馆、市场的坐标；（2）在图中标出小义家（3，﹣1），小锐家（﹣1，﹣1）和学校（﹣1，1）的位置．（3）小义从家途径小锐家到学校最近的路是个单位长度．平面直角坐标系-密码组合1．如图是一组密码的一部分，为了保密，许多情况下可采用不同的密码，请你运用所学的知识找到破译密码的“钥匙”．目前，已破译出“今天考试”的真实意思是“努力发挥”，若“今”所处的位置是（x，y），你找到的密码钥匙是（，），破译“正做数学”的真实意思是“”．平面直角坐标系-诗词调整1．如图，我们从唐代诗人韩愈的《早春呈水部张十八员外》和刘禹锡的《浪淘沙•其一》中各选取一句整齐排列放在平面直角坐标系中，“浪”的坐标是（1，1）．（1）“曲”和“酥”的坐标依次是和．（2）将第2行与第3行对调，再将第4列与第7列对调，“河”由开始的坐标最终变换为．（3）“雨”开始的坐标是，使它的坐标变换到（5，3），应该哪两行对调，同时哪两列对调？1．如图是一个平面直角坐标系．（1）请在图中描出以下6个点：A（0，2）、B（4，2）、C（3，4）A′（﹣4，﹣4）、B'（0，﹣4）、C′（﹣1，﹣2）（2）分别顺次连接A、B、C和A′、B'、C'，得到三角形ABC和三角形A′B′C′；（3）观察所画的图形，判断三角形A′B′C′能否由三角形ABC平移得到，如果能，请说出三角形A′B′C′是由三角形ABC怎样平移得到的；如果不能，说明理由．1.如图，△DEF是△ABC经过某种变换得到的图形，点A与点D，点B 与点E，点C与点F分别是对应点，观察点与点的坐标之间的关系，解答下列问题：（1）分别写出点A与点D，点B与点E，点C与点F的坐标，并说说对应点的坐标有哪些特征；（2）若点P（a+3，4﹣b）与点Q（2a，2b﹣3）也是通过上述变换得到的对应点，求a、b的值．平面直角坐标系-面积求解1．△ABC与△A'B'C'在平面直角坐标系中的位置如图．（1）分别写出下列各点的坐标：A'；B'；C'；（2）说明△A'B'C'由△ABC经过怎样的平移得到？．（3）若点P（a，b）是△ABC内部一点，则平移后△A'B'C'内的对应点P'的坐标为；（4）求△ABC的面积．1.已知：如图，把△ABC向上平移3个单位长度，再向右平移2个单位长度，得到△A′B′C′．（1）写出A′、B′、C′的坐标；（2）求出△ABC的面积；（3）点P在y轴上，且△BCP与△ABC的面积相等，求点P的坐标．1．如图，在平面直角坐标系中，点A（﹣3b，0）为x轴负半轴上一点，点B（0，4b）为y轴正半轴上一点，其中b满足方程3（b+1）＝6．（1）求点A，B的坐标；（2）点C为y轴负半轴上一点，且△ABC的面积为12，求点C的坐标；1．已知点P（a﹣2，2a+8），分别根据下列条件求出点P的坐标．（1）点P在x轴上；（2）点P在y轴上；（3）点Q的坐标为（1，5），直线PQ∥y轴；（4）点P到x轴、y轴的距离相等．1．已知，点P（2m﹣6，m+2）．（1）若点P在y轴上，P点的坐标为；（2）若点P的纵坐标比横坐标大6，求点P在第几象限？（3）若点P和点Q都在过A（2，3）点且与x轴平行的直线上，PQ＝3，求Q点的坐标．平面直角坐标系-文字叙述求解3 1．已知在平面直角坐标系中有一点M（2m﹣1，m﹣3）．（1）当点M到y轴的距离为1时，求点M的坐标；（2）当点M到x轴的距离为2时，求点M的坐标．1．在平面直角坐标系中，已知点M（m，2m+3）．（1）若点M在x轴上，求m的值；（2）若点M在第二象限内，求m的取值范围；（3）若点M在第一、三象限的角平分线上，求m的值．1．已知点P（3m﹣6，m+1），试分别根据下列条件，求出点P的坐标．（1）点P在y轴上；（2）点P在x轴上；（3）点P的纵坐标比横坐标大5；（4）点P在过点A（﹣1，2），且与x轴平行的直线上．1．如图所示，在平面直角坐标系中，点A，B的坐标分别为A（a，0），B（b，0），且a，b满足|a+2|+＝0，点C的坐标为（0，3）．（1）求a，b的值及SABC；△（2）若点M在x轴上，且SACM＝S△ABC，试求点M的坐标．△1．如图，A（﹣1，0），C（1，4），点B在x轴上，且AB＝3．（1）求点B的坐标；（2）求△ABC的面积；（3）在y轴上是否存在点P，使以A、B、P三点为顶点的三角形的面积为10？若存在，请直接写出点P的坐标；若不存在，请说明理由．1．如图在直角坐标系中，已知A（0，a），B（b，0）C（3，c）三点，若a，b，c满足关系式：|a﹣2|+（b﹣3）2+＝0．（1）求a，b，c的值．（2）求四边形AOBC的面积．（3）是否存在点P（x，﹣x），使△AOP的面积为四边形AOBC 的面积的两倍？若存在，求出点P的坐标，若不存在，请说明理由．1．已知：如图，△ABC的三个顶点位置分别是A（1，0）、B（﹣2，3）、C（﹣3，0）．（1）求△ABC的面积是多少？（2）若点A、C的位置不变，当点P在y轴上时，且SACP＝2S△ABC，△求点P的坐标？（3）若点B、C的位置不变，当点Q在x轴上时，且SBCQ＝2S△ABC△求点Q的坐标？1．已知点A（a，0）和B（0，b）满足（a﹣4）2+|b﹣6|＝0，分别过点A、B作x轴、y轴的垂线交于点C，如图所示，点P从原点出发，以每秒1个单位长度的速度沿着O﹣B﹣C﹣A﹣O的路线移动．（1）写出A、B、C三点的坐标；A，B，C；（2）点P在运动过程中，当△OAP的面积为6时，求点P的坐标；（3）当P运动14秒时，连接O、P两点，将线段OP向上平移h个单位（h＞0），得到O'P'，若O'P'将四边形OACB的面积分成相等的两部分，求h的值．1.如图，在平面直角坐标系中，已知A（0，a），B（b，0），C（b，c）三点，其中a、b、c满足关系式|a﹣2|+（b﹣3）2＝0，（c﹣4）2≤0（1）求a、b、c的值；（2）如果在第二象限内有一点P（m，），请用含m的式子表示四边形ABOP的面积；（3）在（2）的条件下，是否存在点P，使四边形ABOP的面积与△ABC的面积相等？若存在，求出点P的坐标，若不存在，请说明理由．1．在平面直角坐标系中，O为坐标原点，过点A（8，6）分别作x轴、y轴的平行线，交y轴于点B，交x轴于点C，点P是从点B出发，沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点，运动时间为t（秒）．（1）直接写出点B和点C的坐标B（，）、C（，）；（2）当点P运动时，用含t的式子表示线段AP的长，并写出t的取值范围；（3）点D（2，0），连接PD、AD，在（2）条件下是否存在这样的t值，使SAPD＝S四边形ABOC，若存在，请求出t值，若不存在，请说明理由．△1.如图，在平面直角坐标系中，一动点从原点O出发，按向上、向右、向下、向右的方向依次平移，每次移动一个单位，得到点A1（0，1），A2（1，1），A3（1，0），A4（2，0），…那么点A2022的坐标为．2.在平面直角坐标系中，点A1（1，0），A2（2，3），A3（3，8），A4（4，15），…，用你发现的规律确定点A n的坐标为．1.如图，在平面直角坐标系中，一动点从原点O出发，沿着箭头所示方向，每次移动1个单位长度，依次得到点P1（0，1），P2（1，1），P3（1，0），P4（1，-1），P5（2，-1），P6（2，0）…，则P2020的坐标是2.如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（﹣1，1），第2次接着运动到点（﹣2，0），第3次接着运动到点（﹣3，2），…，按这样的运动规律，经过第2022次运动后，动点P的坐标是1.点A在y轴正半轴上，OA＝a，点B位于第二象限，且点B到两坐标轴的距离均为b，其中a、b满足b＝++4．（1）a＝，b＝；（2）点C在x轴的负半轴上，射线CD∥AB．①如图1，过C作射线CE交y轴于点E，使∠DCE＝3∠ECO，过A作射线AF交CE于点F，使∠BAF＝3∠OAF，求∠AFE的度数；1.如图，在平面直角坐标系中，点O（0，0），A（0，a），C（b，0）满足+|b﹣2|＝0．（1）直接写出A、C两点的坐标．（2）如图2，点G是第二象限上的点，连OG，且OG∥AC，点F是线段AC上一点，满足∠AOG＝∠AOF．点E是射线OA上一动点，连CE交直线OF于点H，当点E在射线OA上运动的过程中，请确定∠OHC，∠ACE 和∠OEC的数量关系，并说明理由．平面直角坐标---动点和面积压轴1.如图，在平面直角坐标系中，点O（0，0），A（0，a），C（b，0）满足+|b﹣2|＝0．（1）直接写出A、C两点的坐标．（2）如图1，已知坐标轴上有两动点P、Q同时从O点出发，P点沿x轴正方向以2个单位长度每秒的速度匀速移动，Q点以1个单位长度每秒的速度沿y轴正方向移动，点D（1，2）为线段AC上一点，设运动时间为t（t＞0）秒．问：是否存在这样的t，使SDPC＝S三角形DQO，若存在，请求出t的值；三角形若不存在，请说明理由．。