一元线性回归系数比值不确定度的评定

一元线性校准曲线不确定度评定与适用条件的讨论一、引言校准曲线是物质定量分析中最为基础的测量方法之一，常用于化学分析、光谱分析、质谱分析等领域中。

在进行定量分析时，对于复杂的样品或者低浓度测量的样品，我们常常需要使用校准曲线来进行定量分析。

而校准曲线的精确度和可信度直接决定了测量结果的准确性和可靠性，因此，对于校准曲线的不确定度评定与适用条件的讨论，具有重要的理论意义和实际应用价值。

二、一元线性校准曲线的基本原理一元线性校准曲线是一种非常常用的校准曲线，其基本原理是利用已知浓度的标准溶液制备一系列不同浓度的溶液，并以这些溶液的反应值或者信号强度等作为样品中物质的含量来制备一条曲线。

一元线性校准曲线是一条直线，其表达式为：y = ax + b其中，y 代表样品测量值或反应值的大小，x 代表样品中物质的浓度，a 和b 分别是校准曲线的斜率和截距。

三、一元线性校准曲线的不确定度评定1.样品准备误差样品准备误差是样品制备过程中的误差，包括样品的称量误差、体积误差、混匀误差等。

这些误差会导致校准曲线中样品测量值的误差，从而影响到定量测量的准确性。

在确定校准曲线的不确定度时，需要对样品准备误差进行评估，计算其贡献值。

2.样品分析误差样品分析误差是样品测量过程中的误差，包括仪器误差、测量方法误差、操作误差等。

样品分析误差的大小直接影响到校准曲线的精确度和可信度，因此在评定校准曲线的不确定度时，需要对样品分析误差进行评估。

3.校准曲线斜率和截距误差校准曲线的斜率和截距是校准曲线的两个重要参数，它们的大小直接影响到样品浓度与测量值的转换关系。

在进行校准曲线的不确定度评定时，需要对校准曲线的斜率和截距误差进行评估。

4.样品测量值偏差样品测量值偏差是样品测量中产生的偏差，包括零位偏差、系统偏差、随机误差等。

样品测量值偏差的大小会直接影响到校准曲线的精确度和可信度，因此在进行校准曲线的不确定度评定时，需要对样品测量值偏差进行评估。

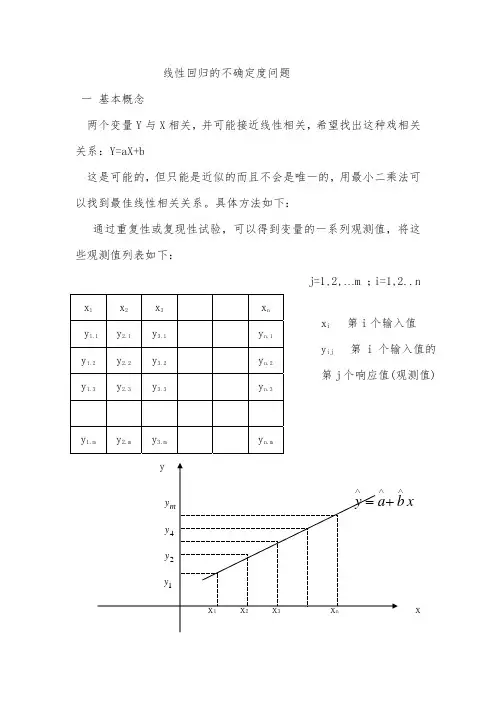
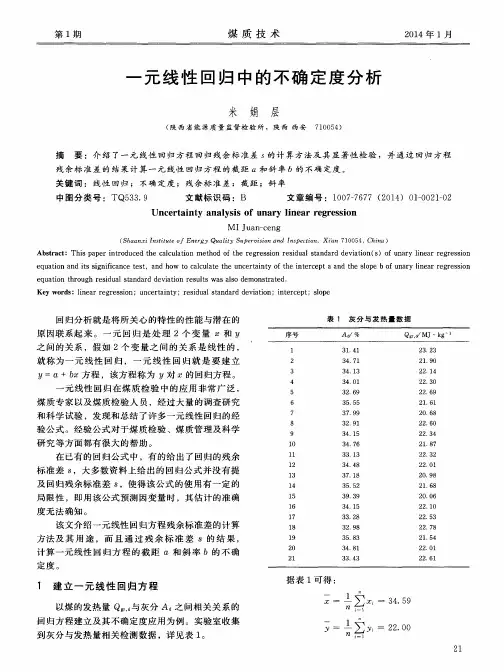
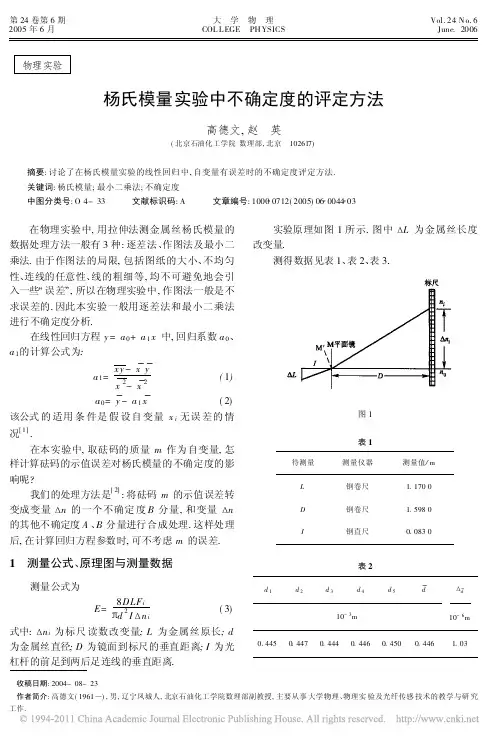
直线回归分析及其测量不确定度评定第一节 一元线性回归分析当输入量X i 的估计值x i 是由实验数据用最小二乘法拟合的曲线上得到时，曲线上任何一点和表征曲线拟合参数的标准不确定度，可以用有关的统计程序评定。

例如有两个估计值x ，y 有线性关系y =a +bx ，对其独立测得若干对数据(x 1,y 1)，(x 2,y 2)，⋯，(x n ,y n )，n >2，欲求取参数a ，b 及其标准不确定度，以及预期估计值及其标准不确定度，则需要应用最小二乘法。

最小二乘法是以“残差平方和最小”为条件求得最佳值并拟合成最佳直线、最佳曲线。

图13.1给出了直线拟合的最小二乘法示意图。

图中，x i ，y i 是观测数据，v i 是残差，a 是拟合直线的截距，b 是拟合直线的斜率。

呈直线的标准曲线用下式表示：y a bx =+ (13.1)式中b 是直线的斜率（回归系数），a 是截距。

各实验数据点可表示为（x i ，y i ）i =1,2,…,n 。

误差方程可用残差v i 表示为：)()()(222111n n n bx a y v bx a y v bx a y v +-=+-=+-=需要使残差平方和最小[]∑∑=+-=m in )(22i i i bx a y v 因此须同时对a 和b 求偏导数并使其为零，得到联立方程[]⎪⎪⎩⎪⎪⎨⎧=-+=---=∂∂=-+=---=∂∂∑∑∑∑∑∑====0222)(2,0222)(21121212ni i i n i i n i i i i n i i i i y x x b x na x bx a y b v y n x nb na bx a y a v式中，1111,nnii i i x x y y n n ====∑∑首先用联立方程求解b0112=+-⋅-⋅∑∑==ni ni i i i y x x b x y n x x nby i y i x ixv i a拟合直线测量数据 图13.1 最小二乘法示意图∑∑==⋅--=ni i ni i i xx n x yx n y x b 121式中，以上各式中，x 是x 值的平均值，y 是y 值的平均值。

仪器分析中线性回归标准曲线法分析结果不确定度评估一、前言对测试方法制定不确定度评估程序是ISO/IEC 17025对实验室的要求[1]，也是检验工作的需要。

由ISO 等7个国际组织联合发布的《测量不确定度表达指南》[2]采用当前国际通行的观点和方法，使涉及测量的技术领域和部门可以用统一的准则对测量结果及其质量进行评定、表示和比较，满足了不同学科之间交往的需要[3]。

采用《测量不确定度表达指南》对测试结果不确定度进行评估，也是检验工作同国际标准接轨的需要。

线性回归标准曲线法是仪器分析中最常用的方法，这类仪器包括原子吸收分光光度计、发射光谱仪、分光光度计、气相（液相）色谱仪等。

这类分析测定结果的不确定度都有相似的来源，可概括为仪器精密度、标准物质不确定度及溶液制备过程中带来的不确定度等。

因此，可用相似的方法对它们进行评估。

本文以ICP-AES 法测定钢铁中磷为例，推导了仪器分析中线性回归标准曲线法测定不确定度的计算方法，并提供了计算过程所需的各参数的采集和计算方法，评估了标准不确定度、自由度和扩展不确定度的数值。

二、测定过程和数学模型仪器分析中线性回归标准曲线测定方法，利用被测物质相应的信号强度与其浓度成正比关系，通过测定已知浓度的溶液（即标准溶液）的信号强度，回归出浓度-信号强度标准曲线，从标准曲线上得到被测定溶液信号强度相应的浓度。

计算过程的数学模型如下：用y i 和y t 分别表示标准溶液和被测溶液的信号线强度，以x i 和x t 分别表示第i 个标准溶液和被测样品溶液的浓度，i=1~n ，n 表示标准溶液个数，则：y a bx t t =+ (1)其中，b xx y y xx ii i nii n=---==∑∑()()()121(2)a y bx =- (3) （1）式也可表示成：x y abt t =- (4) 把式（2）、（3）代入式（4）得：x y y xx xx y y x t t ii nii i n=----+==∑∑()()()()211（5）式（5）表明了被测量x t 与输入量x 1,x 2...x n 和y 1,y 2...y n 、y t 的函数关系，可简写成：x t f x x x n y y y n y t=(,...,,...,)1212 由上式可知，样品溶液浓度测定结果不确定度可分成标准溶液浓度不确定度分量及其信号强度不确定度分量和被测定溶液信号强度不确定度分量，其中标准溶液浓度不确定度分量可由标准样品标称含量不确定度和配制过程引入的不确定度合成得到，而信号强度不确定度分量是由仪器测量的误差引起的，可从仪器的精密度数据得到。

利用回归方程进行不确定度评定黄焕钧 张晋东莞市荣昌化工有限公司摘要本实验通过ICP法测定油漆样品中Ba元素为例，应用数理统计学中的最小二乘法建立其回归方程，同时针对校准曲线引入的不确定度进行评定。

该评定方法在实际工作中可以作为利用回归方程计算检测结果这一类型的不确定度评定的参考。

一切测量结果都不可避免的具有不确定度，一份完整的检测报告应包括对其不确定度的评定。

利用回归方程计算检测结果是分析化学中最常用的计算方法。

本文根据国家技术监督局发布的《测量不确定度评定和表示》(JJF1059-1999)，以使用ICP法测定考核样品中Ba元素为例，利用数理统计学中的最小二乘法进行直线回归计算。

同时由于实验中产生不确定度的因素通常包括检测仪器、实验环境、标准物质、人员操作和分析方法，而本次主要对校准曲线的非线性引起输出值得不确定度U(C)进行评定与评估。

1 实验部分1.1 主要仪器和试剂岛津ICPE-9000，德国利曼的微波消解系统，HNO3（AR）。

浓度为1000μg/mL的Ba单元素标准溶液（从国家有色金属及电子材料分析测试中心购买）。

1.2 标准使用液的配制用2mL移液管吸取浓度为1000μg/mL的Ba标准溶液到100 mL量瓶中，加入3％（v/v）的HNO3介质定容至刻度线，从而得到20μg/mL单元素标准溶液；用13%（v/v）的HNO3分别稀释100、50、33、25和20倍，分别得到浓度为0.2、0.4、0.6、0.8与1.0μg/mL的标准溶液。

1.3 实验方法及过程简述将湿的油漆样品喷在玻璃板上，烘干，用小刀刮取，称量0.1g左右，然后加入约8mL HNO3放入微波消解系统进行消解。

消解完成待冷却后，将其过滤定容于50mL容量瓶中。

然后利用ICPE-9000光谱仪，对标准使用溶液进行测试，测出Ba标准系列的强度值A，计算强度值A与浓度关系的回归方程，然后测量样品溶液中的强度值，由回归方程可计算出样品溶液中被测组分中Ba的浓度。

针对JJF 1305-2011校准规范中几点问题的探讨
解岩;曹春;张曦文
【期刊名称】《计测技术》
【年(卷),期】2016(0)S1
【摘要】针对JJF 1305-2011《线位移传感器校准规范》中一元线性回归参数公
式存在的问题,本文基于最小二乘法从方差角度给出了其正确表达式,并对回归系数
的无偏性加以论证。

同时,从考量线位移传感器重要指标出发,利用不确定度传递率,计算线性度的不确定度,并讨论其回归系数及其重复性等因素引起的不确定度分量。

【总页数】3页(P232-234)
【关键词】元线性参数;线性度;不确定度
【作者】解岩;曹春;张曦文
【作者单位】中航工业第一飞机设计研究院
【正文语种】中文
【中图分类】TB97
【相关文献】
1.《JJF 1057-1998数字存储示波器校准规范》中扫描时间因数校准过程及存在问题探讨 [J], 宋剑波;李坚;刘洪贺;寇琼月
2.对 JJF1064－2010《坐标测量机校准规范》有关问题的探讨 [J], 陈龙;颜宇;李
钢
3.对现行JJF 1066-2000《测长机校准规范》中问题的探讨 [J], 孙云霞;孙友群;周
红光;樊瑞昕;刘瑞峰
4.关于JJF1255-2010《厚度表校准规范》和JJF1488-2014《橡胶、塑料薄膜测厚仪校准规范》几点理解 [J], 王艳;刘钊
5.JJF(浙)1096-2014《药物溶出度仪校准规范》问题探讨 [J], 韩素超;张红中;祖振涛;王昊苏;孙若男
因版权原因，仅展示原文概要，查看原文内容请购买。

一元线性回归系数比值不确定度的评定罗颖【摘要】In this paper regression coefficient correlation was analyzed and the formula of uncertainty of regression coefficient ratio in one dimensional linear regression equation was derived. The shortcomings in some documents about the evaluation of uncertainty of regression coefficient ratio were pointed out in this paper.%分析一元线性回归系数的相关性，导出一元线性回归系数比值不确定度的计算公式，指出了某些文献中有关回归系数比值不确定度评定存在的问题．【期刊名称】《赣南师范学院学报》【年(卷),期】2011(032)006【总页数】4页(P92-95)【关键词】线性回归;回归系数比值;相关系数;不确定度【作者】罗颖【作者单位】赣南师范学院物理与电子信息学院,江西赣州341000【正文语种】中文【中图分类】O212在大学物理实验中，经常遇到二物理量x、y间存在线性关系，常选择线性模型用最小二乘法对测量数据进行拟合(一元线性回归)，得到回归方程y=a+bx中参数的最佳估计值a、b(称为回归系数)以及它们的标准偏差sa、sb，然后根据回归系数比值求出有关物理量. 比如弹簧振子中弹簧的有效质量m有效是回归直线的截距与斜率的比值, 即折合系数文献[1](2000年，第3版)给出了折合系数c的不确定度公式：显然，上式的成立条件是a、b是线性无关的. 回归系数a、b线性无关吗？文献[2](2007年，第4版)修订了上式，给出了折合系数c的不确定度公式：式中的相关系数为回归系数a,b之间的相关系数ra,b等于测量量x,y之间的相关系数r吗？如何计算回归系数a,b之间的相关系数？本文将讨论一元线性回归系数的相关性和评定一元线性回归系数比值C=a/b的不确定度.1 间接测量量的标准偏差传递公式为简单起见，设间接测量量f是直接测量量x,y的函数，即f=f(x,y)(1)在相同的条件下，对x,y作了n次测量：xi,yi(i=1,2,…,n)，其平均值分别为真值分别为X，Y. 则间接测量量的真值为F=f(X,Y).将式(1)在X,Y附近作泰勒展开(只保留到一阶小量)，得令上式移项后在对n次测量值求平方和，得等式两边同除以n，可得引入标准误差(2)将上式可改写为(3)式中rx,y为x,y的相关系数(4)上式中的cov(x,y)称为协方差, cov(x,y)=∑(xi-X)(yi-Y), 式(3)是关于标准误差的方和根法合成公式. 如果x和y彼此独立，则有rx,y=0，这时，式(3)可简化为(5)上述公式只具有理论意义，无法通过测量来实现，因为真值未知，也不可能作无限多次测量.在有限次测量中，直接测量量x,y的最佳值分别为间接测量量f的最佳值为可以取标准偏差(6)作为标准误差σ(X)、σ(Y)的估计值，则式(3)、式(4)可分别改写为(7)(8)相关系数的绝对值│rx,y│≤1，相关系数的数值大小表示了相关程度的好坏.rx,y=±1表示变量x、y完全线性相关，拟合(回归)直线通过全部实验点. 当rx,y=1时，拟合直线的斜率大于零；当rx,y=-1时，拟合直线的斜率小于零；当│rx,y│<1时，实验点之间的线性不大好，│rx,y│越小线性越差，rx,y=0表示变量x与y完全不相关.2 一元线性回归系数的相关性用最小二乘法得到的一元线性回归系数a、b是相关变量，可以证明它们的协方差[3]为(9)式中sy是yi的标准偏差(10)r为x,y之间的相关系数(11)回归直线截距a和斜率b的标准偏差分别为(12)(13)回归直线截距a和斜率b之间的相关系数为(14)由上式可知，回归直线截距与斜率之间的相关系数ra,b<0，表明截距与斜率是相关变量，且呈负相关. 当ra,b=-1时，表示多次“组合测量”得到的回归直线截距ai与斜率bi，在a-b图上描绘的实验点(ai，bi)均在一条斜率小于零的直线上；当│ra,b│<1时，实验点之间的线性不大好，│ra,b│越小线性越差.3 回归直线截距与斜率比值的不确定度令回归直线截距a与斜率b的比值为(15)根据式(7)，有设回归系数a、b不确定度的B类分量较小，可略去不计，则u(a)=sa，u(b)=sb，u(C)=s(C)，令ur(a)=u(a)/a， ur(b)=u(b)/b， ur(C)=u(C)/C，有(16)又根据式(14)，有(17)或(18)式(16)～式(18)是回归直线截距与斜率比值的相对不确定度的计算公式. 回归直线截距与斜率是负相关的，交叉项的相对不确定度分量为(19)4 应用举例4.1 回归直线截距与斜率之间的相关系数不等于零文献[1]的测量举例中，折合系数c=a/(bm0)=C/(m0)，回归系数a、b不确定度的B类分量较小，略去不计，m0是在分析天平上测出的，其不确定度也较小，也略去不计.在此取u(a)=sa，u(b)=sb.应用公式(20)计算结果分别为锥形弹簧振子：r=0.999 992，u(c)=0.002 4(文献[1]中u(c)=0.000 8为笔误)柱形弹簧振子：r=0.999 93，u(c)=0.003由于回归直线截距与斜率是相关变量，若忽略弹簧质量m0的不确定度，则折合系数c=a/(bm0)的不确定度u(c)的计算公式应为(21)笔者根据式(14)、式(21)处理文献[1]的实验数据，正确结果分别为：锥形弹簧振子：r=0.999 992，ra,b=-0.885 12，u(c)=0.002 7,其中折合系数c 的相对不确定度ur(c)及其分量分别为柱形弹簧振子：r=0.999 940，ra,b=-0.904 68，u(c)=0.004 5,其中折合系数c 的相对不确定度ur(c)及其分量分别为显然，回归直线截距与斜率是负相关的，此例的计算结果表明，交叉项的相对不确定度分量是不能忽略不计的，式(20)并不成立.4.2 回归直线截距与斜率之间的相关系数ra,b不等于测量量x,y之间的相关系数r 文献[2]的测量举例中，取u(a)=sa，u(b)=sb，ra,b=r. 应用公式(22)计算结果分别为锥形弹簧振子：ra,b=rx,y=r=0.999 992,u(c)=0.001 9柱形弹簧振子：ra,b=rx,y=r=0.999 93, u(c)=0.000 7笔者根据式(14)、式(21)处理文献[2]的实验数据，正确结果分别为：锥形弹簧振子：rx,y=r=0.999 992，ra,b=-0.885 12，u(c)=0.002 7柱形弹簧振子：rx,y=r=0.999 940，ra,b=-0.904 68，u(c)=0.004 5显然，回归直线截距与斜率的相关系数ra,b不等于测量量x,y的相关系数rx,y=r. 此例中两者是异号的，即测量量x,y之间的相关系数rx,y>0，表明测量量x,y是正相关，回归直线截距与斜率之间的相关系数ra,b<0，表明回归直线截距与斜率是负相关. 由此可知，式(22)并不成立. 根据式(21)计算u(c)值必定大于文献[1]的值.由于文献[2]错误地认为ra,b=rx,y=r，故导致u(c)值反而比文献[1]的还小.综上所述，回归直线截距与斜率之间的相关系数ra,b<0，截距与斜率是负相关变量，其相关系数ra,b不等于测量量x,y的相关系数rx,y.在评定回归系数比值的不确定度时，由于回归直线截距与斜率是相关变量，所以，不仅要计算截距a和斜率b的偏差对总不确定度的贡献，而且必须计入其交叉项对总不确定度的贡献.【相关文献】[1]杨述武,马葭生,贾玉民,等.普通物理实验(一、力学及热学部分)[M].北京:高等教育出版社，2000：143-147.[2]杨述武,赵立竹,沈国土.普通物理实验1力学及热学部分[M].北京:高等教育出版社，2007：95-99.[3]唐象能,戴俭华.数理统计[M].北京: 机械工业出版社，1994：154-167.。

依据JJF1059-1999《测量不确定度评定与表示》和CNAS-CL10：2006《检测和校准实验室能力认可准则在化学检测领域的应用说明》。

应用现代统计学理论对于整个过程的不确定度的来源评定和评估，确定了测试结果的置信区间。

以及对于用同一种制样方法不同的样品的不确定度评定只要考虑样品基体对于测试的影响就可以，具有很强的代表性。

1. 分析方法和测试程序第一步：刮下样品涂层，称取样品重量0.2394g 到烧杯中。

第二步：加入10ml 浓硝酸进行电热板消解（剩下约3-4ml ），将样品过滤后，定容到50ml 的容量瓶中，摇动容量瓶使其混合均匀。

第三步：利用标准溶液采用最小二乘法对仪器ICP 校准。

第四步：用ICP —OES 测试由此得到溶液中各元素的含量，计算材料中可溶性元素的含量。

第五步：计算结果并出具测试报告。

2.被测量及其数学模型样品中重金属含量即为被测量，报告要求结果用每千克样品中含重金属的质量R 来表示：R = 0ml sample C Vd m ⨯其附加参数为：R ：每千克样品中含重金属的质量R （mg/kg ）V ml ：消解液的体积（mL ） m ：样品的质量（g ）d ：稀释因子，由于样品没有稀释，因此d=1.C 0：在消解溶液中各重金属的浓度（mg/L ） 其中：0C =100)(B B A -mg/L其中： C 0：在消解溶液中各重金属的浓度（mg/L ）B 0：校准曲线的截距 B 1：校准曲线的斜率A 0：消解溶液中金属的吸光度3.测量不确定度来源分析产生不确定的因素通常包括检测仪器、实验环境、标准物质、前处理方法、人员操作和分析方法。

本次评定主要考虑A类不确定度（测试重复性的标准偏差）和B类不确定度（包括天平误差和分辨率引入的不确定度、标准物质引入的不确定度、容量瓶误差引入的不确定度、测试设备引入的不确定度、温度变化引入的不确定度等）。

4.不确定度分量的评定4.1样品质量的测量不确度以FA2004N电子天平为例来计算，通常称量先扣除皮重后由天平直接读数给出，此时，称量的不确定度主要包括：测量重复性、分辨率(数字天平的量化误差)及误差，而误差产生的不确定度主要是其线性分量。