《平面的法向量与平面的向量表示》

平面的法向量定义平面的法向量是指垂直于该平面的矢量。

在数学和物理学中，法向量是研究平面性质和解决与平面相关问题的重要工具。

本文将介绍平面的法向量的概念、性质和应用。

一、概念平面的法向量是指与该平面垂直的矢量，它垂直于平面的每一个点。

平面上的每个点都有一个唯一的法向量。

法向量可以用有序数对或坐标表示，也可以用矢量符号表示。

通过法向量，我们可以确定平面的方向和倾斜程度。

二、性质1. 平面的法向量与平面上的任意两个不重合的向量都垂直。

2. 平面的法向量与平面上的任意两个平行的向量也平行。

3. 平面的法向量的模长等于平面上任意两个不重合向量的模长的乘积再乘以它们的夹角的正弦值。

三、求法向量的方法1. 已知平面上的三个点A、B、C，可以通过向量运算求出平面的法向量。

设向量AB=a，向量AC=b，则平面的法向量n=a×b，其中“×”表示向量的叉乘。

2. 已知平面的一般方程Ax+By+Cz+D=0，可以用系数A、B、C构成的向量作为平面的法向量。

四、应用1. 判断平面的位置关系：通过比较两个平面的法向量可以判断它们的位置关系，如平行、垂直或相交。

2. 求直线与平面的交点：直线与平面相交时，可以使用平面的法向量和直线的方向向量求解交点的坐标。

3. 求平面的方程：已知平面上的一点和法向量，可以利用点法式或一般方程求解平面的方程。

4. 求平面的倾斜度：平面的法向量可以用来表示平面的倾斜程度，根据法向量的大小可以判断平面的倾斜程度。

总结：平面的法向量是垂直于该平面的矢量，它可以用来描述平面的方向和倾斜程度。

通过法向量，我们可以判断平面的位置关系、求解直线与平面的交点、求解平面的方程以及判断平面的倾斜程度。

熟练掌握平面的法向量的概念、性质和应用，对于解决与平面相关的问题具有重要意义。

平面向量的平面方程与法向量平面向量是指在平面内既有大小又有方向的向量，通过平面向量可以确定平面上的一些特征，其中包括平面方程和法向量。

本文将详细介绍平面向量的平面方程与法向量的相关概念和性质。

1. 平面向量的表示与性质平面向量通常用箭头表示，箭头的方向表示向量的方向，而箭头的长度表示向量的大小。

平面向量的表示可以用两点表示，即从一个点A指向另一个点B得到的向量，记作AB。

根据平行四边形法则，平面向量的大小等于其对应的对角线的大小。

对于平面向量$\vec{a}$和$\vec{b}$，其性质如下：- 加法性质：$\vec{a}+\vec{b}=\vec{b}+\vec{a}$，即向量的加法满足交换律；- 数乘性质：$k(\vec{a}+\vec{b})=k\vec{a}+k\vec{b}$，即数与向量的加法满足分配律；- 数乘性质：$(k+l)\vec{a}=k\vec{a}+l\vec{a}$，即不同数与向量相乘满足分配律。

2. 平面向量的平面方程平面向量的平面方程表示了该向量所在平面的特征。

平面方程的一般形式为$Ax+By+Cz+D=0$，其中A、B和C是方程的系数，D是常数。

需要注意的是，A、B和C不全为0。

以平面上一点P(x, y, z)为例，该点到平面上已知点Q的向量为$\vec{n}$，若平面上的任意一点M(x', y', z')到点Q的向量为$\vec{p}$，则平面方程可以表示为$\vec{np}=0$。

3. 平面向量的法向量对于平面向量的平面方程而言，平面的法向量起着重要的作用。

法向量是垂直于给定平面的向量，可以用来描述平面的方向和倾斜度。

对于平面的法向量，有以下性质：- 若$\vec{n}$是平面方程$Ax+By+Cz+D=0$的法向量，则$\vec{n}(A, B, C)$；- 若平面有一个与$\vec{n}$同向的法向量，其中$\vec{n}$有大小和方向，$\vec{m}=k\vec{n}$，其中k是一个实数。

平面向量的法向量和单位向量平面向量的法向量和单位向量是数学中常见的概念。

在本文中，将详细介绍平面向量的法向量和单位向量的定义、性质以及求解方法。

通过对这两个概念的深入理解，能够在解决相关问题时做出正确的判断和计算。

1. 平面向量的法向量平面向量的法向量是指与给定向量垂直的向量。

对于一个平面向量[a, b]，其法向量可以表示为[-b, a]或[b, -a]，其中a和b分别表示平面向量的分量。

根据这个定义，可以得到法向量与原向量垂直的性质。

2. 单位向量单位向量是指模长为1的向量。

对于平面向量[a, b]，其单位向量可以表示为[a/|a|, b/|a|]或[a/|b|, b/|b|]，其中|a|和|b|分别表示平面向量的模长。

单位向量的定义使得它可以用来表示方向而不考虑具体的大小。

3. 平面向量的法向量和单位向量的性质平面向量的法向量和原向量垂直，即两个向量的点积为零。

设向量[a, b]和其法向量[-b, a]，则有a*(-b) + b*a = 0。

这可以从向量的乘法和点积的定义出发进行推导。

平面向量的单位向量与原向量的方向相同或相反，即两个向量的夹角为0或π。

设向量[a, b]和其单位向量[a/|a|, b/|a|]，则有acos(a/|a|*a) +bcos(b/|a|*b) = |a||a|/|a| = |a|，其中acos和bcos分别表示两个向量的夹角的余弦值。

4. 求解平面向量的法向量和单位向量的方法平面向量的法向量可以通过简单的计算得到。

对于向量[a, b]，其法向量为[-b, a]或[b, -a]。

通过交换分量的位置并改变其中一个分量的符号即可求得。

单位向量的求解需要先计算出平面向量的模长，然后将分量除以模长即可得到。

对于向量[a, b]，其单位向量为[a/|a|, b/|a|]或[a/|b|, b/|b|]。

分别用向量的分量除以模长即可得到单位向量。

5. 实例应用平面向量的法向量和单位向量在几何学、物理学等领域都有广泛的应用。

平面的法向量和方向向量平面的法向量和方向向量是平面几何中的重要概念，它们在描述平面的性质和运动方向时起到了关键作用。

本文将分别介绍平面的法向量和方向向量，并探讨它们的应用和相关性质。

一、平面的法向量平面的法向量是指垂直于该平面的向量。

设平面P上有一条直线L，经过L上的两点A和B可以确定一条向量AB。

如果向量AB垂直于平面P，那么向量AB就是平面P的法向量。

平面的法向量有以下性质：1. 法向量与平面上任意两个垂直向量的内积为零。

设向量a和向量b是平面P上的两个垂直向量，向量n是平面P的法向量，则有a·n=0，b·n=0。

2. 平面上的两个垂直向量的内积为零时，它们是平面的法向量的倍数关系。

设向量a和向量b是平面P上的两个垂直向量，向量n是平面P的法向量，则有a·n=0，b·n=0，因此存在实数k，使得a=k·n，b=k·n。

3. 平面上的两个非零向量的叉积是平面的法向量的倍数。

设向量a 和向量b是平面P上的两个非零向量，向量n是平面P的法向量，则有向量a×b=k·n，其中k为实数。

平面的法向量在几何和物理学中有广泛的应用。

例如，在计算平面上的点到另一平面的距离时，可以利用平面的法向量来求解。

同时，在力学中，平面的法向量也被用来描述平面上的压力和力的作用方向。

二、平面的方向向量平面的方向向量是指平面上的一个非零向量，它表示了平面上的一个方向。

设平面P上有一条直线L，经过L上的两点A和B可以确定一条向量AB。

如果向量AB不是平面P的法向量，那么向量AB 就是平面P的方向向量。

平面的方向向量有以下性质：1. 平面上的两个非零向量的线性组合是平面的方向向量。

设向量a 和向量b是平面P上的两个非零向量，向量c=k1·a+k2·b，其中k1和k2为实数，则向量c是平面P的方向向量。

2. 平面上的两个方向向量的叉积是平面的法向量。

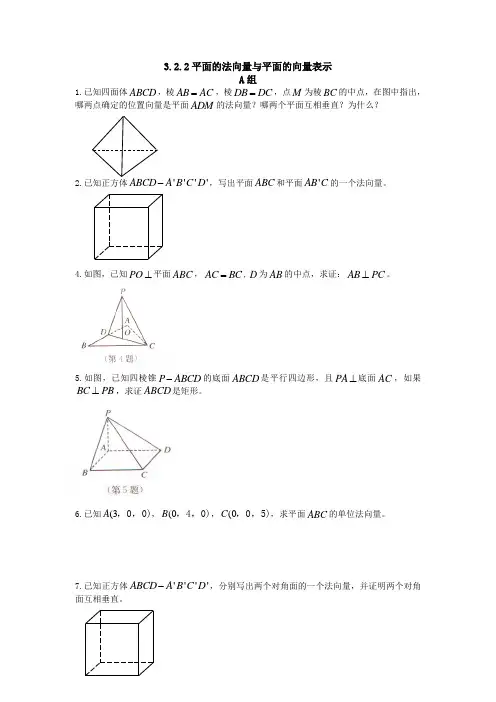
3.2.2平面的法向量与平面的向量表示
A 组
1.已知四面体ABCD ，棱AB AC =，棱DB DC =，点M 为棱BC 的中点，在图中指出，哪两点确定的位置向量是平面ADM 的法向量？哪两个平面互相垂直？为什么？
2.已知正方体''''ABCD A B C D -，写出平面ABC 和平面'AB C 的一个法向量。

4.如图，已知PO ⊥平面ABC ，AC BC =,D 为AB 的中点，求证：AB PC ⊥。

5.如图，已知四棱锥P ABCD -的底面ABCD 是平行四边形，且PA ⊥底面AC ，如果BC PB ⊥，求证ABCD 是矩形。

6.已知(3A ，0，0)，(0B ，4，0)，(0C ，0，5)，求平面ABC 的单位法向量。

7.已知正方体''''ABCD A B C D -，分别写出两个对角面的一个法向量，并证明两个对角面互相垂直。

8.已知四面体ABCD 的棱AB CD ⊥，AC BD ⊥，求证：AD BC ⊥。

B 组
9.直四棱柱1111ABCD A BC D -中，底面ABCD 是矩形，121 3.AB AD AA ===，， M 是BC 的中点.在1DD 上是否存在一点N ，使1MN DC ⊥？。

平面向量的法向量和单位向量平面向量是二维空间中的线段，它具有方向和大小。

在平面向量中，存在着一些特殊的向量，比如法向量和单位向量。

本文将从法向量和单位向量两个方面进行探讨。

一、法向量在平面向量中，法向量是与给定向量垂直的向量，通常用n表示。

对于平面向量a=(a1,a2)，其法向量可以表示为n=(-a2,a1)，或者n=(a2,-a1)。

法向量的方向垂直于给定向量，并且具有相同的大小。

法向量在几何学中有着重要的应用，比如在计算两个向量的夹角时，常常使用法向量来进行计算。

法向量还可以用来表示平面的法线方向，从而帮助求解平面几何中的问题。

二、单位向量单位向量是指长度为1的向量，表示为u。

在二维空间中，单位向量通常表示为u=(cosθ,sinθ)，其中θ为向量与x轴的夹角。

单位向量的大小为1，表示方向而不表示大小。

单位向量在向量运算中起着非常重要的作用。

在计算两个向量的夹角时，可以使用单位向量来表示向量的方向，从而简化计算。

单位向量还常用于表示力的方向，以及在物理学中描述物体的位移和速度方向。

结论平面向量中的法向量和单位向量是非常重要的概念，它们在几何学和向量运算中都具有重要的应用价值。

法向量可以帮助我们求解向量的垂直方向，单位向量则可以帮助我们统一向量的方向，并简化向量运算的复杂度。

深入理解和应用法向量和单位向量，有助于提升数学和物理学等相关学科的学习成绩，同时也为解决实际问题提供了便利。

愿本文对读者有所启发，帮助大家更好地理解平面向量的法向量和单位向量。

3.2.2平面的法向量与平面的向量表示一、选择题1．下列命题中正确的是( )A ．如果一条直线与平面的一条斜线在这个平面内的射影垂直，则它也和这条斜线垂直B ．如果一条直线与平面的一条斜线垂直，则它与斜线在平面上的射影垂直C ．如果一向量和斜线在平面内的射影垂直，则它垂直于这条斜线D ．如果一非零向量和一平面平行，且和一条斜线垂直，则它垂直于斜线在平面内的射影[答案] D[解析] 由三垂线定理知D 成立．2．在正方体ABCD —A 1B 1C 1D 1中，平面ACB 1的一个法向量为( )A.BD 1→B.DB →C.BA 1→D.BB 1→ [答案] A3．点A (a,0,0)，B (0，b,0)，C (0,0，c )，则平面ABC 的一个法向量为( )A ．(bc ，ac ，ab )B ．(ac ，ab ，bc )C ．(bc ，ab ，ac )D ．(ab ，ac ，bc ) [答案] A[解析] 设法向量为n ＝(x ，y ，z )，则AB ·n ＝0，AC →·n ＝0，则⎩⎪⎨⎪⎧－ax ＋by ＝0－ax ＋cz ＝0∴n ＝(bc ，ac ，ab )． 故选A. 4．在正方体ABCD －A 1B 1C 1D 1中，若E 为A 1C 1的中点，则直线CE 垂直于( ) A ．ACB ．BDC ．A 1DD ．A 1A[答案] B[解析] 直线CE 在平面AC 内的射影为AC ，又AC ⊥BD ，∴BD ⊥CE ，故选B.5．正方体AC 1中，E ，F 分别是AB ，CD 的中点，则下列直线中不互相垂直的是( )A ．B 1C 与C 1D 1B ．D 1B 与B 1C C ．D 1B 与EFD ．A 1B 与B 1C 1 [答案] C[解析]D1B与EF所成角等于∠D1BC，其余弦值为33，故选C.6．若平面α、β的法向量分别为u＝(－2,3，－5)，v＝(3，－1,4)，则()A．α∥βB．α⊥βC．α、β相交但不垂直D．以上均不正确[答案] C[解析]∵u＝(－2,3，－5)，v＝(3，－1,4)，∴u与v不平行且u与v不垂直，故选C.7．平面α的一个法向量为v1＝(1,2,1)，平面β的一个法向量v2＝－(2,4,2)，则平面α与平面β()A．平行B．垂直C．相交D．不能确定[答案] A[解析]由v1∥v2故可判定α∥β.8．设平面α的法向量为(1,2，－2)，平面β的法向量(－2，－4，k)，若α∥β，则k＝() A．2B．－4C．4D．－2[答案] C[解析]∵α∥β，∴1－2＝2－4＝－2k，∴k＝4，故选C.9．若直线l的方向向量为a＝(－1,0，－2)，平面α的法向量为u＝(4,0,8)，则() A．l∥αB．l⊥αC．l⊂αD．l与α斜交[答案] B[解析]∵u＝－4a，∴u∥a，∴a⊥α，∴l⊥α.故选B.10．在正方体ABCD—A1B1C1D1中，E、F分别是BB1、CD的中点，则()A．面AED∥面A1FD1B．面AED⊥面A1FD1C．面AED与面A1FD相交但不垂直D．以上都不对[答案] B[解析] 以D 为原点，DA →、DC →，DD 1→分别为x ，y ，z 建立空间直角坐标系求面AED 的法向量n 1与面A 1FD 1的法向量n 2.∵n 1·n 2＝0，∴n 1⊥n 2，∴平面AED ⊥平面A 1FD 1.二、填空题11．若直线l 与β的法向量分别是a ＝(1,0，－2)，b ＝(－1，0,2)，则直线l 与β的位置关系是________．[答案] l ⊥β[解析] ∵a ∥b ，∴l ⊥β.12．已知l ∥α，且l 的方向向量为(2，m,1)，平面α的法向量为⎝⎛⎭⎫1，12，2，则m ＝________.[答案] －8[解析] 设a ＝(2，m,1)，b ＝(1，12，2)． ∵l ∥α，∴a ⊥b ，∴2＋12m ＋2＝0，∴m ＝－8. 13．已知正四棱锥(如图所示)，在向量PA →－PB →＋PC →－PD →，PA→＋PC →，PB →＋PD →，PA →＋PB →＋PC →＋PD →中，不能作为底面ABCD 的法向量的向量是________．[答案] PA →－PB →＋PC →－PD →[解析] ∵PA →－PB →＋PC →－PD →＝BA →＋DC →＝0，不能作为这个平面的法向量，对其它三个化简后可知均与PO →共线．而PO ⊥平面ABCD ，它们可作为这个平面的法向量．14．如图所示，已知矩形ABCD ，AB ＝1，BC ＝a ，P A ⊥平面ABCD ，若在BC 上只有一个点Q 满足PQ ⊥QD ，则a 的值等于________．[答案] 2[解析] 以A 为原点，建立如图所示坐标系，则A (0,0,0)，B (1,0,0)，D (0，a,0)，C (1，a,0)，设Q (1，x,0)，P (0,0，z )，PQ →＝(1，x ，－z )，QD→＝(－1，a －x,0)．由PQ →·QD →＝0，得－1＋x (a －x )＝0，即x 2－ax ＋1＝0.当Δ＝a 2－4＝0，即a ＝2时，Q 只有一个．三、解答题15．已知△ABC 的三个顶点坐标分别为A (0,0,2)，B (4,2,0)，C (2,4,0)，求平面ABC 的单位法向量．[解析] AB →＝(4,2，－2)，AC →＝(2,4，－2)设n ＝(x ，y ，z )是平面ABC 的单位法向量，则有⎩⎪⎨⎪⎧ |n |2＝1，n ·AB →＝0，n ·AC →＝0，⇒⎩⎪⎨⎪⎧ x 2＋y 2＋z 2＝1，2x ＋y －z ＝0，x ＋2y －z ＝0. 取z >0，得x ＝y ＝111，z ＝311 . ∴n ＝111(1,1,3)．16．如图所示，M 、N 、P 分别是正方体ABCD —A 1B 1C 1D 1中的棱CC 1、BC 、CD 的中点．求证：A 1P ⊥平面DMN .[证明] 建立如图所示的空间直角坐标系，设正方体棱长为2，则D (0,0,0)，A 1(2,0,2)，P (0,1,0)，M (0,2,1)，N (1,2,0)．∴向量A 1P →＝(0,1,0)－(2,0,2)＝(－2,1，－2)，DM →＝(0,2,1)－(0,0,0)＝(0,2,1)，DN →＝(1,2,0)．∴A 1P →·DM →＝(－2,1，－2)·(0,2,1)＝(－2)×0＋1×2＋(－2)×1＝0.A 1P →·DN →＝(－2,1，－2)·(1,2,0)＝(－2)×1＋1×2＋(－2)×0＝0.∴A 1P →⊥DM →，A 1P →⊥DN →，即A 1P ⊥DM ，A 1P ⊥DN ，又DM ∩DN ＝D ，∴A 1P ⊥平面DMN .17．棱长为a 的正方体ABCD —A 1B 1C 1D 1中，在棱DD 1上是否存在点P 使B 1D ⊥面P AC?[解析] 以D 为原点建立如图所示的坐标系，设存在点P (0,0，z )，AP →＝(－a,0，z )，AC →＝(－a ，a,0)，DB 1→＝(a ，a ，a )，∴B 1D ⊥面PAC ，∴DB 1→·AP →＝0，DB 1→·AC →＝0.∴－a 2＋az ＝0.∴z ＝a ，即点P 与D 1重合．∴点P 与D 1重合时，DB 1⊥面P AC .18．如图所示，ABCD 为矩形，PA ⊥平面ABCD ，PA ＝AD ，M 、N 、Q 分别是PC 、AB 、CD 的中点，(1)求证：MN ∥PAD ；(2)求证：平面QMN ∥平面PAD ；(3)求证：MN ⊥平面PCD .[解析] (1)如图以A 为原点，以AB ，AD ，AP 所在直线为坐标轴建立空间直角坐标系，设B (b,0,0)，D (0，d,0)，P (0,0，d )，则C (b ，d,0)∵M ，N ，Q 分别是PC ，AB ，CD 的中点，∴M ⎝⎛⎭⎫b 2，d 2，d 2，N ⎝⎛⎭⎫b 2，0，0，Q ⎝⎛⎭⎫b 2，d ，0 ∴MN →＝⎝⎛⎭⎫0，－d 2，－d 2， ∵面PAD 的一个法向量为m ＝(1,0,0)∴MN →·m ＝0，即MN →⊥m ，∴MN 不在面P AD 内，∴MN ∥面PAD ，(2)QN →＝(0，－d,0)，QN →⊥m ，又QN 不在面P AD 内，又QN ∥面PAD .又∵MN ∩QN ＝N ，∴面MNQ ∥平面P AD .(3)PD →＝(0，d ，－d )，DC →＝(b,0,0)， ∴MN →·PD →＝⎝⎛⎭⎫－d 2d ＋⎝⎛⎭⎫－d 2(－d )＝0， MN →·DC →＝0，∴MN →⊥PD →，MN →⊥DC ，又PD ∩DC ＝D ， ∴MN →⊥平面PCD .。

课时分层作业(二十三) 平面的法向量与平面的向量表示(建议用时：45分钟)[基础达标练]1．设平面α的法向量为(1，－2,2)，平面β的法向量为(2，λ，4)，若α∥β，则λ等于( )A ．2B ．4C ．－2D ．－4D [∵α∥β，∴(1，－2,2)＝m (2，λ，4)，∴λ＝－4.]2．若平面α，β的法向量分别为a ＝(－1,2,4)，b ＝(x ，－1，－2)，并且α⊥β，则x 的值为( )A ．10B ．－10 C.12 D ．－12B [因为α⊥β，所以它们的法向量也互相垂直，所以a·b ＝(－1,2,4)·(x ，－1，－2)＝0，即－x －2－8＝0，解得x ＝－10.]3．已知AB →＝(2,2,1)，AC →＝(4,5,3)，则平面ABC 的一个单位法向量可表示为( )A ．a ＝(－1,2，－2)B ．a ＝⎝ ⎛⎭⎪⎫12，－1，1C ．a ＝⎝ ⎛⎭⎪⎫13，－23，23D ．a ＝⎝ ⎛⎭⎪⎫13，23，－23 C [设平面的法向量为a ＝(x ，y ，z )，则有⎩⎨⎧ AB →·a ＝0，AC →·a ＝0∴⎩⎪⎨⎪⎧2x ＋2y ＋z ＝04x ＋5y ＋3z ＝0，令z ＝1，得y ＝－1，x ＝12，∴a ＝⎝ ⎛⎭⎪⎫12，－1，1 故平面ABC 的一个单位法向量为a ＝⎝ ⎛⎭⎪⎫13，－23，23.] 4．已知AB →＝(－3,1,2)，平面α的一个法向量为n ＝(2，－2,4)，点A 不在平面α内，则直线AB 与平面α的位置关系为 ( )【导学号：33242291】A ．AB ⊥αB ．AB ⊂αC ．AB 与α相交但不垂直D ．AB ∥αD [因为n ·AB →＝2×(－3)＋(－2)×1＋4×2＝0，所以n ⊥AB →.又点A 不在平面α内，n 为平面α的一个法向量，所以AB ∥α，故选D.]5．如图3-2-15所示，在三棱锥P -ABC 中，P A ⊥BC ，PB ⊥AC ，点G 是P 在平面ABC 内的射影，则G 是△ABC 的( )图3-2-15A ．内心B ．外心C ．垂心D ．重心C [连接AG ，BG (图略)，则AG ，BG 分别为AP ，BP 在平面ABC 内的射影．因为P A ⊥BC ，所以由三垂线定理的逆定理知AG ⊥BC ，同理，BG ⊥AC ，所以G 是△ABC 的垂心．故选C.]6．已知l ∥α，且l 的方向量为(2，－8,1)，平面α的法向量为(1，y,2)，则y ＝________.12 [∵l ∥α，∴(2，－8,1)·(1，y,2)＝0，而2×1－8y ＋2＝0，∴y ＝12.]7．若A ⎝ ⎛⎭⎪⎫0，2，198，B ⎝ ⎛⎭⎪⎫1，－1，58，C ⎝ ⎛⎭⎪⎫－2，1，58是平面α内的三点，设平面α的法向量a ＝(x ，y ，z )，则x ∶y ∶z ＝________.【导学号：33242292】2∶3∶(－4) [由题意，知AB →＝⎝ ⎛⎭⎪⎫1，－3，－74，AC →＝⎝ ⎛⎭⎪⎫－2，－1，－74.由于a 为平面α的法向量，所以a ·AB →＝0，a ·AC →＝0，即⎩⎪⎨⎪⎧ x －3y －74z ＝0－2x －y －74z ＝0，所以⎩⎪⎨⎪⎧ x ＝23yz ＝－43y ，所以x ∶y ∶z ＝23y ∶y ∶⎝ ⎛⎭⎪⎫－43y ＝2∶3∶(－4)．] 8．已知点P 是平行四边形ABCD 所在的平面外一点，如果AB →＝(2，－1，－4)，AD →＝(4,2,0)，AP →＝(－1,2，－1)．对于结论：①AP ⊥AB ；②AP ⊥AD ；③AP →是平面ABCD 的法向量；④AP →∥BD →.其中正确的是________(填序号)．①②③ [AP →·AB →＝(－1,2，－1)·(2，－1，－4)＝－1×2＋2×(－1)＋(－1)×(－4)＝0，∴AP ⊥AB ，即①正确．AP →·AD →＝(－1,2，－1)·(4,2,0)＝－1×4＋2×2＋(－1)×0＝0.∴AP ⊥AD ，即②正确．又∵AB ∩AD ＝A ，∴AP ⊥平面ABCD ，即AP →是平面ABCD 的一个法向量，③正确．④不正确．]9.如图3-2-16所示，已知四棱锥P -ABCD 的底面是直角梯形，∠ABC ＝∠BCD ＝90°，AB ＝BC ＝PB ＝PC ＝2CD ，侧面PBC ⊥底面ABCD .求证：P A ⊥BD .图3-2-16[证明] 如图，取BC 的中点O ，连接AO 交BD 于点E ，连接PO .因为PB ＝PC ，所以PO ⊥BC .又平面PBC ⊥平面ABCD ，平面PBC ∩平面ABCD ＝BC ，所以PO ⊥平面ABCD ，所以AP 在平面ABCD 内的射影为AO .在直角梯形ABCD 中，由于AB ＝BC ＝2CD ，易知Rt △ABO ≌Rt △BCD ， 所以∠BEO ＝∠OAB ＋∠DBA ＝∠DBC ＋∠DBA ＝90°，即AO ⊥BD .由三垂线定理，得P A ⊥BD .10．已知正方体ABCD -A 1B 1C 1D 1中，E 为棱CC 1上的动点．(1)求证：A 1E ⊥BD ；(2)若平面A 1BD ⊥平面EBD ，试确定E 点的位置．【导学号：33242293】[解] 以D 为坐标原点，以DA ，DC ，DD 1所在直线分别为x 轴，y 轴，z 轴，建立空间直角坐标系．设正方体棱长为a ，则D (0,0,0)，A (a,0,0)，B (a ，a,0)，C (0，a,0)，A 1(a,0，a )，C 1(0，a ，a )．设E (0，a ，e )(0≤e ≤a )．(1)A 1E →＝(－a ，a ，e －a )，BD →＝(－a ，－a,0)，A 1E →·BD →＝a 2－a 2＋(e －a )·0＝0，∴A 1E →⊥BD →，即A 1E ⊥BD .(2)设平面A 1BD ，平面EBD 的法向量分别为n 1＝(x 1，y 1，z 1)，n 2＝(x 2，y 2，z 2)．∵DB →＝(a ，a,0)，DA 1→＝(a,0，a )，DE →＝(0，a ，e )．∴⎩⎨⎧ n 1·DB →＝0，n 1·DA 1→＝0， ⎩⎨⎧ n 2·DB →＝0，n 2·DE →＝0，即⎩⎪⎨⎪⎧ ax 1＋ay 1＝0，ax 1＋az 1＝0， ⎩⎪⎨⎪⎧ax 2＋ay 2＝0，ay 2＋ez 2＝0.取x 1＝x 2＝1，得n 1＝(1，－1，－1)，n 2＝⎝ ⎛⎭⎪⎫1，－1，a e . 由平面A 1BD ⊥平面EBD 得n 1⊥n 2.∴n 1·n 2＝2－a e ＝0，即e ＝a 2.∴当E 为CC 1的中点时，平面A 1BD ⊥平面EBD .[能力提升练]1．已知A (1,0,0)、B (0,1,0)、C (0,0,1)，则平面ABC 的一个单位法向量是 ( ) A.⎝ ⎛⎭⎪⎫33，33，－33 B ．⎝ ⎛⎭⎪⎫33，－33，33 C.⎝ ⎛⎭⎪⎫－33，33，33 D ．⎝ ⎛⎭⎪⎫－33，－33，－33 D [AB →＝(－1,1,0)，AC →＝(－1,0,1)．设平面ABC 的一个法向量为n ＝(x ，y ，z )．∵⎩⎨⎧ AB →·n ＝0，AC →·n ＝0，∴⎩⎪⎨⎪⎧－x ＋y ＝0，－x ＋z ＝0. 令x ＝1，则y ＝1，z ＝1，∴n ＝(1,1,1)，单位法向量为±n |n|＝±⎝ ⎛⎭⎪⎫33，33，33.] 2．已知平面α内有一点M (1，－1,2)，平面α的一个法向量为n ＝(6，－3,6)，则下列点中，在平面α内的是( )【导学号：33242294】A ．P (2,3,3)B ．P (－2,0,1)C ．P (－4,4,0)D ．P (3，－4,4)A [设平面α内一点p (x ，y ，z )，则MP →＝(x －1，y ＋1，z －2)． ∵n ＝(6，－3,6)是平面α的法向量，∴n ⊥MP →，n ·MP →＝6(x －1)－3(y ＋1)＋6(z －2)＝6x －3y ＋6z －21，∴由n ·MP →＝0得6x －3y ＋6z －21＝0，∴2x －y ＋2z ＝7.把各选项的坐标代入上式可知A 选项适合．]3．如图3-2-17所示，已知PO ⊥平面ABC ，且O 为△ABC 的垂心，则AB 与PC 的关系是________．图3-2-17垂直 [∵O 为△ABC 的垂心，∴CO ⊥AB .又∵OC 为PC 在平面ABC 内的射影，∴由三垂线定理知AB ⊥PC .]4．设u ，v 分别是平面α，β的法向量，u ＝(－2,2,5)，当v ＝(3，－2,2)时，α与β的位置关系为________；当v ＝(4，－4，－10)时，α与β的位置关系为________．α⊥β α∥β [∵u ，v 分别为平面α，β的法向量且u ＝(－2,2,5)，当v ＝(3，－2,2)时，u·v ＝－6－4＋10＝0，∴u ⊥v ，即α⊥β，当v ＝(4，－4，－10)时，v ＝－2μ，∴u ∥v ，即α∥β.]5．如图3-2-18所示，在三棱锥P -ABC 中，AB ＝AC ，点D 为BC 的中点，PO ⊥平面ABC ，垂足O 落在线段AD 上．已知BC ＝8，PO ＝4，AO ＝3，OD ＝2.图3-2-18(1)证明：AP ⊥BC ；(2)若点M 是线段AP 上一点，且AM ＝3，试证明平面AMC ⊥平面BMC .【导学号：33242295】[证明] 建立如图所示的空间直角坐标系，则O (0,0,0)，A (0，－3,0)，B (4,2,0)，C (－4,2,0)，P (0,0,4)，(1)AP →＝(0,3,4)，BC →＝(－8,0,0)，所以AP →·BC →＝(0,3,4)·(－8,0,0)＝0，所以AP →⊥BC →，即AP ⊥BC .(2)由(1)知|AP |＝5，又|AM |＝3，且点M 在线段AP 上，所以AM →＝35AP →＝⎝ ⎛⎭⎪⎫0，95，125. 又因为BA →＝(－4，－5,0)，所以BM →＝BA →＋AM →＝⎝ ⎛⎭⎪⎫－4，－165，125， 则AP →·BM →＝(0,3,4)·⎝ ⎛⎭⎪⎫－4，－165，125＝0， 所以AP →⊥BM →，即AP ⊥BM .又根据(1)的结论知AP ⊥BC ，BM ∩BC ＝B ，所以AP ⊥平面BMC ，于是AM ⊥平面BMC .又因为AM ⊂平面AMC ，故平面AMC ⊥平面BMC .。

求平面的法向量平面的法向量是描述平面方向的一个重要概念。

在三维空间中，任意的平面都有一个法向量，它垂直于平面并且指向一个确定的方向。

本文将详细介绍平面的法向量，包括法向量的定义、计算方法以及相关应用。

一、法向量的定义平面的法向量是指垂直于平面的一个向量，在数学中通常用符号n 表示。

对于二维平面，法向量n可以有两个方向，但我们通常取与顺时针方向垂直的那个方向作为法向量。

对于三维平面，法向量只有一个确定的方向。

平面的法向量其实是平面上两个方向垂直向量的叉乘结果。

二、计算方法下面我们将介绍如何计算平面的法向量。

首先，我们需要确定平面上的任意两个非平行的向量A和B。

然后，通过向量A和B的叉乘，我们可以得到平面的法向量n。

具体计算过程如下：1. 向量A和向量B的定义：向量A：A = (x1, y1, z1)向量B：B = (x2, y2, z2)2. 通过向量A和向量B计算法向量n：n = (y1 * z2 - z1 * y2, z1 * x2 - x1 * z2, x1 * y2 - y1 * x2)三、应用场景平面的法向量在几何学以及计算机图形学中有很多应用。

以下列举几个常见的应用场景：1. 确定平面的方向：通过计算平面的法向量，我们可以确定平面的方向。

法向量指向的方向是平面的一个重要属性，它可以帮助我们判断物体在平面上的位置以及平面所处的空间位置。

2. 碰撞检测：在计算机图形学和物理模拟中，平面的法向量常被用于碰撞检测。

通过计算物体与平面的碰撞情况，可以判断物体是否与平面相交或者相切。

3. 光照计算：在计算机图形学中，平面的法向量经常被用于光照计算。

根据平面的法向量和光源的位置，可以计算出光线照射在平面上的强度和颜色。

这个过程对于模拟真实场景中的光照效果非常重要。

4. 三维建模和渲染：在三维建模和渲染中，知道平面的法向量可以帮助我们确定物体表面的方向和形状。

通过对法向量进行计算和处理，可以实现真实感渲染和物体表面的绘制。

平面向量的法向量和单位向量平面向量是二维空间中的箭头，可以用来表示位置、方向和大小。

在平面向量中，除了有定义明确的概念如零向量、负向量和共线向量等，法向量和单位向量也是非常重要的概念。

本文将对平面向量的法向量和单位向量进行详细阐述。

一、平面向量的法向量1. 定义平面向量的法向量，简称法向量，是与给定向量垂直的向量。

对于平面上的向量 A = (a₁, a₂)，其法向量 N = (b₁, b₂)应满足以下条件：a₁ * b₁ + a₂ * b₂ = 0这就是法向量的定义。

2. 求解方法根据定义，可以通过解线性方程组的方法求解平面向量的法向量。

以向量 A = (3, 4)为例，设法向量为 N = (x, y)，代入定义的等式可以得到：3 * x +4 * y = 0根据上述方程，我们可以得到一个关系式 x = -4/3 * y。

取 y = 3，代入公式可以得到一个解 N = (-4, 3)。

同理，可以得到无数个解。

二、平面向量的单位向量1. 定义在平面向量中，单位向量是长度为1的向量，通常用^A 表示。

对于非零向量 A = (a₁, a₂)，其单位向量 ^A = (c₁, c₂)应满足以下条件：c₁² + c₂² = 1这就是单位向量的定义。

2. 求解方法根据定义，可以通过向量的模与法向量来求解平面向量的单位向量。

以向量 A = (3, 4)为例，首先计算向量 A 的模长：|A| = √(3² + 4²) = 5然后根据单位向量的定义，计算单位向量 ^A：^A = (3/5, 4/5)可以看出，单位向量 ^A 的模长为1，符合定义。

三、法向量和单位向量的应用1. 法向量的应用法向量在几何学、物理学等方面有着广泛的应用。

在几何学中，法向量可以用来表示平面的垂直方向；在物理学中，法向量可以用来描述力的作用方向、地形的陡峭程度等。

2. 单位向量的应用单位向量在计算中有着重要的应用。

课题 平面的法向量与平面的向量表示学习目标：1、掌握平面的法向量；会求平面法向量2、利用平面的法向量判定线面、面面的位置关系；学习重点：法向量的应用学习过程（一）、预习检测1、设平面的法向量为(1,2,-2),平面 β 的法向量为(-2,-4,k),若 ，则k= ；若 则 k= 。

2、已知 ，且的方向向量为(2,m,1)，平面的法向量为(1,1/2,2),则m= .3、若 的方向向量为(2,1,m),平面 的法向量为(1,1/2,2),且 ，则m= .4.设 分别是平面α,β的法向量,根据下列条件,判断α,β的位置关系.(二)、复习：1、 直线l 的向量方程：2、与，共面（，不共线）（三）、引入新课1、平面的法向量及求法如果表示向量n 的有向线段所在的直线垂直于平面α,称这个向量垂直于平面α,记作n ⊥α,这时向量n 叫做平面α的法向量.在空间直角坐标系中,如何求平面法向量的坐标呢? 如图,设a =( x 1,y 1,z 1)、b =(x 2,y 2,z 2)是平面α内的两个不共线的非零向量,由直线与平面垂直的判定定理知,若n ⊥a且n ⊥b ,则n ⊥α.换句话说,若n ·a = 0且n ·b = 0,则n ⊥α.可按如下步骤求出平面的法向量的坐标.第一步(设):设出平面法向量的坐标为n =(x,y,z).第二步(列):根据n ·a = 0且n ·b = 0可列出方程组11122200x x y y z z x x y y z z ++=⎧⎨++=⎩ ,α//αβαβ⊥//l αl l αl α⊥(1)(2,2,5),(6,4,4)(2)(1,2,2),(2,4,4)(3)(2,3,5),(3,1,4)u v u v u v =-=-=-=--=-=--第三步(解):把z 看作常数,用z 表示x 、y.第四步(取):取z 为任意一个正数(当然取得越特殊越好),便得到平面法向量n 的坐标.2、平面的向量表示：0AM n =3、设1n 、2n分别是平面α、β的法向量，那么α//β或α与β重合⇔1n //2n αβ⊥⇔12n n ⊥ ⇔120n n =（四）典例分析1、法向量的求解：例1在棱长为2的正方体ABCD-A 1B 1C 1D 1中,O 是面AC 的中心,求面OA 1D 1的法向量.2、法向量的应用1、判断直线与平面的位置关系直线L 的方向向量为a ,平面α的法向量为n ,且L Øα.①若a ∥n ,即a=λn ,则L ⊥α②若a ⊥n ,即a ·n = 0,则L ∥α.例2棱长都等于2的正三棱柱ABC-A 1B 1C 1,D 、E 分别是AC 、CC 1的中点,求证: (I)A 1E ⊥平面DBC 1;(II)AB 1∥平面DBC 1达标检测课后练习A组3,4,5。

平面的法向量平面的法向量确定平面位置的重要向量，指与平面垂直的非零向量，一个平面的法向量可有无限多个，但单位法向量有且仅有两个。

例如在空间直角坐标系中平面Ax+By+Cz+D=0的法向量为n=(A,B,C)，而它的单位法向量即法向量除以法向量的长度，正负代表方向。

平面的法向量1法向量简介法向量，是空间解析几何的一个概念，垂直于平面的直线所表示的向量为该平面的法向量。

法向量适用于解析几何。

由于空间内有无数个直线垂直于已知平面，因此一个平面都存在无数个法向量（包括两个单位法向量）。

定义：三维平面的法线是垂直于该平面的三维向量。

曲面在某点P处的法线为垂直于该点切平面的向量。

法线是与多边形的曲面垂直的理论线，一个平面存在无限个法向量。

在电脑图学的领域里，法线决定着曲面与光源的浓淡处理，对于每个点光源位置，其亮度取决于曲面法线的方向。

如果一个非零向量n与平面a垂直，则称向量n为平面a的法向量。

垂直于平面的直线所表示的向量为该平面的法向量。

每一个平面存在无数个法向量。

计算：对于像三角形这样的多边形来说，多边形两条相互不平行的边的叉积就是多边形的法线。

用方程ax+by+cz=d表示的平面，向量(a,b,c)就是其法线。

如果S是曲线坐标x(s,t)表示的曲面，其中s及t是实数变量，那么用偏导数叉积表示的法线为。

如果曲面S用隐函数表示，点集合(x,y,z)满足F(x,y,z)=0，那么在点(x,y,z)处的曲面法线用梯度表示为。

如果曲面在某点没有切平面，那么在该点就没有法线。

例如，圆锥的顶点以及底面的边线处都没有法线，但是圆锥的法线是几乎处处存在的。

通常一个满足Lipschitz连续的曲面可以认为法线几乎处处存在。