下载文档原格式
hough变换方法Hough变换方法引言Hough变换是一种图像处理方法，主要用于检测和提取图像中的几何形状，如直线、圆等。
它在计算机视觉和模式识别领域有着广泛的应用。
本文将介绍Hough变换的原理、算法和应用，并探讨其优缺点以及未来的发展方向。
一、Hough变换的原理Hough变换的核心思想是将图像中的几何形状转化为参数空间中的曲线或点的形式，从而简化形状检测的问题。
对于直线检测来说，Hough变换可以将直线表示为参数空间中的一个点，通过在参数空间中进行累加操作，找到曲线交点最多的点，从而确定图像中的直线。
二、Hough变换的算法1. 边缘检测：在进行Hough变换之前，需要对图像进行边缘检测，以提取形状的边缘信息。
常用的边缘检测算法包括Sobel、Canny 等。
2. 构建参数空间：对于直线检测来说，参数空间可以理解为直线在参数空间中的表示形式。
通常使用极坐标系表示直线，即每个直线由一个长度和一个角度唯一确定。
3. 累加操作：对于图像中的每个边缘点，计算其在参数空间中的曲线或点，并进行累加操作。
通过累加操作，可以找到曲线交点最多的点，从而确定图像中的直线。
4. 阈值判断：根据累加结果，可以设置一个阈值，只有当累加值超过该阈值时，才认为该点对应的直线存在。
5. 参数反变换：将参数空间中的曲线或点反变换回图像空间，得到检测到的直线。
三、Hough变换的应用1. 直线检测：Hough变换最常见的应用就是直线检测。
在工业检测、路标检测等领域中，直线的检测是一项基础任务，Hough变换可以实现准确地直线检测，从而为后续处理提供便利。
2. 圆检测：除了直线检测，Hough变换还可以用于圆的检测。
通过在参数空间中寻找曲线交点最多的点，可以确定图像中的圆的位置和半径。
3. 图像分割：Hough变换可以将图像中的不同几何形状分割出来，从而实现图像的分割处理。
在医学图像处理、目标跟踪等领域中，图像分割是一项重要的任务。
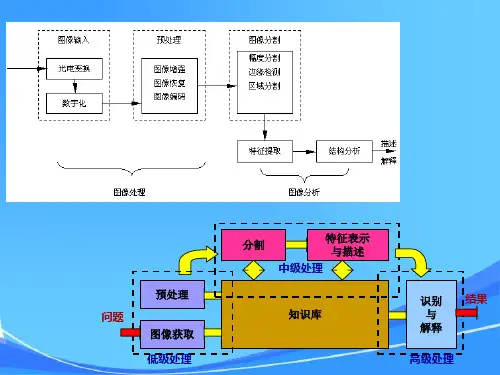
一、概述霍夫变换是一种常用的图像处理技术，它可以用于检测图像中的直线、圆或者其他形状。
它具有很好的鲁棒性，可以应对图像中存在的噪声和其他干扰。
霍夫变换在计算机视觉、图像处理和模式识别领域有着广泛的应用，成为了处理图像中几何形状的重要工具。
二、霍夫变换的原理霍夫变换最初是由美国科学家保罗·霍夫在1962年提出的，用于检测图像中的直线。
后来，霍夫变换被扩展到检测圆或者其他形状。
霍夫变换的基本原理是将空间域中的坐标转换到参数域中，在参数域中对应的曲线经过的点在空间域中具有共线的特点。
通过累加空间域中的点的参数，可以找到曲线或者形状的参数方程，从而实现对图像中形状的检测。
具体来说，对于检测直线来说，可以通过霍夫变换将直线表示为参数空间中的斜率和截距，从而可以在参数空间中进行累加，最终找到直线的参数方程。
三、霍夫变换在直线检测中的应用1. 边缘检测在使用霍夫变换检测直线之前，通常需要对图像进行边缘检测。
边缘检测可以帮助找到图像中明显的过渡区域，这些过渡区域通常对应着直线的轮廓。
常用的边缘检测算法包括Sobel算子、Canny算子等。
2. 参数空间的设置为了使用霍夫变换来检测直线，需要设定参数空间的范围。
对于直线检测来说，一般可以设定直线的斜率和截距的取值范围。
3. 累加过程在设定好参数空间后，需要对图像中的边缘点进行霍夫变换的累加过程。
对于每一个边缘点，都可以在参数空间中找到对应的直线，通过对参数空间的累加，可以找到参数空间中的峰值，这些峰值对应着图像中的直线。
4. 直线检测可以根据参数空间中的峰值来确定图像中的直线。
通常可以设定一个阈值来筛选参数空间中的峰值，从而得到最终的直线检测结果。
四、霍夫变换在圆检测中的应用除了直线检测，霍夫变换也可以用于检测图像中的圆。
与直线检测类似，圆检测也需要进行边缘检测和参数空间的设定。
不同的是，在圆检测中，需要设定圆心和半径的参数空间范围。
五、霍夫变换的改进和应用1. 累加数组的优化在传统的霍夫变换中，需要对参数空间进行离散化，这会导致计算量较大。
Hough 变换Hough 变换是1962年由Hough 提出来的，用于检测图像中直线、圆、抛物线、椭圆等且其形状能够用一定函数关系描述的曲线，它在影像分析、模式识别等很多领域中得到了成功的应用：其基本原理是将影像空间中的曲线（包括直线）变换到参数空间中，通过检测参数空间中的极值点，确定出该曲线的描述参数，从而提取影像中的规则曲线。
直线Hough 变换通常采用的直线模型为θθρsin cos y x +=其中ρ是从原点引到直线的垂线长度；θ是垂线与x 轴正向的夹角（如图）。
对于影像空间直线上任一点(x ，y)，Hough 变换将其映射到参数空间()ρθ，的一条正弦曲线上。
由于影像空间内的一条直线由一对参数()00ρθ，唯一地确定,因而该直线上的各点变换到参数空间的各正弦曲线必然都经过点()00ρθ，，在参数平面(或空间)中的这个点的坐标就代表了影像空间这条直线的参数。
这样，检测影像中直线的问题就转换为检测参数空间中的共线点的问题。
由于存在噪声及特征点的位置误差，参数空间中所映射的曲线并不严格通过一点，而是在一个小区域中出现一个峰，只要检测峰值点，就能确定直线的参数。
其过程为(1)对影像进行预处理，提取特征并计算其梯度方向；(2)将()ρθ，参数平面量化，设置二维累计矩阵()j i H ρθ,；(3)边缘细化，即在边缘点的梯度方向上保留极值点，剔除那些非极值点；(4)对每一边缘点，以其梯度方向ψ为中心，设置一小区间[]00,θψθψ+-，其中0θ为经验，一般可取 10~5，在此小区间上以θ∆为步长，按式(2—3—37)对每一个区间中的θ量化值计算相应的ρ值，并给相应的累计矩阵元素增加一个单位值；(5)对累计矩阵进行阈值检测，将大于阈值的点作为备选点；(6)取累计矩阵(即参数空间)中备选点中的极大值点为所需的峰值点，这些点所对应的参数空间的坐标即所检测直线的参数。
利用Hough 变换也可以提取圆和抛物线：()()222R r y c x =-+- c bx ax y ++=2但此时参数空间是三维空间，因而计算量相当大。
什么是hough变换Hough变换利用图像空间和Hough参数空间的点－线对偶性，把图像空间中的检测问题转换到参数空间。
通过在参数空间里进行简单的累加统计，然后在Hough参数空间寻找累加器峰值的方法检测直线。
例如，图1(a)中的九条线段对应于如图1(b)所示的其Hough参数空间的九个累加器峰值。
图1(b)中，Hough参数空间的横纵坐标分别为直线极坐标方程:ρ＝x×cos(θ) + y×sin(θ) 的两个参数ρ和θ。
九个峰值的ρ和θ值唯一的确定其对应线段所在直线的两个参数。
并且线段的长度决定坐标(ρ,θ)处的累加值的大小。
应用领域理论与实践向来是形影不离，相辅相成，Hough变换之所以有如此长足的发展，主要原因还是在于实践应用上的广泛需求；而在实践中所暴露出的不足又进而促进了它的发展，循环往复，就如同生命的演化。
现枚举其主要应用领域如下：生物医学Hough变换已被成功应用于基于人工智能的专家诊断系统；X射线人体照片和CT图像的处理和判读；光学显微镜和电子显微镜中的细胞核自动分析系统；从超声波诊断中提取三维动脉特征，等等。
自动化、机器人视觉Hough变换已被用于产品部件的自动监视、缺陷诊断、生产过程的自动监控、计算机辅助制造（CAM）等。
例如基于Hough变换的机械零件检测和定位系统；基于Hough变换采用直线、圆弧等作为基本特征的工业产品检查系统。
空间技术、军事防御Hough变换已被用于运动目标轨迹的检测与识别，高空侦察机、间谍卫星和军事雷达等目标自动识别系统的特征提取。
例如应用Hough变换对战斗机的外形特征进行提取和自动识别；应用Hough变换辅以信号检测理论解决并行多运动目标的跟踪问题。
办公自动化Hough变换在许多应用系统中得到了很好的应用。
例如采用Hough变换进行英文字符特征提取并自动识别，其对印刷体字符识别率为99.6%，对手写体字符的平均识别率也达到了86.9%，并已成功应用于邮政信件的自动分拣、文件处理等。
数字图像处理—Hough变换直线检测,matlab实现实验八 Hough变换直线检测一、实验目的理解Hough变换的原理，了解其应用;掌握利用Hough变换进行直线检测的处理过程及编程方法。
二、实验内容利用Hough变换检测直线通常先进行边缘检测，得到只包含边缘的二值图像。
再通过Hough变换，在参数空间检测图像共线点的数量得到直线参数，从而实现直线检测。
1、读入图像(图像需有直线或直线性边缘)2、进行图像边缘，得到二值图像3、实现Hough变换，检测出图像中的直线方程4、输出结果三、实验要求1、编写代码，完成各项实验内容2、总结实验中遇到问题及解决方案，书写实验报告%Hough变换clc;clear;close all f=imread('line.bmp'); %若是彩色图片转灰度化if length(size(f))>2f=rgb2gray(f);end%figure(1)subplot(121);imshow(f); %利用edge函数进行边缘检测j=edge(f,'Sobel');subplot(122);imshow(j); [row,col]=size(j);pinfang=round((row*row+col*col)^0.5);A=zeros(2*pinfang,180);for m=1:rowfor n=1:colif j(m,n)>0for thera=1:180r=thera/180*pi; %角度转弧度rho=round(m*cos(r)+n*sin(r));%ρ=cosθ+sinθrho=rho+pinfang+1;%-l:l转换到1:2l+1A(rho,thera)=A(rho,thera)+1;endendendend[rho,thera]=find(A>40);%交点超过60条线的点，ma,na为参数空间的坐标点nma=length(rho);for i=1:nmahold onm=1:row;%rho=ma(i)-1;r=thera(i)/180*pi;n=(rho(i)-pinfang-m*cos(r))/(0.00001+sin(r));plot(n,m,'r'); end。
实验二、图像分割实验实验目标：掌握图像分割的主流算法。
实验内容：⑴实现边缘检测算法。
⑵实现用Hough变换检测直线的算法。
实验步骤：⑴读入图像。
（设图像中有直线）⑵检测图像边缘⑶实现Hough变换，检测出图像中的直线方程。
⑷输出结果。
实验结果及程序：1.检测图像边缘：①原理：图像边缘是图像最基本的特征，边缘在图像分析中起着重要作用。
所谓边缘是指图像局部特性的不连续性。
灰度或结构等信息的突变处为成为边缘。
边缘是一个区域的结束，也是另一个区域的开始，利用此特征可以分割图像。
边缘检测的实质是采用某种算法来提取出图像中对象与背景间的交界线。
图像灰度的变化情况可以用图像灰度分布的梯度来反映，因此我们可以用局部图像微分技术来获得边缘检测算子。
经典的边缘检测方法是对原始图像中像素的某小邻域来构造检测算子。
拉普拉斯边缘检测算子是基于二阶导数的边缘检测算子，对噪声敏感。
拉普拉斯算子的改进方式是先对图像进行平滑处理，然后再应用二阶倒数的边缘检测算子，其代表是拉普拉斯高斯算子。
②图像边缘检测的程序：I=imread('d.bmp'); %读入原始图像I=rgb2gray(I); %将真彩色图像转化为灰度图像[m,n]=size(I); %确定图片的的长和宽r=m+2; %把图片的长和宽各加2c=n+2;b=zeros(r,c); %定义二维数组b,长、宽比I各多2，成为镜框的尺寸g=zeros(m,n); %定义滤波后的数组d=zeros(3); %定义三阶方阵d,为临时矩阵t=[-1 -1 -1;-1 8 -1;-1 -1 -1]; %定义拉普拉斯算子Result=zeros(3); %定义三阶方阵Result，为运算结果矩阵%原图像矩阵处理，做一个"像框"b(2:m+1,2:n+1)=I; %把原图的矩阵放到新的矩阵b中心，它的第一行、最后一行、第一列、最后一列都是0，即原图矩阵周围有一圈0的边缘，好像给图像加一个像框b(1,:)=b(2,:); %把第二行的值赋给第一行b(r,:)=b(r-1,:); %把倒数第二行的值赋给最后一行b(:,1)=b(:,2); %把第二列的值赋给第一列b(:,c)=b(:,c-1); %把倒数第二列的值赋给最后一列%用拉普拉斯算子进行滤波for i=1:mfor j=1:nd=b(i:i+2,j:j+2); %从b矩阵中依次取出三阶方阵，赋值给临时矩阵dResult=d.*t; %临时矩阵与拉普拉斯算子点乘，赋值给结果矩阵dg(i,j)=sum(sum(Result)); %结果矩阵中"十"字线上元素相加，赋值给输出矩阵中相应的位置，即临时矩阵中心元素所对应的位endendthresh=2.6*mean2(abs(g)); %设定阈值将图像二值化使边缘清晰J=repmat(logical(uint8(0)),m,n); %创建数组J(find(g>thresh))=1; %阈值判断二值化figure,subplot(2,2,1),imshow(I);title('原始图像');%显示原图像subplot(2,2,2),imshow(J); title('拉普拉斯边缘检测后的图像'); %显示拉普拉斯边缘检测后的图像subplot(2,2,3),imshow(g); title('将拉普拉斯边缘检测二值化后的图像')③图像经边缘检测后的MATLAB程序实现效果图如下：2.Hough变换检测直线：①原理：Hough变换用来在图象中查找直线，把直线上点的坐标变换到过点的直线的系数域，通过利用共线和直线相交的关系，使直线的提取问题转化为计数问题。
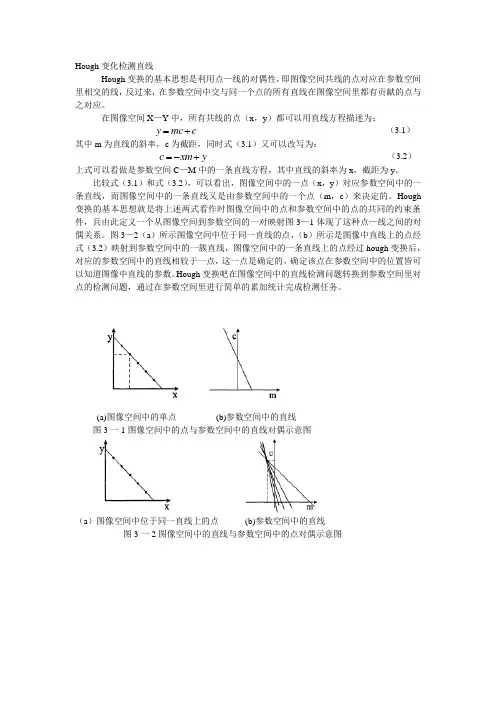
Hough变化检测直线Hough变换的基本思想是利用点—线的对偶性，即图像空间共线的点对应在参数空间里相交的线，反过来，在参数空间中交与同一个点的所有直线在图像空间里都有贡献的点与之对应。
在图像空间X—Y中，所有共线的点（x，y）都可以用直线方程描述为：=（3.1）y+cmc其中m为直线的斜率，c为截距，同时式（3.1）又可以改写为：=（3.2）-yxmc+上式可以看做是参数空间C—M中的一条直线方程，其中直线的斜率为x，截距为y。
比较式（3.1）和式（3.2），可以看出，图像空间中的一点（x，y）对应参数空间中的一条直线，而图像空间中的一条直线又是由参数空间中的一个点（m，c）来决定的。
Hough 变换的基本思想就是将上述两式看作时图像空间中的点和参数空间中的点的共同的约束条件，兵由此定义一个从图像空间到参数空间的一对映射图3—1体现了这种点—线之间的对偶关系。
图3—2（a）所示图像空间中位于同一直线的点，（b）所示是图像中直线上的点经式（3.2）映射到参数空间中的一簇直线，图像空间中的一条直线上的点经过hough变换后，对应的参数空间中的直线相较于一点，这一点是确定的，确定该点在参数空间中的位置皆可以知道图像中直线的参数。
Hough变换吧在图像空间中的直线检测问题转换到参数空间里对点的检测问题，通过在参数空间里进行简单的累加统计完成检测任务。
(a)图像空间中的单点(b)参数空间中的直线图3一1图像空间中的点与参数空间中的直线对偶示意图（a）图像空间中位于同一直线上的点(b)参数空间中的直线图3一2图像空间中的直线与参数空间中的点对偶示意图图3一3参数空间中的累加数组在具体的计算过程中，需要将参数空间M 一C 离散化为二维的累加数组，设这个数组为(m ，c)，如图3一3所示，同时设[[]m ax m in ,m m 和[]m ax m in ,c c 分别为斜率和截距的取值范围。
开始时置数组A 全为零，然后对每一个图像空间中的给定边缘点，让m 取遍[]m ax m in ,m m 内所有可能的值，并根据式 (3.2)算出对应的c 。
