中考数学复习课件系列考前冲刺-解答题——三角形与
- 格式:ppt
- 大小:1.44 MB
- 文档页数:21

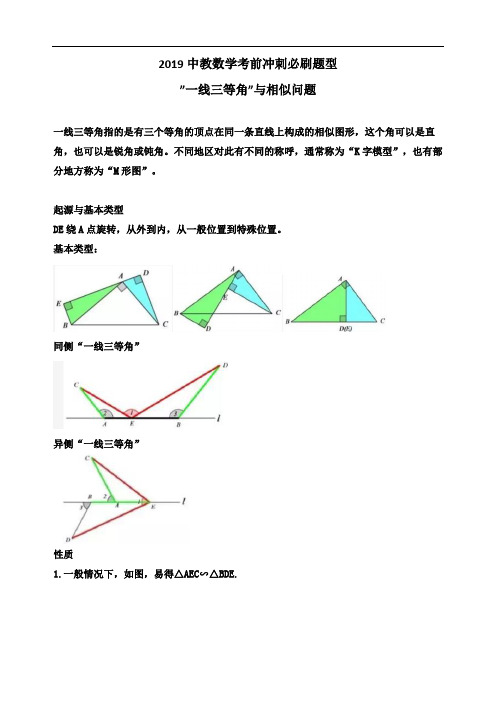
2019中教数学考前冲刺必刷题型”一线三等角”与相似问题一线三等角指的是有三个等角的顶点在同一条直线上构成的相似图形,这个角可以是直角,也可以是锐角或钝角。
不同地区对此有不同的称呼,通常称为“K字模型”,也有部分地方称为“M形图”。
起源与基本类型DE绕A点旋转,从外到内,从一般位置到特殊位置。
基本类型:同侧“一线三等角”异侧“一线三等角”性质1.一般情况下,如图,易得△AEC∽△BDE.2.当等角所对的边相等时,则两个三角形全等。
(若CE=ED,则△AEC≌△BD E)3.中点型“一线三等角”如图,当∠1=∠2=∠3,且D是BC中点时,△BDE∽△CFD∽△DFE.4.“一线三等角”的各种变式应用1.“一线三等角”应用的三种情况。
a.图形中已经存在一线三等角,直接应用模型解题;b.图形中存在“一线二等角”,补上“一等角”构造模型解题;c.图形中只有直线上一个角,补上“二等角”构造模型解题.2.在定边对定角问题中,构造一线三等角是基本手段。
3.构造一线三等角的步骤:找角、定线、构相似。
如上图,线上有一特殊角,就考虑构造同侧型一线三等角,当然只加这两条线通常是不够的,为了利用这个特殊角与线段的关系,过C、D两点作直线l的垂线是必不可少的。
例1.如图,已知E是矩形ABCD的边AB上一点,EF⊥DE交BC于点F,试说明:ΔADE∽ΔBFE。
分析:要证明ΔADE与ΔBFE相似,已经知道∠A=∠B=90°,只需要再找出另外一对相等的角即可。
解答:在矩形ABCD中,∠A=∠B=90°∵EF⊥DE∴∠DEF=90°,∠2+∠3=90°又∵∠1+∠3=90°∴∠1=∠2∴ΔADE∽ΔBFE小结:此时,在直线AB上,∠A=∠DEF=∠B=90°,一条线上有3个直角,两边的ΔADE与ΔBFE相似。
这个相似的基本图形像字母K,可以称为“K”型相似,但更因为图形的结构特征是一条线上有3个垂直关系,也常被称为“一线三垂直”。




2023年江苏省淮安市中考数学考前30天终极冲刺模拟卷学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.如图,在Rt ABC △中,90ACB ∠=.点P 是半圆弧AC 的中点,连接BP 交AC 于点D ,若半圆弧的圆心为O ,点D 、点E 关于圆心O 对称.则图中的两个阴影部分的面积12S S ,之间的关系是( )A .12S S <B .12S S >C .12S S =D .不确定 2.三角形的外心是( ) A . 三条高线的交点B .三条中线的交点C .三条中垂线的交点D .三条内角平分线的交点 3.抛物线2y ax =和22y x =的形状相同,则 a 的值是( )A .2B .-2C .2±D .不确定 4.已知函数y =ax 2+bx +c 的图像如图所示,那么此函数的解析式为( ) A .y =-x 2+2x +3 B .y =x 2―2x ―3 C .y =―x 2―2x +3 D .y =―x 2―2x ―35.下列命题为真命题的是( )A .三角形的中位线把三角形的面积分成相等的两部分B .对角线相等且相互平分的四边形是正方形C .关于某直线对称的两个三角形是全等三角形D .一组对边平行,另一组对边相等的四边形一定是等腰梯形6.用两块全等的有一个角是30°的直角三角板,能拼成不同的平行四边形有( )A .2个B .3个C .4个D .无数个7.如图,在Rt △ABC 中,CD 是斜边AB 上的高,角平分线AE 交CD 于H ,EF ⊥AB 于F ,则下列结论中不正确的是( )A .∠ACD=∠B B . CH=CE=EFC .AC=AFD .CH=HD8.如图,长方体的长为 15、为 10、高为 20,点B 离点 C 的距离为 5,一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ,需要爬行的最短距离是( )A . 521B .25C . 1055D .359.如图,△ABC 是等腰直角三角形,BC 是斜边,将△ABP 绕A 逆时针旋转后,能够与△ACP ′重合,如果AP=3,那么2PP '等于( )A .9B .12C .15D .l810.如图所示,S △ABC=l ,若S △BDE =S △DEC =S △ACE ,则S △ADE 等于( )A .15B .16C .17D .1811.下列各式中,计算正确的是( )A .236+=B .523-=C .1010()10a b a b -=-D .2(3)3-=-12.当n 为整数时,212(1)(1)n n --+-的值为( )A .-2B .0C .1D . 2二、填空题13.如图,DE ∥AC ,BE :EC=2:1,AC=12,则DE= .14.函数22(3)5y x =--,当x= 时,y 有 ,为 .15.在直角坐标系内,点A ,B ,C ,D 的坐标依次为(-2,0),(-4,5),(x ,y),(0,5),要使四边形ABCD 为菱形,则x= ,y= .16.如图是由一些形状相同的长方体搭成的几何体的三视图,则此几何体共由 块长方体搭成.17.笔直的窗帘轨,至少需要钉 个钉子才能将它固定,理由是 .三、解答题18.如图,甲站在墙前,乙在墙后,为了不被甲看到,请你在图中画出乙的活动区域.19.如图,AD 、CE 是△ABG 的高线,A ′D ′、C ′E ′是△A ′B ′C ′的高线,且CD AD C D A D ='''', ∠B=∠B ′,试说明.20.如图所示,在 □ABCD 中,点E ,F 是对角线AC 上的两点,且AE=CF .求证:四边形BEDF 是平行四边形.21.已知:如图,E ,F 分别是□ABCD 的边AD ,BC 的中点,求证:DE =DF.AB C DFE22.解下列方程:(1)22(12)(3)x x-=+;(2)2449x x-+=23.某村过去是一个缺水的村庄,由于兴修水利,现在家家户户都用上了自来水.据村委会主任徐伯伯讲,以前全村400多户人家只有5口水井:第一口在村委会的院子里,第二口在村委会正西1500 m处,第三口在村委会北偏东30°方向,2000 m处,第四口在村委会东南方向1000 m处,第五口在村委会正南900 m处.请你根据徐伯伯的话,画图表示这个村庄5口水井的位置.24.一个包装盒的表面展开图如图所示,请描述这个包装盒的形状,并求出这个包装盒的表面积和容积(纸板厚度忽略不计).25.2008年 10月 18 日上午 10时,经过中国铁建十六局集团和中铁隧道局集团2000多名员工4年零2个月的顽强拼搏,被誉为世界级工程难题的宜万铁路野三关隧道Ⅱ线胜利贯通. 如图,这是工程建设中一个山峰的平面图,施工队在施工之前需要先测量出隧道AB的长度,请你利用三角形全等的知识设计一种测量方法,并说明理由.26.计算机存储容量的基本单位是字节(B),通常还用 KB(千字节)、MB(兆字节)、GB(吉字节)作为存储容量的计量单位. 已知1KB= 210B ,1MB =210 KB ,1GB = 210 MB ,那么372字节相当于多少音字节?27.在所给数轴上表示数-1,3的相反数,7,2-,并把这组数从小到大用“<”连接起来.28.x 为何值时,式子32x -与式子13x -+满足下面的条件? (1)相等(2)互为相反数(3)式子32x -比式子13x -+的值小 129.在数轴上-7 与 37 之间插入三个数,使这五个数的每相邻两个点之间的距离相等. 求插入的三个数.30.利用旧墙为一边(旧墙长为7 m),再用13 m 长的篱笆围成一个面积为20 m 2的长方形场地,则长方形场地的长和宽分别是多少?【参考答案】学校:__________ 姓名:__________ 班级:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息2.请将答案正确填写在答题卡上一、选择题1.C2.C3.C4.A5.C6.B7.D8.B9.D10.B11.CB二、填空题13.814.3-,最大值,-515.-2,1016.417.2,两点确定一条直线三、解答题18.如图中斜线区.19.∵CD ADC D A D='''',且∠ADC =∠A′D′C′,∴△ACD∽△A′C′D′.∴∠ACD=∠A′C′D′.∵∠B=∠B′,△ABC∽△A′B′C′,∴CE AC AD C E A C A D==''''''.20.提示:连结BD,利用对角线互相平分的四边形是平行四边形即可21.提示:四边形BEDF是平行四边形.22.(1)12 3x=-,24x=;(2)15x=,21x=-23.24.该包装盒是一个长方体,它的底面是边长为5厘米的正方形,它的高为25厘米.∴它的表面积为(5×5+25×5+25×5)×2=550(平方厘米),容积为5× 5×25=625(立方厘米) 25.利用全等三角形的判定(AAS,SAS,ASA)来设计完成26.128 GB27.图略,28.(1)245x= (2)12x= (3)185x=29.4,15,2630.宽为 4m,长为 5 m。
中考数学三角形与全等三角形精品课件同学们,咱们今天来好好聊聊中考数学里特别重要的一部分——三角形与全等三角形。
先来说说三角形吧,大家想想看,咱们生活中到处都有三角形的影子。
就像上次我去公园散步,看到那个跷跷板,它的支架就是三角形的。
为啥要用三角形呢?因为三角形具有稳定性呀!这可不是随便说说的,你看那跷跷板上不管小朋友们怎么蹦跶,支架都稳稳当当的,不会晃来晃去。
咱们再回到数学上来,三角形的内角和是 180 度,这可是个重要的知识点。
就好比一个三角形房子,三个角就像三扇窗户,不管窗户大小怎么变,它们加起来的角度永远是 180 度。
还有三角形的三边关系,两边之和大于第三边,两边之差小于第三边。
这就像是三个人排队,前面两个人手拉手的长度一定要比第三个人长,不然就拉不住啦。
接下来重点讲讲全等三角形。
全等三角形那可是中考的常客!全等三角形的判定方法,大家可得牢记在心。
什么 SSS(边边边)、SAS (边角边)、ASA(角边角)、AAS(角角边)、HL(斜边、直角边),就像五个小伙伴,各有各的特点。
比如说,有一次我看到两个一模一样的风筝,形状、大小完全相同。
这其实就相当于两个全等三角形,它们的对应边相等,对应角也相等。
再给大家举个例子,有一道题是这样的:已知在△ABC 和△DEF 中,AB = DE,∠A =∠D,BC = EF,问这两个三角形全等吗?这时候咱们就得用 SAS 来判断啦,因为有两边及其夹角相等,所以这两个三角形全等。
做题的时候,大家一定要仔细审题,看清楚给出的条件,选择合适的判定方法。
可别一着急就选错了,那就像在迷宫里走错了路,得绕好大一圈才能出来。
关于三角形和全等三角形的综合应用,也是中考的热门考点。
比如求角度、边长,或者证明线段相等、角相等。
这就需要咱们把前面学的知识灵活运用起来。
总之,三角形和全等三角形这部分内容,大家一定要认真学,多做练习,把基础打牢。
相信大家在中考中遇到相关题目时,都能轻松应对,取得好成绩!加油哦!。
第1关 以几何图形中的动点最值问题为背景的选择填空题【考查知识点】 “两点之间线段最短”,“垂线段最短”,“点关于线对称”,“线段的平移”。
原型----“饮马问题”,“造桥选址问题”。
考的较多的还是“饮马问题”,出题背景变式有角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等。
【解题思路】找点关于线的对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查.求线段和的最小值需要用到三个基本知识:两点之间,线段最短;轴对称的性质;线段垂直平分线上的点到线段两端点的距离相等.常见情况有三种:“两点一线”型、“一点两线”型和“两点连线” 型. 平面上最短路径问题:(1)归于“两点之间的连线中,线段最短”。
凡属于求“变动的两线段之和的最小值”时,大都应用这一模型。
(2)归于“三角形两边之差小于第三边”。
凡属于求“变动的两线段之差的最大值”时,大都应用这一模型。
(3)平面图形中,直线同侧两点到直线上一点距离之和最短问题。
【典型例题】【例1】如图,ABC ∆是等边三角形,13AD AB =,点E 、F 分别为边AC 、BC 上的动点,当DEF ∆的周长最小时,FDE ∠的度数是______________.【名师点睛】关于最短路线问题:在直线L上的同侧有两个点A、B,在直线L上有到A、B的距离之和最短的点存在,可以通过轴对称来确定,即作出其中一点关于直线L的对称点,对称点与另一点的连线与直线L的交点就是所要找的点(注:本题C,D位于OB的同侧).如下图,解决本题的关键:一是找出最短路线,二是根据一次函数与方程组的关系,将两直线的解析式联立方程组,求出交点坐标.【例2】如图,在⊙O中,弦AB=1,点C在AB上移动,连结OC,过点C作CD⊙OC交⊙O于点D,则CD的最大值为___.【名师点睛】本题考查了垂径定理:垂直于弦的直径平分弦,且平分弦所对的弧.也考查了勾股定理,相似三角形的判定与性质,熟练掌握相似三角形的判定与性质是解答本题的关键.【方法归纳】在平面几何的动态问题中,求几何量的最大值或最小值问题常会运用以下知识:①三角形的三边关系:两边之和大于第三边,两边之差小于第三边;②两点之间线段最短;③连接直线外一点和直线上各点的所有线段中,垂线段最短;④定圆中的所有弦中,直径最长;⑤利用对称的性质求两条线段之和最小的问题,解决此类问题的方法为:如图,要求线段l上的一动点P 到点A、B距离和的最小值,先作点A关于直线L的对称点A′,连接A′B,则A′B与直线L的交点即为P 点,根据对称性可知A′B的长即为PA+PB的最小值,求出A′B的值即可.【针对练习】1.如图,∠AOB=60°,点P是∠AOB内的定点且M、N分别是射线OA、OB上异于点O 的动点,则△PMN周长的最小值是()A B C.6D.32.如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN 周长最小时,则∠AMN+∠ANM的度数为()A.130°B.120°C.110°D.100°3.如图,四边形ABCD中,∠C=,∠B=∠D=,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF的度数为().A .B .C .D .4.如图,已知直线142y x =+与x 轴、y 轴分别交于A , B 两点,将△AOB 沿直线AB 翻折,使点O 落在点C 处, 点P ,Q 分别在AB , AC 上,当PC +PQ 取最小值时,直线OP 的解析式为( )A .y=-34x B .y=-12x C .y=-43x D .23y x =5.如图:等腰△ABC 的底边BC 长为6,面积是18,腰AC 的垂直平分线EF 分别交AC ,AB 边于E ,F 点.若点D 为BC 边的中点,点M 为线段EF 上一动点,则△CDM 周长的最小值为( )A .6B .8C .9D .106.如图,在△ABC 中,5,6AB AC BC ===,动点P ,Q 在边BC 上(P 在Q 的左边),且2PQ =,则AP AQ +的最小值为( )A .8B .C .9D .7.如图,在Rt ABO 中,90OBA ∠=︒,()4,4A ,点C 在边AB 上,且13AC CB =,点D 为OB 的中点,点P 为边OA 上的动点,当点P 在OA 上移动时,使四边形PDBC 周长最小的点P 的坐标为( )A .()2,2B .55,22⎛⎫⎪⎝⎭C .88,33⎛⎫⎪⎝⎭D .()3,38.如图,等腰三角形ABC 底边BC 的长为4 cm ,面积为12 cm 2,腰AB 的垂直平分线EF 交AB 于点E ,交AC 于点F ,若D 为BC 边上的中点,M 为线段EF 上一点,则△BDM 的周长最小值为( )A .5 cmB .6 cmC .8 cmD .10 cm9.如图,周长为16的菱形ABCD 中,点E ,F 分别在边AB ,AD 上,AE =1,AF =3,P 为BD 上一动点,则线段EP +FP 的长最短为( )A .3B .4C .5D .610.在平面直角坐标系中,Rt △AOB 的两条直角边OA 、OB 分别在x 轴和y 轴上,OA=3,OB=4.把△AOB 绕点A 顺时针旋转120°,得到△ADC .边OB 上的一点M 旋转后的对应点为M′,当AM′+DM 取得最小值时,点M 的坐标为( )A .(0)B .(0,34) C .(0 D .(0,3)11.如图,已知点A 是以MN 为直径的半圆上一个三等分点,点B 是弧AN 的中点,点P 是半径ON 上的点.若⊙O 的半径为l ,则AP+BP 的最小值为( )A .2B CD .112.直线y =x +4与x 轴、y 轴分别交于点A 和点B ,点C ,D 分别为线段AB ,OB 的中点,点P 为OA 上一动点,PC +PD 值最小时点P 的坐标为( ).A .(-3,0)B .(-6,0)C .(-,0)D .(-,0)13.如图,MN 是等边三角形ABC 的一条对称轴,D 为AC 的中点,点P 是直线MN 上的一个动点,当PC+PD 最小时,∠PCD 的度数是( )A .30°B .15°C .20°D .35°14.如图,AC 是O 的弦,5AC =,点B 是O 上的一个动点,且45ABC ∠︒=,若点,M N 分别是,AC BC 的中点,则MN 的最大值是_____.15.如图,∠AOB =60°,点M ,N 分别是射线OA ,OB 上的动点,OP 平分∠AOB ,OP =8,当△PMN 周长取最小值时,△OMN 的面积为_____.16.如图,四边形ABCD 中,∠BAD =120°,∠B =∠D =90°,在BC ,CD 上分别找一点M ,N ,使△AMN 周长最小时,则∠AMN +∠ANM 的度数是________17.如图,在Rt ABC ∆中,90ACB ∠=︒,3AC =,4BC =,AD 是BAC ∠的平分线.若P ,Q 分别是AD 和AC 上的动点,则PC PQ +的最小值是__________.18.如图,∠AOB=30°,点M 、N 分别是射线OA 、OB 上的动点,OP 平分∠AOB ,且OP=6,当△PMN 的周长取最小值时,四边形PMON 的面积为 .19.如图,∠AOB 的边OB 与x 轴正半轴重合,点P 是OA 上的一动点,点N (3,0)是OB 上的一定点,点M 是ON 的中点,∠AOB =30°,要使PM +PN 最小,则点P 的坐标为______.20.如图,一副含30°和45°角的三角板ABC和EDF拼合在个平面上,边AC与EF重合,AC=12cm.当点E从点A出发沿AC方向滑动时,点F同时从点C出发沿射线BC方向滑动.当点E从点A滑动到点C时,点D运动的路径长为__cm;连接BD,则△ABD的面积最大值为___cm2.21.如图,Rt△ABC中,∠BAC=90°,AB=3,,点D,E分别是边BC,AC上的动点,则DA+DE 的最小值为_____.第1关 以几何图形中的动点最值问题为背景的选择填空题【考查知识点】 “两点之间线段最短”,“垂线段最短”,“点关于线对称”,“线段的平移”。
专题26 全等三角形的应用(基础)1.如图,A ,B 两点分别位于一个池塘的两端,小明想用绳子测量A 、B 间的距离:现在地上取一个可以直接到达A 点和B 点的点C ,连接AC 并延长到D ,使CD =AC ;连接BC 并延长到E ,使CE =CB ;连接DE 并测量出它的长度. (1)求证:DE =AB ;(2)如果DE 的长度是8m ,则AB 的长度是多少?【分析】(1)利用SAS 直接得出△CDE ≌△CAB ,进而得出答案; (2)利用(1)中所求得出AB 的长即可. 【解答】(1)证明:在△CDE 和△CAB 中, {CD =CA∠DCE =∠BCA CE =CB, ∴△CDE ≌△CAB (SAS ), ∴DE =AB ;(2)解:∵DE =AB ,DE =8m , ∴AB =8m .答:AB 的长度是8m .【点评】此题主要考查了全等三角形的应用,得出△CDE ≌△CAB 是解题关键.2.公路上,A ,B 两站相距25千米,C 、D 为两所学校,DA ⊥AB 于点A ,CB ⊥AB 于点B ,如图,已知DA =15千米,现在要在公路AB 上建一报亭H ,使得C 、D 两所学校到H 的距离相等,且∠DHC =90°,问:H 应建在距离A 站多远处?学校C 到公路的距离是多少千米?【分析】根据同角的余角相等求出∠D =∠CHB ,再利用“角角边”证明△ADH 和△BHC 全等,根据全等三角形对应边相等可得AD =BH ,AH =BC ,再根据AH =AB ﹣BH 计算即可得解. 【解答】解:∵∠DHC =90°, ∴∠AHD +∠CHB =90°, ∵DA ⊥AB ,∴∠D +∠AHD =90°, ∴∠D =∠CHB ,在△ADH 和△BHC 中,{∠D =∠CHB∠A =∠B =90°DH =CH ,∴△ADH ≌△BHC (AAS ), ∴AD =BH =15千米,AH =BC , ∵A ,B 两站相距25千米, ∴AB =25千米,∴AH =AB ﹣BH =25﹣15=10千米, ∴学校C 到公路的距离是10千米.答:H 应建在距离A 站10千米处,学校C 到公路的距离是10千米.【点评】本题考查了全等三角形的应用,全等三角形的性质,熟练掌握全等三角形的判定方法求出两三角形全等是解题的关键.3.如图,有一池塘,要测池塘两端A ,B 的距离,可先在平地上取一个点C ,从点C 不经过池塘可以直接到达点A 和B .连接AC 并延长到点D ,使CD =CA .连接BC 并延长到点E ,使CE =CB .连接DE ,那么量出DE 的长就是A ,B 的距离.为什么?【分析】利用“边角边”证明△ABC 和△DEC 全等,再根据全等三角形对应边相等解答. 【解答】解:量出DE 的长就等于AB 的长,理由如下: 在△ABC 和△DEC 中,{BC =CE∠ACB =∠DCE CA =CD ,∴△ABC ≌△DEC (SAS ), ∴AB =DE .【点评】本题考查了全等三角形的应用,熟练掌握三角形全等的判定方法是解题的关键.4.如图,C 是路段AB 的中点,两人从C 同时出发,以相同的速度分别沿两条直线行走,并同时到达D ,E 两地,DA ⊥AB ,EB ⊥AB ,D ,E 与路段AB 的距离相等吗?为什么?【分析】首先根据题意可知AC =CB ,DC =EC ,再根据HL 定理证明Rt △ACD ≌Rt △BCE ,可得到AD =BE .【解答】解:D ,E 与路段AB 的距离相等,理由:∵点C 是路段AB 的中点, ∴AC =CB ,∵两人从C 同时出发,以相同的速度分别沿两条直线行走, ∴DC =EC ,∵DA ⊥AB ,EB ⊥AB , ∴∠A =∠B =90°, 在Rt △ACD 和Rt △BCE 中 ∵{AC =CB CD =CE, ∴Rt △ACD ≌Rt △BCE (HL ), ∴AD =BE .【点评】此题主要考查了全等三角形的判定与性质,解决此题的关键是证明Rt △ACD ≌Rt △BCE . 5.如图所示,有两个长度相同的滑梯BC 和EF ,CA ⊥BF ,ED ⊥BF ,垂足分别为A ,D ,左边滑梯的高度AC 与右边滑梯水平方向的长度DF 相等.问:两个滑梯的倾斜角∠ABC 和∠DFE 的大小有什么关系?【分析】由图可得,△ABC 与△DEF 均是直角三角形,由已知可根据HL 判定两三角形全等,再根据全等三角形的对应角相等,不难求解.【解答】解:∠ABC +∠DFE =90°,理由如下:由题意可得:△ABC 与△DEF 均是直角三角形,且BC =EF ,AC =DF . 在Rt △ABC 和Rt △DEF 中, {BC =EF AC =DF, ∴Rt △ABC ≌Rt △DEF (HL ), ∴∠ABC =∠DEF , ∵∠DEF +∠DFE =90°, ∴∠ABC +∠DFE =90°.【点评】此题考查了全等三角形的应用.做题时要注意找已知条件,根据已知选择方法得出全等三角形是解题关键.6.某广场是一个四边形区域ABCD ,现测得:AB =60m ,BC =80m ,且∠ABC =30°,∠DAC =60°,试求水池两旁B ,D 两点之间的距离.【分析】以AB 为边在△ABC 外侧作等边△ABE ,连接CE ,求出△EAC ≌△DAB 可得:BD =CE ,证明△EBC 是直角三角形,利用勾股定理求出CE 的长度,即可解答. 【解答】解:以AB 为边在△ABC 外侧作等边△ABE ,连接CE . ∵∠EAB =∠DAC =60°, ∴∠EAB +∠BAC =∠DAC +∠BAC , ∴∠EAC =∠DAB , 在△EAC 和△DAB 中, {AE =AB∠EAC =∠DAB AC =AD, ∴△EAC ≌△DAB (SAS ), ∴BD =CE ,∴∠EBC =60°+30°=90°, ∴△EBC 是直角三角形, ∵EB =60m BC =80m ,∴CE =√BE 2+BC 2=√602+802=100(m ). ∴水池两旁B 、D 两点之间的距离为100m .【点评】本题考查了全等三角形的判定与性质,等边三角形的性质与判定,熟记性质与判定方法是解题的关键,难点在于(灵活运用)作出辅助线构造成等边三角形和直角三角形.7.如图,两只蚂蚁分别位于一个正方形相邻的两个顶点A ,B 上,它们分别沿AE ,BF 的路线向BC 和CD 爬行,如果AE 和BF 相互垂直,那么它们爬行的距离相等吗?【分析】根据题意得出△ABE ≌△BCF (SAS ),可得AE =BF ,进而得出答案. 【解答】解:在正方形ABCD 中,AB =BC ,∠ABC =∠BCD =90°, ∵∠CBF +∠ABO =90°, ∴∠EAB +∠ABO =90°, ∴∠CBF =∠EAB , 在△BFC 和△AEB 中 {∠BFC =∠AEB∠C =∠ABE AB =BC∴△BFC ≌△AEB (AAS ), ∴AE =BF .【点评】此题考查了全等三角形的判定与性质,根据题意得出∠CBF =∠EAB 是解题关键.8.如图,平面上的四边形ABCD 是一只“风筝”的骨架,其中AB =AD ,CB =CD ,某同学观察了这只“风筝”的骨架后,认为四边形ABCD 的两条对角线AC ,BD 垂直,垂足为E ,并且BE =ED ,你同意这位同学的判断吗?请说明理由.【分析】根据中垂线的判定定理:到线段两个端点距离相等的点在线段的中垂线上来判定. 【解答】解:正确;理由如下: ∵AB =AD ,∴点A 在BD 的垂直平分线上. ∵CB =CD ,∴点C 在BD 的垂直平分线上.∴AC 为BD 的垂直平分线,BE =DE ,AC ⊥BD .【点评】本题利用了中垂线的判定定理求解,关键是根据到线段两个端点距离相等的点在线段的中垂线上分析.9.有一张纸片的形状如图所示,其中已知∠1=∠2,纸片中的△ABC 和△ADC 是全等的,小红说:“只要给我一个量角器,我就能验证:这两个三角形是全等.”小明不相信,你知道小红是怎样做的吗?如果知道,请写出小红的验证过程.【分析】直接利用全等三角形的判定方法(AAS ),进而得出答案.【解答】解:只要量出∠B 与∠D 的度数,若两角度数相等,则△ABC 和△ADC 全等. 理由:在△ABC 和△ADC 中,∵{∠B =∠D∠1=∠2AC =AC,∴△ABC ≌△ADC (AAS ).【点评】此题主要考查了全等三角形的应用,熟练应用全等三角形的判定方法是解题关键.10.小红在课外活动时,不小心把老师用的三角形教具弄坏了一个角,如图①所示,她想用一块同样材料的薄板把它补上,想出以下办法:(1)先量出∠AED ,∠BDE 的度数,量出DE 的长;(2)在同样的材料上取D 1E 1=DE ,用量角器∠ME 1D 1=180°﹣∠AED ″,∠ND 1E 1=180°﹣∠BDE ,如图②所示,两射线E 1M ,D 1N 交于点C 1,剪下△C 1D 1E 1,将其与原三角形黏合就能把三角形教具修好,你认为这两种方法可行吗?道理是什么?【分析】利用全等三角形的判定定理ASA 证得△C 1D 1E 1≌△CDE 即可. 【解答】解:这个方法可行,理由如下:∵∠ME 1D 1=180°﹣∠AED ,∠ND 1E 1=180°﹣∠BDE , ∴∠ME 1D 1=∠CED ,∠ND 1E 1=∠CDE , ∴在△C 1D 1E 1与△CDE 中,{∠ME 1D 1=∠CEDD 1E 1=DE ∠ND 1E 1=∠CDE ,∴△C 1D 1E 1≌△CDE (ASA ), ∴该方法可行.【点评】本题考查了全等三角形的应用.在实际生活中,对于难以实地测量的线段,常常通过两个全等三角形,转化需要测量的线段到易测量的边上或者已知边上来,从而求解.11.如图,把一个长为10m 的梯子AB 斜靠在墙上,测得AM =8m ,BM =6m ,梯子沿墙下滑到CD 位置,测得∠ABM =∠DCM ,求梯子下滑的高度.【分析】由全等三角形的判定定理AAS 得到△ABM ≌△DCM ,则其对应边相等:BM =CM ,AM =DM ,故AC =DM ﹣BM =2m .【解答】解:∵在△ABM 与△DCM 中,{∠AMB =∠DMC∠ABM =∠DCM AB =DC ,∴△ABM ≌△DCM (AAS ), ∴BM =CM =6m ,AM =DM =8m , ∴AC =AM ﹣CM =2m . 即梯子下滑的高度是2m .【点评】本题考查了全等三角形的应用.解题时,巧妙地借助两个三角形全等,寻找所求线段与已知线段之间的等量关系.12.如图所示,四边形ABCD 是一条河堤坝的横截面,AE =BF ,且AE ⊥CD ,BF ⊥CD ,垂足分别为E 、F ,AD =BC ,∠C 与∠D 是否相等?为什么?【分析】首先利用HL 定理证明Rt △ADE ≌Rt △BCF ,再根据全等三角形的性质可得∠C =∠D . 【解答】解:∠C =∠D , ∵AE ⊥CD ,BF ⊥CD , ∴∠AED =∠BFC =90°, 在Rt △ADE 和Rt △BCF 中, {AD =BC AE =BF, ∴Rt △ADE ≌Rt △BCF (HL ), ∴∠C =∠D .【点评】此题主要考查了全等三角形的应用,关键是掌握全等三角形的判定方法.13.如图,是小朋友荡秋千的侧面示意图,静止时秋千位于铅垂线BD 上,转轴B 到地面的距离BD =2.5m .小亮在荡秋千过程中,当秋千摆动到最高点A 时,测得点A 到BD 的距离AC =1.5m .点A 到地面的距离AE =1.5m ,当他从A 处摆动后的坐板记为A ′. (1)若A ′B ⊥AB 时,求A '到BD 的距离;(2)若A ′距地面最近时,求A '到地面的距离(结果精确到0.01,√13=3.606).【分析】(1)作A 'F ⊥BD ,垂足为F ,根据全等三角形的判定和性质解答即可; (2)根据全等三角形的性质解答即可.【解答】解:(1)如图2,作A 'F ⊥BD ,垂足为F . ∵AC ⊥BD ,∴∠ACB =∠A 'FB =90°; 在Rt △A 'FB 中,∠1+∠3=90°; 又∵A 'B ⊥AB , ∴∠1+∠2=90°, ∴∠2=∠3; 在△ACB 和△BF A '中, {∠ACB =∠A ′FB∠2=∠3AB =A′B,∴△ACB ≌△BF A '(AAS ); ∴A 'F =BC∵AC ∥DE 且CD ⊥AC ,AE ⊥DE , ∴CD =AE =1.5;∴BC =BD ﹣CD =2.5﹣1.5=1(m ), ∴A 'F =1(m ),即A '到BD 的距离是1m . (2)由(1)知:△ACB ≌△BF A ' ∴BF =AC =1.5m , 作A 'H ⊥DE ,垂足为H . ∵A 'F ∥DE , ∴A 'H =FD ,∴A 'H =BD ﹣BF =2.5﹣1.5=1(m ),即A '到地面的距离是2.5−√1.52−12≈2.5﹣1.8=0.7m .【点评】本题考查全等三角形的应用,解题的关键是正确寻找全等三角形全等的条件,灵活运用所学知识解决问题,属于中考常考题型.14.王强同学用10块高度都是2cm 的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(AC =BC ,∠ACB =90°),点C 在DE 上,点A 和B 分别与木墙的顶端重合. (1)求证:△ADC ≌△CEB ; (2)求两堵木墙之间的距离.【分析】(1)根据题意可得AC =BC ,∠ACB =90°,AD ⊥DE ,BE ⊥DE ,进而得到∠ADC =∠CEB =90°,再根据等角的余角相等可得∠BCE =∠DAC ,再证明△ADC ≌△CEB 即可; (2)利用全等三角形的性质进行解答.【解答】(1)证明:由题意得:AC =BC ,∠ACB =90°,AD ⊥DE ,BE ⊥DE , ∴∠ADC =∠CEB =90°,∴∠ACD +∠BCE =90°,∠ACD +∠DAC =90°, ∴∠BCE =∠DAC在△ADC 和△CEB 中{∠ADC =∠CEB∠DAC =∠BCE AC =BC,∴△ADC ≌△CEB (AAS );(2)解:由题意得:AD =2×3=6cm ,BE =7×2=14cm , ∵△ADC ≌△CEB ,∴EC =AD =6cm ,DC =BE =14cm , ∴DE =DC +CE =20(cm ), 答:两堵木墙之间的距离为20cm .【点评】此题主要考查了全等三角形的应用,关键是正确找出证明三角形全等的条件.15.某中学计划为新生配备如图1所示的折叠凳,图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿AB 和CD 的长度相等,O 是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度AD 设计为35cm ,由以上信息能求出CB 的长度吗?如果能,请求出CB 的长度;如果不能,请说明理由.【分析】根据中点定义求出OA =OB ,OC =OD ,然后利用“边角边”证明△AOD 和△BOC 全等,根据全等三角形对应边相等即可证明. 【解答】解:∵O 是AB 、CD 的中点, ∴OA =OB ,OC =OD , 在△AOD 和△BOC 中, {OA =OB∠AOD =∠BOC OC =OD, ∴△AOD ≌△BOC (SAS ), ∴CB =AD , ∵AD =35cm , ∴CB =35cm ,答:CB 的长度为35cm .【点评】本题考查了全等三角形的应用,证明得到三角形全等是解题的关键.16.如图,工人师傅要在墙壁的O 处用钻打孔,要使孔口从墙壁对面的B 点处打出,墙壁厚是35cm ,B 点与O 点的铅直距离AB 长是20cm ,工人师傅在旁边墙上与AO 水平的线上截取OC =35cm ,画CD ⊥OC ,使CD =20cm ,连接OD ,然后沿着DO 的方向打孔,结果钻头正好从B 点处打出,这是什么道理呢?请你说出理由.【分析】利用“角边角”证明Rt △OAB 和Rt △OCD 全等,根据全等三角形对应边相等可得AB =DC ,从而得解.【解答】解:∵OC =35cm ,墙壁厚OA =35cm , ∴OC =OA , ∵墙体是垂直的,∴∠OAB =90°且CD ⊥OC , ∴∠OAB =∠OCD =90°,在Rt △OAB 和Rt △OCD 中,{∠OAB =∠OCD =90°OC =OA∠AOB =∠COD ,∴Rt △OAB ≌Rt △OCD (ASA ), ∴DC =AB , ∵DC =20cm , ∴AB =20cm ,∴钻头正好从B 点处打出.【点评】本题考查了全等三角形的应用,读懂题目信息确定出全等三角形是解题的关键. 17.课间,小明拿着老师的等腰直角三角板玩,不小心掉到两墙之间,如图AD ⊥DE ,BE ⊥DE . (1)求证:△ADC ≌△CEB ;(2)若三角板的一条直角边AC =25cm ,请你帮小明求出砌墙砖块的厚度a 的大小(每块砖的厚度相等).【分析】(1)根据题意可得AC =BC ,∠ACB =90°,AD ⊥DE ,BE ⊥DE ,进而得到∠ADC =∠CEB =90°,再根据等角的余角相等可得∠BCE =∠DAC ,再证明△ADC ≌△CEB 即可. (2)利用(1)中全等三角形的性质进行解答.【解答】(1)证明:由题意得:AC =BC ,∠ACB =90°,AD ⊥DE ,BE ⊥DE , ∴∠ADC =∠CEB =90°,∴∠ACD +∠BCE =90°,∠ACD +∠DAC =90°, ∴∠BCE =∠DAC ,在△ADC 和△CEB 中,{∠ADC =∠CEB∠DAC =∠BCE AC =BC ,∴△ADC ≌△CEB (AAS );(2)解:∵一块墙砖的厚度为a ,∴AD =4a ,BE =3a ,由(1)得:△ADC ≌△CEB ,∴DC =BE =3a ,AD =CE =4a ,∴AC =√AD 2+CD 2=5a =25,∴a =5,答:砌墙砖块的厚度a 为5cm .【点评】此题主要考查了全等三角形的应用,关键是正确找出证明三角形全等的条件.18.在测量一个小口圆形容器的壁厚时,小明用“X 型转动钳”按如图方法进行测量,其中OA =OD ,OB =OC ,只需测得AB =a ,EF =b ,就可以知道圆形容器的壁厚了.(1)请你利用所学习的数学知识说明AB =CD ;(2)求出圆形容器的壁厚.(用含有a ,b 的代数式表示)【分析】(1)连接AB ,只要证明△AOB ≌△DOC ,可得AB =CD ,即可解决问题;(2)利用(1)中所求即可得出圆形容器的壁厚.【解答】解:(1)连接AB .在△AOB 和△DOC 中,{OA =OD ∠AOB =∠DOC BO =OC,∴△AOB ≌△DOC (SAS ),∴AB =CD ;(2)∵EF =b ,AB =CD =a ,∴圆形容器的壁厚是12(b ﹣a ).【点评】本题考查全等三角形的应用,解题的关键是利用全等三角形的性质解决实际问题.属于中考常考题型.19.某风景区改建中,需测量湖两岸游船码头A 、B 间的距离,于是工作人员在岸边A 、B 的垂线AF 上取两点E、D,使ED=AE.再过D点作出AF的垂线OD,并在OD上找一点C,使B、E、C在同一直线上,这时测得CD长就是AB的距离.请说明理由.【分析】已知等边及垂直,在直角三角形中,可考虑AAS证明三角形全等,从而推出线段相等.【解答】证明:∵AB⊥AD,CD⊥AD∴∠A=∠CDE=90°又∵ED=AE,∠AEB=∠CED∴△ABE≌△CED(AAS)所以AB=CD.【点评】本题考查全等三角形的应用.在实际生活中,对于难以实地测量的线段,常常通过两个全等三角形,转化需要测量的线段到易测量的边上或者已知边上来,从而求解.20.如图所示,有两个长度相等的滑梯,左边滑梯BC的高AC与右边滑梯EF水平方向的长度DF相等,两滑梯倾斜角∠ABC和∠DFE有什么关系?【分析】已知Rt△ABC和Rt△DEF中,BC=EF,AC=DF,利用“HL”可判断两三角形全等,根据确定找对应角相等,根据直角三角形两锐角的互余关系,确定ABC与∠DFE的大小关系.【解答】证明:在Rt△ABC和Rt△DEF中,{BC=EF AC=DF∴Rt△ABC≌Rt△DEF(HL)∴∠ABC=∠DEF又∵∠DEF+∠DFE=90°∴∠ABC+∠DFE=90°即两滑梯的倾斜角∠ABC与∠DFE互余.【点评】本题考查了全等三角形的应用;确定两角的大小关系,通常可证明这两角所在的三角形全等,根据对应角相等进行判定.。