[课件]RBF神经网络的实现过程PPT
- 格式:ppt
- 大小:692.00 KB
- 文档页数:55



径向基函数(RBF)神经⽹络RBF⽹络能够逼近任意的⾮线性函数,可以处理系统内的难以解析的规律性,具有良好的泛化能⼒,并有很快的学习收敛速度,已成功应⽤于⾮线性函数逼近、时间序列分析、数据分类、模式识别、信息处理、图像处理、系统建模、控制和故障诊断等。
简单说明⼀下为什么RBF⽹络学习收敛得⽐较快。
当⽹络的⼀个或多个可调参数(权值或阈值)对任何⼀个输出都有影响时,这样的⽹络称为全局逼近⽹络。
由于对于每次输⼊,⽹络上的每⼀个权值都要调整,从⽽导致全局逼近⽹络的学习速度很慢。
BP⽹络就是⼀个典型的例⼦。
如果对于输⼊空间的某个局部区域只有少数⼏个连接权值影响输出,则该⽹络称为局部逼近⽹络。
常见的局部逼近⽹络有RBF⽹络、⼩脑模型(CMAC)⽹络、B样条⽹络等。
径向基函数解决插值问题完全内插法要求插值函数经过每个样本点,即。
样本点总共有P个。
RBF的⽅法是要选择P个基函数,每个基函数对应⼀个训练数据,各基函数形式为,由于距离是径向同性的,因此称为径向基函数。
||X-X p||表⽰差向量的模,或者叫2范数。
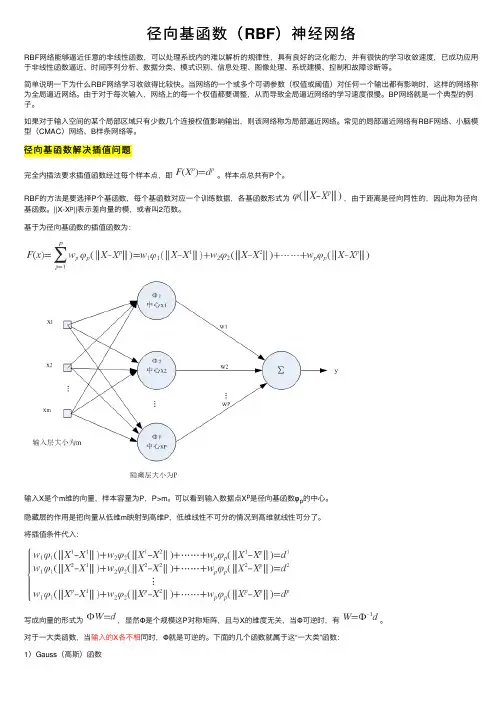
基于为径向基函数的插值函数为:输⼊X是个m维的向量,样本容量为P,P>m。
可以看到输⼊数据点X p是径向基函数φp的中⼼。
隐藏层的作⽤是把向量从低维m映射到⾼维P,低维线性不可分的情况到⾼维就线性可分了。
将插值条件代⼊:写成向量的形式为,显然Φ是个规模这P对称矩阵,且与X的维度⽆关,当Φ可逆时,有。
对于⼀⼤类函数,当输⼊的X各不相同时,Φ就是可逆的。
下⾯的⼏个函数就属于这“⼀⼤类”函数:1)Gauss(⾼斯)函数2)Reflected Sigmoidal(反常S型)函数3)Inverse multiquadrics(拟多⼆次)函数σ称为径向基函数的扩展常数,它反应了函数图像的宽度,σ越⼩,宽度越窄,函数越具有选择性。
完全内插存在⼀些问题:1)插值曲⾯必须经过所有样本点,当样本中包含噪声时,神经⽹络将拟合出⼀个错误的曲⾯,从⽽使泛化能⼒下降。





第7章:多层神经网络设计前面分析可知,神经网络的性能主要取决于神经元类型、神经网络结构及相应的学习算法。
因此可以说神经网络的设计,其实质就是如何选取神经元及其连接形式、如何选择学习算法,确保神经网络性能达到期望值。
我们知道虽然神经网络的形式有许多种,但是用于控制系统的神经网络绝大部分属层状结构。
因此,这里着重讨论多层神经网络的设计问题。
7.1 多层感知器网络设计神经网络的设计涉及到网络的结构、神经元的个数及网络的层数、神经元的激活函数、初始值以及学习算法等。
对于多层感知器网络而言,输入与输出层的神经元数可以根据需要求解的问题来确定。
因此,多层感知器网络的设计一般应从网络的层数、隐含层中的神经元个数、神经元的激活函数、初始值和学习速率等几个方面来进行考虑。
在设计中应当尽可能地减小神经网络模型的规模,以便缩短网络的训练时间。
下面简要地讨论一下各个环节的设计原则。
7.1.1 训练数据的处理一、获取样本数据设计有监督学习的神经网络,获取样本数据集是第一步,也是十分重要和关键的一步。
样本数据的获取包括原始数据的收集、数据分析、变量选择以及数据的预处理,只有经过上述步骤的处理后,神经网络的学习和训练才更加有效。
二、输入数据的变换由于Sigmoid函数的导数计算十分方便,因此神经元的作用函数多选Sigmoid型。
如果神经元的作用函数为一Sigmoid函数,那么根据Sigmoid函数的导数可知,随着的增大,其导数迅速减小。
当很大时,趋于0。
这时,若采用BP学习算法训练神经网络,网络的权值调整量几乎为零。
因此,设计者总是希望神经元工作在较小的区域,这样就需要对神经网络的输入给予适当地处理,一般取。
由于神经网络的输入取决于实际问题,如果提供给神经网络的实际数据很大,则需要做归一化处理,才能保证神经元工作在较小的区域。
由于输入数据发生了变化,那么对神经网络的输出也要进行相应的处理。
如将输出放大倍,的大小视实际而定,且需经验知识的积累。


RBF神经⽹络RBF神经⽹络RBF神经⽹络通常只有三层,即输⼊层、中间层和输出层。
其中中间层主要计算输⼊x和样本⽮量c(记忆样本)之间的欧式距离的Radial Basis Function (RBF)的值,输出层对其做⼀个线性的组合。
径向基函数:RBF神经⽹络的训练可以分为两个阶段:第⼀阶段为⽆监督学习,从样本数据中选择记忆样本/中⼼点;可以使⽤聚类算法,也可以选择随机给定的⽅式。
第⼆阶段为监督学习,主要计算样本经过RBF转换后,和输出之间的关系/权重;可以使⽤BP算法计算、也可以使⽤简单的数学公式计算。
1. 随机初始化中⼼点2. 计算RBF中的激活函数值,每个中⼼点到样本的距离3. 计算权重,原函数:Y=GW4. W = G^-1YRBF⽹络能够逼近任意⾮线性的函数(因为使⽤的是⼀个局部的激活函数。
在中⼼点附近有最⼤的反应;越接近中⼼点则反应最⼤,远离反应成指数递减;就相当于每个神经元都对应不同的感知域)。
可以处理系统内难以解析的规律性,具有很好的泛化能⼒,并且具有较快的学习速度。
有很快的学习收敛速度,已成功应⽤于⾮线性函数逼近、时间序列分析、数据分类、模式识别、信息处理、图像处理、系统建模、控制和故障诊断等。
当⽹络的⼀个或多个可调参数(权值或阈值)对任何⼀个输出都有影响时,这样的⽹络称为全局逼近⽹络。
由于对于每次输⼊,⽹络上的每⼀个权值都要调整,从⽽导致全局逼近⽹络的学习速度很慢,⽐如BP⽹络。
如果对于输⼊空间的某个局部区域只有少数⼏个连接权值影响输出,则该⽹络称为局部逼近⽹络,⽐如RBF⽹络。
RBF和BP神经⽹络的对⽐BP神经⽹络(使⽤Sigmoid激活函数)是全局逼近;RBF神经⽹络(使⽤径向基函数作为激活函数)是局部逼近;相同点:1. RBF神经⽹络中对于权重的求解也可以使⽤BP算法求解。
不同点:1. 中间神经元类型不同(RBF:径向基函数;BP:Sigmoid函数)2. ⽹络层次数量不同(RBF:3层;BP:不限制)3. 运⾏速度的区别(RBF:快;BP:慢)简单的RBF神经⽹络代码实现# norm求模,pinv求逆from scipy.linalg import norm, pinvimport numpy as npfrom matplotlib import pyplot as pltimport matplotlib as mplmpl.rcParams["font.sans-serif"] = ["SimHei"]np.random.seed(28)class RBF:"""RBF径向基神经⽹络"""def__init__(self, input_dim, num_centers, out_dim):"""初始化函数:param input_dim: 输⼊维度数⽬:param num_centers: 中间的核数⽬:param out_dim:输出维度数⽬"""self.input_dim = input_dimself.out_dim = out_dimself.num_centers = num_centersself.centers = [np.random.uniform(-1, 1, input_dim) for i in range(num_centers)] self.beta = 8self.W = np.random.random((self.num_centers, self.out_dim))def _basisfunc(self, c, d):return np.exp(-self.beta * norm(c - d) ** 2)def _calcAct(self, X):G = np.zeros((X.shape[0], self.num_centers), float)for ci, c in enumerate(self.centers):for xi, x in enumerate(X):G[xi, ci] = self._basisfunc(c, x)return Gdef train(self, X, Y):"""进⾏模型训练:param X: 矩阵,x的维度必须是给定的n * input_dim:param Y: 列的向量组合,要求维度必须是n * 1:return:"""# 随机初始化中⼼点rnd_idx = np.random.permutation(X.shape[0])[:self.num_centers]self.centers = [X[i, :] for i in rnd_idx]# 相当于计算RBF中的激活函数值G = self._calcAct(X)# 计算权重==> Y=GW ==> W = G^-1Yself.W = np.dot(pinv(G), Y)def test(self, X):""" x的维度必须是给定的n * input_dim"""G = self._calcAct(X)Y = np.dot(G, self.W)return Y测试上⾯的代码:# 构造数据n = 100x = np.linspace(-1, 1, n).reshape(n, 1)y = np.sin(3 * (x + 0.5) ** 3 - 1)# RBF神经⽹络rbf = RBF(1, 20, 1)rbf.train(x, y)z = rbf.test(x)plt.figure(figsize=(12, 8))plt.plot(x, y, 'ko',label="原始值")plt.plot(x, z, 'r-', linewidth=2,label="预测值")plt.legend()plt.xlim(-1.2, 1.2)plt.show()效果图⽚:RBF训练RBF函数中⼼,扩展常数,输出权值都应该采⽤监督学习算法进⾏训练,经历⼀个误差修正学习的过程,与BP⽹络的学习原理⼀样.同样采⽤梯度下降爱法,定义⽬标函数为:ei为输⼊第i个样本时候的误差。
rbf神经网络
RBF(Radial Basis Function)神经网络是一种广泛应用于模式识别和函数逼近的神经网络模型。
它主要由三个层次
组成:输入层、隐藏层和输出层。
在RBF神经网络中,隐藏层神经元的激活函数是径向基函
数(Radial Basis Function),常用的径向基函数有高斯
函数、多项式函数等。
隐藏层神经元的激活函数用于计算
输入向量与该神经元的权重向量之间的距离或相似性度量。
距离越小,相似度越高。
隐藏层神经元的输出作为输入层神经元到输出层神经元的
连接权重,输出层计算输出结果。
通常情况下,输出层使
用线性激活函数。
RBF神经网络的训练过程可以通过使用最小二乘法或优化
算法进行参数优化。
其训练目标是最小化预测输出与真实
输出之间的误差。
RBF神经网络具有快速训练和良好的泛化能力的特点,由于其可解释性强,因此在模式识别、函数逼近和非线性建模等领域有着广泛的应用。