反比例函数中“K”与面积专题
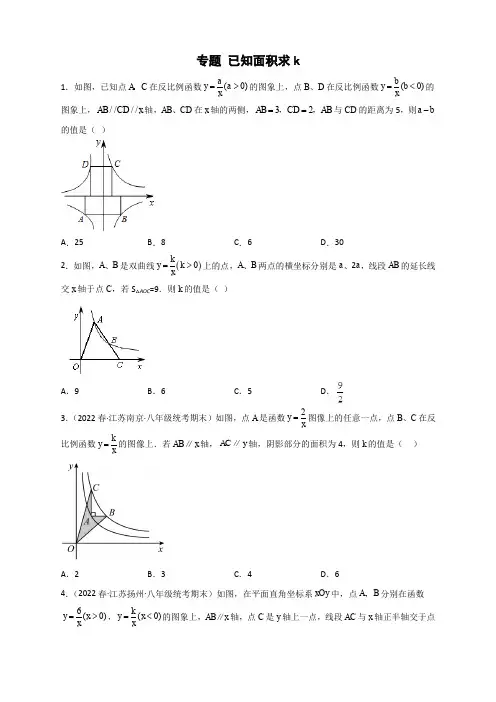
- 格式:docx
- 大小:210.02 KB
- 文档页数:14
A.9 B.6 C.5 D.2x2AD,若ABO的面积为6\kkxDE OC,FG的面积为10,则kmx在平面直角坐标系中,ABO的边若O A B的面积为6,则x,将ABO向右平移到CDE位置,C和DE的中点,则k的值是k(1)设2a =,点(4,2)B 在函数12,y y 的图象上. ①分别求函数12,y y 的表达式;②直接写出使120y y >>成立的x 的范围;(2)如图,设函数12,y y 的图象相交于点B ,点B 的横坐标为3a ,AA B '∆的面积为16,求k 的值. 25.六•一儿童节,小文到公园游玩.看到公园的一段人行弯道MN (不计宽度),如图,它与两面互相垂直的围墙OP 、OQ 之间有一块空地MPOQN (MP ⊥OP ,NQ ⊥OQ ),他发现弯道MN 上任一点到两边围墙的垂线段与围墙所围成的矩形的面积都相等,比如:A 、B 、C 是弯道MN 上的三点,矩形ADOG 、矩形BEOH 、矩形CFOI 的面积相等.爱好数学的他建立了平面直角坐标系(如图),图中三块阴影部分的面积分别记为S 1、S 2、S 3,并测得S 2=6(单位:平方米).OG=GH=HI . (1)求S 1和S 3的值;(2)设T (x ,y )是弯道MN 上的任一点,写出y 关于x 的函数关系式;(3)公园准备对区域MPOQN 内部进行绿化改造,在横坐标、纵坐标都是偶数的点处种植花木(区域边界上的点除外),已知MP=2米,NQ=3米.问一共能种植多少棵花木?A.9 B.6 C.5 D.x22km m m ⎛⎫- ⎪⎝⎭6k =.D .2ADBCDBDASS=【详解】解:如图,过点6kBCDBDASS=ADB=61,若ABO的面积为628AB OA =根据EAB ∠EAB ∴∠=E k x y =⋅设(712E m ,EOF S ∴=△\DBO DBE S S =,根据反比例函数,AD AC =BDA S ∴=△EDB S ∴=△AB AC =AD AB ∴=DBA ∴∠=DBA ∠+ABD ∴∠+D在第一象限,∴=k43故答案为:AOE S =-OBF S =-1+k 2-2k 的值. AOE S +OBF S +S 三点分别在反比例函数y=1k x (x<0AOE S =12OBF S =12△ABC =(,x y=,2∵点A在第二象限,则=-=x y xy2xy=-,即∴反比例函数的解析式为:故答案为:y=、OABC的DE OC,FG 的面积为10,则∴两三角形的相似比为,∵双曲线,可知,,由,得,解得m(,)A a b、∴点O在线段(,)A a b是反比例函数mba∴=,AC∥y轴,∴点C的坐标为|mACa ∴=x【点睛】本题主要考查菱形的性质及反比例函数的比例系数k的几何意义.反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系,即S=|k|.在平面直角坐标系中,ABO的边x若O A B的面积为6,则根据OAB的面积为的坐标,从而得出结论.【详解】解:如图,延长∵OAB的面积为1 2AB OD⋅(1 2AB x⋅-CBDS =,证明BFG BCD ∽,可得BFGS =2k=解方程即分别作x 轴的垂线,垂足分别为四边形Rt Rt OAE CBD ≌CBDS=若点为BC 的中点,△FG CD ∥BFG BCD ∴∽,12BF BC =, 21BFG BCGS BF S⎛⎫∴== ⎪BFGS=OBF +△8k .故答案为:8.【点睛】本题考查了平行四边形的性质,相似三角形的性质与判定,反比例函数与数形结合是解题的关键.,将ABO 向右平移到CDE 位置,C 和DE 的中点,则k 的值是AOD AOB BOC ADCB SS S S +=+四,,2AOD BOC k S S ==AOB S ,列出方程,解出即可.【详解】解:过点,2AOD BOC k S S ==AOD AOB BOC ABCO ADCB S S S S S =+=+四四,AOB ADCB S S ∴=四,2,4,24k k A B ⎛⎫⎛⎫ ⎪ ⎝⎭⎝1222k ⎛∴⨯ ⎝4.k ∴=2a =∴点A 坐标为把()4,2BO 为AA '12AOB S ∆=点A 、36。

专题01 用几何意义探究反比例函数中k 值问题的多种解法如图,反比例函数k y x =(k >0),A 、C 是第一象限上两点,S △OAB =S △OCD =2k ;S △OAC =S 梯形ABDC 在已知面积或比例线段解答反比例函数的问题中,善于利用k 与面积的关系,往往可以事半功倍.典例1.知面积比值,求k 值(2022•山东聊城中考真题)如图,直线与反比例函数在第一象限内的图象交于点,与y 轴交于点B ,过双曲线上的一点C 作x 轴的垂线,垂足为点D ,交直线于点E ,且.()30y px p =+¹()0k y k x=>()2,A q 3y px =+:3:4AOB COD S S =△△(1)求k ,p 的值;(2)若OE 将四边形BOCE 分成两个面积相等的三角形,求点C 的坐标.【答案】(1),;(2)点C 的坐标为(4,2)【解析】【方法一】坐标法(1)解:∵直线与y 轴交点为B ,∴,即.∵点A 的横坐标为2,∴.∵,∴△COD 的面积为4,设,∴,解得.∵点在双曲线上,∴,把点代入,得,∴,;8k =12p =3y px =+()0,3B 3OB =13232AOB S =´´=V :3:4AOB COD S S =△△,k C m m æöç÷èø142k m m×=8k =()2,A q 8y x=4q =()2,4A 3y px =+12p =8k =12p =(2)解:由(1)得8,C m m æöç÷èø,∴.∵OE 将四边形BOCE 分成两个面积相等的三角形,∴,∵32BOE S m =△,,∴,解得或(不符合题意,舍去),∴点的坐标为(4,2).【方法二】k 的几何意义法解:(1)由题意知,△ABO 的面积为3,又,得:△OCD 的面积为4,故k =2S △OCD =8,所以,A (2,4),把点代入,得(2)如图,过A ,E 作y 轴垂线,垂足为M ,N则四边形ODEN 为矩形,所以,S △OEN =S △OED ,又S △OBE =S △OCE ,所以S △BEN =S △OCD =4,1,32E m m æö+ç÷èøBOE COE S S =△△13422COE m S m æö=+-ç÷èø△3134222m m m æö=+-ç÷èø4m =4m =-C :3:4AOB COD S S =△△()2,4A 3y px =+12p =所以S △ABM =1,∵AM ∥NE ,∴△ABM ∽△EBN ,其面积比为1:4,∴AM :NE =1:2,即NE =4,∴C 点坐标为(4,2)典例2.知比例线段,求k 值(2022•贵州铜仁中考真题)如图,点A 、B 在反比例函数k y x=的图象上,AC y ^轴,垂足为D ,BC AC ^.若四边形AOBC 的面积为6,12AD AC =,则k 的值为_______.【答案】3.【解析】【方法一】坐标法设点,k A a a æöç÷èø,∵AC y ^轴,∴AD a =,k OD a =,∵12AD AC =,∴AC 2a =,∴CD =3a ,∵BC AC ^.AC y ^轴,∴BC ∥y 轴,∴点B 3,3æöç÷èøk a a ,∴233k k k BC a a a=-=,∵AOD AOBC OBCD S S S =+V 四边形梯形,四边形AOBC 间面积为6,∴12136232k k a k a a æö+´=+ç÷èø,解得:3k =.【方法二】k 的几何意义法如图,连接OC ,延长CB 交x 轴于E ,则S △AOD =S △BOE =12k ,因为AD :AC =1:2,所以S △AOC =2S △AOD =k ,S △BOC =6-k ,又四边形DOEC 为矩形,OC 为对角线,所以,S △COD =S △COE ,所以12k +k =6-k +12k ,解得:k =3.典例3.知面积值,求k 值(2022•内蒙古呼伦贝尔中考真题)如图,在平面直角坐标系中,Rt OAB △的直角顶点B 在x 轴的正半轴上,点O 与原点重合,点A 在第一象限,反比例函数k y x=(0x >)的图象经过OA 的中点C ,交AB 于点D ,连接CD .若ACD △的面积是1,则k 的值是_________.【答案】43.【解析】【方法一】坐标法解:设C (m ,k m),因为C 为OA 中点,所以A (2m ,2k m),则D (2m ,2k m ),又△ACD 的面积为1,所以12122k k m m m æö×-=ç÷èø,解得:k =43【方法二】k 的几何意义法解:连接OD ,过C 作CE AB ∥,交x 轴于E ,∵∠ABO =90°,反比例函数k y x =(x >0)的图象经过OA 的中点C ,1ACD S =V ,∴12COE BOD S S k ==△△,1ACD OCD S S ==V V ,2OC =OA ,∵CE AB ∥,∴△OCE ∽△OAB ,∴221124OCE S OC S OA æöæö===ç÷ç÷èøèø△△O A B ,∴4OCE OAB ACD OCD OBD S S S S S ==++V V V V V ,∴1141122k k ´=++,∴k =43,故答案为:43.1.(2022•辽宁锦州中考真题)如图,在平面直角坐标系中,△AOB 的边OB 在y 轴上,边AB 与x 轴交于点D ,且BD =AD ,反比例函数y =k x(x >0)的图像经过点A ,若S △OAB =1,则k 的值为___________.【答案】2.【解析】【方法一】坐标法解:设A(a,b) ,如图,作A过x轴的垂线与x轴交于C,则:AC=b,OC=a,AC∥OB,∴∠ACD=∠BOD=90°,∠ADC=∠BDO,∴△ADC≌△BDO,∴S△ADC=S△BDO,∴S△OAC=S△AOD+ S△ADC=S△AOD+ S△BDO= S△OAB=1,∴12×OC×AC=12ab=1,∴ab=2,∵A(a,b) 在y=kx上,∴k=ab=2 .【方法二】k的几何意义法由上知,S△AOC=1,所以,k=2S△AOC=2故答案为:2.2.(2022•辽宁鞍山中考真题)如图,在平面直角坐标系中,O 是坐标原点.在Rt OAB V 中,90OAB Ð=°,边OA 在y 轴上,点D 是边OB 上一点,且:1:2OD DB =,反比例函数()0ky x x=>的图象经过点D 交AB 于点C ,连接OC .若4OBC S =△,则k 的值为_________.【答案】1.【解析】【方法一】坐标法解:∵反比例函数()0k y x x=>的图象经过点D ,∠OAB =90°,∴D (m ,k m ),∵OD :DB =1:2,∴B (3m ,3k m),∴AB =3m ,OA =3k m ,∴反比例函数()0k y x x =>的图象经过点D 交AB 于点C ,∠OAB =90°,∴12AOC S k =△,∵4OBC S △=,∴4AOB AOC S S -△△=,即1313422k m k m ´×-=,解得k =1【方法二】k 的几何意义法如图,过D 作DE ⊥x 轴,则DE ∥AB ,因为OD :BD =1:2,所以DE :AB =1:3,所以S △ODE :S △OAB =1:9,又S △ODE =S △OAC =12k ,所以12k +4=92k ,解得:k =13.(2022•江苏南通中考真题)平面直角坐标系中,已知点是函数图象上的三点.若,则k 的值为___________.【答案】【解析】【方法一】坐标法解:∵点是函数图象上的三点,∴,,∴m =n ,∴,,∴点B 、C 关于原点对称,∴设直线BC 的解析式为,代入得:,解得:,∴直线BC 的解析式为,xOy (,6),(3,2),(3,2)--A m m B m n C m n (0)k y k x=¹2ABC S =△34(,6),(3,2),(3,2)--A m m B m n C m n (0)k y k x =¹260k m =>6k mn =(3,2)B m m (3,2)C m m --()0y kx k =¹(3,2)B m m 23m mk =23k =23y x =不妨设m >0,如图,过点A 作x 轴的垂线交BC 于D ,把x =m 代入得:,∴D (m ,),∴AD =,∴,∴,∴,而当m <0时,可得,故答案为:.【方法二】由题意知,S △OAB =12632m n m m ×-×,O 为BC 中点,因为所以,S △OAB =12632m n m m ×-×=1,即291mn m -=①,又632m m m n k ×=×=②,23y x =23y m =23m 216633m m m -=()11633223ABC S m m m =´×+=V 218m =2136684k m ==´=34k =342ABC S =△由①②可得:4.(2022•湖北十堰中考真题)如图,正方形ABCD 的顶点分别在反比例函数()110k y k x=>和()220k y k x =>的图象上.若BD y ∥轴,点D 的横坐标为3,则12k k +=( )A .36B .18C .12D .9【答案】B .【解析】【方法一】解:连接AC ,与BD 相交于点P ,设PA =PB =PC =PD =t (t ≠0).∴点D 的坐标为(3,23k ),∴点C 的坐标为(3-t ,23k +t ).∵点C 在反比例函数y =2k x 的图象上,34k=∴(3-t )(23k +t )=k 2,化简得:t =3-23k ,∴点B 的纵坐标为23k +2t =23k +2(3-23k )=6-23k ,∴点B 的坐标为(3,6-23k ),∴3×(6-23k )=1k ,整理,得:1k +2k =18.【方法二】先利用D 点坐标,表示出A 和C 点坐标,再根据四边形ABCD 为正方形,BD 与y 轴平行,知AC 平行于x 轴,那么,A 和C 点的纵坐标相等,进而求解23,3k D æöç÷èø,13,3k B æöç÷èø,122123,636k k k C k k æöç÷--ç÷-ç÷-èø,121123,636k k k A k k æöç÷-+ç÷-ç÷+èø所以2112123366k k k k k k =---+,整理得:()212212180k k k k ---=即()()1212108k k k k -+=-因为()120k k -¹所以()12018k k +-=,即1218k k +=5.(2022•黑龙江龙东中考真题)如图,在平面直角坐标系中,点O 为坐标原点,平行四边形OBAD 的顶点B 在反比例函数3y x =的图象上,顶点A 在反比例函数k y x=的图象上,顶点D 在x 轴的负半轴上.若平行四边形OBAD 的面积是5,则k 的值是( )A .2B .1C .1-D .2-【答案】D .【解析】解:设B点坐标为3,mmæöç÷èø,则A3,3kmmæöç÷èø,因为平行四边形OBAD的面积是5,所以353kmmmæö-×=ç÷èø,解得k=-2【方法二】解:如图,连接OA,设AB交y轴于点C,∵四边形OBAD是平行四边形,平行四边形OBAD的面积是5,∴1522AOB OBADS S==V Y,AB∥OD,∴AB⊥y轴,∵点B在反比例函数3yx=的图象上,顶点A在反比例函数kyx=的图象上,∴3,22 COB COAkS S==-V V,∴35222 AOB COB COAkS S S=+=-=V V V,解得:2k=-.故选:D.6.(2022•湖北黄石中考真题)如图,反比例函数kyx=的图象经过矩形ABCD对角线的交点E和点A,点B、C在x轴上,OCE△的面积为6,则k=______________.【答案】8.【解析】设C (m ,0),由题意知E 为AC 中点,因为△OCE 面积为6,所以E 点纵坐标为12m,所以E 12,12km m æöç÷èø,A 24,6km m m æö-ç÷èø,又A 在反比例函数图像上所以246km m k mæö-×=ç÷èø解得k =8【方法二】解:如图作EF ⊥BC ,则12EF AB =,设E 点坐标为(a ,b ),则A 点的纵坐标为2b ,则可设A 点坐标为(c ,2b ),∵点A ,E 在反比例函数k y x=上,∴ab =k =2bc ,解得:a =2c ,故BF =FC =2c -c =c ,∴OC =3c ,故113622OEC S OC EF c b =´´=´´=V ,解得:bc =4,∴k =2bc =8,故答案为:8.7.(2022•贵州六盘水中考真题)如图,正比例函数与反比例函数的图象交于,两点.y x =4y x=A B(1)求,两点的坐标;(2)将直线向下平移个单位长度,与反比例函数在第一象限的图象交于点,与轴交于点,与轴交于点,若,求的值.【答案】(1);(2)【解析】(1)解:联立与,解得,;(2)【方法一】解:如图,过点作轴于点,A B y x =a C x D y E 13CD DE =a ()()2,2,2,2A B --3a =y x =4y x=121222,22x x y y ==-ììíí==-îî()()2,2,2,2A B \--C CF y ^F,,,直线向下平移个单位长度得到,根据图象可知,令,得,令,得,,,,,与反比例函数在第一象限的图象交于点,,将代入,得,解得或(舍去).【方法二】CF OD \∥Q 13CD DE =13OF CD OE DE \==Q y x =a y x a =-0a >0x =y a =-0y =x a =()0,E a \-(),0D a 10,3F a æö\ç÷èø13c y a \=Q y x a =-4y x=C 41213c x aa \==121,3C a a æöç÷èøy x a =-1123a a a=-3a =3a =-如图,连接OC ,过C 作CE ⊥x 轴,因为CD :DE =1:3,CE ∥OE则△CDE ∽△EDO ,相似比为1:3,面积比为1:9,易知△ODE 面积为212a ,△OCE 的面积为12k =2,所以△OCD 的面积为2-2118a ,又△OCD 与△ODE 的面积比为1:3,所以2-2118a =21132a ´,解得:a =3或a =-3(舍)8.(2022•安徽中考真题)如图,平行四边形OABC 的顶点O 是坐标原点,A 在x 轴的正半轴上,B ,C 在第一象限,反比例函数1y x =的图象经过点C ,()0k y k x=¹的图象经过点B .若OC AC =,则k =________.【答案】3.【解析】【方法一】设C 1,m m æöç÷èø,因为OC =AC所以A ()2,0m ,又OABC 为平行四边形所以B 13,m m æöç÷èø因为B 点在k y x =上,所以k =133m m ×=【方法二】解:过点C 作CD ⊥OA 于D ,过点B 作BE ⊥x 轴于E ,∴CD ∥BE ,∵四边形ABCO 为平行四边形,∴CB OA ∥ ,即CB DE ∥,OC =AB ,∴四边形CDEB 为平行四边形,∵CD ⊥OA ,∴四边形CDEB 为矩形,∴CD =BE ,∴在Rt △COD 和Rt △BAE 中,OC AB CD EB =ìí=î,∴Rt △COD ≌Rt △BAE (HL ),∴S △OCD =S △ABE ,∵OC =AC ,CD ⊥OA ,∴OD =AD ,∵反比例函数1yx=的图象经过点C,∴S△OCD=S△CAD=12,∴S平行四边形OCBA=4S△OCD=2,∴S△OBA=11 2OCBAS=平行四边形,∴S△OBE=S△OBA+S△ABE=13122+=,∴3232k=´=.故答案为3.。

专题:反比例函数中k 的几何意义知识要点:反比例函数中k 的几何意义1、反比例函数与矩形面积:若Q(x ,y)为反比例函数y = kx (k≠0)图像上的任意一点如图2所示,过Q 作QA ⊥x 轴于A(或作QB ⊥y 轴于B),连结QO ,则所得矩形的面积为S =|k |.说明:以上结论与点在反比例函数图像上的位置无关. 2、反比例函数与三角形面积:若Q(x ,y)为反比例函数y = k x (k≠0)图像上的任意一点如图2所示,过Q 作QA ⊥x 轴于A(或作QB ⊥y 轴于B),连结QO ,则所得三角形的面积为:S △QOA =|k |2(或S △QOB =|k |2).说明:以上结论与点在反比例函数图像上的位置无关.【跟踪训练】1. (2019∙凉山)如图,正比例函数y=kx 与反比例函数y= 4x 的图象相交于A 、C 两点,过点A 作x 轴的垂线交x 轴于点B ,连接BC ,则△ABC 的面积等于( ) A. 8 B. 6 C. 4 D. 22. (2019∙黑龙江)如图,在平面直角坐标系中,点O 为坐标原点,平行四边形OABC 的顶点A 在反比例函数y=1x上,顶点B 在反比例函数y= 5x 上,点C 在x 轴的正半轴上,则平行四边形OABC 的面积是( ) A. 32B. 52C. 4D. 63. (2019∙山西)如图,在平面直角坐标中,点O 为坐标原点,菱形ABCD 的顶点B 在x 轴的正半轴上,点A 坐标为(−4,0),点D 的坐标为(−1,4),反比例函数y= kx (x>0)的图象恰好经过点C ,则k 的值为___.4. (2019∙巴中)如图,反比例函数y= kx (x>0)经过A. B 两点,过点A 作AC⊥y 轴于点C,过点B 作BD⊥y 轴于点D,过点B 作BE⊥x 轴于点E,连结AD,已知AC=1、BE=1、S 矩形BDOE =4.则S △ACD =___.于点E,BD⊥x轴于点F,AC=2,BD=4,EF=3,则k2−k1=____________.B. 1C. 2D. 3A. 13且与矩形的对角线OB交于点D,连接EF.若OD:OB=2:3,则△BEF的面积为___.。







模型介绍一、反比例函数k 的几何意义1.反比例函数k 的几何意义:如图,在反比例函数图象上任选一点,向两坐标轴作垂线,垂线与坐标轴所围成矩形的面积为k 。
如图二,所围成三角形的面积为2k二、利用k 的几何意义进行面积转化1.如图,直线AB 与反比例函数k y x=(0k ≠)交于A 、B 两点,与x 、y 轴的交点分别为C 、D ,那么OAB OCD OBD OAC S S S S ∆∆∆∆=--,此方法是绝大部分学生选用的方法。
但是,从效率来讲,就比较低2.如图,过点A 、B 作x 轴的垂线,垂足分别为E 、F ,则根据k 的几何意义可得,OBF OAE S S ∆∆=,而OBF OAB OAE ABFE S S S S ∆∆∆+=+梯形,所以OAB ABFE S S ∆=梯形,此方法的好处,在于方便,快捷,不易出错。
【例1】.如图,反比例函数y=在第一象限的图象上有两点A,B,它们的横坐标分别是2,6,则△AOB的面积是8.过点A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,∴x=2时,y=3;x=6时,y=1,=S△OBD=3,故S△ACOS四边形AODB=×(3+1)×4+3=11,故△AOB的面积是:11﹣3=8.故答案为:8.变式训练【变1-1】.如图,点A在反比例函数(x>0)的图象上,点B在x轴负半轴上,直线AB交y轴于点C,若,△AOB的面积为12,则k的值为()A.4B.6C.10D.12解:如图,过点A作AD⊥x轴,垂足为D,∵OC∥AD,,∴,∴,k>0,∴k=12,故选:D.【变1-2】.如图,反比例函数y=(k>0)的图象与矩形ABCO的两边相交于E,F两点,=4,则k的值为16.若E是AB的中点,S△BEF解:设E(a,),则B纵坐标也为,∵E是AB中点,∴F点坐标为(2a,),∴BF=BC﹣FC=﹣=,=4,∵S△BEF∴a•=4,∴k=16.故答案是:16.【例2】.如图,平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为6,4,反比例函数y=(x>0)的图象经过A,B两点,若菱形ABCD的面积为2,则k的值为12.解:解法一:过点A作x轴的垂线,交CB的延长线于点E,∵BC∥x轴,∴AE⊥BC,∵A,B两点在反比例函数y=(x>0)的图象,且纵坐标分别为6,4,∴A(,6),B(,4),∴AE=2,BE=﹣=,∵菱形ABCD的面积为2,∴BC×AE=2,即BC=,∴AB=BC=,在Rt△AEB中,BE===1,∴k=1,∴k=12.解法二:同理知:BE=1,设A(a,6),则B(a+1,4),∴6a=4(a+1),∴a=2,∴k=2×6=12.故答案为12.变式训练【变2-1】.如图,点A、B在反比例函数y=的图象上,A、B的纵坐标分别是3和6,连接OA、OB,则△OAB的面积是()A.9B.8C.7D.6解:∵点A、B在反比例函数y=的图象上,A、B的纵坐标分别是3和6,∴A(4,3),B(2,6),作AD⊥y轴于D,BE⊥y轴于E,=S△BOE=×12=6,∴S△AOD=S△AOD+S梯形ABED﹣S△BOE=S梯形ABED,∵S△OAB=(4+2)×(6﹣3)=9,∴S△AOB故选:A.【变2-2】.如图,在直角坐标系中,O为坐标原点,函数y=与y=(a>b>0)在第一象限的图象分别为曲线C1,C2,点P为曲线C1上的任意一点,过点P作y轴的垂线交C2于点A,作x轴的垂线交C2于点B,则阴影部分的面积S△AOB=a﹣.(结果用a,b表示)解:设B(m,),A(,n),则P(m,n),∵点P为曲线C1上的任意一点,∴mn=a,=mn﹣b﹣b﹣(m﹣)(n﹣)∴阴影部分的面积S△AOB=mn﹣b﹣(mn﹣b﹣b+)=mn﹣b﹣mn+b﹣=a﹣.故答案为:a﹣.1.如图,在△ABC中,AB=AC,点A在反比例函数y=(k>0,x>0)的图象上,点B,C在x轴上,OC=OB,延长AC交y轴于点D,连接BD,若△BCD的面积等于1,则k的值为()A.3B.2C.D.4解:作AE⊥BC于E,连接OA,∵AB=AC,∴CE=BE,∵OC=OB,∴OC=BC=×2CE=CE,∵AE∥OD,∴△COD∽△CEA,∴=()2=4,∵△BCD的面积等于1,OC=OB,=S△BCD=,∴S△COD=4×=1,∴S△CEA∵OC=CE,=S△CEA=,∴S△AOC=+1=,∴S△AOE=k(k>0),∵S△AOE∴k=3,故选:A.2.如图,OC交双曲线y=于点A,且OC:OA=5:3,若矩形ABCD的面积是8,且AB ∥x轴,则k的值是()A.18B.50C.12D.解:延长DA、交x轴于E,∵四边形ABCD是矩形,且AB∥x轴,∴∠CAB=∠AOE,∴DE⊥x轴,CB⊥x轴,∴∠AEO=∠ABC∴△AOE∽△CAB,∴=()2,∵矩形ABCD的面积是8,OC:OA=5:3,∴△ABC的面积为4,AC:OA=2:3,∴=()2=,=9,∴S△AOE∵双曲线y=经过点A,=|k|=9,∴S△AOE∵k>0,∴k=18,故选:A.3.如图,已知点A,B分别在反比例函数y1=﹣和y2=的图象上,若点A是线段OB 的中点,则k的值为()A.﹣8B.8C.﹣2D.﹣4解:设A(a,b),则B(2a,2b),∵点A在反比例函数y1=﹣的图象上,∴ab=﹣2;∵B点在反比例函数y2=的图象上,∴k=2a•2b=4ab=﹣8.故选:A.4.如图,点A(m,n),B(4,)在双曲线y=上,且0<m<n.若△AOB的面积为,则m+n=()A.7B.C.D.3解:∵点A(m,n),B(4,)在双曲线y=上,∴mn=4×=k,∴mn=k=6,∴双曲线为y=,∴n=,作AD⊥x轴于D,BE⊥x轴于E,=S△AOD+S梯形ADEB﹣S△BOE=S梯形ADEB,∵S△AOB∴(+)(4﹣m)=,解得m1=1,m2=﹣16,∵0<m<n.∴m=1,∴n=6,∴m+n=7,故选:A.5.如图,点A,B是反比例函数y=(x>0)图象上的两点,过点A,B分别作AC⊥x轴=3,则S△于点C,BD⊥x轴于点D,连接OA、BC,已知点C(2,0),BD=3,S△BCDAOC为()A.2B.3C.4D.6解:在Rt△BCD中,∵×CD×BD=3,∴×CD×3=3,∴CD=2,∵C(2,0),∴OC=2,∴OD=4,∴B(4,3),∵点B是反比例函数y=(x>0)图象上的点,∴k=12,∵AC⊥x轴,==6,∴S△AOC故选:D.6.如图,平行于y轴的直线分别交y=与y=的图象(部分)于点A、B,点C是y 轴上的动点,则△ABC的面积为()A.k1﹣k2B.(k1﹣k2)C.k2﹣k1D.(k2﹣k1)解:由题意可知,AB=﹣,AB边上的高为x,=×(﹣)•x=(k1﹣k2),∴S△ABC故选:B.7.已知四边形OABC是矩形,边OA在x轴上,边OC在y轴上,双曲线y=与边BC交于点D、与对角线OB交于中点E,若△OBD的面积为10,则k的值是()A.10B.5C.D.解:设E点的坐标是(x,y),∵E是OB的中点,∴B点的坐标是(2x,2y),则D点的坐标是(,2y),∵△OBD的面积为10,∴×(2x﹣)×2y=10,解得,k=,故选:D.8.如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是12,则k=()A.6B.9C.D.解:∵四边形OCBA是矩形,∴AB=OC,OA=BC,设B点的坐标为(a,b),∵BD=3AD,∴D(,b)∵D、E在反比例函数的图象上,∴=k,设E的坐标为(a,y),∴ay=k∴E(a,),=S矩形OCBA﹣S△AOD﹣S△OCE﹣S△BDE=ab﹣k﹣k﹣••(b﹣)=12,∵S△ODE∴4k﹣k﹣+=12k=故选:D.9.如图,一直线经过原点O,且与反比例函数y=(k>0)相交于点A、点B,过点A作AC⊥y轴,垂足为C,连接BC.若△ABC面积为8,则k=8.解:∵反比例函数与正比例函数的图象相交于A、B两点,∴A、B两点关于原点对称,∴OA=OB,∴△BOC的面积=△AOC的面积=8÷2=4,又∵A是反比例函数y=图象上的点,且AC⊥y轴于点C,∴△AOC的面积=|k|,∴|k|=4,∵k>0,∴k=8.故答案为8.10.如图,若反比例函数y=的图象经过等边三角形POQ的顶点P,则△POQ的边长为2.解:如图,过点P作x轴的垂线于M,∵△POQ为等边三角形,∴OP=OQ,OM=QM=OQ,∵反比例函数的图象经过点P,∴设P(a,)(a>0),则OM=a,OQ=OP=2a,PM=,在Rt△OPM中,PM===a,∴=a,∴a=1(负值舍去),∴OQ=2a=2,故答案为:2.11.如图,A(4,3)是反比例函数y=在第一象限图象上一点,连接OA,过A作AB∥x 轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=的图象于点P.则△OAP 的面积为5.解:过P作MN⊥x轴于M,交AB于N,过A作AD⊥x轴于D,∵A(4,3),∴AD=3,OD=4,∴AO==5,∵AB=AO,∴AB=5,∵AB∥x轴,点B的横坐标是4+5=9,纵坐标是3,即点B的坐标是(9,3),设直线OB的解析式是y=ax,把B点的坐标(9,3)代入得:3=9a,解得:a=,即y=x,∵AB∥x轴,∴MN⊥AB,把A(4,3)代入y=,得k=12,即y=,解方程组得:或,∵点P在第一象限,∴点P的坐标是(6,2),∵A(4,3),AB∥x轴,P(6,2),∴MN=AD=3,PN=3﹣2=1,﹣S△APB=3﹣=5,∴△OAP的面积是S△ABO故答案为:5.12.如图,直线y=x+m与双曲线y=相交于A,B两点,BC∥x轴,AC∥y轴,则△ABC 面积的最小值为6.解:方法一:设A(a,),B(b,),则C(a,).将y=x+m代入y=,得x+m=,整理,得x2+mx﹣3=0,则a+b=﹣m,ab=﹣3,∴(a﹣b)2=(a+b)2﹣4ab=m2+12.=AC•BC∵S△ABC=(﹣)(a﹣b)=••(a﹣b)=(a﹣b)2=(m2+12)=m2+6,∴当m=0时,△ABC的面积有最小值6.故答案为6.方法二:因为y=x+m斜率为1,且BC∥x轴,AC∥y轴,∴∠ABC=∠BAC=45°,∴△ABC为等腰直角三角形,∴AC=BC=AB,=AC•BC=AB2,∴S△ABC当AB最小时,m=0,直线为y=x,联立方程,解得或,∴A(,),B(﹣,﹣),AB=×2=2,=×4×6=6.∴S△ABC最小故答案为:6.13.如图,在平面直角坐标系中,△OAB的边OA在x轴正半轴上,其中∠OAB=90°,AO =AB,点C为斜边OB的中点,反比例函数y=(k>0,x>0)的图象过点C,且交线=6,则k的值为8.段AB于点D,连接CD,OD.若S△OCD解:根据题意设B(m,m),则A(m,0),∵点C为斜边OB的中点,∴C(,),∵反比例函数y=(k>0,x>0)的图象过点C,∴k=•=,∵∠OAB=90°,∴D的横坐标为m,∵反比例函数y=(k>0,x>0)的图象过点D,∴D的纵坐标为,作CE⊥x轴于E,=S△AOD,∵S△COES△OCD=S△COE+S梯形ADCE﹣S△AOD=S梯形ADCE,S△OCD=6,∴(AD+CE)•AE=6,即(+)•(m﹣m)=6,∴m2=32,∴k==8,故答案为:8.解法二:作CE⊥OA于E,∵C为AB的中点,OA=AB,∠OAB=90°,=S△AOD=k,S△AOB=2k,∴S△OEC=k,∴S△BOD∵C为斜边OB的中点,=S△BCD=S△BOD=6,∴S△OCD∴×k=6,∴k=8.故答案为:8.14.如图,在平面直角坐标系中,▱OABC的顶点A,B在第一象限内,顶点C在y轴上,经过点A的反比例函数y=(x>0)的图象交BC于点D.若CD=2BD,▱OABC的面积为15,则k的值为18.解:过点D作DN⊥y轴于N,过点B作BM⊥y轴于M,设OC=a,CN=2b,MN=b,∵▱OABC的面积为15,∴BM=,∴ND=BM=,∴A,D点坐标分别为(,3b),(,a+2b),∴•3b=(a+2b),∴b=a,∴k=•3b=•3×a=18,故答案为:18.15.如图,点A在双曲线y=的第一象限的那一支上,AB垂直于y轴于点B,点C在x 轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为.解:连DC,如图,∵AE=3EC,△ADE的面积为3,∴△CDE的面积为1,∴△ADC的面积为4,设A点坐标为(a,b),则AB=a,OC=2AB=2a,而点D为OB的中点,∴BD=OD=b,=S△ABD+S△ADC+S△ODC,∵S梯形OBAC∴(a+2a)×b=a×b+4+×2a×b,∴ab=,把A(a,b)代入双曲线y=,∴k=ab=.故答案为:.16.如图,已知反比例函数y1=与一次函数y2=k2x+b的图象交于点A(1,8),B(﹣4,m)两点.(1)求k1,k2,b的值;(2)求△AOB的面积;(3)请直接写出不等式x+b的解.解:(1)∵反比例函数y1=与一次函数y2=k2x+b的图象交于点A(1,8)、B(﹣4,m),∴k1=8,B(﹣4,﹣2),解方程组,解得;(2)由(1)知一次函数y=k2x+b的图象与y轴的交点坐标为(0,6),=×6×4+×6×1=15;∴S△AOB(3)﹣4≤x<0或x≥1.17.如图,在平面直角坐标系中,A点的坐标为(a,6),AB⊥x轴于点B,cos∠OAB=,反比例函数y=的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为.(1)求反比例函数的解析式;(2)求直线EB的解析式;.(3)求S△OEB解:(1)∵A点的坐标为(a,6),AB⊥x轴,∴AB=6,∵cos∠OAB==,∴,∴OA=10,由勾股定理得:OB=8,∴A(8,6),∴D(8,),∵点D在反比例函数的图象上,∴k=8×=12,∴反比例函数的解析式为:y=;(2)设直线OA的解析式为:y=bx,∵A(8,6),∴8b=6,b=,∴直线OA的解析式为:y=x,则,x=±4,∴E(﹣4,﹣3),设直线BE的解式为:y=mx+n,把B(8,0),E(﹣4,﹣3)代入得:,解得:,∴直线BE的解式为:y=x﹣2;=OB•|y E|=×8×3=12.(3)S△OEB18.如图,直线y=x与反比例函数的图象交于点A(3,a),第一象限内的点B在这个反比例函数图象上,OB与x轴正半轴的夹角为α,且tanα=.(1)求反比例函数的解析式;(2)求点B的坐标;.(3)求S△OAB解:(1)∵直线y=x与反比例函数的图象交于点A(3,a),∴a=×3=4,∴点A的坐标为(3,4),∴k=3×4=12,∴反比例函数解析式y=.(2)∵点B在这个反比例函数图象上,设点B坐标为(x,),∵tanα=,∴=,解得:x=±6,∵点B在第一象限,∴x=6,∴点B的坐标为(6,2).(3)设直线OB为y=kx,(k≠0),将点B(6,2)代入得:2=6k,解得:k=,∴OB直线解析式为:y=x.过A点做AC⊥x轴,交OB于点C,如图所示:则点C坐标为(3,1),∴AC=3.S△OAB的面积=S△OAC的面积+S△ACB的面积=×|AC|×6=9.∴△OAB的面积为9.19.已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(﹣2,0),与反比=4.例函数在第一象限内的图象的交于点B(2,n),连接BO,若S△AOB (1)求该反比例函数的解析式和直线AB的解析式;(2)若直线AB与双曲线的另一交点为D点,求△ODB的面积.=•|x A|•y B,解:(1)由题意得:S△AOB即×2×y B=4,y B=4,∴B(2,4),设反比例函数的解析式为:y=,把点B的坐标代入得:k=2×4=8,∴y=,设直线AB的解析式为:y=ax+b,把A(﹣2,0)、B(2,4)代入得:,解得:,∴y=x+2;(2)由题意得:x+2=,解得:x1=﹣4,x2=2,∴D(﹣4,﹣2),=S△OAD+S△OAB=×2×2+4=6.∴S△ODB20.如图,在平行四边形OABC中,,点A在x轴上,点D是AB 的中点,反比例函数的图象经过C,D两点.(1)求k的值;(2)求四边形OABC的面积.解:(1)过点C作CE⊥x轴于E,∵∠AOC=45°,∴OE=CE,∴OE2+CE2=OC2∵OC=2,∴OE=CE=2,∴C(2,2),∵反比例函数的图象经过点C点,∴k=2×2=4;(2)过点D作DF⊥x轴于F,∵四边形OABC是平行四边形,∴AB=OC=2,∠DAF=∠AOC=45°,又∵点D是AB的中点,∴AD=,AF=DF,∴AF2+DF2=AD2,∴AF=DF=1,∴D点的纵坐标为1,∵反比例函数的图象过点D点,∴D(4,1),∴OF=4,OA=OF﹣AF=4﹣1=3,∴平行四边形OABC的面积S=OA•CE=3×2=6.21.如图,直线y=6x与双曲线y=(k≠0,且x>0)交于点A,点A的横坐标为2.(1)求点A的坐标及双曲线的解析式;(2)点B是双曲线上的点,且点B的纵坐标是6,连接OB,AB,求△AOB的面积.解:(1)将x=2代入y=6x,得:y=12,∴点A的坐标为(2,12),将A(2,12)代入y=,得:k=24,∴反比例函数的解析式为y=;(2)在y=中y=6时,x=4,∴点B(4,6),而A(2,12),如图,过A作AC⊥y轴,BD⊥x轴,交于点E,则OD=4,OC=12,BD=6,AC=2,AE=2,BE=6,=S矩形OCED﹣S△AOC﹣S△BOD﹣S△ABE∴S△AOB=4×12﹣×2×12﹣×4×6﹣×2×6=48﹣12﹣12﹣6=18.22.如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数的图象的两个交点.(1)求反比例函数和一次函数的表达式;(2)求△AOB的面积;(3)若D(x,0)是x轴上原点左侧的一点,且满足,求x的取值范围.解:(1)∵B(2,﹣4)在反比例函数y=的图象上,∴m=﹣8,∴反比例函数的表达式为y=﹣.∵A(﹣4,n)在y=﹣的图象上,∴n=2,∴A(﹣4,2).∵y=kx+b经过A(﹣4,2)和B(2,﹣4),∴,解得∴一次函数的表达式为y=﹣x﹣2.(2)当y=﹣x﹣2=0时,解得x=﹣2.∴点C(﹣2,0),∴OC=2,=S△AOC+S△COB∴S△AOB=×2×2+×2×4=6.(3)根据函数的图象可知:若D(x,0)是x轴上原点左侧的一点,当﹣4<x<0时,满足kx+b﹣<0.23.如图,一次函数y=k1x+b的图象与反比例函数y=(x<0)的图象相交于点A(﹣1,2)、点B(﹣4,n).(1)求此一次函数和反比例函数的表达式;(2)求△AOB的面积;(3)在x轴上存在一点P,使△PAB的周长最小,求点P的坐标.解:(1)∵反比例函数y=(x<0)的图象经过点A(﹣1,2),∴k2=﹣1×2=﹣2,∴反比例函数表达式为:y=﹣,∵反比例y=﹣的图象经过点B(﹣4,n),∴﹣4n=﹣2,解得n=,∴B点坐标为(﹣4,),∵直线y=k1x+b经过点A(﹣1,2),点B(﹣4,),∴,解得:,∴一次函数表达式为:y=+.(2)设直线AB与x轴的交点为C,如图1,当y=0时,x+=0,x=﹣5;∴C点坐标(﹣5,0),∴OC=5.S△AOC=•OC•|y A|=×5×2=5.S△BOC=•OC•|y B|=×5×=.S△AOB=S△AOC﹣S△BOC=5﹣=;(3)如图2,作点A关于x轴的对称点A′,连接A′B,交x轴于点P,此时△PAB的周长最小,∵点A′和A(﹣1,2)关于x轴对称,∴点A′的坐标为(﹣1,﹣2),设直线A′B的表达式为y=ax+c,∵经过点A′(﹣1,﹣2),点B(﹣4,)∴,解得:,∴直线A′B的表达式为:y=﹣x﹣,当y=0时,则x=﹣,∴P点坐标为(﹣,0).24.如图,在平面直角坐标系xOy中,已知四边形DOBC是矩形,且D(0,4),B(6,0).若反比例函数y=(x>0)的图象经过线段OC的中点A(3,2),交DC于点E,交BC于点F.设直线EF的解析式为y=k2x+b.(1)求反比例函数和直线EF的解析式;(2)求△OEF的面积;(3)请结合图象直接写出不等式k2x+b>0的解集.解:(1)∵四边形DOBC是矩形,且D(0,4),B(6,0),∴C点坐标为(6,4),∵A点坐标为(3,2),∴k1=3×2=6,∴反比例函数解析式为y=;把x=6代入y=得x=1,则F点的坐标为(6,1);把y=4代入y=得x=,则E点坐标为(,4),把F(6,1)、E(,4)代入y=k2x+b,得,解得,,∴直线EF的解析式为y=﹣x+5;﹣S△ODE﹣S△OBF﹣S△CEF(2)△OEF的面积=S矩形BCDO=4×6﹣×4×﹣×6×1﹣×(6﹣)×(4﹣1)=;(3)由图象得:不等式k2x+b﹣>0的解集为<x<6.25.如图,已知反比例函数y=(m≠0)的图象经过点(1,4),一次函数y=﹣x+b的图象经过反比例函数图象上的点Q(﹣4,n).(1)求反比例函数与一次函数的表达式;(2)一次函数的图象分别与x轴、y轴交于A、B两点,与反比例函数图象的另一个交点为P,连结OP、OQ.求△OPQ的面积.解:(1)反比例函数y=(m≠0)的图象经过点(1,4),解得m=4,故反比例函数的表达式为y=.一次函数y=﹣x+b的图象与反比例函数的图象相交于点Q(﹣4,n),所以,解得n=﹣1,b=﹣5.∴一次函数的表达式y=﹣x﹣5;(2)由,解得或.∴点P(﹣1,﹣4),在一次函数y=﹣x﹣5中,令y=0,得﹣x﹣5=0,解得x=﹣5,故点A(﹣5,0),S△OPQ=S△OP A﹣S△OAQ=×5×4−×5×1=7.5.26.如图,在平面直角坐标系中,边长为4的等边△OAB的边OB在x轴的负半轴上,反比例函数y=(x<0)的图象经过AB边的中点C,且与OA边交于点D.(1)求k的值;(2)连接OC,CD,求△OCD的面积;(3)若直线y=mx+n与直线CD平行,且与△OAB的边有交点,直接写出n的取值范围.解:(1)∵等边△OAB,∴AB=BO=AO=4,∠ABO=∠BOA=∠OAB=60°,∵点C是AB的中点,∴BC=AC=2,过点C作CM⊥OB,垂足为M,在Rt△BCM中,∠BCM=90°﹣60°=30°,BC=2,∴BM=1,CM=,∴OM=4﹣1=3,∴点C 的坐标为(﹣3,),代入y =得:k =﹣3答:k 的值为﹣3;(2)过点A 作AN ⊥OB ,垂足为N ,由题意得:AN =2CM =2,ON =OB =2,∴A (﹣2,2),设直线OA 的关系式为y =kx ,将A 的坐标代入得:k =﹣,∴直线OA 的关系式为:y =﹣x ,由题意得:,解得:舍去,,∴D (﹣,3)过D 作DE ⊥OB ,垂足为E ,S △OCD =S CMED +S △DOE ﹣S △COM =S CMED =(+3)×(3﹣)=3,答:△OCD 的面积为3.(3)①当与直线CD 平行的直线y =mx +n 过点O 时,此时y =mx +n 的n =0,②当与直线CD 平行的直线y =mx +n 经过点A 时,设直线CD 的关系式为y =ax +b ,把C 、D 坐标代入得:,解得:a =1,b =3+∴直线CD 的关系式为y =x +3+,∵y =mx +n 与直线y =x +3+平行,∴m =1,把A (﹣2,2)代入y =x +n 得:n =2+2因此:0≤n ≤2+2且n .答:n 的取值范围为:0≤n ≤2+2且n ≠3+.。

4.如图,函数y=-x与函数y=-4x的图象相交于A,B两点,过点分别作y轴的垂线,垂足分别为点C则四边形ACBD的面积为A.2 B.4 C.65.如图,点P是反比例函数y=2x图象上的一点积为 .6.如图,在第一象限内,点P,M(2,a 点,PA⊥x轴于点MB⊥x轴于点B,PA7.如图,A,C是函数=1x的图象上任意两点,过点A作y轴的垂线,垂足为B,过点C作△AOB的面积为S1,COD的面积为S2,则A.S1>S2C.S1=S28.如图,点A是反比例函数点C是x轴上的动点,则△A.1 B.2 C9.直线y=kx与反比例函数于y轴于点C,则10.如图,正比例函数x与反比例函数y=的图象相交于A,B两点,BC⊥x轴于点C,则△ABC的面积为( )A.1 B.2 C.3 D.411.如图,Rt△AOB的一条直角边的中点C,与另一直角边交于点12.如图,A,B是双曲线于点D,垂足为C.若△A.43B.8313.如图,过x轴正半轴上的任意一点P作y轴的平行线交反比例函数=2x(x>0)和y=-4x(x>0)的图象于A,B两点,是y轴上任意一点,则△ABC的面积为________.14.如图,在平面直角坐标系中,点P(1,4)Q(m,n)在函数y=kx(x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A、过点Q分别作x轴、 y轴的垂线,垂足为点C D. QD交PA于点E,随着m的增大,四边形ACQE 的面积( )A.减小 B.增大 C.先减小后增大 D.先增大后减小15.如图所示,反比例函数y=kx(x>0)的图象经过矩形OABC的对角线的中点D,若矩形OABC的面积为8,则k的值为.16.如图,反比例函数y=2x的图象经过矩形OABC的边AB的中点D,则矩形OABC的面积为17.如图,已知点P(6,过点P作PM⊥x轴于点M,PN⊥y轴于点N.比例函数y=kx的图象交,若四边形OAPB的面积为12,则k=.19.如图,在平面直角坐标系与反比例函数在第一象限内的图象交于点(1)求该反比例函数的解析式和直线(2)若直线AB与y轴的交点为题型2:已知四边形面积求解析式20.如图,矩形ABOD在第二象限的图象的交点,3.(1)求两函数的解析式;(2)求两函数图象的交点(3)若点P是y轴上一动点,且22.如图,点A在双曲线D两点在x轴上,若矩形解析式.考查形式三.已知反比例函数解析式求图形的面积题型1:利用解析式求面积23.如图,已知反比例函数8),B(-4,m).(1)求k1,k2,b的值;(2)求△AOB的面积;(3)若M(x1,y1),N(xy1<y2,指出点M,N各位于哪个象限,并简要说明理由.题型2:利用对称性求面积25.如图,是由四条曲线围成的广告标志,建立平面直角坐标系,双曲线对应的函数解析式分别为这种钢条加工成矩形产品按面积计算,每单位面积师傅计算一下,所需钢条一共花多少钱?题型3:利用点的坐标及面积公式求面积26.如图,直线y=k1xB,与x轴交于点C,其中点(1)试确定反比例函数的解析式;(2)求△AOC的面积.。
第六章反比例函数及反比例函数k的几何意义专题训练北师大版2024—2025学年九年级上册反比例函数比例系数k的几何意义(1)意义:从反比例函数y=(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|,以该点、一个垂足和原点为顶点的三角形的面积为1/2|k|.(2)常见的面积类型:例1.如图,点P是反比例函数y=(k≠0)的图象上任意一点,过点P作PM⊥x轴,垂足为M,若△POM的面积等于3,则k的值等于()A.﹣6B.6C.﹣3D.3变式1.如图,在▱AOBC中,对角线AB、OC交于点E,双曲线经过A、E两点,若▱AOBC的面积为18,则k的值是()A.5B.6C.7D.8变式2.如图,平行于x轴的直线与函数y=(k1>0,x>0),y=(k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点.若△ABC的面积为4,则k1﹣k2的值为()A.8B.﹣8C.4D.﹣4变式3.如图,点P是反比例函数图象上的一点,PF⊥x轴于F点,且Rt△POF面积为4.则k的值为()A.8B.﹣8C.﹣4D.4变式4.如图,点M是反比例函数y=(x<0)图象上一点,MN⊥y 轴于点N.若P为x轴上的一个动点,则△MNP的面积为()A.2B.4C.6D.无法确定变式5.如图,点P是双曲线C:y=(x>0)上的一点,过点P作x轴的垂线交直线AB:y=x﹣2于点Q,连接OP,OQ,当点P在曲线C上运动,且点P在Q上方时,△POQ面积的最大值为()A.2B.3C.4D.6变式6.如图,已知点A为反比例函数y=(x<0)的图象上一点,过点A作AB⊥y轴,垂足为B,若△OAB的面积为3,则k的值为()A.3B.﹣3C.6D.﹣6变式7.关于x的反比例函数y=的图象如图,A、P为该图象上的点,且关于原点成中心对称.△P AB中,PB∥y轴,AB∥x轴,PB 与AB相交于点B.若△P AB的面积大于12,则关于x的方程(a ﹣1)x2﹣x+=0的根的情况是()A.2个不相等的实数根B.2个相等的实数根C.1个实数根D.无实数根变式8.如图,两个反比例函数y1=和y2=在第一象限内的图象分别是C1和C2,设点P在C1上,P A⊥x轴于点A,交C2于点B,则△POB的面积为()A.4B.2C.1D.6变式9.如图,若反比例函数的图象经过点A,AB⊥x轴于点B,C点是y轴上一点,且△ABC的面积4,则k的值为()A.﹣8B.﹣4C.4D.8变式10.如图,反比例函数的图象经过矩形OABC的边AB的中点D,若矩形OABC的面积为6,则k的值为()A.﹣3B.3C.﹣6D.6变式11.如图,点A是反比例函数的图象上的一点,过点A作AB ⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC 的面积为3,则k的值是()A.3B.﹣6C.6D.﹣3变式12.下面四个图中反比例函数的表达式均为,则阴影部分的图形的面积为3的有()A.1个B.2个C.3个D.4个变式13.如图,将一块含30°角的三角板AOB按如图所示摆放在平面直角坐标系中,∠B=60°,∠BAO=90°,△AOB的面积为4,BO与x轴的夹角为30°,若反比例函数的图象经过点A,则k的值为()A.3B.C.6D.9变式14.如图1,在△OAB中,∠AOB=45°,点B的坐标为,点A在反比例函数的图象上,设△OAB的面积为S1;如图2,在△ABC中,AB=AC,BC在x轴上,且OB:BC=1:2,点A在反比例函数的图象上,设△ABC的面积为S2,则S1+S2的值为()A.B.5C.D.变式15.如图,已知四边形OABC是矩形,边OA在x轴上,边OC在y轴上,双曲线过OB的中点E,且与边BC交于点D,若△DOE的面积为7.5,则k的值是()A.5B.10C.15D.变式16.如图,点A是反比例函数y=(x>0)图象上的一点,AB垂直于x轴,垂足为B,△OAB的面积为8.若点P(a,4)也在此函数的图象上,则a的值是()A.2B.﹣2C.4D.﹣4变式17.如图,在平面直角坐标系xOy中,点A、B分别在y、x 轴上,BC⊥x轴,点M、N分别在线段BC、AC上,BM=CM,NC=2AN,反比例函数y=(x>0)的图象经过M、N两点,P为x轴正半轴上一点,且OP:BP=1:4,△APN的面积为3,则k的值为()A.B.C.D.变式18.如图,在平面直角坐标系中,平行四边形ABCD与y轴分别交于E、F两点,对角线BD在x轴上,反比例函数的图象过点A并交AD于点G,连接DF.若BE:AE=1:2,AG:GD=3:2,且△FCD的面积为,则k的值是()A.B.3C.D.5变式19.如图,平面直角坐标系中,矩形OABC的边与函数y=(x>0)图象交于E,F两点,且F是BC的中点,则四边形ACFE的面积等于()A.4B.6C.8D.不能确定例2.如图,矩形OABC的顶点A,C分别在x轴、y轴的正半轴上,它的对角线OB与函数的图象相交于点D,且,若矩形OABC的面积为24,则k的值是.变式1.如图,已知在平面直角坐标系xOy中,点P是▱ABCO对角线OB的中点,反比例函数的图象经过点A,点P.若▱ABCO的面积为30,且y轴将▱ABCO的面积分为1:3,则k的值为.变式2.如图,在平面直角坐标系xOy中,点A,B都在反比例函数y=(x>0)的图象上,延长AB交y轴于点C,过点A作AD⊥y轴于点D,连接BD并延长,交x轴于点E,连接CE.若AB=2BC,△BCE的面积是4.5,则k的值为.变式3.如图,在平面直角坐标系xOy中,等腰Rt△OAB,∠B=90°,点A在x轴正半轴上,点B在第一象限内,反比例函数y=的图象与AB交于点C,连接OC,若BC=2AC,△OBC的面积为6,则k的值为.变式4.如图,在平面直角坐标系中,C,A分别为x轴、y轴正半轴上的点,以OA,OC为边,在第一象限内作矩形OABC,且S矩形OABC=8,将矩形OABC翻折,使点B与原点O重合,折痕为MN,点C的对应点C'落在第四象限,过M点的反比例函数y=(k ≠0)的图象恰好过MN的中点,则点C'的坐标为.变式5.如图,在平面直角坐标系中,点A、C在y轴上,且,点B(﹣2,0)在x轴上,将△ABC绕点A逆时针旋转90°后得到△AB'C′,线段AB′与双曲线交于点D,连接B′C、C′C,当点D为AB′中点,且S△B'CC′=6时,则k的值是.变式6.如图,在△AOB中,OC平分∠AOB,=,反比例函数y=(k<0)图象经过点A、C两点,点B在x轴上,若△AOB的面积为9,则k的值为.变式7.如图,点A,B,C,D是菱形的四个顶点,其中点A,D在反比例函数y=(m>0,x>0)的图象上,点B,C在反比例函数y=(n<0)的图象上,且点B,C关于原点成中心对称,点A,C的横坐标相等,则的值为;过点A作AE∥x轴交反比例函数y=(n<0)的图象于点E,连结ED并延长交x轴于点F,连结OD.若S△DOF=7,则m的值为.变式8.如图,A(a,b)、B(﹣a,﹣b)是反比例函数y=的图象上的两点,分别过点A、B作y轴的平行线,与反比例函数y=的图象交于点C、D,若四边形ACBD的面积是8,则m、n之间的关系是.变式9.如图,平面直角坐标系xOy中,Rt△ABO的斜边BO在x轴正半轴上,OB=5,反比例函数y=(x>0)的图象过点A,与AB边交于点C,且AC=3BC,则a的值为,射线OA,射线OC分别交反比例函数y=(b>a>0)的图象于点D,E,连接DE,DC,若△DEC的面积为45,则b的值为.变式10.如图,点A、B在反比例函数y=(x>0)的图象上,延长AB交x轴于C点,若△AOC的面积是12,且点B是AC的中点,则k=.变式11.如图,菱形ABCD中,∠ABC=120°,顶点A,C在双曲线上,顶点B,D在双曲线上,且BD经过点O.若k1+k2=2,则菱形ABCD面积的最小值是.变式12.如图,在平面直角坐标系xOy中,正方形ABCD的顶点A、C恰好落在双曲线上,且点O在AC上,AD交x轴于点E.①当A点坐标为(1,m)时,D点的坐标为;②当CE平分∠ACD时,正方形ABCD的面积为.例3.如图,O为坐标原点,点A(﹣1,5)和点B(m,﹣1)均在反比例函数图象上(1)求m,k的值;(2)当x满足什么条件时,﹣x+4>﹣;(3)P为y轴上一点,若△ABP的面积是△ABO面积的2倍,直接写出点P的坐标.变式1.已知点A(a,ma+2)、B(b,mb+2)是反比例函数y=图象上的两个点,且a>0,b<0,m>0.(1)求证:a+b=﹣;(2)若OA2+OB2=2a2+2b2,求m的值;(3)若S△OAB=3S△OCD,求km的值.变式2.如图,双曲线y=上的一点A(m,n),其中n>m>0,过点A作AB⊥x轴于点B,连接OA.(1)已知△AOB的面积是3,求k的值;(2)将△AOB绕点A逆时针旋转90°得到△ACD,且点O的对应点C恰好落在该双曲线上,求的值.。
专题10利用反比例函数中k的几何意义求面积的五种考法目录解题知识必备 (1)压轴题型讲练 (1)类型一、反比例函数中利用k值求三角形的面积 (1)类型二、反比例函数中利用k值求等腰三角形的面积 (2)类型三、反比例函数中利用k值求平行四边形的面积 (3)类型四、反比例函数中利用k值求矩形的面积 (4)类型五、反比例函数中利用k值求阴影部分的面积 (5)压轴能力测评(14题) (6)1.求三角形的面积2.求等腰三角形的面积3.求平行四边形的面积4.求矩形的面积5.求阴影部分的面积坐标是(0,)b ,则ABC V 的面积是()A .30B .3C .60D .6【变式训练】1.(2024·云南昭通·二模)如图,在平面直角坐标系中,A 是反比例函数()0ky x x=<的图像上的一点,过点A 作AB x ⊥轴于点B ,连接OA ,已知ABO 的面积是5,则k =.第1题第2题第3题2.(2024·湖北·模拟预测)如图,点A 在双曲线9y x =上,点B 在双曲线7y x=上,且AB y ∥轴,则ABC V 的面积等于.3.(23-24九年级上·河南郑州·阶段练习)如图所示,是反比例函数3y x=与5y x-=在x 轴上方的图象,点C 是y 轴正半轴上的一点,过点C 作AB x ∥轴分别交这两个图象于A 点和B 点,若点P 在x 轴上运动,则ABP 的面积等于.类型一、反比例函数中利用k 值求三角形的面积例题:(2024·贵州六盘水·二模)如图,点(3,)A a -在反比例函数6y x=-的图象上,点B 的坐标是(3,0)-,点C 的【变式训练】2.(23-24九年级上·广西贺州·期中)如图,若反比例函数y x=的图象上有一点B 与原点和坐标轴上点A 围成一个等腰三角形,则AOB V 的面积是.类型二、反比例函数中利用k 值求等腰三角形的面积【变式训练】2.如图,四边形ABCD 是平行四边形,点D 都在x 轴上,则ABCD Y 3.如图,点A 是双曲线()60y x x =>上的动点,连接BC ,若四边形OABC 为平行四边形,则类型三、反比例函数中利用k 值求平行四边形的面积A .12B .9C .6D .3【变式训练】1.(23-24八年级下·浙江杭州·期末)如图,过()0,0k y k x x=≠>的图象上点A ,分别作x 轴,y 轴的平行线交2y x =-的图象于B ,D 两点,以AB ,AD 为邻边的矩形ABCD 被坐标轴分割成四个小矩形,面积分别记为1S ,2S ,3S ,4S ,若234112S S S ++=,则k 的值为()A .52B .53C .4D .83类型四、反比例函数中利用k 值求矩形的面积例题:(2024·云南文山·模拟预测)如图,在平面直角坐标系xOy 中,点P 在反比例函数6y x=的图象上,过点P 作PA y ⊥轴,PB x ⊥轴,垂足分别为A 、B ,则矩形AOBP 的面积是()的面积为()A .12k k +B .12k k -C .12k kD .21k k -【变式训练】2.(2024·湖南益阳·二模)如图,在反比例函数10y x=的图象上有1P ,2P ,3P ,L ,2025P 等点,它们的横坐标依次为1,2,3,L ,2025,分别过这些点作x 轴与y 轴的垂线,图中所构成的阴影部分的面积从左到右依次为1S ,2S ,3S ,L ,2023S ,2024S ,则12320232024S S S S S +++++=.3.(2023春·八年级单元测试)如图,已知正方形OABC 的面积为9,点,0x >)图象上,点P 是函数ky x=(k 轴的垂线,垂足分别为点E 、F .设矩形OFPE 和正方形=______;的函数关系式.类型五、反比例函数中利用k 值求阴影部分的面积比例函数2(0)y x x =>的图象于点A ,PD y ⊥轴于点D ,交反比例函数2(0)y x x=>的图象于点B ,则四边形PAOB的面积是()A .3B .6C .9D .122.(24-25九年级上·湖南岳阳·阶段练习)如图,点A 在双曲线()20y x x =>上,点B 在双曲线()0ky x x=<上,AB x ∥轴,点C 是x 轴上一点,连接AC BC 、,若ABC V 的面积是6,则k 的值()A .6-B .10C .10-D .12-第2题第3题第4题3.(23-24八年级下·浙江嘉兴·期末)如图,点A ,B 在反比例函数()40y x x=>的图象上,以OA AB ,为邻边作平行四边形OABC ,点C 恰好落在反比例函数()0ky x x=<的图象上,若平行四边形OABC 的面积是6,则k 的值为()A .2-B .3-C .32-D .23-4.(24-25九年级上·河北石家庄·阶段练习)反比例函数k y x =和1y x =在第一象限内的图象如图所示,点P 在k y x=的图象上,PC x ⊥轴,交1y x=的图象于点A ,PD y ⊥轴,交1y x=的图象于点B .当点P 在ky x=的图象上运动时,以下结论:①ODB △与OCA 的面积相等;②PA 与PB 始终相等;③四边形PAOB 的面积不会发生变化;④当点A 是PC 的中点时,点B 一定是PD 的中点.其中一定正确的是()A .①②③④B .①③C .②③④D .①③④一、单选题1.(23-24八年级下·福建泉州·期末)在平面直角坐标系xOy 中,点P 在双曲线12y x=上,PA x ⊥轴于点A ,则PAO第5题第6题6.(2024·辽宁沈阳·模拟预测)如图,点A在双曲线1yx=上,点B在双曲线3yx=上,且AB x∥轴,则ABO的面积是.7.(24-25九年级上·浙江温州·阶段练习)如图,点,,P Q R为反比例函数(0,0)ky k xx=>>图象上从左到右的三个点,分别过这三个点作x轴,y轴的垂线,与y轴的交点分别为点,,C B A,图中所构成的阴影部分的面积从左到右依次记为123,,S S S,其中::1:2:3OA AB BC=,若26S=,则13S S+的值为.8.(2024九年级下·全国·专题练习)如图,在反比例函数8(0)y xx=>的图象上有1P,2P,3P,L,2024P等点,它们的横坐标依次为1,2,3,⋯,2024,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为1S,2S,3S,L,2023S,2024S,则12320232024S S S S S+++++=.二、填空题5.(23-24九年级上·山东泰安·开学考试)反比例函数(0)ky xx=<如图所示,若矩形OAPB的面积是3,则k的值为.10.(2024·山东枣庄·二模)如图,直线24y x =+与y 轴交于点A ,与x 轴交于点E ,点(),6B a 在直线上,ABCD 的顶点D 在x 轴上,反比例函数()0ky x x=>的图像经过点B 、C.(1)求反比例函数的关系式和点C 的坐标;(2)求ABCD 的面积.三、解答题9.(23-24九年级上·河南驻马店·期末)如图,已知A ,B 是反比例函数9(0)y x x=>图象上的两点,AC x ⊥轴于点C ,OB 交AC 于点D ,若OCD 的面积是BCD △的面积的2倍,求AOD △的面积.(1)当点P 的坐标为2,0时,求ABC 的面积.(2)当点P 的坐标为(),0t 时,求ABC 的面积.12.(23-24九年级上·安徽蚌埠·期中)如图,在x 轴的正半轴上依次截取1122312n n OA A A A A A A -===⋯==,过点123n A A A A ⋯、、、分别作x 轴的垂线与反比例函数10y x=的图像相交于点123n P P P P ⋯、、、得直角三角形111222333441n nn OP A A P A A P A A P A A P A -⋯、、、、、,并设其面积分别为123n S S S S ⋯、、、.(1)求23P P Pn 、、、的坐标(2)求n S 的值;11.(2023·山东青岛·模拟预测)如图,P 为x 轴正半轴上一点,过点P 作x 轴的垂线,交函数1y x=(0x >)的图象于点A ,交函数()40y x x =>的图象于点B ,过点B 作x 轴的平行线,交()10y x x=>于点C ,连结AC .y 轴、x 轴作垂线,交y 轴于点D ,交x 轴于点C ,连接AC 、BD .①试探究ADC △与BDC 面积的关系并说明理由;②试探究CD 与AB 之间的位置关系并说明理由.【运用】我们对上述问题进行了实践,如图3,已知点A ,B 在反比例函数20y x =的图像上,且(2,)A m ,B 则是反比例函数20y x=第三象限内图像上的一动点,过点A 作AD x ⊥轴,过点B 作BC y ⊥轴,垂足分别分为D 、C ,若四边形ABCD 的面积为45,求点B 的坐标;【拓展】我们对上述问题进行了延伸,如图4,函数(0)k y k x =<的图像与过原点O 的直线相交于A ,B 两点,点C 是此函数第二象限内图像上的动点(点C 在点B 的右侧),直线BC 分别交于y 轴、x 轴于点D 、G ,连接AC 分别交y 轴、x 轴于点E 、F .若27DC BC =,求CE CA的值?13.(23-24九年级上·四川达州·期末)【感知】如图1,已知反比例函数(0)k y k x=≠上有两点(4,8)A ,(8,4)B --,AD y ⊥轴交y 轴于点D ,BC x ⊥轴交x 轴于点C ,则ADC S =△_____,=BDC S V _____,CD 与AB 的位置关系为:_________.【探究】我们对上述问题进行了思考,如图2,当A ,B 是双曲线(0)k y k x=<同一支上任意两点,过A 、B 分别向(1)初步尝试如图2,点A ,E 分别在反比例函数2y x =和4y x-=的图象上,四边形ABOC 和EFOB 都是矩形,易知四边形EFCA 也是矩形,分别求矩形EFOB 和EFCA 的面积.(2)类比探究如图3,点A ,C 在反比例函数()0a y a x =>的图象上,点B ,D 在反比例函数()0b y b x=<的图象上,AB CD x ∥∥轴,AB 与CD 在x 轴的两侧,3AB =,2CD =,AB 与CD 的距离为5,求a b -的值.【分析】如图4,过A ,B ,C ,D 四点分别作AE 、BF 、CG 、DH x ⊥轴于点E ,F ,G ,H ,设AB ,CD 分别与y 轴交于N ,M ,显然四边形ANOE ,BNOF ,CMOG ,DMOH 均为矩形,且ANOE BNOF CMOG DMOH S S S S a b +=+=-,可设CG 为h ,则5BF h =-,从而可得:()235h h =-,……请根据上述思路,写出完整的解题步骤.(3)拓展延伸如图5,已知反比例函数m y x =和n y x ,0m n >>,若点B ,C 在m y x =图象上,点A ,D 在n y x =图象上,且AB CD x ∥∥轴,53AB =,56CD =,AB 和CD 间的距离为12,求m n -的值.14.(24-25九年级上·湖南郴州·开学考试)知识回顾:在学习反比例函数性质时,我们已经知道:如图1,点A 是反比例函数k y x=上任意一点,则矩形ABOC 的面积为k .。
专题07反比例函数K 值与几何面积综合(1)反比例函数上任何一点与轴线围城的直角三角形面积都相等|k|/2;2OCF k S S S OBN OAM ===∆∆∆图中21|-|2OAB PAB k k S S ∆∆==图中2k ===∆∆∆S S S CBD OBD PDB 图中(2)图像上任意两点与原点构成的三角形的面积等于直角梯形的面积;【真题演练】1.(2023•福建)如图,正方形四个顶点分别位于两个反比例函数y =和y =的图象的四个分支上,则实数n 的值为( )A .﹣3B .﹣C .D .32.(2023•张家界)如图,矩形OABC 的顶点A ,C 分别在y 轴、x 轴的正半轴上,点D 在AB 上,且AD =AB ,反比例函数y =(k >0)的图象经过点D 及矩形OABC 的对称中心M ,连接OD ,OM ,DM .若△ODM的面积为3,则k的值为( )A.2B.3C.4D.53.(2023•黑龙江)如图,△ABC是等腰三角形,AB过原点O,底边BC∥x轴,双曲线y=过A,B两点,=12,则k的值是( )过点C作CD∥y轴交双曲线于点D.若S△BCDA.﹣6B.﹣12C.﹣D.﹣94.(2023•宜宾)如图,在平面直角坐标系xOy中,点A、B分别在y、x轴上,BC⊥x轴,点M、N分别在线段BC、AC上,BM=CM,NC=2AN,反比例函数y=(x>0)的图象经过M、N两点,P为x轴正半轴上一点,且OP:BP=1:4,△APN的面积为3,则k的值为( )A.B.C.D.5.(2022•日照)如图,矩形OABC与反比例函数y1=(k1是非零常数,x>0)的图象交于点M,N,与反比例函数y2=(k2是非零常数,x>0)的图象交于点B,连接OM,ON.若四边形OMBN的面积为3,则k1﹣k2=( )A.3B.﹣3C.D.6.(2022•郴州)如图,在函数y=(x>0)的图象上任取一点A,过点A作y轴的垂线交函数y=﹣(x<0)的图象于点B,连接OA,OB,则△AOB的面积是( )A.3B.5C.6D.107.(2022•十堰)如图,正方形ABCD的顶点分别在反比例函数y=(k1>0)和y=(k2>0)的图象上.若BD∥y轴,点D的横坐标为3,则k1+k2=( )A.36B.18C.12D.98.(2022•黑龙江)如图,在平面直角坐标系中,点O为坐标原点,平行四边形OBAD的顶点B在反比例函数y=的图象上,顶点A在反比例函数y=的图象上,顶点D在x轴的负半轴上.若平行四边形OBAD的面积是5,则k的值是( )A.2B.1C.﹣1D.﹣29.(2023•连云港)如图,矩形OABC的顶点A在反比例函数y=(x<0)的图象上,顶点B、C在第一象限,对角线AC∥x轴,交y轴于点D.若矩形OABC的面积是6,cos∠OAC=,则k= .10.(2023•枣庄)如图,在反比例函数(x>0)的图象上有P1,P2,P3,…P2024等点,它们的横坐标依次为1,2,3,…,2024,分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次为S1,S2,S3,…,S2023,则S1+S2+S3+…+S2023= .11.(2023•朝阳)如图,点A是反比例函数y=(k≠0,x>0)的图象上一点,过点A作AB⊥x轴于点B,点P是y轴上任意一点,连接PA,PB.若△ABP的面积等于3,则k的值为 .12.(2023•衢州)如图,点A,B在x轴上,分别以OA,AB为边,在x轴上方作正方形OACD,ABEF,反比例函数y=(k>0)的图象分别交边CD,BE于点P,Q.作PM⊥x轴于点M,QN⊥y轴于点N.若OA=2AB,Q为BE的中点,且阴影部分面积等于6,则k的值为 .13.(2023•锦州)如图,在平面直角坐标系中,△AOC的边OA在y轴上,点C在第一象限内,点B为AC 的中点,反比例函数y=(x>0)的图象经过B,C两点.若△AOC的面积是6,则k的值为 .14.(2023•黄石)如图,点A(a,)和B(b,)在反比例函数y=(k>0)的图象上,其中a>b>0.过点A作AC⊥x轴于点C,则△AOC的面积为 ;若△AOB的面积为,则= .15.(2023•辽宁)如图,矩形ABCD的边AB平行于x轴,反比例函数y=(x>0)的图象经过点B,D,对角线CA的延长线经过原点O,且AC=2AO,若矩形ABCD的面积是8,则k的值为6 .16.(2023•绍兴)如图,在平面直角坐标系xOy中,函数(k为大于0的常数,x>0)图象上的两点A (x1,y1),B(x2,y2),满足x2=2x1,△ABC的边AC∥x轴,边BC∥y轴,若△OAB的面积为6,则△ABC的面积是 .17.(2022•烟台)如图,A,B是双曲线y=(x>0)上的两点,连接OA,OB.过点A作AC⊥x轴于点C,交OB于点D.若D为AC的中点,△AOD的面积为3,点B的坐标为(m,2),则m的值为 .18.(2022•黄石)如图,反比例函数y=的图象经过矩形ABCD对角线的交点E和点A,点B、C在x轴上,△OCE的面积为6,则k= .19.(2022•衢州)如图,在△ABC中,边AB在x轴上,边AC交y轴于点E.反比例函数y=(x>0)=6,则k= .的图象恰好经过点C,与边BC交于点D.若AE=CE,CD=2BD,S△ABC20.(2022•宜宾)如图,△OMN是边长为10的等边三角形,反比例函数y=(x>0)的图象与边MN、OM分别交于点A、B(点B不与点M重合).若AB⊥OM于点B,则k的值为 .21.(2022•鄂尔多斯)如图,正方形OABC的顶点A、C分别在x轴和y轴上,E、F分别是边AB、OA上的点,且∠ECF=45°,将△ECF沿着CF翻折,点E落在x轴上的点D处.已知反比例函数y1==5,则k1﹣k2= .和y2=分别经过点B、点E,若S△COD22.(2022•东营)如图,△OAB是等腰直角三角形,直角顶点与坐标原点重合,若点B在反比例函数y=(x>0)的图象上,则经过点A的函数图象表达式为 .23.(2022•绍兴)如图,在平面直角坐标系xOy中,点A(0,4),B(3,4),将△ABO向右平移到△CDE 位置,A的对应点是C,O的对应点是E,函数y=(k≠0)的图象经过点C和DE的中点F,则k的值是 .24.(2022•内蒙古)如图,在平面直角坐标系中,Rt△OAB的直角顶点B在x轴的正半轴上,点O与原点重合,点A在第一象限,反比例函数y=(x>0)的图象经过OA的中点C,交AB于点D,连接CD.若△ACD的面积是1,则k的值是 .。
专题四反比例函数中“K”与面积一:问题背景反比例函数y=kx中,比例系数k有一个很重要的几何意义,那就是:过反比例函数y=kx图象上任一点P作x轴、y轴的垂线PM、PN,垂足为M、N(如图1所示),则矩形PMON的面积S=PM·PN=|y|·|x|=|xy|=|k|。
所以,对双曲线上任意一点作x轴、y轴的垂线,它们与x轴、y轴所围成的矩形面积为常数|k|,由此基本图形带来的衍生图形也很多,他们与K都有固定的结论。
在解有关反比例函数的问题时,若能灵活运用这些基本图形,会给解题带来很多方便。
二:基本图形S四边形PEOF =|K|*********************************************************************S△ABO=|K|S△ABM=|K|S △ABC=2|K|S四边形ABCD=2|K|******************************************************************************************************************************************S △AOC=S 四边形ACEF基础题型1、如图,直线y=mx 与双曲线y =kx 交于点A,B 、过点A 作AM ⊥x 轴,垂足为点M,连接BM .若△ABM 的面积为1,则k 的值是________2、如图A,B 是函数y =的图象上关于O 原点对称的任意两点,AC ∥Y 轴,BC ∥X 轴,△ABC 的面积记为S,则S=_________*********************************************************************3、如图,点A 、B 是双曲线y =上的点,分别经过A 、B 两点向X 轴、Y 轴作垂线段,若S 阴影=1,则S 1+S 2=________4、如图,点A 是反比例函数y =k x图象上的一点,过点A 作AB ⊥x 轴,垂足为y 轴上的一点,连接AC ,BC.若△ABC 的面积为3,则k 的值是 。
专题四反比例函数中“K”与面积一:问题背景
反比例函数y=k
x
中,比例系数k有一个很重要的几何意义,那就是:过反
比例函数y=k
x
图象上任一点P作x轴、y轴的垂线PM、PN,垂足为M、N(如
图1所示),则矩形PMON的面积S=PM·PN=|y|·|x|=|xy|=|k|。
所以,对双曲线上任意一点作x轴、y轴的垂线,它们与x轴、y轴所围成的矩形面积为常数|k|,由此基本图形带来的衍生图形也很多,他们与K都有固定的结论。
在解有关反比例函数的问题时,若能灵活运用这些基本图形,会给解题带来很多方便。
二:基本图形
S四边形PEOF =|K|
S△ABO=|K|
S△ABM=|K|
S△ABC=2|K|
S四边形ABCD=2|K| S△AOC=S四边形ACEF
基础题型
1、如图,直线y=mx与双曲线y=k
x
交于点A,B、过点A作AM⊥x轴,垂足为
点M,连接BM.若△ABM的面积为1,则k的值是________
2、如图A,B是函数y=的图象上关于O原点对称的任意两点,AC∥Y 轴,BC∥X轴,△ABC的面积记为S,则S=_________
3、如图,点A、B是双曲线y=上的点,分别经过A、B两点向X轴、Y
轴作垂线段,若S
阴影=1,则S
1
+S
2
=________
4、如图,点A是反比例函数y=k
x
图象上的一点,过点A作AB⊥x轴,垂足为
点B,点C为y轴上的一点,连接AC,BC.若△ABC的面积为3,则k的值是。
5、如图,点A在函数y=的图象上,点B在函数y=k
x
(x﹥0)的图象上,连接
AB,AB垂直x轴于点M,且AM︰MB=1︰2,则k=。
6、如图,点A在双曲线y=上,点B上,且AB∥x轴,
C、D在x轴上,若四边形ABCD为矩形,则S ABCD=。
7、双曲线y1、y2在第一象限的图象如图,y1=,过y1上的任意一点A,作x轴的平行线交y2于B,交y轴于C,若S△AOB=1,则y2的解析式是
_____。
8、(陕西2011中考)如图所示,过y轴正半轴上的任意一点P,作x轴的平行
线,分别与反比例函数y=和y=的图象交于点A和点B,若点C 是x轴上任意一点,连接AC、BC,则S△ABC=____。
9、如图,等边三角形OAB的顶点A在反比例函数y=的图象上,点B在y 轴上,若将△OAB沿x轴正方向平移,当点B落在反比例函数的图象上时,点A的坐标为_____。
10、如图所示,在平面直角坐标系中,点A和点C分别在y轴和x轴正半轴
上,以OA、OC为边作矩形OABC,双曲线y= (x>0)交AB于点E,AE:EB=1:3,则矩形OABC的面积是_____。
11、如图,已知矩形OABC的面积为,它的对角线OB与双曲线y=k
x
相交于点
D,且OB:OD=5:3,则k=_____。
12、如图,点A、B在反比例函数y=k
x
(k>0,x>0)的图象上,过点A、B作
x轴的垂线,垂足分别为M、N,延长线段AB交x轴于点C,若OM=MN=NC,且△AOC的面积为6,则k的值为_____ 。
13、(陕西2017中考)如图,在平面直角坐标系中,过点M(-3,2)分别作x
轴,y轴的垂线与反比例函数y=4
x
的图象交于A,B两点,则四边形MAOB的面
积为________.
14、如图,在Rt△OAB中,∠OBA=90°,点B在x轴上,点A在第二象限,已
知双曲线y=k
x
(k<0)经过Rt△OAB斜边OA的中点D,且与直角边AB相交于
点C.若点A的坐标为(-6,4),△AOC的面积为________.
15、如图,点A是反比例函数y=的图象上任意一点,AB∥x轴交反比例函数
y=的图象于点B,以AB为边作平行四边形ABCD,其中C、D在x轴上,则四边形ABCD的面积为_____ 。
16、反比例函数y=与y=的图像在同一坐标戏中如图所示,P
为y=上任意一点,过P作PQ平行于y轴,交y=于点Q,M为y轴上一点,则S△PMQ是_____ 。
17、如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标
轴,点C在反比例函数y=k
x
(k≠0)的图象上。
若点A的坐标为(-2,-2),则k
的值为_____ 。
提高型
1、如图,反比例函数y=在第二象限的图象上有两点A、B,它们的
横坐标分别为-1,-3,直线AB与x轴交于点C,则△AOC的面积为
_____ 。
2、如图,反比例函数y=k
x
(x>0)的图象经过平行四边形ABCO的顶点A和对角
线的交点E,点A的横坐标为3,对角线AC所在的直线交y轴于(0,6)点,则函
数y=k
x
的表达式为_____ 。
3、如图,A、B是双曲线y=k
x(K>0)
上的点,A、B两点的横坐标分别是a、2a,
线段AB的延长线交x轴于点C,若s△AOC=9,则k=_____ 。
.
4、如图,点A在反比例函数y=图象上,点B在反比例函数y=的图象上,且∠AOB=90°,则tan∠OAB的值为_____ 。
5、如图,已知双曲线y=k
x
(K>0)经过直角三角形OAB斜边OB的中点D,与
直角边AB相交于点C。
若△OBC的面积为3,则k=_____ 。
6、如图,点A在双曲线y=上,过A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,当OA=4时,则△ABC周长为_____。
7、直线y=-与反比例函数y=k
x(X<0)
的图象交于点A,与x轴相交于
点B,过点B作x轴垂线交双曲线于点C,若AB=AC,则k的值为_____ 。
8、如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反
比例函数y=k
x
图象的一个交点为M(﹣2,m).则点B到直线OM的距离为_
____。
9、如图,已知梯形OABC 的底边D 在x 轴上,CB ∥OA ,BA ⊥OA ,过点C 的双曲线y =k x 交OB 于D,且OD :DB=1:2.若s △OBC=3,则k 的值为_____ 。
10、如图,在平面直角坐标系中,经过点A 的双曲线
y =k x
(x >0)同时经过点B ,且点A 在点B 的左侧,点A 的横坐标为,∠AOB=∠OBA=45°,则k 的值为.
11、如图A ,B 两点分别在反比例函数y=(x <0)和y =k x
(k >0,x >0)的图象上,连接OA 、OB ,若OA ⊥OB ,OB=2OA ,则k 的值为_____ 。
12、如图,点E,F在函数y=的图象上,直线EF分别与x轴、y轴交于点
A、B,且BE:BF=1:3,则△EOF的面积是_____ 。
13、如图,已知第一象限内的图象是反比例函数y=图象的一个分支,
第二象限内的图象是反比例函数y=图象的一个分支,在x轴的上方有一条平行于x轴的直线m与它们分别交于点A、B,过点A、B作x轴的垂线,垂足分别为C、D。
若四边形ABCD的周长为8,且AB<AC,则点A的坐标为_____ 。