MATLAB中的三维图形绘制与动画制作技巧

实验9 三维绘图一、实验目的学会MATLAB软件中三维绘图的方法。

二、实验内容与要求1．三维曲线图格式一：plot3(X,Y,Z,S).说明：当X，Y，Z均为同维向量时，则plot3描出点X(i),Y(i),Z(i)依次相连的空间曲线.若X，Y均为同维矩阵，X，Y，Z每一组相应列向量为坐标画出一条曲线，S为‘color﹣linestyle﹣marker’控制字符表1.6～表1.10.【例1.79】绘制螺旋线.>>t=0:pi/60:10*pi;>>x=sin(t);>>y=cos(t);>>plot3(x,y,t,’*-b’)>>grid on图形的结果如图1.16所示.格式二：comet3(x,y,z).说明：显示一个彗星通过数据x,y,z确定的三维曲线.【例1.80】>>t=-20*pi:pi/50:20*pi;>>comet3(sin(t),cos(t),t)可见到彗星头（一个小圆圈）沿着数据指定的轨道前进的动画图象，彗星轨道为整个函数所画的螺旋线.格式三：fill3(X,Y,Z,C) ℅填充由参数X,Y,Z确定的多边形，参数C指定颜色.图1.16 例1.79图形结果图1.17 例1.81图形结果【例1.81】>>X=[2,1,2;9,7,1;6,7,0];>>Y=[1,7,0;4,7,9;0,4,3];>>Z=[1,8,6;7,9,6;1,6,1];>>C=[1,0,0;0,1,0;0,0,1]>>fill3(X,Y,Z,C)>>grid on图形的结果如图1.17所示.问题 1.30：图 1.17中每个三角形按什么规律画出的？（用X,Y,Z的对应列元素值为坐标画三角形）每个三角形内填充的颜色又有何规律？（用C 第i列元素值对应的颜色，从第i个三角形对应顶点向中心过渡）若C=[1,5,10;1,5,10;1,5,10]，结果如何？2.三维网格图格式：mesh(X,Y,Z,C) ℅画出颜色由C指定的三维网格图.meshc(X,Y,Z,C) ℅画出带有等高线的三维网格图.meshz(X,Y,Z,C) ℅画出带有底座的三维网格图.说明：若X与Y均为向量，n=length(X),m=length(Y), Z必须满足[m,n]=size(Z),则空间中的点(X(j),Y(i),Z(i,j))为所画曲面网线的交点，X 对应于Z的列，Y对应于Z的行；若X,Y,Z均为同维矩阵，则空间中的点(X(i,j),Y(i,j),Z(i,j))为所画曲面的网线的交点；矩阵C指定网线的颜色，MATLAB对矩阵C中的数据进行线性处理，以便从当前色图中获得有用的颜色，若C缺省，网线颜色和曲面的高度Z相匹配.在三维作图常用到命令meshgrid，其功能是生成二元函数z=f(x,y)中x-y平面上的矩形定义域中数据点矩阵X和Y.格式：[X,Y]= meshgrid(x,y).说明：输入向量x为x-y平面上x轴的值，向量y为x-y平面上y轴的值.输出矩阵X为x-y平面上数据点的横坐标值，输出矩阵Y为x-y平面上数据点的纵坐标值.【例1．82】>> x=1:4;>> y=1:5;>> [x,y]=meshgrid(x,y)x =1 2 3 41 2 3 41 2 3 41 2 3 41 2 3 4y =1 1 1 12 2 2 23 3 3 34 4 4 45 5 5 5图1.18所示x-y 平面上的矩形定义域中20个数据点（星号点）的坐标就是有X ，Y 决定的。

MATLAB 及仿真技术实验报告
四、实验内容和步骤
1、实验内容
（1）在02πt ≤≤区间内，有3sin x t =，5cos y t =，3z txy =，要求：
① 以子图形式绘出t 与x ,t 与y , t 与z 以及同一标度同一幅图中的三个函数图； ② 绘出三维曲线。

02468-4
-202402468
-505
2
4
6
8
-150
-100-500501000
2
4
6
8
-150
-100-50050100
信息工程学院
3 -2
2
（2）已知
2
)
cos
cos(x
y
x
z+
+
=
绘制三维曲面图，并进行插值着色处理。

510
5
10
（3）用stem绘制离散图象：加网格线
4sin(3π/6)
x n
=+
信息工程学院
5
50
100
150
200
0.5
1
1.5
（4）播放一个直径不断变化的球体。

-1
1
-1
1
2、实验步骤
（1）分析实验内容，写出程序大致框架或完整的程序代码。

（2）进入MATLAB7.0集成环境。

（3）编辑程序并进行保存。

（4）运行程序，若有错误，修改错误后再次运行，如此反复进行到不显示出错为止。

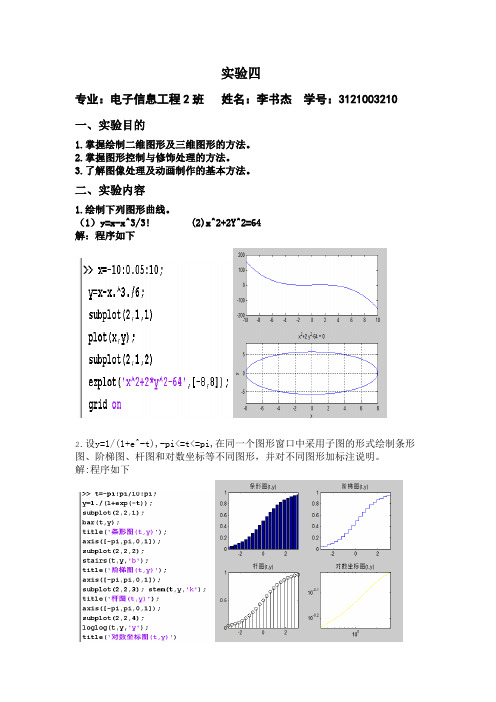
实验四
专业：电子信息工程2班姓名：李书杰学号：3121003210
一、实验目的
1.掌握绘制二维图形及三维图形的方法。

2.掌握图形控制与修饰处理的方法。

3.了解图像处理及动画制作的基本方法。

二、实验内容
1.绘制下列图形曲线。

（1）y=x-x^3/3! (2)x^2+2Y^2=64
解：程序如下
2.设y=1/(1+e^-t),-pi<=t<=pi,在同一个图形窗口中采用子图的形式绘制条形图、阶梯图、杆图和对数坐标等不同图形，并对不同图形加标注说明。

解:程序如下
3.绘制下列极坐标图。

（1）ρ=5cosθ+4 (2)γ=5sin^2φ/cosφ,-π/3<φ<π/3 解：程序如下
思考练习：
2.绘制下列曲线
（1）y=1/2πe^(-x^2/2) (2)x=tsint y=tcost
解：程序如下
（1）
结果如下：
（2）
结果如下：
3.在同一坐标中绘制下列两条曲线并标注两曲线交叉点。

（1）y=2x-0.5
(2)x=sin(3t)cost
Y=sin(3t)sint
解：程序如下
4.分别用plot和fplot函数绘制y=sin(1/x)的曲线，分析两曲线的差别。

解：程序如下
结果如下：
5.绘制下列极坐标图：
(1）p=12/sqrt(θ) (2)γ=3asinφcosφ/(sin^3φ+cos^3φ)解：程序如下
结果如下：。

matlab动画制作例子
在MATLAB中，你可以使用`pause`和`drawnow`命令来制作动画。

以下是一个简单的例子，它展示了如何创建一个动画，该动画显示一个点在二维平面上沿一圆形路径移动。

```matlab
% 初始化参数
t = 0::2pi; % 时间向量
x = sin(t); % x坐标
y = cos(t); % y坐标
% 创建图形窗口
figure;
% 循环动画
for k = 1:length(t)
% 绘制当前点的位置
plot(x(k), y(k), 'ro');
% 添加标题和标签
title('点在圆上的移动');
xlabel('x');
ylabel('y');
% 暂停并更新图形，以便可以看到动画效果
pause();
drawnow;
end
```
这个脚本将会创建一个动画，显示一个点在二维平面上沿着一个圆形路径移动。

这个动画是通过在一个循环中绘制每个点的位置并暂停一段时间来创建的。

`drawnow`命令将立即更新图形窗口，使得你可以看到动画效果。

注意：MATLAB的版本和环境可能会影响动画的表现。

在一些环境中，可能需要使用不同的命令或参数才能获得最佳的动画效果。

Matlab——图形绘制——三维⽴体图形剔透玲珑球动态图——彗星状轨迹图三维绘图函数三维绘制⼯具函数view实例：三维螺旋线>> t=0:pi/50:10*pi;plot3(sin(t),cos(t),t)grid %添加⽹格plot3可以画出空间中的曲线>> t=linspace(0,20*pi, 501);plot3(t.*sin(t), t.*cos(t), t); %注意⽤点乘 .*也可以同时画出两条空间中的曲线>> t=linspace(0,10*pi,501);>> plot3(t.*sin(t),t.*cos(t),t,t.*sin(t),t.*cos(t),-t);正弦曲线图x=linspace(0,3*pi); % 0到 3pi 间100 个数据点z1=sin(x);z2=sin(2*x);z3=sin(3*x);y1=zeros(100); % 含有100 个数据的0数组y3=zeros(100);y2=y3/2;plot3(x,y1,z1,x,y2,z2,x,y3,z3);⽴体⽹状图实例：>> x=linspace(-2, 2, 25); %在x轴上取25点y=linspace(-2, 2, 25); %在y轴上取25点[xx,yy]=meshgrid(x, y); % xx和yy都是21x21的矩阵zz=xx.*exp(-xx.^2-yy.^2); %计算函数值，zz也是21x21的矩阵mesh(xx, yy, zz); %画出⽴体⽹状图曲⾯图>> x=linspace(-2, 2, 25); %在x轴上取25点y=linspace(-2, 2, 25); %在y轴上取25点[xx,yy]=meshgrid(x, y); % xx和yy都是21x21的矩阵zz=xx.*exp(-xx.^2-yy.^2); %计算函数值，zz也是21x21的矩阵surf(xx, yy, zz);%画出⽴体曲⾯图peaks函数>> z = 3*(1-x).^2.*exp(-(x.^2) - (y+1).^2) ...- 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2) ...- 1/3*exp(-(x+1).^2 - y.^2);>> peaks z也可以对peaks函数取点，再以各种不同的⽅法进⾏绘图meshz 可将曲⾯加上围裙[x,y,z]=peaks;meshz(x,y,z);waterfall 可在x ⽅向或y ⽅向产⽣⽔流效果：[x,y,z]=peaks;waterfall(x,y,z);产⽣在y⽅向的⽔流效果：[x,y,z]=peaks;waterfall(x',y',z');meshc 同时画出⽹状图与等⾼线：[x,y,z]=peaks;meshc(x,y,z);surfc 同时画出曲⾯图与等⾼线：[x,y,z]=peaks;surfc(x,y,z);contour3 画出曲⾯在三度空间中的等⾼线contour3(peaks, 20);contour 画出曲⾯等⾼线在XY 平⾯的投影contour(peaks, 20);剔透玲珑球[X0,Y0,Z0]=sphere(30); %产⽣单位球⾯的三维坐标X=2*X0;Y=2*Y0;Z=2*Z0; %产⽣半径为2 的球⾯的三维坐标surf(X0,Y0,Z0); %画单位球⾯shading interp %采⽤插补明暗处理hold on; mesh(X,Y,Z);hold off %画外球⾯hidden off %产⽣透视效果axis off %不显⽰坐标轴动态图形动画效果——彗星状轨迹图R0=1; %以地球半径为⼀个单位a=12*R0;b=9*R0;T0=2*pi; %T0是轨道周期T=5*T0;dt=pi/100;t=[0:dt:T]';f=sqrt(a^2-b^2); %地球与另⼀焦点的距离th=12.5*pi/180; %卫星轨道与x-y平⾯的倾⾓E=exp(-t/20); %轨道收缩率x=E.*(a*cos(t)-f);y=E.*(b*cos(th)*sin(t));z=E.*(b*sin(th)*sin(t)); plot3(x,y,z,'g') %画全程轨线[X,Y,Z]=sphere(30);X=R0*X;Y=R0*Y;Z=R0*Z; %获得单位球坐标grid on,hold on,surf(X,Y,Z),shading interp %画地球x1=-18*R0;x2=6*R0;y1=-12*R0;y2=12*R0;z1=-6*R0;z2=6*R0; axis([x1 x2 y1 y2 z1 z2]) %确定坐标范围view([11737]),comet3(x,y,z,0.02),hold off %设视⾓、画运动轨线。