华师大二附中自主招生数学应试辅导第7讲：函数(3)

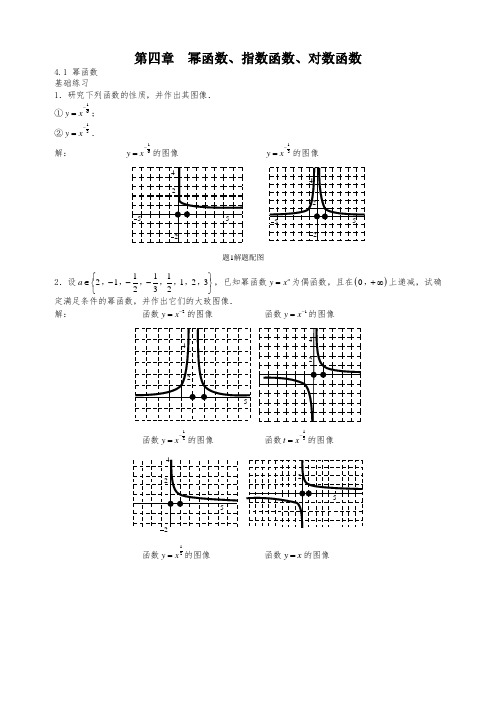
第四章幂函数、指数函数、对数函数4.1 幂函数基础练习1．研究下列函数的性质，并作出其图像．①16y x-=；②13y x-=．解：16y x-=的图像13y x-=的图像题1解题配图2．设11121123232a⎧⎫∈---⎨⎬⎩⎭，，，，，，，，已知幂函数ay x=为偶函数，且在()0+∞，上递减，试确定满足条件的幂函数，并作出它们的大致图像．解：函数2y x-=的图像函数1y x-=的图像函数12y x-=的图像函数13t x-=的图像函数12y x=的图像函数y x=的图像函数2y x =的图像函数3y x =的图像题2解题配图3．已知()()323411mf x m m m x =+--，()0x ≠是幂函数，其图像分布在第一、第三象限，求()f x 的解析式．解：春回大地为()f x 是幂函数，所以3234111m m m +--=，解得3m =-或2m =-或2m =． 由于()()0f x x ≠是幂函数，且图像分布在第一、第三象限，故3m =-． 所以()3f x x -=． 4．已知函数()()223mm f x x m -++=∈Z 为偶函数，且()()35f f <，求m 的值，并确定()f x 的解析式．解：由于()f x 是偶函数，则223m -+应为偶数． 又由于()()35f f <，即22232335mm mm -++-++<，整理，得223315m m -++⎛⎫< ⎪⎝⎭，由于2230m m -++>，则312m -<<． 又由于m ∈Z ，则0m =或1．当0m =时，2233m m -++=为奇数（舍去）；当1m =时，2232m m -++=为偶数． 故m 的值为1，()2f x x =．5．若()()33132m m +<-，试求实数m 的取值范围．解：由于函数3y x =在()-∞+∞，上单调递增，所以132m m +<-，解得23m <． 6．若()()1122132m m +<-，试求实数m 的取值范围． 解：由题6题解配图，10320321m m m m +⎧⎪-⎨⎪->+⎩≥≥，解得213m -<≤．412题6解题配图7．若()()44132m m+<-，试求实数m的取值范围．解：作出幂函数4y x=的图像如题7解题配图所示．由图像知此函数在()()00-∞+∞，，上不具有单调性，若分类讨论步骤较繁，把问题转化到一个单调区间上是关键．考虑4a=时，44x x=．题7解题配图于是有()()44132m m+<-，即44132m m+<-．又由于幂函数4y x=在()0+∞，上单调递增，由于132m m+<-，解得23m<，或4m>．能力提高8．讨论函数()2221k ky k k x--=+在0x>时随着x的增大其函数值的变化情况．解：（1）当20k k+=，即0k=或1k=-时，0y=为常函数．（2）当2210k k--=时，1k=1k=+（3）22210k kk k⎧+>⎪⎨--<⎪⎩，，即01k<<+时，函数为减函数，函数值随x的增大而减小．（4）当22210k kk k⎧+>⎪⎨-->⎪⎩，即1k<-或1k>x的增大而增大．（5）当22210k kk k⎧+<⎪⎨--<⎪⎩，即10k<时，函数为增函数，函数值随x的增大而增大．（6）当22210k kk k⎧+<⎪⎨-->⎪⎩，即11k-<<x的增大而减小．9．已知幂函数()()223m mf x x m--=∈Z为偶函数，且在区间()0+∞，上是减函数，求()f x的解析式，并讨论函数()()b g x xf x =的奇偶性．解：因为幂函数()()223mm f x x x --=∈Z 在区间()0+∞，上是减函数，所以有2230m m --<．解上述不等式得到：13m -<<，而m ∈Z ，所以01m =，或2． 当0m =或2时，2233m m --=-是奇数，不合题意， 当1m =时，2234m m --=-是偶数，故()4f x x -=；()32ag x bx x=-． （1）当0a =，b ≠0时，()3g x bx =-是奇函数．（2）当0a ≠，0b =时，()2ag x x =是偶函数． （3）当0a b ==时，()0g x =既是奇函数又是偶函数． 当0ab ≠时， ()32ag x bx x =-即不奇函数，又不是偶函数． 10．已知函数()()22k k f x x k -++=∈Z ，且()()23f f <． （1）求k 的值．（2）试判断是否存在正数p ，使函数()()()121g x p f x p x =-⋅+-在区间[]12-，上的值域为1748⎡⎤-⎢⎥⎣⎦，；若存在，求出这个p 的值；若不存在，说明理由． 解：（1）220120k k k k -++>⇒-<<⇒=或1．（2）假设存在0p >满足题设，由（1）知()()2211g x px p x =-+-+，[]12x ∈-，． 由于()21g =-，则两个最值点只能在端点()()11g --，和顶点2214124p p p p ⎛⎫-+ ⎪⎝⎭，处取得． 则()()()2max min 4117123448p g x g x g p p +===-=-=-，．解得2p =．则存在2p =满足题意．11．设函数()bf x a x x=+（a ，b 为常数），且：（1）()20f -=．（2）()f x 有两个单调递增区间，写出一个同时满足上述两个条件的有序数对()a b ，． 解：40b a =<，如()14--，．12．已知函数ay x x=+有如下性质：如果常数0a >，那么该函数在区间(0上是减函数，在区间)+∞上是增函数．（1）如果函数()20by x x x =+>的值域为[)6+∞，，求实数b 的值．（2）研究函数22cy x x =+（常数0c >）在定义域内的单调性，并说明理由．（3）对函数a y x x =+和22ay x x=+（常数0a >）作出推广，使它们都是你所推广的函数的特例．研究推广后的函数的单调性． 解：（1）2log 9b =．（2）(1/4c ⎤-∞-⎦，和()1/40c ，递减，()1/40c -，和)1/4c ⎡+∞⎣，递增． （3）/n n y x a x =+（常数0a >）在()1/0n a ，上是减函数，在区间)1/na ⎡+∞⎣，上是增函数；当n 为奇数，则相反． 4.2 指数函数1．利用指数函数的性质，比较下列各组中两个数的大小； （1） 1.4143． （2）230.7-和340.7-．（3）200720082121++和200820092121++．解：（1） 1.4143>．（2）23340.70.7--<．（3）200720082008200921212121++>++． 2．若函数()(]120101x f x m --=∈⇒<，≤． 解：由于10x --≤，则(]120101x m --∈⇒<，≤3．设()442x x f x =+，求出12310001001100110011001f f f f ⎛⎫⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭的值．解：可证：()()11f x f x +-=，进而可得：答案为500．4．某工厂今年1月、2月、3月生产某产品分别为1万件、1.2万件、1.3万件，为了估测以后每个月的产量，以这三个月的产品数量为依据，用一个函数模拟该产品的月产量y 与月份数x 的关系，模拟函数可以选用二次函数或函数x y ab c =+(其中a 、b 、c 为常数)、已知四月份该产品的产量为1.37万件，请问用以上哪个函数作为模拟函数较好?请说明理由． 解：()20.80.5 1.4x f x =-⨯+作为模拟函数较好．理由略． 5．比较a a m m -+与b b m m -+（00a b m >>>，且1m ≠）的大小． 解：()()11a a b b a b a b m m m m m m m --+⎛⎫+-+=-- ⎪⎝⎭，1m >时，()()11a a b b a b a b m m m m m m m --+⎛⎫+-+=-- ⎪⎝⎭，1m >时，则a a b b m m m m --+>+． ()01m ∈，时，则a a b b m m m m --+>+．综上，a a b b m m m m --+>+．6．设()10101010x xx xf x ---=+．(1)证明()f x 在()-∞+∞，上是增函数． （2）求()f x 值域． 解：（1）12x x D ∀<∈()()()()()21122211221122112110102101010101010101010101010x x x x x x x x x x x x x x x x f x f x ---------⨯---=-=++++， 由于21121010x x x x -->，则()()21f x f x >，所以原函数单调递增．（2）()()2210211111010101x x xx f x --⨯=-=-∈-++，． 7．设函数()112x x fx +--=，求使()f x ≥的x 取值范围． 解：()()()()(41411114x x f x x x x ⎧⎪⎪⎪=-<<⇒∈-∞⎨⎪⎪-⎪⎩≥≤．7．(1)求函数()()14102xxf x x -⎛⎫=++ ⎪⎝⎭≥的值域．（2）如果函数()1412xxf x a -⎛⎫=-+- ⎪⎝⎭有两个不同的零点，求实数a 的取值范围． （3）已知函数()(){()()217211xf x a x a x ax =-+-<≥在()-∞+∞，上单调递减，求实数a 的取值范围．解：（1）()211122xxf x ⎛⎫⎛⎫=++ ⎪ ⎪⎝⎭⎝⎭，令(]1012xt ⎛⎫=∈ ⎪⎝⎭，， 则()21g t t t =++，()(]13g t ∈，． （2）()102x t ⎛⎫=∈+∞ ⎪⎝⎭，，()21g t t t a =--+，()0t ∈+∞，，问题转化为()21g t t t a =--+在()0t ∈+∞，有两个不同的零点，可得：()031004a g ∆>⎧⎪⎛⎫⇒∈⎨⎪>⎝⎭⎪⎩，． （3）略．9．已知函数()()219xx a f x a a a --=--，()01a a >≠，在()-∞+∞，上是增函数，求实数a 的取值范围．解：()()()()133x x a f x a a a a --=--+， 1a >时，x x a a --单调递增，则1a >且290a ->；()01a ∈，时，x x a a --单调递减，则2109a a -<-，则()()013a ∈+∞，，． 能力提高10．设()2x x e e f x --=，()2x xe e g x -+=；（1）求证：()()()22f x f x g x =⋅且()2f x 是奇函数．（2）求证：()()()()()222222121g x g x f x f x g x =-=+=+且()2g x 是偶函数．证明：（1）()2222x xe ef x --=，()()()22222x xx x x x e e e e f x g x e e ---+-=-=． 则()()22222x xe ef x f x ---==-，所以()2f x 为奇函数．（2）()2222x xe e g x -+=．()222212x x e e g x -+-=，()222212x x e e f x -++=，()()22222x x e e f x g x -++=， ()()22g x g x =-，则()2g x 为偶函数． 11．设02x ≤≤，求函数1224212x xa y a -=-⋅++的最大值和最小值．解：当1a ≤时，2min 322a y a =-+，2max 492a y a =-+；当512a <≤时，min 1y =，2max 492a y a =-+；当542a <<时，min 1y =，2max 322a y a =-+；当4a ≥时，2min 492a y a =-+，2max 322a y a =-+．12．定义在R 上的增函数()y f x =对任意x ，y ∈R 都有()()()f x y f x f y +=+． （1）求()0f ．（2）求证()f x 为奇函数．（3）若()()33920x x x f k f ⋅+--<对任意x ∈R 恒成立，求实数k 的取值范围． 解：（1）令0x y ==，可得()00f =．（2）令y x =-，可证()()()00f x f x f +-==．（3）即233923113x x x x xk k k ⋅<-++⇒<+-⇒<． 13．已知集合M 是满足下列性质的函数()f x 的体体；存在非零常数T ，对任意x ∈R ，有()()f x T Tf x +=成立．（1）函数()f x x =是否属于集合M ？说明理由．（2）设函数()x f x a =（0a >，且1a ≠）的图像与y x =的图像有公共点，证明：()x f x a M =∈． （3）若函数()sin f x kx M =∈，求实数k 的取值范围．解：（1）对于非零常数T ，()f x T x T +=+，()Tf x Tx =，因为对任意x ∈R ，x T Tx +=不能恒成，所以()f x x M =∉．（2）因为函数()x f x a =（0a >且1a ≠）的图像与函数y x =的图像有公共点， 所以方程组：x y a y x⎧=⎨=⎩有解，消去y 得x a x =，显然0x =不是方程x a x =的解，所以存在非零常数T ，使T a T =．于是对于()x f x a =有()()x T T x x f x T a a a T a Tf x ++==⋅=⋅=，故()x f x a M =∈．（3）当0k =时，()0f x =，显然()0f x M =∈．当0k ≠时，因为()sin f x kx M =∈，所以存在非零常数T ，对任意x ∈R ，有()()f x T Tf x +=成立，即()sin sin kx kT T kx +=．因为0k ≠，且x ∈R ，所以kx ∈R ，kx kT +∈R ，于是[]sin 11kx ∈-，，()[]sin 11kx kT +∈-，, 故要使()sin sin kx kT T kx +=成立，只有1T =±，当1T =时，()sin sin kx k kx +=成立，则2πk m =，m ∈Z ．当1T =-时，()sin sin kx k kx -=-成立，即()sin πsin kx k kx -+=成立， 则π2πk m -+=，m ∈Z ，即()21πk m =--，m ∈Z ． 综合上述得，实数k 的取值范围是{}πk k m m =∈Z ，．14．已知函数ay x x=+有如下性质：如果常数0a >，那么该函数在(0上是减函数，在)+∞上是增函数．（1）如果函数()20by x x x=+>在(]04，上是减函数，在[)4+∞，上是增函数，求b 的值．（2）设常数[]14c ∈，，求函数()()12cf x x x x=+≤≤的最大值和最小值．（3）当n 是正整数时，研究函数()()0n ncg x x c x =+>的单调性，并说明理由． 解：（14=，则4b =．（2）由于[]14c ∈，[]12，，于是，当x ()cf x x x=+取得最小值 ()()2122c f f --=， 当12c ≤≤时，函数()f x 的最大值是()222c f =+； 当24c ≤≤时，函数()f x 的最大值是()11f c =+． （3）设120x x <<，()()()21212121121n n n n nn n n c c c g x g x x x x x x x x x ⎛⎫-=+--=-- ⎪⎝⎭．当12x x <时，()()21g x g x >，函数()g x在)⎡+∞⎣上是增函数；当120x x <<<()()21g x g x >，函数()g x在(0上是减函数．当n 是奇数时，()g x 是奇函数，函数()g x在(-∞-，上是增函数，在)0⎡-⎣上是减函数． 当n 是偶数时，()g x 是偶函数，函数()g x在(-∞-，上是减函数，在0⎡⎤⎣⎦上是增函数．15．若()113x p f x -=，()2223x pf x -=⋅，x ∈R ，1p ，2p 为常数，且()()()()()()()112212f x f x f x f x f x f x f x ⎧⎪=⎨>⎪⎩，≤，． （1）求()()1f x f x =对所有实数x 成立的充要条件（用1p ，2p 表示）．（2）设a b ，为两实数，a b <且1p ，()2p a b ∈，，若()()f a f b =．求证：()f x 在区间[]a b ，上的单调增区间的长度和为2b a-（闭区间[]m n ，的长度定义为n m -）． 解：（1）()()1f x f x =恒成立⇔()()1212323x p x pf x f x --⇔⋅≤≤ 1232x p x p---⇔≤123log 2x p x p ⇔---≤（*）若12p p =，则()30log 2*⇔≤，显然成立；若12p p ≠，记()12g x x p x p =---． 若12p p >时，()()()()12212212112p p x p g x x p p p x p p p x p -<⎧⎪=-++⎨⎪->⎩≤≤所以()12max g x p p =-，故只需123log 2p p -≤． 当12p p <时，()()()()12112122122p p x p g x x p p p x p p p x p -<⎧⎪=--⎨⎪->⎩≤≤所以()21max g x p p =-，故只需213log 2p p -≤．综上所述，()()1f x f x =对所有实数x 成立的充要条件是123log 2p p -≤．（2）第一，如果123log 2p p -≤，则()()1f x f x =的图像关于直线1x p =对称．如题15解题配图()a ． 因为()()f a f b =，所以区间[]a b ，关于直线1x p =对称．因为减区间为[]1a p ，，增区间为[]1p b ，，所以单调增区间的长度和为2b a-． 第二，如果123log 2p p ->，不妨设12p p <，则213log 2p p ->． 于是当1x p ≤时，()()11212333p x p x p x f x f x ---=<<<，从而()()1f x f x =． 当2x p ≥时，()()2312122log 1233333x p p p x p x p f x f x ----==⋅<⋅=，从而()()2f x f x =． 当12p x p <<时，()113x p f x -=及()2223p x f x -=⋅， 由方程0120323x p p x --=⋅，得12031log 222p p x +=+① 显然()10221321log 22p x p p p p <=---<⎡⎤⎣⎦，表明0x 在1p 与2p 之间． 所以()()()()()110202f x p x x f x f x x x p ⎧<⎪=⎨<<⎪⎩≤ 综上可知，在区间[]a b ，上，()()()()()1020f x a x x f x f x x x b ⎧⎪=⎨<⎪⎩≤≤≤如题15解题配图()b ． 故由函数()1f x 及函数()2f x 的单调性可知，()f x 在区间[]a b ，上的单调增区间的长度之和为()()012x p b p -+-，由()()f a f b =，即12323p a b p--=⋅，得123log 2p p a b +=++②故由①得()()[]0121231log 222b ax p b p b p p --+-=-+-=． 综合上述两方面可知，()f x 在区间[]a b ，上的单调增区间的长度和为2b a-．题15解题配图(b )(a )4.3 对数概念及其运算 基础练习1．把下列各题的指数式写成对数式： （1）2416=． （2）031=． （3）42x =． （4）20.5x =． 解：（1）42log 16=． （2）30log 1=． （3）4log 2x =．（4）2log 0.5x =．2．把下列各题的对数式写成指数式： （1）5log 27x =． （2）8log 7x =．（3）4log 3x =． （4）71log 3x =．解：（1）527x =．（2）87x =．（3）43x =．（4）173x =． 3．计算下列各题：（1）22lg lg5⋅ （2）()(21lg5lg8lg1000lg lg0.066++++．（3）2662log 18log 3log 6+． （4）lg 0.7lg30173⎛⎫⋅ ⎪⎝⎭．（5）1log log mm baa b⋅． （6．解：（1）1.（2） 1.（3） 1.（4） 21.5（5） 1.（6）32． 4．（1）已知5log 3a =，5log 4b =，试用a 、b 表示25log 12． （2）已知12log 27a =，求6log 16． （3）已知18log 9a =，185b =，求36log 45． 解：（1）2a b +．（2）()433a a -+．（3）2a ba+-．5．设()0x y z ∈+∞，，，且345x y z ==．（1）求证：1112x y z+=． （2）比较3x ，4y ，6z 的大小．解：（1）换无法，令()3461x y z m m ===>，1log 3m x =，1log 4m y =，1log 6m z=，即可证．（2346x y z <<．6．用log a x ，log a y ，log a z 表示下列各式：（1）log a xyz ．（2）log a ．解：（1）log log log a a a x y z +-．（2）112log log log 23a a a x y z +-．7．求解下列各题：（1）已知lg2a =，103b =，试用a ，b 表示24log 15． （2）已知3log 5a =，5log 7b =，试用a ，b 表示75log 63． （3）已知632236a b c ==，试建立a b c 、、间的关系式．解：（1）13b ab a +-+．（2）221212b ab a a a++=++．（3）123a b c+=或0a b c ===． 8．我们都处于有声世界里，不同场合，人们对音量会有不同的要求，音量大小的单位是分贝()dB ，对于一个强度为I 的声波，分贝的定义是：0101Iy g I =．这里0I 是人耳能听到的声音的最低声波强度，122010W/m I -=，当0I I =时，0y =，即dB 0=．(1)如果21W/m =，求相应的分贝值．(2)70dB 时声音强度I 是60dB 时声音强度I ′的多少倍? 解：(1)21W/m I =，相应的分贝值为()120dB ．(2)70dB 时声音强度I 是60dB 时声音强度I ′的10倍．9．科学研究表明，宇宙射线在大气中能够产生放射性碳14．碳14的衰变极有规律，其精确性可以称为自然界的“标准时钟”．动植物在生长过程中衰变的碳14，可以通过与大气的相互作用得到补充，所以活着的动植物每克组织中的碳14含量保持不变．死亡后的动植物，停止了与外界环境的相互作用，机体中原有的碳14按确定的规律衰减，我们已经知道其“半衰期”为5730年．湖南长沙马王堆汉墓女尸出土时碳14的残余量约占原始含量的76.7％，试推算马王堆古墓的年代． 解：马王堆古墓是近2200年前的遗址． 能力提高10．设1x >，1y >，且2log 2log 30x y y x -+=，求224T x y =-的最小值． 解：令()log 0x t y t =>，则2230t t -+=，22320t t +-=，12t =-，212t =；则1log 2x y =y ， 代入可得：()22424T x x x =-=--． 可知：min 4T =-，当且仅当2x =，y =时取最小值．11．（1）设a b c ，，都是正数，且346a b c ==，求22ab bc acabc-++的值． （2）已知0a b c >，，，且1a b c ≠，，，求：log log log log log log b c a c a b c ab bc a a b c a b c ++---的值． （3）设()20092008f x a x b =⋅+⋅，若()20207log log 2092010f =，求()20209log log 207f 的值． 解：（1）令345a b c m ===，3log a m =，4log b m =，5log c m =，代入，原式0=． （2）利用公式：log log b b c a a c =，证明如下：log log log log lg lg lg lg log lg log lg lg lg lg lg b b b b c a c a b b c aa c a c c a a c a cb b=⇔=⇔=⇔=， 可得：原式为0．（3）利用函数奇偶性，令()()2008g x f x =-，为奇函数， 由于2020920207log log 207log log 209=-， 则原式2006=．12．解方程组：123x y x y x y y x++⎧=⎪⎨=⎪⎩（其中x y +∈R ，）． 解：方程组的解为1111x y =⎧⎨=⎩；2244x y =⎧⎨=⎩．13．对于正整数()a b c a b c ，，≤≤和实数x y z w ，，，，若70x y z w a b c ===，且1111x y z w++=，求证：a b c +=．证明：由70x y z w a b c ===取常用对数得lg lg lg lg70x a y b z c w ===．所以11lg lg70a w x =，11lg lg 70b w y =，11lg lg70c w z=，相加得()1111lg lg lg lg 70a b c w x y z ⎛⎫++=++ ⎪⎝⎭，由题设1111x y z w ++=， 所以lg lg lg lg70a b c ++=，所以lg lg70abc =．所以70257abc ==⨯⨯． 若1a =，则因为lg lg70x a w =，所以0w =与题设矛盾，所以1a >． 又a b c ≤≤，且a b c ，，为70的正约数，所以只有2a =，5b =，7c =． 所以a b c +=． 4.4 反函数 基础练习1．求下列函数的反函数： （1）53y x =-．（2）()220y x x =-≤．（3）32y x =．（4）232x y x +=-（x ∈R 且2x ≠）．解：（1）由53y x =-，得35y x +=，将x 与y 互换，得35x y +=．（2）由()220y x x =-≤，得22x y =+，因为0x ≤，所以有x =将x 与y 互换，得y =()220y x x =-≤的反函数是 )2y x =-≥．（3）由32y x =，得x =x 与y 互换，得y =所以函数32y x =的反函数是y = （4）由232x y x +=-，得223yx y x -=+，即()223y x y -=+． 当2y ≠时，232y x y +=-，将x 与y 互换，得232x y x +=-（x ∈R 且2x ≠）．所以，函数232x y x +=-（x ∈R 且2x ≠）的反函数是232x y x +=-（x ∈R 且2x ≠）．2．若函数()y f x =存在反函数，则下列命题中不正确的是（ ）． Ａ．函数()y f x =与函数()x f y =的图像关于直线y x =对称 Ｂ．若()y f x =是奇函数，则()1y f x -=也是奇函数 Ｃ．若()y f x =在其定义域[]a b ，上是增函数，则()1y f x -=在()()f a f b ⎡⎤⎣⎦，上也是增函数Ｄ．函数()y f x =与()1x f y -=的图像重合．解：Ｃ．3．函数()223f x x ax =--在区间[]12，上存在反函数的充要条件是（ ）． Ａ．(]1a ∈-∞，Ｂ．[)2a ∈+∞， Ｃ．[]12a ∈，Ｄ．(][)12a ∈-∞+∞，，解：抛物线只能是在单调区间上才存在反函数，Ｄ．4．已知()231x f x x +=-，函数()y g x =的图像与()11y f x -=+的图像关于直线y x =对称，则()11g =__________．解：由于()1x f y +=，()()1x f y g x =-=，则()()1g x f x =-，()()3111112g f =-=．5．若点124⎛⎫ ⎪⎝⎭，既是2ax b y +=的图像上，又在它的反函数图像上，则a =__________；b =__________．解：20.2512127410227a b a b a b ++⎧⎧=-⎪=⎪⎪⇒⎨⎨⎪⎪==⎩⎪⎩． 6．若函数()2x f x x =+的反函数是()1f x -，则112f -⎛⎫= ⎪⎝⎭__________．解：解方程122x x =+得1122f -⎛⎫= ⎪⎝⎭．7．若定义在R 上的函数()1y f x =+的反函数是()11y f x -=-，且()01f =，则()2008f =__________．解：()()11f x f x +=+，可得：2009．8．已知函数()y f x =（定义域为D ，值域为A ）有反函数()1y f x -=，则方程00f x =有x a =，且()()f x x x D >∈的充要条件是()1y f x -=满足：__________．解：()10f a -=且()()1f x x x A -<∈．9．设函数()121xf x x-=+，又函数()g x 与()11y f x -=+的图像关于y x =对称，求()2g 的值． 解：由图像可知()()()122g x f x g =-⇒=-． 10．若点（2，1）既在函数()f x =m n ，的值． 解：()()2112f f ⎧=⎪⎨=⎪⎩37m n =-⎧⇒⎨=⎩．11．（1）设函数()y f x =（定义域为D ，值域为A ）的反函数是()1y f x -=，且函数()y f x =在D 上单调递增，证明函数()1y f x -=在A 上也是增函数．（2）设函数()y f x =是D 上的奇函数，证明函数()1y f x -=也是A 上的奇函数．解：（1）21x x >时，()()()()1121212100f x f x f y f y x x --->⇒-=->，()()f x f x -=-．则()()11f y f f x ---=-=⎡⎤⎣⎦()()1f f x x f y --=-=-⎡⎤⎣⎦，得证． （2）略．12．已知函数()()210x f x x x +⎛⎫=> ⎪⎝⎭，（1）求函数()f x 的反函数()1f x -．（2）若2x ≥时，不等式()()(11x f x a a --⋅>恒成立，试求实数a 的取值范围． 解：（1）())11f x x ->，（2）(11-，． 能力提高 13．()1122f x x x-=-．（1）证明函数()f x 有反函数，并求出反函数．（2）反函数的图像是否经过（0，1）点？反函数的图像与y x =有无交点？ （3）设反函数为()1y f x -=，求不等式()10f x -≤的解集． 解：（1）()f x 在正实数集上是增函数，则()f x 有反函数，()(()2114fx x x -=+∈R ；（2）()1f x -经过点（0，1）；无交点；（3）解集为空集．14．已知函数()y f x =的反函数．定义：若对给定的实数()0a a ≠，函数()y f x a =+与()1y f x a -=+互为反函数，则称()y f x =满足“a 和性质”；若函数()y f ax =与()1y f ax -=互为反函数，则称()y f x =满足“a 积性质”．（1）判断函数()()210g x x x =+>是否满足“1和性质”，并说明理由．（2）求所有满足“2和性质”的一次函数．（3）设函数()()0y f x x =>对任何0a >，满足“a 积性质”．求()y f x =的表达式． 解：（1）函数()()210g x x x =+>的反函数是())11g x x -=>． 由于())110g x x -+=>．而()()()21111g x x x +=++>-，其反函数为()11y x =>， 故函数()()210g x x x =+>不满足“1和性质”．（2）设函数()()f x kx b x =+∈R 满足“2和性质”，0k ≠．则()()1x b f x k k --=∈R ，则()122x bf x k-+-+=． 而()()()12f x k x b x +=++∈R ，得反函数2x b ky k--=．由“2和性质”定义可知22x b x b kk k+---=对x ∈R 恒成立， 则1k =-，b ∈R ，即所求一次函数为()()f x x b b =-+∈R ． （3）设0a >，00x >，且点()00x y ，在()y f ax =图像上，则()00y x ，在函数()1y f ax -=图像上．故()()00100f ax y f ay x -⎧=⎪⎨=⎪⎩，可得()()000ay f x af ax ==． 令0ax x =，则0x a x =．()()00xf x f x x ∴=，即()()00x f x f x x=． 综上所述，()()1110n n k b q b f x k x -===≠，此时()k f ax ax =，其反函数就是k y ax =，而()1kf ax ax-=，故()y f ax =与()1y f ax -=互为反函数． 4.5 对数函数 基础练习1．求下列函数的定义域： （1）()22log 1y x =-． （2）y =．（3）1log 1a xy x-=+． （4）y =（5）y =． （6）()()22log log 162x x y x -=+-．解：（1）()()11-∞+∞，，．（2）)(112⎡⎤-⎣⎦，． （3）（-1，1）．（4）()(1131-+，．（5）[)()()200112-，，，． （6）()()2334，，．2．求下列函数的值域：（1）()212log 617y x x =-+． （2）()213log 45y x x =-++．解：（1）[)(]261783x x y -+∈+∞∈-∞-，，，． （2）(]24509x x -++∈，，[)2y ∈-+∞，． 3．利用对数函数的性质，比较下列各题中两个值的大小： （1）0.1log 4和0.1log π；（2）2log 3m 和3log 4m ，其中0m >，1m ≠；（3）log 3a 和log 3b ，其中01a b <<<．解：（1）0.10.1log 4log π<．（2）当1m >时，23log log 34m m <，当01m <<时，23log log 34m m >．（3）log 3log 3a b >．4．函数()2log 2a y x ax =-+在[)2+∞，恒为正，求实数a 的范围．解：首先，由于22x ax -+取值可以正无穷大，可知1a >．所以只要22x ax -+在[)2+∞，恒大于1，即221x ax -+>，在[)2+∞，上恒成立． 转化为：21x ax +>在[)2+∞，上恒成立．即1a x x <+在[)2+∞，上恒成立．则min 1a x x ⎛⎫<+ ⎪⎝⎭．因为1y x x =+在[)2+∞，上单调递增．则min 152x x ⎛⎫+= ⎪⎝⎭，则512a <<．5．设()(32log f x x x =++，则对任意实数0a b a b +，，≥是()()0f a f b +≥的什么条件？ 解：()f x 是奇函数，且单调递增．()()()()00f a f b f a f b a b a b +⇔-⇔-⇔+≥≥≥≥充分必要条件．6．已知函数()x x x x e e f x e e ---=+的反函数是()1f x -，且()()0.810.6f k f --=-，求k 的范围．解：()111ln 21y f x y -+=-，则21ln19log 32ln 4k ==．7．已知函数()11lg11xf x x x+=+--， （1）求函数()f x 的定义域，并判断它的单调性（不用证明）． （2）若()f x 的反函数为()1f x -，证明方程()10f x -=有解，且有唯一解． （3）解关于x 的不等式()11f x x +>⎡⎤⎣⎦．解：（1）()f x 的定义域为()11-，，()f x 在定义域（-1，1）内是增函数． （2）令0x =，得()01f =，即0x =是方程()10f x -=的一个解．设10x ≠是()10f x -=的另一解，则由反函数的定义知()100f x =≠，这与()01f =矛盾，故()10f x -=有且只有一个解．（3）先计算定义域，然后由于()01f =，则()101x x x +>⇒<<-或0x <<． 8．（1）已知()log 4a y ax =-在区间[)02，上是x 的减函数，求实数a 的取值范围．（2）函数()2log a f x ax x =-，()01a a >≠，在区间[]34，上是增函数，求实数a 的取值范围． （3）如果不等式2log 0a x x -<在区间102⎛⎤ ⎥⎝⎦，上恒成立，求实数a 的取值范围．解：（1）分类讨论可得(]12，．（2）1a >，恒成立．()01a ∈，，2ax x -在[]34，单调递减．0∆>恒成立，故14a ≤，18a ≤，且132a ≥，()11164a ⎡⎫∈+∞⎪⎢⎣⎭，，．（3）易知1a <，极限情况2111log 12216a a ⎛⎫⎛⎫=⇒∈ ⎪ ⎪⎝⎭⎝⎭，． 9．若函数()2log 3a y x ax a =-+的值域为R ，求实数a 的取值范围． 解：23x ax a -+可以取遍所有的正数，即()40119⎡⎫∆⇒+∞⎪⎢⎣⎭≥，，．10．已知函数()1log 1a mxf x x -=-是奇函数()01a a >≠，．（1）求出实数m 的值．（2）根据（1）的结果，判断()f x 在()1+∞，上的单调性（不必证明）．（3）如果当()2x r a ∈-，时，()f x 的值域恰为()1+∞，，求a 和r 的值． 解：（1）由定义可知1m =-．（2）1a >，()1x ∈+∞，单调递减；01a <<，()1x ∈+∞，单调递增．（3）即()1011mxr x -∈+∞⇒=-，，2a =+． 11．设函数()()()2221log log 1log 1x f x x p x x +=+-+--，（1）求函数的定义域．（2）问()f x 是否存在最大值与最小值？如果存在，请把它写出来；如果不存在，请说明理由． 解：（1）()f x 的定义域为()()11p p >，．（2）当112p -≤，即13p <≤时，函数()f x 既无最大值又无最小值； 当112p p -<<，即3p >时，函数()f x 有最大值()22log 12p +-，但无最小值．12．已知()()()4log 41f x x kx k =++∈R 是偶函数． （1）求k 的值．（2）证明：对任意实数a ，函数()y f x =的图像与直线12y x b =+最多只有一个交点． （3）设()44log 23x g x a a ⎛⎫=⋅- ⎪⎝⎭，若函数()f x 与()g x 的图像有且只有一个公共点，求实数a 的取值范围．解：（1）12k =-，所以()41log 412x y x =+-．（2）由()411log 4122x x x b +-=+，假设方程有两个不相同的实根12x x 、，则114144x x b +=⋅①224144x x b +=⋅②由②①得()212144444x x x x b -=-，因为1244x x ≠，所以41b =，即0b =，代入①或②不成立，假设错误，命题成立．（3）解法1：由方程()444log 41log 223x x x a a ⎛⎫+-=⋅- ⎪⎝⎭可变形为4142234203x xx x a a a a ⎧+=⋅-⎪⎪⎨⎪⋅->⎪⎩①②，由②得0423x a >⎧⎪⎨>⎪⎩，或0423x a <⎧⎪⎨<⎪⎩， 由①得()242313242x x x a ⨯+=+⨯-⨯，令423xt ⨯+=，则0253a t >⎧⎪⎨>⎪⎩，或02533a t <⎧⎪⎨<<⎪⎩． 则21616117533475334t a t t t t=+=+-++-．当253t >时，75334t t +-单调递增，则753340t t+->，则1a >，此时方程有且只有一个解；当2533t <<时，7543340t t -+-<≤，161375334a t t=+-+-≤，当3a =-时方程有且只有一个解．当3a =-或1a >时，函数()f x 与()g x 的图像有且只有一个公共点． 解法2：()()444142423log 41log 2234203x xx x xx a a x a a a a ⎧+=⋅-⎪⎪⎛⎫+-=⋅-*⇒⎨ ⎪⎝⎭⎪⋅->⎪⎩，()()()22441221011033x x a a a t a t ⇒--⋅-=⇒--⋅-=，两个交点()⇒*式两相异正根()040331101aa a a ⎧⎪∆>⎪⎪⇒>⇒<-⎨-⎪⎪-⎪>-⎩， 一个交点()⇒*式只有一个正根⇒讨论得{}()31a ∈-+∞，， 综上：{}()31a ∈-+∞，时，一个交点．13．已知()2log f x x =，当点()M x y ，在()y f x =的图像上运动时，点()2N x ny -，在函数()n y g x =的图像上运动()n ∈N ．（1）求()n y g x =的表达式．（2）求集合{A a =关于x 的方程()()122g x g x a =-+有实根，a ∈R }．（3）设()()12n g x n H x ⎛⎫= ⎪⎝⎭，函数()()()()110F x H x g x a x b =-<≤≤的值域为22log log ⎡⎢⎣⎦，求实数a b 、的值．解：（1）由条件知002x x y ny=-⎧⎨=⎩，则()020log 2yx n =+则()()2log 2n g x n x =+．（2）由于方程()()122g x g x a =-+x a +， 则求集合Ax a =+有实根时a 的范围．而2199244a x ⎫==-+⎪⎭≤，则94a ≤时原方程总有实根，94A a a ⎧⎫=⎨⎬⎩⎭≤．（3）()()21log 22F x x x =-++，且()F x 在+R 单调递减． 则()()()()22221log 2log 21log 2log2F b b b F a a a ⎧=-+=⎪⎪+⎨⎪=-+=⎪+⎩221log 21log 2b a ⎧=⎪⎪+⎨⎪=⎪+⎩2a ⇒=，3b =． 14．设()()121lgxx xn a n f x n+++-+⋅=，n ∈R ，n ∈N 且2n ≥．若()f x 当()1x ∈-∞，有意义，求a 的取值范围．解：()f x 在()1x ∈-∞，有意义，当且仅当()1210xx x n an +++-+>，对()1x ∈-∞，恒成立．即函数()1210xxxn g x a n n n -⎛⎫⎛⎫⎛⎫=++++> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭对于任意的()1x ∈-∞，恒成立． 因为()g x 在()1-∞，上是减函数，其最小值为()()1211112n g a n a n n n -=++++=-+，所以()0g x >对()1x ∈-∞，恒成立的充要条件是102n a -+>，即12na ->． 故所求实数a 的范围为12n -⎛⎫+∞ ⎪⎝⎭，． 15．已知()()2121x x a f x a -=∈+R ，是R 上的奇函数．（1）求a 的值．（2）求()f x 的反函数．（3）对任意的()0k ∈+∞，解不等式()121log xf x k-+>． 解：（1）由题知()00f =，得1a =，此时()()21212112021212112x x x xx x x xf x f x ------+-=+=+=++++，即()f x 为奇函数．（2）由于21212121x x x y -==-++，得()12111x y y y +=-<<-，则()()121log 111xf x x x-+=-<<-．（3）由于()121log x f x k -+>，则11111x xx k x ++⎧>⎪-⎨⎪-<<⎩，则111x k x >-⎧⎨-<<⎩， ①当02k <<时，原不等式的解集{}11x k x -<<； ②当2k ≥时，原不等式的解集{}11x x -<<． 16．已知()(log a f x x =，其中1a >．（1）试求()f x 的定义域和值域；求出()f x 的反函数()1f x -． （2）求出()f x 的反函数()1f x -． （3）判断函数()1f x -的奇偶性和单调性．（4）若实数m 满足()()112110f m f m ---+-<，求m 的取值范围．解：（1x >，所以，函数()f x 的定义域为R ．函数()f x 的值域为R ．（2）设()y f x =，则y a x =+，利用xx互为倒数，可得y a x -=-，所以，()12y y x a a -=-．所以，()()112x x f x a a --=-，x ∈R ． （3）任取x ∈R ，则()()()1112x x f x a a f x ----=-=-，所以，函数()1f x -为奇函数．任取1x ，2x ∈R ，且12x x <，则由1a >及指数函数的性质可知： 12x x a a <，12x x a a -->，所以，1122x x x x a a a a ---<-，即()()12f x f x <，所以，()1f x -在定义域内单调递增．（4）由()()112110f m f m ---+-<得：()()11211f m f m ---<--，即()()11211f m f m ---<-+．结合()1f x -的单调性可知：上式等价于：211m m -<-+，解之得：1m >或2m <-． 17．已知函数()(()log 01a f x x a a =+>≠，． （1）求反函数()1f x -，并求出其定义域．（2）设()(1log a P n f n -=+．如果()()332n nP n n -+<∈N ，求a 的取值范围．解：（1）设()((log a y f x x x ==．则y y a x a x =-=．两端平方整理得：222222022y y yyyy a a a a xa x a -++-+=⇒==． 则()122x x a a f x --+=由于1a >时，()(log a f x x =值域为)log a ⎡+∞⎣；01a <<时，()f x的值域为(log a -∞，． 则()1f x -的定义域为：1a >时，)log a x ⎡∈+∞⎣， 01a <<时，(log a x ∈-∞，．（2）()(()121log 2n nn a P n f n a a ---⎫=+=+=+⎪⎪⎝⎭， 由333333222n n n n n nn n n n n a a P a a -----+++<⇒<⇒+<+，即()()()3313303nn n n n n n n na a a a a--⎡⎤--⎣⎦+--=<． 由于()30n a >，则()()1331033nn n a a a ⎡⎤--<⇒<<⎣⎦；又由于n ∈N，则log log 1a a n a +>>，即131331a a a ⎧<<⎪⇒<<⎨⎪>⎩． 4.6 指数方程和指数不等式 1．解下列方程：（1）13119133x x x-+=--． （2）31636281x x x ⋅+=⋅．（3）10xx+=．（4（5）14526x x --⋅．（6）()()222121x x x x --=-．解：（1）()1.2x = ()0.5.3 ()2.4±（5）32.（6）1012，，． 2．解下列不等式：（1）282133x x --⎛⎫> ⎪⎝⎭． （2）114123x x>--． （3）22222233x x x x ---->-． 解：（1）（-2，4）． （2）20log 3x <<．（3）()()12+∞-∞-，，．3．已知关于x 的方程2212940x x a a ---+=有一根是2． （1）求实数a 的值．（2）若01a <<，求不等式2212940x x a a ---+<的解集．解：（1）将2x =代入可得12a =或4a =．（2）设1x a t -=后解方程得()12-，．4．设0a >，1a ≠，求证：关于x 的方程2x x a a a -+=的根不在区间[0，1]内． 证明：用反证法证：假设方程有解[]001x ∈，， 由不等式可知：22x x a a a -=+≥，则1a >．则21x x a a a a -=++≤，得出：1a ≤，矛盾． 因此，题目结论成立． 能力提高5．若(]1x ∈-∞-，，不等式()24210x x m m -++>恒成立，则实数m 的取值范围是__________． 解：令2xt =，则对于102t ⎛⎤∈ ⎥⎝⎦，，()2210m m tt -++>恒成立23m ⇒-<<．6．设方程22log 1x x ⋅=的两根为1x ，()212x x x <，则（ ）． Ａ．1200x x <>， Ｂ．101x <<，22x >Ｃ．121x x >Ｄ．1201x x <<解：D ．7．设125236x x xt ⎛⎫⎛⎫⎛⎫=++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则关于x 的方程()()()1230t t t ---=的所有实数解之和为__________．解：125236x x xt ⎛⎫⎛⎫⎛⎫=++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，单调递减，且()03t =，()12t =，()31t =，所以答案为4．4.7 对数方程和对数不等式 基础练习1．解下列方程人：（1）22313log log 30x x +-=． （2）()4log 26x x +=． （3）()141log 1222x x +-=+． （4）5log 15x -=．（5）2lg lg 1020x x x +=．（6）()()212log 21log 2122x x ---⋅+-=-．解：（1）27x =或13x =． （2）2log 3x =． （3）1x =． （4）25或0.2．（5）10或110．（6）2log 3-或25log 4-． 2．解下列不等式： （1）12132log 2x +>． （2）221log 2log 9log 640x x x -+-<． （33121log 202x +>．（4）()2log 21log 21x x x x +->-． 解：（1）()()2701124⎛⎫+∞ ⎪⎝⎭，，，．（2）1613x <<． （3）[)24，． （4）12x >，且1x ≠． 3．若函数()()2lg 43f x ax x a =-+-的值域为R ，则实数a 的取值范围是__________． 解：[]00040a a >⎧=⇒⎨∆⎩≥，，．4．求函数()()213log 56f x x x =-+的单调递增区间．解：首先定义域为()()23-∞+∞，，，再根据复合函数的单调性的性质，可得：()2-∞，．5．已知a b ，是方程()3274log 3log 33x x +=-的两个根，求a b +的值．解：换元法解题，1081a b +=．6．如果0x >，0y >，10log log 3x y y x +=，144xy =，求x y +的值．解：令log x y t =，则1103t t +=⇒．7．设集合()12log 32A x x ⎧⎫⎪⎪=--⎨⎬⎪⎪⎩⎭≥，21a B xx a ⎧⎫=>⎨⎬-⎩⎭，若a B ≠∅，求实数a 的取值范围． 解：(){}()()341003A x x =-⇒-≤，，．8．已知1492320x x +-⋅+≤，求函数1122log log 28x xy =⋅的最大、最小值． 解：令2xt =，则[]2min 183202161t t t y -+⇒∈⇒=-≤，，max 3y =． 9．有关于x 的不等式()lg 37x x a ++->．（1）当1a =时，解此不等式．（2）当a 为何值时，此不等式的集是R ． 解：（1）当1a =时，或7x >或3x <-．（2）[)37101x x a ++-∈+∞⇒<，时此不等式的解集是R ．能力提高10．已知α是函数()log 2008a f x x x =-，()1a >的一个零点，β是函数()2008x g x xa =-的一个零点，求αβ的值．解：2008log a x x =，2008x a x=，log a x 与x a 互为反函数，所以2008αβ=．11．函数()f x 的定义域为D ，若满足①()f x 在D 内是单调函数，②存在[]m n D ⊆，，使()f x 在[]m n ，上的值域为1122m n ⎡⎤⎢⎥⎣⎦，，那么就称()y f x =为“好函数”．现有()()log x a f x a k =+，()01a a >≠，是“好函数”，求k 的取值范围．解：()log 2x a x a k +=有两个实数解104k ⎛⎫⇒∈ ⎪⎝⎭，．12．已知0a >1a ≠，试求使方程()()222log log a a x ak x a-=-有解的k 的取值范围． 解：由对数性质知，原方程的解x 应满足()2222200x ak x a x ak x a ⎧-=-⎪⎪->⎨⎪->⎪⎩①②③若①②同时成立，则③必成立，故只需解()2220x ak x ax ak ⎧-=-⎪⎨->⎪⎩．由①可得()221kx a k =+④当0k =时，④无解；当0k ≠时，④的解是()212a k x k+=，代入②得212k k k+>．。

华师大版八年级数学下《函数及其图像》知识点归纳一．变量与函数1 ．函数的定义：一般的，在某个变化过程中有两个变量x和y，对于x的每一个数值y都有唯一的值与之对应，我们说x叫做自变量，y叫做因变量，y叫做x的函数。

2．自变量的取值范围：（1）能够使函数有意义的自变量的取值全体。

（2）确定函数自变量的取值范围要注意以下两点：一是使自变量所在的代数式有意义；二是使函数在实际问题中有实际意义。

（3）不同函数关系式自变量取值范围的确定：①函数关系式为整式时自变量的取值范围是全体实数。

②函数关系式为分式时自变量的取值范围是使分母不为零的全体实数。

③函数关系式为二次根式时自变量的取值范围是使被开方数大于或等于零的全体实数。

3 ．函数值：当自变量取某一数值时对应的函数值。

这里有三种类型的问题：（1）当已知自变量的值求函数值就是求代数式的值。

（2）当已知函数值求自变量的值就是解方程。

（3）当给定函数值的一个取值范围，欲求自变量的取值范围时实质上就是解不等式或不等式组。

二．平面直角坐标系：1．各象限内点的坐标的特征：（1）点p（x,y）在第一象限→x＞0,y＞0.（2）点p（x,y）在第二象限→x＜0,y＞0.（3）点p（x,y）在第三象限→x＜0,y＜0（4）点p（x,y）在第四象限→x＞0,y＜0.2 ．坐标轴上的点的坐标的特征：（1）点p（x,y）在x轴上→x为任意实数，y=0（2）点p（x,y）在y轴上→x=0,y为任意实数3 ．关于x轴，y轴，原点对称的点的坐标的特征：（1）点p（x,y）关于x轴对称的点的坐标为（x,-y）.（2）点p（x,y）关于y轴对称的点的坐标为（-x,y）.（3）点p（x,y）关于原点对称的点的坐标为（-x,-y）4 ．两条坐标轴夹角平分在线的点的坐标的特征：（1）点p（x,y）在第一、三象限夹角平分在线→x=y.（2）点p（x,y）在第二，四象限夹角平分在线→x+y=0 5．与坐标轴平行的直线上的点的坐标的特征：（1）位于平行于x轴的直线上的所有点的纵坐标相同。

函数图象平移与伸缩的通解对于函数图象的平移与伸缩问题，传统的处理手法过于繁杂，记忆量大，难于掌握.本文试图用代换的手法将其作一般性的探讨. 一、函数图象的平移事实上，设函数()y f x =的图象，向右平移a 个单位，得到的图象的解析式是''()y f x =,令点00(,)x y 是()y f x =的图象上任一点，点00(,)x y 向右平移a 个单位得点''00(,)x y ，则点''00(,)x y 在''()y f x =的图象上，且'00'00x x a y y ⎧=+⎪⎨=⎪⎩，有'00'00x x ay y ⎧=-⎪⎨=⎪⎩，于是，把函数()y f x =的图象，向右平移a 个单位，得到的图象的解析式是()y f x a =-（即以x a -代换x ）.我们定义：当0a >时，表示向右平移；当0a <时，表示向左平移. 例1 函数(21)y f x =-是偶函数，则函数(2)y f x =的对称轴是A ．0x = B.1x =- C. 12x =D. 12x =- 解：函数(21)y f x =-是偶函数，∴其对称轴为0x =，以x a -代换x ，有[2()1]y f x a =--，令2()12x a x --=，解得12a =-，故函数(21)y f x =-的图象向左平移12个单位，得到函数(2)y f x =的图象，其对称轴0x =也相应地向左平移了12个单位，故选D.例2 要得到函数cos(2)4y x π=-的图象，只需要将函数sin 2y x =的图象A. 向左平移8π个单位 B. 向右平移8π个单位 C. 向左平移4π个单位 D.向右平移4π个单位解：∵cos(2)sin[(2)]sin(2)4244y x x x ππππ=-=+-=+，而在sin 2y x =中，以x a -代换x ，有sin 2()y x a =-.令22()4x x a π+=-，解得8a π=-.故选A.方法二：sin 2cos(2)cos(2)22y x x x ππ==-=-.在cos(2)2y x π=-中，以x a -代换x ，有cos[2()]2y x a π=--，令2()224x a x ππ--=-，解得8a π=-.故选A.同样地，把函数()()g y f x =的图象，向右平移a 个单位，再向上平移b 个单位，得到的图象的解析式是()()g y b f x a -=-（即以x a -，y b -分别代换x ，y ）.同样，我们定义：当0b >时，表示向上平移；当0b <时，表示向下平移.例3 函数sin()6y x π=-的图象，经过怎样的平移变换得到函数sin()33y x π=++的图象？ 解：在sin()6y x π=-中，以x a -，y b -分别代换x ，y ，有sin[()]6y b x a π-=--. 即sin()6y x a b π=--+，经对比，有633x a x b ππ⎧--=+⎪⎨⎪=⎩，解得23a b π⎧=-⎪⎨⎪=⎩.故把函数sin()6y x π=-的图象，向左平移2π个单位，再向上平移3个单位，便得函数sin()33y x π=++的图象. 二、函数图象的伸缩与平移事实上，设把函数()y f x =的图象的横坐标伸长到原来的(0)k k >倍（纵坐标不变），得到的图象的解析式是''()y f x =,令点00(,)x y 是()y f x =的图象上任一点，点00(,)x y 的横坐标伸长到原来的k 倍，得点''00(,)x y ，则点''00(,)x y 在''()y f x =的图象上，且'00'00x kx y y ⎧=⎪⎨=⎪⎩，有'00'001x x ky y ⎧=⎪⎨⎪=⎩， 于是，设把函数()y f x =的图象的横坐标伸长到原来的(0)k k >倍（纵坐标不变），得到的图象的解析式是1()y f x k =（即以1x k代换x ）. 我们定义：当1k >时，表示伸长；当01k <<时，表示缩短.例4 函数sin y x =的图象，经过怎样的平移和伸缩变换得到函数sin(2)46y x π=++的图象？解：（先平移后伸缩）在sin y x =中，以x a -，y b -分别代换x ，y ，有s i n ()y b x a -=-，再以1x k代换x ，有1sin()y b x a k -=-，即1sin()y x a b k =-+.对比有1264x a x k b π⎧-=+⎪⎨⎪=⎩，得1,,462a kb π=-==.即把函数sin y x =的图象向左平移6π个单位，再向上平移4个单位，后将横坐标缩短到原来的12倍（纵坐标不变），可得函数sin(2)46y x π=++的图象.方法二：（先伸缩后平移）在sin y x =中，以1x k代换x ，有1sin y x k =，再以x a -，y b -分别代换x ，y ，得1sin ()y b x a k -=-，即1sin ()y x a b k =-+于是1()264x a x k b π⎧-=+⎪⎨⎪=⎩，得12,,46a b k k π=-==，∴1,,4212k a b π==-=.即把函数sin y x =的图象横坐标缩短到原来的12倍（纵坐标不变），再向左平移12π个单位，后向上平移4个单位，可得函数sin(2)46y x π=++的图象.把函数()()g y f x =的图象的横坐标与纵坐标分别伸长到原来的,(,0)k l k l >倍，得到的图象的解析式是11()()g y f x l k=（即分别以1x k ，1y l 代换,x y ）.我们定义：当,1k l >时，表示伸长；当0,1k l <<时，表示缩短.例5 已知函数2()log (1)f x x =+，将()y f x =的图象向左平移1个单位，再将图象上所有点的纵坐标伸长到原来的2倍（横坐标不变），得到函数()y g x =的图象.（I ）求()y g x =的解析式及定义域； （II ）求()()()F x f x g x =-的最大值.解：（I ）依题意，在2log (1)y x =+中，以(1)x --（即1x +）代换x ，得2log [(1)1]y x =++，即2log (2)y x =+，再以12y 代换y ，得21log (2)2y x =+.故得2()2log (2)g x x =+…….下略. 例6 函数3sin(5)3y x π=+的图象，经过怎样的变换得到函数sin()6y x π=-的图象？解：（先伸缩后平移）在3sin(5)3y x π=+中，分别以1x k ，1y l 代换,x y ，有153sin()3y x l k π=+，再以x a -代换x ，得153sin[()]3y x a l k π=-+，即53s i n [()]3y l x a k π=-+，令315()36l x a x kππ=⎧⎪⎨-+=-⎪⎩，得15,,32k l a π===.故把函数3sin(5)3y x π=+的图象，横坐标伸长到原来的5倍（纵坐标不变），再将纵坐标缩短到原来的13倍（横坐标不变），后向右平移2π个单位，即得函数sin()6y x π=-的图象.（本题也可“先平移后伸缩”行变换）。

上海华东师范大学第二附属中学三角函数与解三角形多选题试题含答案一、三角函数与解三角形多选题1．已知函数()2sin (0)6f x x πωω⎛⎫=+> ⎪⎝⎭且对于R x ∀∈都有144f x f x ππ⎛⎫-=- ⎪⎛⎫⎝⎭+ ⎪⎝⎭成立．现将函数()2sin 6f x x πω⎛⎫=+ ⎪⎝⎭的图象向右平移6π个单位长度，再把所有点的横坐标伸长到原来的2倍（纵坐标不变）得到函数()g x 的图象，则下列说法正确的是（ ） A ．函数066g x g x ππ⎛⎫⎛⎫-++=⎪ ⎪⎝⎭⎝⎭B ．函数()g x 相邻的对称轴距离为πC ．函数23g x π⎛⎫+ ⎪⎝⎭是偶函数 D ．函数()g x 在区间,63ππ⎡⎤⎢⎥⎣⎦上单调递增 【答案】ABCD 【分析】先利用已知条件求出()f x 的周期T π=，即可得2ω=，再利三角函数图象的平移伸缩变换得()g x 的解析式，在逐一判断四个选项的正误即可得正确选项. 【详解】因为对于R x ∀∈都有144f x f x ππ⎛⎫-=-⎪⎛⎫⎝⎭+ ⎪⎝⎭成立 所以()12f x f x π=-⎛⎫+ ⎪⎝⎭，()12f x f x ππ⎛⎫+=- ⎪+⎝⎭， 所以()()()11f x f x f x ππ=-=+-+对于R x ∀∈都成立， 可得()f x 的周期T π=，所以22Tπω==， 所以()2sin 26f x x π⎛⎫=+⎪⎝⎭， 将函数()2sin 26f x x π⎛⎫=+⎪⎝⎭的图象向右平移6π个单位长度，可得 2sin 22sin 2666y x x πππ⎡⎤⎛⎫⎛⎫=-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦再把所有点的横坐标伸长到原来的2倍可得()2sin 6g x x π⎛⎫=- ⎪⎝⎭，对于选项A:()2sin 2sin 2sin 2sin 0666666g x g x x x x x ππππππ⎛⎫⎛⎫⎛⎫⎛⎫-++=--++-=-+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，故选项A 正确；对于选项B ：函数()g x 周期为221T ππ==，所以相邻的对称轴距离为2Tπ=，故选项B正确；对于选项C ：222sin 2sin 2cos 3362g x x x x ππππ⎛⎫⎛⎫⎛⎫+=+-=+=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭是偶函数，故选项C 正确； 对于选项D ：当63x ππ≤≤，066x ππ≤-≤，所以函数()g x 在区间,63ππ⎡⎤⎢⎥⎣⎦上单调递增，故选项D 正确， 故选：ABCD 【点睛】关键点点睛：本题解题的关键点是由144f x f x ππ⎛⎫-=-⎪⎛⎫⎝⎭+ ⎪⎝⎭恒成立得出 ()()f x f x π=+可得ω的值，求出()f x 的解析式.2．（多选题）如图，设ABC 的内角、、A B C 所对的边分别为a b c 、、，若a b c 、、成等比数列，、、A B C 成等差数列，D 是ABC 外一点，1,3DC DA ==，下列说法中，正确的是（ ）A ．3B π=B ．ABC 是等边三角形C ．若A B CD 、、、四点共圆，则13AC =D ．四边形ABCD 面积无最大值 【答案】ABC 【分析】根据等差数列的性质和三角形内角和可得3B π=，根据等比中项和余弦定理可得a c =，即ABC 是等边三角形，若A B C D 、、、四点共圆，根据圆内接四边形的性质可得23D π=，再利用余弦定理可求AC =211sin sin 223ACD ABC S S S AD CD D AC π∆∆=+=⋅+和2222cos AC AD CD AD CD D 可得3sin 3sin()23S D D D π=-+=-+. 【详解】由、、A B C 成等差数列可得，2A+C =B ，又A B C π++=， 则3B π=，故A 正确；由a b c 、、成等比数列可得，2b ac =，根据余弦定理，2222cos b a c ac B =+-，两式相减整理得，2()0a c -=，即a c =，又3B π=，所以，ABC 是等边三角形，故B 正确；若A B C D 、、、四点共圆，则B D π+=，所以，23D π=， ADC 中，根据余弦定理，2222cos AC AD CD AD CD D ，解得AC =C 正确； 四边形ABCD 面积为：211sin sin 223ACD ABC S S S AD CD D AC π∆∆=+=⋅+23sin 2D AC = 又2222cos 106cos AC AD CD AD CD D D =+-⋅=-，所以，3sin 3sin()23S D D D π==-+因为(0,)D π∈，当四边形面积最大时，sin()13D π-=，此时max 32S =+，故D 错误. 故选：ABC 【点睛】本题考查解三角形和平面几何的一些性质，同时考查了等差等比数列的基本知识，综合性强，尤其是求面积的最大值需要一定的运算，属难题.3．设函数()sin 6f x M x πω⎛⎫=+ ⎪⎝⎭(0,0)M ω＞＞的周期是π，则下列叙述正确的有（ ）A ．()f x 的图象过点10,2⎛⎫ ⎪⎝⎭B ．()f x 的最大值为MC ．()f x 在区间2,63ππ⎡⎤⎢⎥⎣⎦上单调递减D ．5,012π⎛⎫⎪⎝⎭是()f x 的一个对称中心 【答案】BCD 【分析】已知只有周期的条件，只能求出ω，其中M 未知；A 选项代值判定；B 选项由解析式可知；C 选项由()f x 的单调递减区间在32,2,22k k k Z ππππ⎛⎫++∈ ⎪⎝⎭上化简可得；D 选项由()f x 的对称中心为(),0,k k Z π∈化简可得. 【详解】 由题可知2T ππω==，解得2ω=，即()sin 26f x M x π⎛⎫=+ ⎪⎝⎭当0x =时，()0sin 20sin 662M f M M ππ⎛⎫=⨯+== ⎪⎝⎭，故选项A 错误； 因为()sin 26f x M x π⎛⎫=+ ⎪⎝⎭，所以最大值为M ，故选项B 正确；由解析式可知()f x 在3222,262k x k k Z πππππ+≤+≤+∈ 即2,63x k k ππππ⎡⎤∈++⎢⎥⎣⎦上单调递减，当0k =时，选项C 正确； 由解析式可知()f x 的对称中心的横坐标满足26x k ππ+=，即212k x ππ=- 当1k =时，512x π=，对称中心为5,012π⎛⎫⎪⎝⎭，故选项D 正确. 故选：BCD 【点睛】本题考查()()sin f x A x =+ωϕ型三角函数的性质，其中涉及最值、对称轴、对称中心，属于较难题.4．设函数()sin()(0)4f x x πωω=+>，已知()f x 在[]02π，有且仅有5个零点，则下列结论成立的有（ ）A ．()1y f x =+在()02π，有且仅有2个零点 B ．()f x 在023π⎛⎫⎪⎝⎭，单调递增C ．ω的取值范围是192388⎡⎫⎪⎢⎣⎭，D ．将()f x 的图象先右移4π个单位，再纵坐标不变，横坐标扩大为原来的2倍，得到函数1()sin()2g x x ω=【答案】BC 【分析】首先利用图象直接判断A 选项；再利用函数()f x 在[]02π，有且仅有5个零点，求得ω的范围，并利用整体代入的方法判断B 选项；最后利用图象的变换规律，求得变换之后的解析式，判断D. 【详解】A.如图，[]0,2π上函数仅有5个零点，但有3个最小值点，这3个最小值点就是()1y f x =+在()0,2π上的3个零点；B.[]0,2x π∈时，,2444t x πππωωπ⎡⎤=+∈⋅+⎢⎥⎣⎦ 若函数()f x 在[]02π，有且仅有5个零点，则5264ππωππ≤⋅+<，得192388ω≤<，当023x π⎛⎫∈ ⎪⎝⎭，时，,448t x πππω⎛⎫=+∈ ⎪⎝⎭，此时函数单调递增，故BC 正确； D. 函数()f x 的图象先右移4π个单位后得到sin sin 4444y x x ππωππωω⎡⎤⎛⎫⎛⎫=-+=-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，再将横坐标扩大为原来的2倍，得到()1sin 244g x x ωππω⎛⎫=-+ ⎪⎝⎭，故D 不正确；故选：BC 【点睛】关键点点睛：本题的关键是求出ω的取值范围，首先根据函数在区间[]0,2π有5个零点，首先求4t x πω=+的范围，再分析sin y t =的图象，求得ω的范围.5．已知函数)()lg1( 2.7)x x f x x e e e -=+-+≈⋯，若不等式(sin cos )2(sin 2)f f t θθθ+<--对任意R θ∈恒成立，则实数t 的可能取值为（ ）A ．1BC ．3D ．4【答案】CD 【分析】令)()lgx x g x x e e -=+-，则()()1f x g x =+，可判断()g x 是奇函数且单调递增，不等式可变形可得(sin cos )(sin 2)g g t θθθ+<-，所以sin cos sin 2t θθθ>++，令()sin cos sin 2h θθθθ=++，换元法求出()h θ的最大值，()max t h θ>即可. 【详解】令)()lgx x g x x e e -=+-，则()()1f x g x =+，()g x 的定义域为R ，))()()lglgx x x x g x g x x e e x e e ---+=+-++-0=，所以()()g x g x -=-，所以()g x 是奇函数， 不等式(sin cos )2(sin 2)f f t θθθ+<--等价于[](sin cos )1(sin 2)1f f t θθθ+-<---，即(sin cos )(sin 2)(sin 2)g g t g t θθθθ+<--=-，当0x >时y x =单调递增，可得)lgy x =单调递增，x y e =单调递增，x y e -=单调递减，所以)()lgx x g x x e e -=+-在()0,∞+单调递增，又因为)()lg x x g x x e e -=+-为奇函数，所以)()lgx x g x x e e -=+-在R 上单调递增，所以sin cos sin 2t θθθ+<-，即sin cos sin 2t θθθ>++， 令()sin cos sin 2h θθθθ=++，只需()max t h θ>，令sin cos m θθ⎡+=∈⎣，则21sin 2m θ=+，2sin 21m θ=-，所以()21h m m m =+-，对称轴为12m =-，所以m =()max 211h m ==，所以1t >可得实数t 的可能取值为3或4， 故选：CD 【点睛】关键点点睛：本题解题的关键点是构造函数()g x 奇函数且是增函数，将原不等式脱掉f 转化为函数恒成立问题.6．在ABC 中，下列说法正确的是（ ） A ．若A B >，则sin sin A B > B ．若2C π>，则222sin sin sin C A B >+C ．若sin cos A B <，则ABC 为钝角三角形D ．存在ABC 满足cos cos 0A B +≤ 【答案】ABC 【分析】根据大角对大边，以及正弦定理，判断选项A ；利用余弦定理和正弦定理边角互化，判断选项B ；结合诱导公式，以及三角函数的单调性判断CD. 【详解】 A.A B >，a b ∴>，根据正弦定理sin sin a bA B=，可知sin sin A B >，故A 正确； B.2C π>，222cos 02a b c C ab +-∴=<，即222a b c +<，由正弦定理边角互化可知222sin sin sin C A B >+，故B 正确；C.当02A π<<时，sin cos cos cos 2A B A B π⎛⎫<⇔-<⎪⎝⎭，即22A B A B ππ->⇒+<，即2C π>，则ABC 为钝角三角形，若2A π>，sin cos cos cos 2A B A B π⎛⎫<⇔-< ⎪⎝⎭，即22A B A B ππ->⇒>+成立，A 是钝角，当2A π=是，sin cos A B >，所以综上可知：若sin cos A B <，则ABC 为钝角三角形，故C 正确；D.A B A B ππ+<⇒<-，0,0A B πππ<<<-<，()cos cos cos A B B π∴>-=-，即cos cos 0A B +>，故D 不正确. 故选：ABC 【点睛】关键点点睛：本题考查判断三角形的形状，关键知识点是正弦定理和余弦定理，判断三角形形状，以及诱导公式和三角函数的单调性.7．如图，已知函数()sin()f x A x ωϕ=+（其中0A >，0>ω，||2πϕ≤）的图象与x 轴交于点,A B ，与y 轴交于点C ，2BC BD =，,||23OCB OA π∠==，221||3AD =.则下列说法正确的有（ ）A ．()f x 的最小正周期为12B ．6πϕ=-C ．()f x 的最大值为163D ．()f x 在区间(14,17)上单调递增【答案】ACD 【分析】由题意可得：3|sin |2A πϕω=+，sin(2)0ωϕ+=，可得A ，B ，C ，D 的坐标，根据221||AD =，可得方程22228(1)243A sin πϕω-+=，进而解出ω，ϕ，A ．判断出结论． 【详解】由题意可得：||3||OB OC =，3sin 2A πϕω∴=+，sin(2)0ωϕ+=， (2,0)A ，(2B πω+，0)，(0,sin )C A ϕ，sin 1,22A D πϕω⎛⎫∴+ ⎪⎝⎭， 2213AD =，222sin 281243A πϕω⎛⎫∴-+= ⎪⎝⎭，把|sin |(2)3A πϕω=+代入上式可得：2()2240ππωω-⨯-=，0>ω.解得6πω=，6πω∴=，可得周期212T ωπ==，sin()03πϕ∴+=，||2πϕ≤，解得3πϕ=-.可知：B 不对，3sin 263A π⎛⎫∴-=+ ⎪⎝⎭，0A >，解得163A =，函数16()sin()363f x x ππ=-，可知C 正确. ()14,17x ∈ 时，52,632x ππππ⎛⎫⎛⎫-∈⎪ ⎪⎝⎭⎝⎭，可得：函数()f x 在()14,17x ∈单调递增.综上可得：ACD 正确. 故选：ACD 【点睛】关键点点睛：本题的关键是表示点,,B C D 的坐标，并利用两点间距离表示等量关系后，求解各点的坐标，问题迎刃而解.8．已知函数()2sin (0)6f x x πωω⎛⎫=-> ⎪⎝⎭，则下列结论正确的是（ ） A ．函数()f x 的初相为6π- B ．若函数()f x 在,63ππ⎡⎤⎢⎥⎣⎦上单调递增，则(0,2]ω∈ C ．若函数()f x 关于点,02π⎛⎫⎪⎝⎭对称，则ω可以为12D ．将函数()f x 的图象向左平移一个单位得到的新函数是偶函数，则ω可以为2023 【答案】AB 【分析】根据选项条件一一判断即可得结果. 【详解】A 选项：函数()2sin (0)6f x x πωω⎛⎫=-> ⎪⎝⎭的初相为6π-，正确； B 选项：若函数()f x 在,63ππ⎡⎤⎢⎥⎣⎦上单调递增，则2266k ππωππ-+≤-，2362k πωπππ-≤+，k Z ∈，所以21226k k ω-+≤≤+，k Z ∈，又因为0ω<，则02ω<≤，正确；C 选项：若函数()f x 关于点,02π⎛⎫⎪⎝⎭对称，则,26k k Z πωππ-=∈，所以12,3k k Z ω=+∈故ω不可以为12，错误； D 选项：将函数()f x 的图象向左平移一个单位得到()12sin 6f x x πωω⎛⎫+=+- ⎪⎝⎭是偶函数，则,62k k Z ππωπ-=+∈，所以2,3k k Z πωπ=+∈故ω不是整数，则ω不可以为2023，错误； 故选：AB【点睛】掌握三角函数图象与性质是解题的关键.二、数列多选题9．已知数列{}n a 的前n 项和为n S ，11a =，()1*11,221,21n n n a n ka k N a n k --+=⎧=∈⎨+=+⎩.则下列选项正确的为（ ） A ．614a =B ．数列{}()*213k a k N-+∈是以2为公比的等比数列C ．对于任意的*k N ∈，1223k k a +=-D ．1000n S >的最小正整数n 的值为15 【答案】ABD 【分析】根据题设的递推关系可得2212121,21k k k k a a a a -+=-=-，从而可得22222k k a a +-=，由此可得{}2k a 的通项和{}21k a -的通项，从而可逐项判断正误.【详解】由题设可得2212121,21k k k k a a a a -+=-=-， 因为11a =，211a a -=，故2112a a =+=，所以22212121,12k k k k a a a a +++--==，所以22222k k a a +-=， 所以()222222k k a a ++=+，因为2240a +=≠，故220k a +≠，所以222222k k a a ++=+，所以{}22k a +为等比数列， 所以12242k k a -+=⨯即1222k k a +=-，故416214a =-=，故A 对，C 错. 又112122123k k k a ++-=--=-，故12132k k a +-+=，所以2121323k k a a +-+=+，即{}()*213k a k N -+∈是以2为公比的等比数列，故B 正确.()()141214117711S a a a a a a a =+++=++++++()()2381357911132722323237981a a a a a a a =+++++++=⨯-+-++-+=，15141598150914901000S S a =+=+=>，故1000n S >的最小正整数n 的值为15，故D 正确. 故选：ABD. 【点睛】方法点睛：题设中给出的是混合递推关系，因此需要考虑奇数项的递推关系和偶数项的递推关系，另外讨论D 是否成立时注意先考虑14S 的值.10．（多选）设数列{}n a 是等差数列，公差为d ，n S 是其前n 项和，10a >且69S S =，则（ ）A ．0d >B ．80a =C ．7S 或8S 为n S 的最大值D ．56S S > 【答案】BC【分析】根据69S S =得到80a =，再根据10a >得到0d <，可得数列{}n a 是单调递减的等差数列，所以7S 或8S 为n S 的最大值，根据6560S S a -=>得65S S >，故BC 正确.【详解】由69S S =得，960S S -=，即7890a a a ++=，又7982a a a +=， 830a ∴=，80a ∴=，∴B 正确； 由8170a a d =+=，得17a d =-，又10a >，0d ∴<， ∴数列{}n a 是单调递减的等差数列， ()()0,70,9n n a n N n a n N n **⎧>∈≤⎪∴⎨<∈≥⎪⎩， 7S ∴或8S 为n S 的最大值，∴A 错误，C 正确； 6560S S a -=>，65S S ∴>，所以D 错误. 故选：BC ．【点睛】关键点点睛：根据等差中项推出80a =，进而推出0d <是解题关键.。

第26章 二次函数第七课时 求二次函数的函数关系式①一、教学目标知识与技能：使学生掌握用待定系数法由已知图象上一个点的坐标求二次函数y ＝ax 2的关系式。

过程与方法：使学生掌握用待定系数法由已知图象上三个点的坐标求二次函数的关系式。

情感态度与价值观：让学生体验二次函数的函数关系式的应用，提高学生用数学意识。

二、重点：已知二次函数图象上一个点的坐标或三个点的坐标，分别求二次函数y ＝ax 2、y ＝ax 2＋bx ＋c 的关系式 三、难点：已知图象上三个点坐标求二次函数的关系式是教学的难点。

四、教具准备：投影仪、幻灯片、课外资料。

五、教学过程：一、创设问题情境如图，某建筑的屋顶设计成横截面为抛物线型(曲线AOB)的薄壳屋顶。

它的拱高AB 为4m ，拱高CO 为0.8m 。

施工前要先制造建筑模板，怎样画出模板的轮廓线呢?分析：为了画出符合要求的模板，通常要先建立适当的直角坐标系，再写出函数关系式，然后根据这个关系式进行计算，放样画图。

如图所示，以AB 的垂直平分线为y 轴，以过点O 的y 轴的垂线为x 轴，建立直角坐标系。

这时，屋顶的横截面所成抛物线的顶点在原点，对称轴是y 轴，开口向下，所以可设它的函数关系式为：y ＝ax 2 (a ＜0) (1)因为y 轴垂直平分AB ，并交AB 于点C ，所以CB ＝AB 2＝2(cm)，又CO ＝0.8m ，所以点B 的坐标为(2，－0.8)。

因为点B 在抛物线上，将它的坐标代人(1)，得－0.8＝a×22所以a ＝－0.2因此，所求函数关系式是y ＝－0.2x 2。

请同学们根据这个函数关系式，画出模板的轮廓线。

二、引申拓展问题1：能不能以A 点为原点，AB 所在直线为x 轴，过点A 的x 轴的垂线为y 轴，建立直角坐标系?问题2，若以A 点为原点，AB 所在直线为x 轴，过点A 的x 轴的垂直为y 轴，建立直角坐标系，你能求出其函数关系式吗?问题3：请同学们根据这个函数关系式，画出模板的轮廓线，其图象是否与前面所画图象相同?问题4：比较两种建立直角坐标系的方式，你认为哪种建立直角坐标系方式能使解决问题来得更简便?为什么?请同学们阅渎P20例7。

高考常考的函数定义域的题型总结高考常考的求函数定义域的题型主要有两种：求具体函数（函数解析式已知）的定义域和求抽象函数（函数解析式未知）的定义域.每种形式都有各自的特点和求解规律，而且常以复合函数的形式出现，并和解不等式题型有着紧密的联系.求具体函数的定义域一般较容易，掌握方法后小心计算即可；而求抽象函数的定义域则相对容易出错，需要熟练把握这类题型求解的方法技巧，加强练习.学习本专题必备知识点总结：1. 求具体函数定义域时，要知道：（1）分母不等于0；（2）偶次方根内不小于0，奇次方根内可为一切实数；（3）对数的真数大于0；(4) 函数}{.0|0≠=x x x y 的定义域是2. 当所求函数是由几部分构成的复合函数时，要列出保证每一部分都有意义的不等式，然后解不等式组，不等式组的解集即是该具体函数的定义域. 当函数与实际问题联系在一起时，还要保证实际问题有意义.3. 要熟练掌握专题一中的各种基本不等式以及与之相关的不等式组的解法.4. 抽象函数的定义域求解要切实把握两点：（1）求函数的定义域是求函数表达式中x 的范围；（2）在一个题目里，函数)(f y =括号内的式子的范围一样.一、关于具体函数定义域的题型求具体函数定义域的题型要把握三个常考的原则：（1）分母不等于0；（2）偶次方根内不小于0，奇次方根内可为一切实数；（3）对数的真数大于0.但是我们还要注意一种容易出错的函数的定义域：函数}{.0|0≠=x x x y 的定义域是当然一元一（二）次不等式（组）、指（对）数不等式、三角函数不等式等的解法需要熟练掌握.例1. 求下列函数的定义域：(5) 在ABC △中，已知内角A π=3，边3BC =B x =，周长为y ． 求函数()y f x =的解析式和定义域.解析：例1中的五个题目，基本上把高考常考的求具体函数定义域的形式都包括在内了.既有解一元一次不等式、一元二次不等式，也有解指数、对数、三角函数不等式以及和实际问题联系在一起的求定义域. 我们要在熟练掌握这些不等式的基本解法的基础上，切实把握求具体函数定义域的一些原则.(1) 由偶次方根内不小于0和分母不等于0的原则，知{}为该函数的定义域；实数的原则，知和奇次方根内可为一切域为、正（余）函数的定义、分母不等于、偶次方根内不小于根据对数的真数大于010|01000lg 1000)3(<<⇒⎩⎨⎧><⇒⎩⎨⎧>>-x x x x x x R }.,26526|21sin ,01sin 20)4(为所求函数的定义域的原则，知、正弦函数的定义域为根据偶次方根内不小于Z k k x k x x x R ∈+≤≤+⎩⎨⎧⇒≥⇒≥-ππππ （5）ABC △的内角和A B C ++=π，由00A B C π=>>3，，得20B π<<3．由正弦定理，知 因为y AB BC AC =++，所以224sin 4sin 230.3y x x x ππ⎛⎫⎛⎫=+-+<< ⎪ ⎪3⎝⎭⎝⎭ 总结：求解这类具体函数的定义域时，要求我们牢记一些常用的原则：（1）分母不等于0；（2）偶次方根内不小于0，奇次方根内可为一切实数；（3）对数的真数大于0以及一个容易出错的函数的定义域：}{.0|0≠=x x x y 的定义域是（4）实际问题求定义域时要符合实际意义.练习1.求下列函数的定义域：参考答案：（1）{}}{.)3(;84|)2(;73|R x x x x x ∈<≤<≤二、关于抽象函数定义域的题型求抽象函数的定义域是一种比较容易出错的、而且大部分同学感到有些难度的题，这类题除了需要解不等式的知识外，还要牢记求抽象函数定义域的两个原则. 高考中曾经多次考过这类题，并且有不少考生答错了，因此我们要加强这种类型定义域的求解练习，切实掌握它的解题规律.例2. 求下列函数的定义域：解析：（1）是已知的定义域的定义域，要求函数基本函数)2()(2-==x f y x f y ，即括号内是其他函数形式的定义域, 此题为一元二次函数的形式；而题（2）相反. 题（3）已知函数和所求函数的括号内都为其他函数.上述三题代表了求抽象函数定义域的常见形式.(1) 由条件知，;21,122212≤≤-≤≤-⇒≤-≤-x x x 或}{.010010|)(lg .100010],31lg )(lg ].3,1(12],1,0()12()3();1,0()().1,0(cos 20)(cos )2(≤<=≤<⇒∈=∈+∴∈+=∈=∈∴∈=x x x f y x x x f y x x x f y x x f y x x x f y 的定义域为所以函数，（中从而得函数的定义域，即的定义域为从而也就是），，（的定义域，即 π总结：由上面的求解过程我们可以总结出解这类题的技巧、规律，即抽象函数的定义域 求解要切实把握两点：（1）求函数的定义域是求函数表达式中x 的范围；（2）在一个题目里 函数)(f y =括号内的式子的范围一样.练习2. 求下列函数的定义域：参考答案：本专题典型的求函数定义域的高考真题汇总及解析较容易的基础题：1．函数(1)y x x x =- ）A ．{}|0x x ≥B ．{}|1x x ≥C ．{}{}|10x x ≥D ．{}|01x x ≤≤ 2．函数1y x x =- ( ) A ．{|1}x x ≤ B ．{|0}x x ≥C ．{|10}x x x ≥≤或D ．{|01}x x ≤≤ 3．函数)1(log 221-=x y 的定义域为 （ ）A ．]2,1()1,2[⋃--B ．)2,1()1,2( --C ．[)(]2,11,2 --D ．)2,1()1,2( -- 4. 函数1()12f x x x=+-的定义域为 . 5. 函数)1(log 21-=x y 的定义域是 .6. .,)2lg()1lg()23lg(2的关系，求的定义域为，的定义域为函数G F G x x y F x x y -+-=+-=7. 已知.)1(,2sin )(tan 的值求-=f x x f8. 求下列函数的定义域：（1）;3)2(;log 323-==x y x y ).lg(cos )3(x y =中等难度的提高题：1. .25sin 2的定义域求函数x x y -+=2. 记函数f (x )=132++-x x 的定义域为A, g(x )=lg [(x －a －1)(2a －x )](a <1) 的定义域为B.求集合A 和B.4. 设锐角三角形ABC 的内角A B C ，，的对边分别为a b c ，，，2sin a b A =．求B 的大小和A 的取值范围.较容易的基础题的参考答案：1. C2. D3. A4. [－1, 2)∪(2, +∞)5. }21|{≤<x x6. }{1|)1(.81.7≥-⊆x x F G ⎩⎨⎧⎭⎬⎫≥23|)2(x x .,2222|)3(⎩⎨⎧⎭⎬⎫∈+<<+-Z k k x k x ππππ 第1题解析：..0,1.0,0)1(0C x x x x x 选或且，所以不小于因为偶次方根内的式子∴=≥⇒≥≥- 第3题解析：.110.002A x 选，且对数的真数大于于偶次方根内的式子不小∴≤-<∴ 第4题解析：..02,01.00即得答案，且分母不等于于偶次方根内的式子不小≠-≥+∴x x 第6题解析：}}{{.2|,1,2|0F G x x G x x x F ⊆∴>=<>=∴或，对数的真数大于第7题解析：.2sin .,4,1tan 即得答案代入即令括号内的式子一样，x Z k k x x ∈+-=⇒-=ππ 第8题解析：;23032)2(;10,0log )1(3≥∴≥-≥∴>≥x x x x x 且 中等难度题的参考答案：1. ];,0[],5[ππ⋃--∈x2. A=(－∞,－1)∪[1,+ ∞]，B=(2a ,a +1)；第1题解析：第2题解析：见专题三例2（4）解析.第3题解析：第4题解析：由2sin a b A =，根据正弦定理得sin 2sin sin A B A =，所以1sin 2B =， 由ABC △为锐角三角形得π6B =. 所以23ππ<<A .。

第五讲：函数第一部分概述
函数是自主招生的一个非常重要内容！
⏹就近几年来，本人作了一个统计，复旦和交大自主招生中有关函数的内容
大约占20%—30%。

⏹其中，热点问题是：方程的根的问题、函数的最值问题（
值域）、函数的性质（如周期、有界性等）、函数的迭代、
简单的函数方程、方程的不动点问题、函数的图像及解析式等。

而其中特别提醒同学们注意的是，方程的根的问题是考得最多的一个问题。

第二部分：知识补充：
函数零点的定义：
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点。

结论：
如果函数y=f(x)在区间[a,b]上的图象是连续
不断的一条曲线，并且有f(a)·f(b)<0，那么，函
数y=f(x)在区间(a,b) 内有零点，即存在c∈(a,b)，使得f(c)=0，这个c也就是方程f(x)=0的根。

函数y=f(x)零点的判断方法：
1、方程法：解方程f(x)=0，得函数y=f(x)的零点。

2、图象法：画出函数y=f(x)的图象，其图象与x轴交点的横坐标就是y=f(x)的零点。

3、定理法：函数在区间[a,b]上图象是一条连续不断的曲线，并且有f(a) ·f(b)<0。

例1：若函数f(x)=x2+(k-2)x+2k-1的两个零点中，一个在0和1之间，另一个在1和2之间，求k的取值范围。

三次方程的韦达定理
第三部分：真题精析1、方程根的问题。

华师大版七年级数学上册函数证明专题引言本文档将详细讨论华师大版七年级数学上册中关于函数证明的专题。

我们将重点介绍函数的定义、性质以及相关证明方法，帮助同学们更好地理解和掌握这一重要概念。

函数的定义函数是一种特殊的关系，它将一个集合中的每个元素映射到另一个集合中的唯一元素。

在数学中，我们通常用符号$f(x)$表示函数，其中$x$是定义域中的元素，$f(x)$是值域中的元素。

函数的定义包括定义域、值域以及映射规则。

函数的性质函数具有多个重要的性质，下面我们将介绍其中的几个：1. 单射性：如果对于不同的$x_1$和$x_2$，$f(x_1) \neq f(x_2)$，则函数是单射的。

也就是说，不同的定义域元素映射到不同的值域元素。

单射性：如果对于不同的$x_1$和$x_2$，$f(x_1) \neq f(x_2)$，则函数是单射的。

也就是说，不同的定义域元素映射到不同的值域元素。

2. 满射性：如果对于任意的$y$，存在$x$使得$f(x) = y$，则函数是满射的。

也就是说，函数的值域覆盖了整个值域集合。

满射性：如果对于任意的$y$，存在$x$使得$f(x) = y$，则函数是满射的。

也就是说，函数的值域覆盖了整个值域集合。

3. 双射性：如果函数既是单射的又是满射的，则函数是双射的。

双射性：如果函数既是单射的又是满射的，则函数是双射的。

4. 奇偶性：如果对于任意的$x$，有$f(-x) = f(x)$，则函数是偶函数；如果对于任意的$x$，有$f(-x) = -f(x)$，则函数是奇函数。

奇偶性：如果对于任意的$x$，有$f(-x) = f(x)$，则函数是偶函数；如果对于任意的$x$，有$f(-x) = -f(x)$，则函数是奇函数。

函数证明的方法在进行函数证明时，通常可以使用以下几种方法：1. 直接证明法：通过列举定义或使用已知的数学结论，直接证明待证函数的性质成立。

直接证明法：通过列举定义或使用已知的数学结论，直接证明待证函数的性质成立。