非正态数据转化成正态数据

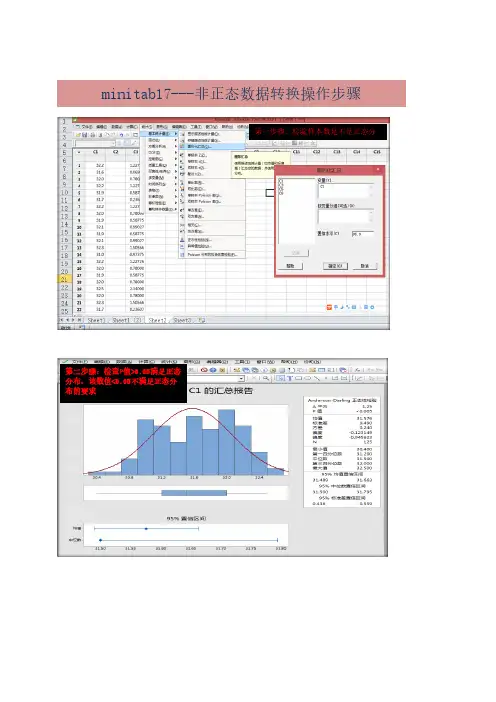
minitab17---非正态数据转换操作步骤
第一步骤：检验样本数是不是正态分
第二步骤：检查P值>0.05满足正态
分布，该数值<0.05不满足正态分
布的要求
第三步骤：个体分布标识确认拟合方式
第四步骤：在会话窗口中查看“拟合优度检验”确认P值，数据越大，说明拟合度就越好，选择
选择数据转第五步骤：使用johnson
变换对非正态数据进行拟合正太分布。

第六步骤：在会话窗口中
复制描述性统计量中的
johnson 函数公式
第七步骤：选择任意单元格，单击鼠右键选择公式，对列设定公式，将复制的描述性统计量中的johnson函数公式炊事员粘贴在“表达式栏内”。

将2处X改写成C5（C5原始的上限规格值，也可以是会话栏中最大值数据。

第八步骤：对拟合后的数据进行正态分布计
第九步骤：将拟后转化的数输入能力分
输入子组数
完成。

关于正态数据与非正态数据及其过程能力计算摘要本文从企业生产现场的实际情况出发，提出数据呈正态或非正态分布时，如何对这些数据进行分析，并准确计算过程能力，将在本文进行讨论。

关键词正态；非正态数据；过程能力1 对数据的管控误区目前企业在流程中对所收集数据的统计、分析以及使用情况，较以前来说，规范性有了长足的进步，但与要求还是存在一定差距，可以通过以下几个方面来说明：1.1 数据来源可评价性差要想弄清楚一件事情，必须要获得现场数据，通过数据还原事实。

但现场数据并非是现存的，要经过人们的有效收集、传递，然后才有数据可以分析。

在此需要强调的是原始记录一定要整洁、规范，只有数据完整，后续才能进行推断性分析，但现实是部分数据在源头上就存在偏差。

这给后续的评价在客观上就带来极大影响。

因此，对数据进行策划和管理时务必确保数据来源的可靠。

1.2 异常数据混在正常数据中通常大家有这样的习惯，在对现场调查时，会对数据进行直接收集，完毕后，会对数据直接使用，所以在此就会存在一个误区，我们分析的数据能代表过程的正常情况吗？当你所收集的数据不能代表这个过程，也就是说数据来源于异常原因而非普通原因时，那所收集的数据就不能代表这个过程的正常情况，所以一定要将异常情况排除后，留下普通原因所引起的质量数据，这样就可以进行分析了。

我们可以通过箱线图进行数据的初步分析，如果数据跑到箱线图的两个尾巴之外的话，说明这样的数据属于异常数据，这样的数据要进行过程改善并予以剔除。

1.3 过程数据的‘伪’正态性在进行过程能力计算前，必须要看数据的分布情况是否符合正态。

在验证数据的时候，我们要关注子组容量的大小，因为子组容量的大小对我们数据的正态性研究也有一定的影响，我们可以通过模拟的125个数据来进行分析。

对于同样的125个数据，当子组容量分别为1和5时，我们可以看到数据正态性的表现情况。

当子组为1时，该125个数据的p值是小于0.05的，是呈非正态分布的。

六西格玛黑带模拟测试题及答案(一)单选题（共84题，每题1分）1、题目：2、题目：某制造企业需求一零件，规格要求为100±3cm，在选择供应商时发现：供应商A提供的零件近似服从正态分布N（100,1），供应商B提供的零件近似服从均匀分布U（97,103）；供应商A、B提供产品的价格相同，同时，该企业非常关注质量损失。

以下哪种说法是正确的？A.从理论上讲，A零件的合格率是99.73%，供应商B提供100%合格品，因此应选择B作为供应商B.从供应商提供产品的分布看，均值相同，选择供应商A或B一样C.A质量损失更低一些，应选择A作为供应商D.根据上述信息无法做出判断3、题目：某轴类加工过程中已知对直径的公差要求为10±0.02mm，假设直径服从正态分布，对该过程进行过程能力分析发现Cp=1.0，Cpk=Cpu=0.8，因此可以判断，该过程分布中心是：A.10.001mmB.10.002mmC.10.004mmD.10.006mm4、题目：黑带小金研究的课题是关于绝缘浇铸件的表面质量问题，在收集数据进行分析之前对现有的测量系统进行分析，以确认测量系统是否可以信赖。

为此，小金设计了MSA方案：取两名测量员，30个被测工件，每人对每个铸件重复测量两次，测量方法是在强光的照射下，目测是否有划痕、磕碰等，判断结果为合格与不合格。

请问在抽取被测工件时按以下哪种方案最为合适？A.用简单随机抽样的方法，从实际生产中随机选取30个样本B.按照日常生产的产品的实际合格率分别抽取合格品和不合格品选取30个样本C.尽可能按照1:1的比例抽取总数为30的合格品和不合格品，不合格品尽可能包括日常出现的缺陷类别D.从最近一个月生产的产品中连续抽取30个样本5、题目：选择项目CTQ（critical to quality）是一项重要的工作，关于如何选择CTQ，下列描述不正确的是：A.CTQ一定是计量型数据B.CTQ一定与顾客需求或企业关键业务指标相关C.当CTQ本身不可测或很难测量时，可以采用待用测量指标D.当CTQ数量较多时，可以采用排列图或质量成本分析确定最重要的CTQ6、题目：冷轧厂的原料是热轧卷，热轧卷用汽车从热轧卷车间运输到冷轧厂，如果对该流程进行增殖性分析，试问，汽车运输热轧卷的过程是否为顾客增值过程？A.增值活动，因为运输本身创造价值B.增值活动，因为运输是必不可少的过程C.非增值活动，应该尽量缩短或消除D.无法确定7、题目：某项目团队在测量阶段要测量其项目指标“温度”的过程能力，收集温度数据时每半小时测量一次，每次测得1个数据，共收集30个数据，过程稳定且数据服从正态分布，采用MINITAB计算得出，Cp=1.3，Pp=0.4，根据这一结果，下列哪个推断可能是正确的？A.过程独立性有问题存在，过程数据存在自相关性B.过程分布中心和公差中心存在较大偏移C.Pp数据不可行，Cp数据是可信的D.以上判断都不对8、题目：对同一个测量对象重复进行测量，不同测量者进行测量时测量结果的差异一般被称为：A.测量系统的稳定B.测量系统的重复性C.测量系统的再现性D.测量系统的线性9、题目：测量产品的特性指标时，不同的产品读数会有差异，造成此差异的原因是：A.产品间真实的差异B.由所使用量具造成的测量系统误差C.测量人员的水平不同D.产品间真实的差异与由所使用量具造成的测量系统误差的综合影响10、题目：实施六西格玛管理最重要的目的在于：A.培养一批黑带，使他们成为统计学专家B.使企业的所有绩效指标都达到六西格玛质量水平C.建立超越ISO9000的质量管理体系D.变革企业文化，成为持续改进的组织11、题目：12、题目：某黑带项目团队在测量阶段计算计量型数据的过程能力指数时，发现数据是非正态数据，而且过程本身稳定，无异常值。

在精益六西格玛持续改进、统计质量管理和SPC中，评价过程的过程能力（Process Capability）都是必不可少的重要步骤。

在用控制图确认过程处于统计受控状态之后，进行过程能力分析可以进一步判断过程能力是否达到客户的要求。

过程能力分析也是六西格玛项目中评价过程基线和改进方向的重要手段。

对计量型的过程数据而言，如果数据服从正态分布，我们可以很方便地计算出相应的过程能力指数Cp，Cpk等。

但当数据呈现非正态分布状态时，如果直接按普通的计算过程能力的方法处理就会存在较大的风险。

一般而言，对此类数据计算过程能力的方法主要有如下几类：第一类方法是将非正态数据转换成正态数据进行计算，常用的转换方式包括我们在Minitab软件中经常用到的Box-Cox转换和Johnson转换等；第二类方法是拟合数据的实际分布，然后根据实际的分布估算其均值、标准差等，进而计算过程能力指数（比如在Minitab和JMP中，我们都可以比较方便地拟合所有连续分布）；第三类方法以非参数统计方法为基础，基于百分位数方法来计算过程能力。

下面分别进行简单说明：方法1：Box-Cox变换法的步骤1.估计合适的Lambda（λ）值；2.计算出变换后的数据Y x，3.根据原数据的USL和LSL，计算求出变换后的USL x和LSL x，4.对Y x用USL x和LSL x计算过程能力指数。

方法2：Johnson变换法的步骤1.根据Johnson判别原则确定转换方式；2.计算出变换后的数据Y x，3.根据原数据的USL和LSL，计算出变换后的USL x和LSL x，4.对Y x用USL x和LSL x计算过程能力指数。

关于上述两种方法的一个重要的问题是，并不是所有的非正态数据都能经过转换得到相应的服从正态分布的数据。

当出现这种情况时，准确的过程能力还是无法计算。

方法3：非参数计算法对于非正态数据，或者说上述两种方法中经过转换仍无法转换为正态分布的数据，我们可以使用这种方法计算过程能力指数，这时不需对原始数据做任何转换，可以直接使用以下公式计算过程能力指数Cp 和Cpk ：X X lower upper LSLUSL Cp --=⎪⎪⎪⎭⎫ ⎝⎛----=X u u u X u lower upper USL USL Min Cpk ****,其中，X upper 和X lower 是随机数据X 的百分位数，通常取X upper 为X 99.865%，取X lower 为X 0.135%，对应于正态分布时覆盖99.73%的数据范围（±3σ）；也可取X upper 为X 99.5%，取X lower 为X 0.5%。

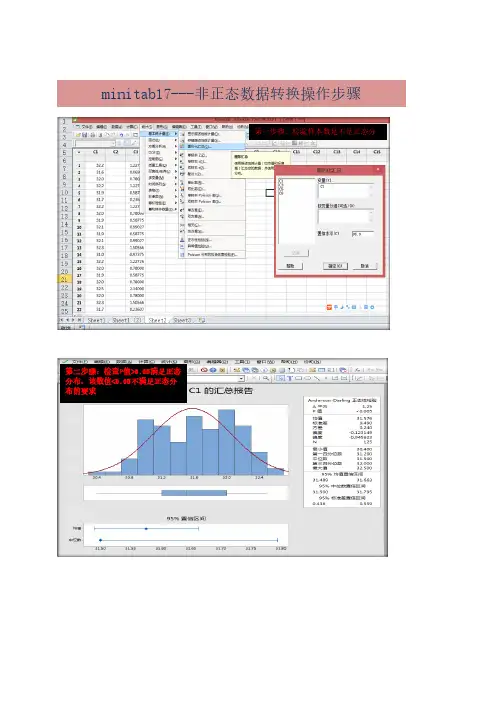
minitab17---非正态数据转换操作步骤
第一步骤：检验样本数是不是正态分
第二步骤：检查P值>0.05满足正态
分布，该数值<0.05不满足正态分
布的要求
第三步骤：个体分布标识确认拟合方式
第四步骤：在会话窗口中查看“拟合优度检验”确认P值，数据越大，说明拟合度就越好，选择
选择数据转第五步骤：使用johnson
变换对非正态数据进行拟合正太分布。

第六步骤：在会话窗口中
复制描述性统计量中的
johnson 函数公式
第七步骤：选择任意单元格，单击鼠右键选择公式，对列设定公式，将复制的描述性统计量中的johnson函数公式炊事员粘贴在“表达式栏内”。

将2处X改写成C5（C5原始的上限规格值，也可以是会话栏中最大值数据。

第八步骤：对拟合后的数据进行正态分布计
第九步骤：将拟后转化的数输入能力分
输入子组数
完成。

如何化标准正态分布标准正态分布是统计学中非常重要的概念，它在各个领域都有着广泛的应用。

在实际应用中，我们经常需要将非正态分布的数据转化为标准正态分布，以便进行统计分析和推断。

本文将介绍如何将非标准正态分布转化为标准正态分布的方法和步骤。

首先，我们需要了解标准正态分布的概念。

标准正态分布是一种均值为0，标准差为1的正态分布。

其概率密度函数可以用数学公式表示为：\[ f(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} \]其中，\( \pi \) 是圆周率，\( e \) 是自然对数的底数。

标准正态分布的特点是钟型曲线，且均值为0，标准差为1。

接下来，我们将介绍如何将非标准正态分布转化为标准正态分布。

假设我们有一个非正态分布的随机变量X，其均值为\( \mu \)，标准差为\( \sigma \)。

我们可以使用以下公式将X转化为标准正态分布的随机变量Z：\[ Z = \frac{X \mu}{\sigma} \]通过这个公式，我们可以将X转化为标准正态分布的随机变量Z。

这样做的好处是，我们可以利用标准正态分布的性质进行统计分析，而不需要考虑原始数据的分布情况。

在实际操作中，我们可以按照以下步骤将非标准正态分布转化为标准正态分布：1. 计算原始数据的均值\( \mu \)和标准差\( \sigma \)；2. 使用上述公式，将原始数据转化为标准正态分布的数据；3. 对转化后的数据进行统计分析和推断。

需要注意的是，在转化数据时，我们要确保原始数据的分布是近似正态分布的。

否则，转化后得到的标准正态分布数据可能无法准确反映原始数据的特征。

除了上述方法外，我们还可以使用统计软件进行标准正态分布的转化。

常见的统计软件如SPSS、R、Python等都提供了相关的函数和工具，可以方便地进行数据转化和分析。

总之，标准正态分布在统计学中具有重要的意义，我们可以通过一定的方法将非标准正态分布的数据转化为标准正态分布，以便进行统计分析和推断。

把数据转化为正态的方法
数据的正态分布是统计分析中常用的一种分布形态，可以帮助我们更准确地描述和分析数据。

然而，很多实际数据并不符合正态分布，需要进行转化。

下面介绍几种常见的数据转化方法：
1. 对数转换：对数转换是将原始数据取对数，以降低数据的变异性和偏斜度。

对于数据集中有很多较大值时效果较好。

2. 平方根转换：平方根转换是将原始数据开平方根，以减小数据的差异性和偏斜度。

通常适用于数据分布相对对称的情况。

3. Box-Cox转换：Box-Cox转换是一种常用的数据转换方法，可以将非正态分布的数据转换为正态分布。

该方法通过一个参数lambda 来确定转换程度，需要根据数据特征来选择lambda值。

4. Yeo-Johnson转换：Yeo-Johnson转换是一种基于Box-Cox转换的改进方法，可以处理负值和零值的数据。

该方法也需要根据数据特征来确定变换参数。

以上是常见的几种数据转化方法，需要根据实际数据情况选择合适的方法来实现数据正态化。

- 1 -。

非标准正态转换为标准正态在统计学中，正态分布是一种非常重要的概率分布，它具有许多良好的性质，因此在实际应用中被广泛使用。

然而，有时候我们遇到的数据并不符合标准正态分布，这时就需要对数据进行转换，使其符合标准正态分布的要求。

本文将介绍如何将非标准正态分布转换为标准正态分布的方法。

首先，我们需要了解什么是标准正态分布。

标准正态分布是均值为0，标准差为1的正态分布，其概率密度函数为：\[f(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\]接下来，我们来讨论如何将非标准正态分布转换为标准正态分布。

常见的方法包括Z分数标准化和Box-Cox变换。

Z分数标准化是一种简单而常用的方法，其思想是将原始数据减去均值，然后除以标准差，得到的新数据就符合标准正态分布。

具体而言，对于原始数据x，其Z分数标准化后的数值为：\[z = \frac{x \mu}{\sigma}\]其中，μ为原始数据的均值，σ为原始数据的标准差。

这样转换后的数据就符合标准正态分布了。

另一种常见的方法是Box-Cox变换，它是一种幂函数变换的方法，可以将非正态分布转换为正态分布。

Box-Cox变换的公式为：\[y(\lambda) = \begin{cases}。

\frac{y^\lambda 1}{\lambda}, & \text{if } \lambda \neq 0 \\。

\log(y), & \text{if } \lambda = 0。

\end{cases}\]其中，λ为变换参数，通过寻找最佳的λ值，可以将原始数据转换为符合正态分布的数据。

除了上述两种方法，还有一些其他的数据转换方法，比如对数变换、幂函数变换等，都可以用来将非标准正态分布转换为标准正态分布。

在实际应用中，我们需要根据数据的特点和要求选择合适的转换方法。

需要注意的是，数据转换只是一种手段，其目的是为了让数据更好地符合统计模型的要求，从而得到更准确的分析结果。

Minitab 操作1、柏拉图：找主要因子，大于或等于80%为主要因子。

路径：统计----质量工具----柏拉图（选已整理成表格的缺陷数据）2、正态分布：正态检验三种方法①概率图：图形---概率图（看P值，P大于0.05说明服从正态分布）;②图形化汇总: 统计---基本统计量----图形化汇总(看P值，P大于0.05说明服从正态分布）;③正态性检验: 统计---基本统计量----正态性检验3、产生随机数据：计算----随机数据（然后再选所需要产生何种数据）4、数据堆叠：数据---堆叠5、计算中行统计量、列统计量分别于计算所在行或列的均值、和、标准偏差等6、文本、数字转换：数据---更改数据类型7、概率计算：计算---概率分布----正态----累积概率8、分位数的计算：计算---概率分布----正态----逆累积概率9、稳定性：统计---控制图---单值的变量控制图----单值（单值控制图选项中S限制）10、测量系统分析①量具研究：统计—质量工具---量具研究---量具R&R研究(交叉)注:非破坏性测试用交叉,破坏性测试用嵌套.②属性一致性分析(合格与不合格)统计---质量工具---属性一致性分析③量具线性与偏倚研究:统计——质量工具——量具研究——量具线性与偏倚研究（看所有的P值，所有P值小于0.05时）11、非正态数据与正态数据转换①正态性检验，②如非正态，转换成正态分布：统计—控制图---BOX-COX12、过程能力分析统计---质量工具---能力分析13、置信区间的算法：①正态总体均值的置信区间（σ已知）用1Z单样本：统计—基本统计量—1Z单样本输入的标准差为已知的总体标准差；样本数量为所取的样本量；均值为样本的均值；请注意选取置信水平②正态总体均值的置信区间（σ未知）用1t单样本：统计—基本统计量—1t单样本请注意汇总数据中的样本数量为所取的样本量；均值为样本的均值；标准差为样本的标准差；请注意选取置信水平④比率P的置信区间用1P单样本：统计—基本统计量—1P单样本（试验数为样本量，事件数为要计算的概率的数）⑤正态总体方差和标准差的置信区间用单方差：统计—基本统计量—σ2单方差（请注意用汇总数据，及置信水平）14、假设检验第一步：首先建立原假设及备择假设；第二步：进行检验；①正态总体均值检验（σ已知）用1Z单样本：统计—基本统计量—1Z单样本输入的标准差为已知的总体标准差；样本数量为所取的样本量；均值为样本的均值；请注意选取置信水平及假设检验，并输入假设的均值及选取相应的备择假设。

不服从正太分布数据的转换
可以应用变量变换的方法,将不服从正态分布的资料转化为非正态分布或近似正态分布。

常用的变量变换方法有对数变换、平方根变换、倒数变换、平方根反正玄变换等，应根据资料性质选择适当的变量变换方法。

1、对数变换即将原始数据X的对数值作为新的分布数据：
X’=lgX
当原始数据中有小值及零时，亦可取X’=lg（X+1）
还可根据需要选用X’=lg（X+k）或X’=lg（k-X）
对数变换常用于（1）使服从对数正态分布的数据正态化。

如环境中某些污染物的分布，人体中某些微量元素的分布等，可用对数正态分布改善其正态性。

（2）使数据达到方差齐性，特别是各样本的标准差与均数成比例或变异系数CV接近于一个常数时。

2、平方根变换即将原始数据X的平方根作为新的分布数据。

X’=sqrt（X）
平方根变换常用于：1）使服从Poission分布的计数资料或轻度偏态资料正态化，可用平方根变换使其正态化。

2）当各样本的方差与均数呈正相关时，可使资料达到方差齐性。

3、倒数变换即将原始数据X的倒数作为新的分析数据。

X’=1/X
常用于资料两端波动较大的资料，可使极端值的影响减小。

4、平方根反正旋变换即将原始数据X的平方根反正玄值做为新的分析数据。

X’=sin-1sqrt（X）
常用于服从二项分布的率或百分比的资料。

一般认为等总体率较小如＜30%时或较大（如＞70%时），偏离正态较为明显，通过样本率的平方根反正玄变换，可使资料接近正态分布，达到方差齐性的要求。

你可以根据自己的资料适当转化。

另外，可以考虑其他分析方法，比如秩和检验。