第16章分式复习课件PPT

第十六章分式知识点和典型例习题第一讲 分式的运算【主要公式】1.同分母加减法则:()0b c b c a a a a ±±=≠2.异分母加减法则:()0,0b d bc da bc daa c a c ac ac ac ±±=±=≠≠; 3.分式的乘法与除法:b d bd ac ac ∙=,b c b d bda d a c ac ÷=∙= 4.同底数幂的加减运算法则:实际是合并同类项5.同底数幂的乘法与除法;a m ● a n =a m+n ; a m ÷ a n =a m －n6.积的乘方与幂的乘方:(ab)m = a m b n , (a m )n = a mn7.负指数幂: a -p =1pa a 0=18.乘法公式与因式分解:平方差与完全平方式 (a+b)(a-b)= a 2- b 2 ;(a ±b)2= a 2±2ab+b 2（一）、分式定义及有关题型题型一：考查分式的定义【例1】下列代数式中：y x yx y x y x ba b a y x x -++-+--1,,,21,22π，是分式的有： .题型二：考查分式有意义的条件【例2】当x 有何值时，下列分式有意义（1）44+-x x （2）232+x x（3）122-x （4）3||6--x x（5）xx 1-题型三：考查分式的值为0的条件【例3】当x 取何值时，下列分式的值为0.（1）31+-x x（2）42||2--x x （3）653222----x x x x题型四：考查分式的值为正、负的条件【例4】（1）当x 为何值时，分式x-84为正； （2）当x 为何值时，分式)1(35-+-x x 为负；（3）当x 为何值时，分式32+-x x 为非负数.（二）分式的基本性质及有关题型1．分式的基本性质：M B MA MB M A B A ÷÷=⨯⨯= 2．分式的变号法则：bab a b a b a =--=+--=-- 题型一：化分数系数、小数系数为整数系数【例1】不改变分式的值，把分子、分母的系数化为整数.（1）y x yx 41313221+- （2）ba ba +-04.003.02.0题型二：分数的系数变号【例2】不改变分式的值，把下列分式的分子、分母的首项的符号变为正号.（1）y x yx --+- （2）b a a --- （3）b a ---题型三：化简求值题【例3】已知：511=+y x ，求yxy x yxy x +++-2232的值.提示：整体代入，①xy y x 3=+，②转化出yx 11+. 【例4】已知：21=-x x ，求221xx +的值. 【例5】若0)32(|1|2=-++-x y x ，求yx 241-的值.（三）分式的运算1．确定最简公分母的方法： ①最简公分母的系数，取各分母系数的最小公倍数； ②最简公分母的字母因式取各分母所有字母的最高次幂. 2．确定最大公因式的方法：①最大公因式的系数取分子、分母系数的最大公约数；②取分子、分母相同的字母因式的最低次幂. 题型一：通分【例1】将下列各式分别通分. （1）cb ac a b ab c 225,3,2--； （2）a b b b a a 22,--；（3）22,21,1222--+--x x x x xx x ； （4）aa -+21,2题型二：约分【例2】约分： （1）322016xy y x -； （2）n m m n --22； （3）6222---+x x x x .题型三：分式的混合运算【例3】计算：（1）42232)()()(abc ab c c b a ÷-⋅-；（2）22233)()()3(xy x y y x y x a +-÷-⋅+；（3）112---a a a（4）mn mn m n m n n m ---+-+22；（5） 2121111x x x ++++- （6）)12()21444(222+-⋅--+--x x x x x x x（四）、整数指数幂与科学记数法题型一：运用整数指数幂计算【例1】计算：（1）3132)()(---⋅bc a（2）2322123)5()3(z xy z y x ---⋅（3）24253])()()()([b a b a b a b a +--+--（4）6223)(])()[(--+⋅-⋅+y x y x y x题型二：科学记数法的计算【例3】计算：（1）223)102.8()103(--⨯⨯⨯；（2）3223)102()104(--⨯÷⨯.第二讲 分式方程（一）分式方程题型分析题型一：用常规方法解分式方程【例1】解下列分式方程 （1）x x 311=-；（2）0132=--x x ；（3）114112=---+x x x ；提示易出错的几个问题：①分子不添括号；②漏乘整数项；③约去相同因式至使漏根；④忘记验根.题型二：求待定字母的值【例4】若关于x 的分式方程3132--=-x mx 有增根，求m 的值.【例5】若分式方程122-=-+x ax 的解是正数，求a 的取值范围. 提示：032>-=ax 且2≠x ，2<∴a 且4-≠a .（三）分式方程求待定字母值的方法例1．若分式方程xmx x -=--221无解，求m 的值。

章复习第16章分式一、分式1、分式的概念一般地，如果A、B表示两个____，并且B中含有____，那么式子____叫做分式．其中A 叫做分子，B叫做分母．注意：分式的分母B不能为____．2、分式有意义、无意义、等于零的条件⑴分式有意义的条件：⑵分式无意义的条件：⑶分式的值等于零的条件：注：①分式的值为正的条件：A的值大于零，反之也成立．若________或________则分式B②分式的值为负的条件：A的值小于零，反之也成立．若________或________则分式B3、分式的基本性质分式的分子与分母都即:4、分式的通分、约分⑴分式的通分利用分式的基本性质，使分子和分母同乘适当的整式，不改变分式的____，把几个分式化成________的分式，这样的分式变形叫做分式的通分．注：分式通分的关键是确定几个分式的________，而最简公分母是指各分母中所有同底数幂因式的最高次幂的积．⑵分式的约分利用分式的基本性质，约去分式的分子和分母的________，这样的分式变形叫做分式的约分．注：分式约分的关键是找出分子与分母的________，当分子、分母是多项式时，要先把分子、分母因式分解，然后约去分子与分母的公因式．二、分式的运算1、分式的乘除⑴分式的乘法法则分式乘分式，________________________________________________________．即：⑵分式的除法法则分式除以分式，________________________________________________________．即：注：运算的结果，若能约分应约分.⑶分式的乘方．分式乘方， ________________________________________________________．即：2、分式的加减分式的加减法则：①同分母分式相加减，_________________________________． ②异分母分式相加减，_________________________________．以上法则用式子表示为：_________________________________________________．3、零指数幂与负整数指数幂⑴零指数幂a =____． 注：①01(0)m m m m a a a a a -÷====/；②00无意义．⑵数学中规定，一般地，当n 是正整数时，n a -=________，这就是说，)0(=/-a a n 是n a的倒数．注：①n a -不能理解为－n 个a 相乘，它是一种规定；②负整数指数幂的底数不能为零；③幂的四条运算法则对负整数指数幂仍然适用．4、用科学记数法表示小于1的正数小于1的正数可以用科学记数法表示为________的形式，其中a 是整数数位只有一位的正数，n 是正整数．注：n a -⨯10中的n 等于小数点向右移动的位数，如=00015.0________．三、分式方程1、分式方程的概念________________的方程叫做分式方程．注：分式方程的重要特征：①含分母；②分母里含未知数．2、分式方程的解法解分式方程的基本思路是将分式方程化为____方程，具体做法是________，即方程两边同乘________，这也是解分式方程的一般思路和做法．解分式方程的一般步骤：①去分母，将分式方程化为整式方程；②解这个整式方程；③验根：把整式方程的根代入最简公分母，如果最简公分母的值不为O ，则整式方程的解是原分式方程的解，否则，这个解不是原分式方程的解，即增根．注：①一般地，解分式方程时，去分母后所得整式方程的解有可能使原方程中分母为0，这就是增根产生的原因．因此解分式方程验根是很重要的，必须进行．②去分母时，方程中的有些项易漏乘，如x x =-11去分母得1-x =x ，右边应为x 2，漏乘了x ．3、分式方程的应用分式方程的应用主要就是列方程解应用题，它与列一元一次方程解应用题的基本思路和方法是一样的，不同的是表示数与数的相等关系时，不再受整式的限制．注：列分式方程解应用题，最后要检验，既要检验是否为所列分式方程的解，又要检验是否符合题意．四、典型例题 先化简，再求值：÷--1222x x x )1121(+---x x x ，其中21=x ．。

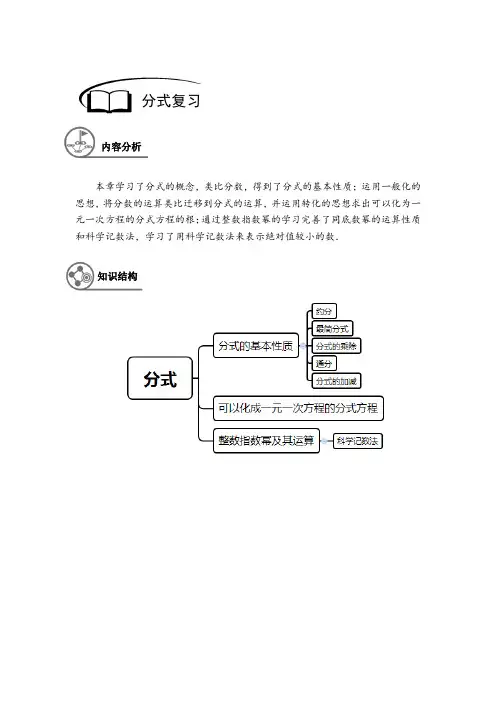
本章学习了分式的概念，类比分数，得到了分式的基本性质；运用一般化的思想，将分数的运算类比迁移到分式的运算，并运用转化的思想求出可以化为一元一次方程的分式方程的根；通过整数指数幂的学习完善了同底数幂的运算性质和科学记数法，学习了用科学记数法来表示绝对值较小的数．分式复习内容分析知识结构【例1】下列判断中，正确的是（）．A．分式的分子中一定含有分母B．当0B=时，分式AB无意义C．当0A=时，分式AB的值为0（A B、无意义）D．分数一定是分式【难度】★【答案】B【解析】分式中分母必须含有字母，分子可以是常数；当分式值为零时，分子为零，同时分母不为零．【总结】考查分式的基本概念及分式有无意义的条件、分式值为0的条件．【例2】若分式36a ba b-+的值为零，则a和b的关系是_________．【难度】★【答案】20a b=≠．【解析】根据分式值为零的条件，分子为零，分母不为零，则3600a b a b-=+≠，，得出20a b=≠．【总结】考查分式值为零的条件．【例3】不改变分式的值，使分式115101139x yx y-+的各项系数化为整数，分子、分母应乘以（）．A．10B．9C．45D．90【难度】★【答案】D【解析】根据分式的分子分母同时乘以一个不为零的整式，分式的值不变，则分式的分子分母都乘以5、10、3、9的最小公公倍数90即可．【总结】考查分式的基本性质．例题解析【例4】在分式()222221332212x a b x y a bx x a b a bx y -+-+++++，，，中，最简分式有__________个． 【难度】★ 【答案】2．【解析】()()()()()()()222221131133112124x x x y x x x y x y x x x x x x y x y x y +------====+++++；． 【总结】考查最简分式的概念，分式的分子、分母中不含有公因式．【例5】（1）用科学记数法表示：0.00003082________=； （2）82.310--⨯=___________． 【难度】★【答案】50.00003082 3.08210-=⨯，82.3100.000000023--⨯=-． 【解析】 小数点移动n 位，则10的指数为n -． 【总结】考查科学计数法含有负指数的表示方法．【例6】已知b a x a b -=，b a y a b+=，则22_____x y -=． 【难度】★【答案】4-． 【解析】()()22224b a b a b a x y x y x y x y a b a b a b ⎛⎫⎛⎫-=+=∴-=+-=-=- ⎪⎪⎝⎭⎝⎭，，．【总结】考查分式的运算结合平方差公式的运用．【例7】甲、乙两班学生植树造林，已知甲班每天比乙班多植5棵树，甲班植80棵树所用的天数与乙班植70棵树所用的天数相等，如果设甲班每天指数x 棵，那么根据题意列出 的方程是（ ）． A ．80703x x =- B ．80705x x =+ C ．80705x x =+ D ．80705x x =- 【难度】★ 【答案】D【解析】根据时间等于所植树总数除以天数列方程． 【总结】先寻找等量关系，再列出分式方程．【例8】已知分式1x yxy+-的值是m ，如果分式中x y 、用它们的相反数代入，那么所得的值为 n ，则m n 、的关系是什么？ 【难度】★★ 【答案】0m n +=． 【解析】()()()01111x y x y x y x ym n m n xy x y xy xy-++--+====-∴+=------，，． 【总结】分式的分子、分母、分式值的符号变化规律，任意改变其中2个符号，分式值不变．【例9】当x 满足_________条件时，分式1111x++有意义．【难度】★★【答案】1x ≠-且2x ≠-． 【解析】11110110020211x x x x x x x +++≠≠-+≠≠∴+≠∴≠-++由，得；由，即，，， 综上：1x ≠-且2x ≠-．【总结】考查分式有意义的条件，分母不为零，注意每一个分母均不为零．【例10】学生有m 个，若每n 个人分配1间宿舍，则还有一人没有地方住，问宿舍的间数为 （ ）．A ．1m n + B ．1m n - C ．1m n- D ．1m n +【难度】★★ 【答案】C ．【解析】分配到房间的人数为1m -，所以宿舍房间数为1m n-． 【总结】考查分式在实际问题中的运用．【例11】如果分式225621x x x x --+-的值等于零，那么x 的值是（）．A ．6B ．1-C ．6-或1D ．1-或6【难度】★★ 【答案】A ． 【解析】22560210x x x x --=+-≠，， ()()()()1601210x x x x ∴+-=+-≠，，1x ∴=-或6x =且1x ≠-且12x ≠， 综上所述：6x =．【总结】考查分式值为零的条件，分子为零分母不为零．【例12】将三个数067⎛⎫- ⎪⎝⎭，123-⎛⎫- ⎪⎝⎭，132-⎛⎫⎪⎝⎭按从小到大的顺序排列：______________________． 【难度】★★【答案】11236327--⎛⎫⎛⎫⎛⎫-<<- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭．【解析】因为01162332173223--⎛⎫⎛⎫⎛⎫-=-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，，，所以11236327--⎛⎫⎛⎫⎛⎫-<<- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭．【总结】考查整数指数中零指数幂与负指数幂的意义．【例13】若13m m +=，则221______m m +=；441_______m m+=． 【难度】★★【答案】2217m m +=；44147m m +=． 【解析】222112927m m m m ⎛⎫+=+-=-= ⎪⎝⎭；2424211249247m m m m ⎛⎫+=+-=-= ⎪⎝⎭．【总结】考查完全平方公式的变形与分式的综合运用．【例14】计算：（1）()2222x y x y x y y x+⋅+--；（2）211121a a a a ⎛⎫-÷ ⎪--+⎝⎭；（3）22222a b a b a ba b a b ab ⎛⎫+---⋅ ⎪-+⎝⎭． 【难度】★★【答案】（1）x + y ；（2）1a -；（3）1a b+． 【解析】（1）()2222x y x y x y y x +⋅+-- ()()()22x y x y x y x y y x =+⋅++-- 22x y x y x y =--- 22x y x y -=- ()()x y x y x y+-=-x y=+；（2）211121a a a a ⎛⎫-÷ ⎪--+⎝⎭()21211a a a a a -+=-+-()2111a a =--1a =-； （3）22222ab a b a b a b a b ab ⎛⎫+---⋅ ⎪-+⎝⎭()()222a b a b a ba b a b a b ab ⎛⎫+--=-⋅ ⎪ ⎪+-+⎝⎭()()2222a b a b a b a b a b a b ab a b ab +---=⋅-⋅+-+()()2222a b a b ab a b +--=+()22ab ab a b =+1a b=+．【总结】考查结合乘法公式、乘法分配律进行分式的计算、分式的化简．【例15】计算：3-3231783211387233--⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫÷+-÷--+ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭．【难度】★★ 【答案】1．【解析】3-3231783211387233--⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫÷+-÷--+ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭3278322118723332111331⎛⎫⎛⎫=⋅+⋅⋅-+⎪ ⎪⎝⎭⎝⎭=+-+= 【总结】考查分式的计算，注意对负整数指数幂的正确计算．【例16】求下列各式中的x ．（1）25168x x =+=；（2）3.6100.036x ⨯=．【难度】★★【答案】（1）3x =；（2）2x =-． 【解析】（1）()()2525438315168222283155153xx x x x x x x x x +++=∴=∴=∴=+∴=∴=，，，，，；（2）220.036 3.61010102x x --=⨯∴=∴=-，，． 【总结】考查整数指数幂的运算，及方程的解法．【例17】已知()()2641212x x A B Cx x x x x x +-=++-+-+，求A B C 、、的值．【难度】★★【答案】2A =；1B =；3C =． 【解析】()()()()()()12211212A x x Bx x Cx x A B Cx x x x x x -++++-++=-+-+()()()()22212A B C x A B C x A x x x ++++--=-+，()()226422x x A B C x A B C x A ∴+-=++++--， 62211243A B C A A B C B A C ++==⎧⎧⎪⎪∴+-==⎨⎨⎪⎪==⎩⎩，解得： ．【总结】考察分式的加法运算，注意先通分再计算．【例18】计算：2222x z y x y zx xy xz yz x xy xz yz+-++--+-+++． 【难度】★★ 【答案】原式222yx y =-．【解析】2222x z y x y zx xy xz yz x xy xz yz +-++--+-+++()()()()()()()()x z x y x y x z x z x y x y x z ++-+++=-+-++ ()()()()1111x z x y x z x y =+--+-++()()11x y x y =--+222y x y =-． 【总结】考查异分母分式的加减运算，注意先分解因式再计算．【例19】已知22x y xy -=，且0xy ≠，求2222x y x y --+的值． 【难度】★★【答案】22223x y x y --+=． 【解析】2222x y x y --+()2222222442222222xy x y x y x yy x x y x y -++=+==，又22x y xy -=，∴原式=2222222222233x y x y x y x y x y+==． 【总结】考查完全平方公式的变形与分式运算的综合运用．【例20】解方程： （1）22133xx x -=--； （2）2222211242x x xx x x x x+---=--+． 【难度】★★ 【答案】（1）53x =；（2）3x =-． 【解析】（1） 解：方程两边同时乘以3x -得：322x x --=-，移项整理的：35x =，方程两边同时除以3得：53x =， 经检验53x =是原方程的解． 所以原方程的解为53x =； （2） 解：方程两边同时乘以()()22x x x +-得：()()()()222112x x x x x +--=--，整理的：26x =-，方程两边同时除以2得：3x =-，经检验3x =-是原方程的解． 所以原方程的解为3x =-．【总结】考查解分式方程的解法，注意求出解后要检验．【例21】当k 为何值时，解关于x 的方程2111x k xx x x -=--+时，不会产生增根． 【难度】★★ 【答案】2k ≠±．【解析】解：方程两边同时乘以()()11x x +-得：()()11x x k x x +-=-，移项整理的：2k x =，因为分式方程的增根为1x =±，所以2k =±． 故当2k ≠±时，不会产生增根．【总结】考查解分式方程的解法及对分式方程增根的理解．【例22】当2x >时，试比较分式21x x --和32x x --的值的大小． 【难度】★★【答案】21x x ->-32x x --． 【解析】()()()()()()()2213231121212x x x x x x x x x x x -------==------， 2x >，()()120x x ∴-->，()()1012x x ∴>--，即 23012x x x x --->--，∴21x x ->-32x x --． 【总结】主要考查利用作差法比较分式的大小．【例23】已知4x y +=-，12xy =-，求1111y x x y +++++的值． 【难度】★★【答案】3415-．【解析】1111y x x y +++++()()()22221x y x y xy x y ++++=+++()()()22221x y xy x y xy x y +-+++=+++， 4x y +=-，12xy =-，∴ 原式=()()()()()2421224234124115--⨯-+⨯-+=--+-+． 【总结】本题一方面考查分式的加减运算，另一方面考查整体思想的运用．【例24】文化用品商店用2000元购进一批学生书包，面市后发现供不应求，商店又购进第二批同样的书包，所购数量是第一批购进数量的3倍，但单价贵了4元，结果第二批用了6300元．（1）求第一批购进书包的单价是多少元？（2）若商品销售这两批书包时，每个售价都是120元，全部售出后，商店共盈利多少元？ 【难度】★★【答案】（1）单价是80元；（2）共盈利3700元． 【解析】解：（1）设第一批购进书包的单价为x 元，则2000363004x x ⨯=+，解得：80x =， 经检验80x =是原方程的解且符合题意，（2）盈利：20002000(12080)(12084)337008080-⨯+-⨯⨯=（元）， 答：（1）第一批购进书包的单价为80元；（2）商店共盈利3700元． 【总结】考查列方程解应用题，寻找出购书数量作为等量关系．【例25】解方程：48755986x x x x x x x x ----+=+----． 【难度】★★★ 【答案】7x =． 【解析】原方程变形为：87549865x x x x x x x x -----=-----， 通分，得：()()()()()()()()()()228795468956x x x x x x x x x x --------=----，化简，得：221117721130x x x x =-+-+， 2217721130x x x x ∴-+=-+， 整理得：642x =，解得：7x =， 经检验7x =是原方程的解， ∴原方程的解为7x =．【总结】考查分式方程的解法，注意方法的合理选择，以及解完后要验根．【例26】已知2520160x x --=，求()()322112x x x ---+-的值．【难度】★★★ 【答案】2020． 【解析】()()()()()32222221111225422x x x x x x x x x x ---+--=--=--=-+--，2520160x x --=，252016x x ∴-=，∴原式=201642020+=．【总结】考查分式的化简求值及整体代入思想的运用．【例27】已知2112x x x =-++，求2232111x x x x x -+-+-的值． 【难度】★★★【答案】32．【解析】解：2112x x x =-++，整理得：212x x x ++=-， 213x x ∴+=-或231x x =--， ∵0x ≠， ∴13x x+=-． 所以()()222322212111111x x x x x x x x x x x x --+=+-+--+-++ 2222111x x x x x =+-+++ ()231142x xx--=+--311111()22222x x x x x x x +=-=--=-+32=． 【总结】考查分式的化简求值，注意整体思想的运用．【例28】如果1110n m m n ++=+，求22m n n m ⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭．【难度】★★★【答案】7． 【解析】()211111110m n m n mn n m m n n m m n mn m n+++=∴+=-∴=-∴+=-+++，，，，()222222222232()2[]2()27m n mn m n m n m n mn n m n m mn mn mn +-+-⎛⎫⎛⎫⎛⎫∴+=+-=-=-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭．【总结】考查与完全平方公式变形相结合的分式的化简求值．【例29】已知a b c 、、为实数，且13ab a b =+，14bc b c =+，15ca c a =+，那么abcab bc ca ++的值 是多少？ 【难度】★★★【答案】61．【解析】∵13ab a b =+，14bc b c =+，15ca c a =+， ∴345a b b c c a ab bc ca +++===，，，111111345a b b c c a +=+=+=即，，， ∴1116a b c ++=， ∴1116ab bc ca abc a b c ++=++=， ∴16abc ab bc ca =++．【总结】考查分式的化简求值，注意方法的恰当运用．【例30】计算：111(1)(2)(1)(2)(3)(98)(99)(100)n n n n n n n n n ++⋅⋅⋅+++++++++． 【难度】★★★ 【答案】见解析． 【解析】解：111(1)(2)(1)(2)(3)(98)(99)(100)n n n n n n n n n ++⋅⋅⋅+++++++++ 1111111112(1)(1)(2)2(1)(2)(2)(3)2(98)(99)(99)(100)11111112(1)(1)(2)(1)(2)(2)(3)(98)(99)(99)(100)112(1n n n n n n n n n n n n n n n n n n n n n n n n n n ⎡⎤⎡⎤⎡⎤=⨯-+⨯-+⋅⋅⋅+⨯-⎢⎥⎢⎥⎢⎥+++++++++++⎣⎦⎣⎦⎣⎦⎡⎤=⨯-+-+⋅⋅⋅+-⎢⎥+++++++++++⎣⎦=⨯+1)(99)(100)119899002(1)(99)(100)994950(1)(99)(100)n n n n n n n n n n n n ⎡⎤-⎢⎥++⎣⎦+=⨯++++=+++【总结】这道题考查了分式运算中的简便计算，解答此类题目时，一是善于观察题目中所隐含的规律，二是根据发现的规律，细心计算，得出正确结果．【习题1】下列各式：3x -，x y x y +-，223x y xy -，110-，25y +，3x，234x y ，1π，其中分式的个数是（）．A ．1B ．2C ．3D ．4【难度】★ 【答案】D【解析】分式必须分母中含有字母，所以x y x y +-，25y +，3x，234x y 是分式． 【总结】考查分式的概念．【习题2】下列等式中，成立的是（）．A ．()()a bc d a b c d +=+++ B ．50.0150010.220y y y y ++=C ．221x y x y x y-=-- D ．1a ba b ---=--【难度】★ 【答案】B【总结】考查利用分式的基本性质进行分式的化简．【习题3】如果把223xyx y-中的x 与y 都扩大5倍，那么分式的值（ ）．A ．扩大5倍B ．不变C ．缩小5倍D ．无法确定【难度】★ 【答案】A【解析】分子扩大了25倍，分母扩大了5倍，分式值扩大了5倍． 【总结】考查分式的基本性质．随堂检测【习题4】已知1纳米910-=米，某植物花粉的直径为3500纳米，那么用科学记数法表示该种花粉的直径为________米．【难度】★ 【答案】63.510-⨯．【解析】9396350010 3.51010 3.510---⨯=⨯⨯=⨯． 【总结】考查科学记数法的表示．【习题5】汽车从甲地开往乙地，每小时行驶1v km ，t 小时可以到达，如果每小时多行驶2v km ，那么可以提前到达的小时数为（ ）．A ．212v t v v +B ．112v tv v +C ．1212v v v v + D ．1221v t v t v v -【难度】★★ 【答案】A 【解析】11212121212v t v t v t v t v tt v v v v v v +--==+++． 【总结】考查运用分式方程求解应用题．【习题6】已知234a b c==，则22222232a b c a ab c -+-+的值为（ ）． A ．32- B ．38- C ．12 D ．2【难度】★★ 【答案】B【解析】设234a k b k c k ===，，，代入原式=()()()()()()()222222222334338822234k k k k k k k k k -+-==--+． 【总结】运用设k 法进行化简求值，也可以代入特殊值求解．【习题7】已知关于x 的方程3211x kx x --=-+有增根，则_______k =． 【难度】★★ 【答案】0k =．【解析】方程两边分别乘以()()11x x -+得：()()()()231121x x k x x -+--=-整理得：2(1)210k x x x -+++=，即：()()2110x k x ++-=， 当1x =时，方程无解； 当1x =-时0k =．【总结】将分式方程转化成整式方程，再将方程的增根代入整式方程，求出k 值．【习题8】把333222111235---、、这三个数按从大到小的顺序排列是______________________． 【难度】★★【答案】111333222523--->>． 【解析】11111111133311122211111111128395895-----⎛⎫⎛⎫⎛⎫===== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，，111111111111589⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， ∴111333222523--->>． 【总结】将幂的形式进行变形，转化成指数相同的形式，则底数越大，值越大．【习题9】已知1122xx x+=--，且2212x y xy +=，求x y 、的值． 【难度】★★ 【答案】32x y ==．【解析】1122x x x +=--， 1122x x x ∴-=--，方程两边同时乘以2x -得：12x x -=-， 整理得：23x =，解得：32x =，经检验32x =是原方程的解，∴原方程的解为32x =，2212x y xy +=， ∴222x y xy +=，即()200x y x y -=∴-=，32x y ∴==． 【总结】通过分式与整式的转化，结合完全平方公式得出x y =，根据解分式方程解得32x =．【习题10】A B 、两地相距36千米，一艘小船从A 地匀速顺流航行至B 地，又立即从B 地匀 速逆流返回A 地，共用去9小时．已知水流速度为3/km h ，若设该轮船在静水中的速度为/xkm h ，则求x 时所列方程式______________________．【难度】★★【答案】3636933x x +=+-．【解析】顺流速度=静水速度+水流速度；逆流速度=静水速度-水流速度；根据：时间=路程÷速度，列出分式方程3636933x x +=+-．【总结】考查顺流速度与逆流速度的公式以及行程问题的运用．【习题11】若2221120x a x b x x ⎛⎫++-++-= ⎪⎝⎭，则a b ，之间的关系式是________________．【难度】★★ 【答案】2a b =．【解析】若2221120x a x b x x ⎛⎫++-++-= ⎪⎝⎭，则22110x a x b x x ⎡⎤⎛⎫+-++-=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦．∴222111100x a x b x a x b a b x x x x ⎛⎫⎛⎫+-=+-=∴+=+=∴= ⎪ ⎪⎝⎭⎝⎭，，，，．【总结】两个非负数的和为零，则每一个非负数值均为零．【习题12】若22103460a b a b +-+-=，求a ba b+-的值． 【难度】★★ 【答案】4．【解析】22103460a b a b +-+-=，()()221025690a a b b ∴-++-+=，()()22530a b -+-=即， 53a b ∴==，，则5384532a b a b ++===--． 【总结】本题一方面考查配方思想的运用，另一方面考查几个非负数的和为零的基本模型的运用．【习题13】先化简，再求值：2234221121x x x x x x ++⎛⎫-÷ ⎪---+⎝⎭，其中x 是不等式组40251x x +>⎧⎨+<⎩的 整数解．【难度】★★ 【答案】值为2．【解析】由 40251x x +>⎧⎨+<⎩， 解得：42x x >-⎧⎨<-⎩，x 是整数解，3x ∴=-．因为 2234221121x x x x x x ++⎛⎫-÷ ⎪---+⎝⎭()()()213421112x x x x x x ⎡⎤-+=-⋅⎢⎥-+-+⎢⎥⎣⎦()()()()234211112x x x x x x +-+-=⋅-++ ()()()212112x x x x x -+=⋅-++ 11x x -=+．所以当3x =-时，原式=3142312---==-+-． 【总结】考查解不等式的求解及分式的乘除运算及求值．【习题14】解方程：（1）232x xx x -=+-；（2）34522341x x x x x x x x +++++=+++++． 【难度】★★【答案】（1）12x =；（2）52x =-．【解析】（1） 解：方程两边同时乘以()()32x x +-得：()()()()23232x x x x x x --+=+-整理得：12x =， 经检验12x =是原方程的解 所以原方程的解为12x =；（2）原方程可变形为：45233412x x x x x x x x ++++-=-++++ ， 两边通分得：()()()()()()()()()()224352133412x x x x x x x x x x +-+++-++=++++，整理得：()()()()113412x x x x =++++， 则()()()()2134x x x x ++=++整理得：410x =-，解得：52x =-， 经检验52x =-是原方程的解，所以原方程的解为52x =-．【习题15】一项工程，甲队单独做完所需天数是乙、丙两队合做所需天数的a 倍，乙队独做 所需天数是甲、丙两队合做所需天数的b 倍，丙队独做所需天数是甲、乙两队合做所需天数的c 倍，求111111a b c +++++的值． 【难度】★★★ 【答案】值为1．【解析】解：设甲、乙、丙单独完成这项工程各需x 天、y 天、z 天，根据题意得， 111ayzx a y zy z=⋅=++，则111xy xz xy yz xz yz a a yz yz a xy yz xz +++=+==+++，所以，所以， 同理可得：1111xz xyb xy yz xzc xy yz xz==++++++；， 1111111yz xz xy a b c xy yz xz++∴++==+++++． 【总结】本题考查了分式方程在工程问题中的应用及分式的加减运算，有一定的难度．根据工作时间=工作总量÷工作效率列出分式方程是解题的关键，根据比例的性质及分式的运算法则进行变形是本题的难点．【习题16】()()()()()()()()2222133********x x x x x x x x +++⋅⋅⋅+++++++++．【难度】★★★【答案】()()1001101x x ++．【解析】解：()()()()()()()()2222133********x x x x x x x x +++⋅⋅⋅+++++++++()()()()()()()()()()()()11111111133557991011111011001101x x x x x x x x x x x x =-+-+-+⋅⋅⋅+-++++++++=-++=++【总结】考查学生对()11111n n n n =-++这一规律的运用．【习题17】如果关于x 的方程21221232a a x x x x ++=---+无解，求a 的值． 【难度】★★★【答案】1a =-或32a =-或2a =-．【解析】方程两边分别乘以()()12x x --得：()()()()231121x x k x x -+--=-整理得：()134a x a +=+，当10a +=，即1a =-时，方程无解，另方程无解，还包含了所得的解是方程的增根，故将1x =代入()134a x a +=+中，得32a =-；将2x =代入()134a x a +=+中，得2a =-， 综上，a 的值为1-或32-或2-．【总结】本题主要考查对方程无解的理解，包含两个方面，一个是所得的整式方程无解，另一个是所得的解是方程的增根．【作业1】无论x 取什么数时，总有意义的分式是（ ）．A ．21x x -+B ．2(1)x x + C ．338xx + D ．25x x - 【难度】★ 【答案】A ．【解析】A 中无论x 取何值时 1110x x -+≥∴-+≠，； B 中当1x =-时2(1)0x +=； C 中当2x =-时380x +=； D 中当0x =时20x =． 【总结】分式有意义的条件是分母不为零．课后作业【作业2】当______x时，分式11x--的值为负数．【难度】★【答案】1x<．【解析】分式值为负，则分子分母异号；则101x x->∴<，．【总结】分式值为正，则分子分母同号；分式值为负，则分子分母异号．【作业3】约分：22229_____________ 215a ba ab b-=--．【难度】★【答案】35a ba b--．【解析】()()()()22223393 215355a b a ba b a ba ab b a b a b a b+---==--+--．【总结】先因式分解，再根据分式的基本性质化简．【作业4】4xxy，326yx，210x yy-的最简公分母是___________．【难度】★【答案】2260x y．【解析】求出4、6、10的最小公倍数60，xy、2x、2y的公分母为22x y，所以最后最简公分母为2260x y．【总结】考查最简公分母的概念．【作业5】计算：201141_______35--⎛⎫⎛⎫-⨯-⨯-=⎪ ⎪⎝⎭⎝⎭．【难度】★【答案】9-．【解析】()2021141131935--⎛⎫⎛⎫-⨯-⨯-=-⨯-⨯=- ⎪ ⎪⎝⎭⎝⎭．【总结】考查整数指数幂的运算．【作业6】计算：（1）222222253214111a a a a a a a a --++-++++；（2）212293m m+--； （3）211x x x -++；（4）2211xy x y x y x y ⎛⎫÷- ⎪--+⎝⎭．【难度】★★ 【答案】（1）2331a a -++；（2）23m -+；（3）11x +；（4）2x．【解析】 （1）222222253214111a a a a a a a a --++-++++222222532143311a a a a a a a a --+-++-+==++；（2）()()()()()21223122122629333333m m m m m m m m m -+--+===---+-+-+；（3）2221111111x x x x x x x x --+=-=++++；（4）2211xy x y x y x y ⎛⎫÷- ⎪--+⎝⎭()()()()2xy yx y x y x y x y =÷+-+-()()()()22x y x y xyxx y x y y+-=⋅=+-．【总结】本题主要考查分式的运算，注意法则的准确运用．【作业7】解方程：（1）2331yy y +=-； （2）23222x x x -=+-；（3）2227461x x x x x +=+--； （4）232133648x x -+-+-=．【难度】★★ 【答案】（1）25y =；（2）27x =；（3）35x =；（4）32x =-． 【解析】（1）解：方程两边同时乘以()1y y -，得：()()221331y y y y -+=-，整理得：52y =， 解得：25y =，经检验25y =是原方程的解， 所以原方程的解为25y =； （2）解：方程两边同时乘以()()22x x +-，得：()()()()2232222x x x x x --+=+-， 整理得：72x =， 解得：27x =， 经检验27x =是原方程的解， 所以原方程的解为27x =； （3） 解：方程两边同时乘以()()11x x x +-，得：()()71416x x x -++=，整理得：53x =，解得：35x =，经检验35x =是原方程的解， 所以原方程的解为35x =； （4） 解：提取公因式： ()212331648x -+-=，整理得：21381x -+=，即21433x -+=，所以：214x -+= 解得：32x =-，所以原方程的解为32x =-．【总结】考查学生解分式方程的能力，注意最后要检验．【作业8】已知22221111x x x y x x x x+++=÷-+--，试说明不论x 为何值，y 的值不变． 【难度】★★ 【答案】略【解析】()()()()22221121111111111x x x x x x y x x x x x x x x x x +-+++=÷-+=⋅-+=-+=--+-+化简结果是常数，所以不论x 为何值，y 的值不变．【总结】实际考查分式化简．【作业9】如果11t x t -=+，2332ty t-=-，那么用含x 的代数式表示y 得___________． 【难度】★★★ 【答案】5151x y x -=+．【解析】解：()()()()123213111511111312151321xx x t x x x x t y x t x x x x x--⋅+-----+=∴=∴===-+++--+-⋅+，，． 【总结】将第一个分式方程进行转换成用x 表示t ，再将t 代入y 即可．【作业10】设1x y za b c++=，0a b c x y z ++=，求222222x y z a b c ++的值．【难度】★★★【答案】2222221x y z a b c ++=．【解析】设x y z u v w a b c ===，，，则()()1111102u v w u v w ++=++=，，由（2）得：0vw uw uvuvw++=，u 、v 、w 均不为0，0vw uw uv ∴++=，把（1）两边平方得()22221u v w uv vw uw +++++=2221u v w ∴++= ，即2222221x y z a b c++=．【总结】主要考查换元的思想，同时考查了公式()()22222a b c a b c ab ac bc ++=+++++的灵活运用．【作业11】计算：2422481111x x x x +++-+++． 【难度】★★★【答案】8161x -．【解析】2422481111x x x x +++-+++ ()()()()242121481111x x x x x x ++-=++-+++ 2248448161111x x x x =++=-++-．【总结】考查学生的观察力与规律总结的能力，通过寻找规律，快速的写出结果．。