随机实验理想白噪声和带限白噪声的发生与分析

第3章随机过程思考题3-1 何谓随机过程？它具有什么特点？答：（1）随机过程是指一类随时间作随机变化的过程，它不能用确切的时间函数描述。

随机过程可以从两个不同的角度来说明。

一个角度是把随机过程看成对应不同随机试验结果的时间过程的集合。

从另外一个角度来看，随机过程是随机变量概念的延伸，它在任意时刻的值是一个随机变量（2）随机过程的特点：①随机过程具有不可预知性。

因为根据随机过程的定义，随机过程相当于任意时刻的一个随机变量，随机也就意味着不可预知性。

②随机过程具有集合性。

集合性是指随机过程相当于由许多个随机变量聚合而成的，不仅仅是一个数量的叠加。

3-2 随机过程的数字特征主要有哪些？分别表征随机过程的什么特性？答：（1）随机过程的数字特征主要包括均值，方差和相关函数（2）三个数字特征分别表现了以下特性：①均值表示随机过程的n个样本函数曲线的摆动中心。

②方差表示随机过程在时刻t相对于均值的偏离程度。

③相关函数衡量随机过程在任意两个时刻上获得的随机变量之间的关联程度。

3-3 何谓严平稳？何谓广义平稳？它们之间的关系如何？答：（1）严平稳随机过程：若一个随机过程的统计特性与时间起点无关，即时间平移不影响其任何统计特性，则称该随机过程为严平稳随机过程。

（2）广义平稳随机过程：若一个随机过程的数学期望与时间无关，而自相关函数仅与时间间隔相关，则称该随机过程为广义平稳随机过程。

（3）严平稳随机过程必定是广义平稳的，反之不然。

因此严平稳随机过程的限制条件要高于广义平稳随机过程。

3-4 平稳过程的自相关函数有哪些性质？它与功率谱密度的关系如何？答：（1）平稳过程的自相关函数R（τ）的性质：①R（0）＝E[ξ2（t）]，表示平稳过程ξ（t）的平均功率。

②它是偶函数。

③它的最大值为R（0）。

④，表示平稳过程ξ（t）的直流功率。

⑤，σ2是方差，表示平稳过程ξ（t）的交流功率。

（2）它与功率谱密度是一对傅立叶变换对。

3-5 什么是高斯过程？其主要性质有哪些？答：（1）定义：如果随机过程的任意n维（n＝1，2，·）分布均服从正态分布，则称它为高斯过程。

实验一 随机序列的产生及数字特征估计一、实验目的1、学习和掌握随机数的产生方法；2、实现随机序列的数字特征估计。

二、实验原理1. 随机数的产生随机数指的是各种不同分布随机变量的抽样序列（样本值序列）。

进行随机信号仿真分析时，需要模拟产生各种分布的随机数。

在计算机仿真时，通常利用数学方法产生随机数，这种随机数称为伪随机数。

伪随机数是按照一定的计算公式产生的，这个公式称为随机数发生器。

伪随机数本质上不是随机的，而且存在周期性，但是如果计算公式选择适当，所产生的数据看似随机的，与真正的随机数具有相近的统计特性，可以作为随机数使用。

(0，1)均匀分布随机数是最最基本、最简单的随机数。

(0，1)均匀分布指的是在[0，1]区间上的均匀分布，即U(0，1)。

实际应用中有许多现成的随机数发生器可以用于产生(0，1)均匀分布随机数，通常采用的方法为线性同余法，公式如下：Ny x N ky Mod y y n n n n /))((110===-， （1.1）序列{}n x 为产生的(0，1)均匀分布随机数。

下面给出了上式的3组常用参数： (1) 7101057k 10⨯≈==，周期，N ；(2) （IBM 随机数发生器）8163110532k 2⨯≈+==，周期，N ； (3) （ran0）95311027k 12⨯≈=-=，周期，N ；由均匀分布随机数，可以利用反函数构造出任意分布的随机数。

定理1.1 若随机变量X 具有连续分布函数F X (x)，而R 为(0，1)均匀分布随机变量，则有)(1R F X x -= （1.2）由这一定理可知，分布函数为F X (x)的随机数可以由(0，1)均匀分布随机数按上式进行变换得到。

2. MATLAB 中产生随机序列的函数(1) (0，1)均匀分布的随机序列 函数：rand用法：x = rand(m,n)功能：产生m ×n 的均匀分布随机数矩阵。

(2) 正态分布的随机序列 函数：randn用法：x = randn(m,n)功能：产生m ×n 的标准正态分布随机数矩阵。

随机信号分析目录CONTENTS白噪声的定义白噪声的时频域特性物理可实现的白噪声小结随机过程的分类⚫按分布函数或概率密度函数特性：正态过程、马尔可夫过程、独立增量过程等；⚫按功率谱特性：宽带过程、窄带过程；白噪声、色噪声等。

定义：若N(t)为一个具有零均值的平稳随机过程，其功率谱密度均匀的分布在整个频率区间，即其中，N0为一个正实常数，则称N(t)为白噪声过程或简称白噪声。

“白”字借用光学中的“白光”术语。

N 120S N ω()白噪声的功率谱ω0=ωS N N 2()10∈−∞+∞ω(,)结论：功率谱在整个频率轴上满足均匀分布。

有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）根据维纳-辛钦定理，白噪声的自相关函数为00111()()222j N R N e d N ωττωδτπ+∞−∞==⎰0)(τN R 021N 结论：白噪声的自相关函数是一个δ函数，其面积等于功率谱密度。

白噪声的时频域特征白噪声的自相关系数为⎩≠⎨===⎧=τττττK R r K R N N N N N (0)(0)0 0()()() 1 0 结论：白噪声在任何两个相邻时刻的取值都是不相关的，白噪声过程随时间的起伏极快，过程的功率谱密度极宽。

有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）物理可实现的白噪声实际上，白噪声是不存在的，因为在实际应用中，当研究随机过程通过某一系统时，只要过程的功率谱密度在一个比系统带宽大得多的频率范围内近似均匀分布，就可以把它作为白噪声来处理。

2(0)(0)N N R σδ==→∞白噪声的功率谱在整个频率轴上满足均匀分布。

白噪声的自相关函数是一个δ函数，其面积等于功率谱密度，在任何两个相邻时刻的取值都是不相关的。

理想白噪声不存在，但某些情况下随机过程可近似看作白噪声。

对于一个具有零均值的平稳随机过程，其功率谱密度均匀的分布在整个频率区间，则称其为白噪声。

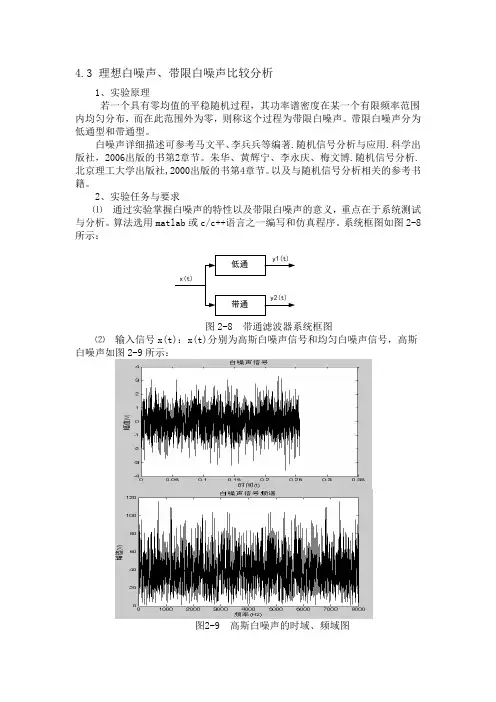
4.3 理想白噪声、带限白噪声比较分析1、实验原理若一个具有零均值的平稳随机过程，其功率谱密度在某一个有限频率范围内均匀分布，而在此范围外为零，则称这个过程为带限白噪声。

带限白噪声分为低通型和带通型。

白噪声详细描述可参考马文平、李兵兵等编著.随机信号分析与应用.科学出版社，2006出版的书第2章节。

朱华、黄辉宁、李永庆、梅文博.随机信号分析.北京理工大学出版社,2000出版的书第4章节。

以及与随机信号分析相关的参考书籍。

2、实验任务与要求⑴通过实验掌握白噪声的特性以及带限白噪声的意义，重点在于系统测试与分析。

算法选用matlab或c/c++语言之一编写和仿真程序。

系统框图如图2-8所示：低通带通x(t)y1(t)y2(t)图2-8带通滤波器系统框图⑵输入信号x(t)：x(t)分别为高斯白噪声信号和均匀白噪声信号，高斯白噪声如图2-9所示：图2-9 高斯白噪声的时域、频域图要求测试白噪声的均值、均方值、方差，自相关函数、概率密度、频谱及功率谱密度并绘图。

分析实验结果，搞清楚均值、均方值、方差，自相关函数、频谱及功率谱密度的物理意义。

例：均值除了表示信号的平均值，它还表示信号中有了什么成分。

相关函数当τ=0时为什么会有一个冲击，表示什么，它又等于什么。

信号的时域波形有哪些特征，频域又有哪些特征。

频谱及功率谱密度有什么差异，什么噪声是白噪声，这个噪声符合白噪声的定义吗等等。

⑶设计一个低通滤波器和一个带通滤波器。

要求白噪声分别通过低通滤波器和带通滤波器后的信号能够表现出带限白噪声的特点。

测试低通滤波器和一个带通滤波器的时频特性和频域特性以验证其正确性。

⑷分别计算高斯白噪声、均匀白噪声经低通滤波、带通滤波器后的均值、均方值、方差、概率密度、自相关函数、频谱及功率谱密度，并加以分析。

⑸所有结果均用图示法来表示。

⑹白噪声在什么情况下为带限白噪声？⑺按要求写实验报告。

第1篇一、实验背景随着城市化进程的加快，噪音污染已成为影响人们生活质量的重要因素之一。

噪音不仅会影响人们的听力健康，还会引起心理压力、睡眠障碍等问题。

为了了解人们对噪音的耐受能力，本研究通过实验方法对一组受试者的噪音耐受力进行测试和分析。

二、实验目的1. 了解受试者在不同噪音水平下的耐受时间。

2. 分析不同性别、年龄、职业等因素对噪音耐受能力的影响。

3. 为噪音治理提供参考依据。

三、实验方法1. 实验对象：招募30名健康成年人，男女各半，年龄在18-60岁之间，职业涵盖教师、工人、医生等。

2. 实验仪器：噪音发生器、秒表、耳机。

3. 实验步骤：（1）将受试者随机分为三组，每组10人。

（2）对每组受试者进行编号，分别为A组、B组、C组。

（3）对A组受试者播放60分贝的噪音，记录耐受时间。

（4）对B组受试者播放80分贝的噪音，记录耐受时间。

（5）对C组受试者播放100分贝的噪音，记录耐受时间。

（6）对受试者的性别、年龄、职业等因素进行统计分析。

四、实验结果1. A组受试者的平均耐受时间为5分钟。

2. B组受试者的平均耐受时间为3分钟。

3. C组受试者的平均耐受时间为1分钟。

通过对受试者的性别、年龄、职业等因素进行统计分析，得出以下结论：1. 女性受试者的平均耐受时间比男性受试者长。

2. 年轻受试者的平均耐受时间比年长受试者长。

3. 教师职业的受试者平均耐受时间较长，工人和医生职业的受试者平均耐受时间较短。

五、实验分析1. 噪音耐受能力与性别、年龄、职业等因素有关。

女性、年轻和教师职业的受试者具有较好的噪音耐受能力。

2. 噪音对人体的危害程度与噪音强度和暴露时间有关。

在本实验中，随着噪音强度的增加，受试者的耐受时间逐渐缩短。

六、实验结论1. 本实验结果表明，人们对噪音的耐受能力存在个体差异，受性别、年龄、职业等因素的影响。

2. 在噪音治理过程中，应针对不同人群采取有针对性的措施，提高人们的噪音耐受能力。

白噪声检验的方法及原理咱得明白啥是白噪声。

白噪声啊，就像是一种杂乱无章但又有规律可循的声音信号。

在统计学和时间序列分析里，白噪声可是个重要的概念呢。

它具有一些特定的性质，比如说均值为零，方差是一个常数，不同时间点的取值相互独立。

简单来说，白噪声就是一种随机的、没有明显趋势和规律的信号。

那为啥要进行白噪声检验呢？这可重要啦！如果一个时间序列是白噪声，那就意味着它没有可预测的模式，是完全随机的。

在很多情况下，我们需要确定一个时间序列是不是白噪声，因为这关系到我们后续的分析和预测方法的选择。

如果一个时间序列不是白噪声，那就可能存在某种趋势、季节性或者周期性，我们就可以利用这些特征来进行预测和分析。

但如果它是白噪声，那我们就知道用传统的预测方法可能不太管用啦。

接下来，咱说说白噪声检验的方法。

常见的方法有好几种呢，比如说自相关函数检验、Ljung-Box 检验和单位根检验等。

自相关函数检验呢，就是看时间序列的自相关函数。

如果一个时间序列是白噪声，那么它的自相关函数在所有的滞后阶数上都应该接近于零。

啥意思呢？就是说不同时间点的取值之间没有明显的相关性。

我们可以通过计算时间序列的自相关函数，并观察它在不同滞后阶数上的值来判断是不是白噪声。

如果自相关函数的值都很小，接近零，那很可能就是白噪声；如果自相关函数在某些滞后阶数上有较大的值，那就不是白噪声啦。

Ljung-Box 检验也是个常用的方法。

这个检验主要是通过计算统计量来判断时间序列的自相关性。

它会比较实际的自相关系数和在白噪声假设下的预期自相关系数。

如果统计量的值很大，那就说明时间序列不是白噪声；如果统计量的值比较小，那就有可能是白噪声。

Ljung-Box 检验通常会给出一个p 值，我们可以根据p 值来判断是否拒绝白噪声假设。

如果p 值小于某个显著性水平，比如0.05，那就拒绝白噪声假设，说明时间序列不是白噪声；如果p 值大于显著性水平，那就不能拒绝白噪声假设，可能是白噪声。

实验八理想白噪声和带限白噪声的产生与分析１．实验目的了解理想白噪声和带限白噪声的基本概念并能够区分它们，掌握用matlab或c/c++软件仿真和分析理想白噪声和带限白噪声的方法。

⒉实验原理所谓白噪声是指它的概率统计特性服从某种分布而它的功率谱密度又是均匀的。

确切的说，白噪声只是一种理想化的模型，因为实际的噪声功率谱密度不可能具有无限宽的带宽，否则它的平均功率将是无限大，是物理上不可实现的。

然而白噪声在数学处理上比较方便，所以它在通信系统的分析中有十分重要的作用。

一般地说，只要噪声的功率谱密度的宽度远大于它所作用的系统的带宽，并且在系统的带内，它的功率谱密度基本上是常数，就可以作为白噪声处理了。

白噪声的功率谱密度为：其中为单边功率谱密度。

2 ) ( 0 N f S n 0 N白噪声的自相关函数位：白噪声的自相关函数是位于τ =0 处，强度为的冲击函数。

这表明白噪声在任何两个不同的瞬间的取值是不相关的。

同时也意味着白噪声能随时间无限快的变化，因为它含一切频率分量而无限宽的带宽。

) ( 20 N R ）（ 20 N若一个具有零均值的平稳随机过程，其功率谱密度在某一个有限频率范围内均匀分布，而在此范围外为零，则称这个过程为带限白噪声。

带限白噪声分为低通型和带通型。

⒊实验任务与要求⑴用matlab 或c/c++语言编写和仿真程序。

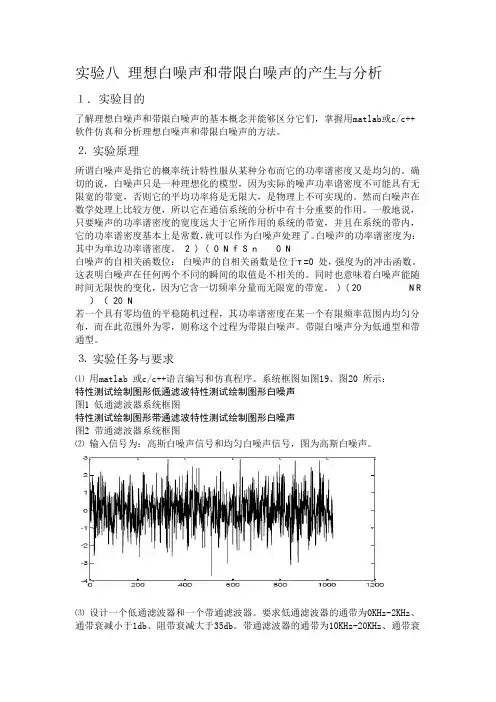
系统框图如图19、图20 所示：特性测试绘制图形低通滤波特性测试绘制图形白噪声图1 低通滤波器系统框图特性测试绘制图形带通滤波特性测试绘制图形白噪声图2 带通滤波器系统框图⑵输入信号为：高斯白噪声信号和均匀白噪声信号，图为高斯白噪声。

⑶设计一个低通滤波器和一个带通滤波器。

要求低通滤波器的通带为0KHz-2KHz、通带衰减小于1db、阻带衰减大于35db。

带通滤波器的通带为10KHz-20KHz、通带衰减小于1db、阻带衰减大于35db。

⑷首先计算白噪声的均值、均方值、方差、概率密度、频谱及功率谱密度、自相关函数。

实验一 随机序列的产生及数字特征估计一、实验目的1、学习和掌握随机数的产生方法；2、实现随机序列的数字特征估计。

二、实验原理1. 随机数的产生随机数指的是各种不同分布随机变量的抽样序列（样本值序列）。

进行随机信号仿真分析时，需要模拟产生各种分布的随机数。

在计算机仿真时，通常利用数学方法产生随机数，这种随机数称为伪随机数。

伪随机数是按照一定的计算公式产生的，这个公式称为随机数发生器。

伪随机数本质上不是随机的，而且存在周期性，但是如果计算公式选择适当，所产生的数据看似随机的，与真正的随机数具有相近的统计特性，可以作为随机数使用。

(0，1)均匀分布随机数是最最基本、最简单的随机数。

(0，1)均匀分布指的是在[0，1]区间上的均匀分布，即U(0，1)。

实际应用中有许多现成的随机数发生器可以用于产生(0，1)均匀分布随机数，通常采用的方法为线性同余法，公式如下：Ny x N ky Mod y y n n n n /))((110===-， （1.1）序列{}n x 为产生的(0，1)均匀分布随机数。

下面给出了上式的3组常用参数：(1) 7101057k 10⨯≈==，周期，N ；(2) （IBM 随机数发生器）8163110532k 2⨯≈+==，周期，N ； (3) （ran0）95311027k 12⨯≈=-=，周期，N ；由均匀分布随机数，可以利用反函数构造出任意分布的随机数。

定理1.1 若随机变量X 具有连续分布函数F X (x)，而R 为(0，1)均匀分布随机变量，则有)(1R F X x -= （1.2）由这一定理可知，分布函数为F X (x)的随机数可以由(0，1)均匀分布随机数按上式进行变换得到。

2. MATLAB 中产生随机序列的函数(1) (0，1)均匀分布的随机序列 函数：rand用法：x = rand(m,n)功能：产生m ×n 的均匀分布随机数矩阵。

(2) 正态分布的随机序列 函数：randn用法：x = randn(m,n)功能：产生m ×n 的标准正态分布随机数矩阵。

理想白噪声和带限白噪声的产生与分析摘要 利用Matlab 仿真分析产生的高斯白噪声和均匀白噪声通过低通滤波器和带通滤波器后的时域及频域波形，以便更好地理解白噪声。

背景 在实际应用中，通信设备的各种电子器件、传输线、天线等都会产生噪声，伴随着信号的产生、传输和处理的全过程。

噪声也是一种随机过程，而白噪声具有均匀功率谱密度，在数学处理上具有方便、简单的优点。

电子设备中的起伏过程如电阻热噪声、散弹噪声等，在相当宽的频率范围内具有均匀的功率谱密度，可以当做白噪声处理，因而研究白噪声的特性显得非常重要。

实验特点与原理（1）随机信号的分析方法在信号系统中，把信号分为确知信号与随机信号两类。

在工程技术中，一般用概率密度、均值、均方值、方差、自相关函数、频谱、功率谱密度等描述随机过程的统计特性。

①均值均值E[x(t)](μ)表示集合平均值或数学期望值。

基于随机过程的各态历经性，可用时间间隔T 内的幅值平均值表示：∑-==10/)()]([N t N t x t x E均值表达了信号变化的中心趋势，或称之为直流分量。

②均方值均方值E[x 2(t)](2ϕ)，或称为平均功率：N t x t x E N t /)()]([(1022∑-==均方值表达了信号的强度，其正平方根值，又称为有效值，也是信号的平均能量的一种表达。

③方差定义： N t x E t x N t /)]]([)([122∑-=-=σ可以证明，2ϕ=2σ+2μ。

其中：2σ描述了信号的波动量；2μ 描述了信号的静态量。

④自相关函数信号的相关性是指客观事物变化量之间的相依关系。

对于平稳随机过程x(t)和y(t)在两个不同时刻t 和t+τ的起伏值的关联程度，可以用相关函数表示。

在离散情况下，信号x(n)和y(n)的相关函数定义为：∑∑-=-+=101N t xy N /)t (y )t (x ),t (N R τττ τ,t=0,1，2,……N-1随机信号的自相关函数表示波形自身不同时刻的相似程度。

一、实验背景白噪声是一种具有平坦频谱特性的噪声，其功率谱密度在所有频率范围内均相等。

白噪声在信号处理、通信、噪声控制等领域具有广泛的应用。

本实验旨在通过搭建实验装置，产生白噪声，并对其进行测量和分析。

二、实验目的1. 了解白噪声的产生原理；2. 掌握白噪声的产生方法；3. 学习白噪声的测量方法；4. 分析白噪声的特性。

三、实验原理白噪声的产生原理是通过随机信号源产生具有平坦频谱特性的噪声。

在实验中，我们可以通过以下方法产生白噪声：1. 采用随机噪声发生器，将随机信号经过滤波器处理后，得到具有平坦频谱特性的白噪声；2. 利用数字信号处理技术，通过随机信号生成算法产生白噪声。

四、实验仪器与设备1. 随机噪声发生器；2. 滤波器；3. 信号分析仪；4. 示波器；5. 数据采集卡；6. 计算机。

五、实验步骤1. 连接实验装置，将随机噪声发生器的输出信号输入滤波器；2. 调整滤波器参数，使滤波器输出信号具有平坦频谱特性；3. 将滤波器输出信号输入信号分析仪，进行频谱分析；4. 使用示波器观察白噪声的波形；5. 使用数据采集卡采集白噪声信号，进行进一步分析。

六、实验结果与分析1. 频谱分析通过信号分析仪对白噪声进行频谱分析，得到白噪声的功率谱密度。

从分析结果可以看出，白噪声的功率谱密度在所有频率范围内均相等，符合白噪声的特性。

2. 波形观察使用示波器观察白噪声的波形，可以看到白噪声的波形具有随机性，无明显规律。

3. 数据分析使用数据采集卡采集白噪声信号，进行进一步分析。

通过分析白噪声的时域特性、频域特性等，可以进一步了解白噪声的特性。

七、实验结论1. 成功搭建了白噪声产生实验装置，并产生了具有平坦频谱特性的白噪声；2. 掌握了白噪声的产生方法、测量方法和特性分析；3. 为后续白噪声在信号处理、通信、噪声控制等领域的应用奠定了基础。

八、实验总结本实验通过对白噪声的产生、测量和分析，使我们了解了白噪声的特性及其应用。

随机信号分析试验随机噪声特性分析院系：通信工程学院班级：011241成员：目录一. 实验摘要二. 实验目的三. 实验步骤四. 实验原理4.1 白噪声特性分析4.2 白化滤波器的设计与分析4.3 理想白噪声、带限白噪声比较分析4.4 色噪声的产生与分析4.5 用硬件实现白噪声五．实验设计与实现六．实验总结与心得、实验摘要本实验主要研究随机信号各种噪声的特性分析。

因此，我们通过利用计算机模拟各种噪声来更好的了解随机噪声的特点，来印证我们所学的基本理论二、实验目的1、了解白噪声信号、色噪声信号自身的特性，包括均值、均方值、方差、相关函数、概率密度、频谱及功率谱密度等。

2、掌握白噪声、色噪声信号的分析方法。

3、熟悉常用的信号处理仿真软件平台：matlab或C/C++语言、EW软件仿真。

4、了解估计功率谱密度的几种方法，掌握功率谱密度估计在随机信号处理中的作用。

三、实验步骤1、根据选题的内容和要求查阅相关的文献资料，设计具体的实现程序流程或电路。

2、自选matlab、EW或c仿真软件。

如用硬件电路实现，需用面包板搭建电路并调试成功。

3、按设计指标测试电路。

分析实验结果与理论设计的误差，根据随机信号的特征，分析误差信号对信号和系统的影响。

四、实验原理4.1 白噪声特性分析白噪声是指它的概率统计特性服从某种分布，而它的功率谱密度又是均匀的确切的说，白噪声只是一种理想化的模型，因为实际的噪声功率谱密度不可能具 有无限宽的带宽，否则它的平均功率将是无限大， 是物理上不可实现的。

然而白 噪声在数学处理上比较方便，所以它在通信系统的分析中有十分重要的作用。

一 般地说，只要噪声的功率谱密度的宽度远大于它所作用的系统的带宽，并且在系统的带宽内，它的功率谱密度基本上是常数，就可以作为白噪声处理了。

白噪声 的功率谱密度为：其中N O /2就是白噪声的均方值。

白噪声的自相关函数为:N o No白噪声的自相关函数是位于T =0处、强度为2的冲击函数。

概率统计学中的白噪声检验方法探析概率统计学是一门研究随机现象的学科，而白噪声则是其中的一个重要概念。

白噪声是一种具有特殊统计特性的信号，它在许多领域中都有着广泛的应用，例如通信、金融和医学等。

在进行白噪声的分析和应用时，我们需要对其进行检验，以确保数据的可靠性和准确性。

本文将探讨概率统计学中常用的白噪声检验方法。

首先，我们需要了解什么是白噪声。

简单来说，白噪声是一种具有均值为零、方差为常数、且相邻值之间没有相关性的信号。

在时间序列分析中，白噪声是指一个时间序列中的观测值之间没有任何相关性，即它们是独立同分布的。

这种信号在频域上表现为频谱平坦，即在所有频率上具有相同的能量分布。

为了检验一个时间序列是否为白噪声，概率统计学提供了多种方法。

其中一种常用的方法是利用自相关函数（ACF）和偏自相关函数（PACF）进行分析。

ACF 和PACF可以帮助我们判断时间序列中观测值之间的相关性，并进而判断是否存在白噪声。

在进行ACF和PACF分析时，我们首先需要计算时间序列的自相关系数和偏自相关系数。

自相关系数是指观测值与其滞后值之间的相关性，而偏自相关系数则是指在控制其他滞后项的影响下，观测值与其滞后值之间的相关性。

通过绘制ACF和PACF图，我们可以观察到时间序列在不同滞后阶数下的相关性，从而判断是否存在白噪声。

除了ACF和PACF分析外，还有其他一些常用的白噪声检验方法，例如Ljung-Box检验和Durbin-Watson检验。

Ljung-Box检验是一种基于自相关系数的检验方法，它用于检验时间序列中的相关性是否显著，从而判断是否存在白噪声。

Durbin-Watson检验则是一种基于残差的检验方法，它用于检验时间序列模型的残差是否存在相关性，进而判断是否存在白噪声。

在进行白噪声检验时，我们还需要注意一些常见的误判。

例如，当时间序列存在趋势或周期性变化时，可能会导致对白噪声的误判。

因此，在进行白噪声检验前，我们需要对时间序列进行预处理，以去除趋势和周期性的影响。

实验报告实验课程：随机信号分析实验项目：随机信号通过线性系统的仿真学员姓名：学号：专业班次：队别：实验日期：实验成绩：教员签字：内容要求：一、实验目的; 二、实验内容或任务；三、实验仪器设备（名称、型号、精度、数量）；四、实验原理与线路图；五、实验步骤与结果记录（数据、图表等）；六、实验结果分析与结论。

一、实验目的（1）掌握对随机过程通过线性系统后的统计特性的分析方法。

（2）掌握典型系统对随机过程的影响。

二、实验内容（1）白噪声通过线性系统的仿真和分析；（2）高斯过程通过线性系统的仿真和分析。

三、实验仪器和设备（1）计算机一台。

（2）Matlab软件。

四、实验原理随机信号通过线性系统分析的中心问题是：给定系统的输入函数（或统计特性：均值和自相关函数）和线性系统的特性，求输出函数。

设L为线性变换，信号)(t(tY为系统的输出，也是随机信号。

即有：X为系统输入，)tL=YX)()]([t众所周知，LTI系统又可以表示为=)*(y⎰+∞∞--)()()(t()=uhuxtdutytx其中)]thδL=是系统的冲激响应。

如果考虑傅里叶变换，令[()(t)()(),()(),()(ωωωj Y t y j X t x j H t h ↔↔↔则)()()(ωωωj H j X j Y =下面来分析输出随机信号的均值和相关函数。

依定理5.1，对于任何稳定的线性系统有{}{})]([)]([t X E L t X L E =依定理5.2，如果)(t X 为平稳过程，)(t h 为实LTI 系统，)()()(t h t X t Y *=,则)()(t Y T X 和是联合广义平稳的，并且有)()()()()()()()()()()0(ττττττττττ-**=-*=*==h h R R h R R h R R j H m m X Y X XY X YX X Y 其中，dt t h j H j H ⎰+∞∞-===)()()0(0ωω，是系统的直流增益。

实验三 随机过程通过线性系统的分析实验目的1. 理解和分析白噪声通过线性系统后输出的特性。

2. 学习和掌握随机过程通过线性系统后的特性，验证随机过程的正态化问题。

实验原理1.白噪声通过线性系统设连续线性系统的传递函数为)(ωH 或)(s H ，输入白噪声的功率谱密度为2)(0N S X =ω，那么系统输出的功率谱密度为2)()(02N H S Y ⋅=ωω （3.1） 输出自相关函数为⎰∞∞-=ωωπτωτd e H N R j Y 20)(4)( （3.2）输出相关系数为)0()()(Y Y Y R R ττγ=（3.3） 输出相关时间为⎰∞=00)(ττγτd Y （3.4）输出平均功率为[]⎰∞=202)(2)(ωωπd H N t Y E （3.5）上述式子表明，若输入端是具有均匀谱的白噪声，则输出端随机信号的功率谱主要由系统的幅频特性)(ωH 决定，不再是常数。

2.等效噪声带宽在实际中，常常用一个理想系统等效代替实际系统的)(ωH ，因此引入了等效噪声带宽的概念，他被定义为理想系统的带宽。

等效的原则是，理想系统与实际系统在同一白噪声的激励下，两个系统的输出平均功率相等，理想系统的增益等于实际系统的最大增益。

实际系统的等效噪声带宽为⎰∞=∆022max)()(1ωωωωd H H e （3.6）或⎰∞∞--=∆j j e ds s H s H H j )()()(212maxωω （3.7）3.线性系统输出端随机过程的概率分布 （1）正态随机过程通过线性系统若线性系统输入为正态过程，则该系统输出仍为正态过程。

（2）随机过程的正态化随机过程的正态化指的是，非正态随机过程通过线性系统后变换为正态过程。

任意分布的白噪声通过线性系统后输出是服从正态分布的；宽带噪声通过窄带系统，输出近似服从正态分布。

实验内容设白噪声通过图3.1所示的RC 电路，分析输出的统计特性。

图3.1 RC 电路（1）试推导系统输出的功率谱密度、相关函数、相关时间和系统的等效噪声带宽。

随机信号分析目录CONTENTS限带白噪声的定义及分类低通型限带白噪声带通型限带白噪声色噪声小结限带白噪声的定义及分类定义：如果一个具有零均值的平稳随机过程X(t)，其功率谱密度在某一个频率范围内均匀分布，而在此频率范围外为零，则称这个过程为限带白噪声。

分类：根据功率谱密度的特点，限带白噪声分为低通型和带通型。

有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）S X ω()功率谱密度：⎩⎪>⎨=⎪⎧≤ωωωWS S W X 0 () 00S W -W0ω有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）自相关函数：01sin ()()2j X X WS W R S ed W ωτττωωππτ+∞−∞==⎰0)(τX R π0WS WπWπ2思考：如何从白噪声中提取不相关的随机变量？S 0ω+W 02ω−W 02ω0ω0S X ω()功率谱密度：⎩⎪⎨=⎪−<<+⎧ωωωωelse S S W W X 0()22 000-0ω有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）自相关函数：)(τX R W π2Wπ400sin /2()cos /2X WS W R W ττωτπτ=色噪声按功率谱密度函数形式来区分随机过程，我们将把白噪声以外的所有噪声都称为有色噪声或色噪声。

有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）如果一个具有零均值的平稳随机过程X(t)，其功率谱密度在某一个频率范围内均匀分布，而在此频率范围外为零，则称这个过程为限带白噪声。

根据功率谱密度的特点，限带白噪声分为低通型和带通型，可看作白噪声通过理想低通或理想带通滤波器的输出。

将白噪声以外的所有噪声都称为有色噪声或色噪声。

实验二 白噪声信道实验一、实验目的1、掌握用matlab 中高斯白噪声信道的产生方法。

2、掌握理想低通和高通白噪声的时频域特性。

3、掌握高斯白噪声对信号的影响。

4、掌握白噪声的消除方法。

二、实验原理 1、高斯过程高斯过程又称为随机过程，它的一维概率密度函数为：概率密度221()()exp 22X x a p x σπσ⎡⎤-=-⎢⎥⎣⎦。

式中，σ > 0, a = 常数。

概率密度曲线：正态分布的概率密度特征：（1）p(x)对称于直线 x = a ，即有：()()p a x p a x +=-（2）p(x)在区间(-∞, a)内单调上升，在区间(a, ∞)内单调下降，并且在点a 处达到其极大值1/(2)πσ。

当x → - ∞或 x → + ∞时，p(x) → 0。

（3）()1p x dx ∞-∞=⎰；()()1/2a ap x dx p x dx ∞-∞==⎰⎰（4）若a = 0, σ = 1，则称这种分布为标准化正态分布：21()exp 22x p x π⎡⎤=-⎢⎥⎣⎦2、白噪声 （1）白噪声白噪声是指具有均匀功率谱密度()n P f 的噪声，即0()/2n P f n =，式中，0n 为单边功率谱密度（W/Hz 。

白噪声的自相关函数可以从它的功率谱密度求得：2200()()()22j f j f X n nR P f edf e df πτπττδτ∞∞-∞-∞===⎰⎰由上式看出，白噪声的任何两个相邻时间（即τ ≠ 0时）的抽样值都是不相关的。

白噪声的平均功率：0(0)(0)2n R δ==∞。

上式表明，白噪声的平均功率为无穷大。

若白噪声的概率分布服从高斯分布，则称为高斯白噪声。

（2）低通白噪声低通白噪声：白噪声通过理想低通滤波器的输出。

低通白噪声的功率谱密度：0()/2,()0,n H HnP f n f f f P f =-≤≤⎧⎨=⎩其他其自相关函数为：20002sin 2sin 2()2222HHf j f H H H Hf H H n n f f R e df f n f f f πτπτπττπτπτ-===⎰（3）带通白噪声带通白噪声：带宽受到限制的白噪声。