半刚性节点对单层球面网壳的弹塑性稳定分析

某单层肋环形球面网壳结构的整体稳定分析陈庆烈【摘要】整体稳定分析问题一直是球面网壳设计中的关键问题.理论分析和工程实践表明:网壳结构的设计通常受其稳定性控制.网壳结构的整体稳定分析主要有三种:屈曲分析、弹性整体稳定分析和弹塑性整体稳定分析.本文借助有限元分析软件ANSYS,以某单层肋环型球面网壳为代表,对其进行屈曲分析、弹性整体稳定分析和弹塑性整体稳定分析,同时深入研究不同缺陷模式对整体稳定性能的影响.研究发现,单层球面网壳前六阶屈曲模态的整体稳定系数相接近,且出现相邻的重模态现象;最低阶屈曲模态缺陷对网壳结构的弹性整体稳定承载力影响最大,但对其弹塑性整体稳定承载力的影响未必最大,故有必要考察相邻的较低阶屈曲模态缺陷对网壳结构的影响.【期刊名称】《四川建材》【年(卷),期】2016(042)003【总页数】2页(P87-88)【关键词】单层肋环形球面网壳;整体稳定;极限承载力;有限元;缺陷模式【作者】陈庆烈【作者单位】同济大学建筑工程系,上海200092【正文语种】中文【中图分类】TU399某单层球面网壳的直径为30 m，矢高20 m(网壳底部标高0.000 m，网壳顶点标高20.000 m)。

周边边界点为支座节点，且为固定铰支座。

荷载标准值为：均布恒载q=1.0 kN/m2 (不包括结构自重)；均布活载p=0.7 kN/m2。

钢材种类选用Q235。

为简化分析，本网壳采用同一杆件截面形式，160×5，径向等分为12份，每根杆件长约1.54 m，环向等分为30份，每根杆件长约0.32～3.14 m。

各杆件选用BEAM188单元，且每个杆件为一个杆单元。

杆件各节点理想刚接，且不考虑节点形式，支座节点理想铰接。

在弹性整体稳定分析时，假定材料为无限弹性；在弹塑性整体稳定分析时，假定材料为理想弹塑性[1]。

当网壳受恒载和活载作用时，其稳定性承载力以恒载与活载的标准组合来衡量，根据JGJ7-2010《网壳结构技术规程》[2](以下简称《技术规程》)中大量算例分析表明：荷载的不对称分布(实际计算中取活载的半跨分布)对球面网壳的稳定性承载力无不利影响。

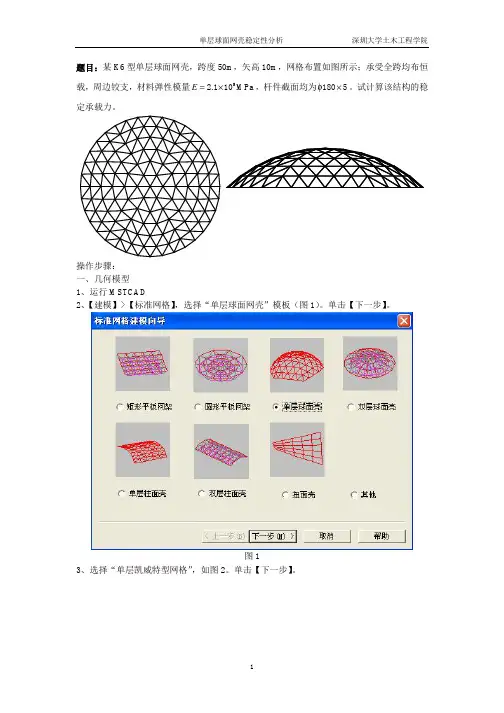
题目：某K6型单层球面网壳，跨度50m，矢高10m，网格布置如图所示；承受全跨均布恒载，周边铰支，材料弹性模量5φ×。

试计算该结构的稳E=×，杆件截面均为18052.110MPa定承载力。

操作步骤：一、几何模型1、运行MSTCAD2、【建模】>【标准网格】，选择“单层球面网壳”模板（图1）。

单击【下一步】。

图13、选择“单层凯威特型网格”，如图2。

单击【下一步】。

图24、输入跨度50m，矢高10m，环向网格数6，径向网格数6，如图3所示。

单击【完成】。

图35、【文件】>【另存为】，保存为dwg文件，如图4所示。

图46、用AutoCAD打开dwg文件，另存为1.dxf文件（R2000版本），关闭AutoCAD。

7、在工作目录中用记事本建立一个文本文件，后缀为“.in”，内容为“loaddxf 1.dxf”，如图5所示。

图58、运行ADINA，并保存文件（路径名及文件名都不能出现中文），例如保存在D:\ADINAEXAMPLE文件夹中（即第7步的工作目录）。

9、在图6所示工具条上单击“Open”按钮，在打开文件对话框中，文件类型选择“ADINA-INCommand Files (*.in)”，选择第7步建立的文本文件，如图7所示。

单击【打开】。

图6图710、在图8所示工具条上单击“Mesh Plot”按钮，显示几何模型，如图9所示。

图8图9二、物理模型11、指定边界条件在图10所示工具条上单击“XZ View”按钮，将模型切换到XZ视图，如图11所示。

图10图11在图12所示工具条上单击“Apply Fixity”按钮。

图12在图13所示对话框中单击“Define”，定义铰支边界约束条件。

图13在图14所示对话框中单击“Add”。

图14在图15所示对话框中输入约束名称，单击【OK】。

图15在图16所示对话框中输入勾选“X-Translation”、“Y-Translation”、“Z-Translation”，单击【OK】。

第24卷第5期 V ol.24 No.5 工 程 力 学 2007年 5 月 May 2007 ENGINEERING MECHANICS17———————————————收稿日期：2005-09-17；修改日期：2005-12-27 基金项目：国家自然科学基金重点资助项目(50338010)作者简介：*曹正罡(1975)，男，黑龙江呼玛县人，讲师，博士生，从事网壳结构稳定性研究(E-mail: caohit@)； 范 峰(1971)，男，安徽安庆人，教授，博士，长期从事大跨空间结构抗震、稳定性能研究；沈世钊(1933)，男，浙江嘉兴市人，教授，中国工程院院士，长期从事大跨空间结构抗风、抗震、稳定性能研究.文章编号：1000-4750(2007)05-0017-07单层球面网壳结构弹塑性稳定性能研究*曹正罡，范 峰，沈世钊(哈尔滨工业大学土木工程学院，黑龙江 哈尔滨 150090)摘 要：有计划地针对六种实际尺寸的常用单层球面网壳结构，利用ANSYS 软件及自编的前后处理程序进行了3200余例网壳双重非线性全过程分析。

求得网壳的弹塑性极限承载力，系统地考察了初始缺陷和荷载不对称分布，支承条件等因素对单层球面网壳结构弹塑性稳定性能的影响，着重研究考虑材料非线性后网壳极限承载力的变化规律。

通过这种大规模参数分析研究，较全面了解单层球面网壳结构的弹塑性稳定性能，为实际工程设计提供了理论依据和设计参考。

关键词：球面网壳；稳定；极限承载力；弹塑性；ANSYS 中图分类号：TU311.2 文献标识码：AELASTO-PLASTIC STABILITY ANALYSIS OF SINGLE LAYER LATTICEDDOMES*CAO Zheng-gang , FAN Feng , SHEN Shi-zhao(School of Civil Engineering, Harbin Institute of Technology, Harbin, Heilongjiang 150090, China)Abstract: A comprehensive parametric analysis of elasto-plastic stability behaviors of six kinds of real latticed domes with various geometric parameters were carried out in the present paper. Based upon geometrical and material nonlinear complete-process analysis, more than 3200 examples of latticed domes were analyzed by Finite Element Method software ANSYS and self-developed pre- and post-processing programs for critical elasto-plastic loads. The effects of initial imperfection, possible unsymmetrical distribution of loads and different supporting conditions, especially the effects of material nonlinearity on the critical loads of these kinds of domes were considered. Through the analytical results, the elasto-plastic stability behaviors of single-layer latticed domes are concluded, and guide-lines for the design of this structure is provided. Key words: latticed domes; stability; critical loads; elasto-plasticity; ANSYS网壳结构在静力作用下的稳定性问题自20世纪80年代后期至90年代中期曾是一个理论研究热点课题，当时许多研究者运用非线性有限元分析方法对网壳结构进行弹性的或弹塑性的荷载-位移全过程跟踪，从各个方面研究其稳定性能。

第3卷　第3期空 间 结 构1997年8月　单层球面网壳的稳定性沈世钊　陈　昕　林有军　汤建南(哈尔滨建筑大学　哈尔滨150001)摘　要　本文有计划地对400余例实际尺寸的单层球面网壳进行了非线性全过程分析,求得了它们的极限承载力,系统地考察了初始缺陷和荷载不对称分布对网壳性能的影响。

通过这种大规模参数分析方法,掌握了单层球面网壳稳定性能的规律性,在此基础上提出了供设计人员使用的实用公式。

关键词　单层球面网壳 稳定 极限承载力一、概　述稳定性问题是单层网壳结构设计中的一个关键课题,文献[1]和[2]解决了这一课题的理论和分析方法问题,并在下列几个方面具有特色:(1)从结构的荷载-位移全过程分析中来考察结构的稳定性问题,因而是在最精确的意义上来研究这一问题的;(2)采用了尽可能精确的理论和灵活的迭代策略,使具有大量自由度的实际网壳结构的全过程分析得以顺利实现;(3)提出了“一致缺陷模态法”这一简便而又有充分理论根据的考虑随机缺陷的分析方法,并把它作为有力武器深入讨论了缺陷这一敏感因素对网壳工作性能的影响,使我们有可能将网壳结构稳定性的研究推进到真正针对实际结构的深度;(4)所采用的方法毋需把网壳的屈曲过程事先设定为节点失稳、局部失稳或整体失稳,是极限屈曲还是分枝屈曲,而是在研究其受力性能全过程中自然地把各种可能的失稳形式均包容在内,并按其先后顺序依次表现出来。

但是,网壳稳定性分析的理论和方法不易为一般设计部门所掌握,要正确、自由地运用所提供的程序也需要较高的理论素养和熟练的计算技术。

所以,要使网壳的稳定设计达到普及的程度,尚需作进一步的细致工作,从上述理论成果出发,搭起必要的桥梁,过渡到便于广大设计人员应用的实用方法。

这一目标就是本文试图解决的任务。

为了正确解决这一任务,最可靠、有效的研究方法就是采用大规模参数分析的方法,也就文稿收到日期:1997.4.12。

3是结合不同类型的网壳结构形式,在基本参数(包括几何参数、构造参数、荷载参数…等)的常用变化范围内,运用上述理论分析方法,进行大规模的实际结构计算,然后对所得计算结果进行统计分析和归纳,考察网壳稳定性的变化规律,最后从理论高度进行概括,提出关于网壳稳定设计的实用方法。

单层球面网壳结构的稳定性分析摘要：网壳结构是近年来在建筑工程中广泛应用的一种空间结构形式，它受力合理,造型美观, 用料经济,施工简便。

其结构形势多样,跨度较大,重量轻，因而网壳结构的稳定性问题是结构设计和施工安装中的十分重要。

本文主要在国内外研究成果的基础上，介绍单层球面网壳结构的发展状况以及其非线性稳定性分析方法，并得出相关结论。

关键词：单层球面网壳结构、非线性、稳定性Abstract:In recent years latticed shell is a widespread spatial structure in the architectural engineering because of the reasonable stress, the beautiful modeling and convenient installation. Its structure diversifies , span is big and the weight is light. So the stability calculation problem on the latticed shell structure becomes important in the structure design and construction installment. Based on the recent research within and without , this paper mainly introduce the development and the nonlinear stability analysis methods of single-layer spherical lattice shells and draws some conclusions.Key words: single-layer spherical lattice shell、nonlinear、stability1 网壳结构的发展概况网壳结构是一种由杆件构成的曲面网格结构，可以看作是曲面状的网架结构，兼有杆系结构和薄壳结构的固有特性。

半刚性单层球面木网壳整体稳定性试验罗伟;陆伟东;孙小鸾;周烨楠【摘要】In order to study the influence of semi-rigid of joints on overall stability of wood reticulated shells,a semi-rigid kind of steel pipe-ear plate with bolts joint was designed and apply it to Kewitte6 single-layer spherical wood reticulated shell models.It has been adopted the static loading method to carry out full span,half span and simplified loading tests.The test results show that the wood reticulated shell with semi-rigid joints has stable bearing capacity.The vertex of the reticulated shell has the largest displacement and is most likely to occur instability when full span are loaded.The local instability occurred when half span areloaded.Increasing the bending stiffness of joints can improve 31 % of the stable capacity of the reticulated shell and reduce 30% of the ultimate displacement of joints during the simplified tests.Finally,it established the numerical models by ANSYS to verify the simplified test results.%为了研究节点半刚性对木网壳整体稳定性的影响，设计一种钢管耳板螺栓节点并应用于 K6型单层球面木网壳模型，采用静力加载方式对其进行了全跨、半跨及简化加载试验。

球面网壳结构是一种独特的结构形式，它具有轻质、高强度、耐腐蚀、耐疲劳等优点。

在现代建筑、桥梁、航空航天等领域得到了广泛应用。

然而，球面网壳结构也存在一些稳定性问题，特别是在承受外力作用下容易发生失稳破坏。

因此，研究球面网壳结构的稳定性是非常重要的。

一、球面网壳结构的基本概念和分类球面网壳结构是由若干根经纬组成的高强度杆件和节点组成的网状结构，呈球面形状。

根据节点连接方式的不同，球面网壳结构可分为刚性节点球面网壳和铰接节点球面网壳两种。

刚性节点球面网壳是由刚性连接件将若干根经纬杆件连接起来组成的网架结构，具有较高的刚度和强度。

由于刚性连接件的存在，刚性节点球面网壳的计算和设计比较容易。

铰接节点球面网壳是通过铰接节点将若干根经纬杆件连接起来，形成一个柔性的球面网壳结构。

由于节点处的连接件和杆件均为铰接，因此在其承载过程中产生较多的应力变形。

因此，设计铰接节点球面网壳结构的过程较为复杂。

二、球面网壳结构的稳定性分析球面网壳结构的稳定性研究是结构设计和计算的重要内容。

与其他结构相比，球面网壳结构的稳定性分析存在以下特点：1.不规则形状球面网壳结构的形状不规则，因此其受力状态也较为复杂。

在球面网壳结构的设计过程中，需要充分考虑其形状和受力状态，进行合理的分析和设计。

2.不同的节点类型根据节点的不同类型，球面网壳结构分为刚性节点球面网壳和铰接节点球面网壳两种形式。

在分析结构的稳定性时，需要分别考虑刚性节点和铰接节点的情况。

3.多个节点位移相互影响球面网壳结构中的多个节点之间存在位移相互影响的情况。

因此，在分析结构的稳定性时，需要考虑节点位移的影响，确定每个节点的位移方向和大小。

4.复杂的边界条件球面网壳结构的边界条件比较复杂，需要考虑框架的边缘受力状态、球面曲率半径、节点位置等多个因素的影响。

因此，在分析结构的稳定性时，需要考虑各种边界条件的复杂性，并进行相应分析和计算。

三、球面网壳结构的稳定性控制球面网壳结构的稳定性受到许多因素的影响，例如材料的强度、形变能力、边界条件等。

目录1 题目 (1)2 验算依据 (1)3 计算简图 (2)4 荷载信息 (2)5 ANSYS有限元分析 (3)5.1 结构线性整体稳定 (3)5.2 完善结构几何非线性整体稳定 (5)2.1 带缺陷结构大位移几何非线性整体稳定 (7)2.2 带缺陷结构大位移弹塑性非线性整体稳定 (10)6 稳定性系数和性态进行分析、比较 (13)6.1 极限承载力分析 (13)6.2 初始缺陷分析 (14)6.3 带初始缺陷的大位移弹塑性分析 (15)附录本文采用的ANSYS有限元分析命令流 (16)1题目单层球面网壳，跨度40m，矢跨比f／L=1／5，网格环向分6份。

杆件材料：Q235，截面均取圆钢管Φ114.0X4.0，网壳节点刚接，周边边界点为支座节点，且为固定铰支座。

结构网格形式采用联方型网壳满跨均布恒载(q)：结构自重(杆件部分)+屋面(0.3kN/m2)半跨均布活载(p)：p =0.5q整体稳定计算内容结构线性整体稳定—给出整体失稳稳定系数值(20)和模态(6)；完善结构几何非线性整体稳定—给出荷载-位移曲线；带缺陷结构大位移几何非线性整体稳定—给出荷载-位移曲线；带缺陷结构大位移弹塑性非线性整体稳定—给出荷载-位移曲线；对各种稳定性系数和性态进行分析、比较，说明特点。

为了便于比较，取各网壳最高点的λ－w曲线作为比较的对象。

2验算依据主要计算根据是：1）罗老师提供的数据文件和资料，以及草图等。

2）我国现行有关规范、规程，主要包括：《建筑结构荷载规范》（GBJ50009-2001）《建筑抗震设计规范》（GBJ50011-2001）《钢结构设计规范》（GBJ50017-2003）《网架与网壳技术规程》（JGJ61-2003）《建筑钢结构焊接技术规程》（JGJ81-2002）《钢结构工程施工及验收规范》（GB50205-2001）本次验算采用了通用有限元软件Ansys进行计算。

3计算简图计算简图4荷载信息1)恒载(1) 屋面 0.30kN/m2(2) 自重（包括表面覆盖） 0.55 kN/m2分项系数：1.2则分散到每个节点上的力为 1.2x3.14x20x20x(0.3+0.55)/109=11.8 kN/m22) 活载(1) 取恒载一半 0.43 kN/m2分项系数：1.4只加半跨则分散到每个节点上的力为 1.4x3.14x20x20/2x0.43/61=6.20 kN/m2加载图5ANSYS有限元分析5.1结构线性整体稳定ANSYS分析结果前20阶稳定系数如下：***** INDEX OF DATA SETS ON RESULTS FILE *****SET TIME/FREQ LOAD STEP SUBSTEP CUMULATIVE1 0.52381 1 1 12 0.52455 1 2 23 0.69295 1 3 34 0.71452 1 4 45 0.81106 1 5 56 0.84886 1 6 67 1.0803 1 7 78 1.1275 1 8 89 1.1316 1 9 910 1.1498 1 10 1011 1.2856 1 11 1112 1.3440 1 12 1213 1.4580 1 13 1314 1.5013 1 14 1415 1.5428 1 15 1516 1.6217 1 16 1617 1.6677 1 17 1718 1.7336 1 18 1819 1.7860 1 19 1920 1.9184 1 20 20其中前六阶失稳模态如下：1JAN 5 2007第1阶失稳模态第2阶失稳模态第3阶失稳模态第4阶失稳模态JAN 5 2007JAN 5 2007第5阶失稳模态第6阶失稳模态5.2完善结构几何非线性整体稳定(1)我们仍然假定顶点产生1000mm的位移时，结构达到承载力极限。

泰姆科节点铝合金单层穹顶结构稳定性能分析徐帅;陈志华;王小盾;刘红波【摘要】针对铝合金单层穹顶结构中常用的泰姆科节点，通过有限元精细化模拟的方式得到其节点的转动刚度。

并且研究了一跨度为95,m 的泰姆科节点铝合金单层球面穹顶实际工程的稳定性，对比在考虑泰姆科节点转动刚度和假定节点为刚接情况两种情况下，穹顶结构的屈曲分析特征值和考虑几何初始缺陷后的结构稳定性能。

分析结果表明：泰姆科节点属于半刚性节点的范畴。

在考虑节点的实际转动刚度之后，结构的屈曲特征值有所降低，节点刚度对结构的稳定性有一定程度的影响。

通过系统地研究泰姆科节点铝合金单层穹顶结构稳定性，可以为工程提供一定参考。

%The rigidity of Temcor joint which is widely used in aluminum single-layer dome is obtained by means of finite element analysis(FEA). The stability of an aluminum single-layer dome with a span of 95,m is investigated. To compare the differences between rigid joint dome and semi-rigid joint dome,buckling and stability analysis consider-ing the initial geometric defect are made by using FEA. Analysis results showed that Temcor joint is semi-rigid. After considering the actual rigidity of joint,the buckling eigenvalue of the structure declines,which means that the rigid-ity of the joint has an effect on the stability of the aluminum single-layer dome. The systematic stability analysisin this paper can provide reference for similar projects.【期刊名称】《天津大学学报》【年(卷),期】2015(000)0z1【总页数】7页(P32-38)【关键词】泰姆科节点;铝合金单层穹顶结构;节点刚度;稳定性【作者】徐帅;陈志华;王小盾;刘红波【作者单位】天津大学建筑工程学院，天津 300072;天津大学建筑工程学院，天津 300072; 滨海土木工程结构与安全教育部重点实验室，天津 300072;天津大学建筑工程学院，天津 300072; 滨海土木工程结构与安全教育部重点实验室，天津300072;天津大学建筑工程学院，天津 300072; 滨海土木工程结构与安全教育部重点实验室，天津 300072【正文语种】中文【中图分类】TU318铝合金因其质轻、耐腐蚀及良好的加工性能，与空间结构的结合使得铝合金的优势发挥更为充分．铝合金与钢材相比，密度仅为钢材的1/3，在相同跨度下，铝结构可减轻自重20%,～30%,，轻盈的结构体系可跨越更大的跨度，同时自重的降低减小了下部支座的负担，轻盈的结构有利于抗震设计[1]．对于空间网壳结构而言，其稳定问题一直备受各国学者的关注[2]．经过多年来的研究，目前已经有比较成熟的计算结构稳定性方面的分析方法和相关理论．然而在众多对网壳结构稳定的影响因素的分析中，主要的关注点在于穹顶结构体系、结构采用的形式以及荷载情况、结构支座边界条件、结构初始缺陷等方面，而在节点刚度方面的研究和关注度还相对缺乏．日本的Shiro等[3]研究了考虑节点半刚性连接和初始缺陷的球面网壳的极限承载力理论，并对结构所用的半刚性节点提出了合理的分析计算方法．英国的Mohammad[4]也针对节点刚度开展了一系列的研究，得到了许多球面穹顶结构稳定性方面的成果．我国许多学者也对节点刚度对穹顶结构稳定的影响进行了一定的研究[5-13]．本文针对铝合金泰姆科(Temcor)节点单层球面穹顶结构开展了稳定性能研究，分析了节点刚度对其的影响．1.1 泰姆科节点对于铝合金单层穹顶结构而言，其常用的节点类型为泰姆科节点体系，如图1所示，由H型铝合金杆件、上下连接盘以及虎克螺栓3部分组成．在安装时首先将虎克螺栓穿过H型铝合金杆件的翼缘和连接盘的螺栓孔，之后通过专用的设备完成安装．虎克螺栓的构造如图2所示，在安装中，螺栓杆受到安装设备的单向拉力作用，同时套环受到推挤而变形，套环被挤压进螺栓杆螺纹，使套环和螺栓杆形成紧密连接．1.2 工程概况新疆已建成的实际单层铝合金穹顶工程，共有3个形式相同的穹顶结构，其结构跨度均为95,m，位于新疆自治区哈密市伊吾县白石湖矿区，在2013年开始施工主体骨架工程，并于2014年11月完成外部蒙皮工程，如图3所示．在结构中采用的典型节点和杆件尺寸以及蒙皮板与杆件连接的详图如图4所示．穹顶结构安装于距地面6.6,m的挡煤墙上，上部穹顶结构高约25,m．挡煤墙共设置60个扶壁柱，柱顶部为混凝土环梁，60个支座均布于环梁上，且支座均为铰接支座．在本工程中采用的杆件和连接板材料均为6061-T6状态的铝合金，上下连接板与杆件之间通过虎克螺栓采用专门工具完成连接．结构杆件尺寸均采用H255,mm×120,mm×4,mm×6,mm的H型铝合金杆件，连接板的尺寸为直径400 mm，厚度10 mm，如图5所示．杆件所用铝合金的弹性模量为70kN/mm2，泊松比为0.3．在本文的分析中仅针对上部的铝合金单层穹顶，建模过程不考虑下部的混凝土柱和混凝土连梁，结构模型如图6所示．结构受到的恒荷载为0.2 kN/m2，活荷载为0.5 kN/m2，在分析中考虑荷载为均匀分布于整个穹顶结构．1.3 泰姆科节点转动刚度分析如果在分析中简单地将泰姆科节点视为刚接节点，不考虑泰姆科节点的承载能力和刚度，得到的结果很可能高于穹顶结构的实际性能，导致结构设计的安全性降低，容易在结构施工或使用过程中出现问题．因此，通过有限元软件ABAQUS对新疆工程中的泰姆科节点进行精细化模拟．模拟中采用软件自带的非协调单元C3D8I模拟泰姆科节点的杆件和上下连接板．为了简化分析，在杆件的本构关系中，取名义屈服强度f0.2为254,MPa，极限抗拉强度为290,MPa；连接板的本构关系中，取名义屈服强度f0.2为256,MPa，极限抗拉强度为313,MPa；虎克螺栓假定为刚体，不考虑其在模拟分析中的变形情况．采用上述方法建立的泰姆科节点平面外受力有限元模型如图7所示．通过有限元分析得到的泰姆科节点的变形情况如图8所示，泰姆科节点向平面外弯曲，模型整体的变形呈对称性．通过分析得到泰姆科节点平面外所受弯矩和连接盘中心竖向位移之间的关系曲线，如图9所示．根据绘制的曲线可得到铝合金泰姆科节点的初始刚度约为1.06×104,kN·m/rad，根据文献[14]中对节点的划分，泰姆科节点属于半刚性节点的范畴．1.4 假定节点为刚接情况时结构的稳定性分析1.4.1 穹顶结构特征值屈曲分析针对铝合金穹顶结构在ANSYS有限元分析软件中建立节点为完全刚接的模型，选用Beam188梁单元模拟穹顶中杆件．对穹顶结构进行线性的特征值屈曲分析，在这个分析中将结构考虑为理想弹性完善结构，得到结构的前6阶模态如图10所示，各个模态所对应的屈曲荷载特征值如表1所示．由于穹顶结构自身的对称性，各阶模态的整体变形对称，从图10可看出结构1阶模态为结构下部出现环形屈曲，之后几阶模态均为局部屈曲．1.4.2 考虑结构初始缺陷的非线性分析在结构的实际施工过程中，难免会出现一定的安装偏差，造成结构在实际使用中与理想结构存在差异．为了在分析铝合金单层穹顶结构稳定性时考虑结构初始缺陷的影响，根据空间网格技术规程的规定，采用结构线性屈曲分析中得到的第1阶整体屈曲失稳时的模态，缺陷的最大计算值按照网壳跨度的1/300取值(铝合金单层穹顶跨度为95,m，因此初始缺陷最大计算值为0.317,m)．通过运用ANSYS有限元软件对铝合金穹顶结构进行全过程分析，绘制结构位移最大的节点的荷载-位移曲线，如图11所示．从图中可以看出在刚接节点情况下，结构的稳定极限荷载为荷载标准值的5.57倍，满足规程中规定的大于4.2倍荷载标准值的规定.1.5 考虑节点实际刚度时穹顶结构的稳定性分析1.5.1 穹顶结构特征值屈曲分析针对铝合金穹顶结构在ANSYS有限元分析软件中建立考虑节点实际转动刚度的模型，在节点处采用ANSYS中的弹簧单元Matrix27，在分析中先建立穹顶结构模型中关键点及连线；之后，确定模型中的关键点，在节点处需要令同一个坐标点生成多个关键点；通过编程，使得新生成的每个关键点与相应的1个杆件相连；定义弹簧单元的属性，给出6个自由度的转动刚度情况；最后在关键点处形成相应的刚度单元号及节点号，并设置弹簧单元．根据文献[15]中试验得到的泰姆科节点平面内转动刚度(2.73×102,kN·m/rad)，同样对穹顶结构进行线性的特征值屈曲分析，得到结构的前6阶模态，如图12所示，各个模态所对应的屈曲荷载特征值如表2所示．1.5.2 考虑结构初始缺陷的非线性分析在分析考虑泰姆科节点转动刚度模型时，考虑网壳结构几何非线性的情况下，同样采用结构线性屈曲分析中得到的第1阶整体屈曲失稳时的模态，缺陷的最大计算值按照网壳跨度的1/300取值，得到考虑了几何初始缺陷的半刚接节点穹顶结构的竖向位移最大点的荷载-位移曲线，如图13所示．从图中可以看出，在考虑泰姆科节点转动刚度情况下，结构的稳定极限荷载为荷载标准值的4.0倍，略低于规程中规定的大于4.2倍荷载标准值的规定，但基本满足要求．相比于将节点假定为刚接的情况，铝合金单层穹顶结构在考虑了节点转动刚度之后，承载力会有一定程度的降低，说明节点刚度的减弱会导致结构的整体稳定性下降．本文介绍了铝合金单层穹顶结构中常用的泰姆科节点，结合使用泰姆科节点的铝合金单层穹顶实际工程，通过有限元分析得到泰姆科节点平面外的转动刚度，并对比假定节点刚接和考虑节点刚度的两个铝合金单层穹顶结构模型结构的稳定情况，得到如下结论．(1) 通过对泰姆科节点进行精细化分析，得到泰姆科节点的弯矩-转角关系曲线，其属于半刚性节点的范畴．(2) 通过铝合金单层穹顶结构的屈曲分析，可以发现前6阶的模态很相似，各阶的屈曲特征值也比较接近，主要的变形出现在结构下部的几圈杆件．(3) 在考虑节点的实际转动刚度之后，结构的屈曲特征值有所降低，降低约15%,，说明节点刚度对结构的稳定性有一定程度的影响．(4) 在考虑结构的初始缺陷之后，无论是节点假定为刚接的铝合金单层球面穹顶结构，还是考虑节点实际刚度的结构，两者的极限承载力均有明显的降低．节点为刚接情况的穹顶结构模型得到的结构极限承载力荷载因子为5.57，满足规程中大于4.2倍荷载标准值的规定．而考虑节点转动刚度的模型极限承载力荷载因子约为4.0，基本满足规程要求．(5) 建议在实际设计中不仅对铝合金单层穹顶结构进行全过程的稳定性分析，还应考虑节点的实际转动性能．【相关文献】［1］刘锡良. 天津市平津战役纪念馆[C]//空间结构新材料新技术研讨会论文集. 北京：中国土木工程学会，1998. Liu Xiliang. Pingjin Campaign Memorial in Tianjin[C]// Proceedings of New Material and New Technique of Spatial Structure. Beijing：China Civil Engineering Society，1998(in Chinese).［2］韩庆华，芦燕，徐杰. 非落地钢管桁架拱结构稳定性能[J]. 天津大学学报：自然科学与工程技术版，2014，47(11)：979-986. Han Qinghua，Lu Yan，Xu Jie. Stability behavior of unlanding latticed steel tubular arch[J]. Journal of Tianjin University：Science and Technology，2014，47(11)：979-986(in Chinese).［3］ Shiro Kato，Itaru Mutoh，Masaaki Shomura. Collapse of semi-rigidly jointed reticulated domes with initial geometric imperfections[J]. Journal of Constructional Steel Research，1998，48(2/3)：145-167.［4］ Mohammad Reza Chenaghlou. Semi-Rigidity of Connections in Space Structures[D]. Guildford：Department of Civil Engineering，University of Surrey，1997.［5］张竟乐，赵金城，许洪明. 单层网壳板式节点的刚度分析[J]. 工业建筑，2005，35(4)：88-90. Zhang Jingle，Zhao Jincheng，Xu Hongming. Analysis of stiffness of gusset-type joint for single-layer reticulated shells[J]. Industrial Construction，2005，35(4)：88-90(in Chinese).［6］张竟乐，赵金城. 节点刚度对凯威特型单层球面网壳稳定性的影响[J]. 空间结构，2004，10(2)：43-45. Zhang Jingle，Zhao Jincheng. The influence of joint stiffness exerted on the stability of Kiewtte-type singlelayer reticulated shells[J]. Spatial Structures，2004，10(2)：43-45(in Chinese).［7］苏玉红. 节点刚度对网壳结构稳定影响的研究[D]. 南京：东南大学土木工程学院，2005. Su Yuhong. Research on the Effect of Joints Stiffness on the Stability of Reticulated Shells[D]. Nanjing：School of Civil Engineering，Southeast University，2005(in Chinese).［8］王星，董石麟，完海鹰. 焊接球节点刚度对网壳内力和挠度的影响分析[J]. 空间结构，1996，2(4)：34-40.Wang Xing，Dong Shilin，Wan Haiying，The influence of stiffness of welded spherical joints on internal force and displacement of space trusses[J]. Spatial Structures，1996，2(4)：34-40(in Chinese).［9］王星，董石麟. 考虑节点刚度的网壳杆件切线刚度矩阵[J]. 工程力学，1999，16(4)：24-32. Wang Xing，Dong Shilin. Tangent stiffness matrix of members of latticed shell considering joint’s stiffness[J]. Engin eering Mechanics，1999，16(4)：24-32(in Chinese). ［10］罗永峰，沈祖炎. 网壳结构节点体对其承载性能的影响[J]. 同济大学学报，1995，23(1)：21-25. Luo Yongfeng，Shen Zuyan. Effects of the joint size of the reticulated shell on its loading capacity[J]. Journal of Tongji University，1995，23(1)：21-25(in Chinese).［11］崔美艳. 半刚性节点单层球面网壳的稳定性分析[D].哈尔滨：哈尔滨工业大学土木工程学院，2006. Cui Meiyan. Stability Analysis of Single Layer Spherical Reticulated Shells with Semi-Rigidity of Joint System [D]. Harbin：School of Civil Engineering，Harbin Institute of Technology，2006(in Chinese).［12］单晨. 毂形节点承载力分析及其对单层球面网壳整体稳定性影响[D]. 天津：天津大学建筑工程学院，2010. Shan Chen. Analysis of Hub-Shape Inlay Joint and Its Influence on the Stability of Single-Layer Lattice Domes [D]. Tianjin：School of Civil Engineering，Tianjin University，2010(in Chinese).［13］ Ma H H，Fan F，Shen S Z. Numerical parametric investigation of single-layer latticed domes with semi-rigid joints[J]. Journal of the International Association for Shell and Spatial Structures(IASS)，2008，49(2)：99-110.［14］ Kishi N，Chen W F. Moment-rotation relations of semirigid connections with angles[J]. Journal of Structural Engineering，ASCE，1990，116(7)：1813-1834.［15］卜宜都. 曹妃甸储煤仓铝合金网壳结构分析[D]. 天津：天津大学建筑工程学院，2013. Bu Yidu. Structural Mechanical Analysis on Aluminum Alloy Dome of Caofeidian Coal Storage[D]. Tianjin：School of Civil Engineering，Tianjin University，2013(in Chinese).。

K8型单层球面网壳的弹塑性稳定
曹正罡;范峰;沈世钊
【期刊名称】《工业建筑》
【年(卷),期】2007(37)4
【摘要】对1 200多例实际尺寸的K8型单层球面网壳进行双重非线性全过程分析,求得它们的极限承载力,并系统考察初始缺陷和荷载不对称分布等因素对网壳稳定性能的影响,重点讨论材料非线性对网壳极限承载力的影响。

通过这种大规模参数分析研究,较全面揭示K8型单层球面网壳弹塑性稳定性能的规律性,在此基础上对以往仅考虑几何非线性影响的K8型网壳极限承载力实用公式进行修正。

【总页数】4页(P69-72)
【关键词】单层球面网壳;稳定;极限承载力;弹塑性
【作者】曹正罡;范峰;沈世钊
【作者单位】哈尔滨工业大学土木工程学院
【正文语种】中文
【中图分类】TU330.1
【相关文献】
1.支座形式对K8型单层球面网壳非线性动力稳定的影响 [J], 李桐栋;路维;孙超;杨凯;王国菊;张翠英
2.半刚性型螺栓球节点单层K8型网壳弹塑性稳定分析 [J], 范峰;马会环;沈世钊
3.基于strand7的K8单层球面网壳的弹塑性稳定分析 [J], 王剑文
4.火灾下K8型单层网壳弹塑性稳定承载力计算 [J], 白音;石永久;王元清
5.K 6型单层球面网壳的弹塑性稳定 [J], 曹正罡;范峰;沈世钊
因版权原因，仅展示原文概要，查看原文内容请购买。

某单层球面网壳结构整体稳定性分析与研究摘要本文针对目前中国规范《空间网格结构技术规程》中提到的网壳的稳定性计算的三种方法进行了比较分析和研究。

并且通过对一个实际工程中的单层网壳进行研究，分析和探讨了影响单层网壳稳定性的若干参数，得到了一些有价值的设计经验供参考。

关键词单层网壳；整体稳定；非线性屈曲；几何非线性；材料非线性中图分类号TU356 文献标识码 A 文章编号1673-9671-(2012)072-0092-02网壳结构虽然有大的跨度，但由于其高跨比小，整体结构在外荷载作用下表现出强烈的大位移非线性效应，在计算分析中必须考虑这种非线性效应。

又由于网壳结构的大部分构件呈受压状态，典型的破坏形式是失稳破坏。

这种破坏的突发性，使得损失更加严重。

网壳结构发生失稳破坏时钢材实际承受的应力水平很低，常常仅为30 MPa-40 MPa，远未充分发挥钢材的强度优势，这说明网壳结构的稳定研究具有非常重要的意义。

网壳结构的失稳从几何学原理和能量原理的观点来看，都可以归结为一种转移，是处于高位能的结构由平衡的临界状态向低位能的稳定平衡状态的转移。

发生平衡转移的那个瞬间状态，就是临界状态。

1）从变形角度来说，失稳在实际上也可以被认为是一种从弹性变形到几何变形的变形转移。

2）从能量的角度来说，结构失稳就是储存在结构中的应变能形式发生转换。

就网壳结构来说，结构失稳时部分薄膜应变能向弯曲应变能转变。

一般单层网壳均应进行整体稳定性计算。

根据之前的研究和实际工程经验总结，影响网壳结构稳定性的主要因素有曲面形状、网格密度、荷载分布、边界条件、节点刚度、结构刚度、非线性效应、初始缺陷等。

由于篇幅有限，本文主要研究了非线性效应的对网壳整体稳定的影响，非线性效应又可分为几何非线性和材料非线性。

1 工程概况图1 网壳结构形式财富广场商贸城穹顶网壳工程钢结构图纸设计使用年限为50年，建筑安全等级为二级。

其主要技术参数为：1）网壳平面尺寸：D=46 m2）网壳失高：f=12 m3）支承方式：周边多点支承4）网壳总重：56吨2 规范上单层网壳整体稳定性计算方法总结《空间网格结构技术规程》中关于网壳的整体稳定性计算提供了三种方法，整理如下：1）用考虑几何非线性的有限元法进行荷载—位移全过程分析，分析中假定材料保持为弹性。

单层球面网壳结构的弹塑性稳定分析摘要：考虑结构的几何非线性和材料的弹塑性，对一个K6型单层球面网壳进行稳定性分析。

通过对比分析发现，此结构的弹塑性稳定承载力约为其弹性稳定承载力的50％，材料的弹塑性对不对称荷载作用下的稳定承载力的影响更显著。

关键词：单层球面网壳；弹塑性；稳定性；极限承载力网壳结构的稳定性是单层网壳分析设计中的一个关键问题，单层网壳和厚度较小的双层网壳都存在失稳的可能性。

研究表明[1]，影响网壳结构稳定性的主要因素包括：非线性效应；初始缺陷；曲面形状；结构刚度；节点刚度；荷载分布；边界条件。

因此，网壳规程第4.3.4条规定，通过网壳结构的几何非线性全过程分析、并考虑初始缺陷、不利荷载分布等影响而求得的第一个临界点处的荷载值，作为该网壳的极限稳定承载力。

通过规定网壳结构的极限稳定承载力与实际荷载之比大于安全系数K来保证结构的整体稳定性。

由于网壳是一种缺陷敏感性结构，初始缺陷将明显地降低网壳的临界荷载。

许多试验和理论分析也证实结构的几何偏差会降低临界荷载的30％－40％[2]。

因此，网壳规程规定了稳定安全系数K可取为5，该系数是一经验系数，确定时考虑到以下因素：荷载等外部作用和结构抗力的不确定性可能带来的不利影响；计算中未考虑材料弹塑性可能带来的不利影响；结构工作条件中的其他不利因素。

我国网壳规程把材料弹塑性的影响放在安全系数K中考虑，而K依据经验来确定，无法真实地考虑材料弹塑性。

本文利用大型通用有限元软件ANSYS对单层网壳结构进行双重非线性分析，得到了较为精确地网壳结构极限承载力。

工程实例问题描述。

一个K6型施威德勒型球面网壳，球面半径36m，底平面跨度50m，失高10.1m。

网壳结构的所有杆件均采用的Q235钢管，周边铰支。

分析参数。

本文的有限元分析采用ANSYS软件中的BEAM189单元。

BEAM189单元为3结点二次梁元，基于Timoshenko梁元理论，该梁元在非线性分析中能考虑大变形、大转角和大应变效应。