空间混合资料讲解

空间向量混合积空间向量混合积是向量分析中的一个重要概念，它可以用来判断空间中三个向量的方向关系以及确定向量的体积和方向。

在三维欧几里得空间中，给定三个向量$\overrightarrow{a}=(a_1,a_2,a_3)$，$\overrightarrow{b}=(b_1,b_2,b_3)$和$\overrightarrow{c}=(c_1,c_2,c_3)$，它们的混合积定义为：$$\overrightarrow {a}\cdot (\overrightarrow {b}\times\overrightarrow {c})=\begin{vmatrix} a_1&a_2&a_3\\b_1&b_2&b_3\\ c_1&c_2&c_3\\ \end{vmatrix}$$其中，$\overrightarrow{b}\times \overrightarrow{c}$表示$\overrightarrow{b}$和$\overrightarrow{c}$的叉积，即：$$\overrightarrow {b}\times \overrightarrow{c}=\begin{bmatrix}b_2c_3-b_3c_2\\b_3c_1-b_1c_3\\b_1c_2-b_2c_1\end{bmatrix}$$混合积实际上是一个标量，它表示由$\overrightarrow{a}$，$\overrightarrow{b}$和$\overrightarrow{c}$所形成的平行六面体（如图所示）的有向体积，其方向依赖于$\overrightarrow{a}$，$\overrightarrow{b}$和$\overrightarrow{c}$的顺序。

混合积有着很多重要的应用，例如：1. 判断三个向量的方向关系如果向量$\overrightarrow{a}$，$\overrightarrow{b}$和$\overrightarrow{c}$的混合积为正数，那么它们的方向关系符合右手法则。

空间向量混合积空间向量是描述物理空间中物体位置和方向的一种数学工具，往往用于计算三维空间中的物理问题。

空间向量混合积是指三个空间向量的叉积与另一个空间向量做点积所得到的一个标量，通常也被称作混合积（scalar triple product），它可以表示空间中的体积、面积以及方向。

在物理学、工程学等领域中，空间向量混合积具有广泛的应用。

空间向量混合积可以用简单的公式来表示：$[\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}] =\boldsymbol{a} \cdot (\boldsymbol{b} \times \boldsymbol{c})$其中，$[\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}]$ 表示空间向量混合积，$\boldsymbol{a}$、$\boldsymbol{b}$、$\boldsymbol{c}$ 分别表示三个空间向量，$\times$ 表示向量的叉积运算，$\cdot$ 表示向量的点积运算。

这个公式也可以写成：$[\boldsymbol{a},\boldsymbol{b},\boldsymbol{c}] =det(\boldsymbol{a},\boldsymbol{b},\boldsymbol{c})$其中 $det$ 表示行列式。

空间向量混合积的值可以用来判断三个向量是否共面，如果其值为 $0$，则表示三个向量共面；如果其值大于 $0$，则表示这三个向量的方向按右手法则满足正向，也即右手坐标系；如果其值小于 $0$，则表示这三个向量的方向按左手法则满足正向，也即左手坐标系。

空间向量混合积还可以表示所在平行六面体所占据的体积。

例如，三个向量 $\boldsymbol{a}$、$\boldsymbol{b}$、$\boldsymbol{c}$ 共面时，其混合积为 $0$，表示这三个向量围成面积为 $0$ 的平行四边形。

色彩混合训练空间混合空间混合是中性混合的一种。

中性混合是基于人的视觉生理特征所产生的视觉色彩混合，它并不是真正的色彩混合，而是通过人们先看到的颜色的视觉残留加载到后看到的颜色上所产生的视觉混合。

当两种或两种以上的颜色并置时，其混合色彩的明度是混合前两色明度的平均值，纯度有所下降。

中性混合主要有旋转混合和空间混合两种方式。

.1旋转混合旋转混合是指将两种或多种颜色并置于一个圆盘上，通过动力令其快速旋转，我们会感受到另一种新色彩的产生，如图4-1，旋转混合并未将两种颜色真正混合在一起，而是由于转动回旋版使眼睛的视网膜在同一位置上产生不断快速更换色彩刺激的缘故，从而得到视觉内的色彩混合效果。

旋转速度越快则越容易发生混合，当旋转停止，色彩又恢复到原样。

参与混合的色彩面积与我们调配色彩时各色量的比例类似，直接影响混合的效果。

图4-1.2空间混合将众多不同颜色的小色块并置在一起，当他们在视网膜上的投影小到一定程度时，这些不同的颜色刺激就会同时作用到视网膜上，非常邻近的感光细胞，以致眼睛很难将它们独立的分辨出来，就会在视觉中产生色彩混合的效果，这种混合方式必须借助空间距离，才能产生新的视觉效果，我们称之为空间混合，如图4-2。

新印象派修拉、西涅克等人创造的点彩画法、电子分色、套色印刷、彩色电视、纺织物都是利用色彩的空间混合原理而获得一种新的视觉效果。

图4-2凡互补色关系的色彩按一定比例进行空间混合时，可得到无彩色系的灰和有彩色系的灰。

红与绿的空间混合，可得到不同程度的灰红、灰、绿灰；红与蓝的空间混合会获得一种中明度的紫色；蓝色与黄色的空间混合，可获得一种跳跃的绿色。

凡非负互补关系的色彩进行空间混合时，产生两色的中间色。

有彩色系的色与无彩色系的色，经过空间混合时将产生两种色的中间色，如红与灰进行空间混合，可得到不同程度的红灰红与白进行空间混合，可得到不同层明度的浅红。

空间混合方法获得的新色相非常丰富多彩，且有一种跳跃感，适合表现光感。

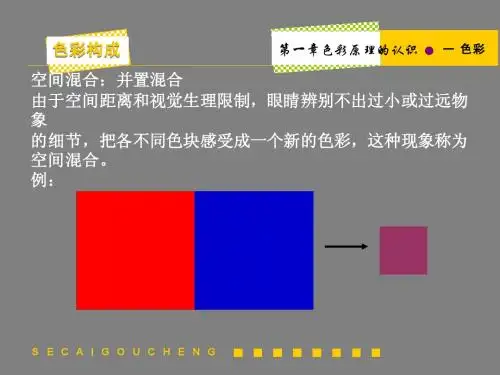
•空间混合也称为并置混合，是指将许多小色块并置在画面上，在一定距离外观看，当它们投影到视网膜上时，由于视觉生理特点，这些不同的色块刺激就会同时作用到视网膜上，xiang邻近各部位的感光细胞辨别不出过小或过远的色彩，就会在视觉中产生色彩混合，自动产生出另外一种颜色感。

由于这种混合受到空间距离和空气清晰度的影响，我们称之为空间混合。

•在空间混合中，颜料本身并未进行混合。

•要取得良好的空间混合效果需注意的是，一是用来并置的小色块的形状，二是小色块之间的对比要强烈。

•作业空间混合练习：选择一幅大家熟知的画面，明星、模特、政治家或风景、绘画图像为蓝本创作一幅色彩空间混合图画，尺寸为20+20cm。

第五章色彩对比•色彩对比是色彩构成整个课程中的组成核心之一。

•色彩对比普遍存在于一切色彩之间。

其本质是通过对比的手段强调反差，增强视觉效果。

•色彩的对比主要为色三元对比。

即色彩的三要素，A色相、B明度、C纯度之间的对比。

A色相对比•因色相之间的差别形成的对比称为色相对比。

在伊顿色相环上，0到90°以内的邻近色之间的对比称为弱对比。

容易获得协调和谐统一的效果，90°以上距离较远的两色之间的对比也叫做强对比，对比色对比。

效果强烈、醒目。

•而类似色对比又可分为a同类色，类似色与邻近色对比。

b对比色对比又包括原色、间色和补色对比。

•a类似而对比同类色对比,是指色环上非常临近的色彩之间的对比——0到15°之间的对比。

其特点是变化微妙、细腻。

类似色对比，色环上两色相之间的距离角度差约为30——45°左右以内的对比，是色彩的弱对比。

邻近色对比，在色环上两色相距60——90°左右以内的对比称为邻近色对比。

如橙与红，蓝与青等。

其特点是在统一中不失对比变化。

•b对比色对比原色对比，红黄蓝三原色之间的对比，色相距离为120°。

它们之间的对比属于强烈的色相对比。

间色对比，橙色、绿色与紫色为三原色相混合所得的间色，色相距离也为120度。

空间向量的混合积与体积空间向量的混合积是向量运算中的一个重要概念，它能够帮助我们求解三维空间中的体积。

本文将详细介绍空间向量的混合积的定义、计算方法以及与体积的关系。

一、空间向量的混合积的定义在三维空间中，我们可以用向量来表示一个点的位置。

空间中的三个向量a、b、c的混合积定义为：(a × b) · c其中，×表示向量的叉乘，·表示向量的点乘。

混合积的结果是一个标量，表示由向量a、b和c所确定的平行六面体的有向体积。

二、空间向量的混合积的计算方法要计算空间向量的混合积，可以按照以下步骤进行：1. 首先求出向量a和向量b的叉乘，得到一个新的向量d：d = a × b2. 然后将向量d与向量c进行点乘，并求出结果：(d · c)3. 最后得到的结果即为空间向量的混合积。

三、空间向量的混合积与体积的关系空间向量的混合积与体积之间有着密切的联系。

根据定义，空间向量的混合积表示了由向量a、b和c所确定的平行六面体的有向体积。

具体而言，当向量a、b和c所确定的平行六面体为直角六面体时，其体积可以直接由混合积计算得出。

设直角六面体的三边长分别为a、b和c，则其体积V等于混合积的绝对值的一半：V = |(a × b) · c| / 2当向量a、b和c不构成直角六面体时，可以通过将空间分解为若干个直角六面体来求解体积。

具体方法是通过向量的投影将空间分解为多个平行于某个坐标轴的直角六面体，然后计算每个直角六面体的体积，并将其相加得到总体积。

需要注意的是，混合积的计算结果为有向体积，其正负性表示了平行六面体的定向。

当混合积为正时，表示平行六面体的定向与坐标系右手定则一致；当混合积为负时，表示平行六面体的定向与坐标系右手定则相反。

结论本文介绍了空间向量的混合积的定义、计算方法以及与体积的关系。

空间向量的混合积是一个重要的向量运算，在计算三维空间中的体积时起到关键作用。

空间混合名词解释
嘿，你知道啥是空间混合不？哎呀，这可神奇啦！就好像你把各种
颜色的小点点撒在一块儿，远看的时候，它们就好像融合在一起变成
了一种新颜色。

举个例子哈，你看那些彩色的印刷品，凑近了看都是
一个个小点点，可离远了看，哇，那就是一幅完整又漂亮的画儿呀！
空间混合就像是一场奇妙的魔术表演！它不是简单地把颜色混在一
起搅拌搅拌哦。

比如说，红色和蓝色的小点点紧密排列，从远处看，
就出现了紫色。

这多有意思呀！这不就跟我们生活中的很多事情一样嘛。

咱就说，有时候我们和不同的人相处，每个人都有自己独特的性格
和特点，就像那些不同颜色的小点点。

但当我们大家聚在一起，相互
影响、相互作用，不就产生了一种新的氛围、新的感觉嘛！这也是一
种空间混合呀！
再想想，音乐也可以这样理解呀！不同的音符、不同的乐器声音，
交织在一起，形成了美妙的乐曲，这不也是一种空间混合嘛。

还有还有，在一个团队里，大家来自不同的背景，有着不同的技能
和想法，当我们共同为了一个目标努力时，就产生了奇妙的化学反应，这也是空间混合的体现呀！
空间混合真的是无处不在，它让这个世界变得丰富多彩，充满了惊
喜和创意。

它让我们看到，单独的个体也许很渺小，但当它们以某种
方式混合在一起时，就能爆发出巨大的能量和魅力。

所以呀，我们要好好去感受和发现空间混合的奇妙之处，让它为我们的生活增添更多的精彩！这就是我对空间混合的理解，你觉得呢？。

空间向量的混合积与体积在数学和物理学中，研究空间向量的混合积与体积是非常重要的。

空间向量是指具有大小和方向的箭头，用来表示空间中的位移、速度、力等物理量。

混合积是一种通过三个向量的叉乘来定义的数。

本篇文章将详细介绍空间向量的混合积的计算方法以及与体积之间的关系。

一、空间向量的混合积的定义与计算方法空间中的向量可以表示为三维坐标系中的三个分量，通常用(i, j, k)表示。

如果我们有三个向量a、b和c，它们的分量分别为(a1, a2, a3)、(b1, b2, b3)和(c1, c2, c3)，那么它们的混合积定义为：V = a·(b×c)其中，"·"表示向量的点乘，"×"表示向量的叉乘。

而叉乘的结果是一个新的向量，可以通过“右手法则”来确定它的方向。

具体计算过程如下：1. 首先，计算向量b和c的叉乘，得到向量d：d = b×c = (b2c3 - b3c2, b3c1 - b1c3, b1c2 - b2c1)2. 然后，将向量a与向量d进行点乘，得到混合积V：V = a·d = a1(b2c3 - b3c2) + a2(b3c1 - b1c3) + a3(b1c2 - b2c1)这样，我们就可以得到三个向量a、b和c的混合积V。

二、混合积与体积之间的关系空间向量的混合积与体积之间有着紧密的联系。

具体而言，当三个向量a、b和c构成一个平行六面体时，该平行六面体的体积等于其混合积的绝对值的一半：V = |a·(b×c)|/2这个结论可以通过对平行六面体进行体积计算的验证来证明。

将平行六面体的一个顶点作为原点，以三个向量a、b和c作为边的向量，我们可以得到平行六面体的体积公式：V = |a·(b×c)|其中，|a·(b×c)|表示空间向量a、b和c的混合积的绝对值。

空间混合知识点总结归纳空间混合是指在三维空间中将不同的元素或物体进行组合和排列，使得它们在空间中形成一种和谐的关系。

在设计、建筑、艺术、工程等领域中，空间混合起着非常重要的作用，它不仅能够给人们带来舒适感和美感，还能够实现实际功能和需求。

通过对空间混合的研究和应用，可以更好地满足人们对于空间的需求，同时也可以拓展空间的应用范围和功能。

二、空间混合的原则1.功能性原则：空间混合的设计应该要符合实际的功能需求，例如厨房、起居室、卧室等功能空间的布局和组合应该合理，便于使用和活动。

2.美学原则：空间混合应该具有美感，即在设计和排列上要追求和谐、统一、平衡，使人在其中感到舒适和愉悦。

3.灵活性原则：空间混合的设计应该具有一定的灵活性，即能够适应不同的使用和需求，可以根据需要进行改变和调整。

4.安全性原则：空间混合的设计应该考虑到安全因素，例如避免有危险的排列、设计和设施，确保人们在其中活动和使用时不会受到伤害。

5.经济性原则：空间混合的设计应该要考虑到实际的经济成本，避免过度的浪费和不必要的花费。

三、空间混合的应用1.建筑设计：在建筑设计中，空间混合可以应用于不同的功能和空间的布局和组合，例如室内的布局、户外的景观设计等，都需要考虑到空间混合的原则和要求。

2.景观设计：在景观设计中，空间混合可以应用于不同的植物、建筑、水景等元素的排列和组合，使得整个景观呈现出一种和谐的感觉。

3.室内设计：在室内设计中，空间混合可以用于不同功能空间的布局和组合，使得整个室内空间更加合理和实用。

4.城市规划：在城市规划中，空间混合可以应用于不同功能和区域的布局和组合，例如商业区和居住区的布局和组合，都需要考虑到空间混合的原则和要求。

5.工程设计：在工程设计中，空间混合可以用于不同设施和设备的布局和组合，使得整个工程更加实用和便于维护。

四、空间混合的案例分析1.建筑设计案例：某一高层建筑，它的室内采用了空间混合的设计，将厨房、客厅、卧室等功能空间进行了合理的布局和组合，使得整个室内空间更加实用和美观。

空间面板混合效应模型
空间面板混合效应模型是运用于面板数据的统计分析方法，该方法融合了时间和空间效应。

在传统面板数据分析中，时间效应指的是不同时间点上的数据差异，而空间效应则指的是不同空间位置上的数据差异。

空间面板混合效应模型考虑到了这两种效应对数据的影响，因此更加准确地分析了面板数据中的相关变量之间的关系。

空间面板混合效应模型可以用来探究空间因素对经济和环境问题的影响。

该方法主要包括四个步骤：首先，应根据研究对象的真实情况设计面板数据；其次，应分析时间和空间效应对面板数据的影响；然后，可以通过时间或空间驱动变量构建混合效应模型；最后，应使用模型评估经济和环境问题的相关因素。

空间面板混合效应模型是一种有效的面板数据分析方法，它能够更全面地考虑数据间的影响，因此被广泛应用于地理学、经济学和环境科学等领域。