《旋转曲面》PPT课件

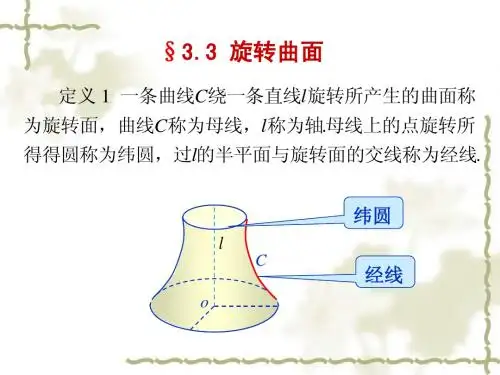
旋转曲面3.3

标。
例1 将下列各曲线绕对应的轴旋转一周，求生成的旋转曲面的方程．
（1）xOz 面上双曲线
x a
绕 x 轴旋转
2 2

z c
2 2
1 分别绕 x 轴和 z 轴；
x
x
x a
2 2

y z
2
2
c
2
1
o z y o z
旋转双叶双曲面
y
（2）xOz 面上双曲线
2
x a
2 2

2
z c
2 2
1 分别绕 x 轴和 z 轴；
. 得旋转单叶双曲面方程为 .
o
x z
2
2
a
2

y b
2 2
a
1
x
z
.
3 旋转锥面两条相交直线
2 x2 y 2 = 0 a2 b z = 0
x
绕 x 轴一周
o
y
3 旋转锥面两条相交直线
2 x2 y 2 = 0 a2 b z = 0
x
z
绕 x 轴一周
点 M 在 S上

M 在过母线 C 上某一点 M 0 ( x0 , y0 , z0 ) 的纬圆上.

M 0 与 M 到轴 l的距离相等（或到轴上一点 M 1的距离相等），且 M 0 M 与 l垂直 .
于是有：
F1 ( x 0 , y 0 , z 0 ) 0 F (x , y , z ) 0 2 0 0 0 M M 1 v M 0M 1 v 或 M M 1 M 0M 1 l ( x x0 ) m ( y y0 ) n ( z z 0 ) 0

第三章 4旋转曲面

z
绕 z 轴旋转一周
.
C
o
y
x
求旋转面的方程
f ( y, z ) 0 曲线 C x 0
得旋转曲面 S
绕 z轴旋转一周
z
M(x,y,z) S
P M
N (0, y1 , z1 )
.
f (y1, z1)=0
z1 z
| y1 | MP
2
S
x2 y2
z
o
z1
C
.
S：f ( x y , z ) 0
一、旋转曲面
通过轴线的平面与旋转曲面相截
所得的平面曲线叫旋转曲面的子

Ｌ
午线。

任意一条子午线都可以当做这个旋转曲面的生成曲线。
Ｃ
求旋转面的方程
1、坐标面上曲线绕坐标轴旋转所成的旋转曲面方程 z
f ( y, z ) 0 曲线 C x 0
绕z轴 C o
y
x
求旋转面的方程
f ( y, z ) 0 曲线 C x 0
பைடு நூலகம்
x y
f (t ) g (t ) cos 2 2 f (t ) g (t ) sin ,(a t b,0 2 )
2 2
z h(t )
例4
x y z 1 ：求直线绕 Z轴旋转所得的旋转曲面的方程 2 1 0
z
例 2：求 oyz 平面上的直线 y=ztanθ 绕 z 轴旋转一周所得旋转曲面方程．
O
y x z tan
2 2
y
x
即： x 2 y 2 z 2 tan2 0

4.3旋转曲面

C
绕y轴旋转一周,所成旋转曲面S S的方程为
f y,

x2 z2 0
o
y
x
xoz平面上的曲线 C f ( x , z ) 0 y0 绕x轴旋转一周,所成旋转曲面S S的方程为
f
o
z
C y

x, y2 z2 0
x
xoy平面上的曲线
f ( x, y ) 0 C z0
所求旋转曲面方程为
x y z 2 2 2 1 2 a a a b
2 2 2
x
P
M0
M
l1
这是由 xoz平面上的双曲线
x z 2 2 1 2 a a b y0
2 2
l2
y
O
z
x
绕z轴旋转而成的单叶旋转双曲面.
z
y
写出下列旋转曲面的方程 (1) 母线
4 x 2 9 y 2 36 : z0
z0 z
2 0
2 2
y x y z z0 0 x2 y2 z2 x 2 y 2 z 2 0 0 0 y0 x 2 y 2 f ( y0 , z0 ) 0 x0 0 f x 2 y 2 , z 0 为S的方程
v i ( 1,0,0 ) 1X 0Y 0Z 0 X 0 v ( 0,Y , Z ) k (0,0,1) Y 0 可设 v ( 0,1, b )
故 l1 的方程为
x a y z 1 b 0
x a y z 设 l1 绕 l2 旋转,所成旋转曲面S l1 : 0 1 b x l1 M ( x , y , z ) 旋转曲面S P M 0 ( x0 , y0 , z0 ) M 0 ( x0 , y0 , z0 ) l1 使得 M 0 M ( x x0 , y y0 , z z0 ) k (0,0,1) M ( x, y, z )

§4.3 旋转曲面

§4.3 旋转曲面一、概念在空间，一条曲线Γ绕着定直线l旋转一周所产生的曲面叫旋转曲面，或称回转曲面。

曲线Γ叫做旋转曲面的母线，定直线l叫做旋转曲面的轴,如图4-3.(1)纬圆：Γ上的任意点M1在旋转时形成一个圆，即为通过点M1且垂直于轴l 的平面与旋转曲面的交线，称为旋转曲面的纬圆（纬线）。

(2)经线：在通过l的平面上，以l为界的半平面都与旋转曲面交成一条曲线（这些曲线在旋转中彼此重合），称为旋转曲面的经线。

二、方程设旋转曲面的母线为旋转轴为直线l：＝＝，其中P0 (x0, y0, z0)为轴l上的一个定点，X, Y, Z为旋转轴l的方向数.设M1(x1, y1, z1)是母线Γ上的任意一点，则过M1的纬圆可以看成是过M1且垂直于旋转轴l的平面与以P0(x0, y0, z0)为中心，为半径的球面的交线，所以过M1(x1, y1, z1)的纬圆的方程为当点M1遍及整个母线Γ时，就得出旋转曲面的所有纬圆，这些纬圆生成旋转曲面.又由于M1(x1, y1, z1)在母线Γ上，所以又有从上述四式中消去参数x1, y1, z1, 最后得一个三元方程F(x, y, z)＝0.即为所求旋转曲面的方程.例1 求直线绕直线旋转一周所得旋转曲面的方程。

解旋转曲面的母线为Γ：，轴为l：.设M1（x1,y1,z1）是母线Γ上的任意点，则过M1的纬圆方程为：由M1在Γ上得（7）由（5）得 z1=z , 由（7）得 x1=2 , y1=1 . 代入（6）得x2+ y2= 5为旋转曲面的方程.一.特殊的旋转曲面：当坐标平面上的曲线Γ绕此坐标平面里的一个坐标轴旋转时，为了求出旋转面的方程，只要将曲线Γ在坐标平面里的方程保留和旋转轴同名的坐标，而以其他两个坐标平方和的平方根来代替方程中的另一坐标即可. 例如Γ：绕y轴旋转所得旋转曲面的方程为F＝0,绕z轴旋转所得旋转曲面的方程为F＝0.结论（规律）：当坐标面上的曲线Γ绕此坐标面上的一个坐标轴旋转，求此旋转曲面的方程，只需将Γ在此坐标面里的方程改变即得，改变的方法是：保留与旋转轴同名的坐标，而以其他两个坐标的平方和的平方根代替方程中的另一坐标。

旋转曲面

解：因为旋转轴是 x 轴，同名坐标就是 x，
长形旋转椭球面
的曲面方程为
x 2 y 2 z2 2 2 1 2 a b b
同样将椭圆绕其短轴旋转的曲面方程为
x2 y 2 z 2 2 2 1 2 a b a
扁形旋转椭球面
z
例 3
将双曲线
y2 z2 2 1 : b2 c x0
P0 x0 , y0 , z0 设点 M1 x1, y1, z1 为Γ上任意一点，为 l 上任意一点。 x
y l
求旋转曲面的方程
过 M 1 的纬圆方程为
X x x1 Y y y1 Z z z1 0 2 2 2 x x y y z z 0 0 0 2 2 2 x x y y z z 1 0 1 0 1 0
2 2 2 2 2 x y z y z 1 1 根来代替方程中的另一坐标。
且有
F y1 , z1 0
消去参数 y1 , z1 求得旋转曲面方程为 F y, x2 z 2 0 同样，把曲线Γ绕 z 轴旋转所得的旋转曲面的方程是 F x2 y 2 , z 0
《解析几何》
§4.3 旋转曲面
content
一、旋转曲面的相关概念二、旋转曲面方程的求法三、特殊的旋转曲面
旋转曲面的相关概念定义：在空间，一条曲线绕着定直线 l 旋转一周所生成的曲面叫做旋转曲面，或称回转曲面. 曲线叫做旋转曲面的母线，定直线 l 叫做旋转曲面的旋转轴，简称为轴.
x1 y1 z1 1 由于M1 x1, y1, z1 在母线上，所以又有 2 1 0

43旋转曲面定义431在空间一条曲线绕着定直线旋转一

x0
绕它的对称轴旋转的旋转曲面方程为
x2 y2 2 pz
曲面（4.3-5）叫做旋转抛物面（图4-11）。
例5 ：
将圆
( y b)2 z2 a2
:
,(b a 0)
x0
(20)
（图4-12(a))绕 z 轴旋转，求所得旋转曲面的方程。
解：因为绕 z 轴旋转，所以在方程( y b)2 z 2 a2 中保留 z 不变，而 y 用 x2 y2 代，就得将圆（20）绕
z 轴旋转而成的旋转曲面的方程为
( x2 y2 b)2 z2 a2
即
x2 y2 z2 b2 a2 2b x2 y2
或
(x2 y2 z2 b2 a2 )2 4b2 (x2 y2 )
这样的曲面叫做环面（图4-12（b)),它的形状像救生圈。
作业
P158 1，2，3
为
x
2
y y1 ( y1, z1) 0
从（12），（13），（14）三式中消去参数得所求旋转曲面的
方程为 F( y, x2 z2 ) 0
同样，把曲线绕z轴旋转所得的旋转曲面的方程为
F( x2 y2 , z) 0
对于其他坐标面上的曲线，绕坐标轴旋转所得的旋转曲面，其方程可类似的求出，这样我们就得出如下的规律：
§4.3 旋转曲面
定义4.3.1 在空间，一条曲线绕着定直线l 旋转一周所生成的曲面叫做旋转曲面，或称回转曲面。曲线叫作旋转曲面的母线，定直线 l 叫做旋
转曲面的旋转轴，简称为轴。
如图就纬交4是圆成-5通或一，过纬条旋点线曲转。线M曲1在，面且通这的垂过些母直旋曲线于转线轴轴显上l然l的在的的任旋平平意转面面点中上与M都，旋1 能以在转l彼旋曲为此转面界重时的的合形交每，成线个这一，半曲个我平线圆们面叫，把都作这它与旋个叫曲转圆做面

柱面锥面和旋转曲面ppt课件

f (y1, z1)=0
.
S
建立旋转曲面的方程：
如图
得方程
规律：一般地，当坐标面上的曲线绕此坐标面里的一个坐标轴旋转时，为求得旋转曲面的方程，只需将曲线方程保留和旋转轴同名的坐标，以其余两坐标平方和的平方根代替方程中的另一个坐标.
例3.1.6 将圆
绕Z轴旋转，求所得旋转曲面的方程.
解：所求旋转曲面的方程为：
l
M1
S
旋转曲面又可看作以轴 l 为连心线的一族纬圆生成的曲面
特例--- 以直线为母线的旋转面
母线和轴共面时
圆柱面 (母线和轴线平行)
圆锥面 (母线和轴线相交而不垂直)
平面 (母线和轴线正交)
母线和轴线异面且直母线与轴线不垂直呢?
母线不是经线
单叶旋转双曲面
解：设P(x1,y1,z1)是母线上的任意点，因为旋转轴通过原点，所以过P的纬圆方程是：
（母线平行于Y轴的椭圆柱面）
（母线平行于x轴的双曲柱面）
（母线平行于y轴的抛物柱面）
注：上述柱面的方程都是二次的，都称为二次柱面。
1、锥面的概念
定义3.1.3 在空间通过一定点且与定曲线相交的一族直线所生成的曲面叫做锥面，这些直线都叫做锥面的母线，那个定点叫做锥面的顶点，定曲线叫做锥面的准线。
补充：
曲线 C
C
绕 z 轴
3、母线在坐标面而旋转轴为坐标轴的旋转曲面
曲线 C
C
绕z 轴
曲线 C
旋转一周得旋转曲面 S
C
S
M
N
z
P
y
z
o
绕 z轴
f (y1, z1)=0
M(x,y,z)
.
S

4.3旋转曲面 4.4椭球面

§4.3 旋转曲面
定义4.3.1 在空间，以一条曲线绕着定直线旋在空间，定义转一周所生成的曲面称为旋转曲面或称回旋曲面旋转曲面或称回旋曲面. 转一周所生成的曲面称为旋转曲面或称回旋曲面.
这条定直线叫旋转曲面的旋转轴．这条定直线叫旋转曲面的旋转轴．旋转轴这条曲线叫旋转曲面的母线．这条曲线叫旋转曲面的母线．母线
y
例卫星接收装置
.
5环面圆（x − R ) 2 + y 2 = r 2 ( R > r > 0) 绕 y轴旋转所成曲面轴
y
o
r
R
x
5环面圆（x − R ) 2 + y 2 = r 2 ( R > r > 0) 绕 y轴旋转所成曲面轴 y
o
x
.
z
5环面圆（x − R ) 2 + y 2 = r 2 ( R > r > 0)
旋转椭球面与椭球面的区别：旋转椭球面与椭球面的区别：与平面 z
= z1 (| z1 |< c)的交线为圆的交线为圆.
2 a2 2 2 x + y 2 = 2 (c − z1 ) . 截面上圆的方程 c z = z 1
( 2) a = b = c ,
x2 y2 z2 1 球面 2 + 2 + 2 = a a a
2
Φ(x, y) ≡ a11x + 2a12xy + a22 y
a11 a12 a13 A = a12 a22 a23 a a a 13 23 33
在平面上，双曲线有渐进线。在平面上，双曲线有渐进线。相仿，单叶双曲面和相仿，单叶双曲面和双叶双曲面渐进锥面。有渐进锥面。去截它们，用z=h去截它们，当|h|无限增大时，双曲面的截口椭圆与它的的截口椭圆与它的渐进锥双曲面的截口椭圆与它的渐进锥的截口椭圆任意接近，面的截口椭圆任意接近，即： x 双曲面和锥面任意接近。双曲面和锥面任意接近。

《面的旋转》课件

的运行效率和安全性至关重要。
04
在航空航天领域，旋转体常用于飞机的发动机、螺旋桨和直升机的旋翼等部件的设计，其动力学特性和稳定性对飞行器的性能和安全性至关重要。
旋转体在数学建模中的应用
旋转体在数学建模中常被用作描述和分析物理现象、工程问题和其他复杂系统的工具。
在物理学中，旋转体用于描述和分析力学、电磁学和流体动力学等领域的现象，如行星运动、磁场分布和流体流动等。
旋转面上的任意一条直线都与旋转轴平行，因此旋转面在任意一
点处的切线都与旋转轴垂直。
旋转面的形状和大小取决于作为旋转轴的定直线和作为旋转对象
的平面曲线的形状和大小。
旋转面的面积和体积
旋转面的面积可以通过计算定直线与平面曲线之间的最小距离和最大距离之间的面积得到。
如果旋转面是一个封闭的曲面，那么它还具有体积。旋转面的体积可以通过计算定直线与平面曲线之间的最小距离和最大距离之间的体积得到。
在工程领域，旋转体常用于描述和分析旋转机械的运动学、动力学和稳定性等问题，如轴承动力学、风力发电机和旋转结构的稳定性分析等。
旋转体在物理模拟中的应用
旋转体在物理模拟中常被用作实验模型，以模拟和分析真实世界的物理现象和过程。
在材料科学中，旋转体用于模拟材料的力学性能和行为，如金属材料的疲劳和断裂等。
《面的旋转》ppt课件
contents
目录
• 面的旋转的定义 • 旋转面的几何性质 • 旋转体的生成 • 旋转体的表面积和体积 • 旋转体的应用实例
01
面的旋转的定义
旋转面的定义
01
02
03
旋转面定义
由定点和定直线确定的平面绕定直线旋转而成的曲面。
旋转轴

4.3：旋转曲面

z
绕 z 轴一周
得单叶旋转双曲面
.
.
o
b
x2 y 2 z 2 2 1 2 b c
y
x
2 双叶旋转双曲面
y2 z2 1 双曲线 b 2 c 2 x 0
y
绕 y 轴一周
0
z
2 双叶旋转双曲面
y2 z2 1 双曲线 b 2 c 2 x 0
2
由于旋转曲面的经线，总可以作为最初的母线来产生旋转曲面. 因此为了方便，今后总是取旋转曲面的某一条经线（显然是平面曲线）作为旋转曲面的母线. 在直角坐标系下导出旋转曲面的方程时，我们又常把母线所
M1
l
在平面取作坐标面而旋转轴取作坐标轴，这时旋转曲面的方程具有特殊的形式.
M
P0

设旋转曲面的母线为
P0

l
设 M1 ( x1 , y1 , z1 )是母线上的任意点，那么过 M 1的纬圆总可以看成是: 过 M 1 且垂直于旋转轴 l 的平面
与以 P0 ( x0 , y0 , z0 ) 为中心,
P0 M 1 为半径的球面的交线.
M1
M
P0

所以过 M1 ( x1 , y1 , z1 ) 的纬线的方程为：
（7）
（8）
由于 M1 ( x1 , y1 , z1 ) 在母线上，所以又有
x1 y1 z1 1 2 1 0
即
( x x1 ) ( y y1 ) ( z z1 ) 0 2 2 2 2 2 2 x y z x1 y1 z1
x1 2 y1 ,
生活中见过这个曲面吗？
o
y
.

BB6_5几种常用的二次曲面与空间曲线PPT课件

x2 a2
z2 c2
1
分别绕
x
轴和 z 轴旋转一周所生成的旋转曲面方程.
解:绕 x 轴旋转所成曲面方程为
x2 a2
y2 z2 c2
1
绕 z 轴旋转所成曲面方程为
x2 y2 a2
z2 c2
1
x
y
z
这两种曲面都叫做旋转双曲面.
21
二、柱面
z
引例. 分析方程 x2 y2 R2
表示怎样的曲面 .
开口向下的旋转抛物面. 例3. 旋转椭球面
0
y
特点:母线C为椭圆,轴为椭圆的
x
对称轴. 例如:yoz面上的椭圆:
y2 a2
z2 b2
1
z
绕z轴旋转得旋转曲面方程:
x2 y2 a2
z2 b2
1
绕y轴旋转得旋转曲面方程:
x
y2 a2
x2 z2 b2
1
y
注:旋转曲面的重要特征是其两个变量的平方项系数相等. 19
例4. 试建立顶点在原点, 旋转轴为z 轴, 半顶角为
的圆锥面方程. 解: 在yoz面上直线L 的方程为
z y cot
z L
绕z 轴旋转时,圆锥面的方程为
z x2 y2 cot
令 a cot
两边平方
x
M (0, y, z)
y
z2 a2( x2 y2 )
20
例5.
求坐标面
xoz
上的双曲线
M
解:在 xoy 面上， x2 y2 R2 表示圆C,
C
o
M1
y
在圆C上任取一点M1(x, y,0) , 过此点作 x
平行 z 轴的直线 l , 对任意 z , 点M (x, y, z)

43旋转曲面

《解析几何》－Chapter 4§3 旋转曲面surface of revolution1、理解旋转曲面及母线和纬圆等概念；2、掌握求旋转曲面方程的一般方法及步骤；3、能熟练写出一类特殊旋转曲面的方程。

Contents一、旋转曲面的有关概念二、旋转曲面的方程（直角坐标系）三、几种特殊的旋转曲面（直角坐标系）l.Sl定义1在空间，一条曲线Γ绕着定直线l 旋转一周所生成的曲面S 称为旋转曲面（或回转曲面）（surface of revolution ）Γ称为旋转曲面的母线（generating curve ）l 称为旋转曲面的旋转轴（axis of rotation ）纬圆Ⅱ以旋转轴l 为边界的半平面与旋转面的交线称为旋转面的经线说明：ⅰ纬圆也可看作垂直于旋转轴l 的平面与旋转面的交线SΓ一、旋转曲面的有关概念Ⅰ母线上任意一点绕旋转轴l 旋转的轨迹是一个圆，称为旋转面的纬圆或纬线ⅱ任一经线都可以作为母线，但母线不一定是经线。

经线和母线一样吗？lM经线π例1求直线绕直线旋转所得的旋转曲面的方程1210x y z -Γ==：:l x y z ==母线不是经线单叶旋转双曲面xyzo经线轴xyzol l纬圆轴旋转曲面可看成经线绕旋转轴旋转一周.旋转曲面也可看成由纬圆族生成.设旋转曲面的母线，()()12,,0:,,0F x y z F x y z =⎧⎪Γ⎨=⎪⎩()1111 ,,M x y z ∀∈母线(),,0F x y z ⇒=1 旋转曲面的一般方程⎧⎪⎪⎨⎪⎪⎩纬圆：约束方程：000:x x y y z z l X Y Z ---==旋转轴为直线当M 1 遍历整个母线Γ时，得出旋转曲面的所有纬圆，这些纬圆生成旋转曲面⎧⎨⎩平面球＝分析：1M ⇔∈纬圆1M S ⇒∈旋转曲面又可看作以轴l 为连心线的一族纬圆生成的曲面yzoP 1M ()()()()X x x Y y y Z z z -+-+-⎧⎪⎨=⎪⎩11110()(),,,,()()F x y z F x y z ==⎧⎪⎨⎪⎩111121114030()()()()()()()x x y y z z x x y y z z -+-+-=-+-+-2222220001010102消参:设旋转曲面的母线，()()12,,0:,,0F x y z F x y z =⎧⎪Γ⎨=⎪⎩1 旋转曲面的一般方程000:x x y y z z l X Y Z ---==旋转轴为直线z1M 普通方法设M 1(x 1, y 1, z 1)为母线上任意一点,①写出纬圆族方程:②写出参数x 1, y 1, z 1的约束条件:③消去参数x 1, y 1, z 1得一个三元方程:()()()()()()()()()()()X x x Y y y Z z x x y y z z x x y y z z z -+-+-=-+-+--+-+-=⎧⎪⎨⎪⎩222222000101011101120()(),,,,()()F x y z F x y z ==⎧⎪⎨⎪⎩111121114030(),,.F x y z =0例1求直线绕直线旋转所得的旋转曲面的方程x y z l -==11210：:l x y z ==2母线轴(0,0,0)解设M 1(x 1, y 1, z 1)为母线l 1上任意一点,则过点M 1的纬圆方程为:()()(),-+-+-=⎧⎨⎩1110x x y y z z ++=222x y z 且有-==1111210x y z ,t 则,,===11121x t y t z 代入上式消去t 得++222111x y z 所求旋转球面方程:()++=++--22225119x y z x y z 即:()()()++-+++++-=22225570x y z xy xz yz x y z 另:,.==11121x y z 代入方程组消参得旋转球面方程.消参中可令1M (,,)0000P {1,1,1}=v l 2xyzo三、旋转曲面的方程特征Γ解则过点M 1纬圆为:(,)F y z =110且y y -=⎧⎨⎩10x y z y z ++=+2222211故旋转曲面方程为22(,)0F y x z ±+=绕y 轴旋转所成曲面的方程.例:给定yoz 面上曲线Γ: (,)F y z x =⎧⎨=⎩0当旋转曲面的母线为坐标面上的曲线,且旋转轴为坐标轴时, 它的方程具有特殊形式.{0,1,0}=v 设M 1(0, y 1, z 1)为母线Г上任意点,{0,1,0}=且v (0,0,0)O y 轴上定点(,,)M y z 1110例2设母线，(),:F y z x =⎧⎪Γ⎨=⎪⎩00规律：一般地，当坐标面上的曲线绕此坐标面里的一个坐标轴旋转时，为求得旋转曲面的方程，只需将曲线方程保留和旋转轴同名的坐标，以其余两坐标平方和的正负平方根代替方程中的另一个坐标xozy⑴绕z 轴旋转所得的旋转面方程；⑵绕y 轴旋转所得的旋转面方程(),F x y z ±+=220(),F y x z±+=2222221:,0x ya b z ⎧+=⎪Γ⎨⎪=⎩()a b >例2.将椭圆o xyz长形旋转椭球面1.绕长轴（即x 轴）旋转的旋转曲面的方程为:2.绕短轴（即y 轴）旋转的旋转曲面的方程为:222222 1.++=x y za b b2222221++=x y za b aoxyzbaab ba 222221++=⇒x y za b222221++=⇒x z y a b例3将双曲线 , ():. y z a b bc x ⎧-=>⎪Γ⎨⎪=⎩2222101.绕虚轴（即z 轴）旋转的旋转曲面的2.绕实轴（即y 轴）旋转的旋转曲面的2222221; +-=x y zb b c2222221; --=y x z b c c 方程为:方程为:单叶旋转双曲面222221+-=⇒x y zb c222221 +-=⇒y x z b c yzoxbxzyo例4将抛物线22 ,:0.⎧=Γ⎨=⎩y pz x 1.绕它的对称轴旋转的旋转曲面的方程为:222+=x y pz旋转抛物面xyzoxyzo>p 生活中见过这个曲面吗？.例5将圆则所得旋转曲面的方程:222() , (b a 0):0.⎧-+=>>Γ⎨=⎩y b z a x -4-224-1-0.500.51-4-224zyOa b绕z 轴旋转,22222(),x y b z a ±+-+=22222222x y z b a b x y+++-=±+即:即:()()2222222224x y z b ab x y+++-=+环面zyoab例5将圆222() , (b a 0):0.⎧-+=>>Γ⎨=⎩y b z a x 绕z 轴旋转,yxo.环面例5将圆222() , (b a 0):0.⎧-+=>>Γ⎨=⎩y b z a x 绕z 轴旋转,zy xo .生活中见过这个曲面吗？环面救生圈.。

4.3 旋转曲面

z
这样的曲面叫做环面
o x y
• 一般旋转曲面的方程
F1 x, y, z 0 设旋转曲面的母线 C : F2 x, y, z 0 旋转轴为直线 l : x x0 y y0 z z0 X Y Z
l
M1
C
平面分析： M1 x1, y1, z1 母线 M1 纬圆＝
球
X x x1 Y y y1 Z z z1 0 1 纬圆： 2 2 2 2 2 2 x x y y z z x x y y z z 0 0 1 0 1 0 1 0 0 F1 x1 , y1 , z1 0 (3) 母线： F2 x1 , y1 , z1 0 (4)
4.3
旋转曲面
定义一条空间曲线C 绕一条定直线旋转一周所产成的曲面称为旋转曲面. 这条定直线称为该曲面的旋转轴，曲线C 称为该曲面的母线.
• 母线上任意一点绕旋转轴 l 旋转的轨迹是一个圆，称
为旋转面的纬圆或纬线. • 以旋转轴 l 为边界的半平面与旋转面的交线称为旋转面的经线. 注： ⅰ 纬圆也可看作垂直于旋转轴 l 的平面与旋转面的交线.
作业：
习题4.3 1
即 x1 2 y1 , z1 1.
因为旋转轴通过原点，所以过 M 1 的纬圆是
( x x1 ) ( y y1 ) ( z z1 ) 0 2 2 2 2 2 2 x y z x y z 1 1 1 5 2 2 2 x y z 1 ( x y z 1)2 9
x 不变
z y2 z2
所以，旋转曲面方程为