中考复习之压轴题选讲(二)

序号：初中数学备课组教师：班级：初三日期：上课时间：学生：学生情况：主课题：抛物线背景下的压轴题教学目标：1. 掌握所学的基本概念和定理公式；2．理解公理定理的来源和用途；3．学会发散思维。

4．经历解综合题的探索过程，领会转化，分类的思想；经历数形结合的探究过程，体会数形结合的思想。

教学重点：怎样解好综合题教学难点：学会对所学知识的串联和并联一、知识概要五、在抛物线背景下的压轴题抛物线的特点是：1、若点在抛物线上，则点的坐标满足相应的抛物线的解析式。

2、会看图象：1）当a＞0时⇔抛物线开口向上，b＞0⇔对称轴在y轴左边，b＜0⇔对称轴在y轴的右边；2）当a＜0时⇔抛物线开口向下b＞0⇔对称轴在y轴的右边，b＜0⇔对称轴在y轴左边。

3）当c＞0⇔抛物线与y轴的交点在x轴上方；当c＜0⇔抛物线与y轴的交点在x轴下方。

4）抛物线与x轴有两交点⇔△＞0抛物线与x轴只有一个交点⇔△=0抛物线与x轴无交点⇔△＜05）对称轴为直线abx 2-=，如果抛物线与x 轴有两交点横坐 标为21x ,x ，那么对称轴与x 轴的交点横坐标0x 与它们之间的关系是2210x x x +=3、解析式要清楚，常用的有三种表达方式：a ≠0))(()3;)())122q x p x a y n m x a y 2 ; c bx ax y --=+-=++=当知道抛物线上任意三点坐标时，可用第一种解析式来求；当知道顶点坐标为（m ，n ）时，可用第二种解析式来求；当知道抛物线与x 轴两交点坐标（p ，0），（q ，0）时，可用第三种解析式来求。

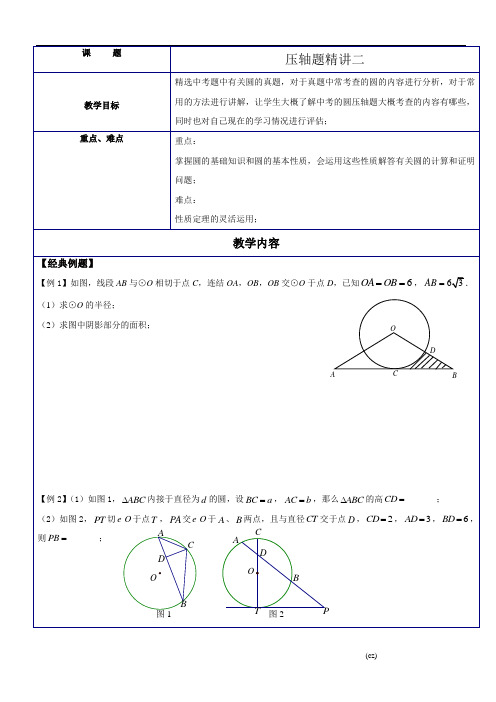
二、精解名题【例1】（2009河北省数学中考题）如图,开口向上的抛物线y=ax 2+2ax-c 与x 轴交于点A,B,与y 轴交于点C,点A 在x 轴的正半轴，点B 在x 的负半轴，OB=OC. （1）如果点A 的坐标为（1，0），求点B 的坐标； （2）求证：ac-2a =1；（3）在(2)的条件下，问此抛物线的对称轴上是否存在点P ，使△PAC 的周长最小？若存在，求出点P 的坐标，不存在，请说明理由.例1题图【例2】（2013年松江）已知抛物线c bx x y ++-=2经过点A （0，1)，B (4，3)．（1）求抛物线的函数解析式； （2）求tan ∠ABO 的值；（3）过点B 作BC ⊥x 轴，垂足为C ，在对称轴的左侧且平行于y 轴的直线交线段AB 于点N ，交抛物线于点M ，若四边形MNCB 为平行四边形，求点M 的坐标．A Boxy（例2题图）【例3】（09年中考题）如图24－1，P 1、P 2、P 3、……、P n 分别是抛物线2y x =与直线y x =、2y x =、3y x =、……、y kx = 的交点，连结P 1P 2、P 2P 3，……，P k －1P k ．⑴求△OP 1P 2的面积，并直接写出△OP 2P 3 的面积； ⑵如图24－2，猜想△OP k －1P k 的面积，并说明理由；⑶若将抛物线2y x =改为抛物线2y ax =，其它条件不变，猜想△OP k －1P k 的面积(直接写出答案)．图24－1【例4】（2010年北京中考题） 在平面直角坐标系xOy 中，抛物线22153244m my x x m m -=-++-+与x 轴的交点分别为原点O 和点A ，点()2B n ，在这条抛物线上．（1）求B 点的坐标；（2）点P 在线段OA 上，从O 点出发向A 点运动，过P 点作x 轴的垂线，与直线OB 交于点E ，延长PE 到点D ，使得ED PE =，以PD 为斜边，在PD 右侧作等腰直角三角形PCD （当P 点运动时，C 点、D 点也随之运动）．① 当等腰直角三角形PCD 的顶点C 落在此抛物线上时，求OP 的长；② 若P 点从O 点出发向A 点作匀速运动，速度为每秒1个单位，同时线段OA 上另一个点Q 从A 点出发向O 点作匀速运动，速度为每秒2个单位（当Q 点到达O 点时停止运动，P 点也同时停止运动）．过Q 点作x 轴的垂线，与直线AB 交于点F ，延长QF 到点M ，使得FM QF =，以QM 为斜边，在QM 的左侧作等腰直角三角形QMN （当Q 点运动时，M 点、N 点也随之运动）．若P 点运动到t 秒时，两个等腰直角三角形分别有一条边恰好落在同一条直线上，求此刻t 的值．三、自我测试图111D P E CBAO yx1、(嘉兴市)如图，已知抛物线y ＝－12x 2＋x ＋4交x 轴的正半轴于点A ，交y 轴于点B ．（1）求A 、B 两点的坐标，并求直线AB 的解析式；（2）设P （x ，y ）（x ＞0）是直线y ＝x 上的一点，Q 是OP 的中点（O 是原点），以PQ 为对角线作正方形PEQF ，若正方形PEQF 与直线AB 有公共点，求x 的取值范围；（3）在（2）的条件下，记正方形PEQF 与△OAB 公共部分的面积为S ，求S 关于x 的函数解析式，并探究S 的最大值．2、（临沂市）如图：二次函数y =﹣x 2 + ax + b 的图象与x 轴交于A （-21，0），B （2，0）两点，且与y 轴交于点C ．OABPEQFxy （第1题）C DOABxy （第1题 备用）PEQF M N（1）求该抛物线的解析式，并判断△ABC 的形状；（2）在x 轴上方的抛物线上有一点D ，且A 、C 、D 、B 四点为顶点的四边形是等腰梯形，请直接写出D 点的坐标；（3）在此抛物线上是否存在点P ，使得以A 、C 、B 、P 四点为顶点的四边形是直角梯形？若存在，求出P 点的坐标；若不存在，说明理由．AC B第2题图。

中考总复习初中数学考前压轴题复习讲义（动点问题详细分层解析，尖子生首选资料 ）所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想：分类思想 函数思想 方程思想 数形结合思想 转化思想 注重对几何图形运动变化能力的考查从变换的角度和运动变化来研究三角形、四边形、函数图像等图形，通过“对称、动点的运动”等研究手段和方法，来探索与发现图形性质及图形变化，在解题过程中渗透空间观念和合情推理。

选择基本的几何图形，让学生经历探索的过程，以能力立意，考查学生的自主探究能力，促进培养学生解决问题的能力．图形在动点的运动过程中观察图形的变化情况，需要理解图形在不同位置的情况，才能做好计算推理的过程。

在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。

二期课改后数学卷中的数学压轴性题正逐步转向数形结合、动态几何、动手操作、实验探究等方向发展．这些压轴题题型繁多、题意创新，目的是考察学生的分析问题、解决问题的能力，内容包括空间观念、应用意识、推理能力等．从数学思想的层面上讲：（1）运动观点；（2）方程思想；（3）数形结合思想；（4）分类思想；（5）转化思想等．研究历年来各区的压轴性试题，就能找到今年中考数学试题的热点的形成和命题的动向，它有利于我们教师在教学中研究对策，把握方向．只的这样，才能更好的培养学生解题素养，在素质教育的背景下更明确地体现课程标准的导向．本文拟就压轴题的题型背景和区分度测量点的存在性和区分度小题处理手法提出自己的观点．函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要内容.动点问题反映的是一种函数思想,由于某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,这种变化关系就是动点问题中的函数关系.那么,我们怎样建立这种函数解析式呢?下面结合中考试题举例分析. 一、应用勾股定理建立函数解析式例1 )如图1,在半径为6,圆心角为90°的扇形OAB 的弧AB 上,有一个动点P,PH ⊥OA,垂足为H,△OPH 的重心为G.(1)当点P 在弧AB 上运动时,线段GO 、GP 、GH 中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度.(2)设PH x =,GP y =,求y 关于x 的函数解析式，并写出函数的定义域(即自变量x 的取值范围).(3)如果△PGH 是等腰三角形,试求出线段PH 的长.解:(1)当点P 在弧AB 上运动时,OP 保持不变,于是线段GO 、GP 、GH 中,有长度保持不变的线段，这条线段是GH=32NH=2132⋅OP=2.(2)在Rt △POH 中, 22236x PH OP OH -=-=, ∴2362121x OH MH -==. 在Rt △MPH 中,2222211HM NGPO AB图1x y.∴y =GP=32MP=233631x + (0<x <6).(3)△PGH 是等腰三角形有三种可能情况:①GP=PH 时,x x =+233631,解得6=x . 经检验, 6=x 是原方程的根,且符合题意. ②GP=GH 时, 2336312=+x ,解得0=x . 经检验, 0=x 是原方程的根,但不符合题意.③PH=GH 时,2=x .综上所述,如果△PGH 是等腰三角形,那么线段PH 的长为6或2.二、应用比例式建立函数解析式例2 如图2,在△ABC 中,AB=AC=1,点D,E 在直线BC 上运动.设BD=,x CE=y . (1)如果∠BAC=30°,∠DAE=105°,试确定y 与x 之间的函数解析式；(2)如果∠BAC 的度数为α,∠DAE 的度数为β,当α,β满足怎样的关系式时,(1)中y 与x 之间的函数解析式还成立?试说明理由.解:(1)在△ABC 中,∵AB=AC,∠BAC=30°,∴∠ABC=∠ACB=75°, ∴∠ABD=∠ACE=105°.∵∠BAC=30°,∠DAE=105°, ∴∠DAB+∠CAE=75°, 又∠DAB+∠ADB=∠ABC=75°, ∴∠CAE=∠ADB,∴△ADB ∽△EAC, ∴ACBD CE AB =,∴11x y =, ∴xy 1=. (2)由于∠DAB+∠CAE=αβ-,又∠DAB+∠ADB=∠ABC=290α-︒,且函数关系式成立, ∴290α-︒=αβ-, 整理得=-2αβ︒90. 当=-2αβ︒90时,函数解析式xy 1=成立. 例3(2005年·上海)如图3(1),在△ABC 中,∠ABC=90°,AB=4,BC=3. 点O 是边AC 上的一个动点,以点O 为圆心作半圆,与边AB 相切于点D,交线段OC 于点E.作EP ⊥ED,交射线AB 于点P,交射线CB 于点F.(1)求证: △ADE ∽△AEP.(2)设OA=x ,AP=y ,求y 关于x 的函数解析式,并写出它的定义域.(3)当BF=1时,求线段AP 的长. 解:(1)连结OD.根据题意,得OD ⊥AB,∴∠ODA=90°,∠ODA=∠DEP.又由OD=OE,得∠ODE=∠OED.∴∠ADE=∠AEP, ∴△ADE ∽△AEDCB 图2A3(1)AEP.(2)∵∠ABC=90°,AB=4,BC=3, ∴AC=5. ∵∠ABC=∠ADO=90°, ∴OD ∥BC, ∴53x OD =,54xAD =, ∴OD=x 53,AD=x 54. ∴AE=x x 53+=x 58. ∵△ADE ∽△AEP, ∴AE AD AP AE =, ∴x x yx 585458=. ∴x y 516= (8250≤<x ). (3)当BF=1时，①若EP 交线段CB 的延长线于点F,如图3(1)，则CF=4.∵∠ADE=∠AEP, ∴∠PDE=∠PEC. ∵∠FBP=∠DEP=90°, ∠FPB=∠DPE, ∴∠F=∠PDE, ∴∠F=∠FEC, ∴CF=CE. ∴5-x 58=4,得85=x .可求得2=y ,即AP=2. ②若EP 交线段CB 于点F,如图3(2), 则CF=2. 类似①,可得CF=CE. ∴5-x 58=2,得815=x . 可求得6=y ,即AP=6.综上所述, 当BF=1时,线段AP 的长为2或6.三、应用求图形面积的方法建立函数关系式例4 如图,在△ABC 中,∠BAC=90°,AB=AC=22,⊙A 的半径为1.若点O 在BC 边上运动(与点B 、C 不重合),设BO=x ,△AOC 的面积为y .(1)求y 关于x 的函数解析式,并写出函数的定义域. (2)以点O 为圆心,BO 长为半径作圆O,求当⊙O 与⊙A 相切时, △AOC 的面积.解:(1)过点A 作AH ⊥BC,垂足为H.∵∠BAC=90°,AB=AC=22, ∴BC=4,AH=21BC=2. ∴OC=4-x . ∵AH OC S AOC ⋅=∆21, ∴4+-=x y (40<<x ). (2)①当⊙O 与⊙A 外切时,在Rt △AOH 中,OA=1+x ,OH=x -2, ∴222)2(2)1(x x -+=+. 解得67=x . 此时,△AOC 的面积y =617674=-. ②当⊙O 与⊙A 内切时,在Rt △AOH 中,OA=1-x ,OH=2-x , ∴222)2(2)1(-+=-x x . 解得27=x . 此时,△AOC 的面积y =21274=-. ABCO 图8HC综上所述,当⊙O 与⊙A 相切时,△AOC 的面积为617或21.动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。

中考数学压轴题复习讲义（动点问题详细分层解析，尖子生首选资料 ）所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想：分类思想 函数思想 方程思想 数形结合思想 转化思想 注重对几何图形运动变化能力的考查从变换的角度和运动变化来研究三角形、四边形、函数图像等图形，通过“对称、动点的运动”等研究手段和方法，来探索与发现图形性质及图形变化，在解题过程中渗透空间观念和合情推理。

选择基本的几何图形，让学生经历探索的过程，以能力立意，考查学生的自主探究能力，促进培养学生解决问题的能力．图形在动点的运动过程中观察图形的变化情况，需要理解图形在不同位置的情况，才能做好计算推理的过程。

在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。

二期课改后数学卷中的数学压轴性题正逐步转向数形结合、动态几何、动手操作、实验探究等方向发展．这些压轴题题型繁多、题意创新，目的是考察学生的分析问题、解决问题的能力，内容包括空间观念、应用意识、推理能力等．从数学思想的层面上讲：（1）运动观点；（2）方程思想；（3）数形结合思想；（4）分类思想；（5）转化思想等．研究历年来各区的压轴性试题，就能找到今年中考数学试题的热点的形成和命题的动向，它有利于我们教师在教学中研究对策，把握方向．只的这样，才能更好的培养学生解题素养，在素质教育的背景下更明确地体现课程标准的导向．本文拟就压轴题的题型背景和区分度测量点的存在性和区分度小题处理手法提出自己的观点．,是初中数学的重要内容.动点问题反映的是一种函数思想,由于某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,这种变化关系就是动点问题中的函数关系.那么,我们怎样建立这种函数解析式呢?下面结合中考试题举例分析. 一、应用勾股定理建立函数解析式例1 )如图1,在半径为6,圆心角为90°的扇形OAB 的弧AB 上,有一个动点P,PH ⊥OA,垂足为H,△OPH 的重心为G.(1)当点P 在弧AB 上运动时,线段GO 、GP 、GH 中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度.(2)设PH x =,GP y =,求y 关于x 的函数解析式，并写出函数的定义域(即自变量x 的取值范围).(3)如果△PGH 是等腰三角形,试求出线段PH 的长.解:(1)当点P 在弧AB 上运动时,OP 保持不变,于是线段GO 、GP 、GH 中,有长度保持不变的线段，这条线段是GH=32NH=2132⋅OP=2.(2)在Rt △POH 中, 22236xPH OP OH -=-=, ∴2362121x OH MH -==.在Rt △MPH 中,.2222233621419x x x MH PH MP +=-+=+=HM NG POAB图1xy∴y =GP=32MP=233631x + (0<x <6). (3)△PGH 是等腰三角形有三种可能情况:①GP=PH 时,x x =+233631,解得6=x . 经检验, 6=x 是原方程的根,且符合题意. ②GP=GH 时, 2336312=+x ,解得0=x . 经检验, 0=x 是原方程的根,但不符合题意.③PH=GH 时,2=x .综上所述,如果△PGH 是等腰三角形,那么线段PH 的长为6或2.二、应用比例式建立函数解析式例2 如图2,在△ABC 中,AB=AC=1,点D,E 在直线BC 上运动.设BD=,x CE=y . (1)如果∠BAC=30°,∠DAE=105°,试确定y 与x 之间的函数解析式；(2)如果∠BAC 的度数为α,∠DAE 的度数为β,当α,β满足怎样的关系式时,(1)中y 与x 之间的函数解析式还成立?试说明理由.解:(1)在△ABC 中,∵AB=AC,∠BAC=30°,∴∠ABC=∠ACB=75°, ∴∠ABD=∠ACE=105°.∵∠BAC=30°,∠DAE=105°, ∴∠DAB+∠CAE=75°, 又∠DAB+∠ADB=∠ABC=75°, ∴∠CAE=∠ADB,∴△ADB ∽△EAC,∴ACBD CE AB =,∴11x y=, ∴xy 1=.(2)由于∠DAB+∠CAE=αβ-,又∠DAB+∠ADB=∠ABC=290α-︒,且函数关系式成立, ∴290α-︒=αβ-, 整理得=-2αβ︒90.当=-2αβ︒90时,函数解析式xy 1=成立. 例3(2005年·上海)如图3(1),在△ABC 中,∠ABC=90°,AB=4,BC=3. 点O 是边AC 上的一个动点,以点O 为圆心作半圆,与边AB 相切于点D,交线段OC 于点E.作EP ⊥ED,交射线AB 于点P,交射线CB 于点F.(1)求证: △ADE ∽△AEP.(2)设OA=x ,AP=y ,求y 关于x 的函数解析式,并写出它的定义域.(3)当BF=1时,求线段AP 的长.解:(1)连结OD.根据题意,得OD ⊥AB,∴∠ODA=90°,∠ODA=∠DEP. 又由OD=OE,得∠ODE=∠OED.∴∠ADE=∠AEP, ∴△ADE ∽△AEP.(2)∵∠ABC=90°,AB=4,BC=3, ∴AC=5. ∵∠ABC=∠ADO=90°, ∴OD ∥BC, ∴53x OD =,54xAD =,AEDCB 图2A3(2)3(1)∴OD=x 53,AD=x 54. ∴AE=x x 53+=x 58. ∵△ADE ∽△AEP, ∴AE AD AP AE =, ∴x x yx 585458=. ∴x y 516= (8250≤<x ). (3)当BF=1时，①若EP 交线段CB 的延长线于点F,如图3(1)，则CF=4.∵∠ADE=∠AEP, ∴∠PDE=∠PEC. ∵∠FBP=∠DEP=90°, ∠FPB=∠DPE, ∴∠F=∠PDE, ∴∠F=∠FEC, ∴CF=CE. ∴5-x 58=4,得85=x .可求得2=y ,即AP=2. ②若EP 交线段CB 于点F,如图3(2), 则CF=2. 类似①,可得CF=CE.∴5-x 58=2,得815=x . 可求得6=y ,即AP=6.综上所述, 当BF=1时,线段AP 的长为2或6. 三、应用求图形面积的方法建立函数关系式例4 如图,在△ABC 中,∠BAC=90°,AB=AC=22,⊙A 的半径为1.若点O 在BC 边上运动(与点B 、C 不重合),设BO=x ,△AOC 的面积为y .(1)求y 关于x 的函数解析式,并写出函数的定义域.(2)以点O 为圆心,BO 长为半径作圆O,求当⊙O 与⊙A 相切时, △AOC 的面积.解:(1)过点A 作AH ⊥BC,垂足为H.∵∠BAC=90°,AB=AC=22, ∴BC=4,AH=21BC=2. ∴OC=4-x. ∵AH OC S AOC⋅=∆21, ∴4+-=x y (40<<x ). (2)①当⊙O 与⊙A 外切时,在Rt △AOH 中,OA=1+x ,OH=x -2, ∴222)2(2)1(x x -+=+. 解得67=x . 此时,△AOC 的面积y =617674=-. ②当⊙O 与⊙A 内切时,在Rt △AOH 中,OA=1-x ,OH=2-x , ∴222)2(2)1(-+=-x x . 解得27=x . 此时,△AOC 的面积y =21274=-. 综上所述,当⊙O 与⊙A 相切时,△AOC 的面积为617或21. 分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。

中考数学压轴题复习讲义（动点问题详细分层解析，尖子生首选资料 ）所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想：分类思想 函数思想 方程思想 数形结合思想 转化思想 注重对几何图形运动变化能力的考查从变换的角度和运动变化来研究三角形、四边形、函数图像等图形，通过“对称、动点的运动”等研究手段和方法，来探索与发现图形性质及图形变化，在解题过程中渗透空间观念和合情推理。

选择基本的几何图形，让学生经历探索的过程，以能力立意，考查学生的自主探究能力，促进培养学生解决问题的能力．图形在动点的运动过程中观察图形的变化情况，需要理解图形在不同位置的情况，才能做好计算推理的过程。

在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。

二期课改后数学卷中的数学压轴性题正逐步转向数形结合、动态几何、动手操作、实验探究等方向发展．这些压轴题题型繁多、题意创新，目的是考察学生的分析问题、解决问题的能力，内容包括空间观念、应用意识、推理能力等．从数学思想的层面上讲：（1）运动观点；（2）方程思想；（3）数形结合思想；（4）分类思想；（5）转化思想等．研究历年来各区的压轴性试题，就能找到今年中考数学试题的热点的形成和命题的动向，它有利于我们教师在教学中研究对策，把握方向．只的这样，才能更好的培养学生解题素养，在素质教育的背景下更明确地体现课程标准的导向．本文拟就压轴题的题型背景和区分度测量点的存在性和区分度小题处理手法提出自己的观点．函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要内容.动点问题反映的是一种函数思想,由于某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,这种变化关系就是动点问题中的函数关系.那么,我们怎样建立这种函数解析式呢?下面结合中考试题举例分析. 一、应用勾股定理建立函数解析式例1 )如图1,在半径为6,圆心角为90°的扇形OAB 的弧AB 上,有一个动点P,PH ⊥OA,垂足为H,△OPH 的重心为G.(1)当点P 在弧AB 上运动时,线段GO 、GP 、GH 中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度.(2)设PH x =,GP y =,求y 关于x 的函数解析式，并写出函数的定义域(即自变量x 的取值范围).(3)如果△PGH 是等腰三角形,试求出线段PH 的长.解:(1)当点P 在弧AB 上运动时,OP 保持不变,于是线段GO 、GP 、GH 中,有长度保持不变的线段，这条线段是GH=32NH=2132⋅OP=2.(2)在Rt △POH 中, 22236xPH OP OH -=-=, ∴2362121x OH MH -==.在Rt △MPH 中,.2222233621419x x x MH PH MP +=-+=+=HM NGPO AB图1x y∴y =GP=32MP=233631x + (0<x <6). (3)△PGH 是等腰三角形有三种可能情况:①GP=PH 时,x x =+233631,解得6=x . 经检验, 6=x 是原方程的根,且符合题意. ②GP=GH 时, 2336312=+x ,解得0=x . 经检验, 0=x 是原方程的根,但不符合题意.③PH=GH 时,2=x .综上所述,如果△PGH 是等腰三角形,那么线段PH 的长为6或2.二、应用比例式建立函数解析式例2 如图2,在△ABC 中,AB=AC=1,点D,E 在直线BC 上运动.设BD=,x CE=y . (1)如果∠BAC=30°,∠DAE=105°,试确定y 与x 之间的函数解析式；(2)如果∠BAC 的度数为α,∠DAE 的度数为β,当α,β满足怎样的关系式时,(1)中y 与x 之间的函数解析式还成立?试说明理由.解:(1)在△ABC 中,∵AB=AC,∠BAC=30°, ∴∠ABC=∠ACB=75°, ∴∠ABD=∠ACE=105°. ∵∠BAC=30°,∠DAE=105°, ∴∠DAB+∠CAE=75°, 又∠DAB+∠ADB=∠ABC=75°, ∴∠CAE=∠ADB,∴△ADB ∽△EAC, ∴AC BD CE AB =,∴11x y =, ∴xy 1=. (2)由于∠DAB+∠CAE=αβ-,又∠DAB+∠ADB=∠ABC=290α-︒,且函数关系式成立, ∴290α-︒=αβ-, 整理得=-2αβ︒90.当=-2αβ︒90时,函数解析式xy 1=成立. 例3(2005年·上海)如图3(1),在△ABC 中,∠ABC=90°,AB=4,BC=3. 点O 是边AC 上的一个动点,以点O 为圆心作半圆,与边AB 相切于点D,交线段OC 于点E.作EP ⊥ED,交射线AB 于点P,交射线CB 于点F.(1)求证: △ADE ∽△AEP.(2)设OA=x ,AP=y ,求y 关于x 的函数解析式,并写出它的定义域.(3)当BF=1时,求线段AP 的长. 解:(1)连结OD.根据题意,得OD ⊥AB,∴∠ODA=90°,∠ODA=∠DEP.又由OD=OE,得∠ODE=∠OED.∴∠ADE=∠AEP, ∴△ADE ∽△AEP.(2)∵∠ABC=90°,AB=4,BC=3, ∴AC=5. ∵∠ABC=∠ADO=90°,∴OD ∥BC, ∴53x OD =,54xAD =,AEDCB 图2A3(2)3(1)∴OD=x 53,AD=x 54. ∴AE=x x 53+=x 58. ∵△ADE ∽△AEP, ∴AE AD AP AE =, ∴x x yx 585458=. ∴x y 516= (8250≤<x ). (3)当BF=1时，①若EP 交线段CB 的延长线于点F,如图3(1)，则CF=4.∵∠ADE=∠AEP, ∴∠PDE=∠PEC. ∵∠FBP=∠DEP=90°, ∠FPB=∠DPE, ∴∠F=∠PDE, ∴∠F=∠FEC, ∴CF=CE. ∴5-x 58=4,得85=x .可求得2=y ,即AP=2. ②若EP 交线段CB 于点F,如图3(2), 则CF=2. 类似①,可得CF=CE.∴5-x 58=2,得815=x . 可求得6=y ,即AP=6.综上所述, 当BF=1时,线段AP 的长为2或6. 三、应用求图形面积的方法建立函数关系式例4 如图,在△ABC 中,∠BAC=90°,AB=AC=22,⊙A 的半径为1.若点O 在BC 边上运动(与点B 、C 不重合),设BO=x ,△AOC 的面积为y .(1)求y 关于x 的函数解析式,并写出函数的定义域. (2)以点O 为圆心,BO 长为半径作圆O,求当⊙O 与⊙A 相切时, △AOC 的面积.解:(1)过点A 作AH ⊥BC,垂足为H. ∵∠BAC=90°,AB=AC=22, ∴BC=4,AH=21BC=2. ∴OC=4-x . ∵AH OC S AOC ⋅=∆21, ∴4+-=x y (40<<x ). (2)①当⊙O 与⊙A 外切时,在Rt △AOH 中,OA=1+x ,OH=x -2, ∴222)2(2)1(x x -+=+. 解得67=x . 此时,△AOC 的面积y =617674=-. ②当⊙O 与⊙A 内切时,在Rt △AOH 中,OA=1-x ,OH=2-x , ∴222)2(2)1(-+=-x x . 解得27=x . 此时,△AOC 的面积y =21274=-. 综上所述,当⊙O 与⊙A 相切时,△AOC 的面积为617或21.动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。

中考数学压轴题复习讲义（动点问题详细分层解析，尖子生首选资料 ）所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想：分类思想 函数思想 方程思想 数形结合思想 转化思想 注重对几何图形运动变化能力的考查从变换的角度和运动变化来研究三角形、四边形、函数图像等图形，通过“对称、动点的运动”等研究手段和方法，来探索与发现图形性质及图形变化，在解题过程中渗透空间观念和合情推理。

选择基本的几何图形，让学生经历探索的过程，以能力立意，考查学生的自主探究能力，促进培养学生解决问题的能力．图形在动点的运动过程中观察图形的变化情况，需要理解图形在不同位置的情况，才能做好计算推理的过程。

在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。

二期课改后数学卷中的数学压轴性题正逐步转向数形结合、动态几何、动手操作、实验探究等方向发展．这些压轴题题型繁多、题意创新，目的是考察学生的分析问题、解决问题的能力，内容包括空间观念、应用意识、推理能力等．从数学思想的层面上讲：（1）运动观点；（2）方程思想；（3）数形结合思想；（4）分类思想；（5）转化思想等．研究历年来各区的压轴性试题，就能找到今年中考数学试题的热点的形成和命题的动向，它有利于我们教师在教学中研究对策，把握方向．只的这样，才能更好的培养学生解题素养，在素质教育的背景下更明确地体现课程标准的导向．本文拟就压轴题的题型背景和区分度测量点的存在性和区分度小题处理手法提出自己的观点．函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要内容.动点问题反映的是一种函数思想,由于某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,这种变化关系就是动点问题中的函数关系.那么,我们怎样建立这种函数解析式呢?下面结合中考试题举例分析. 一、应用勾股定理建立函数解析式例1 )如图1,在半径为6,圆心角为90°的扇形OAB 的弧AB 上,有一个动点P,PH ⊥OA,垂足为H,△OPH 的重心为G.(1)当点P 在弧AB 上运动时,线段GO 、GP 、GH 中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度.(2)设PH x =,GP y =,求y 关于x 的函数解析式，并写出函数的定义域(即自变量x 的取值范围). (3)如果△PGH 是等腰三角形,试求出线段PH 的长.解:(1)当点P 在弧AB 上运动时,OP 保持不变,于是线段GO 、GP 、GH 中,有长度保持不变的线段，这条线段是GH=32NH=2132⋅OP=2.(2)在Rt △POH 中, 22236x PH OP OH -=-=, ∴2362121x OH MH -==. 在Rt △MPH 中,HM NG POAB图1xy.∴y =GP=32MP=233631x + (0<x <6). (3)△PGH 是等腰三角形有三种可能情况:①GP=PH 时,x x =+233631,解得6=x . 经检验, 6=x 是原方程的根,且符合题意. ②GP=GH 时, 2336312=+x ,解得0=x . 经检验, 0=x 是原方程的根,但不符合题意.③PH=GH 时,2=x .综上所述,如果△PGH 是等腰三角形,那么线段PH 的长为6或2. 二、应用比例式建立函数解析式例2 如图2,在△ABC 中,AB=AC=1,点D,E 在直线BC 上运动.设BD=,x CE=y . (1)如果∠BAC=30°,∠DAE=105°,试确定y 与x 之间的函数解析式；(2)如果∠BAC 的度数为α,∠DAE 的度数为β,当α,β满足怎样的关系式时,(1)中y 与x 之间的函数解析式还成立?试说明理由.解:(1)在△ABC 中,∵AB=AC,∠BAC=30°, ∴∠ABC=∠ACB=75°, ∴∠ABD=∠ACE=105°. ∵∠BAC=30°,∠DAE=105°, ∴∠DAB+∠CAE=75°, 又∠DAB+∠ADB=∠ABC=75°, ∴∠CAE=∠ADB,∴△ADB ∽△EAC, ∴AC BD CE AB =,∴11x y =, ∴xy 1=. (2)由于∠DAB+∠CAE=αβ-,又∠DAB+∠ADB=∠ABC=290α-︒,且函数关系式成立, ∴290α-︒=αβ-, 整理得=-2αβ︒90.当=-2αβ︒90时,函数解析式xy 1=成立.例3(2005年·上海)如图3(1),在△ABC 中,∠ABC=90°,AB=4,BC=3.点O 是边AC 上的一个动点,以点O 为圆心作半圆,与边AB 相切于点D,交线段OC 于点E.作EP ⊥ED,交射线AB 于点P,交射线CB 于点F.(1)求证: △ADE ∽△AEP.(2)设OA=x ,AP=y ,求y 关于x 的函数解析式,并写出它的定义域.(3)当BF=1时,求线段AP 的长.2222233621419x x x MH PH MP +=-+=+= AEDCB 图2A3(2)3(1)解:(1)连结OD.根据题意,得OD ⊥AB,∴∠ODA=90°,∠ODA=∠DEP.又由OD=OE,得∠ODE=∠OED.∴∠ADE=∠AEP, ∴△ADE ∽△AEP.(2)∵∠ABC=90°,AB=4,BC=3, ∴AC=5. ∵∠ABC=∠ADO=90°, ∴OD ∥BC, ∴53x OD =,54xAD =, ∴OD=x 53,AD=x 54. ∴AE=x x 53+=x 58. ∵△ADE ∽△AEP, ∴AE AD AP AE =, ∴x x yx 585458=. ∴x y 516= (8250≤<x ). (3)当BF=1时，①若EP 交线段CB 的延长线于点F,如图3(1)，则CF=4.∵∠ADE=∠AEP, ∴∠PDE=∠PEC. ∵∠FBP=∠DEP=90°, ∠FPB=∠DPE, ∴∠F=∠PDE, ∴∠F=∠FEC, ∴CF=CE. ∴5-x 58=4,得85=x .可求得2=y ,即AP=2. ②若EP 交线段CB 于点F,如图3(2), 则CF=2. 类似①,可得CF=CE.∴5-x 58=2,得815=x . 可求得6=y ,即AP=6.综上所述, 当BF=1时,线段AP 的长为2或6. 三、应用求图形面积的方法建立函数关系式例4 如图,在△ABC 中,∠BAC=90°,AB=AC=22,⊙A 的半径为1.若点O 在BC 边上运动(与点B 、C 不重合),设BO=x ,△AOC 的面积为y .(1)求y 关于x 的函数解析式,并写出函数的定义域. (2)以点O 为圆心,BO 长为半径作圆O,求当⊙O 与⊙A 相切时, △AOC 的面积.解:(1)过点A 作AH ⊥BC,垂足为H. ∵∠BAC=90°,AB=AC=22, ∴BC=4,AH=21BC=2. ∴OC=4-x .∵AH OC S AOC ⋅=∆21, ∴4+-=x y (40<<x ). (2)①当⊙O 与⊙A 外切时,在Rt △AOH 中,OA=1+x ,OH=x -2, ∴222)2(2)1(x x -+=+. 解得67=x . 此时,△AOC 的面积y =617674=-. ②当⊙O 与⊙A 内切时,AB CO 图8HC在Rt △AOH 中,OA=1-x ,OH=2-x , ∴222)2(2)1(-+=-x x . 解得27=x . 此时,△AOC 的面积y =21274=-. 综上所述,当⊙O 与⊙A 相切时,△AOC 的面积为617或21.动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。

第1题如图，抛物线y ＝－x 2－2x ＋3的图象与x 轴交于A 、B 两点（点A 在点B 的左边），与y 轴交于点C ，点D 为抛物线的顶点． （1）直接写出A 、B 、C 三点的坐标；（2）点M 为线段AB 上一点（点M 不与点A 、B 重合），过点M 作x 轴的垂线，与直线AC 交于点E ，与抛物线交于点P ，过点P 作PQ ∥AB 交抛物线于点Q ，过点Q 作QN ⊥x 轴于点N ，若点P 在点Q 左边，当矩形PMNQ 的周长最大时，求△AEM 的面积； （3）在（2）的条件下，当矩形PMNQ 的周长最大时，连接DQ ，过抛物线上一点F 作y 轴的平行线，与直线AC 交于点G （点G 在点F 的上方）．若FG ＝22DQ ，求点F 的坐标．解：（1）由题设，依题意，得：A （－3，0），B （1，0），C （0，3）（2）∵y ＝－x 2－2x ＋3＝－( x ＋1 )2＋4 ∴抛物线的对称轴为直线x ＝－1设M （x ，0），P （x ，－x 2－2x ＋3），其中－3＜x ＜－1 ∵P 、Q 关于直线x ＝－1对称， ∴设Q 的横坐标为a则a －( －1 )＝－1－x ，∴a ＝－2－x∴Q （－2－x ，－x 2－2x ＋3）∴MP ＝－x 2－2x ＋3，PQ ＝－2－x －x ＝－2－2x ∴周长d ＝2( －2－2x －x 2－2x ＋3 )＝－2x 2－8x ＋2＝－2( x ＋2 )2＋10∴当x ＝－2设，d 取最大值 此时M （－2，0），∴AM ＝－2－( －3 )＝1 设直线AC 的解析式为y ＝kx ＋b则 ⎩⎪⎨⎪⎧－3k ＋b ＝0b ＝3 解得 ⎩⎪⎨⎪⎧k ＝1b ＝3 ∴直线AC 的解析式为y ＝x ＋3 将x ＝－2代入y ＝x ＋3得y ＝1xyPB N O M AQCD E xyB O A Q DK GF∴E（－2，1），∴EM＝1∴S△AEM ＝12AM·ME＝12×1×1＝12（3）由（2）知，当矩形PMNQ的周长最大时，x＝－2 此时点Q（0，3），与点C重合，∴OQ＝3∵y＝－x2－2x＋3＝－(x＋1)2＋4，∴D（－1，4）过D作DK⊥y轴于K，则DK＝1，OK＝4∴QK＝OK－OQ＝4－3＝1∴△DKQ是等腰直角三角形，DQ＝ 2∴FG＝22DQ＝4设F（m，－m2－2m＋3），则G（m，m＋3）FG＝m＋3－(－m2－2m＋3)＝m2＋3m∴m2＋3m＝4，解得m1＝－4，m2＝1当m＝－4时，－m2－2m＋3＝－5当m＝1时，－m2－2m＋3＝0∴F（－4，－5）或（1，0）第2题如图，抛物线y＝ax2＋4ax＋34与x轴交于点A、B（A在B的左侧），过点A的直线y＝kx＋3k交抛物线于另一点C．（1）求抛物线的解析式；（2）连接BC，过点B作BD⊥BC，交直线AC于点D，若BC＝5BD，求k的值；（3）将直线y＝kx＋3k向上平移4个单位，平移后的直线交抛物线于E、F两点，求△AEF 的面积的最小值．解：（1）∵y＝kx＋3k＝k(x＋3)，∴A（－3，0）把A（－3，0）代入抛物线y＝ax2＋4ax＋3 49a－12a＋34＝0，解得a＝14xyA OBCMD∴抛物线的解析式为y ＝ 1 4 x 2＋x ＋ 3 4（2）令1 4 x 2＋x ＋ 34＝0，解得x 1＝－1，x 2＝－3 ∴B （－1，0）联立 ⎩⎪⎨⎪⎧y ＝kx ＋3k y ＝ 1 4 x 2＋x ＋ 3 4得C （4k －1，4k 2＋2k ）作DF ⊥x 轴于F ，CG ⊥x 轴于G ，则△BDF ∽△CBG∵BC ＝5BD ，∴CG ＝5BF ，BG ＝5DF设BF ＝m ，则CG ＝5m ，DF ＝k ( －m －1 )＋3k ＝2k －km ，BG ＝10k －5km∴⎩⎪⎨⎪⎧4k －1＋1＝10k －5km 5m ＝4k 2＋2k解得k ＝－32或k ＝1 （3）将直线y ＝kx ＋3k 向上平移4个单位， 平移后的直线为y ＝kx ＋3k ＋4 当x ＝－3时，y ＝4过A 作AG ∥y 轴交直线EF 于G ，则AG ＝4 设E （x 1，y 1），F （x 2，y 2）联立 ⎩⎪⎨⎪⎧y ＝kx ＋3k ＋4y ＝ 1 4 x 2＋x ＋ 3 4 得x 2＋( 4－4k ) x －13－12k ＝0∴x 1＋x 2＝4k －4，x 1x 2＝－13－12k∴| x 2－x 1|＝( x 1＋x 2 )2－4x 1x 2 ＝( 4k －4 )2－4( －13－12k ) ＝16k 2＋16k ＋68 ＝16( k ＋1 2)2＋64∴S △AEF ＝ S △AEG ＋ S △AFG ＝ 12AG ·| x 2－x 1| ＝ 12×4×16( k ＋1 2)2＋64 ∴当k ＝－ 12 时，△AEF 的面积有最小值16第3题如图，已知抛物线y ＝－x 2＋2x ＋3与x 轴交于A 、B 两点（点A 在点B 的左边），与y 轴交于点C ，连接BC ．（1）直接写出A 、B 、C 三点的坐标；xyA OB CM DF GyxOA B GEF（2）点P 为线段BC 上的一点（不与B 、C 重合），PM ∥y 轴交抛物线于M ，交x 轴于N ，当△BCM 的面积最大时，求△BPN 的周长；（3）在（2）的条件下，在抛物线的对称轴上存在点Q ，使△CNQ 为直角三角形，求点Q 的坐标．解：（1）由题设，依题意，得：A （－1，0），B （3，0），C （0，3）（2）设直线BC 的解析式为y ＝kx ＋b则 ⎩⎪⎨⎪⎧3k ＋b ＝0b ＝3 解得 ⎩⎪⎨⎪⎧k ＝－1b ＝3 ∴y ＝－x ＋3 ∵S △BCM ＝S △BPM ＋ S △CPM ＝1 2 PM ·OB ＝ 32PM ∴当线段PM 的长度取最大值时，△BCM 的面积最大 设P （t ，－t ＋3），则M （t ，－t 2＋2t ＋3）（0＜t ＜3） PM ＝－t 2＋2t ＋3－( －t ＋3 )＝－t 2＋3t ＝－( t － 3 2 )2＋ 9 4∴当t ＝32时，△BCM 的面积最大 此时P （3 2 ，3 2 ），N （32 ，0）∴BN ＝PN ＝ 3 2 ，PB ＝ 32 2∴△BPN 的周长为3 2 ＋ 3 2 ＋ 3 2 2＝3＋ 322 （3）∵y ＝－x 2＋2x ＋3＝－( x －1 )2＋4∴抛物线的对称轴为直线x ＝1， 与x 轴交于点E （1，0）设Q （1，y ），由N （3 2 ，0），C （3，0），得CN 2＝ 454过点Q 作QD ⊥y 轴于D ，则D （0，y ）∴CQ 2＝( y －3 )2＋1 2＝y 2－6y ＋10，NQ 2＝y 2＋ 14∵△CNQ 为直角三角形，∴有以下三种情况：xyMCOB NAPxy MCO B N APQ DE①当CN 2＋CQ 2＝NQ 2时，45 4 ＋y 2－6y ＋10＝y 2＋1 4解得y ＝ 7 2 ，∴Q 1（1，72 ）②当CN 2＋NQ 2＝CQ 2时，45 4 ＋y 2＋ 1 4＝y 2－6y ＋10 解得y ＝－ 1 4 ，∴Q 2（1，－ 14）③当CQ 2＋NQ 2＝CN 2时，y 2－6y ＋10＋y 2＋ 1 4 ＝454解得y ＝3±112 ，∴Q 3（1，3＋112），Q 4（1，3－112） 综上所述，点Q 的坐标为（1，7 2 ），（1，－ 14 ），（1，3＋112），（1，3－112）第4题如图，在平面直角坐标系中，直线y ＝kx ＋1与y 轴交于点C ，与抛物线y ＝1 4x 2交于点A 、B （点A 在点B 左侧），分别过A 、B 两点作直线y ＝－1的垂线，垂足为E 、F ． （1）求证：AC ＝AE ；（2）设△ACE 、△BCF 、△ECF 的面积分别为S 1、S 2、S 3，若S 1＋S 2 S 3 ＝ 32，求k 的值； （3）M 为EF 的中点，连接MC 并延长交抛物线于点P ，连接PA 、BM ．是否存在这样的点M ，使△PAC 与△BMC 相似？若存在，求出所有符合条件的点M 的坐标；若不存在，请说明理由．解：（1）由题设，依题意，设A （x ，y ），其中y ＝ 14x 2则AC 2＝x 2＋( y －1 )2＝4y ＋y 2－2y ＋1＝( y ＋1 )2 AE 2＝( y ＋1 )2 ∴AC ＝AE（2）设A （x 1，y 1），B （x 2，y 2） x y B A OE F M CxyBAO EFC G由 ⎩⎪⎨⎪⎧y ＝kx ＋1y ＝ 1 4 x2 得x 2－4kx －4＝0 则x 1＋x 2＝4k ，x 1x 2＝－4∴AE ＋BF ＝y 1＋1＋y 2＋1＝kx 1＋1＋kx 2＋1＋2 ＝k ( x 1＋x 2 )＋4＝4k 2＋4∵S 1＋S 2＝S 梯形AEFB －S 3＝ 1 2 ( AE ＋BF )·EF － 12 EF ·CGS 3＝ 1 2 EF ·CG ，S 1＋S 2 S 3 ＝ 32∴AE ＋BF －CG CG ＝ 3 2∴4k 2＋4－2 2 ＝3 2 ，解得k ＝± 1 2（3）连接AM∵AC ＝AE ，∴∠ACE ＝∠AEC ∵AE ⊥EF ，∴AE ∥y 轴 ∴∠AEC ＝∠ECO ∴ACE ＝∠ECO同理可得∠BCF ＝∠FCO∴∠ECF ＝∠ECO ＋∠FCO ＝ 12 ( ∠ACO ＋∠BCO )＝90°∵M 为EF 的中点，∴CM ＝EM ∴△ACM ≌△AEM∴∠AMC ＝∠AME ，∠ACM ＝∠AEM ＝90° ∴∠PCA ＝∠BCM ＝90°∴∠MAC ＝∠BMC ＝90°－∠ABM ①若△PAC ∽△BMC ，则∠PAC ＝∠BMC ＝∠MAC ∴△APC ≌△AMC ，∴PC ＝CM 即C 是PM 中点作PH ⊥EF 于H ，设直线EF 交y 轴于G 则G 是HM 中点，PH ＝2CG ＝2( 1＋1 )＝4 ∴点P 的纵坐标为3，代入y ＝1 4x 2，得x ＝±2 3 ∴M 1（23，－1），M 2（－23，－1）②若△PAC ∽△MBC ，则∠PAC ＝∠MBC ，∴PA ∥BM∵∠ACM ＝90°，∠MAC ＝∠BMC ∴∠AMB ＝90°，∴∠PAM ＝90° 作PH ⊥EF 于H ，AG ⊥PH 于G ，交PM 于K ， 则AG ∥EF ，∴∠KAM ＝∠AME ＝∠AMC ∴AK ＝MK ，∴AK ＝PK ∴PK ＝KM ，∴PG ＝GH ＝AE 设EF 交x 轴于N ，则CN ＝2∠CEN ＝∠ECM ＝∠BMC ＝∠APC ∴△ECN ∽△PAC∴EN CN ＝ PC AC ＝ PH AE ＝ PHGH ＝2，∴EN ＝2CN ＝4 设MN ＝x ，则CM ＝EM ＝4－x ，yO xA BC ME FPHGxyO PABM E FC在Rt △CMN 中，x 2＋2 2＝( 4－x )2 解得x ＝3 2 ，∴M 3（－ 3 2，－1） 综上所述，符合条件的点M 的坐标为M 1（23，－1）， M 2（－23，－1），M 3（－ 32，－1）第5题如图，抛物线y ＝－1m( x ＋2)( x －m )（m ＞0）与x 轴交于A 、B 两点（A 在B 的左侧），与y 轴交于点C ，连接AC 、BC ． （1）若△ABC 为直角三角形，求m 的值；（2）在（1）的条件下，点D 是第一象限抛物线上一动点，过D 点的直线交x 轴、y 轴的正半轴于E 、F ，连接OD ，当OD 的长最小时，求△OEF 面积的最小值； （3）直线y ＝12x ＋b 经过点B ，与抛物线交于另一点G ，点P 在y 轴上，点Q 在抛物线上，以点B 、G 、P 、Q 为顶点的四边形能否成为矩形？若能，求出点P 的坐标；若不能，请说明理由．解：（1）令－1m(x ＋2)(x －m)＝0，解得x 1＝－2，x 2＝m ∵m ＞0，A 在B 的左侧，∴A （－2，0），B （m ，0） 令x ＝0，得y ＝2，∴C （0，2）∴OA ＝OC ＝2，∴∠ACO ＝∠CAO ＝45° △ABC 为直角三角形，只能∠ACB ＝90° ∴∠BCO ＝∠CBO ＝45°，∴OB ＝OC ＝2 ∴m ＝2（2）∵m ＝2，∴y ＝－ 1 2 ( x ＋2)( x －2 )＝－ 12 x 2＋2∴x 2＝4－2yCBAxy CBAxy 备用图x yM EFB GHAO C PKN设D（x，y），作DH⊥x轴于H则OH＝x，DH＝y∴OD2＝OH2＋DH2＝x2＋y2＝4－2y＋y2＝(y－1)2＋3 ∴当点D的纵坐标为1时，OD2最小，OD最小由－12x2＋2＝1，解得x＝± 2∵点D在第一象限，∴D（2，1）设直线EF的解析式为y＝kx＋n则1＝2k＋n，n＝1－2k ∴y＝kx＋1－2k令y＝0，得x＝2－1k；令x＝0，得y＝1－2k∴OE＝2－1k，OF＝1－2k∴S△OEF ＝12OE·OF＝12(2－1k)(1－2k)＝－12k－k＋2＝(1－2k－－k)2＋2 2∴△OEF面积的最小值为2 2（3）∵直线y＝12x＋b经过点B（m，0），∴0＝12m＋b∴b＝－12m，∴y＝12x－12m令－1m(x＋2)(x－m)＝12x－12m，解得x＝m或x＝－12m－2∴G（－12m－2，－34m－1）①若BG是矩形的一条对角线，显然点P只能在直线BG的下方由PG＝∥BQ，可得点Q的横坐标为12m－2∴y＝－1m(12m－2＋2)(12m－2－m)＝14m＋1，∴Q（12m－2，14m＋1）点P的纵坐标为：－34m－1－14m－1＝－m－2∴P（0，－m－2）作QM⊥x轴于MBM＝m－(12m－2)＝12(m＋4)，QM＝14m＋1＝14(m＋4)∵四边形BPGQ为矩形，∴BP⊥BQxyODCBAHFEyCQBAOGPxM∴△BQM ∽△PBO ，∴OP OB ＝ BMQM， ∴ m ＋2 m＝ 12 ( m ＋4 )1 4( m ＋4 )∵m ＞0，∴m ＋2m＝2，∴m ＝2 ∴P （0，－4）②若BG 是矩形的一条边，显然点P 只能在直线BG 的下方由点B 的横坐标为m 、点P 的横坐标为0，可得矩形对角线交点的横坐标为 m2由点G 横坐标为－ 1 2 m －2可得点Q 的横坐标为 3 2m ＋2 ∴y ＝－ 1 m ( 3 2 m ＋2＋2 )( 32m ＋2－m ) ＝－3 4m －5－8m ∴Q （3 2 m ＋2，－ 3 4m －5－8m ） 点P 的纵坐标为－ 3 4 m －1－ 3 4m －5－8m ＝－ 3 2 m －6－ 8 m∴P （0，－3 2m －6－8m ） 作QM ⊥x 轴于M ，GN ⊥x 轴于N BM ＝3 2 m ＋2－m ＝ 1 2 ( m ＋4 )，QM ＝ 3 4 m ＋5＋8 m ＝ 14m( m ＋4 )( 3m ＋8 ) BN ＝m ＋1 2 m ＋2＝ 3 2 m ＋2＝ 3 2 ( m ＋4 )，GN ＝ 3 4 m ＋1＝ 34( m ＋4 ) ∵四边形BPEQ 为矩形，∴BQ ⊥BG∴△BQM ∽△GBN ，∴BM QM ＝ GN BN，∴12( m ＋4 ) 1 4m ( m ＋4 )( 3m ＋8 ) ＝34( m ＋4 )3 2 ( m ＋4 ) ∵m ＞0，∴2m 3m ＋8＝ 12 ，∴m ＝8 ∴P （0，－19）综上所述，以点B 、E 、P 、Q 为顶点的四边形能成为矩形 点P 的坐标为（0，－4）或（0，－19）By OA CxGPQNM第6题如图，抛物线y ＝x 2－( m ＋2 )x ＋4的顶点C 在x 轴正半轴上，直线y ＝x ＋2与抛物线交于A 、B 两点（点A 在点B 的左侧）． （1）求m 的值；（2）点P 是抛物线上一点，当△PAB 的面积是△ABC 面积的2倍时，求点P 的坐标； （3）将直线AB 向下平移t （t ＞0）个单位，平移后的直线与抛物线交于A ′、B ′ 两点（A ′ 在B ′ 的左侧），当△A ′B ′C 为直角三角形时，求t 的值．解：（1）抛物线y ＝x 2－( m ＋2 )x ＋4的顶点坐标为C （m ＋2 2 ，4－( m ＋2 )24） ∵顶点C 在x 轴正半轴上，∴m ＋2 2 ＞0，4－ ( m ＋2 )24＝0解得m ＞－2，m ＝2或m ＝－6 ∴m ＝2（2）过C 作CD ⊥AB 于D ，过P 作PE ⊥AB 于E过C 作CF ∥y 轴，交直线AB 于F ，过P 作PG ∥y 轴，交直线AB 于G则PG ∥CF ，∴∠PGE ＝∠CFD ∴Rt △PGE ∽Rt △CFD ，∴PG CF ＝PECD∵S △PAB ＝2S △ABC ，∴1 2 AB ·PE ＝2 · 12AB ·CD ∴PE ＝2CD ，∴PG ＝2CF∵m ＝2，∴抛物线的解析式为y ＝x 2－4x ＋4∵y ＝x 2－4x ＋4＝( x －2 )2，∴C （2，0） 把x ＝2代入y ＝x ＋2，得y ＝4 ∴CF ＝4，∴PG ＝8设P （x ，x 2－4x ＋4），则G （x ，x ＋2）ABxy COABxy CO备用图ABxy C OPG DFE∴PG ＝x 2－4x ＋4－( x ＋2 )＝x 2－5x ＋2 ∴x 2－5x ＋2＝8，解得x ＝－1或x ＝6 ∴P 1（－1，9），P 2（6，16）（3）设直线A ′B ′ 的解析式为y ＝x ＋b ，A ′（x 1，y 1），B ′（x 2，y 2） 显然，∠A ′B ′C ≠90° ①若∠B ′A ′C ＝90°，过A ′ 作FG ⊥x 轴于G ，B ′F ⊥FG 于F 则△A ′CG ∽△B ′A ′F∴A ′G CG ＝ B ′FA ′F ＝ x 2－x 1 y 2－y 1 ＝ x 2－x 1 x 2＋b －( x 1＋b ) ＝1 ∴A ′G ＝CG ＝2－x 1，∴A ′（x 1，2－x 1）∴2－x 1＝( x 1－2 )2，解得x 1＝1或x 1＝2（舍去） ∴A ′（1，1），代入y ＝x ＋b ，得b ＝0 ∴t ＝2②若∠B ′A ′C ＝90°，作A ′G ⊥x 轴于G ，B ′H ⊥x 轴于H则△A ′CG ∽△CB ′H ，∴A ′G CG ＝CHB ′H ∴y 12－x 1＝ x 2－2 y 2 ，∴y 1y 2＝2( x 1＋x 2 )－x 1x 2－4令x 2－4x ＋4＝x ＋b ，即x 2－5x ＋4－b ＝0则x 1＋x 2＝5，x 1x 2＝4－by 1y 2＝( x 1＋b )( x 2＋b )＝x 1x 2＋b ( x 1＋x 2 )＋b 2＝b 2＋4b ＋4∴b 2＋4b ＋4＝10－( 4－b )－4 解得b ＝－1或b ＝－2当b ＝－2时，y ＝x －2，直线过点C ，A ′ 与C 重合 ∴b ＝－2不合题意，舍去 ∴b ＝－1，t ＝2－( －1 )＝3 综上所述，t ＝2或t ＝3第7题已知抛物线y ＝－x 2＋bx ＋c 与x 轴交于点A （m －2，0）和B （2m ＋1，0）（点A 在点B 的左侧），与y 轴交于点C ，顶点为P ，对称轴为直线x ＝1． （1）求抛物线的解析式；（2）直线y ＝kx ＋2（k ≠0）与抛物线相交于不同两点M （x 1，y 1）、N （x 2，y 2）（x 1＜x 2），当| x 1－x 2|最小时，求M 、N 两点的坐标；（3）若线段OB 在x 轴上移动，首尾顺次连接点O 、B 、P 、C 构成多边形的周长为L ，求L 最小值时点O 、B 移动后的坐标及L 的最小值．xy ABCO A ′ B ′F GxyABCOA ′B ′G H解：（1）∵对称轴为直线x ＝1，∴－b2×( －1)＝1，∴b ＝2∵A （m －2，0），B （2m ＋1，0），∴m －2＋2m ＋12＝1∴m ＝1，∴A （－1，0），B （3，0）∴⎩⎪⎨⎪⎧－1－b ＋c ＝0－9＋3b ＋c ＝0 解得 ⎩⎪⎨⎪⎧b ＝2c ＝3 ∴抛物线的解析式为y ＝－x 2＋2x ＋3（2）令－x 2＋2x ＋3＝kx ＋2，得x 2＋( k －2 )x －1＝0 则x 1＋x 2＝2－k ，x 1x 2＝－1∴( x 1－x 2 )2＝( x 1＋x 2 )2－4x 1x 2＝( k －2 )2＋4∴当k ＝2时，( x 1－x 2 )2的最小值为4即| x 1－x 2|的最小值为2，∴x 2－1＝0∵x 1＜x 2，∴x 1＝－1，x 2＝1，∴y 1＝0，y 2＝4 ∴M （－1，0），N （1，4） （3）O （0，0），B （3，0），P （1，4），C （0，3）O 、B 、P 、C 构成多边形的周长为L ＝OB ＋BP ＋PC ＋CO ∵线段OB 平移过程中，OB 、PC 的长度不变 ∴要使L 最小，只需BP ＋CO 最小平移线段OC 到BC ′，四边形OBC ′C 是矩形 ∴C ′（3，3）作点P 关于x 轴的对称点P ′（1，－4），连接C ′P ′ 与x 轴 交于B ′可求直线C ′P ′ 的解析式为y ＝ 7 2 x －152当y ＝0时，x ＝15 7 ，∴B ′（157，0） 又3－ 15 7 ＝ 6 7 ，∴点B 向左平移 67个单位到B ′xyOABCPxyOC ′AB O ′ B ′CPP ′同时点O 向左平移6 7 个单位到O ′（－ 67 ，0） 即线段OB 向左平移67个单位时，L 最小 此时BP ＋CO 最小为C ′P ′＝ 7 2＋2 2 ＝53O ′B ′＝OB ＝3，CP ＝ 2∴周长L 的最小值为 53＋2＋3第8题如图，已知二次函数的图象M 经过A （－1，0），B （4，0），C （2，－6）三点． （1）求该二次函数的解析式； （2）点G 是线段AC 上的动点（点G 与线段AC 的端点不重合），若△ABG 与△ABC 相似，求点G 的坐标；（3）设图象M 的对称轴为l ，点D （m ，n ）（－1＜m ＜2）是图象M 上一动点，当△ACD 的面积为278时，点D 关于l 的对称点为E ，能否在图象M 和l 上分别找到点P 、Q ，使得以点D 、E 、P 、Q 为顶点的四边形为平行四边形．若能，求出点P 的坐标；若不能，说明理由．解：（1）设二次函数的解析式为y ＝ax 2＋bx ＋c ，由题意得：⎩⎪⎨⎪⎧a －b ＋c ＝016a ＋4b ＋c ＝04a ＋2b ＋c ＝－6 解得 ⎩⎪⎨⎪⎧a ＝1b ＝－3b ＝－4 ∴二次函数的解析式为y ＝x 2－3x －4（2）若△ABG 与△ABC 相似，则 AB AC ＝ AG AB易求AB ＝5，AC ＝3 5 ∴AG ＝ AB 2 AC ＝ 535过G 、C 分别作x 轴的垂线，垂足为F 和HlyBAOGDCxl yBAOG DCxHF ly BAOKDC x则△AGF ∽△ACH ，AH AF ＝ GH CF ＝AGAC∴AH 3 ＝ GH 6 ＝ 5 35 35 ，解得AF ＝ 5 3 ，GF ＝10 3 ∴点G 的坐标为（2 3 ，－103） （3）过D 作DK ∥y 轴交AC 于K 设直线AC 的解析式为y ＝kx ＋t∴⎩⎪⎨⎪⎧－k ＋t ＝02k ＋t ＝－6 解得 ⎩⎪⎨⎪⎧k ＝－2t ＝－2 ∴直线AC 的解析式为y ＝－2x －2∵D （m ，n ）在二次函数的图象上，∴D （m ，m 2－3m －4） ∴K （m ，－2m －2）∴KD ＝－2m －2－( m 2－3m －4 )＝－m 2＋m ＋2 ∴S △ACD ＝S △AKD ＋ S △CKD ＝ 1 2 KD ( x D －x A )＋ 12KD ( x C －x D ) ＝1 2 KD ( x C －x A )＝ 1 2( －m 2＋m ＋2 )×3 ∵S △ACD ＝27 8 ，∴1 2 ( －m 2＋m ＋2 )×3＝ 278解得m ＝ 12∴D （1 2 ，－214） ∵y ＝x 2－3x －4＝( x －3 2 )2－254∴图象M 的对称轴l 为直线x ＝ 32∵点D 关于l 的对称点为E ，∴DE ＝2( 3 2 － 12 )＝2设P （x ，x 2－3x －4）①若PQ 为平行四边形的一条边 则PQ ∥DE ，且PQ ＝DE ＝2∴| x － 3 2 |＝2，解得x ＝－ 1 2 或x ＝ 72∴P 1（－1 2 ，－ 9 4 ），P 2（7 2 ，－ 94） ②若PQ 为平行四边形的一条对角线则PQ 、DE 互相平分∴此时P 点是抛物线的顶点ly BAODCxQEPlyBAODC xQEPlyBAOPDCxQE∴P 3（3 2 ，－254） 综上所述，满足条件的点P 的坐标为 （－1 2 ，－ 9 4 ）或（7 2 ，－ 9 4 ）或（3 2 ，－254）第9题如图，抛物线y ＝ax 2－2ax －3a （a ＜0）与x 轴交于A 、B 两点（A 在B 的左侧），与y 轴交于点C ，顶点为P ，对称轴与x 轴交于点M ，抛物线的对称轴与抛物线交于点P ，与直线BC 交于点M ，且PM ＝AB ． （1）求抛物线的解析式； （2）点K 是x 轴正半轴上一点，点A 、P 关于点K 的对称点分别为A 1、P 1，连接PA 1、P 1A 1，若PA 1⊥P 1A 1，求点K 的坐标；（3）矩形ADEF 的边AF 在x 轴负半轴上，边AD 在第二象限，AD ＝2，DE ＝3．将矩形ADEF 沿x 轴正方向平移t （t ＞0）个单位，直线AD 、EF 分别交抛物线于G 、H ．问：是否存在实数t ，使得以点D 、F 、G 、H 为顶点的四边形是平行四边形？若存在，求出t 的值；若不存在，说明理由．解：（1）根据题意，由y ＝ax 2－2ax －3a ＝a ( x ＋1 )( x －3 )令y ＝0，则x 1＝－1，x 2＝3∵A 在B 的左侧，∴A （－1，0），B （3，0），∴AB ＝4 ∵PM ＝AB ，∴PM ＝4∵y ＝ax 2－2ax －3a ＝a ( x －1 )2－4a ∴P （1，－4a ），PM ＝－4a ∴－4a ＝4，∴a ＝－1∴抛物线的解析式为y ＝－x 2＋2x ＋3 （2）∵a ＝－1，∴P （1，4），PM ＝4 作P 1Q ⊥x 轴于Q∵点A 、P 关于点K 的对称点分别为A 1、P 1 ∴AK ＝A 1K ，PK ＝P 1K ，∠PKM ＝∠P 1KQxyPCBAOMxyCBAODEF备用图xyPCBA O M∴△PKM ≌△P 1KQ ，∴P 1Q ＝PM ＝4，MK ＝QK ∴A 1Q ＝AM ＝2∵PA 1⊥P 1A 1，∴△PA 1M ∽△A 1P 1Q ∴A 1M PM ＝ P 1Q A 1Q ，∴A 1M 4 ＝4 2∴A 1M ＝8，∴A 1（9，0） ∴K （4，0） （3）存在由题意，点G 的横坐标为t －1，点H 的横坐标为t －4 若GH 为平行四边形的一条边，则DG ＝FH∴－( t －4 )2＋2( t －4 )＋3－2＝－( t －1 )2＋2( t －1 )＋3 解得t ＝23 6若GH 为平行四边形的一条对角线，则DG ＝FH ∴－( t －4 )2＋2( t －4 )＋3＝( t －1 )2－2( t －1 )－3＋2 解得t ＝ 7±32xyPCBAOMKP 1A 1QxyC BOA DG H EF x y CBO A DGHEFxBOADEF GHy第10题如图，已知抛物线y ＝ax 2＋bx ＋c 的顶点坐标为（1，－92），且与x 轴交于A （4，0）、B 两点，与y 轴交于点C ，P 点是抛物线上的一个动点，且横坐标为m ．（1）求抛物线的解析式；（2）若动点P 满足∠PAO 不大于45°，求P 点的横坐标m 的取值范围；（3）当P 点的横坐标m ＜0时，过P 点作y 轴的垂线PQ ，垂足为Q ．问：是否存在P 点，使∠QPO ＝∠BCO ？若存在，求出P 点坐标；若不存在，请说明理由．解：（1）∵抛物线的顶点坐标为（1，－ 92）∴设抛物线为y ＝a ( x －1 )2－ 9 2∵点A （4，0）在抛物线上 ∴a ( 4－1 )2－92 ＝0，∴a ＝ 1 2∴抛物线的解析式为y ＝ 1 2 ( x －1 )2－ 92即y ＝ 12 x 2－x －4（2）由y ＝1 2x 2－x －4，令x ＝0，得y ＝－4 ∴C （0，－4） ∵A （4，0），∴OA ＝OC ∴∠OAC ＝45°过A 作AP ⊥AC 交抛物线于P ，则∠PAO ＝45°xyBAOC xyMB AQ QO P PCP作PM ⊥x 轴于M ，则PM ＝AM ∴P （m ，－m ＋4），∴－m ＋4＝1 2m 2－m －4 解得m ＝4（舍去）或m ＝－4 ∴P （－4，8）∴动点P 满足∠PAO 不大于45°时，P 点的横坐标m 的取值范围是－4≤m ≤0 （3）存在点P 使∠QPO ＝∠BCO当P 点在第二象限时，由题意△PQO ∽△COB ∴PQ CO ＝ QO OB∵B （－2，0），C （0，－4），∴PQ ＝2QO ∴P （m ，－ 1 2 m ），∴－ 1 2 m ＝ 12m 2－m －4 解得m ＝1±332∵m ＜0，∴P （1－332 ，33－14） 当P 点在第三象限时，同理可得P （m ，12m ） ∴1 2 m ＝ 1 2m 2－m －4，解得m ＝3±412 ∵m ＜0，∴P （3－412 ，3－414） 综上所述，满足条件的点P 坐标为（1－332 ，33－14）或（3－412 ，3－414）第11题如图，抛物线y ＝－1 2x 2＋bx ＋c 与x 轴分别相交于点A （－2，0）、B （4，0），与y 轴交于点C ，顶点为点P ． （1）求抛物线的解析式；（2）动点M 、N 从点O 同时出发，都以每秒1个单位长度的速度分别在线段OB 、OC 上向点B 、C 方向运动，过点M 作x 轴的垂线交BC 于点F ，交抛物线于点H ． ①当四边形OMHN 为矩形时，求点H 的坐标；②是否存在这样的点F ，使△PFB 为直角三角形？若存在，求出点F 的坐标；若不存在，请说明理由．xyOMNP H CABF解：（1）由题设，依题意，得：y＝－12x2＋x＋4（2）①设H（x，－12x2＋x＋4）由题意，OM＝ON∵四边形OMHN为矩形，∴MH＝ON∴OM＝MH，∴x＝－12x2＋x＋4解得x＝－22（舍去）或x＝2 2∴H（22，22）②存在设抛物线的对称轴交x轴于D，作PG⊥MF于G∵y＝－12x2＋x＋4＝－12(x－1)2＋92∴P（1，9 2）易求直线BC的解析式为y＝－x＋4 设F（m，－m＋4）当∠PFB＝90°时在y＝－12x2＋x＋4中，当x＝0时，y＝4∴C（0，4），∴OB＝OC，∴∠OBC＝45°∴△BFM和△PFG均为等腰直角三角形∴PG＝FG，∴1－m＝92－(4－m)解得m＝14，∴F（14，154）当∠FPB＝90°时，则△PFG∽△PBD∴PGFG＝PDBD，∴1－m92－(4－m)＝923解得m＝110，∴F（110，3910）综上所述，存在点F（14，154）或（110，3910），使△PFB为直角三角形xyO MNPHCA BFxyO MPGCA BFDxyO MNPGCA BFD第12题如图，已知抛物线C1：y＝－12x2，平移抛物线y＝x2，使其顶点D落在抛物线C1位于y轴右侧的图象上，设平移后的抛物线为C2，且C2与y轴交于点C（0，2）．（1）求抛物线C2的解析式；（2）抛物线C2与x轴交于A、B两点（点B在点A的右侧），求过A、B、C三点的圆的圆心E的坐标；（3）在过点（0，12）且平行于x轴的直线上是否存在点F，使四边形CEBF为菱形，若存在，求出点F的坐标，若不存在，请说明理由．解：（1）由题意，设D（a，－12a2）则抛物线C2的解析式为y＝(x－a)2－12a2∵点C（0，2）在抛物线C2上∴2＝(0－a)2－12a2，解得a＝±2∵D在y轴右侧，∴a＝2∴抛物线C2的解析式为y＝(x－2)2－2（2）在y＝(x－a)2－2中，令y＝0，得x＝2± 2∵点B在点A的右侧，∴A（2－2，0），B（2＋2，0）∵过A、B、C三点的圆的圆心E一定在AB 的垂直平分线上∴设E（2，m）由CE＝AE得22＋(2－m)2＝(2－2＋2)2＋m2解得m＝3 2∴圆心E的坐标为（2，3 2）（3）假设存在F（t，12）使四边形CEBF为菱形，则BF＝CF＝CExyCABODxyCABODEF∴( 2＋2－t )2＋( 1 2 )2＝t 2＋( 2－ 1 2 )2 解得t ＝2，∴F （2，12） 易求CE ＝17 2 ，CF ＝172∴BF ＝CF ＝CE ＝BE即存在点F （2，12 ）使四边形CEBF 为菱形第13题如图，抛物线y ＝－x 2＋bx ＋c 与x 轴交于A 、B 两点（A 在B 的左侧），与y 轴正半轴交于点C ，抛物线的顶点为P ，对称轴为直线x ＝1，且OC ＝3OA ． （1）求抛物线的解析式；（2）点D （2，m ）在抛物线上，点E 在直线AP 上，使DE ⊥OE ，求点E 的横坐标；（3）连接BC 与抛物线的对称轴交于点F ，在抛物线上是否存在点G ，使△GPF 与△GBF 的面积相等，若存在，求出点G 的坐标；若不存在，请说明理由.解：（1）∵抛物线y ＝－x 2＋bx ＋c 的对称轴为直线x ＝1∴－ b 2×( －1 ) ＝1，∴b ＝2，∴y ＝－x 2＋2x ＋c∵OC ＝3OA ，∴OA ＝ 1 3 OC ＝ 1 3 c ，∴A （－ 13 c ，0）∴－( －1 3 c )2＋2( － 1 3c )＋c ＝0，∴c ＝3 ∴抛物线的解析式为y ＝－x 2＋2x ＋3 （2）由（1）知，A （－1，0），C （0，3） ∵D （2，m ）在抛物线上，∴m ＝－2 2＋4＋3＝3 ∴D （2，3）当x ＝1时，y ＝4，∴P （1，4） 易求直线AP 的解析式为y ＝2x ＋ 2xyABOPCxyABONPCMEDxyABOFPC备用图设E （m ，2m ＋2），过E 作MN ∥x 轴，交y 轴于M ，DN ⊥MN 于N ∵DE ⊥OE ，∴△OME ∽△END ∴OM EN ＝ ME ND ，∴2m ＋2 2－m ＝m2m ＋2－3 解得m ＝± 10 5 ∴点E 的横坐标为± 10 5（3）存在令－x 2＋2x ＋3＝0，解得x ＝－1或x ＝3∴B （3，0）易求直线BC 的解析式为y ＝－x ＋3 当x ＝1时，y ＝2，∴F （1，2）∵S △GPF ＝S △GBF ，∴P 、B 两点到直线FG 的距离相等 分两种情况讨论：①当P 、B 在直线FG 同侧时，则FG ∥PB 易求直线PB 的解析式为y ＝－2x ＋6 设直线PB 的解析式为y ＝－2x ＋n 把F （1，2）代入，得n ＝4 ∴y ＝－2x ＋4由 ⎩⎪⎨⎪⎧y ＝－2x ＋4y ＝－x 2＋2x ＋3 解得 ⎩⎨⎧x 1＝2－3y 1＝23 ⎩⎨⎧x 2＝2＋3y 2＝－23∴G 1（2－3，23），G 2（2＋3，－23）②当P 、B 在直线FG 异侧时，则直线FG 过PB 的中点 设对称轴交x 轴于H ∵F （1，2），P （1，4），∴F 为PH 中点 ∴FG ∥x 轴，∴点G 的纵坐标为2令－x 2＋2x ＋3＝2，解得x ＝1± 2 ∴G 3（1－2，2），G 4（1＋2，2）综上所述，存在满足条件的点G ，其坐标为：（2－3，23）或（2＋3，－23）或（1－2，2）或（1＋2，2）xyA BO PCG FxyA BO H PCGF第14题如图，点D 在第一象限，以D 为圆心的⊙D 与y 轴相切于点C （0，4），与x 轴交于A 、B 两点，AB ＝6，抛物线y ＝ax 2＋bx ＋c 经过A 、B 、C 三点． （1）求抛物线的解析式； （2）设抛物线的顶点为M ，（3）点P 是抛物线上的动点，线段PA 与线段BC 相交于点Q ，当PQ ＝4AQ 时，求点P 的坐标．解：（1）连接CD 、DB ，作DE ⊥AB 于E ，则AE ＝BE ＝12AB ＝3∵⊙D 与y 轴相切于点C （0，4），∴DC ⊥OC ，∴DE ＝OC ＝4 ∴OE ＝CD ＝DB ＝BE 2＋DE 2 ＝ 3 2＋4 2 ＝5∴A （2，0），B （8，0）∵抛物线y ＝ax 2＋bx ＋c 经过A 、B 、C 三点∴⎩⎪⎨⎪⎧4a ＋2b ＋c ＝064a ＋8b ＋c ＝0c ＝4解得a ＝ 1 4 ，b ＝－ 52，c ＝4∴抛物线的解析式为y ＝ 1 4 x 2－ 52 x ＋4（2）直线BM 与⊙D 相切，理由如下：连接DM 交AB 于E ，由对称性可知DM ⊥AB ∴∠BEM ＝∠DEB ＝90° ∵y ＝1 4 x 2－ 52 x ＋4＝ 1 4 ( x －5 )2－ 9 4∴EM ＝9 4 ，∴BE EM ＝ 3 9 4＝ 43yDxCABO MyDxCA BO ME yDxCABOME∵DE BE ＝ 4 3，∴BE EM ＝DE BE ∴△BEM ∽△DEB ，∴∠MBE ＝∠BDE ∵∠BDE ＋∠DBE ＝90° ∴∠MBE ＋∠DBE ＝90°，∴∠DBM ＝90° ∴BM 与⊙D 相切 （3）∵B （8，0），C （0，4）， ∴直线BC 的解析式为y ＝－ 12 x ＋4分别过P 、Q 作x 轴的垂线，垂足为F 、G 设P （m ，1 4 m 2－ 52m ＋4） 由PQ ＝4AQ 得AF ＝1 5 AG ＝ 15( m －2 )， OF ＝2＋15 ( m －2 )＝ m ＋8 5QF ＝ 1 5 PG ＝ 1 5 ( 1 4 m 2－ 52 m ＋4 )＝ m 2－10m ＋16 20∴Q （m ＋8 5 ，m 2－10m ＋16 20 ） ∵点Q 在直线y ＝－ 12x ＋4上∴－ 1 2 ( m ＋85 )＋4＝ m 2－10m ＋16 20解得m 1＝－4，m 2＝12 ∴P 1（－4，18），P 2（12，10）第15题如图，抛物线y ＝ax 2＋bx ＋c （a ＜0）与x 轴交于点A （x 1，0）、B （x 2，0），与y 轴交于点C ，OA ＜OB ，OB ＝2OC ，x 1，x 2是方程x 2－4x －5＝0的两个根． （1）求抛物线的解析式；（2）点D 是第一象限抛物线上一点，且∠BDC ＝90°，求点D 的坐标；（3）在（2）的条件下，点P 是抛物线上B 、D 两点之间的一个动点（不与点B 、D 重合），过点P 分别作x 轴和直线OD 的垂线，垂足为M 、N ，求PM ＋PN 的最大值．yDxPCAB O QFGxy OABCxyOABC备用图解：（1）解方程x 2－4x －5＝0，得x 1＝－1，x 2＝5∴A （－1，0），B （5，0） ∵OB ＝2OC ，∴OC ＝ 5 2∵a ＜0，∴C （52，0） ∵抛物线y ＝ax 2＋bx ＋c 经过A 、B 、C 三点∴⎩⎪⎨⎪⎧a －b ＋c ＝025a ＋5b ＋c ＝0c ＝52解得a ＝－1 2，b ＝2，c ＝5 2∴抛物线的解析式为y ＝－1 2 x 2＋2x ＋ 52（2）作DE ⊥x 轴于E ，DF ⊥y 轴于F ， 设D （x ，－1 2 x 2＋2x ＋ 52） 则BE ＝5－x ，DE ＝－ 1 2 x 2＋2x ＋ 5 2 ＝ 12( x ＋1 )( 5－x ) CF ＝－1 2 x 2＋2x ＋ 5 2 － 5 2 ＝－ 12x ( x －4 )，DF ＝x ∵∠BDC ＝90°，∴△DBE ∽△DCF ∴DE BE ＝ DF CF ，∴12 ( x ＋1 )( 5－x )5－x ＝x－ 12x ( x －4 )∵x ≠0，x ≠5，∴12( x ＋1 )＝1－ 12( x －4 )整理得：x ( x －3 )＝0，∴x ＝3 ∴点D 的坐标为（3，4） （3）延长MP 、OD 交于点G 易求直线OD 的解析式为y ＝4 3x 设P （x ，－ 1 2 x 2＋2x ＋ 5 2 ），则G （x ，43 x ）GP ＝4 3 x －( － 1 2 x 2＋2x ＋5 2 )＝ 1 2 x 2－ 2 3 x － 5 2∵PM ⊥OM ，PN ⊥OG ，∴△GPN ∽△GOM 得PN ＝3 5 GP ＝ 3 10 x 2－ 2 5 x － 32∴PM ＋PN ＝－1 2 x 2＋2x ＋ 5 2 ＋ 3 10 x 2－ 2 5 x － 32xy O A B CDE F xyO AB CD GM P N＝－15x2＋85x＋1＝－15(x－4)2＋215∴PM＋PN的最大值为215第16题如图，抛物线y＝14x2＋bx＋c与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，抛物线的顶点为M，对称轴交x轴于E，点D在第一象限，且在抛物线的对称轴上，DE＝OC，DM＝25 4．（1）求抛物线的对称轴；（2）若DA＝DC，求抛物线的解析式；（3）在（2）的条件下，点P是抛物线对称轴上的一个动点，若在直线BM上只存在一个点Q，使∠PQC＝45°，求点P的坐标．解：（1）由题意，DE＝OC＝c∵y＝14x2＋bx＋c＝14(x＋2b)2＋c－b2∴M（－2b，c－b2）∵DM＝254，∴c－(c－b2)＝254∴b2＝254，∴b＝52（舍去）或b＝－52∴－2b＝5∴抛物线的对称轴为x＝5 （2）设A（x1，0），B（x2，0）则x1，x2是方程14x2－52x＋c＝0的两个根yMA BO xDECyMA BO xDEC∴x1＋x2＝－10，x1x2＝4c∴AB2＝(x1－x2 )2＝(x1＋x2 )2－4x1x＝100－16c易知AE＝12AB，∴AE2＝14AB2＝25－4c在Rt△DAE中，DA＝DC＝5，DE＝c ∴AE2＝DA2－DE2＝25－c2∴25－4c＝25－c2，∴c＝4∴抛物线的解析式为y＝14x2－52x＋4（3）取△PQC的外心K，连接KC、KP、KQ则KC＝KP＝KQ∵∠PQC＝45°，∴∠PKC＝90°过点K作GH∥x轴，分别交y轴、对称轴于G、H 则△CKG≌△KPH，∴KG＝PH，CG＝KH＝5－KG 设点K的横坐标为m，则点K的纵坐标为4－(5－m)＝m－1∴K（m，m－1），P（m，2m－1）方法一：易求BE＝AE＝3，EM＝94，∴B（8，0），M（5，－94）易求直线BM的解析式为y＝34x－6设Q（n，34n－6）∵KC＝KQ，∴m2＋(m－1－4)2＝(m－n)2＋(m－1－34n＋6)2整理得：2516n2－(72m＋152)n＋20m＝0∵在直线BM上只存在一个点Q，使∠PQC＝45°∴△＝(72m＋152)2－4×2516×20m＝0整理得：49m2－290m＋225＝0 即(m－5)(49m－45)＝0解得m＝5或m＝45 49∴P1（5，9），P2（5，41 49）方法二：∵在直线BM上只存在一个点Q，使∠PQC＝45°∴△PQC的外接圆与直线BM相切∴KQ⊥BM过点K作KN∥y轴，交直线BM于N易求BE＝AE＝3，EM＝94，∴B（8，0），M（5，－94）yMA BO xDECQPKG HyMA BO xDECQPKG HN∴BM＝BE2＋EM2 ＝15 4易求直线BM的解析式为y＝34x－6∴N（m，34m－6），KN＝m－1－(34m－6)＝14m＋5∵KN∥EM，∴∠BNK＝∠BME∴sin∠BNK＝sin∠BME＝BEBM＝45∴KQ＝KN·sin∠BNK＝45(14m＋5)＝15m＋4∵KC＝KQ，∴m2＋(m－1－4)2＝(15m＋4)2整理得49m2－290m＋225＝0，即(m－5)(49m－45)＝0解得m＝5或m＝4549∴P1（5，9），P2（5，4149）第17题已知抛物线y＝－x2＋3x＋4交y轴于点A，交x轴于点B、C（点B在点C的右侧），过点A作垂直于y轴的直线l．点P是直线l下方的抛物线上一动点，过点P作直线PQ平行于y轴交直线l于点Q，连接AP．（1）写出A，B，C三点的坐标；（2）当点P在抛物线对称轴的右侧时①若以A、P、Q三点构成的三角形与△AOC相似，求出点P的坐标；②若将△APQ沿AP对折，点Q的对应点为点M．是否存在这样的点P，使得点M落在坐标轴上？若存在，求出点P的坐标；若不存在，请说明理由．解：（1）A（0，4），B（4，0），C（－1，0）（2）①若以A、P、Q三点构成的三角形与△AOC相似则AQAO＝PQCO或AQCO＝PQAOxOyC BQl AMPxOyC BQl AP设点P 的横坐标为x ，则PQ ＝4－(－x2＋3x ＋4)＝x2－3x∴x4＝x2－3x1或x1＝x2－3x4解得x ＝134或x ＝7，均在抛物线对称轴的右侧 ∴点P 的坐标为（134，5116）或（7，－24）②假设存在，设P （x ，－x2＋3x ＋4），则Q （x ，4），PQ ＝x2－3x （i ）当点M 落在x 轴上时，PM ＝PQ ＝x2－3x过M 作y 轴的平行线EF ，交直线l 于E ，过点P 作PF ⊥EF 于F易证△AEM ∽△MFP ，得AMME＝MPPF∵ME ＝OA ＝4，AM ＝AQ ＝x ，PM ＝PQ ＝x2－3x∴x4＝x2－3xPF，∴PF ＝4x －12，∴OM ＝(4x －12)－x ＝3x －12 在Rt △AOM 中，OM 2＋OA 2＝AM 2∴(4x －12)2＋42＝x2，解得x 1＝4，x 2＝5，均在抛物线对称轴的右侧 ∴P 1（4，0），P 2（5，－6）（ii ）当点M 落在y 轴上时，则∠PAQ ＝∠PAM ＝45° ∴△APQ 是等腰直角三角形，∴PQ ＝AQ∴x2－3x ＝x ，解得x ＝0（舍去）或x ＝4 ∴存在点P 1（4，0）或P 2（5，－6），使得点M 落在坐标轴上第18题如图，顶点为A 的抛物线y ＝1 4x 2＋bx ＋c 经过点B （5，3），对称轴为直线x ＝1，且与x 轴交于C 、D 两点（点C 在点D 的左侧），与y 轴交于点E ． （1）求抛物线的解析式；（2）点P 是抛物线上的动点，过点P 作PQ ∥y 轴，交直线BE 于点Q ，连接PE ．若点Q 关于直线PE 的对称点Q ′ 恰好落在y 轴上，求点P 的坐标；（3）点M 在第二象限内的抛物线上，点N 在x 轴上，且∠MNB ＝∠OAB ，当△BMN 与△OAB 相似时，求点M 的横坐标．xOyC BQlAE PMF yOC Dx E A BPQ y x O B A 备用图C D E解：（1）由题意得：⎩⎪⎨⎪⎧14×25＋5b ＋c ＝3－b2×14＝1解得b ＝－1 2，c ＝－34∴抛物线的解析式为由y ＝ 1 4 x 2－ 1 2 x － 3 4（2）连接PQ ′ 由y ＝1 4 x 2－ 12 x －34 可得E （0，－ 34） 易求直线BE 的解析式为y ＝3 4 x － 34设直线BE 与x 轴相交于点F ，则F （1，0） ∴EF ＝ OE 2＋OF 2 ＝3 2＋4 2＝ 5 4∵Q 与Q ′ 关于直线PE 对称，∴∠Q ′EP ＝∠QEP ∵PQ ∥y 轴，∴∠QPE ＝∠Q ′EP ∴∠QEP ＝∠QPE ，∴PQ ＝EQ又EQ ＝EQ ′，∴四边形PQEQ ′ 为菱形 设P （x ，1 4 x 2－ 1 2 x － 3 4 ），则Q （x ，3 4 x － 34） ∴PQ ＝1 4 x 2－ 12 x －34 －( 3 4 x － 3 4 )＝ 1 4 x 2－5 4x 作QH ⊥y 轴于H ，则△EHQ ∽△EOF ∴EQ HQ ＝ EF OF ＝ 5 4 ，EQ ＝ 5 4 HQ ＝| 54x | ∴1 4 x 2－ 5 4 x ＝ 5 4 x 或 1 4 x 2－ 5 4 x ＝－ 54x 解得x 1＝0（舍去），x 2＝10 ∴点P 的坐标为（10，774） （3）过A 作GH ∥x 轴，交y 轴于G ，作BH ⊥GH 于H 当x ＝1时，y ＝1 4 x 2－ 12 x － 34＝－1，∴A （1，－1） ∴AG ＝OG ＝1，∴∠OAG ＝45°∵B （5，3），∴AH ＝BH ＝4，∴∠BAH ＝45° ∴∠OAB ＝90°∵∠MNB ＝∠OAB ，∴∠MNB ＝90° 设M （m ，1 4 m 2－ 12 m － 34），BH 交x 轴于K ，作MT ⊥x 轴于T 则△MNT ∽△NBK ，∴MT NK ＝ NT BK ＝ MNNByO C D x E ABPH QQ ′ F yxOMB N AGHK T①若△BMN∽△BOA，则MNNB＝OAAB＝AGAH＝14∴MTNK＝NTBK＝14∴NK＝4MT＝4(14m2－12m－34)＝m2－2m－3NT＝14BK＝34∵OT＝ON＋NT＝NK－OK＋NT∴－m＝m2－2m－3－5＋3 4解得m＝1－302或m＝1＋302（舍去）即点M的横坐标为1－302②若△BMN∽△OBA，则MNNB＝ABOA＝AHAG＝4∴MTNK＝NTBK＝4∴NK＝14MT＝14(14m2－12m－34)＝116m2－18m－316NT＝4BK＝12∵OT＝NK－OK＋NT，∴－m＝116m2－18m－316－5＋12即116m2＋78m＋10916＝0，方程无实数解∴这种情况不存在综上所述，点M的横坐标为1－302第19题如图，直线y＝12x＋c（c≠0）与x轴交于点A，与y轴交于点C，抛物线y＝－12x2＋bx＋c的对称轴是直线x＝－32，且经过A、C两点，与x轴交于另一点B．（1）求抛物线的解析式；（2）过原点O的直线交抛物线于E、F两点（点E在第二象限），连接AE、CF，若∠EOC ＝∠ACO，求证：∠EAC＝∠EFC；（3）在（2）的条件下，设抛物线的对称轴交x轴于D，点P是对称轴上的一个动点，若在直线EF上有且只有一个点Q，使得∠PQD＝45°，请求出所有满足条件的点P的坐标．解：（1）∵抛物线y＝－12x 2＋bx＋c的对称轴是直线x＝－32∴－b2×(－12)＝－32，∴b＝－32，∴y＝－12x2－32x＋c在y＝12x＋c中，当y＝0时，x＝－2c；当x＝0时，y＝c∴A（－2c，0），C（0，c）∵抛物线y＝－12x2－32x＋c经过点A，∴－12(－2c)2－32(－2c)＋c＝0∵c≠0，∴－2c＋3＋1＝0，∴c＝2∴抛物线的解析式为y＝－12x2－32x＋2（2）作EG⊥x轴于G，FH⊥y轴于H，设E（x，－12x2－32x＋2）则∠OEG＝∠EOC由（1）知，A（－4，0），B（1，0），C（0，2）∵∠EOC＝∠ACO，∴∠OEG＝∠ACO∴OGEG＝tan∠OEG＝tan∠ACO＝OAOC＝2xyCA BOEFxyCA BOEFD备用图xyCA BOEFGH。