小学数学总复习专题 15图文搭配应用题
- 格式:docx
- 大小:112.56 KB
- 文档页数:11

搭配的应用题答案1. 题目:小明有5件不同的上衣和4条不同的裤子,他想要搭配出不同的着装方案。
请问小明一共有多少种不同的搭配方式?答案:小明有5件不同的上衣,每件上衣可以搭配4条不同的裤子,所以总共的搭配方式是5件上衣乘以4条裤子,即5×4=20种不同的搭配方式。
2. 题目:一个班级有30名学生,其中有15名男生和15名女生。
老师要从中选出5名学生组成一个小组,要求小组中至少有1名男生和1名女生。
请问有多少种不同的选法?答案:首先,我们计算总的选法,即从30名学生中选出5名,不考虑性别限制,共有C(30,5)种选法。
然后,我们减去不符合条件的选法,即全是男生或全是女生的选法。
全是男生的选法有C(15,5)种,全是女生的选法也有C(15,5)种。
所以符合条件的选法是C(30,5) -C(15,5) - C(15,5)。
计算得:C(30,5) = 142506C(15,5) = 3003符合条件的选法 = 142506 - 3003 - 3003 = 135500种。
3. 题目:一个水果店有苹果、香蕉和橙子三种水果,每种水果有10个。
小华想要购买至少一种水果,每种水果最多买5个。
请问小华有多少种不同的购买方式?答案:小华可以购买0个、1个、2个、3个、4个或5个苹果,同样也可以购买0个、1个、2个、3个、4个或5个香蕉和橙子。
所以每种水果有6种购买方式。
总的购买方式是每种水果的购买方式相乘,即6×6×6=216种。
4. 题目:一个学校有3个不同的班级,每个班级有10名学生。
学校要组织一个由3名学生组成的篮球队,要求每个班级至少有1名学生。
请问有多少种不同的组队方式?答案:首先,我们计算从每个班级中选出1名学生的组合数,即C(10,1)×C(10,1)×C(10,1)。
然后,我们需要考虑剩下的1名学生可以来自任何一个班级,所以有3种选择。
计算得:C(10,1) = 10每个班级选出1名学生的组合数= 10×10×10 = 1000剩下的1名学生有3种选择总的组队方式= 1000 + 3×(10×9×8) = 1000 + 3×720 = 1000 + 2160 = 3160种。




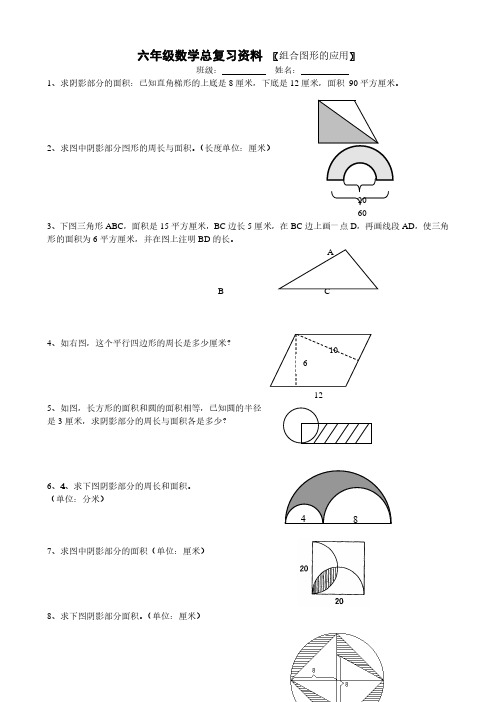
4 8 六年级数学总复习资料 〖组合图形的应用〗班级: 姓名:1、求阴影部分的面积:已知直角梯形的上底是8厘米,下底是12厘米,面积 90平方厘米。
2、求图中阴影部分图形的周长与面积。
(长度单位:厘米)20 603、下图三角形ABC ,面积是15平方厘米,BC 边长5厘米,在BC 边上画一点D ,再画线段AD ,使三角形的面积为6平方厘米,并在图上注明BD 的长。
AB C4、如右图,这个平行四边形的周长是多少厘米?12 5、如图,长方形的面积和圆的面积相等,已知圆的半径 是3厘米,求阴影部分的周长与面积各是多少?6、4、求下图阴影部分的周长和面积。
(单位:分米)7、求图中阴影部分的面积(单位:厘米)8、求下图阴影部分面积。
(单位:厘米) 6109、三角形ABC的面积是24.6平方厘米,BF是FC的2倍,E是AC的中点,连接EF,求阴影部分的面积。
10、如右图,已知甲三角形面积为3.6平方厘米,乙三角形的面积为5.4平方厘米。
线段BD的长是DC的长的多少倍?)11、下图是一个直角三角形,AD为底边BC上的高。
根据图中的已知条件,求出AD的长度。
(单位:厘米413、有一块长20米,宽10米的长方形地,若在这块地四周修2米宽的小路,中间植草皮,草地面积是多少?小路的面积是多少?14、把一个四条边都是5厘米的平行四边形拉成一个正方形后,面积增加了7.5平方厘米,原平行四边形的高是多少?15、有一个正方形水池(如图的阴影部分),在它的周围修一条宽 8米的花坛,花坛的面积是480平方米,水池的边长是多少米?16、如图,两个正方形的边长分别是4分米和3分米,阴影部分的面积是多少平方分米?17、求出下列各图中阴影部分图形的周长与面积:(单位;厘米)北师大版三年级上册数学期末试卷(完卷时间:60分钟)一、填空。
19分(4+2+6+2+2+3)1、一年有( )个月,今年2月份有( )天,第三季度的月份是( ),共有( )天。
小学搭配问题练习题数学
在小学数学教学中,搭配问题是一个常见的练习题类型。
搭配问题要求学生根据给定的条件,合理地搭配事物或数据,找出满足条件的正确答案。
通过搭配问题的练习,可以培养学生的逻辑思维能力和解决问题的能力。
以下是一些小学搭配问题的练习题,供学生练习。
练习题一:
1. 一共有10只动物,其中有5只是鸟。
那么还有多少只动物不是鸟?
2. 一袋子里有红、黄、蓝三种颜色的球,其中红球的数量是黄球的2倍,蓝球的数量是红球和黄球的和。
如果一共有30个球,请问每种颜色的球各有多少个?
练习题二:
1. 一条船上有15个水桶,其中3个是空的,剩下的桶里装着150升水。
那么每个有水的桶里都装了多少升水?
2. 一只箱子里有红、黄、蓝三色的苹果,其中红苹果是黄苹果的2倍,蓝苹果比红苹果多3个。
如果一共有50个苹果,请问每种颜色的苹果各有多少个?
练习题三:
1. 某班同学进行了一次篮球比赛,其中1/4的同学是女生,还有10名同学没有参加比赛。
如果这个班共有40名同学,请问男生共有多少名?
2. 李明去水果店买了苹果、香蕉、橙子三种水果,他买了苹果和香蕉共7个,买了苹果和橙子共9个,买了香蕉和橙子共6个。
请问他各买了多少个苹果、香蕉和橙子?
以上的练习题涵盖了小学搭配问题的一些经典类型。
学生可以根据给定的条件,通过逻辑推理和计算,找出正确的答案。
在解答搭配问题的过程中,学生需要灵活运用加减乘除等数学运算符号,培养数学思维和计算能力。
通过不断地练习,学生可以更好地掌握搭配问题的解题方法,提高数学解决问题的能力。
三年级数学搭配题一、服装搭配类。
1. 小明有3件上衣,分别是红色、蓝色、绿色,2条裤子,分别是黑色和白色。
小明搭配服装,一共有多少种不同的搭配方法?- 解析:每件上衣都可以和2条裤子搭配。
红色上衣可以搭配黑色裤子和白色裤子,这是2种搭配;蓝色上衣也可以搭配黑色和白色裤子,又是2种搭配;绿色上衣同样可以搭配黑色和白色裤子,还是2种搭配。
所以总的搭配方法有3×2 = 6种。
2. 小红有2件裙子,一件是粉色的长裙,一件是黄色的短裙,她还有3件上衣,分别是白色、灰色和棕色。
小红的裙子和上衣搭配,共有多少种不同的穿法?- 解析:对于粉色长裙,可以和3件上衣分别搭配,有3种穿法;对于黄色短裙,也可以和3件上衣分别搭配,又有3种穿法。
所以总共的搭配方法是2×3 = 6种。
3. 小刚有4件T恤,颜色分别为红、黄、蓝、白,3条短裤,颜色为黑、灰、棕。
小刚选择一件T恤和一条短裤搭配,有多少种不同的搭配?- 解析:每件T恤都有3种短裤的搭配选择。
红T恤有3种搭配(和黑、灰、棕短裤),黄T恤有3种搭配,蓝T恤有3种搭配,白T恤有3种搭配。
所以总的搭配数为4×3 = 12种。
二、饮食搭配类。
4. 早餐店有3种主食,分别是包子、油条、馒头,还有2种饮品,豆浆和牛奶。
顾客选择一种主食和一种饮品,有多少种不同的搭配?- 解析:包子可以和豆浆、牛奶搭配,这是2种搭配;油条可以和豆浆、牛奶搭配,是2种搭配;馒头也可以和豆浆、牛奶搭配,是2种搭配。
所以共有3×2 = 6种搭配。
5. 食堂有2种荤菜,红烧肉和糖醋排骨,3种素菜,炒青菜、炒土豆丝、凉拌黄瓜。
一份套餐包含一种荤菜和一种素菜,有多少种不同的套餐组合?- 解析:红烧肉可以和3种素菜分别搭配,有3种组合;糖醋排骨也可以和3种素菜分别搭配,有3种组合。
所以总的套餐组合数为2×3 = 6种。
6. 水果店里有4种水果,苹果、香蕉、橙子、梨,还有3种果盘,小果盘、中果盘、大果盘。
小学数学总复习专题15 图文搭配应用题1.根据如图提供的信息,可知每支网球拍与每支乒乓球拍的单价分别为()。
A.75元,50元 B.70元,45元 C.70元,60元 D.80元,40元2.体育馆内排球的个数是篮球的75%,篮球比排球多6个。
篮球和排球各有多少个?3.现有一个圆柱,底面直径是5厘米,高是12厘米。
求它的侧面积。
4.如图是一块长方形草地,长方形的长是16米,宽是10米。
中间有两条道路,一条是长方形,一条是平行四边形。
草地部分的面积有多大?5.小明星期天请6名同学来家做客,他选用一盒用长方体(如图(1))包装的饮料招待同学,给每个同学倒上一满杯(如图(2))后,他自己还有喝的饮料吗?(写出主要过程)6.如图,A至B是下坡,B至C是平路,C至D是上坡.小张和小王在上坡时步行速度是每小时4千米,平路时步行速度是每小时5千米,下坡时步行速度是每小时6千米.小张和小王分别从A和D同时出发,1小时后两人在E点相遇.已知E在BC上,并且E 至C的距离是B至C距离的1/5.当小王到达A后9分钟,小张到达D.那么A至D全程长是多少千米?7.现有两种酒精溶液,已知甲种酒精溶液中含酒精18千克,含水12千克;乙种酒精溶液中含酒精3千克,含水9千克。
现在要得到含酒精7千克,含水7千克的酒精溶液,问应取甲、乙两种酒精溶液各多少千克?8.以下反映的是昨天的股市行情:项目开盘价(元)收盘价(元)青岛海尔 15.00 16.00中国石化 20.50 19.00(1)青岛海尔一天的涨幅是多少?(2)中国石化一天的跌幅是多少?(3)若某股民原来买等总价的两种股票,昨天是盈还是亏?请举例说明.9.幼儿园有三个班,甲班比乙班多4人,乙班比丙班多4人,老师给小孩分枣,甲班每个小孩比乙班每个小孩少分3个枣.乙班每个小孩比丙班每个小孩少分5个枣,结果甲班比乙班总共多分了3个枣,乙班比丙班总共多分5个枣,问三个班总共分了多少个枣?参考答案1.D【解析】根据图示,1支网球拍比1支乒乓球拍贵200-160=40(元),假设每支乒乓球拍多加40元,那么乒乓球拍的价格就和网球拍的价格相同,而2支网球拍与1支乒乓球拍的总价要增加到200+40=240(元),也就是240元相当于3支网球拍的价格,所以每支网球拍的单价是240÷3=80(元)。
解:每支网球拍的单价:[200+(200-160)]÷3,=[200+40]÷3,=240÷3,=80(元);每支乒乓球拍:80-(200-160),=80-40,=40(元);答:每支网球拍的单价是80元,每支乒乓球拍的单价是40元.故选:D.考点:图文应用题。
点评:先求出1支网球拍比1支乒乓球拍贵40元,然后根据关系式:(和+差)÷2=大数,求出每支网球拍的单价,再求每支乒乓球拍的单价。
2.篮球有24个,排球有18个。
【解析】排球的个数是篮球的75%,是把篮球个数看作单位“1”。
排球的个数是篮球的75%,等量关系式:篮球-排球=6个。
解:设篮球有x个,则排球有75%x个。
x-75%x=60.25x=6x=2475%x=24×0.75=18答:篮球有24个,排球有18个。
3.188.4平方厘米【解析】沿着圆柱侧面的一条高剪开,将侧面展开,就得到一个长方形。
这个长方形的长等于圆柱底面的周长,宽等于圆柱的高。
因此,用圆柱的底面周长乘圆柱的高就得到这个长方形的面积,即圆柱的侧面积。
解:3.14×5×12=188.4(平方厘米)答:它的侧面积是188.4平方厘米。
点评:圆柱的侧面是个曲面,不能直接求出它的面积。
推导出侧面积的计算公式也用到了转化的思想。
把这个曲面沿高剪开,然后平展开来,就能得到一个长方形,这个长方形的面积就是这个圆柱的侧面积。
考点分析:1、圆柱上、下两个面叫做圆柱的底面,它们是完全相同的两个圆。
形成圆柱的面还有一个曲面,叫做圆柱的侧面。
圆柱两个底面之间的距离叫做圆柱的高。
2、圆锥的底面是个圆,圆锥的侧面是一个曲面。
从圆锥的顶点到底面圆心的距离是圆锥的高。
3、把圆柱的侧面展开得到一个长方形,这个长方形的长等于圆柱底面的周长,宽等于圆柱的高。
4、圆柱的侧面积=底面周长×高5、圆柱的表面积=侧面积+底面积×2总结:1、使学生在观察、操作、交流等活动中感知和发现圆柱、圆锥的特征,知道圆柱和圆锥的底面、侧面和高。
2、使学生理解圆柱侧面积和圆柱表面积的含义,掌握圆柱侧面积和表面积的计算方法。
4.112平方米【解析】求草地部分的面积,可以用大长方形的面积减去两条道路的面积,但要考虑两条道路的重叠部分,因此计算比较复杂。
可以将图1转化成图2,两条道路转化到了长方形草地的边上,很明显,图2草地部分(阴影部分)的面积和图1相等,现在求草地的面积转化成了求长方形的面积,计算比较简单。
解:(16-2)×(10-2)=112(平方米)答:草地部分的面积是112平方米。
总结:这分割法是在一个复杂的几何图形中,添上一条或几条辅助线,把图形分割成若干个已学过的基本图形,然后分别计算出各图形的面积或体积,再将所得结果相加的解题方法。
5.他自己还有喝的饮料。
【解析】结合图形已知条件,求出长方体的体积和圆柱体的体积即可.解:15×12×6=1080(立方厘米),20×8=160(立方厘米),160×6=960(立方厘米),1080立方厘米>960立方厘米;答:他自己还有喝的饮料。
考点:图文应用题。
总结:1、联系生活,注重实际意义,结合数学知识即可解决问题,2、注意观察给出的图片、图形,继而总结出对解题有帮助的信息。
6.11.5千米【解析】BE是BC的4/5,CE是BC的1/5,说明DC这段下坡,比AB这段下坡所用的时间多,也就是DC这一段,比AB这一段长,因此可以在DC上取一段DF和AB一样长,如下图:另外,再在图上画出一点G,使EG和EC一样长,这样就表示出,小王从F到C。
小张从B 到G。
小王走完全程比小张走完全程少用9分钟,这时因为小张走C 至F 是上坡,而小王走F 至C 是下坡(他们两人的其余行程走下坡、平路、上坡各走一样多)。
解答:因此,小王从F 至C ,走下坡所用时间是9÷(6/4-1)=18(分钟)。
因此得出小张从B 至G 也是用18分钟,走GE 或CE 都用6分钟.走B 至C 全程(平路)要30分钟。
从A 至曰下坡所用时间是60-18-6=36(分钟);从D 至C 下坡所用时间是60-6=54(分钟);A 至D 全程长是(36+54)×6/60+30×5/60=11.5千米。
总结:在一些数学问题中要用以题中的等量为等量关系建立方程。
综合法——先把应用题中已知数(量)和所设未知数(量)列成有关的代数式,再找出它们之间的等量关系,进而列出方程。
这是从部分到整体的一种 思维过程,其思考方向是从已知到未知。
7.甲种酒精溶液应取10千克,乙种酒精溶液应取4千克。
【解析】此题是溶液的混合配制问题,这类问题中有三个等量关系:混合前后溶液的重量和不变、溶质重量和不变及溶剂重量和不变。
需要先算出甲种、乙种酒精溶液的浓度,再根据等量关系列出方程。
设应取甲种酒精溶液x 千克,那么乙种酒精溶液应取(77)x +-千克,所取的甲种酒精溶液含酒精18100%1812x ⋅⨯+千克,所取的乙种酒精溶液含酒精3(77)100%39x +-⋅⨯+千克,根据题意,得183100%(77)100%7181239x x ⋅⨯++-⋅⨯=++ 解方程,得10x =7714104x +-=-=答:甲种酒精溶液应取10千克,乙种酒精溶液应取4千克。
总结:根浓度问题是列方程解应用题的常见类型之一,关键是要找出配制前后溶液中哪些量不发生变化,从而寻找出等量关系,进而列出方程求解。
从上述例题我们知道,列方程解应用题的步骤是(1)审题:弄清题意,确定已知量、未知量及它们的关系;(2)设元:选择适当未知数,用字母表示;(3)列代数式:根据条件,用含所设未知数的代数式表示其他未知量;(4)列方程:利用列代数式时未用过的等量关系,列出方程;(5)解方程:正确运用等式的性质,求出方程的解;(6)检验并答题。
8.6.7%;7.3%;亏损【解析】根据图表所给信息可知,(1)青岛海尔一天的涨幅是(16-15)÷15;(2)中国石化一天的跌幅是(20.5-19)÷20.5;(3)设定这他分别买了同样钱数的这两只股票,只要根据这两只股票的涨幅和跌幅分别算出青岛海尔和中国石化的盈利的亏损是多少,进行比较一下即可得出他这天是盈利还是亏损.解:(1)(16-15)÷15≈6.7%,答:青岛海尔一天的涨幅约是6.7%.(2)(20.5-19)÷20.5≈7.3%,答:中国石化一天的跌幅约是7.3%.(3)假设他分别买了4000元的青岛海尔和中国石化,其盈亏情况为:盈利:4000×6.7%=268(元),亏损:4000×7.3%=292(元),盈利<亏损.答:他昨天是亏损的.考点:图文应用题。
总结:有的数量及其关系适合用文字叙述,而有的数量及其关系适合用表格表示,还有的数量及其关系适合用图形来表达。
我们应该把它们表示为易于理解的形式。
另外,对于十进制数该如何表示也应该掌握。
9.673个【解析】先画长方形图,见图4。
在图4中,AB、BD、DG分别表示丙、乙、甲三班小孩的人数,GH、DK、BN分别表示甲、乙、丙三班小孩每人分的枣数,则BD=AB+4,DG=BD+4=AB+8,这里CD=EF=FG=4.BN=DK+5,DK=HG+3,这里PN=5,KY=3.这一来长方形DGHY、BDKP、ABNO的面积便分别表示甲、乙、丙三班小孩分得枣的总数.添辅助线后,从图4中可以看出:长方形ABRQ、BCXR、DEJY的面积相等.根据题意,长方形EGHJ的面积等于长方形QRNO的面积加8(=3+5).而长方形EGHJ的面积等于8HG,长方形QRNO的面积等于AB×RN=8AB.即8HG=8AB+8,所以HG=QA=AB+1.另外长方形BDYR与长方形DFIY的面积相等,根据题意长方形FGHI的面积等于长方形RYKP的面积加3,而长方形FGHI的面积等于4GH,长方形RYKP的面积等于3RY,所以4GH=3RY+3=3(BC+4)+3=3BC+15,即4(AB+1)= 3AB+15,最后可求出AB=11,HG=12,有了这两个数便可求出总共分了多少个枣。
甲班总分枣数为:(11+4+4)×12=228(个)乙班总分枣数为:(11+4)×(12+3)=225(个)丙班总分枣数为:11×(12+3+5)=220(个)三班共分枣数为:228+225+220=673(个)答:三个班总共分枣673个。