SLAM算法简介—1PPT学习课件
- 格式:ppt
- 大小:86.14 KB
- 文档页数:20



SLAM基础算法(1):卡尔曼滤波对于⼀个正在运动中的⼩车来说,如何准确的知道它所处的位置?理论家说:我可以通过⽜顿公式来计算!实践家说:给它装个GPS不就得了!好吧,你们说的听上去都很有道理,但我们到底该相信谁?现实情况是:理论家没有考虑到现实存在的摩擦⼒、空⽓阻⼒、时间测量误差等因素,算出来的结果存在较⼤误差;实践家没有考虑GPS的测量存在较⼤误差。
这样⼀说,感觉两位半⽄⼋两,都有误差,感觉谁都不可信。
不过,我们还是要解决问题的嘛,能不能让这两位合作⼀下呢,理论联系实际嘛,马克思他⽼⼈家说的准没错。
我们知道,误差其实是⼀种噪声,那么是不是可以⽤滤波的⽅法呢?感觉可以,我们把他俩的结果加起来,再除⼆嘛,均值滤波谁不会呢!但是,但是传感器的测量值(不⼀定是GPS)有时候简直会上天哪,这样简单粗暴肯定不靠谱,那有没有更⽜X的⽅法呢?-------------------------------------------------------------------------------------------------严肃的分隔线----------------------------------------------------------------------------------------在刚刚提出的例⼦⾥,⼩车的状态向量可以表⽰为:这时候,理论家提出,他可以预测k时刻的⼩车状态,并很难受的承认,这个预测是有误差的,假设这个误差服从正态分布:给出误差的协⽅差矩阵假设⼩车是匀速⾏驶,使⽤基本的运动学公式来表⽰,有:即:其中:称为预测矩阵。
现实中,⼩车肯定不是匀速的,因为各种阻⼒的存在,需要时不时的给⼩车⼀个向前的⼒,才能使它继续向前⾏驶:假设某个时刻给了⼩车⼀个向前的⼒,产⽣了⼀个向前的加速度a,那么:即:其中:称为控制矩阵。
对于施加给⼩车的加速度a,它也称为⼀个向量,叫做控制向量,常⽤来表⽰,即有:到这⾥,理论家的事情也差不多了,我们为他补上最后⼀步。
SLAM从定位到建图基本概念:(1)特征点:选取图像(视频)中具有代表性的点来进行图像的特征表示(或者说是进行图像的描述),简单的说就是一种图像表示的方式。
(2)世界坐标系:选取一个固定的坐标系(世界坐标系)作为固定参照,相当于在真实世界中选取一个固定不变的坐标系,以便于后续的图像和相机的相对位置参照。
(3)相机坐标系:相机坐标系随相机的运动而变化,一般从相机中观察到的图像都是以相机坐标系作为直观的表示,比如某一个像素点在相机坐标系下的坐标为(X,Y,Z)。
(4)位姿:就是相机的运动轨迹的描述,也就相当于相机坐标系原点在世界(固定)坐标系的位置表示,一般以对应时间下的坐标系的旋转和平移作为参数进行表达。
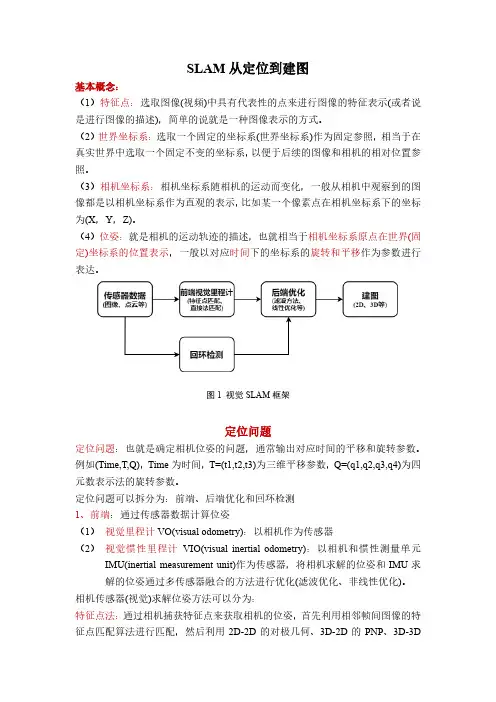
图1 视觉SLAM框架定位问题定位问题:也就是确定相机位姿的问题,通常输出对应时间的平移和旋转参数。
例如(Time,T,Q),Time为时间,T=(t1,t2,t3)为三维平移参数,Q=(q1,q2,q3,q4)为四元数表示法的旋转参数。
定位问题可以拆分为:前端、后端优化和回环检测1、前端:通过传感器数据计算位姿(1)视觉里程计VO(visual odometry):以相机作为传感器(2)视觉惯性里程计VIO(visual inertial odometry):以相机和惯性测量单元IMU(inertial measurement unit)作为传感器,将相机求解的位姿和IMU求解的位姿通过多传感器融合的方法进行优化(滤波优化、非线性优化)。
相机传感器(视觉)求解位姿方法可以分为:特征点法:通过相机捕获特征点来获取相机的位姿,首先利用相邻帧间图像的特征点匹配算法进行匹配,然后利用2D-2D的对极几何、3D-2D的PNP、3D-3D的ICP 求解位姿。
直接法:通过相邻帧间图像的光照变化来计算位姿。
2、后端:对求解的位姿进行优化,或者说是对求解的位姿进行除噪的过程。
利用滤波优化或者非线性优化算法,现在一般都用非线性优化算法。






SLAM概念学习之随机SLAM算法 这⼀节,在熟悉了Featue maps相关概念之后,我们将开始学习基于EKF的特征图SLAM算法。
1. 机器⼈,图和增强的状态向量随机SLAM算法⼀般存储机器⼈位姿和图中的地标在单个状态向量中,然后通过⼀个递归预测和量测过程来估计状态参数。
其中,预测阶段通过增量航迹估计来处理机器⼈的运动,并增加了机器⼈位姿不确定性的估计。
当再次观测到Map中存储的特征后,量测阶段,或者叫更新阶段开始执⾏,这个过程可以改善整个的状态估计。
当机器⼈在运动过程中观测到新特征时,便通过⼀个状态增强的过程将新观测的特征添加到状态向量中。
机器⼈的状态,即⼀个相对于参考笛卡尔坐标系的⾃⾝位姿参数通过均值和协⽅差来定义:(1)(2) 图的协⽅差矩阵P m包含特征之间的互相关信息(即⾮对⾓项),这些交叉关联信息表征了每个特征对Map中其他特征相关信息的依赖。
由于特征的位置是静态的,当周围的环境也即Map是刚性的话,特征之间的交叉关联将会随着的特征的⼆次观测增强。
图中的特征可以表⽰如下(3)(4) SLAM中的图通过⼀个串联了机器⼈位姿和特征图状态的增强状态向量定义,如图1所⽰。
这是很有必要的,因为⼀致的SLAM依赖于机器⼈位姿和图之间相关性P v m(5)(6)Fig. 1 增强的状态向量. 需要注意的是,状态的初始化时通常为和.也就是说,还没有特征被机器⼈观测到,并且初始时刻机器⼈位于参考坐标系的原点。
2. 预测阶段随机SLAM算法的过程模型根据航迹推算运动估计来确定机器⼈相对于先前时刻位姿的运动,图特征仍然保持静⽌。
这个模型对状态估计的影响存在于状态向量部分和状态协⽅差矩阵中的以及项。
⽽和这些图特征相关项仍保持不变。
估计带来的机器⼈(这⾥以移动⼩车为例)位姿变化和协⽅差通常⽤车轮的编码器测量和⼩车对应的运动学模型获取。
本⽂⾥⾯的位姿改变通过基于激光测距的航迹推算获取,该算法可以通过批处理数据关联算法来找出序列激光扫描之间的相对位姿关系。
