2013年4月10日_动态规划思考题
- 格式:pdf
- 大小:310.69 KB
- 文档页数:8

什么是动态规划算法,常见的动态规划问题分析与求解理解动态规划动态规划中递推式的求解⽅法不是动态规划的本质。
我曾经给学校参加NOIP的同学多次讲过动态规划,我试着讲⼀下我理解的动态规划,争取深⼊浅出。
希望你看了我的答案,能够喜欢上动态规划。
0. 动态规划的本质,是对问题状态的定义和状态转移⽅程的定义。
引⾃维基百科dynamic programming is a method for solving a complex problem by breaking it down into a collection of simpler subproblems.动态规划是通过拆分问题,定义问题状态和状态之间的关系,使得问题能够以递推(或者说分治)的⽅式去解决。
本题下的其他答案,⼤多都是在说递推的求解⽅法,但如何拆分问题,才是动态规划的核⼼。
⽽拆分问题,靠的就是状态的定义和状态转移⽅程的定义。
1. 什么是状态的定义?⾸先想说⼤家千万不要被下⾯的数学式吓到,这⾥只涉及到了函数相关的知识。
我们先来看⼀个动态规划的教学必备题:给定⼀个数列,长度为N,求这个数列的最长上升(递增)⼦数列(LIS)的长度.以 1 7 2 8 3 4 为例。
这个数列的最长递增⼦数列是 1 2 3 4,长度为4;次长的长度为3,包括 1 7 8; 1 2 3 等.要解决这个问题,我们⾸先要定义这个问题和这个问题的⼦问题。
有⼈可能会问了,题⽬都已经在这了,我们还需定义这个问题吗?需要,原因就是这个问题在字⾯上看,找不出⼦问题,⽽没有⼦问题,这个题⽬就没办法解决。
所以我们来重新定义这个问题:给定⼀个数列,长度为N,设为:以数列中第k项结尾的最长递增⼦序列的长度.求中的最⼤值.显然,这个新问题与原问题等价。
⽽对于来讲,都是的⼦问题:因为以第k项结尾的最长递增⼦序列(下称LIS),包含着以第中某项结尾的LIS。
上述的新问题也可以叫做状态,定义中的“为数列中第k项结尾的LIS的长度”,就叫做对状态的定义。

动态规划练习题USACO 2.2 Subset Sums题目如下:对于从1到N的连续整集合合,能划分成两个子集合,且保证每个集合的数字和是相等的。
举个例子,如果N=3,对于{1,2,3}能划分成两个子集合,他们每个的所有数字和是相等的:and {1,2}这是唯一一种分发(交换集合位置被认为是同一种划分方案,因此不会增加划分方案总数)如果N=7,有四种方法能划分集合{1,2,3,4,5,6,7},每一种分发的子集合各数字和是相等的:{1,6,7} and {2,3,4,5} {注1+6+7=2+3+4+5}{2,5,7} and {1,3,4,6}{3,4,7} and {1,2,5,6}{1,2,4,7} and {3,5,6}给出N,你的程序应该输出划分方案总数,如果不存在这样的划分方案,则输出0。
程序不能预存结果直接输出。
PROGRAM NAME: subsetINPUT FORMAT输入文件只有一行,且只有一个整数NSAMPLE INPUT (file subset.in)7OUTPUT FORMAT输出划分方案总数,如果不存在则输出0。
SAMPLE OUTPUT (file subset.out)4参考程序如下:#include <fstream>using namespace std;const unsigned int MAX_SUM = 1024;int n;unsigned long long int dyn[MAX_SUM];ifstream fin ("subset.in");ofstream fout ("subset.out");int main() {fin >> n;fin.close();int s = n*(n+1);if (s % 4) {fout << 0 << endl;fout.close ();return ;}s /= 4;int i, j;dyn [0] = 1;for (i = 1; i <= n; i++)for (j = s; j >= i; j--)dyn[j] += dyn[j-i];fout << (dyn[s]/2) << endl;fout.close();return 0;}USACO 2.3 Longest Prefix题目如下:在生物学中,一些生物的结构是用包含其要素的大写字母序列来表示的。

动态规划讲解大全含例题及答案动态规划讲解大全动态规划(dynamic programming)是运筹学的一个分支,是求解决策过程(decision process)最优化的数学方法。
20世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程(multistep decision process)的优化问题时,提出了著名的最优化原理(principle of optimality),把多阶段过程转化为一系列单阶段问题,逐个求解,创立了解决这类过程优化问题的新方法——动态规划。
1957年出版了他的名著Dynamic Programming,这是该领域的第一本著作。
动态规划问世以来,在经济管理、生产调度、工程技术和最优控制等方面得到了广泛的应用。
例如最短路线、库存管理、资源分配、设备更新、排序、装载等问题,用动态规划方法比用其它方法求解更为方便。
虽然动态规划主要用于求解以时间划分阶段的动态过程的优化问题,但是一些与时间无关的静态规划(如线性规划、非线性规划),只要人为地引进时间因素,把它视为多阶段决策过程,也可以用动态规划方法方便地求解。
动态规划程序设计是对解最优化问题的一种途径、一种方法,而不是一种特殊算法。
不象前面所述的那些搜索或数值计算那样,具有一个标准的数学表达式和明确清晰的解题方法。
动态规划程序设计往往是针对一种最优化问题,由于各种问题的性质不同,确定最优解的条件也互不相同,因而动态规划的设计方法对不同的问题,有各具特色的解题方法,而不存在一种万能的动态规划算法,可以解决各类最优化问题。
因此读者在学习时,除了要对基本概念和方法正确理解外,必须具体问题具体分析处理,以丰富的想象力去建立模型,用创造性的技巧去求解。
我们也可以通过对若干有代表性的问题的动态规划算法进行分析、讨论,逐渐学会并掌握这一设计方法。
基本模型多阶段决策过程的最优化问题。
在现实生活中,有一类活动的过程,由于它的特殊性,可将过程分成若干个互相联系的阶段,在它的每一阶段都需要作出决策,从而使整个过程达到最好的活动效果。

C++中的动态规划算法及常见题⽬汇总什么是动态规划在⾯试过程中如果是求⼀个问题的最优解(通常是最⼤值或者最⼩值),并且该问题能够分解成若⼲个⼦问题,并且⼦问题之间好友重叠的更⼩⼦问题,就可以考虑⽤动态规划来解决这个问题。
动态规划的分类 ⼤多数动态规划问题都可以被归类成两种类型:优化问题和组合问题优化问题 优化问题就是我们常见的求⼀个问题最优解(最⼤值或者最⼩值)组合问题 组合问题是希望你弄清楚做某事的数量或者某些事件发⽣的概率两种不同动态规划解决⽅案⾃上⽽下:即从顶端不断地分解问题,知道你看到的问题已经分解到最⼩并已得到解决,之后只⽤返回保存的答案即可⾃下⽽上:你可以直接开始解决较⼩的⼦问题,从⽽获得最⼩的解决⽅案。
在此过程中,你需要保证在解决问题之前先解决⼦问题。
这种⽅法叫做表格填充法。
常见的动态规划例⼦1.2.3.4.5.6.7.8.9.10.11. 猜数字⼤⼩ 1. 裴波那契数列 裴波那契数列就是典型的组合问题,要求出做某事的数量或者概率问题分析:对于题⽬中的青蛙爬楼梯问题,初试情况下是只有⼀级台阶时,只有⼀种跳法,只有两级台阶时,有两种跳法,当有n级台阶时,设n级台阶的跳法总数是f(n),如果第⼀步跳⼀级台阶,则和剩下的n-1级台阶的跳法是⼀样的,如果第⼀级跳两级台阶,则和剩下的n-2级台阶的跳法是⼀样的,因此最终n级台阶的跳法是f(n)=f(n-1)+f(n-2),即其是可以被分解为更⼩的⼦问题的,下⾯我们以求解f(10)为例来分析递归的过程 我们从这张图中不难发现,在这棵树中有很多节点都是重复的,⽽且重复节点会随着n的增⼤⽽急剧增⼤,因此我们采⽤⾃顶向下的⽅式会有很低的效率,因此我们采⽤⾃下⽽上的⽅法,⾸先根据f(1)和f(2)计算出f(3),再根据f(2)和f(3计算出f(4),以此类推求出f(n) 实现的代码如下1int jumpFloor(int number) {2if(number<0)3return0;4else if(number==0||number==1||number==2)5return number;6else7 {8int result=0;9int f1=1;10int f2=2;11for(int i=3;i<=number;++i)12 {13 result=f1+f2;14 f1=f2;15 f2=result;16 }17return f2;18 }19 }矩形覆盖问题问题分析:由于2*1的⼩矩形可以横着放,也可以竖着放,当n=1时,其只有⼀种⽅式,f(1)=1,n=2时,有两种覆盖⽅式f(2)=2如图 当要构成2*n的⼤矩形时,如果第⼀个⼩矩形竖着放,则其和后⾯n-1个⼩矩形的⽅法相等,如果第⼀个⼩矩形横着放,则第⼆个⼩矩形也只能横着放,即上图右边的⽅法,因此其和后⾯n-2个⼩矩形的放法相等。


动态规划思想:⽯⼦合并问题描述:在⼀个圆形操场的四周摆放着n 堆⽯⼦。
现要将⽯⼦有次序地合并成⼀堆。
规定每次只能选相邻的2 堆⽯⼦合并成新的⼀堆,并将新的⼀堆⽯⼦数记为该次合并的得分。
试设计⼀个算法,计算出将n堆⽯⼦合并成⼀堆的最⼩得分和最⼤得分。
开始以为通过贪⼼算法可能很快解决问题,可是是⾏不通的。
⾸先我们可以把这么堆⽯⼦看成⼀列我们假如5堆的⽯⼦,其中⽯⼦数分别为7,6,5,7,100•按照贪⼼法,合并的过程如下:每次合并得分第⼀次合并 7 6 5 7 100 =11 第⼆次合并 7 11 7 100=18 第三次合并 18 7 100 =25第四次合并 25 100 =125总得分=11+18+25+125=179•另⼀种合并⽅案每次合并得分 第⼀次合并 7 6 5 7 100 ->13第⼆次合并 13 5 7 100->12第三次合并 13 12 100 ->25第四次合并 25 100 ->125总得分=13+12+25+125=175显然利⽤贪⼼来做是错误的,贪⼼算法在⼦过程中得出的解只是局部最优,⽽不能保证使得全局的值最优。
如果N-1次合并的全局最优解包含了每⼀次合并的⼦问题的最优解,那么经这样的N-1次合并后的得分总和必然是最优的。
因此我们需要通过动态规划算法来求出最优解。
在此我们假设有n堆⽯⼦,⼀字排开,合并相邻两堆的⽯⼦,每合并两堆⽯⼦得到⼀个分数,最终合并后总分数最少的。
我们设m(i,j)定义为第i堆⽯⼦到第j堆⽯⼦合并后的最少总分数。
a(i)为第i堆⽯⼦得⽯⼦数量。
当合并的⽯⼦堆为1堆时,很明显m(i,i)的分数为0; 当合并的⽯⼦堆为2堆时,m(i,i+1)的分数为a(i)+a(i+1); 当合并的⽯⼦堆为3堆时,m(i,i+2)的分数为MIN((m(i,i)+m(i+1,i+2)+sum(i,i+2)),(m(i,i+1)+m(i+2,i+2)+sum(i,i+2)); 当合并的⽯⼦堆为4堆时......代码实现如下:1 #include<stdio.h>2#define N 1003/*4 *求合并过程中5 *最少合并堆数⽬6 **/7int MatrixChain_min(int p[N],int n)8 {9//定义⼆维数组m[i][j]来记录i到j的合并过成中最少⽯⼦数⽬10 //此处赋值为-11112int m[N][N];13for(int x=1;x<=n;x++)14for(int z=1;z<=n;z++)15 {16 m[x][z]=-1;17 }1819int min=0;2021//当⼀个单独合并时,m[i][i]设为0,表⽰没有⽯⼦22for(int g = 1;g<=n;g++) m[g][g]=0;2324//当相邻的两堆⽯⼦合并时,此时的m很容易可以看出是两者之和25for(int i=1;i<=n-1;i++)26 {27int j=i+1;28 m[i][j]=p[i]+p[j];29 }3031//当相邻的3堆以及到最后的n堆时,执⾏以下循环32for(int r=3; r<=n;r++)33for(int i=1;i<=n-r+1;i++)34 {35int j = i+r-1; //j总是距离i r-1的距离36int sum=0;37//当i到j堆⽯⼦合并时最后⾥⾯的⽯⼦数求和得sum38for(int b=i;b<=j;b++)39 sum+=p[b];4041// 此时m[i][j]为i~j堆⽯⼦间以m[i][i]+m[i+1][j]+sum结果,这是其中⼀种可能,不⼀定是最优42 //要与下⾯的情况相⽐较,唉,太详细了4344 m[i][j] = m[i+1][j]+sum;4546//除上⾯⼀种组合情况外的其他组合情况47for(int k=i+1;k<j;k++)48 {49int t=m[i][k]+m[k+1][j]+sum;50if(t<m[i][j])51 m[i][j] = t;5253 }54 }55//最终得到最优解56 min=m[1][n];57return min;585960 }6162/*63 *求合并过程中64 *最多合并堆数⽬65 **/6667int MatrixChain_max(int p[N],int n)68 {69int m[N][N];70for(int x=1;x<=n;x++)71for(int z=1;z<=n;z++)72 {73 m[x][z]=-1;74 }757677int max=0;78//⼀个独⾃组合时79for(int g = 1;g<=n;g++) m[g][g]=0;80//两个两两组合时81for(int i=1;i<=n-1;i++)82 {83int j=i+1;84 m[i][j]=p[i]+p[j];85 }8687for(int r=3; r<=n;r++)88for(int i=1;i<=n-r+1;i++)89 {90int j = i+r-1;91int sum=0;92for(int b=i;b<=j;b++)93 sum+=p[b];94 m[i][j] = m[i+1][j]+sum;9596for(int k=i+1;k<j;k++)97 {98int t=m[i][k]+m[k+1][j]+sum;99if(t>m[i][j])100 m[i][j] = t;101102 }103 }104105 max=m[1][n];106return max;107108109 }110int main()111 {112int stone[N];113int min=0;114int max=0;115int n;116 scanf("%d",&n);117for(int i=1;i<=n;i++)118 scanf("%d",&stone[i]);119120 min= MatrixChain_min(stone,n);121 max= MatrixChain_max(stone,n);122123//因为题⽬要求圆的原因,要把所有情况都要考虑到,总共有n种情况。

第1篇一、实验目的本次实验旨在让学生理解动态规划算法的基本概念,掌握动态规划解决问题的基本思想和步骤,并能运用动态规划算法解决实际问题。
通过实验,学生应能够:1. 理解动态规划算法的概念及其应用领域。
2. 掌握动态规划的基本思想和解决问题的基本步骤。
3. 学习动态规划算法设计策略,并能够运用到实际问题中。
4. 通过实际编程,提高编程能力和问题解决能力。
二、实验环境1. 操作系统:Windows 102. 编程语言:Python3.83. 开发环境:PyCharm三、实验内容本次实验选择了三个典型的动态规划问题进行实践:1. 最长公共子序列问题2. 矩阵连乘问题3. 剪绳子问题四、实验步骤1. 最长公共子序列问题(1)问题描述:给定两个序列X和Y,找出X和Y的最长公共子序列。
(2)算法设计:- 使用二维数组dp[i][j]表示X的前i个字符和Y的前j个字符的最长公共子序列的长度。
- 初始化dp[0][j] = 0和dp[i][0] = 0。
- 对于i > 0和j > 0,如果X[i-1] == Y[j-1],则dp[i][j] = dp[i-1][j-1] + 1;否则,dp[i][j] = max(dp[i-1][j], dp[i][j-1])。
(3)代码实现:```pythondef longest_common_subsequence(X, Y):m, n = len(X), len(Y)dp = [[0] (n + 1) for _ in range(m + 1)]for i in range(1, m + 1):for j in range(1, n + 1):if X[i - 1] == Y[j - 1]:dp[i][j] = dp[i - 1][j - 1] + 1else:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])return dp[m][n]```2. 矩阵连乘问题(1)问题描述:给定n个矩阵A1, A2, ..., An,其中Ai与Ai-1是可乘的,i = 1, 2, ..., n-1。
动态规划动态规划是运筹学的一个分支,它是解决多阶段决策过程最优化问题的一种方法。
该方法是由美国数学家贝尔曼(R.Bellman)等人在本世纪50年代初提出的。
他们针对多阶段决策问题的特点,提出了解决这类问题的“最优化原理”,并成功地解决了生产管理、工程技术等方面的许多实际问题,从而建立了运筹学的一个新分支——动态规划。
他的名著《动态规划》于1957年出版,该书是动态规划的第一本著作。
动态规划是现代企业管理中的一种重要决策方法,在工程技术、经济管理、工农业生产及军事及其它部们都有广泛的应用,并且获得了显著的效果。
动态规划可用于解决最优路径问题、资源分配问题、生产计划与库存问题、投资分配问题、装载问题、设备更新与维修问题、排序问题及生产过程的最优控制等。
由于它所具有独特的解题思路,在处理某些优化问题时,常常比线性规划或非线性规划方法更有效。
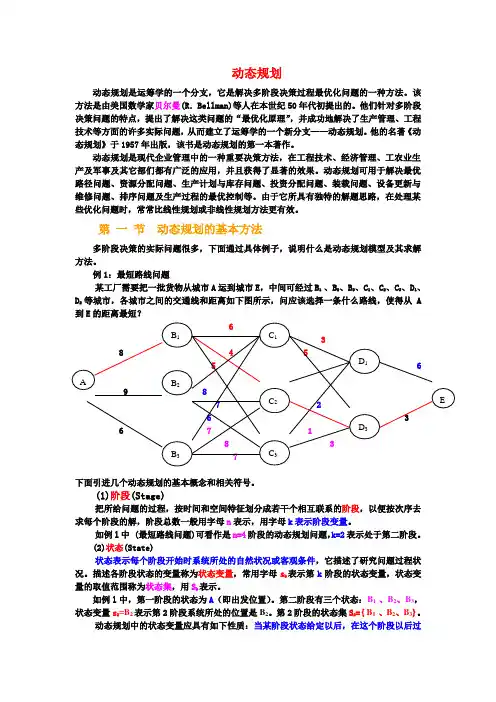
第一节动态规划的基本方法多阶段决策的实际问题很多,下面通过具体例子,说明什么是动态规划模型及其求解方法。
例1:最短路线问题某工厂需要把一批货物从城市A运到城市E,中间可经过B1 、B2、B3、C1、C2、C3、D1、D2等城市,各城市之间的交通线和距离如下图所示,问应该选择一条什么路线,使得从A到E的距离最短?下面引进几个动态规划的基本概念和相关符号。
(1)阶段(Stage)把所给问题的过程,按时间和空间特征划分成若干个相互联系的阶段,以便按次序去求每个阶段的解,阶段总数一般用字母n表示,用字母k表示阶段变量。
如例l中 (最短路线问题)可看作是n=4阶段的动态规划问题,k=2表示处于第二阶段。
(2)状态(State)状态表示每个阶段开始时系统所处的自然状况或客观条件,它描述了研究问题过程状况。
描述各阶段状态的变量称为状态变量,常用字母sk表示第k阶段的状态变量,状态变量的取值范围称为状态集,用Sk表示。
如例l中,第一阶段的状态为A(即出发位置)。
第二阶段有三个状态:B1 、B2、B3,状态变量s2=B2表示第2阶段系统所处的位置是B2。

常见的动态规划问题分析与求解 转载⾃:动态规划(Dynamic Programming,简称DP),虽然抽象后进⾏求解的思路并不复杂,但具体的形式千差万别,找出问题的⼦结构以及通过⼦结构重新构造最优解的过程很难统⼀,并不像回溯法具有解决绝⼤多数问题的框架()。
为了解决动态规划问题,只能靠多练习、多思考了。
本⽂主要是对⼀些常见的动态规划题⽬的收集,希望能有所帮助。
难度评级受个⼈主观影响较⼤,仅供参考。
⽬录(点击跳转)动态规划求解的⼀般思路: 判断问题的⼦结构(也可看作状态),当具有最优⼦结构时,动态规划可能适⽤。
求解重叠⼦问题。
⼀个递归算法不断地调⽤同⼀问题,递归可以转化为查表从⽽利⽤⼦问题的解。
分治法则不同,每次递归都产⽣新的问题。
重新构造⼀个最优解。
备忘录法: 动态规划的⼀种变形,使⽤⾃顶向下的策略,更像递归算法。
初始化时表中填⼊⼀个特殊值表⽰待填⼊,当递归算法第⼀次遇到⼀个⼦问题时,计算并填表;以后每次遇到时只需返回以前填⼊的值。
实例可以参照矩阵链乘法部分。
1.硬币找零难度评级:★ 假设有⼏种硬币,如1、3、5,并且数量⽆限。
请找出能够组成某个数⽬的找零所使⽤最少的硬币数。
解法: ⽤待找零的数值k描述⼦结构/状态,记作sum[k],其值为所需的最⼩硬币数。
对于不同的硬币⾯值coin[0...n],有sum[k] = min(sum[k-coin[0]] , sum[k-coin[1]], ...)+1。
对应于给定数⽬的找零total,需要求解sum[total]的值。
typedef struct {int nCoin; //使⽤硬币数量//以下两个成员是为了便于构造出求解过程的展⽰int lastSum;//上⼀个状态int addCoin;//从上⼀个状态达到当前状态所⽤的硬币种类} state;state *sum = malloc(sizeof(state)*(total+1));//initfor(i=0;i<=total;i++)sum[i].nCoin = INF;sum[0].nCoin = 0;sum[0].lastSum = 0;for(i=1;i<=total;i++)for(j=0;j<n;j++)if(i-coin[j]>=0 && sum[i-coin[j]].nCoin+1<sum[i].nCoin){sum[i].nCoin = sum[i-coin[j]].nCoin+1;sum[i].lastSum = j;sum[i].addCoin = coin[j];}if(sum[total].nCoin == INF){printf("can't make change.\n");return 0;}else//output ; 通过sum[total].lastSum和sum[total].addCoin,很容易通过循环逆序地或者编写递归调⽤的函数正序地输出从结束状态到开始状态使⽤的硬币种类。

动态规划算法动态规划算法基本思想:1、将待求解问题分阶段处理2、每个阶段有若干个状态S3、通过决策X将目前的状态S转到下一个状态S4、从目前的状态到如何到终点与如何到此状态无关5、从最后一阶段往前递推6、找到递推公式,对于最短路径问题:=Min{ }= Min{ +}【最短路径问题】如图所示,节点间的路长已标出,求A至E点的最短路径。
解决方法:将问题分4个阶段,自低向上讨论。
当k=4(阶段4)只考虑从本阶段到终点E的路径选择。
在这一阶段有两个状态:D1和D2,D1:目前已到达D1,要从D1到E;D2:目前已到达D2,要从D2到E:在阶段4,从当前状态到达终点的决策(应选择哪一个点到达终点路径最短):阶段4 从当前状态到达终点的最短距离k=3k=2或或k=1或所以,110为从A到E的最短路径值。
【0-1背包问题】一个旅行者有一个最多能用M公斤的背包,现在有N件物品,它们的重量分别是W1,W2,...,Wn,它们的价值分别为P1,P2,...,Pn.若每种物品只有一件求旅行者能获得最大总价值。
测试数据:10 33 44 55 6(表示M=10,N=3,W1=3,P1=4,w2=4,P2=5,W3=5,P3=6)分析:阶段:在前i件物品中,选取若干件物品放入背包中;状态:在前i件物品中,选取若干件物品放入所剩空间为W的背包中的所能获得的最大价值;决策:第i件物品放或者不放;递推公式:c(i,j)=max{c(i-1,j), c(i-1,j-w[i])+vl(i)}i :处理到第i件物品j:剩余的空间为jc(i,j):在前i件物品中选取若干件放到背包的最大价值c(i-1,j):第i件物品不放所能得到的价值c(i-1,j-w[i])+vl(i):第i件物品放入所能得到的价值所以,获得的最大总价值是11。
【0-1完全背包问题】一个旅行者有一个最多能用M公斤的背包,现在有N种物品,它们的重量分别是W1,W2,...,Wn,它们的价值分别为P1,P2,...,Pn.若每种物品有无限件,求旅行者能获得最大总价值。

动态规划转移方程1. 资源问题1-----机器分配问题总公司拥有高效生产设备M台,准备分给下属的N个公司。
各分公司若获得这些设备,可以为国家提供一定的盈利。
问:如何分配这M台设备才能使国家得到的盈利最大?求出最大盈利值。
其中M<=15,N<=10。
分配原则:每个公司有权获得任意数目的设备,但总台数不得超过总设备数M。
数据文件格式为:第一行保存两个数,第一个数是设备台数M,第二个数是分公司数N。
接下来是一个M*N的矩阵,表明了第I个公司分配J台机器的盈利。
用机器数来做状态,数组F[I,J]表示前I个公司分配J台机器的最大盈利。
则状态转移方程为:F[I,j]:=max(f[i-1,k]+w[i,j-k])2. 资源问题2------01背包问题有N件物品和一个容量为V的背包。
第i件物品的费用是c,价值是w。
求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量,且价值总和最大。
F[I,j]:=max(f[i-1,j-v[i]]+w[i],f[i-1,j]);3. 线性动态规划1-----朴素最长非降子序列设有由n个不相同的整数组成的数列,记为:a(1),a(2),……,a(n)且a(i)<>a(j) (i<>j)例如3,18,7,14,10,12,23,41,16,24。
若存在i1<I2<I3< span < ie …>且有a(i1)<A(I2)< span … <a(ie)<>则称为长度为e的不下降序列。
如上例中3,18,23,24就是一个长度为4的不下降序列,同时也有3,7,10,12,16,24长度为6的不下降序列。
程序要求,当原数列给出之后,求出最长的不下降序列。
F[i]:=max{f[j]+1}4. 剖分问题1-----石子合并在一个园形操场的四周摆放N堆石子(N≤100),现要将石子有次序地合并成一堆。
动态规划之01背包问题首先是问题描述:给定n种物品和一背包,物品i的重量是wi,其价值是pi,背包的容量是M,问如何选择装入背包中的物品总价值最大?可以这样理解:背包的背负有上限,因此在这个上限内尽可能多的装东西,并且价值越多越好。
在这里我之想讨论动态规划解决这个问题的详细过程。
动态规划是用空间换时间的一种方法的抽象。
其关键是发现子问题和记录其结果。
然后利用这些结果减轻运算量。
因为背包的最终最大容量未知,所以,我们得从1到M一个一个的试,比如,刚开始任选N件物品中的一个,看对应的M的背包,能不能放进去,如果能放进去,并且还有多少空间,则,多出来的空间能放N-1物品中的最大价值,怎么能保证总选则是最大价值呢,看下表:测试数据:10,33,44,55,6c[i][j]数组保存了1,2,3号物品依次选择后的最大价值.这个最大价值是怎么得来的呢?从背包容量为0开始,1号物品先试,0,1,2,的容量都不能放.所以置0,背包容量为3则里面放4.这样,这一排背包容量为4,5,6,....10的时候,最佳方案都是放4.假如1号物品放入背包.则再看2号物品.当背包容量为3的时候,最佳方案还是上一排的最价方案c为4.而背包容量为5的时候,则最佳方案为自己的重量5.背包容量为7的时候,很显然是5加上一个值了。
加谁??很显然是7-4=3的时候.上一排c3的最佳方案是4.所以。
总的最佳方案是5+4为9.这样.一排一排推下去。
最右下放的数据就是最大的价值了。
(注意第3排的背包容量为7的时候,最佳方案不是本身的6.而是上一排的9.说明这时候3号物品没有被选.选的是1,2号物品.所以得9.从以上最大价值的构造过程中可以看出。
f(n,m)=max{f(n-1,m), f(n-1,m-w[n])+P(n,m)}这就是书本上写的动态规划方程.下面是一种实现过程:(C语言描述)#include<stdio.h>int c[10][100];int knapsack(int m,int n){int i,j,w[10],p[10];for(i=1;i<n+1;i++)scanf("\n%d,%d",&w[i],&p[i]);for(i=0;i<10;i++)for(j=0;j<100;j++)c[i][j]=0;for(i=1;i<n+1;i++)for(j=1;j<m+1;j++){if(w[i]<=j){if(p[i]+c[i-1][j-w[i]]>c[i-1][j])c[i][j]=p[i]+c[i-1][j-w[i]];elsec[i][j]=c[i-1][j];}elsec[i][j]=c[i-1][j];}return(c[n][m]);}int main(){int m,n;int i,j;printf("input the max capacity and the number of the goods:\n"); scanf("%d,%d",&m,&n);printf("Input each one(weight and value):\n");printf("%d",knapsack(m,n));printf("\n");for(i=0;i<10;i++)for(j=0;j<15;j++){printf("%d ",c[i][j]);if(j==14)printf("\n");}system("pause");}下面是思路的基本过程问题的特点是:每种物品一件,可以选择放1或不放0。
1
第五章 动态规划作业题及答案
1.用动态规划法求解求最短路径
从起点A 到终点E 之间各点的距离如图所示。
求A 到E 的最短路径。
B A
C B
D B C D E
C 21
23
12
31
2
5
11214
10610
41312113
96
5810
5
2
2.用动态规划法求解资源分配问题
有资金4万元,投资A 、B 、C 三个项目,每个项目的投资效益与投入该项目的资金有关。
三个项目A 、B 、C 的投资效益(万吨)和投入资金(万元)的关系见下表:
用动态规划法求解对三个项目的最优投资分配,使总投资效益最大。
3.用动态规划法求解生产库存问题
一个工厂生产某种产品,1~7月份生产成本和产品需求量的变化情况如下表:
为了调节生产生产和需求,工厂设有一个产品仓库,库容量H=9。
已知期初库存量为2,要求期末(七月低)库存量为0。
每个月生产的产品在月末入库,月初根据当月需求发货。
求七个月的生产量,能满足各月的需求,并使生产成本最低。
4.用动态规划法求解背包问题
第i 种每件价值c 1=65,c 2=85,c 3=40元; 第i 种物品每件重量为:w 1=2,w 2=3,w 3=1公斤;现有一只可装载重量为5公斤的背包,求各种物品应各取多少件放入背包,使背包中物品的价值最高。
2.某公司有资金4百万元向A,B和C3个项目追加投资,各个项目可以有不同的投资额(百万元计),相应的效益如表所示。
问怎样分配资金,使总效益值最大?##表8-47W k (X k)投资额(项目k#012341#(A)-414860662#(B )40425060-3#(C)-64687884解:设S1-A,B,C项目的总投资额,S2-B、C项目的总投资额S3-C项目的投资额;X k-k项目的投资额;(X1-A项目的投资额,X2-B项目的投资额,X3-C项目的投资额)W k(S k,X k)-对K项目投资X k后的收益:W k(S k,X k)=W k (X k)T k (S k,X k)-S k+1=S k-X kf k (S k)-当K至第3项目允许的投资额为S k时所能获得的最大收益。
为获得最大利润,必须将4百万全部投资,假设有4阶段存在,有S4=0,建立递归方程f4 (S k)=0f k (S k)=max{ W k (X k)+f k +1(S k+1)} k=3,2,1X k∈D k(S k)第一步,K=3f4(S4)=0f3 (S3)=max{W3 (X3)+f4 (S4)}X3∈D3(S3)S4=S3-X3S3f3 (S3)X3* 1641268237834844第二步:K=2 f2 (S2)=max{W2 (X2)+f3 (S3)}X2∈D2(S2)S3=S2-X2W2 (X2)+f3 (S2-X2)S2X2 =0X2 =1X2 =2X2 =3f2 (S2)X2 * 140+64---1040 240+6842+64--1080 340+7842+6850+64-1180 440+8442+7850+6860+641240,3第三步:K=1 f1 (S1) =max {W1 (X1)+ f2 (S2)}X1∈D1(S1)S2= S1- X1W1 (X1)+ f2 (S1- X1)S1X1=0X1=1X1=2X1=3f1 (S1)X1 * 4-41+118 48+10860+1041643S1=4 →S2=1 →S3=1↓↓↓X1*=3 X2*=0 X3*=1A投资3百万,B不投资C投资1百万。
第七章动态规划规划问题的最终目的就是确定各决策变量的取值,以使目标函数达到极大或极小。
在线性规划和非线性规划中,决策变量都是以集合的形式被一次性处理的;然而,有时我们也会面对决策变量需分期、分批处理的多阶段决策问题。
所谓多阶段决策问题是指这样一类活动过程:它可以分解为若干个互相联系的阶段,在每一阶段分别对应着一组可供选取的决策集合;即构成过程的每个阶段都需要进行一次决策的决策问题。
将各个阶段的决策综合起来构成一个决策序列,称为一个策略。
显然,由于各个阶段选取的决策不同,对应整个过程可以有一系列不同的策略。
当过程采取某个具体策略时,相应可以得到一个确定的效果,采取不同的策略,就会得到不同的效果。
多阶段的决策问题,就是要在所有可能采取的策略中选取一个最优的策略,以便得到最佳的效果。
动态规划(dynamic programming)同前面介绍过的各种优化方法不同,它不是一种算法,而是考察问题的一种途径。
动态规划是一种求解多阶段决策问题的系统技术,可以说它横跨整个规划领域(线性规划和非线性规划)。
当然,由于动态规划不是一种特定的算法,因而它不象线性规划那样有一个标准的数学表达式和明确定义的一组规则,动态规划必须对具体问题进行具体的分析处理。
在多阶段决策问题中,有些问题对阶段的划分具有明显的时序性,动态规划的“动态”二字也由此而得名。
动态规划的主要创始人是美国数学家贝尔曼(Bellman)。
20世纪40年代末50年代初,当时在兰德公司(Rand Corporation)从事研究工作的贝尔曼首先提出了动态规划的概念。
1957年贝尔曼发表了数篇研究论文,并出版了他的第一部著作《动态规划》。
该著作成为了当时唯一的进一步研究和应用动态规划的理论源泉。
1961年贝尔曼出版了他的第二部著作,并于1962年同杜瑞佛思(Dreyfus)合作出版了第三部著作。
在贝尔曼及其助手们致力于发展和推广这一技术的同时,其他一些学者也对动态规划的发展做出了重大的贡献,其中最值得一提的是爱尔思(Aris)和梅特顿(Mitten)。
动态规划经典教程引言:本人在做过一些题目后对DP有些感想,就写了这个总结:第一节动态规划基本概念一,动态规划三要素:阶段,状态,决策。
他们的概念到处都是,我就不多说了,我只说说我对他们的理解:如果把动态规划的求解过程看成一个工厂的生产线,阶段就是生产某个商品的不同的环节,状态就是工件当前的形态,决策就是对工件的操作。
显然不同阶段是对产品的一个前面各个状态的小结,有一个个的小结构成了最终的整个生产线。
每个状态间又有关联(下一个状态是由上一个状态做了某个决策后产生的)。
下面举个例子:要生产一批雪糕,在这个过程中要分好多环节:购买牛奶,对牛奶提纯处理,放入工厂加工,加工后的商品要包装,包装后就去销售……,这样每个环节就可以看做是一个阶段;产品在不同的时候有不同的状态,刚开始时只是白白的牛奶,进入生产后做成了各种造型,从冷冻库拿出来后就变成雪糕(由液态变成固态)。
每个形态就是一个状态,那从液态变成固态经过了冰冻这一操作,这个操作就是一个决策。
一个状态经过一个决策变成了另外一个状态,这个过程就是状态转移,用来描述状态转移的方程就是状态转移方程。
经过这个例子相信大家对动态规划有所了解了吧。
下面再说说我对动态规划的另外一个理解:用图论知识理解动态规划:把动态规划中的状态抽象成一个点,在有直接关联的状态间连一条有向边,状态转移的代价就是边上的权。
这样就形成了一个有向无环图AOE网(为什么无环呢?往下看)。
对这个图进行拓扑排序,删除一个边后同时出现入度为0的状态在同一阶段。
这样对图求最优路径就是动态规划问题的求解。
二,动态规划的适用范围动态规划用于解决多阶段决策最优化问题,但是不是所有的最优化问题都可以用动态规划解答呢?一般在题目中出现求最优解的问题就要考虑动态规划了,但是否可以用还要满足两个条件:最优子结构(最优化原理)无后效性最优化原理在下面的最短路径问题中有详细的解答;什么是无后效性呢?就是说在状态i求解时用到状态j而状态j求解又用到状态k…..状态N。
求大神解答一下这题的解题过程尤其是第3步到第4步
的过程
这道题目是一道动态规划题目,我们可以使用动态规划的方法来解决它。
首先,在解决动态规划问题之前,我们必须首先定义一个子问题。
在
这里,我们的子问题是对于cur容量为i时,能够与最大的值。
那么,我
们可以定义一个状态数组dp[i],表示容量为i时,能够获取的最大价值。
第二步,我们要确定问题的状态转移方程,即当前状态与其之前的状
态有什么关系。
由于我们在容量为cur时,只能选择剩余的货物中的一个,因此可以将状态转移方程定义为:
dp[i] = max (dp[i], dp[i - weights[j]] + values[j]),其中i表
示剩余容量,weights[j]表示第j件货物的重量,values[j]表示第j件
货物的价值。
这里,max代表我们要取最大值,因为我们想要获得最大的价值,所
以取最大值。
dp[i - weights[j]] + values[j]表示的是在不选择第j件
货物的情况下,容量为i时,能够获取的最大值加上选择第j件货物时,
获取的价值。
第三步,我们要确定边界条件。
由于在容量为cur时,我们只能选择
货物中的一件,所以我们可以分成两种情况:一种是不选择任何货物,即
当容量为0时,最大价值为0,另一种是选择货物,当容量不为0时,最
大价值初始化为负无穷。
因此,我们可以设置如下的边界条件:
dp[0] = 0 // 容量为0时,最大价值为0。