浙教版八年级上册 2.6 直角三角形专题培优(附答案)

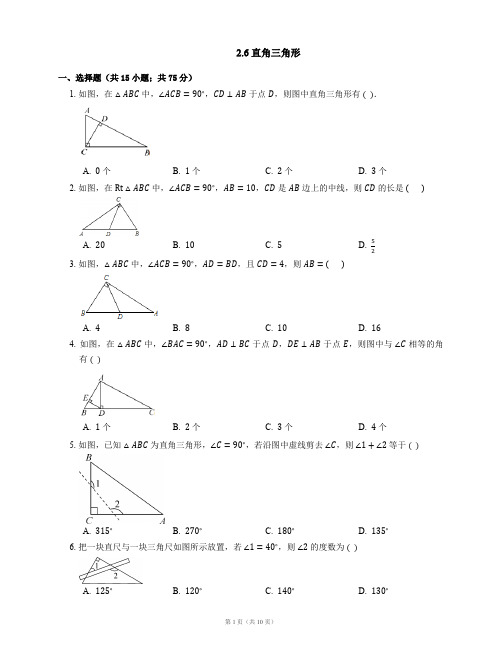
2.6 直角三角形一、选择题（共15小题；共75分）1. 如图，在△ABC中，∠ACB=90∘，CD⊥AB于点D，则图中直角三角形有( )．A. 0个B. 1个C. 2个D. 3个2. 如图，在Rt△ABC中，∠ACB=90∘，AB=10，CD是AB边上的中线，则CD的长是 ( )A. 20B. 10C. 5D. 523. 如图，△ABC中，∠ACB=90∘，AD=BD，且CD=4，则AB= ( )A. 4B. 8C. 10D. 164. 如图，在△ABC中，∠BAC=90∘，AD⊥BC于点D，DE⊥AB于点E，则图中与∠C相等的角有( )A. 1个B. 2个C. 3个D. 4个5. 如图，已知△ABC为直角三角形，∠C=90∘，若沿图中虚线剪去∠C，则∠1+∠2等于( )A. 315∘B. 270∘C. 180∘D. 135∘6. 把一块直尺与一块三角尺如图所示放置，若∠1=40∘，则∠2的度数为( )A. 125∘B. 120∘C. 140∘D. 130∘7. 若直角三角形的两条直角边的长分别为9 cm和12 cm，则斜边上的中线长为( )A. 4.5 cmB. 6 cmC. 7.5 cmD. 10 cm8. 如图，已知在Rt△ABC中，∠ABC=90∘，点D是BC边的中点，分别以B、C为圆心，大于线段BC长度一半的长为半径圆弧，两弧在直线BC上方的交点为P，直线PD交AC于点E，连接AB中，一定BE，则下列结论：① ED⊥BC；② ∠A=∠EBA；③ EB平分∠AED；④ ED=12正确的是 ( )A. ①②③B. ①②④C. ①③④D. ②③④9. 如图，CD是Rt△ABC斜边AB上的高，将△BCD沿CD折叠，B点恰好落在AB的中点E处，则∠A等于 ( )A. 25∘B. 30∘C. 45∘D. 60∘10. 如图，在Rt△ACB中，∠ACB=90∘,∠A=25∘，D是AB上一点，将Rt△ABC沿CD折叠，使B点落在AC边上的Bʹ处，则∠ADBʹ等于( )A. 25∘B. 30∘C. 35∘D. 40∘11. 如图，已知OP平分∠AOB，∠AOB=60∘，CP=2，CP∥OA，PD⊥OA于点D，PE⊥OB于点E．如果M是OP的中点，那么DM的长是( )A. 2B. √2C. √3D. 2√312. 如图，已知点A(−1,0)和点B(1,2)，在坐标轴上确定点P，使得△ABP为直角三角形，则满足这样条件的点P共有 ( )A. 2个B. 4个C. 6个D. 7个13. 如图，在△ABC中，∠CAB=90∘，∠B<∠C，AD，AE，AF分别是△ABC的高、角平分线、中线．则∠DAE与∠FAE的大小关系是( )A. ∠DAE>∠FAEB. ∠DAE=∠FAEC. ∠DAE<∠FAED. 与∠C的度数有关，无法判断14. 如图，直角三角板的直角顶点落在直尺边上，若∠1=56∘，则∠2的度数为 ( )A. 56∘B. 44∘C. 34∘D. 28∘15. 如图，m∥n，直线l分别交m，n于点A、点B，AC⊥AB，AC交直线n于点C，若∠1=35∘，则∠2等于 ( )A. 35∘B. 45∘C. 55∘D. 65∘二、填空题（共15小题；共75分）16. 在Rt△ABC中，∠C=Rt∠，∠A=70∘，则∠B=．17. 在Rt△ABC中，锐角∠A=35∘，则另一个锐角∠B=18. 如图，有两个互相垂直的滑槽（滑槽宽度忽略不计），一根没有弹性的木棒的两端A，B能在滑槽内自由滑动，将笔插入位于木棒中点P处的小孔中，随着木棒的滑动就可以画出一个圆来．若AB=20 cm，则画出的圆的半径为 cm．19. 如图，将一副三角尺叠放在一起，使直角的顶点重合于点O，则∠AOC+∠BOD=．20. 已知一个直角三角形的两条直角边长分别为3 cm和4 cm，则这个直角三角形斜边上的高线长为cm，斜边上的中线长为cm．21. 在直角三角形中，斜边及其中线长之和为3，那么该三角形的斜边长为．22. 如图，在Rt△ABC中，∠ACB=90∘，BC=6，AC=8，分别以点A，B为圆心，大于线段AB长度一半的长为半径作弧，相交于点E，F，过点E，F作直线EF，交AB于点D，连接CD，则CD的长是．23. 如图，在△ABC中，∠ACB=90∘，CD是AB边上的高，则图中与∠A相等的角是．24. 如图，AB，CD相交于点O，AC⊥CD于点C．若∠BOD=38∘，则∠A=．25. 在△ABC中，2∠B=∠A+∠C，最小角∠A=30∘，最长边的中线为8cm，则最短边的长为cm．26. 如图，在Rt△ABC中，D，E为斜边AB上的两个点，且BD=BC，AE=AC，则∠DCE的大小为．27. 如图，直线m∥n，Rt△ABC的顶点A在直线n上，∠C=90∘．若∠1=25∘，∠2=70∘，则∠B=∘．28. 如图，△ABC中，CD⊥AB于D，E是AC的中点，若AD=6，CD=8，则DE的长等于．29. 如图，有一块含有60∘角的直角三角板的两个顶点放在矩形的对边上．如果∠1=15∘，那么∠2的度数是 .30. 已知边长为a的正三角形ABC，两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动，点C在第一象限，连结OC，则OC的长的最大值是．三、解答题（共5小题；共65分）31. 如图，在四边形ABCD中，∠ABC=∠ADC=90∘，M，N分别是AC，BD的中点，连接MN．Ⅰ试猜想MN与BD的位置关系，并证明你的结论．Ⅱ如果∠BCD=45∘，BD=2，求MN的长．32. 如图，O是等边三角形ABC内一点，∠AOB=110∘，∠BOC=α .将△BOC绕点C按顺时针方向旋转60∘得到△ADC，连接OD .Ⅰ求证：△COD是等边三角形．Ⅱ当α=150∘时，试判断△AOD的形状，并说明理由．Ⅲ探究：当α为多少度时，△AOD是等腰三角形?33. 如图，在Rt△ABC中，∠ACB=90∘，D是AB上一点，且∠ACD=∠B．求证：CD⊥AB．34. 如图，在Rt△ABC中，∠ACB=90∘，M是边AB的中点，CH⊥AB于点H，CD平分∠ACB．Ⅰ求证：∠1=∠2．Ⅱ过点M作AB的垂线交CD的延长线于点E，求证：CM=EM．35. 已知：如图，D为线段AB上一点（不与点A，B重合），CD⊥AB，且CD=AB，AE⊥AB，BF⊥AB，且AE=BD，BF=AD．Ⅰ如图 1，当点D恰是AB的中点时，请你猜想并证明∠ACE与∠BCF的数量关系；Ⅱ如图2，当点D不是AB的中点时，你在（1）中所得的结论是否发生变化，写出你的猜想并证明；Ⅲ若∠ACB=α，直接写出∠ECF的度数（用含α的式子表示）．答案第一部分1. D2. C3. B4. B5. B6. D7. C8. B9. B 10. D11. C 12. C 13. B 14. C 15. C第二部分16. 20∘17. 55 度18. 1019. 180∘20. 125；52 21. 222. 523. ∠BCD24. 52∘25. 826. 45∘27. 4528. 529. 15∘30.√3+12a第三部分31. （1） MN ⊥BD ．证明如下：连接 BM ，DM ．因为 ∠ADC =90∘，M 是 AC 的中点，所以 AC =2DM =2CM ．同理，AC =2BM =2CM ，所以 BM =DM ．因为 N 是 BD 的中点，所以 MN ⊥BD ．（2） 由（1），得 BM =CM ，DM =CM ，所以 ∠BCM =∠CBM ，∠DCM =∠CDM ．因为 ∠AMB 是 △BCM 的一个外角，所以 ∠AMB =∠BCM +∠CBM =2∠BCM ．同理，∠AMD =2∠DCM ．因为∠BCD=45∘，所以∠BCM+∠DCM=45∘．所以∠BMD=∠AMB+∠AMD=2(∠BCM+∠DCM)=90∘．所以△BMD是直角三角形．因为N是BD的中点，BD=1．所以MN=1232. （1）∵将△BOC绕点C按顺时针方向旋转60∘得到△ADC，∴CO=CD，∠OCD=60∘，∴△COD是等边三角形．（2）当α=150∘时，△AOD是直角三角形．理由如下：∵△BOC≌△ADC，∴∠ADC=∠BOC=α=150∘ .∵△COD是等边三角形，∴∠ODC=60∘，∴∠ADO=90∘，∴△AOD是直角三角形．（3）分类讨论：①要使AO=AD，需∠AOD=∠ADO .∵∠AOD=190∘−α，∠ADO=α−60∘，∴190∘−α=α−60∘，∴α=125∘ .②要使AO=OD，需∠OAD=∠ADO .可得2(α−60∘)=180∘−(190∘−α)，∴α=110∘ .③要使OD=AD，需∠OAD=∠AOD .可得2(190∘−α)=180∘−(α−60∘)，∴α=140∘ .综上所述，当α的度数为125∘或110∘或140∘时，△ABC是等腰三角形．33. ∵∠ACB=90∘，∴∠A+∠B=90∘．∵∠ACD=∠B，∴∠A+∠ACD=90∘ .∴∠ADC=90∘ .∴CD⊥AB．34. （1）因为∠ACB=90∘，所以∠BCH+∠ACH=90∘ .因为CH⊥AB，所以∠CAH+∠ACH=90∘，所以∠CAH=∠BCH .因为M是斜边AB的中点，所以CM=AM=BM，所以∠CAM=∠ACM .所以∠BCH=∠ACM .因为CD平分∠ACB，所以∠BCD=∠ACD，所以∠BCD−∠BCH=∠ACD−∠ACM，即∠1=∠2 .（2）因为CH⊥AB，ME⊥AB，所以ME∥CH，所以∠1=∠MED .因为∠1=∠2，所以∠2=∠MED，所以CM=EM .35. （1）猜想：∠ACE=∠BCF．证明：∵D是AB中点，∴AD=BD，又AE=BD，BF=AD，∴AE=BF．∵CD⊥AB，AD=BD，∴CA=CB．∴∠1=∠2．∵AE⊥AB，BF⊥AB，∴∠3=∠4=90∘．∴∠1+∠3=∠2+∠4．即∠CAE=∠CBF．∴△CAE≌△CBF．∴∠ACE=∠BCF．（2）∠ACE=∠BCF仍然成立．证明：连接BE，AF．∵CD⊥AB，AE⊥AB，∴∠CDB=∠BAE=90∘．又BD=AE，CD=AB，△CDB≌△BAE．∴CB=BE，∠BCD=∠EBA．在Rt△CDB中，∵∠CDB=90∘，∴∠BCD+∠CBD=90∘．∴∠EBA+∠CBD=90∘．即∠CBE=90∘．∴△BCE是等腰直角三角形．∴∠BCE=45∘．同理可证：△ACF是等腰直角三角形．∴∠ACF=45∘．∴∠ACF=∠BCE．∴∠ACF−∠ECF=∠BCE−∠ECF．即∠ACE=∠BCF．（3）∠ECF的度数为90∘−α．。

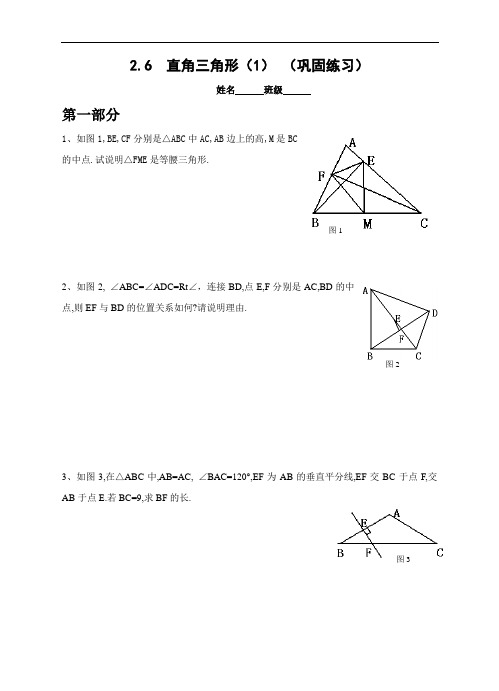
2.6 直角三角形（1）（巩固练习）姓名班级第一部分1、如图1,BE,CF分别是△ABC中AC,AB边上的高,M是BC的中点.试说明△FME是等腰三角形.图12、如图2, ∠ABC=∠ADC=Rt∠，连接BD,点E,F分别是AC,BD的中点,则EF与BD的位置关系如何?请说明理由.图23、如图3,在△ABC中,AB=AC, ∠BAC=120°,EF为AB的垂直平分线,EF交BC于点F,交AB于点E.若BC=9,求BF的长.图34、如图4，ABC ∆中，∠C=90°，∠ABC=60°，BD 平分∠ABC ，若AD=6，则CD= .第二部分1.在△ABC 中, ∠A ＝90°,∠B=2∠C,则∠C= 度.2. 在△ABC 中, ∠C ＝90°, AB=8cm,点D 是AB 的中点,则CD= .3. 在△ABC 中, ∠C ＝90°,点D 是AB 的中点,则图中有 个等腰三角形.4. 在△ABC 中, ∠C ＝90°,AC=BC,CD ⊥AB,且AB=8cm,则CD= .5. 如图8，△ABC 中，∠ABC ＝90°，D 是AB 的中点，∠A=66°,则∠BCD= 度.6.如图9,某市为改善交通状况，修建了大量的高架桥．一汽车在坡度为30°的笔直高架桥点A 开始爬行，行驶了150米到达点B ，则这时汽车离地面的高度为 米．7.直角三角形斜边长是6，以斜边的中点为 圆心，斜边上的中线为半径的圆的面积是 ．8. 如图10，在等腰三角形ABC 中，12cm AB AC ==，BAC ∠=120°，那么底边上的高AD = cm ． 9.如图11，△ABC 是房梁的一部分，其中BC ⊥AC ，垂足为C ，∠A=30°，D 是AB 的中点，且DC=3m ，求AB ，BC 的长.图 430o图9ADCＢ图10图1110.如图12,在Rt △ABC 中，∠ACB ＝90°，∠CAB ＝30°，用两种方法把它分成两个三角形，且要求一个三角形是等腰三角形．图12A CBACB参考答案第一部分中，∠C=90°，∠ABC=60°，BD平分∠ABC，若AD=6，则CD= .4、如图4，ABC答案：3第二部分1.在△ABC中, ∠A＝90°,∠B=2∠C,则∠C= 度.答案：302. 在△ABC中, ∠C＝90°, AB=8cm,点D是AB的中点,则CD= .答案：4cm3. 在△ABC 中, ∠C ＝90°,点D 是AB 的中点,则图中有 个等腰三角形.答案：24. 在△ABC 中, ∠C ＝90°,AC=BC,CD ⊥AB,且AB=8cm,则CD= .答案：4cm5. 如图8，△ABC 中，∠ABC ＝90°，D 是AB 的中点，∠A=66°,则∠BCD= 度.答案：246.如图9,某市为改善交通状况，修建了大量的高架桥．一汽车在坡度为30°的笔直高架桥点A 开始爬行，行驶了150米到达点B ，则这时汽车离地面的高度为 米．答案：757.直角三角形斜边长是6，以斜边的中点为 圆心，斜边上的中线为半径的圆的面积是 ． 答案：9π8. 如图10，在等腰三角形ABC 中，12cm AB AC ==，BAC ∠=120°，那么底边上的高AD = cm ． 答案：19.如图11，△ABC 是房梁的一部分，其中BC ⊥AC ，垂足为C ，∠A=30°，D 是AB 的中点，且DC=3m ，求AB ，BC 的长.解：∵BC ⊥AC, D 是BC 的中点, ∴AB=2DC=6m. ∵∠A=30°，∴BC=12AB=3m. 10.如图12,在Rt △ABC 中，∠ACB ＝90°，∠CAB ＝30°，用两种方法把它分成两个三角形，且要求一个三角形是等腰三角形．30o图9ADCＢ 图10图11图12A CBACB解：可参考的作法有：(1)作AC的中垂线交AB于D，连接CD，得等腰△DAC；(2)作∠B的平分线交AC于D，得等腰△DAB；(3)在BA上截取BD＝BC，连接CD，得等腰△BCD；(4)在AB上截取AD＝AC，连结CD，得等腰△ACD．。

2.6 直角三角形第1课时直角三角形的性质知识点1.直角三角形的两个锐角互余1．Rt△ABC中，∠C＝90°，∠B＝36°，则∠A的度数是(C)A．44°B．36°C．54°D．64°2．如图1，已知AB⊥BD，AC⊥CD，∠A＝40°，则∠D的度数为(A)图1A．40°B．50°C．60°D．70°【解析】∵AB⊥BD，∠A＝40°，∴∠AEB＝50°，∴∠DEC＝50°，又∵AC⊥CD，∴∠D＝40°.3．如图2，在Rt△ABC中，CD是斜边AB上的高，∠A＝35°.则∠BCD的度数为__35°__．图2 图34．如图3，AC⊥BC于点C，DE⊥BE于点E，BC平分∠ABE，∠BDE＝58°，则∠A＝__58°__．5．在Rt△ABC中，∠C＝90°，∠B＝2∠A，求∠B，∠A的度数．解：设∠A为x，则∠B为2x，由题意，得x＋2x＝90°，解得x＝30°，则2x＝60°，∴∠B＝60°，∠A＝30°.6．如图4，DE⊥AB于E，∠A＝40°，∠D＝30°，求∠ACD的度数．图4解：∵DE⊥AB于E，∠D＝30°，∴∠B＝90°－30°＝60°，在△ABC中，∠ACB＝180°－∠A－∠B＝180°－40°－60°＝80°，∴∠ACD＝180°－∠ACB＝180°－80°＝100°.知识点2.直角三角形斜边上的中线等于斜边的一半7．[邗江区期中]在Rt△ABC中，∠ACB＝90°，点D为斜边AB的中点，如果CD＝3，那么AB的长是(C)A．1.5 B．3 C．6 D．128．如图5，在△ABC中，AB＝AC＝3，BC＝4，AE平分∠BAC交BC于点E，点D为AB的中点，连结DE，则△BDE的周长是(C)图5A．3 B．4C．5 D．6【解析】由题意，得△ABC是等腰三角形，∵AE平分∠BAC交BC于点E，∴AE⊥BC，∴BE＝CE＝12BC＝2，∠AEB＝90°.又∵D是AB中点，∴DE＝BD＝12AB＝32，∴△BDE的周长为BE＋DE＋BD＝2＋32＋32＝5.故选C.9．[西城区校级模拟]如图6，在Rt△ABC中，∠BAC＝90°，AD是BC边上的中线，ED⊥BC于D，交BA延长线于点E，若∠E＝35°，求∠BDA的度数．图6解：∵∠E＝35°，ED⊥BC，∴∠B＝55°.∵∠BAC＝90°，AD是BC边上的中线，∴DA＝DB，∴∠B＝∠DAB＝55°，∴∠BDA＝180°－55°－55°＝70°.【易错点】直角三角形中如果遇斜边上的中点，连斜边上的中线，应利用“直角三角形中，斜边上的中线等于斜边的一半”解题．10．[来宾期末]如图7，在四边形ABCD中，∠ABC＝∠ADC＝90°，连结AC，BD，E，F分别是AC，BD的中点，连结EF，试证明：EF⊥BD.图7 第10题答图证明：如答图，连结BE，DE，∵∠ABC＝∠ADC＝90°，E是AC的中点，∴BE＝DE＝12AC，∵F是BD的中点，∴EF⊥BD.第2课时直角三角形的判定知识点有两个角互余的三角形是直角三角形1．[平邑校级月考]在△ABC中，满足下列条件：①∠A＝60°，∠C＝30°；②∠A ＋∠B＝∠C；③∠A∶∠B∶∠C＝3∶4∶5；④∠A＝90°－∠C，能确定△ABC 是直角三角形的有(C)A．1个B．2个C．3个D．4个【解析】①∠A＝60°，∠C＝30°时，∠B＝180°－60°－30°＝90°，是直角三角形；②∠A＋∠B＝∠C时，∠C＝90°，是直角三角形；③∠A∶∠B∶∠C＝3∶4∶5时，∠C＝180°×53＋4＋5＜90°，是锐角三角形；④∠A＝90°－∠C时，∠A＋∠C＝90°，∠B＝90°，是直角三角形．综上所述，是直角三角形的有①②④，共3个．故选C.2．已知∠A＝37°，∠B＝53°，则△ABC为__直角__三角形．3．如图1，点E是△ABC中AC边上的一点，过E作ED⊥AB，垂足为D.若∠1＝∠2，则△ABC是直角三角形吗？为什么？图1解：△ABC是直角三角形．理由如下：∵ED⊥AB，∴∠ADE＝90°，△ADE是直角三角形．∴∠1＋∠A＝90°.又∵∠1＝∠2，∴∠2＋∠A＝90°，∴△ABC是直角三角形．4．[阜宁期中]已知：如图2，在△ABC 中，点D 是AB 的中点，连结CD ，且CD ＝12AB ，求证：△ABC 为直角三角形．图2证明：由条件可知，AD ＝BD ＝CD ，则∠A ＝∠DCA ，∠B ＝∠DCB ，又∵∠A ＋∠DCA ＋∠B ＋∠DCB ＝180°，∴∠DCA ＋∠DCB ＝90°，即∠ACB ＝90°，∴△ABC 为直角三角形．5．如图3，四边形ABCD 中，∠ABC ＝∠ADC ＝90°，E 是对角线AC 的中点，连结BE ，DE .(1)求证：△BDE 是等腰三角形；(2)当∠BCD ＝__45__°时，△BDE 是等腰直角三角形．图3解：(1)证明：∵∠ABC ＝∠ADC ＝90°，E 是对角线AC 的中点，∴BE ＝DE ＝CE ＝AE ，∴△BDE 是等腰三角形；(2)∵BE ＝CE ＝DE ，∴∠CBE ＝∠ACB ，∠DCE ＝∠CDE ，由三角形的外角性质，得∠AEB ＝∠ACB ＋∠CBE ＝2∠ACB ，∠AED ＝∠CDE ＋∠DCE ＝2∠DCE ，∴∠BED ＝∠AEB ＋∠AED ＝2(∠ACB ＋∠DCE )＝2∠BCD ，∵△BDE是等腰直角三角形，∴∠BED＝90°，∴2∠BCD＝90°，∴∠BCD＝45°.【易错点】混淆直角三角形的性质和判定．6．如图4，在Rt△ABC中，∠BAC＝90°，BD平分∠ABC，M为直线AC上一点，ME⊥BC，垂足为E，∠AME的平分线交直线BD于点F.求证：△DMF是直角三角形．图4解：∵∠BAC＝90°，ME⊥BC，∴∠ABC＋∠C＝∠AME＋∠C＝90°，∴∠ABC＝∠AME.∵BD平分∠ABC，MF平分∠AME，∴∠ABD＝∠AMF.∵∠ABD＋∠ADB＝90°，∴∠AMF＋∠ADB＝90°，∴△DEF是直角三角形．。

第1章《三角形的初步认识》培优提升卷班级______ 姓名_______一、选择题（每题3分，共30分）1.现有四根木棒，长度分别为4cm ，6cm ，8cm ，10cm ，从中任取三根木棒，能组成三角形的个数为（ ）A ．1个B ．2个C ．3个D ．4个2.如图所示，一个60°角的三角形纸片，剪去这个60°角后，得到一个四边形，则∠+∠12 的度数为（ ）A.120°B. 180°C. 240°D. 300°第2题 第4题 第5题 3.根据下列已知条件，能惟一画出△ABC 的是（ ）A ．AB ＝3，BC ＝4，CA ＝8 B ．AB ＝4，BC ＝3，∠A ＝30° C ．∠A ＝60°，∠B ＝45°，AB ＝4D ．∠C ＝90°，AB ＝64.如图，A ，B ，C ，D ，E ，F 是平面上的6个点，则∠A+∠B+∠C+∠D+∠E+∠F 的度数是（ ）A. 180°B.360°C.540°D.720°2160°5.如图，一副分别含有30°和45°角的两个直角三角板，拼成如下图形，其中∠C=90°，∠B=45°，∠E=30°，则∠BFD的度数是（）A．15°B．25°C．30°D．10°6.下列命题:(1)无限小数是无理数(2)绝对值等于它本身的数是非负数(3) 垂直于同一直线的两条直线互相平行(4) 有两边和其中一边的对角对应相等的两个三角形全等, (5)面积相等的两个三角形全等，是真命题的有（）A.1个B.2个C.3个D.4个7.如图，在△ABC和△DEB中，已知AB=DE，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是（）A.BC=EC，∠B=∠EB. BC=ECC. BC=DC，∠A=∠DD.∠B=∠E，∠A=∠D8.如图，在△ABC中，AD是角平分线，AE是高，已知∠BAC=2∠B，∠B=2∠DAE，那么∠ACB为（）A. 80°B. 72°C. 48°D. 36°第7题第8题第10题9.若三角形的周长为18，且三边都是整数，则满足条件的三角形的个数有（）A、4个B、5个C、6个D、7个10.如图所示，点B、C、E在同一条直线上，△ABC与△CDE都是等边三角形，则下列结论不一定成立的是（）A.△ACE ≌△BCDB.△BGC ≌△AFCC.△DCG ≌△ECFD.△ADB ≌△CEA二、填空题（每题4分，共24分）11.已知三角形的三边长分别是3、x 、9，则化简135-+-x x = 12.如图，长方形ABCD 中(AD>AB)，M 为CD 上一点，若沿着AM 折叠，点N 恰落在BC 上，则∠ANB+∠MNC=___________13.如图，在△ABC 中，∠B=47°，三角形的外角∠DAC 和∠ACF 的平分线交于点E ，则∠AEC=______°BFB第12题 第13题 第16题14.在△ABC 中，AB=8，AC=6，则BC 边上的中线AD 的取值范围是 15.已知三条不同的直线a ，b ，c 在同一平面内，下列四个命题：①如果a ∥b ，a ⊥c ，那么b ⊥c ；②如果b ∥a ，c ∥a ，那么b ∥c ；③如果b ⊥a ，c ⊥a ，那么b ⊥c ；④如果b ⊥a ，c ⊥a ，那么b ∥C ．其中为真命题的是__________．(填写所有真命题的序号)16.在数学活动课上，小明提出这样一个问题：如图,∠B=∠C=900，E 是BC 的中点，DE 平分∠ADC ，∠CED=35°，，则∠EAB 是多少度？大家一起热烈地讨论交流，小英第一个得出正确答案，是______。

浙教版八年级数学上册第二章特殊三角形2.6《直角三角形》同步练习题一、选择题1．如果三角形的三个内角之比为1∶2∶3，那么这个三角形是(C)A．锐角三角形B．钝角三角形C．直角三角形D．锐角三角形或钝角三角形2．如图，在△ABC中，∠C＝90°，BD平分∠ABC，CD＝3，则点D到AB的距离是(C)A．5 B．4 C．3 D．2(第2题) (第3题)3．如图，图中直角三角形的个数为(D)A. 6B. 7C. 8D. 94．如图，CD是等腰直角三角形AB C斜边AB上的中线，DE⊥BC于点E，则图中等腰直角三角形的个数是(C)A．3 B．4 C．5 D．6(第4题) (第5题)5．如图，在△ABC中，AB＝AC，AD⊥BC于点D，E为AC的中点，AB＝6，则DE 的长是(B)A．2 B．3 C．4 D．2.56．把等边△ABC的一边AB延长一倍到点D，连结CD，则△ADC是(B)A．等腰三角形B．直角三角形C．等边三角形D．不能确定7．如图，在△ABC中，AB＝AC＝6，BC＝8，AE平分∠BAC交BC于点E，点D为AB的中点，连结DE，则△BDE的周长是(B)A．7＋ 5 B．10C．4＋2 5 D．12二填空题8．在△ABC中，∠A∶∠B∶∠C＝5∶2∶3，则△ABC是______三角形．9. 直角三角形斜边上的高与中线分别为5 cm和6 cm，则它的面积是_____cm2. 10．如图，在△ABC中，∠C＝90°，∠A＝45°，则△ABC是_______直角三角形．11．(1)在Rt△ABC中，∠C＝90°，∠A＝45°，则∠B＝________；(2)在Rt△ABC中，∠A＝90°，∠B＝30°，则∠C＝_________.(第12题)12．如图，在Rt△ABC中，∠ACB＝90°.(1)CD是斜边AB上的高线，则∠ACD＝_______，∠A＝_____；(2)若E是AB的中点，则图中的等腰三角形有____；(3)若CE＝3 cm，则AB＝______cm；(4)若∠A－∠B＝10°，则∠A＝_______．(第13题)13．如图所示，在Rt△ABC中，∠BAC＝90°，AB＝AC，AD是BC边上的高线，则∠BAD的度数是_____，∠C的度数是_____．若BC＝8 cm，则BD＝_____cm，AD ＝____cm.三、解答题14．如图，在Rt△ABC中，∠ACB＝90°，CD是AB边上的中线，过点D作DE⊥BC于点E，F是BD的中点，连结EF.求证：CD＝2EF.15．如图，在△ACB中，∠ACB＝90°，∠B＝30°.求证：AC＝12AB.(第16题)16．如图，在△ABC中，∠B＝∠C，AD是∠BAC的平分线，点E，F分别是AB，AC的中点，问：DE，DF的长度有什么关系？并说明理由．(第17题)17．如图，在△ABC中，AB＝AC，∠A＝90°，CD平分∠ACB，E在AC上，且AE＝AD，EF⊥CD交BC于点F，交CD于点O.求证：BF＝2AD.18．如图，在等腰Rt△ABC中，P是斜边BC上的中点，以P为顶点的直角的两边分别与边AB，AC交于点E，F，连结EF.当∠EPF绕顶点P旋转时(点E不与点A，B重合)，△PEF始终是等腰直角三角形，请你说明理由．(第18题)(第19题)19．如图，在△ABC中，∠ACB＝90°，AC＝BC，D为BC的中点，CE⊥AD于点E，BF∥AC交CE的延长线于点F.求证：AB垂直平分DF.参考答案：1.C 2.C 3.D 4.C 5.B 6.B 7.B8. 直角; 9. 30; 10. 等腰; 11. 45°, 60°; 12. ∠B，∠BCD, △ACE和△BCE,6，50°; 13. 45°,45°,4，414. 【解】在Rt△ABC中，∵∠ACB＝90°，CD是AB边上的中线，∴CD＝BD＝AD.∵F是BD的中点，∴EF是BD上的中线．又∵DE⊥BC，∴EF ＝12BD ＝12CD ， ∴CD ＝2EF.15. 【解】 作AB 边上的中线CD.∵∠ACB ＝90°，∴BD ＝CD ＝AD ＝12AB. 又∵∠B＝30°，∴∠BCD ＝∠B＝30°.∵∠ACB ＝90°，∴∠B ＋∠A＝90°，∠ACD ＋∠BCD＝90°，∴∠A ＝∠ACD＝60°.∵∠ADC ＝∠B＋∠BCD＝60°，∴∠A ＝∠ACD＝∠ADC，∴△ACD 是等边三角形．∴AC ＝CD ＝12A B. 16. 【解】 DE ＝DF.理由如下：∵∠B ＝∠C，∴AB ＝AC.又∵AD 平分∠BAC，∴AD ⊥BC ，∴△ABD ，△ACD 都为直角三角形．∵E ，F 分别为AB ，AC 的中点，∴DE ＝12AB ，DF ＝12AC ，∴DE＝DF.17. 【解】连结DF，过点D作DG⊥BC于点G. ∵∠A＝90°，AD＝AE，AB＝AC，∴∠ADE＝∠AED＝45°，∠B＝∠A CB＝45°，∴∠ADE＝∠B，∴DE∥BC，∴∠EDC＝∠BCD.∵CD平分∠ACB，∴∠BCD＝∠ACD，∴∠EDC＝∠ACD，∴DE＝EC.∵EF⊥CD，∴EF垂直平分CD.∴FD＝FC，∴∠FDC＝∠FCD.∴∠FDC＝∠ACD，∴DF∥AC.∴∠DFB＝∠ACB＝45°.∴∠B＝∠BFD＝45°，∴BD＝DF，∠BDF＝90°，∴△DBF为等腰直角三角形．∵DG⊥BF，∴DG为斜边BF上的中线，∴DG＝12BF.又∵CD平分∠ACB，∠A＝∠DGC＝90°，∴AD＝DG.∴AD＝12BF，即BF＝2AD.18. 【解】 连结PA.∵PA 是等腰Rt△ABC 底边上的中线，∴AP ⊥BC ，∠B ＝∠C＝45°.∴∠PAB ＝∠PAC＝45°.∴∠PAB ＝∠C.∵AP ⊥BC ，PE ⊥PF ，∴∠APE ＋∠APF＝∠APF＋∠CPF＝90°，∴∠APE ＝∠CPF.∵PA 是Rt△ABC 斜边上的中线，∴PA ＝12BC ＝PC. 在△PAE 和△PCF 中，∵∠PAE ＝∠C，PA ＝PC ，∠APE ＝∠CPF，∴△PAE ≌△PCF(ASA)，∴PE ＝PF.∴△PEF 始终是等腰直角三角形．19.【解】 ∵∠ACB＝90°，A C ＝BC ，∴∠CAB ＝∠CBA＝45°，∠CAD ＋∠CDE＝90°.∵CE ⊥AD ，∴∠CED ＝90°.∴∠CDE ＋∠DCE＝90°，∴∠CAD ＝∠DCE ，即∠CAD＝∠BCF. ∵BF ∥AC ，∴∠CBF ＋∠ACB＝180°，∴∠CBF ＝180°－∠ACB＝90°.∴∠CBF ＝∠ACD＝90°.在△ACD 和△CBF 中，∵⎩⎪⎨⎪⎧∠ACD＝∠CBF，AC ＝CB ，∠CAD ＝∠BCF，∴△ACD ≌△CBF(ASA)，∴CD ＝BF.∵D 为BC 的中点，∴CD ＝BD ，∴BD ＝BF. 又∵∠CBF＝90°，∴△DBF 为等腰直角三角形．∵BF ∥AC ，∴∠ABF ＝∠CAB＝∠DBA＝45°， ∴AB 是等腰Rt△DBF 的顶角平分线， ∴AB 垂直平分DF.。

2.6直角三角形（1）1、在△ABC中，∠C = 90º，∠A = 50º,则∠B的度数为（）A．50ºB．60ºC．30ºD．40º2、等腰直角三角形的一个底角的度数是（）A． B． C． D．3、直角三角形三条边长分别是5、12、13,则斜边上的中线长( )A.5B.6C.6.5D.124、若等腰三角形的顶角为，则它一腰上的高与底边的夹角等于（）A． B． C． D．5、如图，△ABC中，∠ACB=Rt∠，在AB上截取AE=AC，BD=BC，则∠DCE等于（）A、45°B、60°C、50°D、65°6、在△ABC中，∠C=90°，∠A =2∠B，则∠A= ，∠B= 。

7、直角三角形两锐角之差是12度，则较大的一个锐角是度。

8、在Rt△ABC中，∠C=90°，AB=15㎝，D是AB边的中点，则CD= 。

9、如图，Rt△ABC中，∠ACB=90°，AB=8cm，D为AB中点，DE⊥AC于E，∠A=30°，则BC= ，CD= ，DE= 。

10、等腰三角形的底角为15度，腰长为2a，则三角形的面积为。

11、△ABC中，∠C=90°，∠BAC=2∠B， AE平分∠CAB。

求证：AE=BE。

12、如图，在△ABC中，∠B=∠C，AD⊥BC于D，E为AC的中点，AB=6，求DE的长。

13、如图，等腰△ABC，AB=AC，∠C=30°，AB⊥AD,AD=2，求BC的长.14、如图，△ABC和△ABD中，∠ACB=∠ADB=Rt∠，E是BC边上的中点，求证：CE=DE15、阅读下面短文：如图1，△ABC是直角三角形，∠C=90°，现将△ABC补成长方形，使△ABC的两个顶点为长方形一边的两个端点，第三个顶点落在长方形这一边的对边上，那么符合要求的长方形可以画出两个：长方形ACBD和长方形AEFB（如图2）。

初中数学浙教版八年级上册2.6直角三角形（2）同步练习一、单选题（共9题；共18分）1・具备下列条件的三角形中，不是直角三角形的是（）A. Z A+Z B=Z CB. Z B=Z C= g Z AC. Z A=90β-Z B2.—个三角形的三个内角的度数之比为1: 2: 3,这个三角形一定是（）D. Z A-Z B=90oA •直角三角形B •锐角三角形 C.钝角三角形 D.无法判泄3•具备下列条件的AABC中，不是直角三角形的是（）A. Z A+Z B = Z CB. ZA = ZB = 2ZCC. Z A： Z B: Z C=I: 2： 3D.Z A=2Z B = 2Z C 4•在△ ABC 中, ZJ = Z3+ZC,则AABC 是（）A •钝角三角形B∙直角三角形 C.锐角三角形 D.无法确左5•已知△ ABC中，Z A=20o, Z B = 70o,那么AABC 是（）A •直角三角形B •锐角三角形 C.钝角三角形 D •正三角形6・如图，在AABC中，AB=AC, D是BC的中点，Z B=40∖则Z BAD=（）A.IOO0B. 80oC. 50oD. 40°7・如图，⅛Δ ABC中，BD=CD z AD丄BC,垂足为D, E是AC的中点.若AB二5,则DE的长为（）A. 2B. 2.5C.3D.48.如果一个三角形的三条髙的交点恰是三角形的一个顶点，那么这个三角形是（）A.锐角三角形B.钝角三角形C.直角三角形D.都有可能9.Δ ABC的内角分别为ZA, ZB, ZC,下列能判⅛Δ ABC是直角三角形的条件是（）A.ZA=2ZB = 3ZC B・ Z C=2Z B C. Z A： Z B: Z C = 3: 4： 5 D. Z A+Z B = Z C二、填空题（共3题；共3分）10.如图，处是△ ABC的角平分线，AD丄BC于点D ,若Z3JC = 128°, ZC = 36*.Z DAE__________ 度.AB二2,作AC的垂直平分线交AC, BC于点E, D,则BD的长12・如图,在Δ ABC中，Z ACB=90o.CD为AB边上的中线，若ZA=CG则Z BCD的度数为________________________ （用含α的代数式表示）・度为 _______三.解答题（共1题；共5分）13・证明：如果一个三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形.答案解析部分一、单选题1.【答案】D【考点】直角三角形的性质【解析】【解答】解：A// Z A+Z B=Z C,Z A+Z B+Z C=180o.∙. 2Z C=180°,解得Z 090°,此三角形是直角三角形，故本选项不符合题意；B.■/ Z B=Z C= gz A,.∙.设Z B=Z C=x,则Z A=2x.T Z A+Z B+Z C=180o,.∙. x+x+2x=180°,解得x=45°,Z A=2x=90o,此三角形是直角三角形，故本选项不符合题意；C.∙.∙ Z A=90o-Z B,.∙. Z A+Z B=90o,此三角形是直角三角形，故本选项不符合题意；D.,.∙ Z A-Z B=90°,.∙. Z A=Z B+90o,.∙.此三角形不是直角三角形，故本选项符合题意.故答案为D.【分析】根据宜角三角形的性质结合三角形内角和为180。

2.6 直角三角形（2） （巩固练习）姓名 班级第一部分1、如图1，△ABC 中，∠A BC=45°，AD 是高，点E 在AD 上，且∠BED=∠C.试说明BE=AC的理由.2、如图2，△ACB 、△ECD 都是等腰直角三角形，且C 在AD 上，AE 的延长线与BD 交于F.请你在图中找出一对全等三角形，并写出它们全等的过程．3、如图3,在44⨯方格中作以AB 为一边的Rt ΔABC,要求点C 也在格点上,这样的Rt ΔABC 能作出……………………………（ ）A. 2个B. 3个C. 4个D. 5个4、如图4所示，每个小方格都是边长为1的正方形，点A B ，是方格纸的两个格点（即正方形的顶点），在这个66⨯的方格纸中，找出格点C ，使ABC △的面积为1个平方单位的直角三角形的个数是 ．图2 图3 图4AB图1图8图9第二部分1. 在Rt ABC △中，BAC ∠=90°，AD ⊥BC 于D,则图中共有 个直角三角形.2. 在Rt ABC △中，BAC ∠=90°，若∠B=36°, 则∠C= 度.3.等腰直角三角形的底角等于 度.4. Rt △ABC 中，∠C=Rt ∠，∠A ∶∠B=2∶3，则∠A= 度.5.如图8，一块等腰直角的三角板ABC ，在水平桌面上绕点C 按顺时针方向旋转到A B C ''的位置，使A C B '，，三点共线，那么旋转角度的大小为．6. 如图9，B 、C 是河岸边两点，A 是对岸岸边一点，测得ABC ∠=ACB ∠=45°，BC=60米，则点A 到岸边BC 的距离是________米.7.如图10, 已知CD ∥AE, ∠DCA 与∠CAE 的平分线相交于点B.判断ABC △是否直角三角形,并说明理由.8.如图11,已知ABC △是等腰直角三角形,把ABC △绕点A 逆时针旋转成ADE △,连接DB.求∠BDE 的度数.图10图119.如图12,在ABC △中，AB AC ，BAC ∠=90°，AD 是∠BAC 的平分线,且AD=4,求ABC △的面积.图12参考答案第一部分AB1个单位的两条平行线上.答案：14第二部分图8图91. 在Rt ABC △中，BAC ∠=90°，AD ⊥BC 于D,则图中共有 个直角三角形.答案：32. 在Rt ABC △中，BAC ∠=90°，若∠B=36°, 则∠C= 度.答案：543.等腰直角三角形的底角等于 度.答案：454. Rt △ABC 中，∠C=Rt ∠，∠A ∶∠B=2∶3，则∠A= 度.答案：365.如图8，一块等腰直角的三角板ABC ，在水平桌面上绕点C 按顺时针方向旋转到A B C ''的位置，使A C B '，，三点共线，那么旋转角度的大小为．答案：135°6. 如图9，B 、C 是河岸边两点，A 是对岸岸边一点，测得ABC ∠=ACB ∠=45°，BC=60米，则点A 到岸边BC 的距离是________米.答案：307.如图10, 已知CD ∥AE, ∠DCA 与∠CAE 的平分线相交于点B.判断ABC △是否直角三角形,并说明理由.解：∵BA 平分∠CAE , BC 平分∠DCA , ∴∠BAC =12∠CAE , ∠BCA =12∠DCA . ∵CD ∥AE , ∴∠CAE +∠DCA =180°,∴∠BAC +∠BCA =90°, 即△ABC 是直角三角形.8.如图11,已知ABC △是等腰直角三角形,把ABC △绕点A 逆时针旋转成ADE △,连接DB.求∠BDE 的度数.图10图11解：∵△ABC 绕点A 逆时针旋转成△ADE , ∴∠DAE =∠ADE =45°, AD=AB .∴∠ADB =67.5°, ∴∠BDE =∠ADB -∠ADE =22.5°.9.如图12,在ABC △中，AB AC ，BAC ∠=90°，AD 是∠BAC 的平分线,且AD=4,求ABC △的面积.解：∵AB=AC , ∠BAC =90°, ∴∠B=∠C =45°.∵AD 是∠BAC 的平分线, ∴∠BAD =∠CAD =45°. ∴∠B=∠BAD =∠CAD =∠C =45°, ∴BD =AD=DC =4. ∴BC =8. ∴S △ABC =12BC ·AD =16.图12。

2.6 直角三角形一、选择题（共15小题；共75分）1. 如图，在△ABC中，∠ACB=90∘，CD⊥AB于点D，则图中直角三角形有( )．A. 0个B. 1个C. 2个D. 3个2. 如图，在Rt△ABC中，∠ACB=90∘，AB=10，CD是AB边上的中线，则CD的长是 ( )A. 20B. 10C. 5D. 523. 如图，△ABC中，∠ACB=90∘，AD=BD，且CD=4，则AB= ( )A. 4B. 8C. 10D. 164. 如图，在△ABC中，∠BAC=90∘，AD⊥BC于点D，DE⊥AB于点E，则图中与∠C相等的角有( )A. 1个B. 2个C. 3个D. 4个5. 如图，已知△ABC为直角三角形，∠C=90∘，若沿图中虚线剪去∠C，则∠1+∠2等于( )A. 315∘B. 270∘C. 180∘D. 135∘6. 把一块直尺与一块三角尺如图所示放置，若∠1=40∘，则∠2的度数为( )A. 125∘B. 120∘C. 140∘D. 130∘7. 若直角三角形的两条直角边的长分别为9 cm和12 cm，则斜边上的中线长为( )A. 4.5 cmB. 6 cmC. 7.5 cmD. 10 cm8. 如图，已知在Rt△ABC中，∠ABC=90∘，点D是BC边的中点，分别以B、C为圆心，大于线段BC长度一半的长为半径圆弧，两弧在直线BC上方的交点为P，直线PD交AC于点E，连接AB中，一定BE，则下列结论：① ED⊥BC；② ∠A=∠EBA；③ EB平分∠AED；④ ED=12正确的是 ( )A. ①②③B. ①②④C. ①③④D. ②③④9. 如图，CD是Rt△ABC斜边AB上的高，将△BCD沿CD折叠，B点恰好落在AB的中点E处，则∠A等于 ( )A. 25∘B. 30∘C. 45∘D. 60∘10. 如图，在Rt△ACB中，∠ACB=90∘,∠A=25∘，D是AB上一点，将Rt△ABC沿CD折叠，使B点落在AC边上的Bʹ处，则∠ADBʹ等于( )A. 25∘B. 30∘C. 35∘D. 40∘11. 如图，已知OP平分∠AOB，∠AOB=60∘，CP=2，CP∥OA，PD⊥OA于点D，PE⊥OB于点E．如果M是OP的中点，那么DM的长是( )A. 2B. √C. √3D. 2√312. 如图，已知点A(−1,0)和点B(1,2)，在坐标轴上确定点P，使得△ABP为直角三角形，则满足这样条件的点P共有 ( )A. 2个B. 4个C. 6个D. 7个13. 如图，在△ABC中，∠CAB=90∘，∠B<∠C，AD，AE，AF分别是△ABC的高、角平分线、中线．则∠DAE与∠FAE的大小关系是( )A. ∠DAE>∠FAEB. ∠DAE=∠FAEC. ∠DAE<∠FAED. 与∠C的度数有关，无法判断14. 如图，直角三角板的直角顶点落在直尺边上，若∠1=56∘，则∠2的度数为 ( )A. 56∘B. 44∘C. 34∘D. 28∘15. 如图，m∥n，直线l分别交m，n于点A、点B，AC⊥AB，AC交直线n于点C，若∠1=35∘，则∠2等于 ( )A. 35∘B. 45∘C. 55∘D. 65∘二、填空题（共15小题；共75分）16. 在Rt△ABC中，∠C=Rt∠，∠A=70∘，则∠B=．17. 在Rt△ABC中，锐角∠A=35∘，则另一个锐角∠B=18. 如图，有两个互相垂直的滑槽（滑槽宽度忽略不计），一根没有弹性的木棒的两端A，B能在滑槽内自由滑动，将笔插入位于木棒中点P处的小孔中，随着木棒的滑动就可以画出一个圆来．若AB=20 cm，则画出的圆的半径为 cm．19. 如图，将一副三角尺叠放在一起，使直角的顶点重合于点O，则∠AOC+∠BOD=．20. 已知一个直角三角形的两条直角边长分别为3 cm和4 cm，则这个直角三角形斜边上的高线长为cm，斜边上的中线长为cm．21. 在直角三角形中，斜边及其中线长之和为3，那么该三角形的斜边长为．22. 如图，在Rt△ABC中，∠ACB=90∘，BC=6，AC=8，分别以点A，B为圆心，大于线段AB长度一半的长为半径作弧，相交于点E，F，过点E，F作直线EF，交AB于点D，连接CD，则CD的长是．23. 如图，在△ABC中，∠ACB=90∘，CD是AB边上的高，则图中与∠A相等的角是．24. 如图，AB，CD相交于点O，AC⊥CD于点C．若∠BOD=38∘，则∠A=．25. 在△ABC中，2∠B=∠A+∠C，最小角∠A=30∘，最长边的中线为8cm，则最短边的长为cm．26. 如图，在Rt△ABC中，D，E为斜边AB上的两个点，且BD=BC，AE=AC，则∠DCE的大小为．27. 如图，直线m∥n，Rt△ABC的顶点A在直线n上，∠C=90∘．若∠1=25∘，∠2=70∘，则∠B=∘．28. 如图，△ABC中，CD⊥AB于D，E是AC的中点，若AD=6，CD=8，则DE的长等于．29. 如图，有一块含有60∘角的直角三角板的两个顶点放在矩形的对边上．如果∠1=15∘，那么∠2的度数是 .30. 已知边长为a的正三角形ABC，两顶点A、B分别在平面直角坐标系的x轴、y轴的正半轴上滑动，点C在第一象限，连结OC，则OC的长的最大值是．三、解答题（共5小题；共65分）31. 如图，在四边形ABCD中，∠ABC=∠ADC=90∘，M，N分别是AC，BD的中点，连接MN．Ⅰ试猜想MN与BD的位置关系，并证明你的结论．Ⅱ如果∠BCD=45∘，BD=2，求MN的长．32. 如图，O是等边三角形ABC内一点，∠AOB=110∘，∠BOC=α .将△BOC绕点C按顺时针方向旋转60∘得到△ADC，连接OD .Ⅰ求证：△COD是等边三角形．Ⅱ当α=150∘时，试判断△AOD的形状，并说明理由．Ⅲ探究：当α为多少度时，△AOD是等腰三角形?33. 如图，在Rt△ABC中，∠ACB=90∘，D是AB上一点，且∠ACD=∠B．求证：CD⊥AB．34. 如图，在Rt△ABC中，∠ACB=90∘，M是边AB的中点，CH⊥AB于点H，CD平分∠ACB．Ⅰ求证：∠1=∠2．Ⅱ过点M作AB的垂线交CD的延长线于点E，求证：CM=EM．35. 已知：如图，D为线段AB上一点（不与点A，B重合），CD⊥AB，且CD=AB，AE⊥AB，BF⊥AB，且AE=BD，BF=AD．Ⅰ如图 1，当点D恰是AB的中点时，请你猜想并证明∠ACE与∠BCF的数量关系；Ⅱ如图2，当点D不是AB的中点时，你在（1）中所得的结论是否发生变化，写出你的猜想并证明；Ⅲ若∠ACB=α，直接写出∠ECF的度数（用含α的式子表示）．答案第一部分1. D2. C3. B4. B5. B6. D7. C8. B9. B 10. D11. C 12. C 13. B 14. C 15. C第二部分16. 20∘17. 55 度18. 1019. 180∘20. 125；52 21. 222. 523. ∠BCD24. 52∘25. 826. 45∘27. 4528. 529. 15∘30.√3+12a第三部分31. （1） MN ⊥BD ．证明如下：连接 BM ，DM ．因为 ∠ADC =90∘，M 是 AC 的中点，所以 AC =2DM =2CM ．同理，AC =2BM =2CM ，所以 BM =DM ．因为 N 是 BD 的中点，所以 MN ⊥BD ．（2） 由（1），得 BM =CM ，DM =CM ，所以 ∠BCM =∠CBM ，∠DCM =∠CDM ．因为 ∠AMB 是 △BCM 的一个外角，所以 ∠AMB =∠BCM +∠CBM =2∠BCM ．同理，∠AMD =2∠DCM ．因为∠BCD=45∘，所以∠BCM+∠DCM=45∘．所以∠BMD=∠AMB+∠AMD=2(∠BCM+∠DCM)=90∘．所以△BMD是直角三角形．因为N是BD的中点，BD=1．所以MN=1232. （1）∵将△BOC绕点C按顺时针方向旋转60∘得到△ADC，∴CO=CD，∠OCD=60∘，∴△COD是等边三角形．（2）当α=150∘时，△AOD是直角三角形．理由如下：∵△BOC≌△ADC，∴∠ADC=∠BOC=α=150∘ .∵△COD是等边三角形，∴∠ODC=60∘，∴∠ADO=90∘，∴△AOD是直角三角形．（3）分类讨论：①要使AO=AD，需∠AOD=∠ADO .∵∠AOD=190∘−α，∠ADO=α−60∘，∴190∘−α=α−60∘，∴α=125∘ .②要使AO=OD，需∠OAD=∠ADO .可得2(α−60∘)=180∘−(190∘−α)，∴α=110∘ .③要使OD=AD，需∠OAD=∠AOD .可得2(190∘−α)=180∘−(α−60∘)，∴α=140∘ .综上所述，当α的度数为125∘或110∘或140∘时，△ABC是等腰三角形．33. ∵∠ACB=90∘，∴∠A+∠B=90∘．∵∠ACD=∠B，∴∠A+∠ACD=90∘ .∴∠ADC=90∘ .∴CD⊥AB．34. （1）因为∠ACB=90∘，所以∠BCH+∠ACH=90∘ .因为CH⊥AB，所以∠CAH+∠ACH=90∘，所以∠CAH=∠BCH .因为M是斜边AB的中点，所以CM=AM=BM，所以∠CAM=∠ACM .所以∠BCH=∠ACM .因为CD平分∠ACB，所以∠BCD=∠ACD，所以∠BCD−∠BCH=∠ACD−∠ACM，即∠1=∠2 .（2）因为CH⊥AB，ME⊥AB，所以ME∥CH，所以∠1=∠MED .因为∠1=∠2，所以∠2=∠MED，所以CM=EM .35. （1）猜想：∠ACE=∠BCF．证明：∵D是AB中点，∴AD=BD，又AE=BD，BF=AD，∴AE=BF．∵CD⊥AB，AD=BD，∴CA=CB．∴∠1=∠2．∵AE⊥AB，BF⊥AB，∴∠3=∠4=90∘．∴∠1+∠3=∠2+∠4．即∠CAE=∠CBF．∴△CAE≌△CBF．∴∠ACE=∠BCF．（2）∠ACE=∠BCF仍然成立．证明：连接BE，AF．∵CD⊥AB，AE⊥AB，∴∠CDB=∠BAE=90∘．又BD=AE，CD=AB，△CDB≌△BAE．∴CB=BE，∠BCD=∠EBA．在Rt△CDB中，∵∠CDB=90∘，∴∠BCD+∠CBD=90∘．∴∠EBA+∠CBD=90∘．即∠CBE=90∘．∴△BCE是等腰直角三角形．∴∠BCE=45∘．同理可证：△ACF是等腰直角三角形．∴∠ACF=45∘．∴∠ACF=∠BCE．∴∠ACF−∠ECF=∠BCE−∠ECF．即∠ACE=∠BCF．（3）∠ECF的度数为90∘−α．。

浙教版八年级数学上册第二章特殊三角形2.6《直角三角形》同步练习题一、选择题1．如果三角形的三个内角之比为1∶2∶3，那么这个三角形是(C)A．锐角三角形B．钝角三角形C．直角三角形D．锐角三角形或钝角三角形2．如图，在△ABC中，∠C＝90°，BD平分∠ABC，CD＝3，则点D到AB的距离是(C) A．5 B．4 C．3 D．2(第2题) (第3题)3．如图，图中直角三角形的个数为(D)A. 6B. 7C. 8D. 94．如图，CD是等腰直角三角形AB C斜边AB上的中线，DE⊥BC于点E，则图中等腰直角三角形的个数是(C)A．3 B．4 C．5 D．6(第4题) (第5题)5．如图，在△ABC中，AB＝AC，AD⊥BC于点D，E为AC的中点，AB＝6，则DE 的长是(B)A．2 B．3 C．4 D．2.56．把等边△ABC的一边AB延长一倍到点D，连结CD，则△ADC是(B)A．等腰三角形B．直角三角形C．等边三角形D．不能确定7．如图，在△ABC中，AB＝AC＝6，BC＝8，AE平分∠BAC交BC于点E，点D为AB的中点，连结DE，则△BDE的周长是(B)A．7＋ 5 B．10C．4＋2 5 D．12二填空题8．在△ABC中，∠A∶∠B∶∠C＝5∶2∶3，则△ABC是______三角形．9. 直角三角形斜边上的高与中线分别为5 cm和6 cm，则它的面积是_____cm2. 10．如图，在△ABC中，∠C＝90°，∠A＝45°，则△ABC是_______直角三角形．11．(1)在Rt△ABC中，∠C＝90°，∠A＝45°，则∠B＝________；(2)在Rt△ABC中，∠A＝90°，∠B＝30°，则∠C＝_________.(第12题)12．如图，在Rt △ABC 中，∠ACB ＝90°.(1)CD 是斜边AB 上的高线，则∠ACD ＝_______，∠A ＝_____；(2)若E 是AB 的中点，则图中的等腰三角形有____；(3)若CE ＝3 cm ，则AB ＝______cm ； (4)若∠A －∠B ＝10°，则∠A ＝_______．(第13题)13．如图所示，在Rt △ABC 中，∠BAC ＝90°，AB ＝AC ，AD 是BC 边上的高线，则∠BAD 的度数是_____，∠C 的度数是_____．若BC ＝8 cm ，则BD ＝_____cm ，AD ＝____cm.三、解答题14．如图，在Rt △ABC 中，∠ACB ＝90°，CD 是AB 边上的中线，过点D 作DE ⊥BC 于点E ，F 是BD 的中点，连结EF.求证：CD ＝2EF.15．如图，在△ACB 中，∠ACB ＝90°，∠B ＝30°.求证：AC ＝12AB.(第16题)16．如图，在△ABC中，∠B＝∠C，AD是∠BAC的平分线，点E，F分别是AB，AC的中点，问：DE，DF的长度有什么关系？并说明理由．(第17题)17．如图，在△ABC中，AB＝AC，∠A＝90°，CD平分∠ACB，E在AC上，且AE＝AD，EF⊥CD交BC于点F，交CD于点O.求证：BF＝2AD.18．如图，在等腰Rt△ABC中，P是斜边BC上的中点，以P为顶点的直角的两边分别与边AB，AC交于点E，F，连结EF.当∠EPF绕顶点P旋转时(点E不与点A，B重合)，△PEF始终是等腰直角三角形，请你说明理由．(第18题)(第19题)19．如图，在△ABC中，∠ACB＝90°，AC＝BC，D为BC的中点，CE⊥AD于点E，BF∥AC交CE的延长线于点F.求证：AB垂直平分DF.参考答案：1.C 2.C 3.D 4.C 5.B 6.B 7.B8. 直角; 9. 30; 10. 等腰; 11. 45°, 60°; 12. ∠B，∠BCD, △ACE和△BCE,6，50°; 13. 45°,45°,4，414. 【解】在Rt△ABC中，∵∠ACB＝90°，CD是AB边上的中线，∴CD＝BD＝AD.∵F是BD的中点，∴EF是BD上的中线．又∵DE⊥BC，∴EF＝12BD＝12CD，∴CD＝2EF.15. 【解】作AB边上的中线CD.∵∠ACB＝90°，∴BD＝CD＝AD＝12 AB.又∵∠B＝30°，∴∠BCD ＝∠B ＝30°.∵∠ACB ＝90°，∴∠B ＋∠A ＝90°，∠ACD ＋∠BCD ＝90°，∴∠A ＝∠ACD ＝60°.∵∠ADC ＝∠B ＋∠BCD ＝60°，∴∠A ＝∠ACD ＝∠ADC ，∴△ACD 是等边三角形．∴AC ＝CD ＝12A B. 16. 【解】 DE ＝DF.理由如下：∵∠B ＝∠C ，∴AB ＝AC.又∵AD 平分∠BAC ，∴AD ⊥BC ，∴△ABD ，△ACD 都为直角三角形．∵E ，F 分别为AB ，AC 的中点，∴DE ＝12AB ，DF ＝12AC ， ∴DE ＝DF.17. 【解】 连结DF ，过点D 作DG ⊥BC 于点G. ∵∠A ＝90°，AD ＝AE ，AB ＝AC ，∴∠ADE ＝∠AED ＝45°，∠B ＝∠A CB ＝45°，∴∠ADE ＝∠B ，∴DE ∥BC ，∴∠EDC＝∠BCD.∵CD平分∠ACB，∴∠BCD＝∠ACD，∴∠EDC＝∠ACD，∴DE＝EC.∵EF⊥CD，∴EF垂直平分CD.∴FD＝FC，∴∠FDC＝∠FCD.∴∠FDC＝∠ACD，∴DF∥AC.∴∠DFB＝∠ACB＝45°.∴∠B＝∠BFD＝45°，∴BD＝DF，∠BDF＝90°，∴△DBF为等腰直角三角形．∵DG⊥BF，∴DG为斜边BF上的中线，∴DG＝12 BF.又∵CD平分∠ACB，∠A＝∠DGC＝90°，∴AD＝DG.∴AD＝12BF，即BF＝2AD.18. 【解】连结PA.∵PA是等腰Rt△ABC底边上的中线，∴AP⊥BC，∠B＝∠C＝45°.∴∠PAB＝∠PAC＝45°.∴∠PAB＝∠C.∵AP⊥BC，PE⊥PF，∴∠APE ＋∠APF ＝∠APF ＋∠CPF ＝90°，∴∠APE ＝∠CPF.∵PA 是Rt △ABC 斜边上的中线，∴PA ＝12BC ＝PC. 在△PAE 和△PCF 中，∵∠PAE ＝∠C ，PA ＝PC ，∠APE ＝∠CPF ，∴△PAE ≌△PCF(ASA)，∴PE ＝PF.∴△PEF 始终是等腰直角三角形．19.【解】 ∵∠ACB ＝90°，A C ＝BC ，∴∠CAB ＝∠CBA ＝45°，∠CAD ＋∠CDE ＝90°.∵CE ⊥AD ，∴∠CED ＝90°.∴∠CDE ＋∠DCE ＝90°，∴∠CAD ＝∠DCE ，即∠CAD ＝∠BCF. ∵BF ∥AC ，∴∠CBF ＋∠ACB ＝180°，∴∠CBF ＝180°－∠ACB ＝90°.∴∠CBF ＝∠ACD ＝90°.在△ACD 和△CBF 中，∵⎩⎪⎨⎪⎧∠ACD ＝∠CBF ，AC ＝CB ，∠CAD ＝∠BCF ，∴△ACD ≌△CBF(ASA)，∴CD ＝BF.∵D 为BC 的中点，∴CD ＝BD ，∴BD ＝BF.又∵∠CBF ＝90°，∴△DBF为等腰直角三角形．∵BF∥AC，∴∠ABF＝∠CAB＝∠DBA＝45°，∴AB是等腰Rt△DBF的顶角平分线，∴AB垂直平分DF.。