燕山大学空间机构学作业PPT
- 格式:ppt
- 大小:3.81 MB
- 文档页数:25

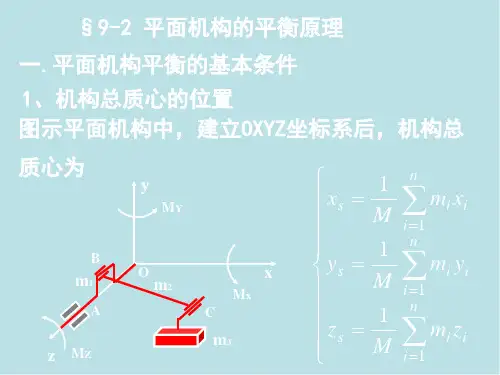



1. 机构简图X2. 计算机构自由度该机构是单环闭链空间机构,无公共约束,但是AB 杆两端都是球面副,存在一局部自由度。
自由度的计算如下所示:161331611pi t i F f f ==--=+++--=∑所以该机构的自由度为1。
3. 位移分析1).建立0AA 绕0B B 轴的转动方程010[][][]α-=-a u A A R A A100[][][][]α=-+a u A R A A A其中cos sin 0[]sin cos 0001ααααα-⎛⎫⎪= ⎪ ⎪⎝⎭a u R所以()cos sin 010cos []sin cos 000sin 1001011αααααα-⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪=+= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭A2).建立0BB 绕b u 轴的转动方程010[][][]β-=-b u B B R B B100[][][][]β=-+b u B R B B B100[]0cos sin 0sin cos βββββ⎛⎫⎪=- ⎪ ⎪⎝⎭b u R 所以()100022[]0cos sin 303cos 20sin cos 003sin ββββββ⎛⎫⎛⎫⎛⎫⎛⎫⎪⎪ ⎪ ⎪=-+= ⎪⎪ ⎪ ⎪⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭B3).建立连杆AB 的定杆长约束方程()211113[][][][]113--=--==T T B A B A B A B A l将矩阵[A]、矩阵[B]代入式(3)2cos [2cos ,3cos sin ,3sin 1]3cos sin 113sin 1ααβαββαβ-⎛⎫⎪----= ⎪ ⎪-⎝⎭整理得3sin 3cos sin 22cos ββαα+=+cos β=从动件0BB 的转角变化为:β=arcc 4. 速度分析1).建立A 点的速度方程0[][][][][]αα=-=- a u ua A w A A P A A , 其中010[]100000-⎛⎫⎪= ⎪ ⎪⎝⎭ua P所以()010cos sin []100sin cos 400000αααααα--⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪== ⎪⎪ ⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭A2).建立B 点的速度方程00[][][][][]ββ=-=- bb u u B w B B P B B , 其中000[]001010⎛⎫⎪=- ⎪ ⎪⎝⎭b u P()00000[]0013cos 3sin 50103sin 3cos ββββββ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪=-=- ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭B3).建立速度约束方程把式(4)和式(5)带入式(6)中得cos 2[sin ,cos 3sin ,3cos ]sin 3cos 013sin αααααββββαββ-⎛⎫⎪-+-⨯-= ⎪⎪-⎝⎭故3cos cos 2sin 3sin sin 3cos ααβααβαββ-=-式中10.628s α-=,22sin (1cos )os(3(sin 1)arcc ααβα-±=+ 5. 加速度分析1).建立A 点的加速度方程200[][][[[]][][]][]αααα=-=+- a a b u u u A w A A P P P A A , 式中010[]100000-⎛⎫⎪= ⎪ ⎪⎝⎭a u P ,0α=()2cos sin 70ααα-⎛⎫⎪=- ⎪⎪⎝⎭A2).建立B 点的加速度方程200[][][[[]][][]][]ββββ=-=+- b b b u u u B w B B P P P B B ,[][]0T AB A B --=其中000[]001010⎛⎫ ⎪=- ⎪ ⎪⎝⎭b u P ,得203cos 3sin (8)3cos 3sin ββββββββ⎛⎫ ⎪=-- ⎪ ⎪-⎝⎭B3).建立加速度约束方程[][][][]0(9)--+--= T T AB A B A B A B其中2222cos cos 2[][]sin 3cos 3sin sin 3cos 13sin 3sin 3cos TT A B A B αααααββββαββββββ⎛⎫--⎛⎫⎪ ⎪--=-++- ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭sin sin [][]cos 3sin cos 3sin 3cos 3cos TT A B A B ααααααββααββββββ-⎛⎫-⎛⎫⎪ ⎪--=++ ⎪⎪ ⎪ ⎪--⎝⎭⎝⎭可解到()2222222cos 3cos sin 3sin cos 3sin 9sin 9cos 96cos sin 103(cos sin sin 4sin cos )ααββαααββββββββαβαβββαβββ+++--++=--+ 式中22sin (1cos )arccos 3(sin 1)ααβα-±=+3cos cos 2sin 3sin sin 3cos ααβααβαββ-=-6. 编程#include <stdio.h> #include <stdlib.h> #include <math.h> #include <conio.h> #define pi 3.14159265float displacement (float a){floatc,b;c= (2*sin(a)*(1-cos(a))+sqrt(14+8*cos(a)-13*cos(a)*cos(a)))/(3*(1+sin(a)*sin(a)));if(c>=-1&&c<=1)b=acos(c);else b=4;return b;}float velocity (float a,float b){ float v;v=(3*0.628*cos(a)*cos(b))/(3*sin(a)*sin(b)-3*cos(b));return v;}float acceleration (float a ,float b,float b1){ float z;z=( 2*0.628*0.628*+3*b1*cos(b)*cos(a)+3*0.628*sin(a)*cos(b) +3*b1*sin(b)-9*b1*cos(b)*cos(b)-9*sin(b)*sin(b)+9*b1*b1)/(3*(cos(b)-sin(b)*sin(b)-4*sin(b)*cos(b)));return z;}main(){float a,b1,b2;int i;float b=0.0;clrscr();printf("\nAA1 Dispacement(rad)BB1Dispacement(rad)Velocity(rad/s)Acceleration(rad/s\n)");for(i=1;i<=360&&b!=4;i+=2){a=pi*i/180;b=displacement(a);b1 =velocity(a,b);b2=acceleration(a,b,b1);if(b!=4)printf("%8.4f%8.4f%8.4f%8.4f\n",a,b,b1,b2);} }。





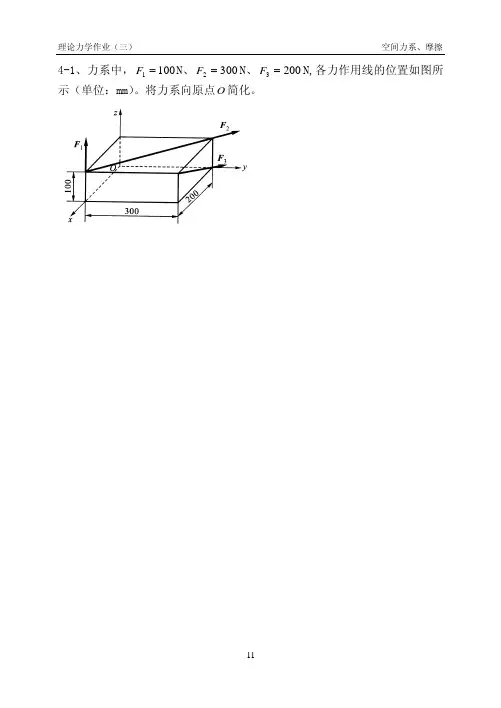
4-1、力系中,1001=F N、N、3002=F 2003=F N,各力作用线的位置如图所示(单位:mm)。
将力系向原点简化。
O4-2、水平圆盘的半径为r ,外缘处作用有已知力C F 。
力F 位于铅垂平面内,且与处圆盘切线夹角为,其他尺寸如图所示。
求力C o 60F 对z y x ,,轴之矩。
4-3、图示空间构架由三根无自重直杆组成,在端用球铰链连接,如图所示。
、D A B 和端则用球铰链固定在水平地板上。
如果挂在端的物重,试求铰链、C D KN 10=P A B 和的反力。
C4-4、图示六杆支撑一水平板,在板角处受铅直力F作用。
设板和杆自重不计,求各杆的内力。
4-5、无重曲杆有两个直角,且平面与平面垂直。
杆的端为球铰链支座,另一端受轴承支持,如图所示。
在曲杆的、BC 和CD 上作用三个力偶,力偶所在平面分别垂直于、和CD 三线段。
已知力偶矩和,求使曲杆处于平衡的力偶矩和支座反力。
ABCD ABC BCD D A AB AB BC 2M 3M 1M5-1、物重A KN 5=A P ,B 物重,物与KN 6=B P A B 物间的静滑动摩擦系数,1.01=s f B 物与地面间的静滑动摩擦系数2.02=s f ,两物体块由绕过一定滑轮的无重水平绳相连。
求使系统运动的水平力F 的最小值。
5-2、鼓轮B 重,放在墙角里,如图所示。
已知鼓轮与水平地板间的摩擦系数为0.25,而铅直墙壁则假定是绝对光滑的。
鼓轮上的绳索下端挂着重物。
设半径,N 500mm 200=R mm 100=r ,求平衡时重物的最大重量。
A5-3、均质圆柱重P 、半径为r ,搁在不计自重的水平杆和固定斜面之间。
杆端为光滑铰链,D 端受一铅直向上的力A F ,圆柱上作用一力偶,如图所示。
已知P F =,圆柱与杆和斜面间的静滑动摩擦系数皆为3.0=s f ,不计滚动摩阻,当时,045=αBD AB =。
求此时能保持系统静止的力偶矩M 的最小值。