abaqus有限元建模小例子

abaqus cae解析实例Abaqus CAE（Computer-Aided Engineering）是一个强大的有限元分析（FEA）软件，用于模拟复杂结构的力学行为。

以下是一个简单的Abaqus CAE分析实例，以演示如何使用该软件进行有限元分析。

假设我们要分析一个简单的悬臂梁在受到集中载荷作用下的弯曲行为。

1. 启动Abaqus CAE：打开Abaqus CAE软件，创建一个新的模型。

2. 创建几何体：在几何模块中，创建一个悬臂梁的几何体。

可以使用线、面、体等基本元素来构建。

3. 划分网格：在网格模块中，将悬臂梁划分为有限个小的元素，这些元素被称为“网格”或“有限元”。

可以选择不同的元素类型和大小来模拟悬臂梁的不同部分。

4. 应用材料属性：在材料模块中，为悬臂梁指定材料属性，如弹性模量、泊松比和密度等。

5. 定义载荷和边界条件：在载荷和边界条件模块中，定义悬臂梁受到的集中载荷以及支座的边界条件。

在这个例子中，可以在悬臂梁的末端施加一个集中力。

6. 选择分析类型：在分析类型模块中，选择静态分析类型。

因为我们要模拟的是恒定载荷下的弯曲行为，所以选择静态分析是合适的。

7. 运行分析：完成以上步骤后，运行分析。

Abaqus CAE将自动求解有限元方程，并输出结果。

8. 后处理：在后处理模块中，查看分析结果。

可以查看应力、应变、位移等结果云图和数据。

9. 优化设计：根据分析结果，优化悬臂梁的设计，例如改变梁的截面形状或材料属性等。

以上是一个简单的Abaqus CAE分析实例，通过这个实例可以了解如何使用该软件进行有限元分析。

当然，实际的分析可能会更加复杂，需要更多的步骤和考虑因素。

建议参考Abaqus CAE的官方文档和教程以获得更详细的信息和指导。

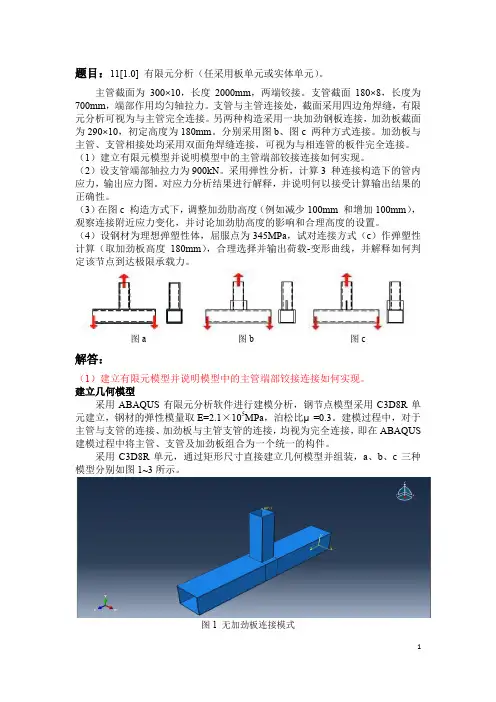
题目：11[1.0] 有限元分析（任采用板单元或实体单元）。

主管截面为300×10，长度2000mm，两端铰接。

支管截面180×8，长度为700mm，端部作用均匀轴拉力。

支管与主管连接处，截面采用四边角焊缝，有限元分析可视为与主管完全连接。

另两种构造采用一块加劲钢板连接，加劲板截面为290×10，初定高度为180mm。

分别采用图b、图c 两种方式连接。

加劲板与主管、支管相接处均采用双面角焊缝连接，可视为与相连管的板件完全连接。

（1）建立有限元模型并说明模型中的主管端部铰接连接如何实现。

（2）设支管端部轴拉力为900kN。

采用弹性分析，计算3 种连接构造下的管内应力，输出应力图。

对应力分析结果进行解释，并说明何以接受计算输出结果的正确性。

（3）在图c 构造方式下，调整加劲肋高度（例如减少100mm 和增加100mm），观察连接附近应力变化，并讨论加劲肋高度的影响和合理高度的设置。

（4）设钢材为理想弹塑性体，屈服点为345MPa，试对连接方式（c）作弹塑性计算（取加劲板高度180mm），合理选择并输出荷载-变形曲线，并解释如何判定该节点到达极限承载力。

图a 图b 图c解答：（1）建立有限元模型并说明模型中的主管端部铰接连接如何实现。

建立几何模型采用ABAQUS有限元分析软件进行建模分析，钢节点模型采用C3D8R单元建立，钢材的弹性模量取E=2.1×105MPa，泊松比μ=0.3。

建模过程中，对于主管与支管的连接、加劲板与主管支管的连接，均视为完全连接，即在ABAQUS 建模过程中将主管、支管及加劲板组合为一个统一的构件。

采用C3D8R单元，通过矩形尺寸直接建立几何模型并组装，a、b、c三种模型分别如图1~3所示。

图1 无加劲板连接模式图2加劲板纵向布置连接模式图3加劲板横向布置连接模式划分网格采用structured方式进行网格划分，划分精度为0.03，划分网格后的模型如图4~6所示。

本科生"工程软件及应用"大作业高速移动冲击内压下夹层圆柱壳的构造分析与设计XX：孙亚川〔学号：〕肖立〔学号：〕班级：力硕1101指导教师：周加喜学院：机械与运载工程学院XX大学2021.12大作业成绩高速移动冲击内压下夹层圆柱壳的构造分析与设计1前言脉冲爆震发动机〔Pause Detonation Engine，PDE〕是21世纪最有前途的革命性航空航天动力之一。

它是一种利用脉冲式爆震波产生推力的新概念发动机。

具有如下优点：①热循环效率高；②构造简单、重量轻、推重比大〔大于20〕以及比冲大〔大于2100s〕；③单位燃料消耗率低；④适用范围广；⑤工作范围广等。

对于此类发动机的工作原理国内外已经有了很多研究，但是对发动机构造强度、振动以及寿命技术研究却很少。

PDE的工作环境很特殊：高温〔2000-3000K〕、高压〔20-30atm〕、间歇性高速移动〔1500-3000m/s〕的热机冲击，为保证爆震燃烧室〔爆震管〕在如此恶劣的环境下要稳定、可靠的运行，其强度设计、减振降噪和寿命技术等都是关键课题。

多孔金属材料具有很多良好的性能：超轻、高比强度比刚度、高韧性耐冲击、高效散热隔热以及噪声管理等，尤其是通过合理设计材料微构造可以实现多功能集成。

用ABAQUS软件对多孔金属夹层圆柱壳及其等效模型在移动冲击内压作用下的构造响应进展分析。

比照两种模型在不同工况下的应变能、圆管跨中内、外面板的径向位移以及周向〔环向〕应力等响应，计算冲击内压的临界移动速度〔构造响应最大时的移动荷载冲击速度〕。

2分析模型2.1实际模型建模过程①部件：截面草图如图1图1截面草图三维拉伸壳模型如图2。

图2三维模型及材料方向②属性：设置并分配材料的弹性常数及密度。

赋截面属性时内外表的ShellOffset 设为Top surface，中间夹芯设为Middle surface，外外表设为Bottom surface，所得模型如图3。

线性静力学分析实例—-以悬臂梁为例线性静力学问题是简单且常见的有限元分析类型，不涉及任何非线性(材料非线性、几何非线性、接触等）,也不考虑惯性及时间相关的材料属性。

在ABAQUS 中,该类问题通常采用静态通用（Ｓta ｔi ｃ,Gen ｅr ａｌ)分析步或静态线性摄动(Sta ｔi ｃ,Ｌi ｎear p ｅrturbation ）分析步进行分析。

线性静力学问题很容易求解,往往用户更关系的是计算效率和求解效率，希望在获得较高精度的前提下尽量缩短计算时间，特别是大型模型。

这主要取决于网格的划分，包括种子的设置、网格控制和单元类型的选取。

在一般的分析中,应尽量选用精度和效率都较高的二次四边形/六面体单元,在主要的分析部位设置较密的种子；若主要分析部位的网格没有大的扭曲,使用非协调单元（如CPS4I 、C3D8Ｉ）的性价比很高.对于复杂模型，可以采用分割模型的方法划分二次四边形/六面体单元;有时分割过程过于繁琐，用户可以采用精度较高的二次三角形/四面体单元进行网格划分。

悬臂梁的线性静力学分析1。

1 问题的描述一悬臂梁左端受固定约束,右端自由,结构尺寸如图1—1所示,求梁受载后的Ｍises 应力、位移分布。

材料性质:弹性模量32e E =,泊松比3.0=ν均布载荷:Ｆ＝103N图1—1 悬臂梁受均布载荷图1.2 启动ＡB ＡQU Ｓ启动AB ＡＱUS 有两种方法,用户可以任选一种．（1）在Ｗin ｄow ｓ操作系统中单击“开始”—-“程序"——A ＢＡQU Ｓ 6.10-—AＢAQUS/ＣＡE。

（2）在操作系统的DOS窗口中输入命令:aｂaqｕs cａｅ。

启动ＡＢAQＵS／CAE后,在出现的Staｒt Sｅctioｎ（开始任务)对话框中选择Crｅate ModeｌDataｂａse。

1。

３创建部件在AＢAQUＳ／ＣAＥ顶部的环境栏中，可以看到模块列表：Module：Pａrt，这表示当前处在Part（部件)模块,在这个模块中可以定义模型各部分的几何形体。

基于ABAQUS软件环件冷轧三维有限元仿真建模分析引言：冷轧是金属制造过程中的重要工艺环节之一，通过冷轧可以改变金属材料的形状和性能，提高产品的质量和性能。

在冷轧工艺中，有限元仿真分析是一种常用的研究方法。

本文将基于ABAQUS软件环境，对冷轧过程进行三维有限元仿真建模分析。

首先介绍冷轧过程的基本原理，然后介绍ABAQUS软件环境及其在冷轧仿真中的应用，最后通过一个实例进行具体的仿真建模分析。

一、冷轧过程的基本原理冷轧是将热轧产生的热轧卷板进行再加工，使其通过冷变形和退火等工艺，获得更好的表面质量和机械性能。

冷轧过程通常包括以下几个步骤：1.卷取：将热轧卷板经辊道系统传送至轧机，进行裁剪和焊接，形成卷取材料。

2.进料：将卷取材料通过入口辊道装置，引入冷轧机。

3.冷轧：在冷轧机辊道系统中，通过辊轧将卷取材料冷变形。

4.处理：经过冷轧后，需要对材料进行切割、切边、去尾等处理。

5.包装：对处理后的材料进行包装，出厂运输。

冷轧过程的成功与否，关键取决于轧机辊道系统的设计和操作参数的选择。

有限元仿真分析可以为冷轧过程的优化设计和参数选择提供有效的支持。

二、ABAQUS软件环境及其在冷轧仿真中的应用ABAQUS是一种常用的商业有限元分析软件，它提供了强大的建模和分析功能，能够模拟各种工程问题。

在冷轧仿真中，ABAQUS可以用来建立三维有限元模型，通过数值计算得到轧机辊道系统的应力分布、变形量等重要参数。

ABAQUS在冷轧仿真中的应用主要包括以下几个方面：1.材料建模：ABAQUS提供了多种材料模型，可以根据所使用的金属材料性质进行选取。

通过材料模型的选取，可以对冷轧过程中的材料行为进行准确的描述。

2.辊道系统建模：轧机辊道系统是冷轧过程中的核心装置，其形状和参数会直接影响到冷轧效果。

在ABAQUS中，可以通过建立几何模型和定义辊道系统的运动参数来进行仿真分析。

3.边界条件设置：冷轧过程中，边界条件的设置对模拟结果的准确性和可靠性有重要影响。

abaqus经典例题集下面是一些abaqus的经典例题，以帮助大家更好地理解和掌握这款强大的有限元分析软件。

1.线性弹性问题例题1：在一个长方形平板上施加均匀分布的载荷，求解板的应力和应变。

解题步骤：-创建模型，定义几何参数和材料属性；-划分网格；-应用边界条件；-施加载荷；-求解；- 后处理，查看结果。

2.非线性问题例题2：一个简支梁在受力过程中，梁的横截面半径发生变化。

求解梁的挠度和应力。

解题步骤：-创建模型，定义几何参数、材料属性和边界条件；-划分网格；-应用材料的本构关系；-施加载荷；-求解；- 后处理，查看结果。

3.热力学问题例题3：一个平板在均匀温度差的作用下，求解热应力和温度分布。

解题步骤：-创建模型，定义几何参数、材料属性、边界条件和温度差；-划分网格；-应用热力学本构关系；-施加温度边界条件；-求解；- 后处理，查看结果。

4.耦合问题例题4：一个悬臂梁在受到弯曲应力和剪切应力的同时，还受到温度的变化。

求解梁的应力和温度分布。

解题步骤：-创建模型，定义几何参数、材料属性、边界条件、载荷和温度变化；-划分网格；-应用耦合场本构关系；-施加边界条件、载荷和温度边界条件；-求解；- 后处理，查看结果。

5.接触问题例题5：两个物体相互挤压，求解接触面上的应力和接触力。

解题步骤：-创建模型，定义几何参数、材料属性、边界条件和接触属性；-划分网格；-应用接触算法；-施加边界条件和接触力；-求解；- 后处理，查看结果。

通过以上五个经典例题的讲解，相信大家对abaqus的应用有了更深入的了解。

在实际应用中，我们应根据具体问题选择合适的分析类型，并灵活运用所学知识。

希望大家能在实践中不断提高，成为优秀的有限元分析工程师。

Abaqus是一款功能强大的有限元分析（FEA）软件，广泛应用于各种工程领域。

以下是一个简单的Abaqus仿真案例，演示了如何对一个简单的结构进行静态分析。

案例描述：
假设我们要分析一个简单的矩形板，其长度为1m，宽度为0.5m，厚度为0.01m。

该板材由线性弹性材料制成，其弹性模量为200GPa，泊松比为0.3。

分析步骤：
1.创建模型：在Abaqus中创建一个新的模型，并设置模型单位为m。

2.创建材料属性：在Abaqus中定义材料的弹性模量和泊松比。

3.创建网格：对模型进行网格划分，选择合适的网格大小和类型。

4.施加载荷和约束：在模型的边界上施加固定约束，并在上表面施加均匀分布
的载荷。

5.运行分析：进行静态分析，并查看分析结果。

分析结果：
通过查看分析结果，我们可以得到矩形板的应力分布和变形情况。

在本案例中，最大应力出现在矩形板的中心位置，其值为199.8MPa。

最大变形出现在矩形板的边缘位置，其值为0.002m。

结论：
本案例演示了如何使用Abaqus进行静态分析，并得到了矩形板的应力分布和变形情况。

通过调整材料属性和载荷条件，可以对不同结构的静态性能进行分析和优化。

ABAQUS有限元分析实例详解有限元分析（Finite Element Analysis，简称FEA）是一种工程分析方法，它将连续物体分割为无数个小的有限元单元，并在每个有限元上分别进行力学方程求解，最终得到整个物体的力学性能。

ABAQUS是目前使用最广泛的有限元分析软件之一，本文将详细介绍ABAQUS有限元分析的实例。

一、准备工作在进行ABAQUS有限元分析之前，首先需要准备以下工作：1.模型准备：将需要分析的物体建模为几何模型，并进行网格划分，划分成有限元单元，以便进行分析。

2.边界条件：设定物体的边界条件，即模拟施加在物体上的外力或约束条件，如支撑条件、加载条件等。

3.材料属性：设定物体的材料属性，包括弹性模量、泊松比等。

4.分析类型：选择适合的分析类型，如静态分析、动态分析、热分析等。

二、材料建模在进行ABAQUS有限元分析时，需要将材料的力学性质进行建模。

通常有以下几种材料建模方法：1.线弹性模型：认为材料的应力-应变关系在整个材料的应力范围内都是线性的，即满足胡克定律。

2.非线性弹性模型：考虑材料的应变硬化效应，即材料的刚度随加载的增加而增大。

3.塑性模型：考虑材料的塑性行为，在达到屈服点后，材料会发生塑性变形。

4.屈服准则模型：通过引入屈服准则，将材料的屈服破坏进行建模。

5.破坏模型：考虑材料的破坏行为，通常采用层间剪切应力、最大主应力等作为破坏准则。

三、加载和约束在进行ABAQUS有限元分析时，需要模拟实际工程中施加在物体上的外部载荷和约束条件。

常见的加载和约束方式有以下几种：1.固定支撑：将物体的一些边界固定，使其不能发生位移。

2.约束位移：设定物体一些节点的位移值，模拟实际固定住的情况。

3.压力加载：施加在物体上的压力载荷。

4.弯曲加载：施加在物体上的弯曲载荷。

5.温度加载：通过施加温度场来模拟温度载荷。

四、求解过程在进行ABAQUS有限元分析时，求解过程主要有以下几个步骤：1.指定分析步数：指定分析的总时间和分析步数，也可以根据需要进行自适应时间增量控制。

abaqus案例Abaqus是一款由法国达索系统公司开发的有限元分析软件。

它提供了强大的分析工具和高度可定制的建模环境，使工程师能够在各种领域进行准确的仿真分析。

在本文中，我们将介绍一些使用Abaqus的真实案例，以便更好地了解该软件的功能和应用。

1. 案例一：汽车碰撞分析汽车碰撞是交通事故中最常见的一种，也是最危险的一种。

利用Abaqus进行汽车碰撞仿真分析可以帮助工程师更好地理解碰撞过程和车辆的结构变形情况。

在这个案例中，我们将对一辆小型轿车进行碰撞测试。

首先，我们需要建立一个准确的车辆模型。

通过CAD软件，我们可以设计出车辆的外形，并将其导入Abaqus中。

接下来，我们需要添加材料属性和约束条件，以便对车辆进行仿真分析。

在这个案例中，我们使用了钢材作为车辆的材料，并设置了车辆的边界条件和碰撞速度。

通过Abaqus进行汽车碰撞仿真分析后，我们可以得到车辆在碰撞过程中的应力、应变和变形情况。

此外，我们还可以观察到车辆的安全性能和结构强度是否符合标准要求。

这些结果可以帮助汽车制造商更好地设计和改进汽车结构，以提高车辆的安全性能和耐用性。

2. 案例二：桥梁结构分析桥梁是重要的基础设施之一，其结构的稳定性和安全性对人们的出行和生活具有重要影响。

利用Abaqus进行桥梁结构分析可以帮助工程师更好地了解桥梁的结构特性和受力状态，以便更好地设计和改进桥梁结构。

在这个案例中，我们将对一座悬索桥进行分析。

首先，我们需要建立一个准确的桥梁模型，并添加材料属性和约束条件。

接下来，我们需要对桥梁进行荷载分析，以便了解桥梁在不同荷载下的受力状态和变形情况。

通过Abaqus进行桥梁结构分析后，我们可以得到桥梁在不同荷载下的应力、应变和变形情况。

此外，我们还可以观察到桥梁的结构稳定性和安全性能是否符合标准要求。

这些结果可以帮助桥梁工程师更好地设计和改进桥梁结构，以提高其安全性能和耐用性。

3. 案例三：电子设备热分析电子设备的热管理是一个重要的问题，因为过热会导致设备故障或损坏。

Abaqus有限元分析实例——非线性斜板这个例子如图8-11所示。

已经应用ABAQUS/Standard模拟了板的线性响应，现在你将应用ABAQUS/Standard对它进行重新分析，包含几何非线性的影响。

从线性模拟的结果表明对于此问题非线性的效应可能是重要的，由此次分析的结果，你将判断这个结论是否正确。

图8-11 斜板如果你愿意，可以根据本例题后面的指导，应用ABAQUS/Explicit将模拟扩展到动态分析。

在本手册的在线文档第 A.6节“Norlinear skew plate”提供了输入文件。

当通过ABAQUS/CAE运行这个输入文件时，将创建关于该问题的完整的分析模型。

根据下面给出的指导如果你遇到困难，或者如果你希望检查你的工作，则可以运行这个输入文件。

在附录A“Example Files”中，给出了如何提取和运行输入文件的指导。

如果你没有进入ABAQUS/CAE或者其它的前处理器，可以人工创建关于这个问题的输入文件，关于这方面的讨论，见Getting Started with ABAQUS/Standard：Keywords Version，第7.4节“Example：norlinear skew plate”。

8.4.1 修改模型打开模型数据库文件SkewPlate.cae，从主菜单栏中，选择Model-->Copy Model-->Linear，将名字为Linear的模型复制成名字为Nonlinear的模型。

对于非线性斜板模型，你将考虑包含几何非线性效应和改变输出要求。

定义分析步进入分析步Step模块，从主菜单栏中，选择Step-->Edit-->Apply Pressure来编辑分析步定义。

在Edit Step对话框的Basic页中，选中Nlgeom（注：几何非线性的缩写）以考虑几何非线性的效应，并设置分析步的时间周期为1.0。

在Incrementation （增量步）页中，设置初始增量步的值（initial increment size）为0.1。

1■应用背景概述随着科学技术的发展，汽车已经成为人们生活中必不可少的交通工具。

但当今由于交通事故造成的损失日益剧增，研究汽车的碰撞安全性能，提高其耐撞性成为各国汽车行业研究的重要课题。

目前国内外许多著名大学、研究机构以及汽车生产厂商都在大力研究节省成本的汽车安全检测方法，而汽车碰撞理论以及模拟技术随之迅速发展，其中运用有限元方法来研究车辆碰撞模拟得到了相当的重视。

而本案例就是取材于汽车碰撞模拟分析中的一个小案例 ----------------------------------- 保险杠撞击刚性墙。

2■问题描述该案例选取的几何模型是通过导入已有的*.IGS文件来生成的（已经通过Solidworks软件建好模型的），共包括刚性墙（PART-wall）、保险杠（PART-bumpe）、平板（PART-plane）以及横梁（PART-rail）四个部件，该分析案例的关注要点就是主要吸能部件（保险杠）的变形模拟，即发生车体碰撞时其是否能够对车体有足够的保护能力？这里根据具体车体模型建立了保险杠撞击刚性墙的有限元分析模型，为了节省计算资源和时间成本这里也对保险杠的对称模型进行了简化，详细的撞击模型请参照图1所示，撞击时保险杠分析模型以2000mm/s的速度撞击刚性墙，其中分析模型中的保险杠与平板之间、平板与横梁之间不定义接触，采用焊接进行连接，对于保险杠和刚性墙之间的接触采用接触对算法来定义。

1.横梁（rail）2.平板（plane）3保险杠（bumper）4.刚性墙（wall）图2.1碰撞模型的SolidWorks图为了使模拟结果尽可能真实，通过查阅相关资料，定义了在碰撞过程中相关的数据以及各部件的材料属性。

其中，刚性墙的材料密度为7.83 >10-9,弹性模量为2.07 >05,泊松比为0.28;保险杠、平板以及横梁的材料密度为7.83 >0-9, 弹性模量为2.07 >05,泊松比为0.28，塑形应力-应变数据如表2.1所示。

abaqus铰接经典案例
ABAQUS是一款强大的有限元分析软件，可以用于模拟各种复杂的机械系统，包括铰接结构。

以下是一个简单的ABAQUS铰接经典案例：
案例描述：
考虑一个简单的四连杆结构，其中包含两个相互铰接的杆件。

我们需要使用ABAQUS来模拟这两个杆件之间的铰接约束。

步骤：
1. 创建模型：在ABAQUS中创建一个新的模型，并设置模型的基本单位。

2. 创建材料：为每个杆件创建一个材料，并为其分配适当的弹性模量和泊松比。

3. 创建网格：对每个杆件进行网格划分，确保网格的大小和密度适合于模拟铰接约束。

4. 定义约束：在两个杆件之间的铰接点上定义约束。

在这个案例中，我们需要定义一个耦合约束，以确保两个杆件在铰接点上具有相同的旋转自由度。

5. 定义载荷和边界条件：根据实际情况定义适当的载荷和边界条件。

例如，如果有一个固定的杆件，则需要在该杆件的端部定义固定约束。

6. 运行模拟：运行模拟以计算模型的响应。

7. 结果分析：分析模拟结果，以了解铰接结构的性能和行为。

这个案例是一个简单的示例，用于说明如何使用ABAQUS模拟铰接结构。

在实际应用中，可以根据需要进行更复杂的建模和模拟。

工字型截面压弯构件有限元分析简例为了让初学者对ABAQUS软件建模有一个较为详细的认识，本实例取用的是受集中荷载的工字形压弯构件，以此构件进行ABAQUS有限元建模并进行简略分析。

1 问题描述图1-1所示Q235钢焊接工字形截面压弯构件，翼缘为火焰切割变，承受的轴线压力设计值为600kN，在构件的中央有一横向集中荷载150kN。

构件的梁端铰接并在中央有一侧向支撑点。

要求验算构件的整体稳定。

（《钢结构》P154，例6-2）图1-1附图2 启动ABAQUS/CAE启动ABAQUS/CAE，选择Create Model Database下的With Standard/Explicit Model，进入ABAQUS的主窗口进行创建新模型操作，如图所示。

图2-1 ABAQUS/CAE主窗口3创建部件3.1工字形梁在主窗口界面中的工具区找到并点击Create Part()命令，弹出如图所示的操作窗口。

构件名称（Name）建议修改成读者熟知的名称，以方便之后的操作。

这里笔者将其命名为“beam”。

这里要创建的是三维（3D）可变形（Deformable）实体（Solid）模型，三维构件由二维图形拉伸（Extrusion）形成Approximate size设置为和模型尺寸接近尺寸（这里设为1000）。

点击Continue 进入如图所示的操作界面。

图3-1创建部件对话框图3-2二维草图绘制界面点击Create LinesConnected()命令，按照所设计的柱尺寸画线。

在提示区的输入框内输入起始坐标（-125，380），回车或点击鼠标中键进行确认；按照以上方法依次输入坐标（-125,392），（125,392），（125,380），（6,380），（6,-380），（125,-380），（125,-392），（-125,-392），（-125,-380），（-6，-380），（-6,380），（-125,380），便画出工字形钢梁的横截面。

abaqus介绍_带⼩例⼦ABAQUS ⼊门教程1.什么是有限元对于连续的实体，或者流体，如果形状，边界条件较复杂，是不能得到位移或者应⼒应变的解析解的，因此提出了利⽤有限个单元（Finite Element）的集合来离散（Discretize）表⽰结构的实际⼏何形状，如下图，该实体由六⾯体单元和四⾯体单元(Element)组成，每⼀个单元代表这个实际结构的⼀个离散部分。

单元由节点构成，单元和单元之间通过共有的节点（Node）连接。

节点与单元的集合称为⽹格（Mesh）。

在⼀个特定⽹格中的单元数⽬称为⽹格密度（Mesh Density），可以很轻易地得到⽹格密度是和计算精度密切相关的，但是过密的⽹格会导致庞⼤的计算量，因此需要根据情况合理确定⽹格尺⼨。

各种单元类型，不同的单元类型适⽤于不同的情况。

有限元求解⽅法：隐式⽅法(Implicit)由胡克定理得：=-F Kx其中F代表⼒矩阵，K为刚度矩阵，由每个单元的局部刚度矩阵结合得到，x为位移矩阵，代表每个节点的各个⽅向的位移。

隐式⽅法主要就是求解该⽅程。

位移法步骤如下：1.结构离散2.单元分析，形成单元刚度矩阵3.结构分析，形成总刚度矩阵（包含所有单元刚度矩阵）4.约束处理5.求解线性⽅程组，求得节点位移（求得所有节点的位移）6.根据节点位移求出各个单元的内⼒和应变如下图所⽰，桁架及其离散化模型：显⽰⽅法（explicit）显⽰⽅法与隐式⽅法不同，例如应⽤在ABAQUS/Explicit中的显⽰⽅法，并不需要求解⼀套⽅程组或计算整体刚度矩阵。

求解式通过动态⽅法从⼀个增量步前推到下⼀个增量步得到的，简单来说，就是假设有⼀个炸弹爆炸的过程，将该过程分成很多个时间增量步，从初始炸弹只有⼀个点开始，根据增量步⼀步步递推计算炸弹的冲击波膨胀的过程。

ABAQUS/Explicit适⽤于求解复杂⾮线性动⼒学问题和准静态问题，特别是模拟短暂、瞬时的动态时间，如冲击和爆炸问题。

abaqus案例
Abaqus是一种广泛使用的有限元分析软件，用于模拟各种工程问题。

以下是一个关于抗风塔设计的Abaqus案例。

针对抗风塔的设计，需要进行结构分析来确定其承受最大风荷载
的能力。

这个案例使用了Abaqus这一强大的有限元分析工具，其中包
括了以下步骤：
首先，建立三维模型。

这个模型代表了一个矩形筒体形的抗风塔，其尺寸和几何形状与实际设计一致。

其次，定义材料性能。

结构材料
是铝合金，使用Abaqus的材料数据库来定义材料的应力-应变曲线。

接下来，设置边界条件。

在这个案例中，地面为固定边界，风荷
载通过侧面分布在塔身上。

对于风荷载，使用预定义的速度和压力分布，这相当于对风场进行了划分并进行平均计算。

完成了这些步骤后，可以进行结构稳态解的计算。

在这个阶段，Abaqus将使用所定义的材料和边界条件，对模型进行处理，来计算塔
结构的稳态响应和位移。

这个过程可以帮助我们确定抗风塔当前的承载能力及其弹性变形情况。

最后，我们可以将模型加入最大风荷载，以模拟超载情况下的反应。

这可以帮助确定抗风塔的耐久性，以及可能的破坏形式。

整个过程都可以通过Abaqus快速灵活地完成，它可以模拟出各种不同的条件下的结构响应，并且提供了极为详尽的计算结果。

这可以帮助设计人员更好地优化结构设计，并确保其能够承受最大的负载。