极小范数最小二乘解

解析线性方程组中的若干问题施妮沙【摘要】解线性方程组是线性代数课程的最重要内容之一,通过线性方程组的一般解析法对相容线性方程组进行了一般的介绍,用微积分方法给出不相容方程组的最小二乘解以及相容线性方程组极小范数解.循序渐进的对线性方程组的求解法进行了延伸.【期刊名称】《贵阳学院学报（自然科学版）》【年(卷),期】2013(008)001【总页数】3页(P28-29,33)【关键词】相容方程组;不相容方程组;极小范数解;最小二乘解【作者】施妮沙【作者单位】贵阳学院数学与信息科学学院,贵州贵阳550008【正文语种】中文【中图分类】O151线性代数是大学理、工、经济管理、医药、农业等学科必修的一门数学基础课，是除算术外，应用最为广泛的数学方法，它是从初等数学到高等数学学习的桥梁，对学生数学的学习起重要作用。

虽然这门课所安排的学时数不是太多，但其与微积分并驾齐驱的重要性已成为人们的共识。

线性代数在工农业生产实践中也有广泛应用，如钢板受力后的变形，大气的流场，都可以用若干个微分方程来描述。

通常对微分方程进行离散，得到线性方程组，再用数值方法求解。

在试验数据处理和曲线拟合问题中，在无法完全满足给定条件的情况下，求一个比较接近的解，最常用的方法是最小二乘法。

［1－3］通过介绍基础的线性方程组在求解中的如干问题，然后用微积分方法给出不相容方程组的最小二乘解，在介绍完以上两点后笔者再来讨论特殊情况下能否找到一组解向量使它在范数意义下长度是所有解向量中最短的，这就归结为求相容线性方程组的极小范数解。

在(*)式中系数矩阵、未知数向量和常数向量分别为:则方程组(*)也可表示为矩阵的形式:Ax= b (1)当向量b=0时线性方程组被称为齐次线性方程组，方程组(1)只有零解的充分必要条件是矩阵A的秩r(A)=R=n;有非零解的充分必要条件是矩阵A的秩r(A)=R＜n;其中n表示未知量个数，n－r是自由未知量个数。

特别地，当m=n(即方程个数与未知量个数相等)时，由Gramer［4］法则知(1)只有零解的充分必要条件为|A|≠0(r(A) =n)。

20世纪最好的十个算法( Computing in Science & Engineering 评选)1.1946.Los Alamos的Von Neumann,Stan Vlam,Nick Metropolis编的Metropolis算法,即Monte Carlo方法2.1947兰德公司的Grorge Dantzig创造的线性规划的单纯性算法3.1950.美国国家标准局数值分析所的Magnus Hestenes,Edward Stiefel, Cornelius Lanczos的Krylovz空间迭代法4.1951 橡树岭国家实验室的Alston Householder矩阵计算的分解方法5.1951 John Backus在IBM领导的小组研制的Fortron最优编译程序6.1959-61 伦敦的Ferranti Ltd的J.G.F.Francis的称为QR的算法的计算机本征值的稳定的算法7.1962London的Elliot Brothers Ltd的Tony Hoare提出的快速(按大小)分类法8.1965 IBM的Cooley与Princeton及Bell的Turkey的FFT算法9.1977 Brighham Young大学的Helaman Ferguson和Rodney Forcede的整数关系侦察算法10.1987 Yale的Leslie Greengard和Vladinimir Rokhlin发明的快速多级算法数值代数上课内容：一、预备知识（基础）1）误差分析2）范数理论3）初等变换与矩阵分解二、线性方程组的求解1）直接法2）迭代法3）最小二乘问题与矩阵广义逆三、矩阵特征值问题1）普通特征值问题a)幂法和反幂法b)QR方法2）对称特征值问题各部分的主要知识要点：（主要看上课笔记）一、预备知识（基础）§1 误差分析基本要求：1）了解数值代数的研究对象与特点及主要研究内容2）了解误差的基本知识及误差来源、误差种类3）了解浮点运算和舍入误差分析4）了解算法的评价及算法的向后稳定§2范数理论基本要求：1）熟练掌握向量范数的定义，会判断给定的某个函数是否是向量范数（范数的三个条件正定性、齐次性和三角不等式）2）了解常用向量范数、范数等价定理3）熟练掌握矩阵范数的定义，会判断给定的某个函数是否是矩阵范数（范数的三个条件正定性、齐次性和三角不等式）4）熟练掌握几个特殊的矩阵范数－算子范数、相容范数、酉不变范数的定义5）掌握常用矩阵范数1－范数，2－范数， －范数，F－范数的定义，并清楚且会证明它们分别属于算子范数、相容范数、酉不变范数的那一种范数6）会证明常用的范数不等式7）了解矩阵的谱和谱半径的定义二、初等变换与矩阵分解§1初等变换（主要看上课笔记）基本要求：1）了解初等变换的一般形式和一般初等变换的性质2）熟练掌握两种特殊的初等变换－Gauss消元变换、Household变换a)熟练掌握Gauss消元变换的定义和性质，特别是消元性质，会利用Gauss消元变换对向量进行消元b) 熟练掌握Householder变换/初等Hermit阵的定义和性质，特别是变换性质和消元性质，会利用Householder变换对向量进行消元，会求Householder变换矩阵3)熟练掌握Givens旋转变换的定义和性质，特别是消元性质即消元特点，会灵活运用Givens 旋转变换对向量进行消元（消调某一个变量）4）了解交换阵的定义即性质§2 矩阵分解1、基于Gauss消元阵的分解基于Gauss消元阵的分解，包括无主元LU分解、列主元LU分解、对称正定阵的Cholesky 分解基本要求：1）熟练掌握无主元LU分解的具体过程，会写出相应的程序，给定一个矩阵，会计算它的LU 分解矩阵2） 了解LU 分解的不稳定性和LU 分解的唯一性及存在条件det()0(1,2,,).1n n k k n A R D A k n A L U A LU ⨯∈=≠== 若阶方阵的顺序主子式则可唯一地分解为一个单位下三角阵和非奇异的上三角阵的乘积。

矩阵论线性空间定义：本质是个集合，满足一定条件下的集合。

首先定义了加法运算（满足加法的交换结合律），在这个集合中能找到零元素，与负元素；然后定义数乘运算（数域上的元素与集合当中的元素相乘），并且满足数乘的分配，结合律（集合中的元素能否进行乘法运算并没有定义）。

最后指出，这些运算都是封闭的，运算的结果与集合中的元素唯一对应。

称这样的一个集合为线性空间。

注意：运算结果与集合中的元素对应。

例如0*a=0（此零非彼零，不是数域里的零，而是线性空间当中的零，即集合当中的零元素<很可能不是零>）核空间：矩阵A对应于齐次线性方程组Ax=0的解空间。

子空间：线性空间对应集合的一个子集，并且也满足线性空间的定义的一个子集。

其中，零空间，与线性空间本身构成平凡子空间，还存在的其他子空间构成非平凡子空间。

矩阵A的核空间就是他的一个子空间，相当于对矩阵A构成的空间中的元素进行了限定。

矩阵A的列向量的线性组合构成了矩阵A的值域空间（其中的基为最大无关组的个数）。

注意：子空间交，与子空间的和任然为子空间，但子空间的并集不一定再是子空间。

属于两个子空间的线性无关的两个基的并基构成新的元素，但是这个元素不在属于原来的两个子空间的任意一个。

子空间中的几个等价定义：（1）直和定义为V1与V2的交空间只包含零元素（不一定是数字零），构成零子空间（2）直和空间中的元素表达式唯一。

（3）V1的基于V2的基直接构成直和空间的基。

（4）和空间的维度等于V1与V2维度的和。

线性映射性质：（1）V1的零元素经过线性映射变为V2的零元素（2）线性相关组经过线性映射之后任然为线性相关（3）线性无关组经过单射线性映射后任然为线性无关同构：两个线性空间之间存在一个一一对应的线性变换，则称这两个矩阵是同构的。

相应的线性变换称为同构映射。

任一线性空间都能够找到一个数域向量与其同构，这个向量就是坐标。

线性变换T的秩，线性映射的坐标表示：T表示线性空间到线性空间的映射，在具体的基底下（两个线性空间基都确定的情况），可以由一个矩阵A表示T，为V到V‘的线性映射。

最小二乘法（least sqauremethod）专栏文章汇总文章结构如下：1：最小二乘法的原理与要解决的问题2 ：最小二乘法的矩阵法解法3：最小二乘法的几何解释4：最小二乘法的局限性和适用场景5：案例python实现6：参考文献1：最小二乘法的原理与要解决的问题最小二乘法是由勒让德在19世纪发现的，形式如下式：标函数 = \sum（观测值-理论值）^2\\观测值就是我们的多组样本，理论值就是我们的假设拟合函数。

目标函数也就是在机器学习中常说的损失函数，我们的目标是得到使目标函数最小化时候的拟合函数的模型。

举一个最简单的线性回归的简单例子，比如我们有 m 个只有一个特征的样本： (x_i, y_i)(i=1, 2, 3...,m)样本采用一般的 h_{\theta}(x) 为 n 次的多项式拟合，h_{\theta}(x)=\theta_0+\theta_1x+\theta_2x^2+...\theta_nx^n,\theta(\theta_0,\theta_1,\theta_2,...,\theta_n) 为参数最小二乘法就是要找到一组\theta(\theta_0,\theta_1,\theta_2,...,\theta_n) 使得\sum_{i=1}^n(h_{\theta}(x_i)-y_i)^2 (残差平方和) 最小，即，求 min\sum_{i=1}^n(h_{\theta}(x_i)-y_i)^22 ：最小二乘法的矩阵法解法最小二乘法的代数法解法就是对 \theta_i 求偏导数，令偏导数为0，再解方程组，得到 \theta_i 。

矩阵法比代数法要简洁，下面主要讲解下矩阵法解法，这里用多元线性回归例子来描：假设函数h_{\theta}(x_1,x_2,...x_n)=\theta_0+\theta_1x_1+...+\t heta_nx_n 的矩阵表达方式为：h_{\theta}(\mathbf{x})=\mathbf{X}\theta\\其中，假设函数 h_{\theta}(\mathbf{x})=\mathbf{X}\theta 为 m\times1 的向量, \theta 为 n\times1 的向量，里面有 n 个代数法的模型参数。

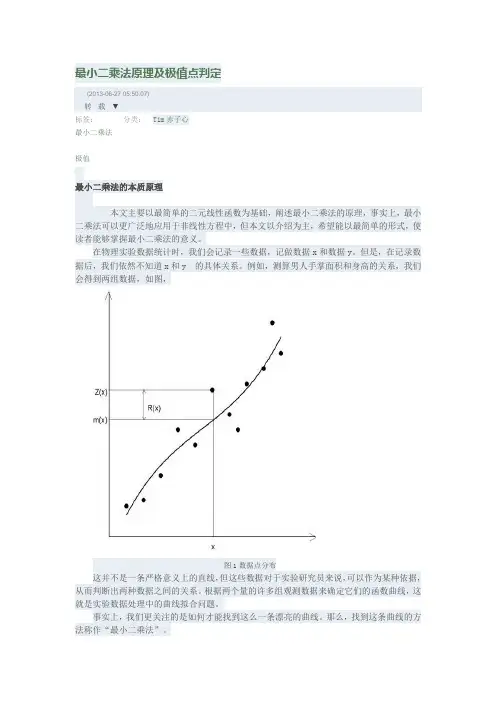
最小二乘法原理及极值点判定(2013-06-27 05:50:07)转载▼标签：最小二乘法极值分类：Tim赤子心最小二乘法的本质原理本文主要以最简单的二元线性函数为基础，阐述最小二乘法的原理，事实上，最小二乘法可以更广泛地应用于非线性方程中，但本文以介绍为主，希望能以最简单的形式，使读者能够掌握最小二乘法的意义。

在物理实验数据统计时，我们会记录一些数据，记做数据x和数据y。

但是，在记录数据后，我们依然不知道x和y 的具体关系。

例如，测算男人手掌面积和身高的关系，我们会得到两组数据，如图，图1数据点分布这并不是一条严格意义上的直线，但这些数据对于实验研究员来说，可以作为某种依据，从而判断出两种数据之间的关系。

根据两个量的许多组观测数据来确定它们的函数曲线，这就是实验数据处理中的曲线拟合问题。

事实上，我们更关注的是如何才能找到这么一条漂亮的曲线。

那么，找到这条曲线的方法称作“最小二乘法”。

曲线拟合中最基本和最常用的是直线拟合。

设x和y之间的函数关系由直线方程y=ax+b给出。

式中有两个待定参数，b代表截距，a代表斜率。

下面的问题在于，如何找到“最合适”的a和b使得尽可能多的数据落在或者更加靠近这条拟合出来的直线上。

即数据对这条直线的逼近程度最佳。

当然，当我们将直线拟合出来之后，就可以反过来进行预测了。

所以说最小二乘法是很有用的一种测算方法。

实际上，我们并不关心x和y到底是多少，因为x和y是给定的，当然x和y与其本质的内在关系之间肯定存在误差。

我们关心的是方程中的a和b，也就是说，在这个待定的方程中，a和b才是所求的变量，它们可以描述出x和y的关系。

所以我们接下来的任务就是找到一组最好的a和b。

我们对a和b的要求就是，使得所有x和y相对拟合直线的误差总和最小。

也就是说，我们要考虑的是，要使这些数据点距离拟合直线的和最小，距离最短，这样就可以使得尽可能多的数据成为有效点。

接下来我们的工作就是，最小化误差了。

文献综述信息与计算科学关于非齐次线性方程组Ax=b两类解法的对比矩阵理论既是学习经典数学的基础，又是一门最有实用价值的数学理论。

它不仅是数学的一个重要的分支，而且业已成为现代各科技领域处理大量有限维空间形式与数量关系的强有力的工具。

特别是计算机的广泛应用，为矩阵论的应用开辟了广阔的前景。

广义逆矩阵是对逆矩阵的推广。

若A为非奇异矩阵，则线性方程组Ax=b的解为x=A^(-1)b，其中A的A的逆矩阵A^(-1)满足A^(-1)A=AA^(-1)=I(I为单位矩阵)。

若A 是奇异阵或长方阵，Ax=b可能无解或有很多解。

若有解，则解为x=Xb+(I-XA)у，其中у是维数与A的列数相同的任意向量，X是满足AXA=A的任何一个矩阵，通常称X为A的广义逆矩阵，用A^g、A^-或A^(1)等符号表示，有时简称广义逆。

线性方程组的逆矩阵解法一般只适用于一种特殊情况,即适用于系数矩阵为方阵的时候，用于一般的线性方程组,可以应用矩阵的广义逆来研究并表示它的解而且与其它解法相比解的讨论更完整,表达形式更简洁系统本文探讨了线性方程组的广义逆矩阵解法。

对一般的线性方程组,可以应用矩阵的广义逆来研究并表示它的解而且与其它解法相比解的讨论更完整,表达形式更简洁系统。

本文通过运用相关定理，进行线性方程组的广义逆矩阵解法和初等矩阵法的对比。

这对于我们理解相关广义逆矩阵的应用会有帮助。

白素英（2010）在《关于非齐次线性方程组 A x=b两类解法的对比》一文中给出相容的非齐次线性方程组的两种不同的解法，即矩阵的初等变换法及广义逆矩阵法，并证明了两种方法通解的等价性，通过实例给出了惟一的极小范数解。

对于不相客的非齐次线性方程组，用广义逆矩阵法由实例给出了惟一的极小范数最小二乘解。

侯双根（1992）在《广义分块对角矩阵的广义逆矩阵》一文中对广义分块对角矩阵的广义逆矩阵给出了一个运算规则，并且利用它可以简化求广义分块对角矩阵的广义逆矩阵。

最小范数解和最小二乘解在数学和工程学中，最小范数解和最小二乘解是两个常用的概念。

它们在解决线性方程组和最优化问题时具有重要的意义。

最小范数解是指在所有解中，范数最小的解。

范数是一种度量向量或者矩阵大小的函数。

在线性代数中，常用的范数有L1范数、L2范数和无穷范数等。

对于给定的线性方程组Ax=b，如果存在一个向量x使得Ax=b成立，同时x的范数最小，那么x就是该线性方程组的最小范数解。

最小二乘解是指在所有解中，使得误差平方和最小的解。

在实际问题中，往往会遇到超定线性方程组，即方程组的未知数个数多于方程个数。

这时候，很可能无法找到一个精确的解使得方程组成立。

最小二乘解可以通过最小化误差平方和来找到一个最接近的解。

对于给定的超定线性方程组Ax=b，最小二乘解x可以通过求解最小化目标函数||Ax-b||2的优化问题得到。

最小范数解和最小二乘解在一些问题中具有相似的性质，但在某些情况下它们的解可能不同。

在实际应用中，最小范数解和最小二乘解都有广泛的应用。

例如，在信号处理中，最小范数解可以用于信号恢复和降噪；在图像处理中，最小范数解可以用于图像复原和去噪；在机器学习中，最小二乘解常用于线性回归和参数估计等问题。

最小范数解和最小二乘解的求解方法也有很多。

对于最小范数解，可以使用线性代数中的求解方法，如矩阵的奇异值分解（SVD）等。

对于最小二乘解，可以使用数值优化算法，如梯度下降法、牛顿法等。

这些方法可以有效地求解最小范数解和最小二乘解，并且在实际应用中具有较好的性能。

总结来说，最小范数解和最小二乘解是解决线性方程组和最优化问题中常用的概念。

它们在实际应用中具有广泛的应用价值，并且可以通过不同的数学方法和算法进行求解。

无论是在工程领域还是在科学研究中，了解和掌握最小范数解和最小二乘解的概念和求解方法都是非常重要的。