当前位置：文档之家 › 《电路理论》第三章ppt课件

《电路理论》第三章ppt课件

  • 格式：ppt
  • 大小：1.92 MB
  • 文档页数：62

下载文档原格式

  / 62

合集下载

电路理论课件

电路理论课件


(5) 校核：选一新回路。
例2. 用回路法求含有受控电压源电路的各支路电流。
1
2
① 将看VCVS作独立源建立方程；
I1+ 2V
_
I2 I3
Ia 3
U2 +
Ib
将②代入①，得
I4 1
+ –3U2
Ic
I5 ② 找出控制量和回路电流关系。
2 解： ①
4Ia-3Ib=2 -3Ia+6Ib-Ic=-3U2
第三章 线性网络的分析方法
目录
3.1 支路电流法和支路电压法 3.2 网孔分析法 3.3 节点分析法 3.4 网络拓扑的概念 3.5 割集分析法 3.6 电路的计算机辅助分析法
第三章 线性网络的分析方法
掌握支路电流法 和支路电压法 重点掌握网孔（电流）分析法 重点掌握节点（电压）分析法 了解网络拓扑的基本概念
1. 对每一支路假设一未 知电流（I1--I6）
2. 列电流方程 对每个节点有
I 0
3. 列电压方程 对每个回路有
E U
4. 解联立方程组
b I2
列电流方程
I1 a
I6 R6
I3 I4
d
+E3
R3
节点数 N=4 支路数 B=6
c I5
节点a： I3 I4 I1 节点b： I1 I6 I2
-Ib+3Ic=3U2
U2=－3（Ia － Ib）
4Ia-3Ib=2
解得
③ -12Ia+15Ib-Ic=0
9Ia-10Ib+3Ic=0
Ia=1.19A
Ib=0.92A Ic=-0.51A
各支路电流为：
I1= Ia=1.19A, I2= Ia- Ib=0.27A, I3= Ib=0.92A,
中南 电路理论基础课件 电路第3章

中南 电路理论基础课件 电路第3章


P发=715 W
a I1 R1 US1 + – I2 R2 + I3 R3 b
PR 1吸=R1I12=100 W PR 2吸=R2I22=15 W PR 3吸=R3I32=600 W
01:44:50
US2
–
16
支路中含有无伴电流源的情况 例2
I1 支路电流未知数共5个，I3为已知：
a I2
R1 b I5 R2
基本思想： 以假想的网孔电流为未知量，列写电路方程分析电 路的方法。求出网孔电流，则可得各支路电流。 a
i1 R1
uS1 +
–
i2 R2 im1 + uS2 –
im2 uS3
i3 R3
图示的两个网孔即是一组独立回 路，网孔电流分别为im1、 im2 支路电流可由网孔电流求出 i1= im1，i2= im1- im2， i3= im2
im2
uS3
R3 +
–
标准形式
b R11=R1+R2 —网孔1的自电阻。等于网孔1中所有电阻之和。 R22=R2+R3 —网孔2的自电阻。等于网孔2中所有电阻之和。 R12= R21= –R2 :网孔1、网孔2之间的互电阻。当两个网孔电流 流过相关支路方向相同时，互电阻取正号；否则为负号。 us11= uS1-uS2 —网孔1中所有电压源电压的代数和。 us22= uS2 –uS3 —网孔2中所有电压源电压的代数和。
uS1 R6
#2
R2
#1
#3
R5
R5
R6
#2
R4
+ uS5 _
R3
R4
+ uS5 _
R3
平面电路：可以画在平面上,不出现支路交叉的电路。
电工学第三章三相交流电ppt课件

电工学第三章三相交流电ppt课件

结论：电源 Y形联结时, 线电压Ul 3UP, 且超 前相应的相电压 30 , 三相线电压也是对称的 。
6
3.1.2 三相电路中负载的联结方法
1. 三相负载
分类
三相负载：需三相电源同时供电
负载
三相电动机等
单相负载：只需一相电源供电
照明负载、家用电器
对称三相负载：ZA=ZB= ZC
三相负载
如三相电动机
此时负载中性点N´即为 A, 因此负载各相电压为 N
UA 0 , UA 0
B
UB UB A, UB 380 V UC UC A , UC 380 V C
+
U A
iA
iC
– –
N´
–
iB
+ U C U B +
此情况下，B相和C相的电灯组由于承受电压上所加 的电压都超过额定电压（220V) ，这是不允许的。
(2) 相UA电B=流UBC=UIIICABCABCA=UUUUZZZClCAABB=AABBCCUP
A
+–
U AB
– U CA
B U+ BC C–
+
IB IC
ICA
ZCA
IAB
ZBC ZAB
IBC
相电流： 线电流：
IIAA、B、IIB、BC、IC ICA
线电流不等于相电流
20
(3) 线电流
IA IAB ICA
16
(2) A相断路
A
1) 中性线未断
B、C相灯仍承受220V N
电压, 正常工作。
2) 中性线断开
B
变为单相电路，如图(b) C 所示, 由图可求得
I UBC 380 12 .7 A RB RC 10 20
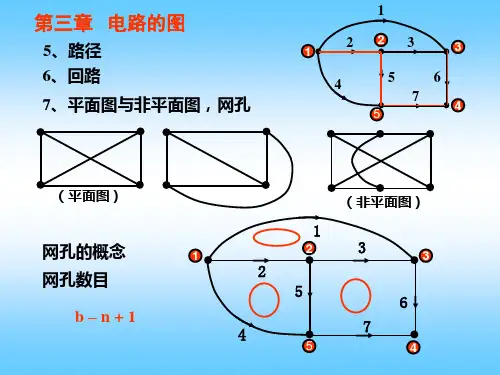
电路理论(邱光源)第三章ppt

电路理论(邱光源)第三章ppt


注：不能根据 不能根据KCL检验计算结果 根据 检验计算结果
支路电流法
以支路电流为求解对象，直接根据 以支路电流为求解对象，直接根据KCL和KVL建立 和 建立 方程。将以支路电流表示支路电压的支路方程代入KVL 方程。将以支路电流表示支路电压的支路方程代入 方程。 方程。
∑ ik = 0
I1
∑Rkik= ∑uSk
3-6
节点电压法
节点电压
3-6-1
节点电压法是以n-1个节点到参考节点的电压为求解对 节点电压法是以 个节点到参考节点的电压为求解对 根据KCL建立方程（支路电流要用节点电压表示）。 建立方程（ 象，根据 建立方程 支路电流要用节点电压表示）。 3-6-2 节点电压方程
（1） ） i6 R2 R1 R6 i2 （2） ） i3 R3 R5 R5 R4 i4 i5 （3） ）
例
回路电流法
−
3-5-2 回路电流方程 写出图示电路的回路 电流方程。 电流方程。
us
+
R6
R1 R5
R2
i1
R3
i2
(R1+R5+R4+R7)i1+(R4+R5)i2 – R4i3+(R4+R7)i4=uS (R4+R5)i1+(R2+R4+R5+R8)i2 −(R4+R8)i3+R4i4= – R8iS
第三章 电路的图
5、路径 、 6、回路 、 7、平面图与非平面图，网孔 、平面图与非平面图，
1
1 2 4
5 2
3 5 7 6
3
4
平面图） （平面图）
非平面图） （非平面图）
电路理论(新教材第3章)

电路理论(新教材第3章)

φ2 x– +14A
φ1
–
R1 12V + – R3
+
R2 φ3
+ –
0.5Vx R4
Vy
0.2Vy
φ4
例5
设网络的结点方程为： 设网络的结点方程为：
4 2 1 1 1 0 5 3 2 = 0 4 3 8 3 2
试给出该节点电压方程对应的最简电路图。 试给出该节点电压方程对应的最简电路图。 将系数矩阵不对称的方程调整为系数矩阵对称的方程。 解：将系数矩阵不对称的方程调整为系数矩阵对称的方程。
a i1 R1 uS1 + – i2 R2 il1 + uS2 – b i3 il2 R3 (R1+ R2) il1-R2il2=uS1-uS2 - R2il1+ (R2 +R3) il2 =uS2
代入支路特性（将支路电流用结点电压表示）： 代入支路特性（将支路电流用结点电压表示）： un1 un2 un1 un2 un1 un2 + + + = iS1 iS2 + iS3 R1 R2 R3 R4
un1 un2 un1 un2 un2 + = iS3 R3 R4 R5
un1 un2 un1 un2 un1 un2 + + + = iS1 iS2 + iS3 R1 R2 R3 R4
iS3 1 i3 i4 R4 0 R3 un2 2 i5 R5
令: Gk=1/Rk，k=1, 2, 3, 4, 5 上式简记为
iS1
i1 R1
i2 iS2 R2
G11un1+G12un2 = iSn1 G21un1+G22un2 = iSn2
《电路理论基础》课件

《电路理论基础》课件

详细描述
零输入响应是指没有外加激励信号时，电路的初始状态对时间的变化规律；零状态响应 则是电路在初始时刻为零状态下，外加激励引起的响应。这两种响应是分析一阶动态电
路的基本方法。
一阶动态电路的冲激响应和阶跃响应
总结词
描述冲激响应和阶跃响应的特点
详细描述
冲激响应是指一阶动态电路在单位冲激函数激励下的输 出响应，其特点是响应瞬间达到最大值并随后迅速衰减 至零；阶跃响应则是激励为阶跃函数时的输出响应，其 特点是响应在激励发生后缓慢变化至稳态值。这两种响 应对于理解和分析一阶动态电路具有重要意义。
02
电路分析基础
电路分析的基本概念
总结词
理解电路的基本构成和元件
详细描述
介绍电路的基本构成，包括电源、电阻、电容、电感等元件，以及它们在电路中的作用和工作原理。
电路分析的基本定律
总结词
掌握基尔霍夫定律和欧姆定律
详细描述
介绍基尔霍夫电流定律和电压定律，以及欧姆定律，说明这些定律在电路分析中的重要性和应用。
总结词
描述一阶动态电路的数学模型
详细描述
一阶动态电路的微分方程是描述电路 中电压或电流随时间变化的数学模型 ，通常表示为RC电路的V(t) = V0*(1exp(-t/RC))或RL电路的i(t) = i0*(1exp(-t/RL))。
一阶动态电路的零输入响应和零状态响应
总结词
解释零输入响应和零状态响应的概念
电路分析的基本方法
总结词
掌握等效变换、支路电流法、节点电压法等基本分析方法
详细描述
介绍等效变换、支路电流法、节点电压法等基本分析方法， 以及如何运用这些方法进行电路分析和计算。
03
线性电阻电路分析
电路第三章高等教育出版社

电路第三章高等教育出版社


连支数： bl b bt b n 1
第3-12页
■
二、KCL、KVL的独立方程数
1.独立方程组（线性无关）
(1)组中方程不能由其余方程组合得到； (2)方程组包含全部有关变量。
2.KCL独立方程数
n个结点的电路，独立的KCL 方程为n-1个，其对应的n-1个 结点称为独立结点。
第3-13页
KVL : uk 0 VCR : uk f (ik ) KCL : ik g(ilk )
KVL : f [g(ilk )] 0
uk f [g(ilk )]
第3-31页
■
2.回路电流方程的标准形式
a
i1
i2
R1
R2
+ il1 + il2
uS1
uS2
–
–
b
i3 KVL: u1 u2 , u2 u3 R3 VCR : u1 R1i1-uS1
假想的一组沿独立回路，按指定 绕向流动的电流 il ，b-n+1个。 网孔电流也是一组独立变量。
63
2
1
1
4
32 5
i1= -il1 i2=il1-il3 i3=il1-il2
i4=il2-il3 i5=il2 i6=il3
第3-29页
■
结点电压
任选一结点作为参考结点，其它
结点到参考结点的电压un ，n-1个。 参考方向：独立结点恒为正，参


b 个方程

b个支路电流
支路电压法

KVL
b
uk＝0
b-(n-1)个方程


KCL(VCR)
k=1
《电路理论基础》学习指导(李晓滨) 第3章.ppt

《电路理论基础》学习指导(李晓滨) 第3章.ppt

第3章 线性电阻电路的一般分析法
第3章 线性电阻电路的一般分析法
3.1 内容提要 3.2 重点、难点 3.3 典型例题 3.4 习题解答
第3章 线性电阻电路的一般分析法
3.1 内容提要
1. KCL、KVL方程的独立性 图：点与线的集合。 电路的图：每一支路用一“线段”表示，每一节点用 一“点”表示。 回路：一个路径的起点和终点为同一点。 平面电路：若一个电路可画在一个平面上，且在非节 点处不相交，则称之为平面电路，否则为非平面电路。 网孔：内部不含其他支路的回路。
含电流源、受控源电路网孔电流方程的列写： (1) 当电路中含有理想电流源时，尽可能使电流源的电 流成为网孔电流，这样，网孔电流就成为已知量，可以不用 列该网孔的网孔方程； (2) 当电流源的电流不能成为网孔电流时，设该电流源 的两端电压为u ， 再列一个该电流源支路的补充方程。 (3) 当电路中含有受控源时，将受控源当作独立源用上 述(1)、(2)同样的方法列方程，然后列一个有关控制量的补 充方程。
第3章 线性电阻电路的一般分析法 解 选取网孔电流im1、im2、im3， 列网孔电流方程:
(R1 R2 R3)im1 R3im2 R2im3 us3 R3im1 (R3 R4 R5)im2 R4im3 us3 R2im1 R4im2 (R2 R4 R6 )im3 us6
第3章 线性电阻电路的一般分析法 2. 节点分析法 若电路的节点数为n，则独立的节点数为n-1。只含电 阻和电流源的电路的节点方程为
G11un1 G12un2
G21un1
G22un2
G u 1(n1) n(n1) is11 G u 2(n1) n(n1) is22
G u G u G u i (n1)1 n1
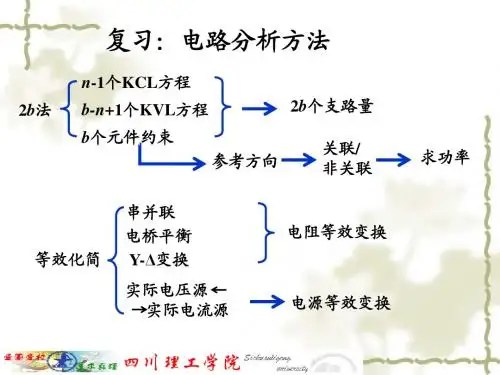
电路第3章ppt课件

电路第3章ppt课件


(n − 1)
b − (n − 1)
说明： 3、说明：
(1) KVL:
树支数 独立方程数
(n − 1)
连支数 独立回路数
b − (n − 1)
单连支回路组
b-(n-1) 个
独立回路：每个回路至少有一条新支路 独立回路： 平面图上的全部网孔是一组独立回路 平面图上的全部网孔是一组独立回路 (2) KCL: 独立方程数 n -1 单树支割集组
复习： 复习：电路分析方法
n-1个KCL方程 个 方程 2b法 法 b-n+1个KVL方程 个 方程 b个元件约束 个元件约束 参考方向 串并联 电桥平衡 Y-∆变换 变换 实际电压源 实际电流源 2b个支路量 个支路量 关联/ 关联 非关联 求功率
电阻等效变换
等效化简
电源等效变换
第三章 电阻电路的一般分析
2
基本回路: 基本回路:
只含一条连支的回路称为单连支回路 单连支回路， 只含一条连支的回路称为单连支回路，它们的总和为 一组独立回路 称为“基本回路” 树一经选定， 独立回路， 一组独立回路，称为“基本回路”。树一经选定，基本回路 唯一地确定下来。 唯一地确定下来。 基本回路数( 基本回路数(组)
3-3、支路电流法
A
I6 I5
I1+I3+I6=0 -I1+I2=0 -I3+I4+I5=0 I5+I6+I7=0 U1+U2-U3-U4=0 U3-U5-U6=0 U4+U5-U7=0
I1
R1
I3
R3
R6
U1=R1I1 U2=US U3=R3I3 U4=R5I5 U5=R5I5 U6=R6I6 U7=R7I7 尝试用支路电流表示支路电压
高等教育出版社《电路(第五版)》第三章课件

高等教育出版社《电路(第五版)》第三章课件


如把结点移去，则应把与它联接的全部支路同时移去。 c. 如把结点移去，则应把与它联接的全部支路同时移去。 支路的端点必须是结点，但结点则允许是孤立结点。 支路的端点必须是结点，但结点则允许是孤立结点。
上 页 下 页
3.2 KCL和KVL的独立方程数 和 的独立方程数
1. KCL的独立方程数 的独立方程数
7 I1 − 11I 2 + 6 − 70 = 0
11I 2 + 7 I 3 − 6 = 0
解得 I 1 = 6 A
I 2 = −2 A
I 3 = I1 + I 2 = 6 − 2 = 4 A
P70V发 = 6 × 70 = 420 W
P6V发 = 6 × (−2) = −12W
上 页 下 页
例2
U 2
7 I1 − 11I 2 + U − 70 = 0
11I 2 + 7 I 3 − U = 0
增补方程： 增补方程：I2=6A 由于I 已知， 由于 2已知，故只列写两个方程
− I1 − 6 + I 3 = 0
避开电流源支路取回路： 避开电流源支路取回路：
7 I1 + 7 I 3 − 70 = 0
R4 R3 4
2
i4 3
1 2 3
R1
3
R5
i5 i6
i1 + i2 − i6 = 0 − i 2 + i 3 + i4 = 0 − i4 − i5 + i6 = 0
取网孔为基本回路，沿顺时 取网孔为基本回路， 针方向绕行列KVL方程 方程: 针方向绕行列 方程
R6
+ u – S
回路1 回路 回路2 回路 回路3 回路
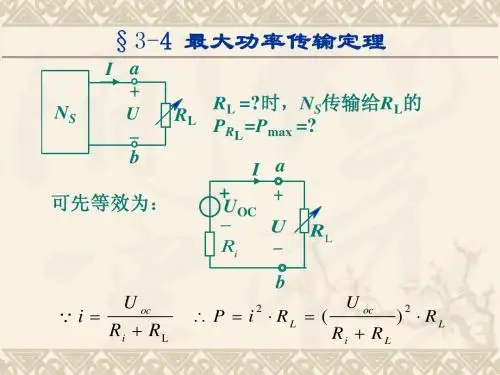
电路理论 第3章第4节最大功率传输定理

电路理论 第3章第4节最大功率传输定理


将上式对R 求导， 即可求得R 将上式对 L求导，并令 dP = 0 ，即可求得 L
dRL
获得最大功率的条件： 获得最大功率的条件：
2 2 U oc ( Ri + RL ) 2 − U oc ⋅ 2 RL ( Ri + RL ) dP = dRL ( Ri + RL ) 4
U ( Ri − RL ) = =0 3 ( Ri + RL )
∴ U = −5I0
I + U -
I0 5
6I0
+
7
3 I1
3 15 = (−5) × (− I) = I 2 2
U ∴ Ri = = 7.5Ω I
（3）求最大功率
+
UOC=15V
－
RL
2 OC
∴当RL = Ri = 7.5Ω时 Pmax
2 U = = 15 = 7.5 W 4 Ri 4 × 7.5
I
6I
+
7
9 2A
3
6I
+
2A
-
3
6I 1 1 ( + )U oc = 2 − 3 ∴ U oc = 15 V 5 3 U oc = − 5 I
外加电源法） （2）求Ri（外加电源法）
5 I 0 = 3 I1 + 6 I 0 I1 = − I − I 0 3 ∴ I0 = − I 2
§3-4 最大功率传输定理 4
I a + NS
Ubຫໍສະໝຸດ RLRL =?时，NS传输给 L的 传输给R 时 PRL =Pmax =? + UOC
－
可先等效为： 可先等效为：
I a +

现代电路理论第三章PPT 邱关源版


无源滤波器中元件变换
作业
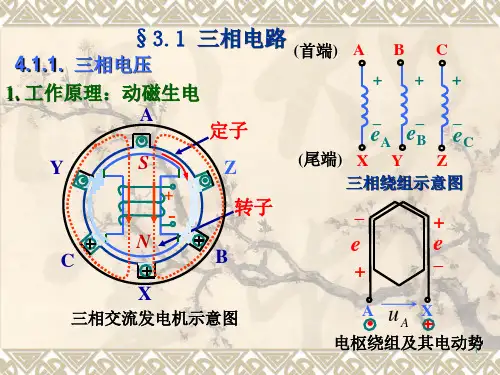
第四节 仿真电路
一、阻抗变换器
V ( s) Z1Z 3 Z 5 Zin I ( s) Z2Z4
当Z 2 1 , Z k Rk (k 1,2,3,4,5) sC2
R1 R3 R5 则Z in s C2 R4 等效电感Leq R1 R3 R5C2 R4
1 , 则Z in 2 c cC5 C1
频变电阻
D

1 2D
二.RLC-CRD变换： 如果用K/s乘以各个阻抗，其中K为任意常数，经变换后的电 路的电压转移函数仍将与原电路的相同。但电路中的各个元 件的性质发生了改变： 电容：
如
Vi ( s)
R
L
Vo ( s)

sL K s
若10log
1 1
2n
(100.1 A 1) A则n 2 log
取N=7
二、Chebyshev函数
1 H( j ) 1 2C2 n ( )
2
C0 ( ) 1 C1 ( ) Cn ( ) 2Cn 1 ( ) Cn 2 ( )
第三节 滤波函数的转换
经过频率域的变换，可实现滤波函数的变换。 一、低通函数→高通函数
H H( s ) 2 0 s s 1
p 1 s
H0s2 H( s ) 2 s s 1
物理意义: 电容： Z
1 sc
无源滤波器中元件变换
电感： Z sL
二、低通函数→带通函数
2 2 s 2 0 Q(sn 1) p sBW sn
作业：3-1,3-2
Design issues of analog filters: The analog filters using inductor works well at high frequencies, however, in low frequency applications that is in the frequency range (0- 20 kHz), the inductors cannot be used for the reasons : The size and weight of the inductors are large and physically bulky and the quality factor becomes very low Their characteristics are quite non-ideal Inductors are impossible to fabricate in monolithic form and are incompatible with any of the modern techniques for assembling electronic systems. Design analog filters without the use of inductors-simulated inductor.

《电路理论》幻灯片


1.设计分压器。 已知R1为1k ，试确定 R2 R3及R4的值。
电阻R0＝1k ，满幅 电流（最大允许电流） I0＝50A。
R1
•
+
R2
+
•
- 10V R3
+
8V
• + 5V
R4 2V
• - --
+R0 ,-I0 R1 R2 R3
• •
1V 10V
K 100V
+
-
电路基础
2.4 电阻的Y形连接与形连接的等效变 换 Resistor’s Wye-Delta Transformations
电路基础
i
i1 Gi12 G2 in Gn
(c)
显然Geq>Gk , k=1,2,…,n;
G eq R 1 eq ,G kR 1 k,R eq R k
等效电阻总小于并联各电阻中任一电阻，
且等效电阻为
1 11 1
R RR R
eq 1
2
n
电电阻路的基并础联
i
+
u
i1
-
Gi12
G2
in
Gn
1 .3 5
R1
R2
R3
30 K 15 K 0 .8
当 R 1R 3,R 2R 3 等, 效电阻估算为 R 3。
阻值相差很大的两个电阻串联，小电阻的分压作用 常可忽略不计；
阻值相差很大的两个电阻并联，大电阻的分流作用 常可忽略不计。
三、电阻的串并联
i
+ R1
u
R2
R3
-
R4
电路基础
R e q R 3 R 4 /R 2 / R 1 R ( R 3 3 R R 4 4 ) R R 2 2 R 1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

a
解 ① n–1=1个KCL方程：
I1 +
70V –
7 I2 11 +
61V
2
–
b
I3 结点a： –I1–I2+I3=0
7 ② b–( n–1)=2个KVL方程：
7I1–11I2=70-6=64
11I2+7I3= 6
返回 上页 下页
a
1 1 1
I1 7 I2 11 I3
Δ 7 11 0 203
R2 i2
i3
11
R1 i1
R4 应用欧姆定律消去支路电压得：
i4
R3 2
3
R5 i5
R 2i2R 3i3R 1 i10
R 4i4R 5i5R 3 i30 R 1 i1R 5 i5R 6 i6 u S
34
i6
R6 + uS –
返回 上页 下页
小结 （1）支路电流法的一般步骤：
①标定各支路电流（电压）的参考方向； ②选定(n–1)个结点，列写其KCL方程； ③选定b–(n–1)个独立回路，指定回路绕行方向，结合
不
23 5
12
是
75
回 路
84
1）对应一个图有很多的回路；
明 2）基本回路的数目是一定的，为连支数； 确 3）对于 b(n1)
返回 上页 下页
基本回路(单连支回路) 基本回路具有独占的一条连支
6
5
6
4
5
2
1
3
2
1
3
2
1
3
结论
支路数＝树支数＋连支数 ＝结点数－1＋基本回路数
减运算可以得到其他回路的KVL方程：
返回 上页 下页
结论 ①KVL的独立方程数=基本回路数=b－(n－1)
②n个结点、b条支路的电路, 独立的KCL和KVL方程数 为：
(n 1 ) b (n 1 ) b
返回 上页 下页
3.3 支路电流法
1. 支路电流法
以各支路电流为未知量列写电 路方程分析电路的方法。
第3章 电阻电路的一般分析
本章主要内容
3.1 电路的图 3.2 KCL和KVL的独立方程数 3.3 支路电流法 3.4 回路电流法 3.5 网孔电流法 3.6 结点电压法
首页
第三章
重点
KCL和KVL独立方程数的概念。 回路电流法（无伴电流源情况） 结点电压法（无伴电压源情况）
难点
独立回路的确定。 正确理解每一种方法所依据的电路 基本定律、选取的方程变量及列写的 方程式。
含有受控源的各种情况。
本章与其它章节的联系
本章内容以基尔霍夫定律为基础。介绍的支 路电流法、回路电流法和节点电压法适用于所有 线性电路问题的分析，在后面章节中都要用到。
预习知识
线性代数方程的求解、线性代数方程的特点
3.1 电路的图
1.网络图论 图论是拓扑学的一个分支，是富有趣 味和应用极为广泛的一门学科。
图G的任意两结点间至少有一条路径 时称为连通图，非连通图至少存在两 个分离部分。
返回 上页 下页
(4)子图
若图G1中所有支路和结点都是图G 中的支路和结点，则称G1是G的子 图。
①树(Tree)
T是连通图的一个子图且满足下列 条件： a. 连通 b.包含所有结点 c. 不含闭合路径
返回 上页 下页
+
70V –
+ 61V
– b
7 2
0 11 7 0 1 1
Δ1 64 11 0 1218
I112210 8 6A 3
⑴图的定义(Graph)
G={支路，结点}
①图中的结点和支路各自是一个整体。 ②移去图中的支路，与它所联接的结点依然存在，
因此允许有孤立结点存在。
③如把结点移去，则应把与它联接 的全部支路同时移去。
返回 上页 下页
(2)路径 (3)连通图
从图G的一个结点出发沿着一些支路 连续移动到达另一结点所经过的支路 构成路径。
KVL和支路方程列写；
R kik uSk
④求解上述方程，得到b个支路电流； ⑤进一步计算支路电压和进行其它分析。
返回 上页 下页
（2）支路电流法的特点： 支路法列写的是 KCL和KVL方程， 所以方程列写
方便、直观，但方程数较多，宜于在支路数不多的情
况下使用。
例1 求各支路电流及各电压源发出的功率。
对于有n个结点、b条支路的电路，要求解支路电流, 未知量共有b个。只要列出b个独立的电路方程，便可 以求解这b个变量。
2. 独立方程的列写
①从电路的n个结点中任意选择n-1个结点列写KCL方
程 ②选择基本回路列写b-(n-1)个KVL方程。
返回 上页 下页
例
R2
i2
1
1
2
R4
i3
i4
R3 2
有6个支路电流，需列写6个方程。 KCL方程:
bnl1 结点、支路和基
本回路关系
返回 上页 下页
例 图示为电路的图，画出三种可能的树及其对应
的基本回路。
1 45
86 3 72
5
86 7
4 86
3
4
8 2
3
注意
网孔为基本回路。
返回 上页 下页
3.2 KCL和KVL的独立方程数
1.KCL的独立方程数
2
1
2
1 i1i4i60 2 i1i2i30
1 43
1 i1i2i60
3
2 i2i3i40
R1 i1 34
R5 i5
3 i4i5i60
取网孔为独立回路，沿顺时针
i6 方向绕行列写KVL方程:
R6
+
uS
– 回路1
u2u3u10
回路2 u4u5u30
回路3 u1u5u60
返回 上页 下页
这一步可
回路1 u2u3u10
以省去
回路2 u4u5u30
2
回路3 u1u5u60
3
6
5
3 i2i5i60 4 i3i4i50
4
1 ＋ 2 ＋ 3 ＋ 4 ＝0
结论
n个结点的电路, 独立的KCL方程为n-1个。
返回 上页 下页
2.KVL的独立方程数
2
1
2
1 43
6
5
4
对网孔列KVL方程：
1 u1u3u40 3 2 u2u3u50
3 u4u5u60
1 - 2 u1u2u4u50
注意 可以证明通过对以上三个网孔方程进行加、
A A
B
D
C
哥尼斯堡七桥难题
B
D
C
返回 上页 下页
2.电路的图
i
R1 R2
R3 R5
R4
+ uS _ R6
元件的串联及并联组 合作为一条支路
n4b6
抛开元 件性质
n5 b8
1
8 3
5
2
4
1
3
5
2
4
6
7
6
一个元件作为 一条支路
有向图
返回 上页 下页
结电论路的图是用以表示电路几何结构的图形，图中
的支路和结点与电路的支路和结点一一对应。
树
不 是 树
树支：构成树的支路 连支：属于G而不属于T的支路
明确 ①对应一个图有很多的树
②树支的数目是一定的
bt n1
连支数： b l b b t b (n 1 )
返回 上页 下页
②回路(Loop)
1 23 75
6 84
回路
L是连通图的一个子图，构成一条闭
合路径，并满足：(1)连通，(2)每个
结点关联2条支路。