叠加定理和齐性定理的验证

实验二 叠加原理的验证一、 实验目的验证线性电路叠加原理和基尔霍夫定律的正确性，从而加深对线性电路的叠加性和齐次性的认识和理解。

二、 原理说明叠加原理指出：在有几个独立源共同作用下的线性电路中，通过每一个元件的电流或其两端的电压，可以看成是由每一个独立源单独作用时在该元件上产生的电流或电压的代数和。

线性电路的齐次性是指当激励型号（某独立源的值）增加或减少K 倍时，电路的响应（即在电路其他各电阻元件上所建立的电流和电压值）也将增加和减少K 倍。

基尔霍夫电流定律：任何集中参数电路中，任意时刻流进任意一个结点的所有支路电流的代数和总是为零。

基尔霍夫电压定律：任何集中参数电路中，任意时刻绕任意一个回路一周所有支路电压的代数和总是为零。

三、 实验设备四、 实验内容实验电路如图2-1所示1、按图2-1电路接线，取V E VE 61221+=+=。

2、令1E 电源单独作用，用直流数字电压表和毫安表测量各支路电流及各电阻元3、令2E 电源单独作用，用直流数字电压表和毫安表测量各支路电流及各电阻元件两端电压，数据记入表格中。

4、令1E 、2E 电源共同作用，用直流数字电压表和毫安表测量各支路电流及各电阻元件两端电压，数据记入表格中。

5、将2E 的数值调至+12V ，用直流数字电压表和毫安表测量各支路电流及各电阻元件两端电压，数据记入表格中。

五、 实验注意事项1、测量各支路电流时，应注意仪表的极性，及数据表格中的“+”“—”号的记录。

2、注意仪表的量程的及时更换。

六、 预习思考题1、叠加原理中1E 、2E 分别单独作用，在实验中应该如何让操作？，可否直接将不作用的电源致零？2、 实验电路中，若有一个电阻器改为二极管，试问叠加原理的叠加性和齐次性还成立吗，为什么？七、 实验报告1、根据实验数据验证线性电路的叠加性和齐次性。

2、根据实验数据验证基尔霍夫定律。

3、各电阻器所消耗的功率能否用叠加原理计算得出？试用上述实验数据，进行计算并得出结论。

实验一 叠加定理的验证一、实验目的验证线性电路叠加定理的正确性，加深对线性电路的叠加性和齐次性的认识和理解。

二、原理说明叠加定理指出：在有多个独立源共同作用下的线性电路中，通过每一个元件的电流或其两端的电压，可以看成是由每一个独立源单独作用时在该元件上所产生的电流或电压的代数和。

线性电路的齐次性是指当激励信号（某独立源的值）增加或减小K 倍时，电路的响应（即在电路中各电阻元件上所建立的电流和电压值）也将增加或减小K 倍。

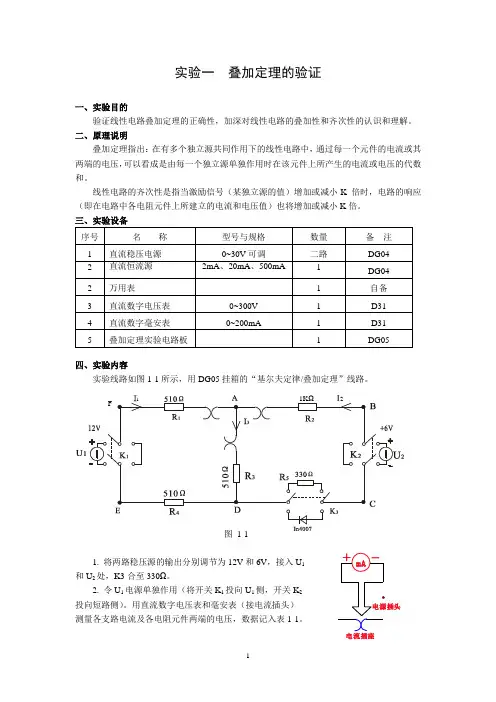
四、实验内容实验线路如图1-1所示，用DG05挂箱的“基尔夫定律/叠加定理”线路。

图 1-11. 将两路稳压源的输出分别调节为12V 和6V ，接入U 1和U 2处，K3合至330Ω。

2. 令U 1电源单独作用（将开关K 1投向U 1侧，开关K 2投向短路侧）。

用直流数字电压表和毫安表（接电流插头） 测量各支路电流及各电阻元件两端的电压，数据记入表1-1。

电流插座3. 令U2电源单独作用（将开关K1投向短路侧，开关K2投向U2侧），重复实验步骤2的测量和记录，数据记入表1-1。

4. 令U1和U2共同作用（开关K1和K2分别投向U1和U2侧），重复上述的测量和记录，数据记入表1-1。

5. 将R5（330Ω）换成二极管1N4007（即将开关K3投向二极管IN4007侧），重复1～4的测量过程，数据记入表1-2。

表1-2五、实验注意事项1. 用电流插头测量各支路电流时，或者用电压表测量电压降时，应注意仪表的极性，正确判断测得值的＋、－号后，记入数据表格。

2. 注意仪表量程的及时更换。

六、预习思考题1. 在叠加定理实验中，要令U1、U2分别单独作用，应如何操作？可否直接将不作用的电源（U1或U2）短接置零？2. 实验电路中，若有一个电阻器改为二极管，试问叠加定理的迭加性还成立吗？为什么？七、实验报告1. 根据实验数据表格，进行分析、比较，归纳、总结实验结论，即验证线性电路的叠加性。

2. 各电阻器所消耗的功率能否用叠加定理计算得出？试用上述实验数据，进行计算并作结论。

实验4-3---叠加定理和齐次定理的验证
叠加定理和齐次定理是电路分析中的重要定理，它们理解了特定的电路运行的原理和
类型，本文旨在验证它们的正确性。

首先，让我们来证明叠加定理，它规定，两个电压源可以被放在一起以形成一个总电
压源，其值等于它们之和。

对于证明，我们将考虑一个简单的电路，由两个电池和一个放
电灯泡组成，如图1所示。

图1
我们以另一个简单电路作为对照，如图2所示。

该电路由单个电池和一个放电灯泡组成，电池电势与图1中所示的两个等电势的电池的输出之和相同。

然后，我们测量了两个
电路中的灯泡的明亮度，结果发现，两者的亮度是相同的。

由此可见，我们可以得出结论，两个电路中的灯泡得到的总电量是相同的，这也就证实了叠加定理的正确性。

图2
接下来，让我们来证明齐次定理，它规定，具有相同电势的两个电源的输出的总电量
是相同的。

为了证明这一点，我们将比较两个不同电路，分别由两个电池组成，但它们的
电势不同，情况一如图3所示，电池的电势分别为27V和13V；情况二如图4所示，电池
的电势分别为27V和27V。

图3
图4
以上证明叠加定理和齐次定理的正确性。

叠加定理规定，两个电压源可以被放在一起
以形成一个总电压源，其值等于它们之和；而根据齐次定理，具有相同电势的两个电源的
输出的总电量是相同的。

因此，叠加定理和齐次定理是正确的，为电路分析提供了有力支持。

实验一：叠加定理实验一、实验目的1.验证线性电路中叠加定理的正确性；2.掌握叠加定理的适用范围。

二、实验仪器1.直流电压源2.直流电流源3.Ground4.普通电阻5.直流电压表6.直流电流表三、实验原理叠加定理指出，对于线性电路，任一电压或电流都是电路中各个独立电源单独作用（其余激励源置为0）时，在该处产生的电压或电流的叠加。

对于不作用的激励源，电压源应视为短路，电流源应视为开路。

使用叠加定理时应注意以下几点：（1）叠加定理适用于线性电路，不适用于非线性电路；（2）在叠加的各分电路中，不作用的电压源置零，在电压源处用短路代替；不作用的电流源置零，在电流源处用开路代替。

电路中所有电阻都不予更动，受控源则保留在各分电路中；（3）叠加时各分电路中的电压和电流的参考方向可以取为与原电路中的相同。

取和时，应注意各分量前的“+”、“-”号；（4）原电路的功率不等于按各分电路计算所得的功率的叠加，这是因为功率是电压和电流的乘积。

四、实验内容实验任务：验证叠加定理及线性电路的齐次性。

按照图1搭建实验电路，其中直流电压表和直流电流表内阻采用默认值。

图1实验电路1.叠加定理的验证（1）运行实验，记录激励源共同作用情况下电路中各处电流及电压于表1；（2）测量E s1单独作用时数据：设置电流源断路，电压源E s2短路，记录直流电压源U s1单独作用情况下电路中各处电流及电压于表1；（3）测量E s2单独作用时数据：设置电流源断路，电压源E s1短路，记录直流电压源E s2单独作用情况下电路中各处电流及电压于表1；（4）测量I s单独作用时数据：设置电压源E s1和E s2均短路，记录直流电流源I s单独作用情况下电路中各处电流及电压于表1；（5）补充完整表1，验证叠加定理的正确性。

表1叠加定理的实验数据I1（A）U1（V）I2（A）U2（V）I3（A）U3（V）激励源共同作用 1.00 3.000.00-50.00 2.00 4.00E s1单独作用 2.447.310.00 4.69 2.34 4.69E s2单独作用-0.98-2.930.00 2.93-1.04-2.07I s单独作用-0.40-1.200.00-50.000.60 1.20叠加定理的验证∑x单独=X共同1.06 3.180.0044.38 1.80 3.82五、实验仿真结果图：（截图说明）1、激励源共同作用仿真结果图：单独作用仿真结果图2、Es13、E单独作用仿真结果图s2单独作用仿真结果图4、Is六：实验结果分析及结论（理论数据与仿真数据对比，实验结论！手写拍照粘上去）。

实验3_线性电路叠加原理和齐次性的验证(自动)一、实验目的1. 理解线性电路叠加原理和齐次性原理的基本概念和意义；2. 掌握叠加原理和齐次性原理的实验验证方法和实验步骤；3. 培养学生使用实验仪器测试线性电路的能力。

二、实验原理1. 线性电路叠加原理：叠加原理是对于由多个不同的独立源作用于同一电路中的电压和电流的关系，可以通过叠加各个源的作用来求得最终的电压和电流的规律的一种方法。

线性电路在满足叠加原理的情况下，可以将各个电源的作用逐一地计算出来，最后进行叠加求和。

叠加原理的表述如下：对于多个独立源同时作用于线性电路中，每个电源单独作用时，电路中的电压、电流和功率等物理量的值，等于这个电源在电路中单独存在时引起的电压、电流和功率等物理量的值的代数和。

2. 齐次性原理：齐次性原理是指在电路中，如果所有的初始条件（即在某一初始状态下的电压、电流、充电等状态）都为零，则电路的响应也将为零。

这是由于电路的状态不发生变化，导致了电路中的各个元件的电压、电流等物理量都不发生变化，相应的电路响应也为零。

齐次性原理的表述如下：如果线性电路的输入为零，则输出也为零。

三、实验装置与设备1. 普通电压源；2. 万用电表；3. 实验电路图（如图1、图2）。

四、实验步骤（1）按照实验电路图1搭建线性电路。

（2）将普通电压源V1和V2的正负极分别接入电路中的两个不同的电阻上，调节电压源的电压为10V和5V。

（3）使用万用电表测量R1、R2、R3的电阻值，并记录下来。

（4）测量电路中R1两端的电压（记作V1）和R2两端的电压（记作V2）。

（6）根据叠加原理和测量结果，计算出电路中R1和R2两端的电压的大小。

（7）与测量结果进行比较，观察并分析误差的产生原因。

（3）分别记录电源开关开关前后各个电阻的电压值，并记录下来。

（4）打开电源开关使电流通过电路。

五、实验结果与分析（1）测得R1的电阻值为45.6Ω，R2的电阻值为33.3Ω，R3的电阻值为67.9Ω。

叠加定理的验证原理与内容叠加定理是数学中一个重要的定理，它在各个数学领域中都有广泛的应用，如微积分，线性代数和物理学等，是数学中的基本工具之一。

叠加定理主要用于将复杂的问题分解为简单的部分，并通过叠加这些简单的部分来解决整个问题。

下面我将详细介绍叠加定理的验证原理和内容。

叠加定理的验证原理是基于线性性质的。

线性性质是指在某个数学对象中，如果满足特定的条件，它的求和或求积等运算可以分解为若干个部分的求和或求积。

这种分解使得我们可以将原问题分解为多个简单的子问题，并最终将它们叠加起来得到原问题的解。

对于叠加定理来说，它的线性性质是指对于任意两个满足特定条件的函数，它们的线性组合的求和等于这两个函数分别求和的结果的线性组合。

对于叠加定理的内容，我们首先需要明确它的应用范围。

叠加定理适用于满足线性微分方程的函数，具体可以分为两种情况：齐次线性微分方程和非齐次线性微分方程。

对于齐次线性微分方程，叠加定理告诉我们，如果给定两个满足齐次线性微分方程的解函数f(x)和g(x)，那么它们的线性组合a*f(x) + b*g(x)也是这个方程的解函数，其中a和b是常数。

换句话说，对于齐次线性微分方程，解的线性组合仍然是方程的解。

对于非齐次线性微分方程，叠加定理告诉我们，如果给定了方程的一个特解函数p(x)和它的对应齐次方程的通解函数h(x)，那么方程的一般解可以表示为p(x) + h(x)，其中p(x)是方程的特解，h(x)是方程的齐次方程的通解。

换句话说，对于非齐次线性微分方程，一般解可以表示为特解和通解的线性组合。

叠加定理的验证原理可以通过数学推导来证明。

对于齐次线性微分方程，我们可以将求和后的函数代入方程中，利用线性微分方程的性质，将方程分解为两个部分，然后再验证这两个部分分别满足方程，最终证明线性组合是方程的解。

对于非齐次线性微分方程，我们可以通过将方程的一般解代入方程中，然后利用线性微分方程的性质将方程分解为一个特解和一个齐次方程的解，最终证明一般解是方程的解。

叠加定理的验证实验报告叠加定理的验证实验报告引言：叠加定理是物理学中一个重要的定理，它在解决复杂问题时起到了重要的作用。

本实验旨在验证叠加定理的有效性，并通过实验数据来加深对该定理的理解。

实验目的：验证叠加定理在电路中的应用，了解其原理和实际效果。

实验材料：1. 电源：直流电源、交流电源2. 电阻：不同阻值的电阻器3. 电流表、电压表、万用表4. 连接线、开关等实验器材实验步骤：1. 搭建直流电路：将直流电源与电阻器相连，通过电流表测量电流大小，并记录数据。

2. 搭建交流电路：将交流电源与电阻器相连，通过电流表测量电流大小，并记录数据。

3. 切换电源：将直流电源与交流电源同时连接到电阻器上，通过电流表测量电流大小，并记录数据。

4. 分析数据：根据实验数据，比较直流电路和交流电路的电流大小，以及叠加电路的电流大小，验证叠加定理的有效性。

实验结果：通过实验记录的数据，我们可以得到以下结论：1. 在直流电路中，电流大小与电源电压和电阻大小成正比。

即I=U/R，其中I为电流，U为电压，R为电阻。

2. 在交流电路中，电流的大小与电源电压和电阻大小成正比，但还受到频率和电感、电容等因素的影响。

3. 在叠加电路中，当直流电源和交流电源同时连接到电阻器上时，电流的大小等于直流电路和交流电路电流的代数和。

即I_total = I_direct + I_alternating，其中I_total为总电流，I_direct为直流电路电流，I_alternating为交流电路电流。

讨论与分析：通过实验结果的分析，我们可以得到以下结论：1. 叠加定理在电路中是成立的，无论是直流电路还是交流电路，都可以通过叠加定理来计算电流大小。

2. 叠加定理的有效性源于电流的线性特性，即电流满足叠加原理。

3. 在实际应用中，叠加定理可以简化复杂电路的分析和计算，提高解决问题的效率。

结论：通过本实验的验证，我们可以得出结论：叠加定理在电路中是有效的，可以用来计算电流大小。

简述叠加定理和齐次定理
叠加定理（superposition principle）和齐次定理（homogeneity principle）是电路分析中常用的两个基本原理。

叠加定理指出，对于一个线性电路，其响应可以认为是各个输入信号分别作用时产生的响应的叠加。

简单来说，就是将复杂的电路分解为若干个简单的子电路，分别计算每个子电路的响应，然后将它们叠加起来得到整个电路的响应。

这个原理适用于任何线性电路，无论是直流电路还是交流电路，只要满足线性条件，就可以使用叠加定理进行分析。

通过叠加定理，我们可以更好地理解电路中各个元件之间的相互作用。

齐次定理是叠加定理的一个特殊情况。

它指出，如果一个线性电路的输入信号为零，即没有任何外部激励作用在电路上，那么电路的响应也为零。

这意味着在没有输入信号的情况下，电路不会产生任何输出。

齐次定理可以用来分析电路的初始条件，即在没有任何输入信号时电路的状态。

在实际电路分析中，叠加定理和齐次定理常常一起使用。

首先使用叠加定理将复杂的电路拆解成若干个简单的子电路，然后对每个子电路应用齐次定理，计算出每个子电路的响应。

最后将这些响应叠加起来，得到整个电路的响应。

这种方法简化了电路分析的过程，使得计算更加方便和快速。

总之，叠加定理和齐次定理是电路分析中常用的两个基本原理，它们使得对复杂
电路的分析和计算变得更加简单和直观。

通过利用叠加定理和齐次定理，我们可以更好地理解电路的行为和特性，并且能够更高效地设计和优化电路。

第四章电路定理第一节叠加定理一、叠加定理1、内容：在多个电源共同作用的线性电路中，任一电压（或电流）是各独立电源单独作用时，在该处产生的电流（或电压）的代数和。

2、定理的证明R1R(2)电压源单独作用电流源单独作用(1)(2)111(1)(2)222u u ui i i=+=+证明：11211212121212s sssR R Ru u iR R R Ru Ri iR R R R=-++=+++122121ssu R i uui iR+=+=(1)1112sRu uR R=+(2)12112sR Ru iR R=-+(1)2121si uR R=+(2)1212sRi iR R=+(1)(2)1121111212(1)(2)121112121s ss sR R Ru u u u iR R R RRi i i u iR R R R=+=-++=+=+++几点说明：（1）叠加定理只适用于线性电路；（2）一个电源作用，其余电源为零（电压源为零——短路；电流源为零——开路）。

（3）叠加时各分电路中电压和电流的参考方向一般取为与原电路中的相同。

（4）含受控源电路亦可用叠加定理，但叠加只适用于独立源，受控源应始终保留。

（5）功率不能叠加例1：试用叠加定理计算图示电路中的I 和U 。

12A(1)(2)12A解：(1)(1)120315,154203(24)366324I A UV ===⨯⨯=⨯+++++(2)(2)2,6424I A U V ==-⨯=- (1)(2)(1)(2)17,4I I IA U UUV=+==+=- 例2：用叠加定理求电压3u 。

解：(1)(2)333u u u =+ (1)(2)333625.619.6u u u V =+=-+= (1)(1)1210146i i A ===+ (1)(1)(1)3121046u i i V =-+=-(2)1441.646i A =-⨯=-+ (2)(2)(2)31110616(1.6)25.6u i i V =--=-⨯-= 例3：用叠加定理计算U 。

简述叠加定理和齐次定理叠加定理和齐次定理是电路分析中常用的重要理论工具。

它们帮助我们更好地理解和分析复杂的电路系统，解决电路中的各种问题。

首先，我们来谈谈叠加定理。

叠加定理是基于线性电路特性的定理，它指出一个线性电路中的各种效应（如电流、电压、功率等）可以分别计算，然后将它们叠加起来得到最终的结果。

也就是说，叠加定理允许我们将电路中的多个独立源的影响分别看待，再将它们的效应叠加起来，得到与真实情况完全一致的结果。

叠加定理的核心思想是，对于一个具有多个独立源（如电压源和电流源）的电路系统，在计算某一特定效应时，我们可以将除了待计算的源之外的其他源“短路”或“断路”，然后计算待计算源的效应。

最后，将各个结果相加，即可得到整个系统的总效应。

这样做的好处是，通过将复杂的多源电路分解为简单的单源电路，我们可以化繁为简，一步步地解决问题，简化了计算过程。

接下来，我们来探讨齐次定理。

齐次定理也是基于线性电路特性的一个重要定理，它指出如果一个电路系统中所有独立源都为零（包括电压源和电流源），那么该电路中的各种效应也都为零。

也就是说，没有独立源的电路系统是一个平衡的系统，其中不存在电流和电压的产生。

齐次定理告诉我们，如果我们想要分析一个电路系统中某一特定效应的大小、方向或分布情况，我们可以首先将所有独立源置零，然后分析得到的电路系统就是一个“齐次电路”。

齐次电路的分析相对简单，一般可以采用基本的电路分析方法求解。

在求解完成后，我们再将独立源重新接入，根据叠加定理就可以得到默认所有独立源对电路造成的影响，从而求解出我们关心的效应。

综上所述，叠加定理和齐次定理是电路分析中不可或缺的重要工具。

通过这两个定理的运用，我们能够更好地理解电路系统的行为规律，快速解决各种电路问题。

在实际应用中，我们可以根据电路的具体情况，适时地采用叠加定理和齐次定理进行分析，准确地提取出我们所关心的信息，从而为电路设计、故障诊断和性能优化等方面提供理论指导。

实验4-3 叠加定理和齐次定理的验证一.实验目的1.验证叠加定理和齐次定理,加深对线形电路的理解。

2.掌握叠加定理的测定方法。

3.加深对电流和电压参考方向的理解。

图表 1 K1 K2 均闭合时的电路图图表 2 K1断开K2 闭合时的电路图图表 3 K2断开K1 闭合时的电路图I1的照片图表 4 当开关都闭合时电流计的值图表 5 K2断开K1 闭合时的电路图图表 5 K1断开K2 闭合时的电路图图表 6 2U1时的电路图U ab的测试数据图表7当开关都闭合时电流计的值图表8 K2断开K1 闭合时的电路图图表9 K1断开K2 闭合时的电路图图表 6 2U1时的电路图4.3 叠加定理和齐次定理的验证表4.3-1 叠加定理和齐次定理的验证数据已知两个电源电压分别为U S1=13V，U S2=12V，电阻R1=510Ω，R2=1kΩ，R3=510Ω，计算电流I1、I2和I3，以及电压U AB、U BC、U BD。

解；1.以Us1为激励时：R总=R1+R2//R3=847.691I1=Us1/R总=22.0m AI2=R3/（R2+R3）*I1=7.571m AI3=R2/（R2+R3）*I1=0.15mAU AB=R1*I1=11.430VU BC=R2*I2=7.570VU BD=R3*I3=7.570V2. 以Us2为激励时：R总=R2+R1//R3=1.254kI2=Us2/R2=-1.992mAI1=R3/（R1+R3）*I2=1.992mAI3=R1/（R1+R3）*I2=3.984mAU AB=R1*I1=1.0VU BC=R2*I2=3.984VU BD=R3*I3=-1.016V所以：I1=22.0+1.992=24.0mAI2=7.571-1.992=5.580mAI3=0.15+3.984=0.014781AU AB=11.43+1.0=12.43VU BC=7.570+3.984=11.554VU BD=7.570-1.016=6.554V二.实验结论：1、由上述计算结果证明：在一个线性电路中，由几个独立电源共同作用所形成的各支路电流或电压，等于各个独立电源分别单独作用时在各相应支路中形成的电流或电压的代数和。