概率论与数理统计lec01 11
- 格式:ppt
- 大小:397.00 KB
- 文档页数:27





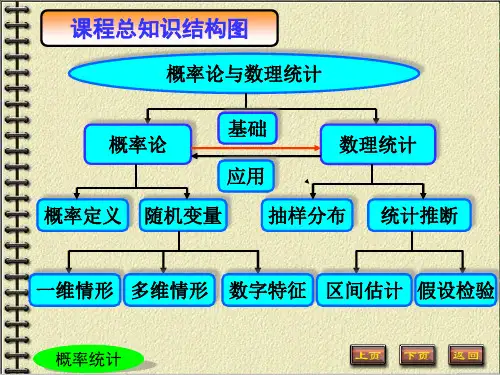





概率论与数理统计首先,概率论是研究随机事件发生的可能性的数学理论。
概率论的基本概念包括样本空间、事件、概率等。
样本空间是指所有可能结果的集合,事件是样本空间的子集,概率是用来描述事件发生可能性的大小。
概率论主要研究的是随机事件的规律性和性质,通过概率论的基本概念和理论,可以对随机事件进行合理的量化和分析。
数理统计是根据概率论的基本原理,通过对样本观测数据的分析来对总体的性质进行推断和估计的一门学科。
数理统计主要包括描述统计和推断统计两个部分。
描述统计是通过对样本数据进行整理、分析和表示,来描述总体数据的特征和分布情况。
推断统计是根据样本统计量,对总体参数进行推断和估计。
数理统计在许多领域中都有广泛的应用,如社会科学、自然科学、医学、工程等。
相关分析是数理统计中的一个重要方法,它研究两个变量之间的相关性。
相关性指的是两个变量之间的关系,既可以是正相关,也可以是负相关,还可以是没有相关性。
通过相关分析,可以帮助我们了解两个变量之间的关系及其强度,从而可以进行进一步的预测和分析。
在相关分析中,常用的统计量包括相关系数和相关显著性检验。
相关系数是衡量两个变量之间相关性强度的指标,其取值范围在-1到1之间。
当相关系数接近1时,表示两个变量正相关,相关系数接近-1时,表示两个变量负相关,相关系数接近0时,表示两个变量没有相关性。
相关显著性检验可以用来检验相关系数是否显著不等于0,从而判断两个变量之间是否存在相关性。
相关分析在实际应用中具有广泛的应用价值。
例如,在金融领域中,可以利用相关分析来研究不同股票之间的相关性,从而帮助投资者进行风险分散和资产配置。
在医学研究中,可以利用相关分析来研究因变量和自变量之间的关系,从而帮助医生和研究人员了解疾病的发展和治疗效果。
在市场调查中,可以利用相关分析来研究不同因素之间的相关性,从而帮助企业做出有效的营销策略。
综上所述,概率论与数理统计及其相关分析是一门重要的学科,它在现实生活和科学研究中具有广泛的应用价值。
概率论与数理统计1. 前言概率论与数理统计是数学的一个重要分支,它是研究随机现象规律性的数学学科。
概率论是研究随机现象的规律性和数量关系的学科,而数理统计则是利用数学方法研究大量数据中的规律性和趋势的学科。
本文将介绍概率论与数理统计的基本概念、方法和应用。
2. 概率论概率论是研究随机现象的规律性和数量关系的数学学科。
随机现象是指在一定条件下,每次实验的结果无法预知,但在一系列相同实验中,某些现象出现的频率具有稳定的规律性。
概率论通过概率分布、概率密度函数、条件概率等概念来描述随机现象,并提供了一系列计算概率的方法。
2.1 基本概念•样本空间:样本空间是随机现象所有可能结果的集合,常用符号为S。
例如,抛一枚硬币的样本空间为$\\{H, T\\}$,其中H表示正面,T表示反面。
•事件:事件是样本空间的一个子集,表示随机现象的一个可能结果或一组可能结果组成的集合。
如果随机事件A中包含了样本空间S中的某些结果,则称事件A发生。
•概率:概率是描述随机事件发生可能性大小的数值,通常用P(A)表示,表示事件A发生的可能性大小。
概率的取值范围在[0,1]之间。
•概率分布:概率分布是随机变量所有可能取值及其发生的概率的描述。
常见的概率分布包括二项分布、泊松分布、正态分布等。
2.2 概率计算概率计算是概率论的核心内容之一,常用的计算方法包括加法法则、乘法法则、全概率公式和贝叶斯定理等。
这些方法可以帮助我们计算复杂事件的概率,进行概率分布的推导和分析。
3. 数理统计数理统计是利用数学方法研究大量数据中的规律性和趋势的学科。
在现代社会中,大量的数据被广泛应用于科学研究、经济分析、医学诊断等领域,而数理统计提供了一系列工具和方法来处理和分析这些数据。
3.1 基本概念•总体与样本:总体是指研究对象的全部个体或事物的集合,样本是从总体中选取的一部分个体或事物。
数理统计的目标通常是通过对样本的统计量进行分析来进行对总体的推断。