基于双因子定价模型的投资组合风险价值的多分辨率特征研究
- 格式:pdf
- 大小:383.89 KB
- 文档页数:15

基于多因子模型的量化投资研究基于多因子模型的量化投资研究1. 引言量化投资是近年来发展迅速的一种投资策略,其核心思想是利用数学模型和计算机技术对市场进行分析和预测,以期获得超越市场的收益。
而多因子模型作为一种有效的量化投资方法,通过考量多个因子对股票价格的影响,量化地评估股票的价值和风险。
2. 多因子模型概述多因子模型是一种基于统计分析的投资模型,通过将股票的收益率与多个因子进行回归分析,来解释股票收益率的波动。
多因子模型通常包括市场因子、规模因子、价值因子、动量因子等。
市场因子衡量股票相对市场的表现,规模因子衡量股票的市值大小,价值因子衡量股票的估值水平,动量因子衡量股票的价格趋势。
通过综合考虑多个因子,可以更全面地评估股票的投资价值。
3. 多因子模型的构建在构建多因子模型时,首先需要选择适合的因子。
这需要根据市场的特点和投资者的偏好进行选择。
随后,需要进行因子的数据处理和归一化处理,以消除不同因子之间的量纲差异。
然后,通过回归分析对股票收益率与因子之间的关系进行建模。
最后,通过模型的参数估计,可以量化地评估股票的价值和风险,并进行投资决策。
4. 多因子模型的优势与传统的单因子模型相比,多因子模型具有以下优势:(1)全面性:多因子模型综合考虑了多个因子对股票收益率的影响,可以更全面地评估股票的价值和风险。
(2)稳定性:多因子模型通过考虑多个因子,可以降低单个因子的不确定性对投资组合的影响,提高投资策略的稳定性。
(3)有效性:多因子模型通过统计分析和回归分析,可以对不同因子的权重进行优化调整,从而提高投资组合的收益率。
5. 多因子模型的应用多因子模型在量化投资中有广泛的应用。
一方面,多因子模型可以用于股票的选择和投资组合的构建。
通过量化评估股票的价值和风险,可以选择具有良好投资价值的股票,并构建具有较高收益率和较低风险的投资组合。
另一方面,多因子模型还可以用于市场的预测和交易信号的生成。
通过对多个因子的综合分析,可以预测市场的走势,并基于此生成交易信号。


金融风险定价模型的多因子分析与优化研究一、引言金融市场的不确定性和风险性使得风险定价模型在金融领域中扮演着重要的角色。
随着时间的推移,传统的单因子模型已经不足以满足风险定价的需求。
因此,多因子分析和优化成为了研究的热点。
本文旨在探讨金融风险定价模型的多因子分析与优化研究。
二、多因子模型的概念和应用1. 多因子模型的概念多因子模型是指将金融资产的收益率分解为多个因素的线性组合,以揭示背后的经济和市场趋势。
通常,这些因子包括市场因子、公司特定因子和宏观经济因子等。
2. 多因子模型的应用多因子模型的应用广泛,包括股票选取、投资组合管理和风险分析等。
通过使用多因子模型,投资者可以更准确地评估投资组合的风险和收益,优化资产配置,并进行有效的风险管理。
三、金融风险定价模型的多因子分析1. 市场因子分析市场因子是多因子模型中最重要的因素之一,通常是指市场指数的表现。
通过分析市场因子,可以帮助我们预测市场的整体风险和收益。
一些常用的市场因子包括市场收益率、市场波动率以及市场流动性等。
2. 公司特定因子分析公司特定因子是指影响个别公司或行业的因素。
这些因素包括公司的盈利情况、行业竞争力、财务状况和管理层能力等。
通过分析公司特定因素,可以帮助我们理解某个公司或行业的风险和收益特征。
3. 宏观经济因子分析宏观经济因子是指宏观经济环境的变化对金融资产收益率的影响。
例如,利率、通货膨胀率、国内生产总值(GDP)增长率等。
通过分析宏观经济因素,可以更好地理解金融市场的风险和收益。
四、金融风险定价模型的多因子优化1. 基于协方差矩阵的优化在多因子模型中,协方差矩阵是优化构建投资组合的关键。
通过分析各个因子之间的协方差,可以更好地实现资产的多样化和风险的分散。
在优化投资组合时,可以通过最小化投资组合的方差或最大化投资组合的效用函数来优化投资组合的风险和收益。
2. 约束优化约束优化是在投资组合构建中常用的一种方法,在优化过程中引入约束条件来满足特定的投资目标。


多因子模型在投资组合中的应用投资组合是指将资金分配到不同的资产中,以实现风险分散和收益最大化的投资策略。
在投资组合中,多因子模型是一种常用的工具,用于解释资产收益率的变动,并辅助投资者进行资产配置和风险管理。
本文将探讨多因子模型在投资组合中的应用,并分析其优势和局限性。
多因子模型是基于资本资产定价模型(CAPM)的扩展,通过引入更多的因子来解释资产收益率的变动。
传统的CAPM模型认为资产收益率仅受市场因素的影响,而多因子模型则认为资产收益率还受其他因素的影响,如公司规模、估值、盈利能力等。
通过考虑多个因子,多因子模型能够更全面地解释资产收益率的波动。
在投资组合中,多因子模型的应用主要体现在两个方面:资产配置和风险管理。
首先,多因子模型可以帮助投资者进行资产配置。
通过分析不同因子对资产收益率的影响程度,投资者可以选择合适的因子组合来配置资产。
例如,如果某个因子对资产收益率的解释力较强,投资者可以增加该因子在投资组合中的权重,以获得更高的收益。
其次,多因子模型还可以用于风险管理。
通过分析不同因子对资产收益率的敏感性,投资者可以评估投资组合的风险水平,并采取相应的风险控制措施。
例如,如果某个因子对资产收益率的敏感性较高,投资者可以减少该因子在投资组合中的权重,以降低投资组合的风险。
多因子模型在投资组合中的应用具有一定的优势。
首先,多因子模型能够更全面地解释资产收益率的波动,相比于传统的CAPM模型,能够提供更准确的预测和评估。
其次,多因子模型能够帮助投资者进行更精细的资产配置和风险管理,提高投资组合的收益和风险控制能力。
此外,多因子模型还能够帮助投资者发现市场中的投资机会和价值股,提高投资决策的准确性和效果。
然而,多因子模型在投资组合中的应用也存在一些局限性。
首先,多因子模型的构建和参数估计需要大量的数据和复杂的计算,对投资者的数据处理和模型建立能力提出了较高的要求。
其次,多因子模型仍然存在一定的误差和不确定性,无法完全准确地预测和解释资产收益率的变动。

金融市场风险管理中的多因子模型与价值评估方法探究概述:金融市场风险管理是投资者、机构和金融机构的重要任务之一。
多因子模型和价值评估方法是衡量金融市场风险和评估资产价值的两种常用工具。
本文将探讨多因子模型和价值评估方法在金融市场风险管理中的应用和有效性。
一、多因子模型的基本原理多因子模型是通过考虑多个因素对金融资产收益的影响来评估市场风险的一个方法。
该模型基于以下假设:1)资产的收益可以被多个因素解释;2)这些因素之间具有一定程度的相关性;3)通过对这些因素的权重进行组合,可以预测资产收益。
常用的多因子模型包括CAPM (Capital Asset Pricing Model)、FF模型(Fama-French模型)等。
CAPM是最早的多因子模型之一,它考虑市场因素对资产收益的影响。
该模型认为资产的预期回报率与其系统风险成正比,系统风险即与市场整体相比的波动性。
CAPM 的优点是简单易用,但也存在一些缺点,如没有考虑其他具体因素对资产收益的影响。
FF模型是建立在CAPM基础上的一种改进模型,它进一步考虑了三个因素:市场风险因素、市场规模因素和市场价值因素。
通过引入这些因素,FF模型可以更准确地解释金融资产的收益。
尽管FF模型相对于CAPM有更高的解释能力,但它仍然无法覆盖所有的市场因素。
二、多因子模型在金融市场风险管理中的应用多因子模型在金融市场风险管理中有着广泛的应用。
它可以帮助投资者和机构更准确地估计资产的风险,优化资产组合,并制定合理的投资策略。
以下是一些具体的应用场景:1. 评估投资组合的风险多因子模型可以用来评估投资组合的风险水平。
通过考虑不同因素对组合收益的影响,可以更准确地估计投资组合的风险暴露,并进行风险控制。
2. 优化资产配置多因子模型还可以用于优化资产配置。
根据不同因子的权重,可以调整资产的权重分配,以最大化组合收益或最小化组合风险。
3. 补充单因子模型的不足传统的单因子模型无法完全解释资产收益的波动,而多因子模型可以更全面地考虑市场因素对资产收益的影响。
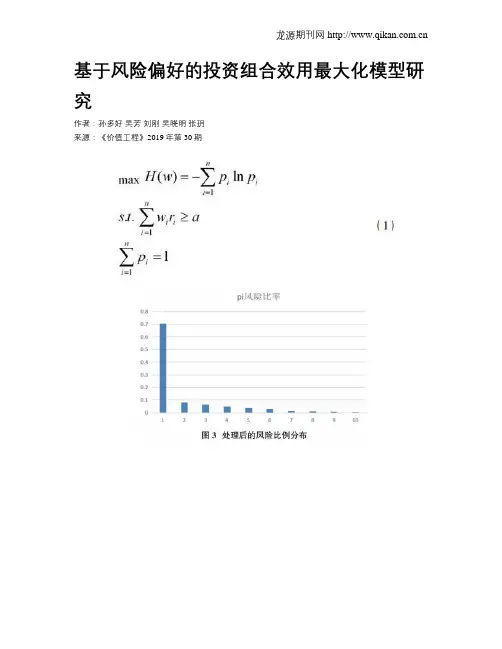
基于风险偏好的投资组合效用最大化模型研究作者:孙多好吴芳刘刚吴晓明张玥来源:《价值工程》2019年第30期摘要:在投资过程中,风险和收益之间存在着一种权衡,这种权衡是根据投资者风险偏好的不同而不同,这就要求我们在构建投资组合时应该充分考虑投资者的风险偏好从而达到投资效用最大化。
本文通过建立均值—最大熵优化模型,将风险因子引入所构建的投资组合模型中,通过调整风险因子,得到符合投资者风险偏好的投资组合,并通过汇添富消费混合基金的实证研究,验证了该投资组合效绩明显优于市场组合及样本组合。
Abstract: In the process of investment, there is a trade-off between risk and return. This trade-off varies according to investor's risk preferences, which requires that we should fully consider investor's risk preferences in the construction of portfolio so as to maximize the utility of investment.By establishing the mean-maximum entropy optimization model and introducing the risk factors into the portfolio model, this paper adjusts the risk factors to get the portfolio that meets the investor's risk preferences. The empirical study of the mixed fund of Huitian Rich Consumption verifies that the performance of the portfolio is obviously better than that of the market portfolio and sample portfolio.关键词:风险;投资组合;均值—最大熵优化模型Key words: risk;portfolio investment;mean-maximum entropy optimization model中圖分类号:F830.59;F224 ; ; ; ; ; ; ; ; ; ; ; ; ; ;文献标识码:A ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ;文章编号:1006-4311(2019)30-0265-040 ;引言构建投资组合的目的是为了对投资风险进行分散化,从而达到既定投资收益下有效降低风险目的。

基于双因子模型的量化投资策略初探作者:张力来源:《商情》2016年第01期摘要:随着投资策略研究不断发展,量化投资无论在投资理论研究还是实践中表现优异。
本文首先简单介绍了超额收益Alpha投资策略,然后对基于双因子模型超额收益Alpha量化投资策略进行了探讨,为后续的基于双因子模型的量化投资策略深入研究提供参考。
关键词:双因子模型量化投资超额收益Alpha1前言随着我国股市体制改革,股票市场迅猛发展,股票投资新增账户和新股扩张飞速,截止到2015年7月,股票账户数已经突破2亿,两市A股约有多2700多只股票,并推行多种利好政策逐步为股票投资者铺平了道路。
在牛短熊长的中国股票市场,众多依赖传统方法进行投资的投资者往往会损失惨重,此时利用量化投资策略以寻求较为稳定超额收益的投资方法愈来愈受到投资者青睐,其中尤其是超额收益Alpha量化投资策略广为受到关注。
2量化投资与超额收益Alpha投资策略量化投资就是通过收集整理现有已发生的大量数据,并利用数学、统计学、信息技术建立数学模型对收集到的数据进行分析研究,从而构建最优投资组合以获得超额收益。
简而言之,它是一个将传统投资理念、风险、收益等进行量化并付诸实现的过程。
在国内量化投资起步较晚,但随着国内金融市场的不断对外开放并与国际接轨,在国际上较为盛行的金融研究技术也逐步在国内铺展开来,但目前投资策略的系统化研究仍是我国量化投资长远发展的薄弱之处。
因此,更加系统的投资策略研究和实践成为当下迫切的需求。
系统投资策略及组合能推动量化投资的快速发展,对中国金融生态系统的良性循环起到积极的作用。
所谓超额收益Alpha指的就是实际收益率中高于对应的预期收益率的超额收益部分,严格地来讲,超额收益Alpha是用来衡量一个在风险调整下由投资所产生的“主动收益”。
超额收益Alpha量化投资策略主要来源于CAPM模型,在CAPM模型中,投资组合的收益率等于无风险利率加上风险溢价,只有承担更多的风险才能获得更高的收益。


河北工业大学硕士学位论文两类风险因子线性投资组合的条件风险价值姓名:***申请学位级别:硕士专业:应用数学指导教师:***20071201河北工业大学硕士学位论文两类风险因子线性投资组合的条件风险价值摘要本文把离散型随机变量为一维情景预设模型时线性投资组合的CVaR推广到风险因子服从多项分布和多维Poisson分布时线性投资组合的CVaR;此外,利用CVaR与ES在随机变量可积时的相等关系推导出连续型风险因子服从多维逻辑斯特分布与多维指数幂分布时线性投资组合的CVaR;最后给出一种特殊的连续型风险因子线性投资组合的CVaR.本文共分五章.第二章是预备知识.第三,第四章是本文的主体:首先,第三章给出了风险因子服从多项分布与多维泊松分布时线性投资组合的CVaR;而后,第四章第一节给出了风险因子服从多维逻辑斯特分布和多维指数幂分布时线性投资组合的CVaR,第二节给出风险因子为一种特殊的随机变量----多维泊松分布随机变量与多维指数幂分布随机变量之和----时线性投资组合的CVaR.第五章为结论.关键词:风险价值,条件风险价值,期望亏空,线性投资组合,离散型随机变量,连续型随机变量i各类风险因子线性投资组合条件风险价值iiCONDITIONAL V ALUE-AT-RISK FOR LINEAR PORTFOLIOS WITH TWO CATEGORY DISTRIBUTIONSRISK FACTORSABSTRACTIn the paper, we have extended CVaR of linear portfolios about discrete random variableof scenario models in space of one dimension to CVaR of linear portfolios of multinomial distribution and multi-Poisson power distribution in the hyperspace. In the same time, it presents CVaR of linear portfolios about random variables which have a logistic distribution and an exponential power distribution in use of the equivalence of CVaR and ES when the variables are integral. Finally, it gives CVaR of linear portfolios about the sum of different forms of random variables.There are five chapters in the paper. The first chapter is the introduction. The second one is the pre-knowledge of the paper. The third one and the forth one are the main body of the paper. At first, the third chapter offers CVaR of linear portfolios about random variables with multinomial distribution and multi-Poisson power distribution. Then the forth chapter presents CVaR of linear portfolios about random variables which have a logistic distribution and an exponential power distribution as well as CVaR of linear portfolios about the sum of different form of random variables. The last chapter is the conclusion.KEY WORDS:VaR, CVaR, ES, linear portfolios, discrete random variable, continue random variable河北工业大学硕士学位论文第一章 绪 论金融市场风险已成为金融机构和监管当局关注的焦点,许多金融机构投入大量资源开发金融风险技术.作为风险管理核心和基础的风险测量技术自上世纪九十年代以来,取得了许多重要进展,其中VaR 模型成了金融市场风险测量的主流模型.然而,研究发现,VaR存在两个重大缺陷:不满足一致性公理以及尾部损失测量的不充分(见文献[1,2,3 ]).著名的一致性公理是由Artzner等在1997年提出的,其内容是:若某种风险计量满足次可加性、正齐次性,单调性和传递不变性四个条件,则该风险计量是一致性风险计量.Artzner等指出,只有满足一致性要求的风险计量方法才能充当投资组合管理工具.一致性公理表达的是金融风险最基本的常识.通过这些条件将检验风险计量工具对投资组合的局部和总体的风险度量是否保持一致性.在一致性公理的四大条件中,次可加性是最为重要的.若VaR不满足次可加性,它就不是凸性的风险计量,我们也就不能通过优化来求得最小风险投资组合.而且,当VaR不满足次可加性时,投资组合的VaR值会大于投资组合中各项资产的VaR值的和,这将产生一个错误的风险规避策略:一个包含多个部门的金融机构只要将其资产分别划分给其下的各个部门,由各个部门分别计算VaR再求和,就能实现整个金融机构的风险降低.显然违背次可加性将有可能给金融监管系统带来系统漏洞.另外,我们可以证明,当且仅当投资组合的收益或损失呈正态分布时,VaR才满足次可加性,进而满足一致性要求.但是许多文献已经给出证明,无论是在国内还是国外的证券市场,投资组合的收益或损失分布都是厚尾或有偏的,即不满足正态性.这也意味着,用VaR来度量投资组合风险是不满足次可加性的,不符合一致性公理的要求.根据Jorion给出的定义(见文献[4]),VaR是指在给定的置信水平和投资期内投资组合可能遭受的最大损失.可见,VaR本质上只是对应于某置信水平的分为数,故又称之为分位点VaR.因此它无法考查分位点下方的信息,即所谓的左尾损失,这就是VaR尾部损失测量的非充分性.VaR方法的这一缺陷使人们忽略了小概率发生的巨额损失事件甚至是金融危机,而这又恰恰正是金融监管部门所必须重点关注的.正是因为VaR方法越来越为人们所熟知和认可而广泛应用于金融系统的风险度量,但其本质又有着上述的缺陷,故研究界纷纷试图对其进行改良,找到一个既具有可操作性又满足一致性公理,特别是考虑到左尾损失极值的风险测量.其中Rockafellar等学者在1997年提出的CVaR(条件风险价值)这一概念(见文献[5,6,7 ])引起了证券界金融风险管理人员的重点关注,并得到了越来越多业界人士的认可.CVaR是指在投资组合的损失大于某个给定的VaR值条件下的期望损失.从数学上看,CVaR实际上1各类风险因子线性投资组合条件风险价值是个期望值.由此不难发现CVaR与VaR的区别:首先,CVaR不是一个单一的分为数,而是尾部损失的均值,只有将所有大于VaR的损失值都考虑到才能计算,因此它对尾部损失的测量是充分的.其次,Artzner[8]、Acerbi[9]等通过不同渠道证明CVaR是满足次可加性的,因此不论回报是否服从正态分布,CVaR都是一致的风险计量.所以,我们可以认为与VaR相比,CVaR无疑是更加完善的资产组合风险管理工具,也是以后资产组合风险管理技术发展的重要方向之一.本文受文献[5], [9], [16], [17]的启发,把 [5]中离散型随机变量为一维情景预设模型时线性投资组合的CVaR推广到风险因子服从多项分布和多维Poisson分布(见文献[10,11,12])时线性投资组合的CVaR;此外,利用文献[9]给出的CVaR与ES(见文献[13,14,15])在随机变量可积时的相等关系以及文献[16,17]得出的椭圆分布(见文献[18,19])的ES值,推导出连续型风险因子服从多维逻辑斯特分布与多维指数幂分布时线性投资组合的CVaR;最后给出一种特殊的连续型风险因子线性投资组合的CVaR.本文共分五章.第二章是预备知识,介绍了本文的相关概念与相关引理.第三,第四章是本文的主体:首先,第三章给出了投资组合的收益或损失为多项分布和多维Poisson随机变量的线性函数的CVaR;而后,第四章第一节给出了投资组合的收益或损失为随机变量服从逻辑斯特分布与指数幂分布的线性函数的CVaR,第二节给出了投资组合的收益或损失是一类特殊的随机变量——两种类型随机变量之和(见文献[20])——的线性函数的CVaR.第五章为结论,对本文的主要工作进行总结.2河北工业大学硕士学位论文第二章 预备知识3r 记1212(,,...,),(,,...,)r x x x x y y y y ==,…,则相应的列向量记作t x ,ty ,…,其中表示矩阵的转置.记r 矩阵,t r ×()ij r r A ×=A ()ij r r B ×=B ,…,满足通常所定义的矩阵的乘法.特别的, 左乘列向量A t y ,记作t y A ,右乘行向量A x ,记作x A ;2212r 2x x x x x =++⋅⋅⋅+i 表示欧氏内积.我们称[0上种投资产品的投资组合价值的收益损失函数,]t r ()()(0)t t ΔΠ=Π−Π是线性的,如果是各种投资产品收益或损失()t ΔΠ()j X t (1,2,...,)j r =的线性函数,即:()()(0)t t ΔΠ=Π−Π=1122()()...()r r X t X t X t δδδ+++.为了便于书写,我们把()t ΔΠ简记作ΔΠ,()j X t 简记作j X .令12(,,...,)r δδδδ=,12(,,...,)r X X X X =,则:1rtj j j X X X δδδ=ΔΠ===∑i .§2-1 相关概念定义 (Va [15]2.1.1R β) 设(0,1]β∈是个固定值,X 是概率空间(,,P)ΩF 上一实随机变量,定义in .我们称f ∅=∞ ()inf{:[]}q X x P X x ββ=∈≤≥ (1)为X 的分为数,VaR ()()X q X ββ=−为置信水平为β时X 的风险价值(VaR β).定义 (ES [9]2.1.2β) 设(0,1]β∈是个固定值,X 是概率空间(,,P)ΩF 上一实随机变量,且.设为(1)中定义的分为数,我们称E[max(0,)]X −<∞)q X β(q X β−1{()}ES ()(1)(E[1](){[()]})X q X X q X P X βββββ−−≥−=−−+−−−<−为X 在置信水平为β时的期望亏空(ES β).定义 ([5]2.1.3CVaR β) 设(0,1]β∈是个固定值,X 是概率空间(,,P)ΩF 上一实随机变量,则X 的β-尾分布的均值称作条件风险价值(CVaR β).各类风险因子线性投资组合条件风险价值定义 ([5]2.1.4CVaR β+ 和CVaR β−) 设(0,1]β∈是个固定值,X 是概率空间(,上一实随机变量,则,P)ΩF CVaR ()E[|VaR ]X X X ββ+=−<− (2) 称作X 在置信水平为β时的上条件风险价值(CVaR β+).CVaR ()E[|VaR ]X X X ββ−=−≤−称作X 在置信水平为β时的下条件风险价值(CVaR β−).定义 ( r 维逻辑斯特分布) 若随机向量[19]2.1.5X 满足如下条件,我们称它的分布为n 维逻辑斯特分布.1)X 的密度生成元形式为:2φ()(1)uu e u e −−=+. 2)X 的联合密度函数具有如下形式:121121exp(()())2f ()||1(1exp(()()))2t X r t x x x c x x μμμμ−−−−−−=+−−−ΣΣΣ (3) 其中211121(2)[(1)]r rj r j c jπ∞−−−−==−∑.定义 ( r 维指数幂分布) 若随机向量[19]2.1.6X 满足如下条件,我们称它的分布为r 维指数幂分布.1)X 的密度生成元形式为:φ()sr u u e′−= ,其中,0r s ′>.2)X 的联合密度函数具有如下形式:1102f ()||exp{[()()]}2t s X r r x c x x μμ−−=−−−ΣΣ (4) 其中(2)2(2)(2)(2)r s r r s r c r r s πΓ=Γ. 定义 (r 维泊松分布) 设[11]2.1.712(,,...,)r X X X X =是r 元随机变量,如果12(,,,)r X x x x =⋅⋅⋅的联合概率密度函数为121112(12121211(,,,)!()!()!rr r x x x x xr r r r P x x x e x x x x x )λλλλλλ−−−−+++−⋅⋅⋅⋅⋅⋅=−⋅⋅⋅− (5)4河北工业大学硕士学位论文其中0k λ>,.1,2,,k r =⋅⋅⋅12r x x x ≤≤⋅⋅⋅≤,0,1,2,k x =⋅⋅⋅,1,2,,k r =⋅⋅⋅.则称X 服从参数为12(,,,)r λλλ⋅⋅⋅的r 元泊松分布,记作12~(,,,)r r X P λλλ⋅⋅⋅.定义 ( r 维多项分布) 设[10]2.1.812(,,...,)r X X X X =是r 元随机变量,如果12(,,,)r X x x x =⋅⋅⋅的联合概率密度函数为11211!(,,,)!!r x x r r n P x x x p p x x r ⋅⋅⋅=⋅⋅⋅⋅⋅⋅ , (6)其中诸i x 为非负整数,且1rii xn ==∑,01i p ≤≤,1,,i r =⋅⋅⋅,11ri i p ==∑,则称12(,,,)r x x x ⋅⋅⋅服从多项分布,记为1(,,,)r M n p p ⋅⋅⋅.注2.1.9 由定义2.1.3和2.1.4可知当X 为连续型随机变量时,CVaR β=CVaR β+=CVaR β−. 注2.1.10 一般情况下我们默认置信水平为β时X 的风险价值(VaR β)为正值,X 表示投资组合的收益或损失,当X 表示投资组合的损失时为负值.§2-2 相关引理现在,我们定义,X ΔΠ的表示形式同上,i X 为满足均值为μ,协方差为的椭圆分布,即:t=ΣAA 12(,,...,)~E (,,)r r X X X μψΣ()ψi 表示X 的特征生成元.则X 的概率密度函数具有如下形式:121f ()||g(()())t X x x x μμ−−=−−ΣΣ||Σ其中表示的行列式;,通过傅立叶变换,上Σ0g :+→ ≠n 2g(||||)x 可化作2(||||)ψξ形式.引理 设[17]2.2.1(0,1)β∈,t X X δδΔΠ==i 是r 维风险因子12(,,...,)r X X X X =的线性函数,其中12(,,...,)r δδδδ=,j δ(1,2,...,)j r =是j X 投资权重,且12(,,...,)~E (,,)r r X X X μψΣ,即X 的概率密度函数为121f ()||g(()())t X x x x μμ−−=−−ΣΣ,为g + 上连续可积且处处不为零的函数.若记g (1),VaR r q βδμ−+=i ,则置信水平为β时该投资组合的期望亏空ES β为:g 2(1),1g 22(1),()ES (())g()r r rq u qu du βββδμ−−+∞−=−+−i .引理 设[9]2.2.2(0,1)β∈是个固定值,X 是概率空间(,,P)ΩF 上一实可积随机变量,则5各类风险因子线性投资组合条件风险价值ES β=CVaR β.引理(条件风险价值作为加权平均) 设[5]2.2.3(0,1)β∈是个固定值,X 是概率空间(,,P)ΩF 上一实随机变量,VaR β为置信水平为β时X 的风险价值,CVaR β+为置信水平为β时X 的上条件风险价值.令(|VaR )1P X X βββλβ≤−−=−,则(i )当时,(|VaR )1P X X β≤−<1βλ<,即存在比VaR β大的损失,有CVaR VaR (1)CVaR ββββλλβ+=+−(ii )当时,(|VaR )1P X X β≤−=1βλ=,即VaR β为所有可能发生损失的最大值,此时CVaR β+没有意义.有CVaR VaR ββ=6第三章 两种离散型风险因子线性投资组合的CVaR关于多元离散型分布,由于其复杂性,除了多项分布和多元Poisson 分布外,对其研究一直较少.本文利用数学分析与概率统计相关知识(见文献[21, 22])给出多项分布和多元Poisson 分布的条件风险价值.定理3.1 设(0,1)α∈是个固定值,[0上种投资产品的投资组合的收益损失函数,]t r X δΔΠ=it X δ=是r 维风险因子12(,,...,)r X X X X =的线性函数,其中j X (1,2,...,)j r =是各种投资产品收益或损失,12(,,...,)r δδδδ=,j δ(1,2,...,)j r =是j X 投资权重.若 12(,,...,)r X X X X −=−−−服从r 维Possion 分布,则X −的概率密度函数为定义2.1.7中(5)式形式.若记1VaR α−为置信水平为1α−时投资组合的风险价值,则:(i )当时,1(|VaR )P α−ΔΠΔΠ≤−<111(|VaR )1P αααλα−−−ΔΠΔΠ>−=<,置信水平为1α−时投资组合的条件风险价值12111212()11112()11(,,,)11211CVaR (1)!()!()!rr r r rr j j j j n k j j x x x x x rr j tX x x x j r r x i jx X ex xx x x αλλλαααδδλλλδδλ−+==−−−+++−−=⋅⋅⋅=−<−⋅⋅⋅=+−−⋅⋅⋅−∑∑∑∑其中 12111212()111()121(,,,)1211(|VaR )!()!()!rr r r r r j j j j n k j j x x x x xr X x x x r r x i P e x x x x x αλλλαδδλλλ−+==−−−+++−=⋅⋅⋅−>−⋅⋅⋅ΔΠΔΠ>−=−⋅⋅⋅−∑∑∑,(1)(2)()111(,,,)kkkr n n n X i i i αααα+++=⋅⋅⋅()0,1,2,k m n ,i =⋅⋅⋅,1,2,,m r =⋅⋅⋅.(ii )当时,1(|VaR )P α−ΔΠΔΠ≤−=111(|VaR )1P αααλα−−−ΔΠΔΠ>−==,置信水平为1α−时投资组合的条件风险价值11CVaR VaR αα−−=()11krj j n j i αδ+==∑t X αδ=其中1(|VaR P )α−ΔΠΔΠ>−,X α同(i ).证明:X −服从r 维Possion 分布,当12(,,...,)r X n n n −=时,由定义2.1.7中(5)式,有121112()1211221211(,,,)!()!()!rr r n n n n nr r r r r P x n x n x n e n n n n n λλλλλλ−−−−+++−⋅⋅⋅−=−=⋅⋅⋅−==−⋅⋅⋅−可知当12(,,...,)r X n n n =−−−时,121112(1211221211(,,,)!()!()!rr r n n n n nr r r r r P x n x n x n e n n n n n )λλλλλλ−−−−+++−⋅⋅⋅=−=−⋅⋅⋅=−=−⋅⋅⋅− (7)对固定参数0k λ>,1,2,,k r =⋅⋅⋅.记,则121122(,,,r n n n r r P P x n x n x ⋅⋅⋅==−=−⋅⋅⋅=−)n 12r n n n P ⋅⋅⋅共有可列个点,按损失从小到大排序相应的损失点记为:(1)(2)()(1)(2)()(1)(2)()000111(,,,)(,,,)(,,,)k k k r r n n n i i i i i i i i i −−⋅⋅⋅−<−−⋅⋅⋅−<⋅⋅⋅<−−⋅⋅⋅−<⋅⋅⋅r )其中对应的概率为,(1)(2)()(,,,kk k r n n n i i i −−⋅⋅⋅−(1)(2)()r n n n kkkii i P ⋅⋅⋅()0,1,2,km n i =⋅⋅⋅,,,.1,2,,m r =⋅⋅⋅0,1,2,k n =⋅⋅⋅1,2,,k r =⋅⋅⋅对任意(0,1)α∈,存在非负整数k n α使得(1)(2)()(1)(2)()1r r n n n n n n kk k kk k k k k k ii i ii i n n n n P P ααα∞∞⋅⋅⋅⋅⋅⋅==+≥>∑∑由定义2.1.1中(1)式可得置信水平为1α−时投资组合的风险价值1VaR α−=,(1)(2)()12111(,,...,)(,,,)kkkr t r n n n i i i αααδδδ+++⋅⋅⋅i ()11krj j n j i αδ+==∑其中,1,2,,j k r α=⋅⋅⋅, 0,1,2,k n α=⋅⋅⋅)令(1)(2)()111(,,,kkkr n n n X i i i αααα+++=⋅⋅⋅则1VaR t X ααδ−=. (8)根据引理2.2.3(i )当时,1(|VaR )P α−ΔΠΔΠ≤−<111(|VaR )1P αααλα−−−ΔΠΔΠ>−=<,置信水平为1α−时投资组合的条件风险价值111CVaR VaR (1)CVaR 1αααλ+−−−=+−α− (9)由定义2.1.4,以及(7)式可知置信水平为1α−时投资组合的上条件风险价值11CVaR [|VaR ]E αα+−−=−ΔΠΔΠ<−12(,,,)0,1,2,,1,2,,()(|r k t t t X x x x x k r)t X P X X X αδδδδ=⋅⋅⋅=⋅⋅⋅=⋅⋅⋅=−<−∑)12()11112(,,,)1()(,,,r r r j j j j n k j j rj j r X x x x j x i x P x x x αδδδ+===⋅⋅⋅=<−=−⋅⋅⋅∑∑∑∑12111212()111()12(,,,)11211()()!()!()!rr r r r r j j j j n k j j x x x x xrr j j X x x x j r r x i x e x x x x x αλλλδδλλλδ−+==−−+−+−+++=⋅⋅⋅=−<−⋅⋅⋅=−−−+⋅⋅⋅−+∑∑∑∑12111212()11112()(,,,)11211()!()!()r r r r rr j j j j n k j j x x x x x rr j jX x x x j r r x i !x ex xx x x αλλλδδλλλδ−+==−−+−+−+++=⋅⋅⋅=−<−⋅⋅⋅=−−−+⋅⋅⋅−+∑∑∑∑则由(9)式,111CVaR VaR (1)CVaR 1αααλα+−−−=+−−12111212()11112()1(,,,)11211(1)()!()!()rr r r rr j j j j n k j j x x x x x rr j jtX x x x j r r x i x X ex xx x x αλλλααδδλλλδδλ−+==−−+−+−+++−=⋅⋅⋅=−<−⋅⋅⋅=−−−−+⋅⋅⋅−+∑∑∑∑ !其中11(|VaR P )αααλα−−−ΔΠΔΠ>−=,12111212()11112()1(,,,)1211(|VaR )()!()!()!rr r r r r j j j j n k j j x x x x x r j jX x x x r r x i x P e x x x x x αλλλαδδλλλδ−+==−−+−+−+++−=⋅⋅⋅−>−⋅⋅⋅ΔΠΔΠ>−=−−+⋅⋅⋅−+∑∑∑(ii )当时, 1(|VaR )P α−ΔΠΔΠ≤−=111(|VaR )1P αααλα−−−ΔΠΔΠ>−==,由(8)式,1VaR α−为置信水平为1α−时投资组合可能发生的最大损失,1CVaR α+−没有意义,置信水平为1α−时投资组合的条件风险价值11CVaR VaR αα−−=()11k rj j n j i αδ+==∑tX αδ=. 证毕. 定理3.2 设(0,1)α∈是个固定值,[0上种投资产品的投资组合的收益损失函数,]t r X δΔΠ=it X δ=是r 维风险因子12(,,...,)r X X X X =的线性函数,其中j X (1,2,...,)j r =是各种投资产品收益或损失,12(,,...,)r δδδδ=,j δ(1,2,...,)j r =是j X 投资权重.若 12(,,...,)r X X X X −=−−−服从r 维多项分布,则X −的概率密度函数为定义2.1.8中(6)式形式.若记1VaR α−为置信水平为1α−时投资组合的风险价值,则:ΔΠ1(i )当时,置信水平为11(|VaR )P α−ΔΠΔΠ≤−<α−时投资组合的条件风险价值112()111111(,,,)11CVaR !(1)!!r r r r j j j j n k j j rj jx x tr X x x x j rx i x X n px x ααααδδp δδλ+==−−=⋅⋅⋅=<−=+−⋅⋅⋅⋅⋅⋅∑∑∑∑其中11(|VaR )1P αααλα−−−ΔΠΔΠ>−=<112()11111(,,,)1(|VaR )!!rrrr j j j j n k j j j jx x r X x x x r x i x P p x x ααδδp δ+==−=⋅⋅⋅>−ΔΠΔΠ>−=⋅⋅⋅⋅⋅⋅∑∑∑, (1)(2)()111(,,,)kkkr n n n X i i i αααα+++=⋅⋅⋅()0,1,2,k m n ,i =⋅⋅⋅,1,2,,m r =⋅⋅⋅.(ii )当时,1(|VaR )P α−ΔΠΔΠ≤−=111(|VaR )1P αααλα−−−ΔΠΔΠ>−==,置信水平为1α−时投资组合的条件风险价值11CVaR VaR αα−−=()11krj j n j i αδ+==∑t X αδ=其中1(|VaR P )α−ΔΠΔΠ>−,X α同(i ).证明: X −服从r 维多项分布,当12(,,...,)r X n n n −=时,由定义2.1.8中(6)式有1112211!(,,,)!!r n n r r r r n P x n x n x n p p n n −=−=⋅⋅⋅−==⋅⋅⋅⋅⋅⋅可知当12(,,...,)r X n n n =−−−时,1112211!(,,,)!!r n r r r r n P x n x n x n p p n n =−=−⋅⋅⋅=−=⋅⋅⋅⋅⋅⋅n )n (10)记,则121122(,,,r n n n r r P P x n x n x ⋅⋅⋅==−=−⋅⋅⋅=−12r n n n P ⋅⋅⋅共有可列个点,按损失从小到大排序相应的损失点记为:(1)(2)()(1)(2)()(1)(2)()000111(,,,)(,,,)(,,,)k k k r r n n n i i i i i i i i i −−⋅⋅⋅−<−−⋅⋅⋅−<⋅⋅⋅<−−⋅⋅⋅−<⋅⋅⋅r )其中对应的概率为,(1)(2)()(,,,kk k r n n n i i i −−⋅⋅⋅−(1)(2)()r n n n kkkii i P ⋅⋅⋅()0,1,2,km n i =⋅⋅⋅,,,.1,2,,m r =⋅⋅⋅0,1,2,k n =⋅⋅⋅1,2,,k r =⋅⋅⋅对任意(0,1)α∈,存在非负整数k n α使得(1)(2)()(1)(2)()1r r n n n n n n kk k kk k k k k k ii i ii i n n n n P P ααα∞∞⋅⋅⋅⋅⋅⋅==+≥>∑∑由定义2.1.1中(1)式可得置信水平为1α−时投资组合的风险价值1VaR α−=,(1)(2)()12111(,,...,)(,,,)kkkr t r n n n i i i αααδδδ+++⋅⋅⋅i ()11krj j n j i αδ+==∑其中,1,2,,j k r α=⋅⋅⋅, 0,1,2,k n α=⋅⋅⋅)令(1)(2)()111(,,,kkkr n n n X i i i αααα+++=⋅⋅⋅,则1VaR t X ααδ−=. (11)根据引理2.2.3(i )当时,1(|VaR )P α−ΔΠΔΠ≤−<111(|VaR )1P αααλα−−−ΔΠΔΠ>−=<,置信水平为1α−时投资组合的条件风险价值111CVaR VaR (1)CVaR 1αααλ+−−−=+−α− (12)又由定义2.1.4,以及(10)式可知置信水平为1α−时投资组合的上条件风险价值11CVaR E[|VaR ]αα+−−=−ΔΠΔΠ<−12(,,,)0,1,2,,1,2,,()(|r k t t t X x x x x k r)t X P X X X αδδδδ=⋅⋅⋅=⋅⋅⋅=⋅⋅⋅=−<−∑12()11112(,,,)1()(,,,r r r j j j j n k j j rj j r X x x x j x i )x P x x x αδδδ+===⋅⋅⋅=<−=−⋅⋅⋅∑∑∑∑112()1111(,,,)11!()()!()!r r r r j j j j n k j j rx x j j r X x x x j r x i n x p p x x αδδδ+==−−=⋅⋅⋅=<−=−⋅⋅⋅−⋅⋅⋅−∑∑∑∑112()1111(,,,)11!()!()!r r r r j j j j n k j j rj jx x r X x x x j rx i x n x x αδδpp δ+==−=⋅⋅⋅=<−=−⋅⋅⋅−⋅⋅⋅−∑∑∑∑−1则由(12)式,111CVaR VaR (1)CVaR αααλα+−−−=+−−112()11111(,,,)11!(1)()!()!r r r r j j j j n k j j rj jx x tr X x x x j rx i x X n px x αααδδp δδλ+==−−−=⋅⋅⋅=<−=−−⋅⋅⋅−⋅⋅⋅−∑∑∑∑其中11(|VaR P )αααλα−−−ΔΠΔΠ>−=,112()11111(,,,)1(|VaR )()!()!r r r r j j j j n k j j j jx x r X x x x r x i x P p x x ααδδp δ+==−−−=⋅⋅⋅>−ΔΠΔΠ>−=⋅⋅⋅−⋅⋅⋅−∑∑∑(ii )当时, 1(|VaR )P α−ΔΠΔΠ≤−=111(|VaR )1P αααλα−−−ΔΠΔΠ>−==,由(11)式,1VaR α−为置信水平为1α−时投资组合可能发生的最大损失,1CVaR α+−没有意义,置信水平为1α−时投资组合的条件风险价值11CVaR VaR αα−−=()11krj j n j i αδ+==∑t X αδ=.证毕.注3.3 本文之所以研究X −服从r 维多项分布或Possion 分布,是因为当X 服从多项分布或Possion 分布时,投资组合只有收益没有损失,失去了研究风险价值的意义.第四章 几种连续型风险因子线性投资组合的CVaR§4-1 投资组合收益或损失为椭圆分布随机变量线性函数的CVaR定理4.1.1 设(0,1)α∈是个固定值,[0上r 种投资产品的投资组合的收益损失函数,]t X δΔΠ=it X δ=是维逻辑斯特分布风险因子r 12(,,.X ..,)r X X X =的线性函数,其中j X (1,2,...,)j r =是各种投资产品收益或损失,12(,,...,)r δδδδ=,j δ(1,2,...,)j r =是j X 投资权重,则X 的概率密度函数为定义2.1.5中(3)式形式.记g,r q α=,1VaR α−为置信水平为1α−时投资组合的风险价值,则置信水平为1α−时该投资组合的条件风险价值1CVaR α−为:g 2,()112211CVaR (1)r q r i i i ieααδμ−∞−−+−==−+−i ,其中11121(1)]rj r j c j∞−−−=′=−∑.证明:对任意(0,1)α∈,由定义2.1.4可知X 为可积随机变量,又由引理2.2.2可知1ES CVaR 1αα−−= (13)由引理2.2.1可知1ES α−=g 2,1g 22,()(())g()r r r q u q u du ααδμ−+∞−−∫i则由(13)式1CVaR α−=g 2,1g 22,()(())g()r r r q u q u du ααδμ−+∞−+−i其中12122g()(1)u ru eu c e −−=+.211121(2)[(1)]r rj r j c j π∞−−−−==−∑则1CVaR α−=g 2,112g22,1()22(())(1)r u r r q u eu q du e ααδμ−−+∞−−−+i令2112220122()(1)u r qu eI u q du e−−+∞−=−+∫则2111222201222()222(1)u r r q u u q eu I de −+−+∞−=−+∫211222222()2(1)r r xq x q e x dx e +−−+∞−=−+∫1212r I +=又2122121()21r q xq I x d e−+∞−x ′⎛⎞=−⎜⎟+⎝⎠∫ 212202()()2r x i q i q x e d −∞+∞−=x ′⎛⎞=−−⎜⎟⎝⎠∑∫ 2121212()(1)2r i ix q i q x i e −∞+∞+−=⎛⎞=−−⎜⎟⎝⎠∑∫dx2121212(1)()2r i i q i q i x e −∞+∞+−==−−∑∫x dx21()1221(1)r q i v i i i ve −∞+∞−++==−∑∫dv2112201(1)q r ii i i i eve −∞+∞−+−==−∑∫vdv21112221(1)()()r q r i i i i ieiv e d iv −−∞+∞−−+−==−∑∫v21112221(1)()r q r i i y i iey e d −−∞+∞−−+−==−∑∫y2112211(1)()2r q i i i r ie −∞−−+=+=−Γ∑ 故2,11222,1()22(())(1)g r u r gr q u eI u q du eαα−−+∞−′=−+∫2,()111222112(1)(2gr q r r i i i r ie α+−∞−−+=+=−Γ∑ 2,()11122112((1)2gr q r r i i i r i eα+−∞−−+=+=Γ−∑2则1CVaR α−I δμ′=−+i (14) 把I ′,带入(14)rc g 2,()11122111CVaR 2()(1)2r q r r i i i r i eααδμ+−∞−−+−=+=−+Γ−∑i 2g2,()111112211(1)](1)r q r i rj i j i ji eαδμ−∞∞−−−−−+===−−−∑∑i2g 2,()11221(1)r q r i i i ieαδμ−∞−−+==−+−i其中11121(1)]rj r j c j∞−−−=′=−∑证毕.定理4.1.2 设(0,1)α∈是个固定值,[0上r 种投资产品的投资组合的收益损失函数,]t X δΔΠ=it X δ=是r 维指数幂分布风险因子12(,,...,)r X X X =的线性函数,其中j X (1,2,...,)j =X r 是各种投资产品收益或损失,12(,,...,)r δδδδ=,j δ(1,2,...,)j r =是j X 投资权重,则X 的概率密度函数为定义2.1.6中(4)式形式.记g,r q α=,1VaR α−为置信水平为1α−时投资组合的风险价值,则置信水平为1α−时该投资组合的条件风险价值1CVaR α−为:11CVaR r c αδμα−′=−+i ,其中1122221100221g 2,,11()()122()(())(())112!!()()22r r g 2si s r r i i r r r r i i r r c c r c si q q r r i i ααππ−−i r +++−−∞∞−==−−+′′=−−+++ΓΓ∑∑+ 1220g 21,11()(1)2((1)21)...((1)21)12[(())(!!r si ir i j r r r r j r q j i j α−++∞∞)]2si −==−−⋅−−⋅⋅−−++−−∑∑ 证明:对任意(0,1)α∈,由定义2.1.5可知X 为可积随机变量,又由引理2.2.2可知1ES CVaR 1αα−−= (15)由引理2.2.1可知g 2,1g 221,()ES (())g()r r r q u q u du αααδμ−+∞−=−−∫i由(15)式g 2,1g 221,()CVaR (())g()r r r q u q u du αααδμ−+∞−=−−i其中02g()s r u r u c e−=.(2)02(2)(2)(2)r s r r s r c r r s πΓ=Γ,. 0,0r s >则1CVaR α−0g 2,1g 222,()(())s r r r u r q u q e du ααδμ−+∞−=−+−iδμ′=−i 令021220()sr r u qI u q edu −+∞′−=−∫则2120201()()!r s iqi r u I u q du i −∞+∞=′−=−∑∫ 212021()()!r isi qi r u q u du i −∞+∞=′−=−∑∫011()!ii r I i ∞=′−=∑其中21221()r si qI u q u du −+∞=−∫令1u v=,则 210221111()()r si q 1I q d vv −=−∫v1112222112222()(1)()r r si si r q q vq vq −−++−−−−=−∫2dvq令2x vq =,则111222112210()(1)r r si si r I q x x−−++−−−=−∫dx11222()r si q I −++=即12211220(1)r si r I x xd −−−−−=−∫x122101(1)2((1)21)...((1)21)[1]!r si j j r r r j x x d j −−−−∞=−⋅−−⋅⋅−−+=+∑∫x 11222211001(1)2((1)21)...((1)21)[]!r r si si j j r r r j xdx x x dx j −−−−−−−−∞=−⋅−−⋅⋅−−+=+∑∫∫1221112201(1)2((1)21)...((1)21)!r si r j si j r r r j xdx x dx j −−−−−∞−−−=−⋅−−⋅⋅−−+=+∑∫∫ 171221112201(1)2((1)21)...((1)21)!r si r j si j r r r j xdx x dx j −−−−−∞−−=−⋅−−⋅⋅−−+=+∑∫∫ 1111(1)2((1)21)...((1)21)1()(2!j r r r r j r si j si j ∞)2−−=+−⋅−−⋅⋅−−++=−−+−−∑i a =则0011()!ii r I I i ∞=′−=∑1122021())!r si i i r q I i −++∞=′−=∑112201())!r si i i i r q a i −++∞=′−=∑1121201()1())2!r si i i r r si q i −++∞−=′−+=−−∑11221011()(1)2((1)21)...((1)21)1()()!!r si i i j r r r r j r q j i j −++∞∞2si −==′−−⋅−−⋅⋅−−+++−∑∑− 所以0g 2,1g 222,()(())s r r r r q I u q edu αα−+∞−′=−∫12201g 2,1(12()))2!r si i r i rr si q i α−++∞−=−+=−−∑1220g 21,11()(1)2((1)21)...((1)21)12(())()!!r si ir i j r r r r j r q j i j α−++∞∞2si −==−−⋅−−⋅⋅−−+++−∑∑− 则1CVaR αδμ−′=−+i1r c δμα′=−+i18其中121()2r r r c c I r π−′′′=+Γ1122221100221g 2,,11(()122()))(())112!!()()22r r g 2si s r r i i r r r r i i r r c c r si q q r r i i ααππ−−i ++−−∞∞−==−−+=−−+++ΓΓ∑∑+ 1220g 21,11((1)2((1)21)...((1)21)12[))(!!r si i r i j rr r r j r q j i j α−++∞∞)]2si −==−−⋅−−⋅⋅−−++−−∑∑ 证毕.注4.1.3 当X 服从维指数幂分布时,由定义2.1.5中r X 密度函数可知,r 维正态分布是定义2.1.6中(4)式时的特殊情况,由此可知满足定理4.1.2中条件的r 维正态分布的条件风险价值.01,1r s ==注4.1.4 当X 服从维指数幂分布时,由定义2.1.5中r X 密度函数可知,r 维拉普拉斯分布是定义2.1.6中(4)式012r s ==时的特殊情况,由此可知满足定理4.1.2中条件的维拉普拉斯分布的条件风险价值. r§4-2 投资组合收益或损失为不同类型随机变量之和的线性函数的CVaR除了离散型与连续型随机变量以外,下面我们将给出随机变量为一个离散型随机变量与一个连续型随机变量和的条件风险价值.定理4.2.1 设(0,1)α∈是个固定值,某投资组合在[0上收益或损失函数,]t t Y Y δδΔΠ==i 是维风险因子的线性函数,其中r 12(,,...,)r Y Y Y Y =j Y 是各种投资产品的收益或损失,12(,,...,)r δδδδ=,j δ(1,2,...,)j r =是j Y 投资权重,若Y X X ′′′=+, X ′=12(,,...,)r X X X ′′′,12(,,...,X X X ′′′′′′=)r X ′′,,j j X X ′′′为每个j Y (1,2,...,)j =r 的分支投资产品的收益或损失,其中,X X ′′′相互独立,X ′服从均值为μ,协方差为的维指数幂分布,tΣ=AA r X ′′−服从维泊松分布.记r 1VaR α−为置信水平为1α−时投资组合的风险价值,,tr q α′′=,12(,,,r n n n n )′′=−−− ,则置信水平为1α−时该投资组合的条件风险价值1CVaR α−为:19121112102()12100112111,2,...,()2CVaR 1!()!()!!()2r r r k n in n n n n i r r n k i r r k r r a c e n n n n n n i λλλαπλλλα−−−−∞∞∞−+++−===−=−⋅⋅⋅=−−−⋅⋅⋅−Γ∑∑∑212122,,,,||||(){[(1)()][(1)()]}(21)(2)t r si r si r si r si r r r r n q k q k q k q k r si r si ααααδδμ++++++′′+++−++++−++++A 其中1111(3)2((3)21)...((3)21)1()(1)(2!j i j r r r r j r a si j j ∞)2si −−=+−⋅−−⋅⋅−−++=−−+−−−∑证明:由X ′服从维指数幂分布,则r X ′的概率密度函数具有如下形式:1102f ()||exp{[()()]}2t s X r r x c x x μμ−−′′′=−−−ΣΣ′ 其中12(,,,)r x x x x ′′′′= ,)02(2)(2)(2)r s r r s r c r r s πΓ=Γ,. 0,0r s >又X ′′−服从r 维泊松分布,则12(,,...,)r X n n n ′′−=时,有121112()1211221211(,,,)!()!()!rr r n n n n nr r r r r P x n x n x n e n n n n n λλλλλλ−−−−+++−⋅⋅⋅′′′′′′−=−=⋅⋅⋅−==−⋅⋅⋅−可知当12(,,...,)r X n n n ′′=−−−时,121112()1211221211(,,,)!()!()!rr r n n n n nr r r r r P x n x n x n e n n n n n λλλλλλ−−−−+++−⋅⋅⋅′′′′′′=−=−⋅⋅⋅=−=−⋅⋅⋅−对固定参数0k λ>, ,0,1,2,k n =⋅⋅⋅12r n n n ≤≤⋅⋅⋅≤,1,2,,k r =⋅⋅⋅.记,则Y X 121122(,,,r n n n r r P P x n x n x ⋅⋅⋅′′′′′′==−=−⋅⋅⋅=−)n X ′′′=+的分布函数:F ()()()Y y P Y y P X X y ′′′=<=+<1201,2,...,((,,,);k r n k rP X n n n X y X ∞==)′′′==−−−<∑′′−=<∑∞′⋅⋅⋅′′′<−==1201,2,...,()r k n n n n k rP P X y X ∞⋅⋅⋅==′′′−1201,2,...,f ()r k n n n Xx y x n k rP x dx ′′=∑∫dx 1201,2,...,f ()r k n n n X x y x n k rP x ∞′⋅⋅⋅′′′<−==′′=∑∫由连续型随机变量的定义可知Y 为连续型随机变量,其分布密度函数为:1201,2,...,f ()f ()r k Y n n n X n k ry P y ∞′⋅⋅⋅==x ′′=−∑令,则由条件风险价值的定义,置信水平为112(,,,r n n n n ′′=−−− )α−时投资组合的条件风险价值1CVaR =CVaR 1αα+−−1E[|VaR ]α−=−ΔΠΔΠ<−201VaR 1()f ()Y y y y d αδδα−<−=−∫i i y1VaR 1f ()tt Y y y y d αδδy α−<−=−∫121VaR 01,2,...,1f ()t r k tn n n X y n k ryP y n αδδα−∞′⋅⋅⋅<−==dy ′′=−−∑∫121VaR 01,2,...,1[f (t r k t n n n X y n k rP y y αδδα−∞′⋅⋅⋅<−==′′=−−∑∫)]n dy121112()12012111,2,...,1!()!()!rr r k n n n n nr n r r k re n n n n n λλλλλλα−−−∞−+++=−=⋅⋅⋅=−−⋅⋅⋅−∑11102VaR [||exp{[()()]}]2t tt r y r s y c y n y n αδδμ−−−<−′′′′−−−−−∫ΣΣdy μ121112()12012111,2,...,!()!()!rr r k n n n n nrr n r r k rc en n n n n λλλλλλα−−−∞−+++=−=⋅⋅⋅=−−⋅⋅⋅−∑11102VaR [||exp{[()()]}]2t t t y r s y y n y n dy αδδμ−−−<−′′′′−−−−−∫ΣΣμ (16)令111021VaR ||exp{[()()]}2t t t y r s I y y n y n αδδμ−−−<−′′′′=−−−Σ−−∫Σdy μ设,()tu y n μ−′′=−−A ty u n μ′′=++A ,||dy du =A ,.tΣ=AA 则201||||21()VaR ()s t t ru t tu n I u n ed αδμδμ−−′′++<−′′=++∫A A u201||||2()VaR ()()s t t tru t tu n u n ed αδδμδμ−−′′<−−+′′=++∫A A u201||||2VaR ()[()]s tru tu n u n ed αδδμδδμ−−′′<−−+′′=++∫A A i i u设为把R δA 映射为(||||,0,...,0)δA ,把映射为的旋转,则12(,,...,)r u u u 12(,,...,)r v v v 2011||211||||VaR ()[||||()]s trv tv n I v n ed αδδμδδμ−−′′<−−+′′=++∫A A v2122 2若,,则221||||||||v v v ′=+1r v −′∈ 221011VaR ()(||||)||||211{[||||()]ts r n rv v t1}I v n edv d αδμδδδμ−−′′−−+′−+−∞v ′′′=++∫∫A A作球面坐标变换v l ξ′=,2r S ξ−∈,为2r S −1r −维球面,则,22||r r dv S l dl −−′=2122||1()2r n S n π−−=−Γ为1r −维球面面积.221012VaR ()()2||||2110||{[||||()]}ts r n rv l r t1I S lv n edv αδμδδδμ−−′′−−+∞−+−−∞′′=++∫∫A A dl令1,VaR ()||||t rn q ααδμδ−′′++=A ,则220,12()22110||{[||||()]}s r r rq v l r t1I S l v n e dv αδδμ−∞−−+−−∞′′=++∫∫A dl 2令,则21m v l =+0,21132222111()[||||()]1()2s rn r r q m tv 1I m v v n edmdv n απδδμ−−−∞−−∞′′=−++−Γ∫∫A0,2113222211[||||()]()1()2s rn r r q tv v n m v edmd n απδδμ−−−∞−−∞′′=++−−Γ∫∫A 1v,1211[||||()]1()2rn q t v n I d n απδδμ−−−∞v ′′′=+−Γ∫A +令2132221()sr r m v I m v e dm −∞′−=−∫则21322211()()!r s i v i r m I m v dm i −∞∞=′−=−∑∫2132211()()!r isiv i r m v m dm i −∞+∞=′−=−∑∫31()!ii r I i ∞=′−=∑2132231()r si v I m v m dm −+∞=−∫令1m z=,则21322131111()()r siv 23I v d zz z −=−∫331222211322221110()(1)()r r si si r v v zv zv −−++−−−−=−∫21dzv令21x zv =,则3312223122310()(1)()r r si si r I v x x dx −−++−−−−=−∫312214()r si v I −++=即32231240(1)()r si r I x x d −−−−−=−∫x322101(3)2((3)21)...((3)21)[1()]!r si jj r r r j x x d j −−−−∞=−⋅−−⋅⋅−−+=+−∑∫x 3311222201(3)2((3)21)...((3)21)[(!r r si si j j r r r j )]xdx x x dx j −−∞−−−−−−=−⋅−−⋅⋅−−+=+−∑∫∫3311222201(3)2((3)21)...((3)21)(1)!r r si j si jj r r r j xdx x dxj −−∞−−−−−−=−⋅−−⋅⋅−−+=+−∑∫∫3311222201(3)2((3)21)...((3)21)(1)!r r si j si jj r r r j xdx x dx j −−∞−−−−−−=−⋅−−⋅⋅−−+=+−∑∫∫ 1111(3)2((3)21)...((3)21)1()(1)(2!j j r r r r j r si j si j ∞−−=+−⋅−−⋅⋅−−++=−−+−−−∑)2(17)i a =则2132221()sr r m v I m v e dm −∞′−=−∫31()!i i r I i ∞=′−=∑3122141()()!r si i i r v I i −+∞=′−=∑312211())!r si i i i a r v i −++∞=′−=∑所以02132221()s r r v I m v edm −∞−′=−∫3120211()2)!r si i i i ra v i −++∞=−=∑则,1211[||||()]1()2rn q t 1I v n I d n απδδμ−−−∞v ′′′=+−Γ∫A +。

基于双风险因子调整的剩余收益经营与投资最优决策模型王立夏【摘要】一般来说,公司净资产基于投向可以分为净经营性资产和净金融性资产.这两种净资产所面临的风险属性是不同的,净经营性资产承担的是经营性风险,而净金融性资产承担的则是金融性风险.作为公司多元化经营的决策者,在公司净资产一定的情况下,如何合理分配经营性投资与金融性投资间的比例并作出最优的投资决策,以达到公司价值最大化?本文基于一般形式的三阶段剩余收益模型,根据净经营性资产具有经营风险,净金融性资产则具有金融风险的风险识别与判断,从理论上构建出双风险因子调整的剩余收益经营与投资决策模型(Opera-tion and Investment Decision Model of Dual-risks RIM,OIDM-DRRIM).同时,利用中国资本市场1997年到2014年的经验数据进行实证检验,研究结果表明,所构建的OIDM-DRRIM具有非常好的适用性,公司经营决策者可以根据该模型计算出净经营性资产和净金融性资产之间的最优分配比例,进而作出使公司价值最大化的经营与投资决策.【期刊名称】《运筹与管理》【年(卷),期】2019(028)006【总页数】8页(P53-60)【关键词】经营风险;金融风险;双风险因子;剩余收益;经营与投资决策【作者】王立夏【作者单位】上海大学悉尼工商学院,上海 200899【正文语种】中文【中图分类】F230.9;F2020 引言公司投资的本质,从公司金融的角度定义,是指在一定期间内,通过改变自身的资本存量来换取未来公司财富的增值活动[1]。
根据投资形式进行分类,主要有:按照投资期限可以分为短期投资和长期投资;按照投资对象则分为对内投资和对外投资;按照投资的具体形式则可分为直接投资和间接投资,也有学者把其分为实业投资和股权投资[2]。
现有研究认为公司进行投资的目的主要有两方面,一方面是为了获取收益,另一方面则是为了分散风险[3]。
基于双因子CIR强度式定价的信用债券投资组合优化李鸿禧;宋宇【期刊名称】《运筹与管理》【年(卷),期】2022(31)12【摘要】信用风险和利率风险是相互关联影响的。
资产组合优化不能将这两种风险单独考虑或简单的相加,应该进行整体的风险控制,不然会造成投资风险的低估。
本文的主要工作:一是在强度式定价模型的框架下,分别利用CIR随机利率模型刻画利率风险因素“无风险利率”和信用风险因素“违约强度”的随机动态变化,衡量在两类风险共同影响下信用债券的市场价值,从而构建CRRA型投资效用函数。
以CRRA型投资效用函数最大化作为目标函数,同时控制利率和信用两类风险。
弥补了现有研究中仅单独考虑信用风险或利率风险、无法对两种风险进行整体控制的弊端。
二是将无风险利率作为影响违约强度的一个因子,利用“无风险利率因子”和“纯信用因子”的双因子CIR模型拟合违约强度,考虑了市场利率变化对于债券违约强度的影响,反映两种风险的相关性。
使得投资组合模型中既同时考虑了信用风险和利率风险、又考虑了两种风险的交互影响。
避免在优化资产组合时忽略两种风险间相关性、可能造成风险低估的问题。
【总页数】8页(P120-127)【作者】李鸿禧;宋宇【作者单位】中央国债登记结算有限责任公司博士后科研工作站;中国人民银行金融研究所博士后流动站;中国东方资产管理股份有限公司评估管理部【正文语种】中文【中图分类】F830.3【相关文献】1.双指数跳CIR利率模型下无违约零息票债券定价2.CIR利率模型中基于对数效用的投资组合最优化问题3.基于信用风险的双因素可转换债券定价模型研究4.考虑信用风险的债券投资组合优化模型5.含信用等级迁移的公司债券基于双资产的结构化定价因版权原因,仅展示原文概要,查看原文内容请购买。
基金投资中的多因子模型分析随着金融市场的发展和投资者需求的不断增长,基金投资成为了越来越多人关注的话题。
在投资基金时,多因子模型是一种常用的分析方法,它帮助投资者评估基金的收益风险特征。
本文将就基金投资中的多因子模型进行分析,从理论和实践两个方面探讨其应用。
一、多因子模型的理论基础多因子模型是指用多个因子来解释和预测资产或投资组合收益的模型。
它基于资本资产定价模型(CAPM)的基础上,引入了多个影响资产价格的因素。
常用的因子包括市场因子、价值因子、规模因子、动量因子等。
这些因子各自代表了不同的市场现象和投资特征,通过综合考虑这些因子可以更准确地评估基金的风险与收益。
二、多因子模型的实践应用1. 市场因子分析市场因子是多因子模型中最基本的因子之一,它代表了整个市场的波动情况。
通过市场因子的分析,我们可以了解到基金的整体表现如何受到市场波动的影响。
例如,当市场因子为正时,说明市场表现良好,基金投资的机会也相对较好;而当市场因子为负时,说明市场走势不佳,投资者需谨慎对待。
2. 价值因子分析价值因子是指衡量资产估值相对便宜还是昂贵的因素。
通过分析价值因子,我们可以评估基金的低估或高估程度。
具体而言,价值因子较高的基金可能具有较低的市盈率、较高的股息率等特征,而价值因子较低的基金则相反。
投资者可以根据价值因子的分析结果来选择适合自己风险偏好和投资目标的基金。
3. 规模因子分析规模因子是指衡量公司规模对基金表现的影响程度。
较小规模的公司往往具有较高的成长性和回报潜力,而较大规模的公司则更加稳定可靠。
通过规模因子的分析,投资者可以了解基金所投资的公司规模结构,从而更好地把握市场机会。
4. 动量因子分析动量因子是指衡量资产或投资组合在一段时间内涨跌幅的因素。
通过动量因子的分析,我们可以评估基金近期的涨跌情况以及是否存在持续的趋势。
若分析结果显示基金具有较好的动量因子,则可能意味着其投资策略较为成功,值得投资者关注。
双风险因子调整的剩余收益定价模型理论研究1王立夏上海大学悉尼工商学院摘要:本文在一般形式的三阶段剩余收益模型基础上,针对第三阶段的非明确预测期,将公司的净资产按不同属性划分为净经营性资产和净金融性资产,这两种不同属性的净资产具有不同的风险特性,即净经营性资产具有经营风险,净金融性资产则具有金融风险。
基于两种不同属性净资产具有不同风险因子的特性,从理论上构建出双风险因子调整的剩余收益定价模型(Double Risks Residual Income Model, DR-RIM)。
本模型有利于公司经营者或投资人对风险进行全面且合理的评估,从而做出正确的经营或投资决策。
同时,本模型还可以使公司做出保持净经营性资产和净金融性资产最优比例的决策,以使公司的价值最大化。
关键词:经营风险、金融风险、双风险因子、定价模型0. 引言Preinreich(1938)最早提出剩余收益概念,Edward和Bell(1961)继续就剩余收益进行研究,他们提出清洁盈余即净剩余关系假设,并利用权益回报率等变量指标来替代未来难于预测的股利变量,提出了一般剩余收益模型,即公司的内在价值就等于公司权益的账面价值与未来超常收益折现的总和。
该模型的建立对于利用财务会计信息对公司价值进行评估具有重要的理论意义。
Ohlson(1995),Feltham and Ohlson(1995)和Feltham and Ohlson(1996)基于一般剩余收益模型,从会计信息有用观的角度,提出了对会计实证研究意义意义重大的三个剩余收益模型,即Feltham and Ohlson系列剩余收益模型。
Feltham and1收稿日期:2016-作者简介:王立夏(1974—),男,江西修水人,上海大学悉尼工商学院讲师,中国注册会计师,中国注册税务师,高级会计师,高级经济师,博士Ohlson 系列剩余收益模型利用线性信息动态假设,顺利地解决了对于未来无限期的预测问题。
金融市场中多因素风险因子定价模型研究概述:金融市场中的风险是投资者和市场参与者普遍面临的重要问题之一。
了解和准确定价金融市场中的风险因素对于投资组合管理和风险控制至关重要。
多因素风险因子定价模型是通过分析多个风险因素对证券收益的影响,揭示市场风险背后的内在规律的统计模型。
近年来,该模型受到广泛关注和研究,并在实际投资决策中得到了应用。
1. 多因素风险因子定价模型的理论基础:多因素风险因子定价模型的核心理论基础来源于资本资产定价模型(Capital Asset Pricing Model, CAPM)和套利定价理论(Arbitrage Pricing Theory, APT)。
CAPM模型表达了资产收益与资产系统性风险的关系,而APT模型则认为资产收益受到多个因素的影响。
2. 多因素风险因子定价模型的构建:构建多因素风险因子定价模型需要确定适当的风险因素并收集相关数据。
一般来说,风险因素可以分为宏观经济因素、行业因素和公司特定因素等。
通过研究市场历史数据并运用统计方法,可以识别和选择最能解释证券收益波动的关键因素。
然后,需要将这些风险因素与证券收益进行回归分析,以估计因子的影响系数。
3. 多因素风险因子定价模型的优势:与传统的CAPM模型相比,多因素风险因子定价模型具有以下几个优势:首先,多因素模型考虑了更多的影响因素,因此能够更准确地解释和预测证券收益的波动。
这对于投资者和基金经理来说,提供了更可靠的风险评估和投资决策支持。
其次,通过分析各种风险因素的影响,多因素模型能够帮助投资者理解市场波动背后的根本原因,并掌握市场的变化趋势。
最后,多因素模型的广泛应用可以帮助投资者在构建投资组合时更好地分散风险,实现资产配置的优化。
4. 多因素风险因子定价模型的应用:多因素风险因子定价模型已经在实际投资中得到了广泛应用。
许多基金公司和机构投资者利用这种模型来评估投资组合的风险和预测证券的未来表现。
此外,该模型还可应用于风险管理和资产定价等领域,为投资者提供更准确的决策依据。
基于双因素模型的银行信用风险评估研究1.引言银行是财经领域的关键组织之一,信用风险是银行风险管理中的关键问题。
随着银行业务的不断扩展,信用风险成为银行风险管理中最重要的一种风险。
因此,建立一种科学有效的银行信用风险评估模型,对于银行风险管理具有至关重要的意义。
2.双因素模型简介传统的信用风险模型主要基于客户画像的一些基本指标来进行风险评估,比如其年龄、职业及财务状况等等。
这些因素虽然代表了客户的个人情况,但由于个体差异很大,因此效果并不理想。
基于双因素模型的信用风险模型引入了历史行为与个人特征两个维度,将客户的信用风险评估转化为从客户的历史信用行为与个人特征两个方面对其预测未来信用风险。
其中历史信用行为可以通过对客户的过往信用记录的评估得到;而个人特征则需要客户自身提供相关信息,如客户的性别、学历、职业等信息。
3.借鉴国外的双因素模型研究国外学者在研究双因素模型时,通常会引入很多特征属性,用于提高模型的预测准确率。
例如,Tobias J. Moskowitz, Annette Vissing-Jorgensen和Luo Zeng等学者以被动组合贝塔和Alpha作为历史信用表现评估指标,以包括性别、种族、年龄、家庭收入等个人特征属性作为个人特征因子。
实证结果表明,双因素模型可以有效提高个体客户的信用评级的预测准确度。
4.建立基于双因素模型的银行信用风险评估模型基于国内银行特点,我们建议在个人特征中考虑以下指标:年龄、性别、学历、职业、职称、家庭住址和政治等级;在历史行为中,我们建议关注的有:存款余额、贷款余额、信用卡额度、信用卡使用率、逾期次数等。
在建立双因素模型的过程中,需要充分做好数据预处理工作,使得原始数据经处理后更符合模型假设。
模型参数的求解可以用统计学习算法来解决,如逻辑回归算法。
5.实证研究我们以某国内银行为例展开了实证研究。
实证结果表明,基于双因素模型的银行信用风险评估模型的预测准确率比传统的基于客户画像模型的信用评级模型有明显的提高,可以更好地识别风险,为我行的信用审批提供参考意见。
财务风险管理中的基于因子模型的投资组合优化研究财务风险管理一直是企业发展中的重要环节,尤其是当市场波动加剧,经济环境不稳定时,有效的财务风险管理显得尤为必要。
而投资组合优化是财务风险管理中的一个重要方面,通过因子模型进行投资组合优化可有效降低风险,提高资产收益率。
一、因子模型的介绍因子模型是用来解释多个证券收益率与共同的系统风险因素之间关系的一种方法。
这种方法假设证券收益率与一些共同的因子有关,将证券收益率分解为系统风险因子和非系统风险因子,从而得到了这些证券之间的相关性。
因子模型通常采用线性回归分析的方法进行计算,并可通过调整模型中因子的权重,来实现投资组合优化的目的。
二、基于因子模型的投资组合优化借助因子模型进行投资组合优化,可将每个证券的收益率分解为系统风险因子和非系统风险因子。
系统风险因子是所有证券之间的共同风险因素,而非系统风险因子则是与个别证券自身特性相关的风险因素。
通过对投资组合中的证券进行分类,使用因子模型分析每个证券的因子权重,就可以选择合适的证券组合,从而实现投资组合优化。
三、因子模型各因子的解释在因子模型中,重要的因子包括风险因子和收益因子。
其中,风险因子是所有证券共同具备的风险特征,如市场风险、行业风险等;而收益因子则是与各个证券个别特征相关,如公司规模、资产质量、盈利能力等。
通过对风险与收益因子的分析,可以有效识别投资组合中存在的风险问题,并制定相应的风险管理策略。
四、因子模型的实践应用因子模型可应用于各种金融机构的投资组合管理、资产评估和风险控制等重要环节。
在投资组合管理中,应用因子模型能够更好地确定投资组合中证券的权重,从而合理配置风险,平衡风险与收益。
在资产评估中,因子模型可作为一个比较客观的评估工具,对证券的价格进行合理评估。
在风险控制方面,应用因子模型可更好地发现投资组合中存在的风险问题,预测市场波动,降低风险损失。
综上所述,投资组合优化基于因子模型的理论与实践应用具有重要意义。