测距仪LM50 说明书

激光测距仪操作说明书一．激光测距仪硬件介绍HUDLCD显示器RS232数据串口扳机LCD显示器二．测距仪的技术指标a)罗盘(抗磁性传感器，Post-Fluxgate 技术)i."0.5 º 精确度b)磁倾仪i."0.1 º 倾斜精度ii."40 º 倾斜范围c)测距i.精度–测８５米外的白目标精度为０.１米ii.最大距离–１８５０米(反射目标)iii.最小距离–３米iv.高压输电线１７５米v.杆状标志４００米vi.树（无叶）４００米vii.建筑物，树（有叶）８００米三．激光测距仪的基本操作3．1 如何校对激光测距仪●开启电源●按“MENU” 健●用>?键来进行功能选择●选择“COMP” 并按下“Enter” 键●选择“CAL” 并按下“Enter” 键●LCD显示窗显示“Initializing Please Wait!” &“Rotate Unit for Calibration” 信息●以射击的姿势扣住扳机. LCD显示窗显示“Data PointCount” 信息●慢慢转动Contour枪1-2圈. 每圈用45-60秒钟完成●慢慢转动Contour枪1-2圈. 每圈用45-60秒钟完成●在转动中，慢慢地从上到下，从左到右移动(±40º的范围)●虽着 Contour 的移动, 你将看到数据点(Data PointCount) 在增加。

当其值增加到275时，罗盘校对操作就完成了。

松开板机，系统恢复原来的设置●每次系统上电都必须要重复以上操做3.2 开机自检自检信息：仪器开机后将进行自检，自检信息将显示在LCD 显示屏上:Selft TestControur XLRic当自检信息结束后回到以前的测量界面时，说明自检成功，否则会出现以下错误信息:End Of Self Test*** Fall3.3 标准测量模式下的测量标准模式是仪器在开机后默认的模式，在这种模式下，仪器将显示所测目标的距离、方位和倾斜值。

激光测距仪LMD2000用户手册常州潞城传感器有限公司目录1.0概述 (2)1.1系统原理 (2)1.2技术性能与指标 (2)1.3接线表 (3)2.0参数代码说明 (3)2.0.1模拟量输出范围的起点Range Beginning（RB） (3)2.0.2模拟量输出范围的终点Range End（RE） (3)2.0.3报警值选择（OPT） (4)2.0.4报警点1（DL） (4)2.0.5报警点2（DH） (4)2.0.6报警迟滞Alarm Hysteresis（AH） (5)2.0.7RS485或RS232选择 (6)2.0.8串口地址设置 (6)2.0.9软件版本号 (6)3.0操作说明 (7)3.0.1后面板示意图 (7)3.0.2参数设置过程 (7)3.0.2.1按键功能 (7)3.0.2.2参数设置步骤及说明 (7)4.0串口参数设定 (8)4.0.1串口连接 (8)4.0.2定义ASCII码RS485和RS232通讯协议 (8)4.0.2.1RS232通讯 (8)4.0.2.2RS485通讯 (10)5.0错误信息 (12)6.0机械尺寸 (12)1.0概述LMD2000激光测距仪专门用于对固定和移动物体的距离测量。

主要特点如下：•在恶劣的户外环境下，仍能保持很高的测量精度和可靠性•测量范围最大可达100米•使用可见激光束，易于瞄准被测物•灵活的可扩展的连接电缆，便于供电、电平信号、开关量和模拟量输出•可用不同的参数对开关量输出和模拟量输出分别编程•随意设定距离范围，并能用开关量输出表示距离的正负超差1.1系统原理LMD2000激光测距仪采用相位比较原理进行测量。

激光传感器发射不同频率的可见激光束，接收从被测物返回的散射激光，将接收到的激光信号与参考信号进行比较，最后，用微处理器计算出相应相位偏移所对应的物体间距离，可以达到mm级测量精度。

1.2技术性能与指标测量范围1：0.2～30m内，可直接测量；30～100米，需使用特制反射器测量精度2：0.2～30米：±2mm；30～100米：±3mm；分辨率：1mm激光发散角：0.6mrad供电电压：DC24V直流或交流AC（100～240）V(用户选择)数据接口：通过按键或串口（RS232或RS485）进行参数设置继电器输出：AC250V，10A；DC30V，5A响应时间小于320ms电平输出：PNP高电平DC24V，低电平0V；最大负载电流300mA；响应时间小于160ms。

徕卡测距仪使用说明书徕卡测距仪使用说明书:一、使用前的准备,一,电池的装入/更换打开仪器尾部的固定挡板。

向前推卡钮～向下将底座取下。

按住红色的卡钮推开电池盒盖。

安装或更换电池。

关闭电池盒盖～安装底座和卡扣。

当电池的电压过低时～显示屏上将持续闪烁显示电池的标志{B～21}。

此时应及时更换电池。

1、按照极性正确装入电池。

2、使用碱性电池,建议不要使用充电电池,。

3、当长时间不使用仪器时～请取出电池～以避免电池的腐蚀。

更换电池后～设置和储存的值都保持不变。

,二,多功能底底座固定挡板可以在下面的测量情况下使用:边缘测量～将固定挡板拉出～直到听到卡入的声音。

1、从2、从角落测量～将固定挡板拉出～直到听到卡入的声音～轻轻将固定挡板向右推～此时固定挡板完全展开。

仪器自带的传感器将辨认出固定挡板的位置～并将自动设置测量其准点。

,三,内置的望远镜瞄准器在仪器的右部有一个内置的望远镜瞄准器。

此望远镜瞄准器为远距离测量起到辅助的作用。

通过瞄准器上的十字丝可以精确地观察到测量目标。

在30米以上的测量距离～激光点会显示在十字线的正中。

而在30米以下的测量距离～激光点不在十字线中间。

,四,气泡一体化的水泡使仪器更容易调平。

,五,键盘1、开/测量键2、第二级菜单功能3、加+键4、计时,延迟测量,键5、等于[=]键6、面积/体积键7、储存键8、测量基准边键9、清除/关键10、菜单键11、照明键12、间接测量,勾股定律,键13、减-键14、BLUETOOTH ,六,显示屏1、关于错误测量的信息2、激光启动3、周长4、最大跟踪测量值5、最小跟踪测量值6、测量基准边7、调出储存值8、储存常数9、主显示10、单位～包括乘方立方,2/3,11、顶的面积12、墙面积13、3个额外显示,如:测量中间值,14、BLUETOOTH蓝牙开/关15、第二级菜单功能开16、硬件故障17、间接测量-利用勾股定律18、间接测量-利用勾股定律-部分高度19、面积/体积20、带常数的测量21、电池充电量显示二、菜单功能,一,设置在菜单中可以改变设置～并将其长久保存～并在关机和更换电池后不改变。

A Method of Calculating Measuring Interval forLarge-Size StraightnessShengzhou Luline 1:Mechanical and Electrical Engineering line 2: Harbin Institute of Technologyline 3: Harbin, Chinaline4:e-mail:*****************Zhongxi Shaoline 1:Mechanical and Electrical Engineering line 2: Harbin Institute of Technologyline 3: Harbin, Chinaline4:e-mail:*********************Weishun Wangline 1:Research and Development Center line 2: Qiqihar Heavy CNC Equipment CORP. LTDline 3: Qiqihar, Chinaline4:e-mail:138****************Hongya Fuline 1:Mechanical and Electrical Engineering line 2: Harbin Institute of Technologyline 3: Harbin, Chinaline4:e-mail:****************.cnAbstract—Accurately straightness measuring has a direct relation to the promotion of the machine precision. In the process of straightness measurement, since the measuring interval has a great impact on the accuracy and efficiency of large-size straightness measurement, and there is no detailed measurement interval calculation method at present, it is necessary to make a deeply research to the measuring interval. This paper gives theoretical derivation to the measuring interval based on the Nyquist sampling theorem. Maximum frequency M and the number of measuring points in one period N are determined based on measurement tolerance, and then calculate the optimal theoretical measuring interval. Finally, measure the straightess of the guide rail under diferent measuring interval including the optimal one. Validate the calculation method through the straightess measuring experiment. The experimental results show that the optimal theoretical measuring interval derived in this paper is suitable, which proves the correctness of the calculating method.Keywords-Straightness; Measuring interval; Large-size; Accuracy; Optimal theoretical measuring interval.I.I NTRODUCTIONStraightness tolerance is one of the geometric tolerances which are specified in the national standard and the international organization for standardization (ISO), and it is mainly used to control the shape error of straight line in plane or space[1]. The accurate measurement and evaluation of the straightness error is very important to eligibility judgment and guarantee of geometry parts with the straightness tolerance requirements[2]. Straightness measurement usually adopts the method of equal intervals measurement to measure the measured object through the measuring interval. There isn’t convincingly theoretical basis about the definition of the measuring interval in the related standard of country and enterprise[3], while the definition mostly depends on the experience of the technician[4][5]. The large measuring interval brings few measuring points,which will result in part of information losing that can cause the shape of the measured object cannot be accurately measured. Conversely, if the measuring interval is too small and the measuring points are too many, it will bring some interference information and useless data, especially for large-size straightness measurement, therefore this will cause low measuring efficiency and untrusted measuring results. So it is necessary to make a deeply theoretical analysis about how to choose the straightness measuring interval of large-size, and to choose suitable measuring interval in measurement of large-size under the premise of measurement requirement,aiming to improve the efficiency of straightness measurement and evaluation and to ensure the credibility of the measurement results.II.T HE DETERMINATION OF MEASURING INTERVAL IN LARGE-SIZE STRAIGHTNESS MEASUREMENTA.Nyquist sampling theoremAt present, the theoretical basis of determining the measuring interval is the Nyquist sampling theorem at home and abroad [6], the content of the theorem is as follows: If the maximum frequency of a continuous single value analog is M and the sampling frequency is 2M, it will completely determine the analog waveform. It means that there must be sampled at least twice times in one changing cycle of the maximum frequency. The sampling period now is presented by Eq.(1)12M∆<(1) where ∆and M respectively stand for sampling period and the maximum frequency of single value analog.International Conference on Chemical, Material and Food Engineering (CMFE-2015)The measuring interval corresponds to the sampling period of the signal in the time domain[7]. By the Nyquist sampling theorem, the number of measuring points in total length K can be determined by the maximum frequency M and the number of sampling in one changing cycle N of the maximum frequency. With the total measurement length L, the measuring interval can be determined as Eq.(2)=L L K MN∆= (2)where L,K,M and N respectively represent total measuring length, theoretical optimum measurement points in total measurement length, the maximum frequency and the number of sampling N in one changing cycle of the maximum frequency(2N >).It is observed that the measuring interval ∆ can be determined by total measurement length L, the maximum frequency M of the signal of the surface shape of the measured guide rail and the number of measuring points N in one changing cycle of the maximum frequency. Figure.1 describes the calculation process of theoretical measuringLarge-size StraightnessB. The determination of the maximum frequency MSince the determination of the maximum frequency of surface profile signal M is related with the measurement tolerance δ, there needs to introduce the measurement tolerance δ. The purpose of straightness measurement is to truly express the measured surface shape. The measurement errors from the measuring method and instrument will cause that the machining errors of the measured object cannot be accurately measured, so we should try to reduce measuring errors which mainly refers to errors from the method. Inpractice, the measurement method of equal interval is often used in straightness measurement, but the uncertainty of measuring interval brings the uncertainty of the position of measuring. The measuring errors from the method are mainly caused by mismatching between the measurement points and the extreme values points of the measured surface profile, and the measurement tolerance δ is used to restrict the measuring errors especially from measuring methods. Literature [8] points out that measurement tolerance δ relate with tolerance grade level and size of the measured object. By selecting the appropriate measurement tolerance δ based on the characteristics of the measured object, we can determine the maximum frequency M of the measured object surface shape of the signal.The error signal of the surface profile in the measured guide rail contains geometrical form error 、 surface waviness and surface roughness. In terms of frequency and amplitude, the low frequency and large amplitude makes the geometrical form error be the major factor affecting the surface appearance. The surface roughness frequency is high and amplitude is small. The frequency and amplitude of the surface wave are between both the above[9]. In the actual measurement, because of the difference of measured surface, the maximum frequency M of surface profile signal is not the same. The specific way to determine the M is to find out the former M order harmonic components of the measured surface profile signal, then compare each order harmonic amplitude with the measurement tolerance δ, find the maximum frequency M whose amplitude is above the measurement tolerance δ.In summary, according to the selected measuring interval determined by the total length L of the measured object and related national standards, measure the object and get the measurement data, and then modify the data through least square method to eliminate the influence of the installation inclination of the measured surface. Process the revised data by Fourier transform and data X(k) after Fourier transform which is described as Eq.(3)21()[()]()j ikn ni X k DFT x i x i eπ−−===∑ (3)where x(i) and n respectively represent the original measurement data and the total number of measuring points. Compare each order harmonic amplitude C i with the measurement tolerance δ, find the harmonic C m whose amplitude is above the measurement tolerance δ and order is the highest, then the maximum frequency is M.C. The determination of the number of meauring points in one cycle NIn the process of straightness measurement,the extreme values ultimately determine the straightness error value. Any one periodic signal can be formed by a number of sinusoidal signals, so we can assume that the measured surface profile is a sine wave, its period is T and its amplitude is a as Figure.2 describes, then we can see B and D is the determinant to straightness error value. As can be seen from Figure.2, thedecrease of the measuring interval will make the measurement points much closer to the extreme values points and then finally decrease the deviation caused by the mismatching between the measurement points and the extreme values points. But the decrease of the measuring interval and the increasing of the measurement points reduce the measurement efficiency and increase the amount of calculation, there is need to discuss the optimum number of Y PositionAssume that the number of measuring points in one changing cycle of the maximum frequency on the measured surface is N, the amplitude of the frequency component is a and its period T=2π,so the measuring interval is 2π/N . The measuring starting point is zero A, and B fall between K and K+1（K=0,1,2……N ）, then the difference between K and B ∆Y K. and K and B ∆Y K+1 are determined as Eq.(4) and Eq.(5)sin(2/)Y a a K N K π∆=− (4)sin(2(+1)/)+1Y a a K N K π=−∆ (5) In actual measurement, the position of the measured point is unknown. Assume that the actual positions of the measured points and the measuring point position deviation is △X, then the difference of B value and K and K+1 point measurements are respectively determined as Eq.(6) and Eq.(7) sin((2/N)X)K Y a a K π∆=−+∆ (6) 1sin((2(1)/N)X)K Y a a K π+∆=−++∆ (7) Point B is between point K and point K+1, so when the actual position of measuring point changes, the variation trend of ΔY K and ΔY K+1 is just the opposite, one increases, another reduces. It can be proved that the limitation of measurement error caused by the mismatching between the measurement points and the extreme values points.ΔY K =ΔY K+1, the change of the actual measurement point △X is as Eq.(8) (42)/(2)X N K N π∆=−− (8) Take Eq.(8) into Eq.(6) and Eq.(7), the limit of measurement error near B is as Eq.(9) max (1cos(/N))B Y a π∆=− (9) Similarly, the limit of measurement error near the extreme value point D is as Eq.(10) max (1cos(/N))D Y a π∆=− (10)Therefore, the limit of straightness measurement error ΔY max caused by mismatching between the measurement points and the extreme values points are determined as Eq.(11)max max max2(1cos(/N))B D Y Y Y a π∆=∆+∆=−(11)As can be seen from Eq(11), with the number of measuring points N increasing,limit error of straightness measurement gets smaller. Therefore, as long as we know the amplitude of the maximum frequency of the measured surface signal a , we can get the number of measuring in one cycle of the maximum frequency N with measurement tolerance δ.D. Determination of straightness measuring interval Δ Combine the maximum frequency M and the number of sampling in one changing cycle of the maximum frequency N , we can get the number of measuring points K in the total measuring length which descibes the determination of theoretically optimal measuring points as Eq.(12) =K MN(12) And theoretically optimal measuring interval in total measurement length is determined as Eq.(13)=L L K MN∆= (13)III. E XPERIMENTAL VERIFICATION TO THE CALCULATIONMETHOD FOR MEASURING INTERVAL OF L ARGESTRAIGHTNESS Theoretically optimal measuring interval can be deduced according to the large-size straightness measuring interval calculation method with the original experimental data obtained. Validate the theoretically optimal measuring interval derived in this paper is reasonable, through measuring the straightness by different measuring interval including the optimal one.The measuring object in experiment is straightness within the vertical plane of the 5m guide rail whose accuracy index T is 0.02mm and the measuring instruments is Renishaw XL-80 laser interferometer. In order to eliminate the effect of the tilt of the rail to straightness measurements, use the least squares method to assess the straightness. It is recommended that the measurement tolerance δ in the calculation can be T/5~T/10.Figure.3 Measuring the Straightness of Guide Rail The length of bridgeboard used in straightness measurement are 160mm,500mm,750mm and 1000mm. Figure.3 describes straightness measurement by Renishaw XL-80 laser interferometer. TABLE 1 describes the impact of different measurement tolerance δto the measuring intervals that are derived.TABLE 1 The Impact of Different Measurement Tolerance δ to theMeasuring IntervalsMeasurement tolerance Theoretically optimal measuring interval [mm] δ=T/10 544δ=T/8 544δ=T/6 620δ=T/5 620As can be seen from TABLE 1, the theoretically optimal measuring interval derived under the case of δ=T/10 is 544mm, so the raw data obtained by the 160mm can be used to calculate as true values. TABLE 2 below describes the results of straightness measurement under the case of different measuring intervals by laser interferometer.TABLE 2 Straightness under Different Measuring IntervalsMeasuring interval [mm] Straightness [μm]160 40.922500 43.782750 33.81000 26.846The theoretically optimal measuring interval derived is about 550mm, and the interval less than 550mm can be used in practical. Taking the purpose of measuring efficiency and true expression of the straightness of the measured object into account, we can choose 500mm as measuring interval. As can be seen from TABLE 2, the results of straightness measurement got under the case of interval 160mm and 500mm are basically the same, while the results are significantly smaller under the case of interval 750mm and 1000mm, so the interval 500mm can be the optimal measuring interval.IV.C ONCLUSIONThis article proposes a calculation method for the large-size straightness measuring interval based on Nyquist sampling theorem. The results of validation experiments indicate that the method is feasible. According to the rail experimented, the interval 500mm through theoretical derivation can be its optimal measuring interval. Because the measurement tolerance δis from experiment in this paper, the subsequent research should give theoretical derivation and inspect the relationship between the measurement tolerance δ and measurement length.A CKNOWLEDGMENTThis work is supported by the National Science and Technology Major Project of China (2013ZX04013-011-09) and Heilongjiang Postdoctoral Fund in 2013 (LBH-Z13209). The authors would like to express their appreciation to the contribution of Xiaozhong Lou and Zhonghe Xu, who are the engineers at Qiqihar Heavy CNC Equipment CO., LTD, for offering help in experiments.R EFERENCES[1] F.G. Huang. The Number of Measurement Extraction Points forStraightness Error Evaluation[J]. Journal of Huaqiao university: Natural Science Edition, 2011, 32(6): 615-617.[2] F.G. Huang and Y.J. Zheng. Research straightness error measurementsampling scheme[J].Tool and Technology, 2007,10:95-98.[3]X.F. Hou. Research of Sampling Spacing in Measuring StraightnessBased on CMM[J].Tool and Technology, 2008, 42(6): 102-103. [4]M. M. Dowling, P. M. Griffin, K.-L. Tsui and C. Zhou. StatisticalIssues in Geometric Feature Inspection Using Coordinate Measuring Machines. Tchnometrics, 1997,39(1)3~24.[5] A. Weckenmann, H. Eitzert, M. Garmer and H. Weber. Functionality-Oriented Evaluation and Sampling Strategy in Coordinate Metrology.Precision Engineering,1995,17:244~252.[6]Y.H Zheng, L.N. Zhang and K.W. Qing. Extraction scheme of the newgeneration GPS and its application research[J]. Machinery Design & Manufacture, 2008 (6): 193-194.[7]L.L. Huang, L.X. Wang, Yu Wang, H.L. Wang and F.G. Huang.Extraction of Straightness Error Signal with Harmonic Analysis. [J].Journal of Huaqiao university: Natural Science Edition, ,2014,01:7-10.[8]Z Li and Z.G. Xu and X.Q.Jiang. Interchangeability andMeasurement Technology——Geometrical Product Specifications and Verification(Higher Education Press,China 2004). pp.67.[9] B.Fei, Y.J. Fan and WenXiong Xu. Adaptive Sampling Method——Anew method used in measuring the shape error[J]. Journal of Applied Sciences, 1994, 12(4): 423-430.[10]F.X Zhang and H. Zhao. Theoretical research between sample step anddeviation shape in straightness measurement[J]. Aiavtion method & measurement technology. 1995, 15(2): 9-11.。

lomvum测距仪说明书Lomvum测距仪是一款精密测量工具，可以快速、准确地测量各种长度、面积、体积以及间距等。

一、产品外观Lomvum测距仪外观简洁，主要由测量部分、显示屏、控制按键和电池仓组成。

二、产品特点1、高精度测量：Lomvum测距仪采用激光技术，具有高精度、高速度的测量能力，测量范围从0.05米到60米不等。

2、多功能：Lomvum测距仪支持长度、面积、体积、连续测量、最大/最小值测量等多种测量方式，满足不同测量需求。

3、易操作：Lomvum测距仪采用大尺寸LCD液晶显示屏，界面简洁、易读，同时操作简单方便，适用于各种人群使用。

4、自动校准：Lomvum测距仪自动支持校准，准确度高，保证了测量数据的可靠性。

三、使用方法1、按下电源键开启测距仪，在显示屏上可以看到“0.00”数值。

2、选择需要进行的测量方式：(1) 按功能键进行选择，如：长度、面积、体积等。

(2) 点击单位键，选择需要的单位，如：米/英尺/英寸等。

3、使用参考位标记测量：(1) 将测量仪对准需要测量的起始点，按下“测量”按键。

(2) 将测量仪对准需要测量的终点，按下“测量”按键。

(3) 显示屏会显示所测得的数值。

4、键入参数测量：(1) 直接通过键盘键入需要测量的数值，然后按下“测量”按键。

(2) 显示屏会显示所测得的数值。

5、最大/最小测量：(1) 点击“MAX/MIN”键，选择需要测量的模式。

(2) 将测量仪对准需要测量的目标，按下“测量”按键。

(3) 显示屏会显示所测得的最大/最小数值。

四、注意事项1、使用时请避免阳光直射、划痕、碰撞等情况。

2、请使用干燥的抹布清洁测距仪，避免使用含酸性或碱性的清洁剂。

3、使用时请遵循使用说明，避免误操作或酿成其他危害。

4、在不使用时请关闭电源，避免耗电等情况。

5、Lomvum测距仪只能在室内环境下使用，不能在室外使用，避免影响精度。

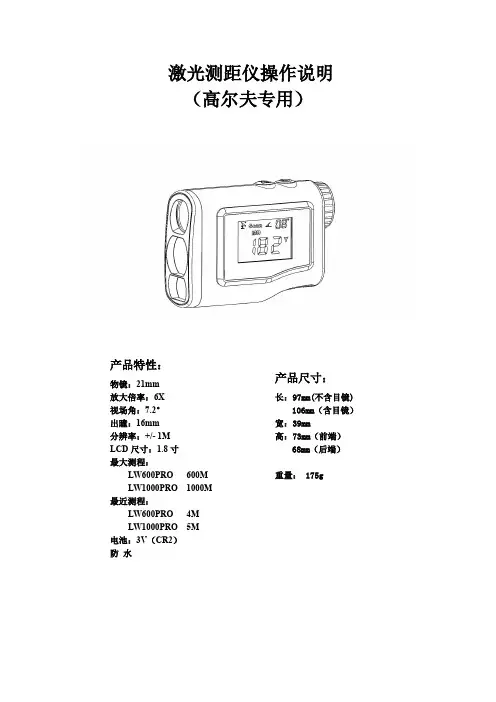
激光测距仪操作说明（高尔夫专用）产品特性：物镜：21mm放大倍率：6X视场角：7.2°出瞳：16mm分辨率：+/-1MLCD尺寸：1.8寸最大测程：LW600PRO600MLW1000PRO1000M 最近测程：LW600PRO4MLW1000PRO5M电池：3V（CR2）防水产品尺寸：长：97mm(不含目镜)106mm（含目镜）宽：39mm高：73mm（前端）68mm（后端）重量：175g1、开机按键开机开机画面，是上次操作后的功能界面。

2、单位转换长按键可切换距离单位，M和Y。

在“测距”，“旗杆锁定”，“高尔夫距离修正”，“雾天”4种模式中，都可以通过长按键来切换M,Y单位，单位切换后将在4种模式中统一使用。

3、模式选择短按键可在“测距”，“旗杆锁定”，“高尔夫距离修正”，“雾天”，之间切换选择。

侧屏的内容将与望远镜内显示内容同步。

侧屏中有出现MD符号时表示显示的是实测距离，出现RD时表示显示的是建议距离。

3-1测距原理望远镜显示界面侧屏显示界面短按键开始测距望远镜显示界面侧屏显示界面3-2“旗杆锁定”模式原理说明在旗杆锁定模式中，可以将点D从众多的背景点中分离出来，并只保留该点的距离d1。

从而达到自动锁定旗杆，并清除旗杆背后的树林等杂散目标的目的。

望远镜显示界面侧屏显示界面在旗杆扫描模式画面出现后，按住启动旗杆扫描功能，此时画面中的旗帜周围的方框会闪动，将测距机的瞄准点在被测旗杆的两侧来回扫描，当旗杆的数据被测到后，数据将被保留，而画面中旗帜周围的方框也不再闪动，表示旗杆数据被锁定。

望远镜显示界面侧屏显示界面3-3高尔夫距离修正：将测距值AB与坡度值(<±20°）带入到高尔夫飞行弹道的方程中，根据距离解算出高尔夫的建议击球距离。

在坡度为正时，击球距离要远。

距离：AB点间距=AD点间距若按实际距离，击球抛物线为1，此时由于坡度为正，实际只能飞行到C 点。

要达到B点，需要按抛物线2击球，此时的飞行距离应该是AE点间的距离。

激光测距仪带速度测量功能的SNDWAYSW-600A,SW-1000A,SW-1500A具有距离、速度、坡度和高度测量功能的多功能设备操作说明该产品的设计符合标准：GB/T14267-2009广东制造，货号：00000950安全说明使用前仔细阅读安全要求和操作说明在使用该设备之前，请阅读所有的安全和操作说明。

任何未在这些说明中描述的措施都可能导致设备发生故障，影响测量的准确性或对用户或第三方造成伤害。

请勿自行打开或修理该装置。

严禁对激光发射器的功能做任何修改或调整。

妥善存放设备，不要让儿童接触到它，避免未经授权的人使用。

切勿将激光发射器对准自己或旁人，对准你身体的任何部位或任何高度反射的物体。

该设备的电磁辐射会对其他电子设备造成干扰。

不要在飞机上或医疗设备附近使用本装置。

不要在爆炸性或易燃性环境中使用本设备。

不要将废旧电池和无法使用的电器与家庭垃圾一起处理。

请按照现行法律和关于处理此类设备的规定来处理设备。

如果您在使用过程中遇到任何问题或疑问，请立即联系您的SNDWAY官方代表，我们将尽快帮助您解决问题。

感谢你购买SNDWAY手持式激光测距仪!带倾斜测量功能的SNDWAY多功能激光测距仪是一款集双筒望远镜和激光测距仪功能于一体的便携式激光倾斜测距仪。

主要应用。

•对于物体的详细检查，测量静态物体或低速移动且在可视范围内的物体。

该仪器的特点是测量精度高，测量速度快，可检测参数的可视化。

经济性：提供自动断电和低耗电。

•多功能激光测距仪结合了最新技术，可同时显示物体的距离和倾角。

在确定与物体的距离时，它可以显示到目标点的线路与地面的角度（仰角定义为正，俯角定义为负），相对高度和可见地平线的范围。

激光发射器的功率足够低，对人眼来说很安全。

它能够测量任何物体的范围，其体积小、重量轻，便于携带。

它由一个可充电的锂离子电池供电。

测距仪广泛用于电力设施（复杂的测量和扫描功能可以方便地检查远处的物体，如电力线和电线杆）、高速铁路、公用事业、林业设计、建筑、互联网通信设计、通信线路的检查和维修等，在开放的乡村和高尔夫、狩猎和野营旅行中使用。

测距仪说明书测距仪是一种仪器，主要用于测量物体之间的距离。

它可以用于各种应用，包括建筑、制造、测绘、激光标记和机器人等。

这是一种非常有用的工具，下面我们将为您介绍一下如何使用测距仪。

1. 开机使用测距仪前，需要将其开机。

按下电源按键，屏幕将显示菜单，然后进入测量模式。

2. 选择模式在菜单中选择适当的模式，例如测量距离、面积或体积。

选择模式后，设备将开始测量。

3. 对准目标在进行测量之前，需要先对准目标。

选择需要测量的对象，将测距仪对准目标并保持稳定。

4. 测量距离在目标对准之后，对其进行测量。

点击测量键，设备将发出一个激光束，直接照射到目标的表面。

设备将在屏幕上显示测量的数值。

如果需要进行连续测量，则可以按住测量键并更新结果。

5. 测量面积选中面积模式后，将激光射向首个角落，并使用设备的功能测量每个角落的距离。

在完全测量后，设备将计算面积并在屏幕上显示结果。

6. 测量体积如果需要测量物体的体积，则可以选择体积模式。

在测量距离和面积后，可以通过选择物体高度和单击计算键来完成测量。

7. 单次测量和连续测量测距仪可以执行一次或连续测量。

在单次测量中，设备进行一次测量并显示测量结果。

在连续测量中，设备将在点击测量键时连续进行测量，并显示测量结果。

8. 显示单位在使用设备时，需要选择合适的度量单位。

可以选择米、英尺、英寸等单位。

您将需要根据项目的需求选择适当的单位。

9. 存储测量结果测距仪还可以存储测量结果。

在测量完成后，可以将数据存储在设备的内存中，以备将来使用。

10. 翻转显示屏有些测距仪具有翻转显示屏的功能，可以根据使用者的需求实现自动翻转屏幕。

在使用过程中，还需要注意以下几点：1. 将设备保持平稳，以确保测量结果的正确性。

2. 在使用设备时要避免划痕或损坏。

3. 在不使用设备时，建议将其放置在盒子或软垫中以保护它。

4. 某些设备具有防水或防尘功能，但并不是所有设备都配备此类功能，使用前请确保知道设备的全面性。

测距传感器操作说明
一、接口
整机选用7芯航插接口，管脚定义是：⑴电源正极，电压为5V供电；⑵电源地；
⑶空；⑷传感器的RS232发送信号TXD；⑸传感器的RS232接收信号RXD；⑹信号地；
⑺空。

二、操作
通电5V即刻开始连续测距，并通过RS232接口发送数据，数据单位固定为米。

三、通讯
采用RS232接口，波特率是9600Bit/S；校验位：None；数据位：8；停止位：1。

数据发送格式（16进制）：DA数据高位数据低位EE，其中“DA”表示字头，“EE”表示字尾，数据均为BCD码。

例如：DA0275EE则表示距离为275m；DA0000EE则表示脱靶，距离无效。

以下是通讯截图：
四、参数
1、供电：直流5V；
2、功耗：<1W；
3、最近测程：>5m；
4、最远测程：1500m；
5、最快频率：约30Hz（30m以内的近距离目标）；
6、最慢频率：约0.8Hz（对空测量）；
7、一般频率：约10Hz
8、重量：0.125kg
9、尺寸104*72*41mm
10、精度：正负1米。