2011~2009年浙江省高中数学竞赛试题及详细解析答案

浙江高三高中数学竞赛测试班级:___________ 姓名：___________ 分数：___________一、选择题1.集合}，且,则实数取值范围为（）A．B．C．或D．2.若则是的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件3.已知等比数列{}：且第一项至第八项的几何平均数为9，则第三项是（）A．B．C．D．4.已知复数为虚数单位），且，则（）A．B．C．或D．或5.已知直线与抛物线交于两点，为的中点，为抛物线上一个动点，若满足，则下列一定成立的是（）。

A．B．其中是抛物线过的切线C．D．6.某程序框图如下，当E0.96时，则输出的K=（）A．20B．22C．D．257.若三位数被7整除，且成公差非零的等差数列，则这样的整数共有（）个。

A．4B．6C．7D．88.设函数，则函数的极大值点为（）A．B．C．D．9.已知为一次函数，若对实数满足，则的表达式为（）。

A．B．C．D．二、填空题1.若，则_________________。

2.已知，若当时恒大于零，则的取值范围为_____________ 。

3.数列，则数列中最大项的值为______________。

4.若，满足，则 ,。

5.设直线与曲线有三个不同的交点,且,则直线的方程为_________________。

6.若则________________________。

7.某动点在平面直角坐标系第一象限的整点上运动（含第一象限轴上的整点），其运动规律为或。

若该动点从原点出发，经过6步运动到（6,2）点，则有__________________种不同的运动轨迹。

三、解答题1.已知抛物线，过轴上一点的直线与抛物线交于点两点。

证明，存在唯一一点，使得为常数，并确定点的坐标。

2.设二次函数在[3,4]上至少有一个零点，求的最小值。

3.设满足数列是公差为，首项的等差数列；数列是公比为首项的等比数列，求证：。

4.设证明。

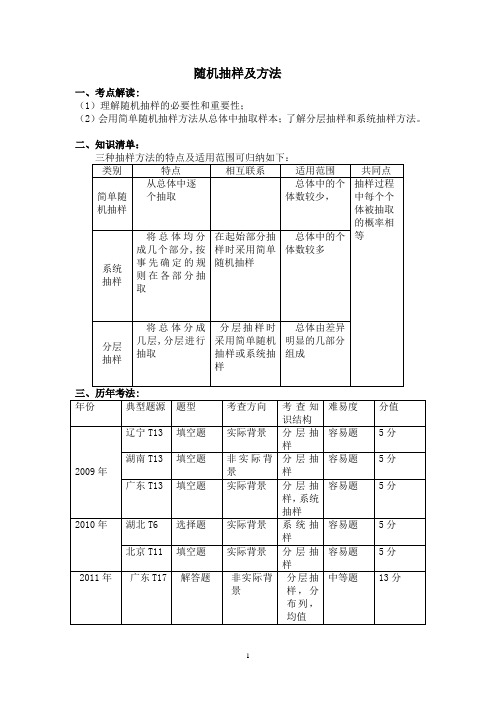
随机抽样及方法一、考点解读:（1）理解随机抽样的必要性和重要性；（2）会用简单随机抽样方法从总体中抽取样本；了解分层抽样和系统抽样方法。

二、知识清单：四、真题剖析：【例1】（2010湖北,6题,5分）将参加夏令营的600名学生编号为：001，002，……600，采用系统抽样方法抽取一个容量为50的样本，且随机抽得的号码为003．这600名学生分住在三个营区，从001到300在第Ⅰ营区，从301到495住在第Ⅱ营区，从496到600在第Ⅲ营区，三个营区被抽中的人数一次为（）A．26, 16, 8, B．25，17，8 C．25，16，9 D．24，17，9【答案】B【解析】依题意可知,在随机抽样中,首次抽到003号,以后每隔12个号抽到一个人,则分别是003、015、027、039……构成以3为首项,12为公差的等差数列,故可分别求出在001到300中有25人,在301至495号中共有17人,则496到600中有8人,所以B正确【丢分陷阱】：本题主要考查系统抽样方法．并能转化等差数列的思想【例2】（2010安徽，14题，5分）某地有居民100 000户，其中普通家庭99 000户,高收入家庭1 000户．从普通家庭中以简单随机抽样方式抽取990户，从高收入家庭中以简单随机抽样方式抽取l00户进行调查，发现共有120户家庭拥有3套或3套以上住房，其中普通家庭50户，高收人家庭70户．依据这些数据并结合所掌握的统计知识，你认为该地拥有3套或3套以上住房的家庭所占比例的合理估计是________ .【答案】5.7%【解析】该地拥有3套或3套以上住房的家庭可以估计有：户，所以所占比例的合理估计是÷=.5700100000 5.7%【丢分陷阱】：利用题目给出的比例采用分层抽样模型，【方法总结】：本题分层抽样问题,首先根据拥有3套或3套以上住房的家庭所占的比例，得出100 000户，居民中拥有3套或3套以上住房的户数，它除以100 000得到的值，为该地拥有3套或3套以上住房的家庭所占比例的合理估计. 【例3】（2010北京,题11,5分）（11）从某小学随机抽取100名同学，将他们的身高（单位：厘米）数据绘制成频率分布直方图（如图）。

2009年浙江省高中数学竞赛试卷(含答案)2009年浙江省高中数学竞赛试卷 参考答案一、选择题（本大题共10小题，每小题5分，共计50分）1. 已知集合{1,2}M =，{21}N a M a =-∈，则M N ⋂＝（ A ）。

A ．{}1 B ．{}2,1 C ．{}3,2,1 D ．空集 解： 由于{21}{1,3}N M a a ∈=-=，所以{1}M N ⋂=。

答案为 A 。

2. 已知椭圆192522=+y x 上一点P 到点（4, 0）距离等于4，则P 点到直线425-=x 的距离为（ C ）。

A ．4 B ． 6 C ．152 D ．54解：因为5,3a b ==，则4c =。

于是P 到另一个焦点(4,0)-的距离等于2546⨯-=。

由于直线425-=x 为椭圆的左准线方程，则P 到直线425-=x 的距离为667.545d e ===。

答案为 C 。

3. 等差数列{}na 中，01>a，13853a a=，则部分和nS 中最大的是（ C ）A ． 10S B ． 11S C ． 20S D ． 21S解： 由题意知，13853a a =1113(7)5(12392)0a d a d d a ⇒+=+⇒=-<。

所以{}n a 是单调递减数列。

又11122(1)2039(1)()[1]039naa n a a n n =+--=->≤⇒-。

由此可得当20n =时，nS 最大。

答案为 C4. 已知平面上单位向量51243(,),(,)131355a b ==r r ，则下列关系式正确的是（ B ） A ．a b⊥r rB.()()a b a b +⊥-r r r r C.()//()a b a b +-r r r r D.()a ab ⊥+r r r解： 因为,a br r 都是非零单位向量，以,ab r r 为边，,a b a b -+r r r r为对角线构成一个菱形。

2011年浙江省高中数学竞赛试题一、选择题（本大题共有10小题，每题5分，共50分）1. 已知53[,]42ππθ∈ ） A ．2sin θ B. 2sin θ- C. 2cos θ- D. 2cos θ2．如果复数()()21a i i ++的模为4，则实数a 的值为（ ）A. 2B.C. 2±D. ±3. 设A ，B 为两个互不同集合，命题P ：x A B ∈⋂， 命题q ：x A ∈或x B ∈，则p 是q 的（ ） A. 充分且必要条件 B. 充分非必要条件 C. 必要非充分条件 D. 非充分且非必要条件4. 过椭圆2212x y +=的右焦点2F 作倾斜角为45弦AB ，则AB 为（ ）A. B. C. 3 D. 5. 函数150()510xx x f x x -⎧-≥=⎨-<⎩，则该函数为（ ） A. 单调增加函数、奇函数 B. 单调递减函数、偶函数C. 单调增加函数、偶函数D. 单调递减函数、奇函数8. 在平面区域{}(,)||1,||1x y x y ≤≤上恒有22ax by -≤，则动点(,)P a b 所形成平面区域的面积为（ ）A. 4 B.8 C. 16 D. 329. 已知函数()sin(2)6f x x m π=--在0,2π⎡⎤⎢⎥⎣⎦上有两个零点，则m 的取值范围为（ ） A. 1, 12⎛⎫ ⎪⎝⎭ B 1, 12⎡⎤⎢⎥⎣⎦ C. 1, 12⎡⎫⎪⎢⎣⎭ D. 1, 12⎛⎤ ⎥⎝⎦10. 已知[1,1]a ∈-，则2(4)420x a x a +-+->的解为（ ）A. 3x >或2x <B. 2x >或1x <C. 3x >或1x <D. 13x <<二、填空题（本大题共有7小题，将正确答案填入题干后的横线上，每空7分，共49分）11. 函数()2sin 2x f x x =的最小正周期为_________。

浙江省高中数学竞赛（a卷）参考答案2007年浙江省高中数学竞赛（Ａ卷）参考答案一、选择题1.如果23()1log 2log 9log 64x x x f x =-+-，则使()0f x <的x 的取值范围为（ B ）A. 01x << B. 813x << C. 1x <<+∞ D. 8 3x <<+∞ 解：显然0x >，且1x ≠。

23()1log 2log 9log 64x x x f x =-+-1log 2log 3log 4x x x =-+-3log 8x x =。

要使()0f x <。

当1x >时，318x <，即813x <<；当01x <<时，318x >，此时无解。

由此可得，使()0f x <的x 的取值范围为813x <<。

2.已知集合{}c o s 22)s i n A x x x xR =++-+>∈，{}sin cos ,B x x x x R =≥∈，则A B ?＝（ C ）A. 4xx ππ??<<B. ＲC. ?D. 2(21),4xk x k k πππ??+<<+∈Z解：cos 22(11)0x x ++->2sin (10x x ?-+(sin 1)0x x ?-<没有实数x 可以使上述不等式成立。

故A =?。

从而有A B ?=?。

3.以（ B ）A. 2B. 3C. 4D. 6解：以这些边为三角形仅有四种：(1,1,1)，，，。

固定四面体的一面作为底面：当底面的三边为(1,1,1)时，另外三边的取法只有一种情况，即；当底面的三边为时，另外三边的取法有两种情形，即，。

其余情形得到的四面体均在上述情形中。

由此可知，四面体个数有３个。

4.从１至169的自然数中任意取出３个数构成以整数为公比的递增等比数列的取法有（ C ）种。

2009 年全国高中数学联赛受中国数学会委托，2009 年全国高中数学联赛由黑龙江省数学会承办。

中国数学会普及工作委员会和黑龙江数学会负责命题工作。

2009 年全国高中数学联赛一试命题范围不超出教育部2000 年《全日制普通高级中学数学教学大纲》中所规定的教学要求和内容，但在方法的要求上有所提高。

主要考查学生对基础知识和基本技能的掌握情况，以及综合和灵活运用的能力。

全卷包括8 填空题和3 道大题，满分100 分。

答卷时间为80 分钟。

全国高中数学联赛加试命题范围与国际数学奥林匹克接轨，在知识方面有所扩展，适当增加一些竞赛教学大纲的内容。

全卷包括4 道大题，其中一道平面几何题，试卷满分200 分。

答卷时问为150 分钟。

、填空（每小题 7分，共56 分） f f fL f x，贝U f 99 11 4 442 4 4 雄n2 22. 已知直线L:x y 9 0和圆M :2x 2yC 为圆M 上两点，在 ABC 中， BAC 45 ， 为 .y > 03. 在坐标平面上有两个区域 M 和N , M 为y w x , N 是随t 变化的区域，它由y w 2 x不等式t w x w t 1所确定，t 的取值范围是 0 w t w 1，贝y M 和N 的公共面积是函数 f t .1 1 1 14.使不等式 La 2007-对一切正整数n 都成立的最小正整数n 1 n 2 2n 13a 的值为 _____ .2 25. 椭圆—2 爲1 a b 0上任意两点 P , Q ，若OP OQ ，则乘积|OP OQ|的a b最小值为 _____ .6.若方程lgkx 2lg x 1仅有一个实根，那么 k 的取值范围是 _________________ .7. 一个由若干行数字组成的数表，从第二行起每一行中的数字均等于其肩上的两个数 之和，最后一行仅有一个数，第一行是前 100个正整数按从小到大排成的行，则最后一行的 数是 （可以用指数表示）8. 某车站每天8： 00〜9： 00, 9： 00〜10： 00都恰有一辆客车到站，但到站的时刻是随 机的，且两者到站的时间是相互独立的，其规律为到站时刻8：108：308：509：109： 309： 50概率111623一旅客8： 20到车站，则它候车时间的数学期望为 __________ （精确到分） 二、解答题2 21. （14分）设直线l : y kx m （其中k , m 为整数）与椭圆 ——1交于不同两16 122 2点A , B ，与双曲线—也1交于不同两点 C , D ，问是否存在直线l ，使得向量4 12AC BD 0 ,若存在，指出这样的直线有多少条？若不存在，请说明理由.8x 8y 1 0 ,点A 在直线L 上，B ,AB 过圆心M ,则点A 横坐标范围1.若函数(n)X2,,数列a n2. （15 分）已知p , q q 0是实数，方程x px q 0有两个实根满足a i p , a2 p2 q , a. pa n 1 qa. 2 n 3,4, L（I ）求数列a n的通项公式（用，表示）；1（H ）若p 1, q —,求a n的前n项和.43. （15分）求函数y 宀―27 • 13—x .. x的最大和最小值.加试一、解答题(共4小题，每小题50分，共200分)1、如图，M , N分别为锐角三角形ABC ( A B )的外接圆中点•过点C作PC II MN交圆于P点，I为ABC的内心，连接T •⑴求证：MP MT NP NT ；⑵在弧A B (不含点C )上任取一点Q ( Q工A , T , B )，记心分别为I i, I2,求证：Q , I i , I2, T四点共圆.2、求证不等式:1In n w , n 1 , 2,2上弧B C、A C的PI并延长交圆于AQC , △ QCB 的内k 1 k2 1PAB13、设k , l是给定的两个正整数•证明：有无穷多个正整数m > k，使得c m与l互素.4、在非负数构成的39数表X11X12X13X14X15X16X17X18X19P X21X22X23X24X25X26X27X28X29X31X32X33X34X35X36X37X38X39中每行的数互不相同，前 6 列中每列的三数之和为1，x17 x28 x39 0，x27，x37，x18，x38，X19，X29均大于•如果P的前三列构成的数表X 11X12X13S X21X22X23X31X32X33x1k满足下面的性质(O)：对于数表P 中的任意一列x2k( k 1 ，2,…，9)均存在某个x3ki 1 ，2，3 使得⑶x ik< u i minx i1 ，x i 2，x i 3求证：(i)最小值u i min xi1，x i2，x i3 ，i 1，2，3一定自数表S的不同列.(11)存在数表P 中唯一的一列x1k*x2k* ，k*x3k*丰1 ,2，3 使得33数表X11 X12 X1k*S X21 X22 X2k*X31 X32 X3k* 仍然具有性质(O) •2009年全国高中数学联合竞赛一试试题参考答案及评分标准说明： 1.评阅试卷时，请依据本评分标准，选择题只设7分的0分两档；其它各题的评阅，请严 格按照本评分标准的评分档次给分，不要增加其他中间档次。

2009年全国高中数学联合竞赛一试试题参考答案及评分标准说明：1．评阅试卷时，请依据本评分标准，填空题只设7分和0分两档；其他各题的评阅，请严格按照本评分标准的评分档次给分，不要增加其他中间档次．2．如果考生的解答方法和本解答不同，只要思路合理、步骤正确，在评卷时可参考本评分标准适当划分档次评分，解答题中至少4分为一个档次，不要增加其他中间档次． 一、填空（共8小题，每小题7分，共56分） 1． 若函数()f x =且()()()n nfx f f f f x ⎡⎤=⎡⎤⎣⎦⎣⎦，则()()991f=．【答案】 110【解析】 ()()()1fx fx ==，()()()2fx f fx ==⎡⎤⎣⎦……()()99fx =．故()()991110f=．2． 已知直线:90L x y +-=和圆22:228810M x y x y +---=，点A 在直线L 上，B ，C 为圆M 上两点，在A B C ∆中，45B A C ∠=︒，A B 过圆心M ，则点A 横坐标范围为 ．【答案】 []36， 【解析】 设()9A a a -，，则圆心M 到直线A C 的距离sin 45dA M =︒，由直线A C 与圆M 相交，得2d ≤解得36a ≤≤．3．在坐标平面上有两个区域M 和N ，M 为02y y xy x⎧⎪⎨⎪-⎩≥≤≤，N 是随t 变化的区域，它由不等式1t x t +≤≤所确定，t 的取值范围是01t ≤≤，则M 和N 的公共面积是函数()f t = ．【答案】 212tt -++【解析】 由题意知()f t S =阴影部分面积A OB OCD BE FS S S ∆∆∆=--()22111122t t =---212t t =-++4． 使不等式1111200712213a n n n +++<-+++ 对一切正整数n 都成立的最小正整数a的值为 ．【答案】 2009 【解析】 设()1111221fn n n n =++++++ ．显然()fn 单调递减，则由()fn 的最大值()1120073f a <-，可得2009a=．5． 椭圆22221x y ab+=()0a b >>上任意两点P ，Q ，若OPOQ⊥，则乘积O PO Q⋅的最小值为 ．【答案】22222a ba b+【解析】 设()c o s s in P O P O P θθ，，ππc o s s in22Q O Q O Q θθ⎛⎫⎛⎫⎛⎫±± ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，．由P ，Q 在椭圆上，有222221c o s s in abO P θθ=+① 222221s in c o s abO Qθθ=+②①+②得22221111abO PO Q+=+．于是当O PO Q ==时，O PO Q达到最小值22222a ba b+．6． 若方程()lg 2lg 1k x x =+仅有一个实根，那么k 的取值范围是 ．【答案】 0k<或4k= 【解析】 ()20101k x x k x x ⎧>⎪⎪+>⎨⎪=+⎪⎩当且仅当0kx >① 10x +>② ()2210x k x +-+= ③对③由求根公式得1x，2122x k ⎡=-±⎣④2400k k k ∆=-⇒≥≤或4k ≥．(ⅰ)当0k<时，由③得12122010x x k x x +=-<⎧⎨=>⎩所以1x ，2x 同为负根． 又由④知121010x x +>⎧⎨+<⎩所以原方程有一个解1x ． (ⅱ)当4k =时，原方程有一个解112k x =-=．(ⅲ)当4k>时，由③得12122010x x k x x +=->⎧⎨=>⎩所以1x ，2x 同为正根，且12x x ≠，不合题意，舍去．综上可得0k<或4k=为所求．7． 一个由若干行数字组成的数表，从第二行起每一行中的数字均等于其肩上的两个数之和，最后一行仅有一个数，第一行是前100个正整数按从小到大排成的行，则最后一行的数是 （可以用指数表示）【答案】 981012⨯ 【解析】 易知：(ⅰ)该数表共有100行；(ⅱ)每一行构成一个等差数列，且公差依次为11d =，22d =，232d =，…，98992d =(ⅲ)100a 为所求．设第()2n n ≥行的第一个数为n a ，则 ()22111222n n nn n n a a a a-----=++=+3222222n n n a ---⎡⎤=++⎣⎦24223222222n n n n a ----⎡⎤=++⨯+⎣⎦323232n n a --=+⨯……()121212n n a n --=+-⨯()212n n -=+故981001012a =⨯．8． 某车站每天800~900∶∶，900~1000∶∶都恰有一辆客车到站，但到站的时刻是随一旅客820∶到车站，则它候车时间的数学期望为 （精确到分）．【答案】 27 【解析】 旅候车时间的数学期望为1111110305070902723361218⨯+⨯+⨯+⨯+⨯=二、解答题1． （本小题满分14分）设直线:l ykx m=+（其中k ，m 为整数）与椭圆2211612xy+=交于不同两点A ，B ，与双曲线221412xy-=交于不同两点C ，D ，问是否存在直线l ，使得向量0A CB D +=，若存在，指出这样的直线有多少条？若不存在，请说明理由．【解析】 由2211612y k x m x y =+⎧⎪⎨+=⎪⎩消去y 化简整理得()2223484480k xkm x m +++-=设()11A x y ，，()22B x y ，，则122834km x x k+=-+()()()222184344480km km∆=-+->① ………………………………………………4分由221412y k x m x y =+⎧⎪⎨-=⎪⎩消去y 化简整理得()22232120k xkm x m ----=设()34C x y ，，()44D x y ，，则34223km x x k+=-()()()2222243120km km∆=-+-+>② ………………………………………………8分 因为A CB D +=，所以()()42310x x x x -+-=，此时()()42310y y y y -+-=．由1234x x x x +=+得2282343km km kk-=+-．所以20km =或2241343k k-=+-．由上式解得0k=或0m=．当0k=时，由①和②得m -<因m 是整数，所以m 的值为3-，2-，1-，0，1，2，3．当m =，由①和②得k <<k 是整数，所以1k=-，0，1．于是满足条件的直线共有9条．………14分2． （本小题15分）已知p ，()0q q≠是实数，方程20x p x q -+=有两个实根α，β，数列{}n a 满足1a p=，22a p q=-，()1234n n n a p a q a n --=-=，，(Ⅰ)求数列{}n a 的通项公式（用α，β表示）； (Ⅱ)若1p=，14q =，求{}n a 的前n 项和．【解析】 方法一：(Ⅰ)由韦达定理知0q αβ⋅=≠，又pαβ+=，所以()1212n n n n n a p x q x a a αβαβ------=+-，()345n=，，，整理得()112n n n n a a a a βαβ----=-令1nn nb a a β+=-，则()112n n b b n α+== ，，．所以{}n b 是公比为α的等比数列． 数列{}n b 的首项为：()()222121b a a pq p ββαβαββαβα=-=--=+--+=．所以21n n n b ααα-+=⋅=，即11n n n a a βα++-=()12n=，，．所以11n n n a a βα++=+()12n=，，．①当240p q ∆=-=时，αβ=≠，12a p ααα==+=，11n n n a a βα++=+()12n=，，变为11n n n a a αα++=+()12n=，，．整理得，111n nn na a αα++-=，()12n = ，，．所以，数列n n a α⎧⎫⎨⎬⎩⎭成公差为1的等差数列，其首项为122a ααα==．所以()2111nna n n α=+-=+．于是数列{}n a 的通项公式为()1nn a n α=+；……………………………………………………………………………5分 ②当240p q ∆=->时，αβ≠，11n n n a a βα++=+1n n a βαβαβα+-=+-11n n n a βαβααβαβα++=+---()12n=，，．整理得211n n n n a a ααββαβα+++⎛⎫+=+ ⎪--⎝⎭，()12n=，，．所以，数列1n n a αβα+⎧⎫+⎨⎬-⎩⎭成公比为β的等比数列，其首项为2221a ααβαββαβαβα+=++=---．所以121n n na αβββαβα+-+=--．于是数列{}n a 的通项公式为11n n n a βαβα++-=-．………………………………………………10分(Ⅱ)若1p =，14q =，则240p q ∆=-=，此时12αβ==．由第(Ⅰ)步的结果得，数列{}n a 的通项公式为()11122nn nn a n +⎛⎫=+= ⎪⎝⎭，所以，{}n a 的前n 项和为231234122222n n nn n s -+=+++++ 234112341222222n n nn s n ++=+++++以上两式相减，整理得1133222n n n s ++=-所以332n nn s +=-．……………………………………………………………………………15分 方法二：(Ⅰ)由韦达定理知0q αβ⋅=≠，又pαβ+=，所以1a αβ=+，222a αβαβ=++．特征方程20p q λλ-+=的两个根为α，β．①当0αβ=≠时，通项()()1212nna A A n nα=+=，，由12a α=，223a α=得()()122212223A A A A αααα+=⎧⎪⎨+=⎪⎩解得121A A ==．故()1nn a n α=+．……………………………………………………5分②当αβ≠时，通项()1212nnn a A A n αβ=+=，，．由1a αβ=+，222a αβαβ=++得12222212A A A A αβαβαβαβαβ+=+⎧⎪⎨+=++⎪⎩ 解得1A αβα-=-，2A ββα=-．故1111n n n n n a αββαβαβαβα++++--=+=---．…………………………………………………………10分 (Ⅱ)同方法一．3． （本小题满分15分）求函数y =的最大和最小值．【解析】 函数的定义域为[]013，.因为y =≥ =当0x =时等号成立．故y的最小值为．……………………………………………5分又由柯西不等式得22y=()()()11122731312123x x x ⎛⎫+++++-= ⎪⎝⎭≤所以11y ≤． ………………………………………………………………………………10分由柯西不等式等号成立的条件，得()491327x x x =-=+，解得9x=．故当9x=时等号成立．因此y的最大值为11． (15)分2009年全国高中数学联合竞赛加试 试题参考答案及评分标准（A 卷）说明：1．评阅试卷时，请严格按照本评分标准的评分档次给分．2．如果考生的解答方法和本解答不同，只要思路合理、步骤正确，在评卷时可参考本评分标准适当划分档次评分，10分为一个档次，不要增加其他中间档次． 一、填空（共4小题，每小题50分，共200分）9． 如图，M ，N 分别为锐角三角形A B C ∆（A B ∠<∠）的外接圆Γ上弧 B C 、 A C 的中点．过点C 作P C M N ∥交圆Γ于P 点，I 为A B C ∆的内心，连接P I 并延长交圆Γ于T ．⑴求证：M P M T N P N T ⋅=⋅；⑵在弧 A B （不含点C ）上任取一点Q （Q A≠，T ，B ），记A Q C ∆，Q C B △的内心分别为1I ，2I ，B求证：Q ，1I ，2I ，T 四点共圆．【解析】 ⑴连N I ，M I ．由于P C M N ∥，P ，C ，M ，N 共圆，故P C M N 是等腰梯形．因此N P M C =，P M N C =．ABCMNPTI连A M ，C I ，则A M 与C I 交于I ，因为M IC M A C A C I M C B B C I M C I∠=∠+∠=∠+∠=∠，所以M CM I=．同理N C N I=．于是N P M I=，P M N I =．故四边形M P N I 为平行四边形．因此P M TP N TS S =△△（同底，等高）．又P ，N ，T ，M 四点共圆，故180T N PP M T ∠+∠=︒，由三角形面积公式1sin 2P M T S P M M T P M T=⋅∠△1s i n 2P N TS P N N T P NT ==⋅∠△1s i n 2P N N T P MT =⋅∠ 于是P M M T P N N T⋅=⋅．⑵因为1111N C I N C A A C I N Q C Q C I C I N∠=∠+∠=∠+∠=∠，B所以1N CN I =，同理2M C M I =．由M P M T N P N T⋅=⋅得N T M T M PN P=．由⑴所证M PN C=，N PM C=，故12N T M T N I M I =．又因12I N T Q N T Q M T I M T∠=∠=∠=∠，有12I N T I M T∆∆∽． 故12N T I M T I ∠=∠，从而1212I Q I N Q M N T M I T I ∠=∠=∠=∠．因此Q ，1I ，2I ，T 四点共圆． 10． 求证不等式：2111ln 12nk k n k =⎛⎫-<- ⎪+⎝⎭∑≤，1n =，2，…【解析】 证明：首先证明一个不等式：⑴ln (1)1x x xx<+<+，0x>．事实上，令()ln (1)h x x x =-+，()ln (1)1x g x x x =+-+．则对0x>，1()101h x x'=->+，2211()1(1)(1)x g x xx x '=-=>+++．于是()(0)0h x h >=，()(0)0g x g >=．在⑴中取1x n=得⑵111ln 11n n n ⎛⎫<+< ⎪+⎝⎭．令21ln 1nnk k x nk==-+∑，则112x =，121ln 111n n nx x nn -⎛⎫-=-+ ⎪+-⎝⎭211n n n<-+210(1)n n=-<+因此1112n n x x x -<<<=．又因为111ln (ln ln (1))(ln (1)ln (2))(ln 2ln 1)ln 1ln 1n k n n n n n k -=⎛⎫=--+---++-+=+⎪⎝⎭∑ ．从而12111ln 11nn n k k k x kk -==⎛⎫=-+ ⎪+⎝⎭∑∑12211ln 111n k k n k k n -=⎛⎫⎛⎫=-++ ⎪ ⎪++⎝⎭⎝⎭∑12111n k k kk -=⎛⎫>- ⎪+⎝⎭∑1211(1)n k kk-==-+∑111(1)n k k k-=-+∑≥111n=-+>-．11． 设k ，l 是给定的两个正整数．证明：有无穷多个正整数m k≥，使得C k m 与l 互素．【解析】 证法一：对任意正整数t ，令(!)mk t l k =+⋅⋅．我们证明()C 1k ml =，． 设p 是l 的任一素因子，只要证明：C kmpŒ．若!p k Œ，则由1!C ()kkm i k m k i ==-+∏1[((!)]ki i t l k =≡+∏1ki i =≡∏()1!m o d k pα+≡．及|!p k α，且1!pk α+Œ，知|!C kmpk α且1!C kmp k α+Œ．从而C kmpŒ．证法二：对任意正整数t ，令2(!)mk t l k =+⋅⋅，我们证明()C 1k ml =，． 设p 是l 的任一素因子，只要证明：C kmpŒ．若!p k Œ，则由1!C ()kkm i k m k i ==-+∏21[((!)]ki i t l k =≡+∏ 1ki i =≡∏()!m o d k p ≡．即p 不整除上式，故C kmp Œ．若|!pk ，设1α≥使|!p k α，但1!p k α+Œ．12|(!)pk α+．故由11!C ()k km i k m k i -==-+∏21[((!)]ki i t l k =≡+∏1ki i =≡∏()1!m o d k pα+≡及|!p k α，且1!p k α+Œ，知|!C kmp k α且1!C kmp k α+Œ．从而C kmpŒ．12． 在非负数构成的39⨯数表111213141516171212223242526272829313233343536373839x xx x x x xxx P xx x x xxxx x x xxxx x xx x ⎛⎫ ⎪= ⎪ ⎪⎝⎭ 中每行的数互不相同，前6列中每列的三数之和为1，1728390x x x ===，27x ，37x ，18x ，38x ，19x ，29x 均大于．如果P 的前三列构成的数表111213212223313233x x x S x x x xx x ⎛⎫⎪= ⎪ ⎪⎝⎭满足下面的性质()O ：对于数表P 中的任意一列123k kkx x x ⎛⎫⎪ ⎪ ⎪⎝⎭（1k =，2，…，9）均存在某个{}123i ∈，，使得 ⑶{}123m in ik i i i i x u x x x =≤，，．求证：（ⅰ）最小值{}123m in ii i i u x x x =，，，1i =，2，3一定自数表S 的不同列．（ⅱ）存在数表P 中唯一的一列***123k k k x x x ⎛⎫⎪ ⎪ ⎪ ⎪⎝⎭，*1k ≠，2，3使得33⨯数表***111212122231323k kk x x xS x x x x x x ⎛⎫⎪'= ⎪ ⎪ ⎪⎝⎭仍然具有性质()O ．【解析】 （ⅰ）假设最小值{}123m in ii i i u x x x =，，，1i =，2，3不是取自数表S 的不同列．则存在一列不含任何i u ．不妨设2i i u x ≠，1i =，2，3．由于数表P 中同一行中的任何两个元素都不等，于是2i i u x <，1i =，2，3．另一方面，由于数表S 具有性质()O ，在⑶中取2k=，则存在某个{}123i ∈，，使得02iix u ≤．矛盾．（ⅱ）由抽届原理知{}1112m in x x ，，{}2122m in x x ，，{}3132m in x x ， 中至少有两个值取在同一列．不妨设{}212222m in x x x =，，{}313232m in x x x =，．由前面的结论知数表S 的第一列一定含有某个i u ，所以只能是111x u =．同样，第二列中也必含某个i u ，1i =，2．不妨设222x u =．于是333u x =，即i u 是数表S中的对角线上数字．111213212223313233x x x S x x x xx x ⎛⎫⎪= ⎪ ⎪⎝⎭记{}129M = ，，，，令集合{}{}12|m in 13ik i i I k Mx x x i =∈>=，，，．显然{}111332|k k I k M x x x x =∈>>，且1，23I ∉．因为18x ，38111x x >≥，32x ，所以8I ∈．故I ∅≠．于是存在*k I ∈使得{}*22m a x |k k x x k I =∈．显然，*1k ≠，2，3．下面证明33⨯数表***111212122231323k kk x x xS x x x x x x ⎛⎫⎪'= ⎪ ⎪ ⎪⎝⎭具有性质()O ． 从上面的选法可知{}{}*1212:m in m in i i i i i ik u x x xxx '==，，，，(13)i =，．这说明{}*111211m in k xx x u >，≥，{}*313233m in kx x x u >，≥． 又由S满足性质()O ．在⑶中取*k k =，推得*22k xu ≤，于是{}**2212222m in k k u x x x x'==，，．下证对任意的k M ∈，存在某个1i =，2，3使得i iku x '≥．假若不然，则{}12m in ik i i x x x >，，1i =，3且*22kk x x>．这与*2k x 的最大性矛盾．因此，数表S '满足性质()O ．下证唯一性．设有k M ∈使得数表111212122231323k kkx x x S x x x xx x ⎛⎫ ⎪= ⎪ ⎪⎝⎭具有性质()O ，不失一般性，我们假定 {}111121311m i n u x x x x ==，，⑷{}221222322m in u x x x x ==，，{}331323333m i n u x x x x ==，，3231x x<．由于3231x x <，2221x x <及（ⅰ），有 {}11112111m in k u x x x x ==，，．又由（ⅰ）知：或者()a {}3313233m in k k u x x x x ==，，，或者 {}2212222()m in k kb u x x x x ==，，．如果()a 成立，由数表 S具有性质()O ，则{}11112111m i n ku x x x x ==，，， ⑸ {}22122222m in k u x x x x ==，，，{}3313233m i n kku x x xx==，，． 由数表S 满足性质()O ，则对于3M∈至少存在一个{}123i ∈，，使得*iik u x ≥．由*k I ∈及⑷和⑹式知， *1111kx x u >=， *3323kx x u >=．于是只能有*222kk xu x =≤．类似地，由S '满足性质()O 及k M ∈可推得*222kk x u x '=≤．从而*k k=．。

浙江高三高中数学竞赛测试班级:___________ 姓名：___________ 分数：___________一、选择题1.若集合，，，则集合（）A．B．C．D．2.若函数（，且）的值域为，则实数的取值范围为（）A．B．C．D．3.如图，在四面体中，已知两两互相垂直，且．则在该四面体表面上与点距离为的点形成的曲线段的总长度为（）A．B．C．D．4.在中，“”是“”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件5.已知函数，则关于的不等式的解集为（）A．B．C．D．6.记为三个数中的最小数，若二次函数有零点，则的最大值为（）A．2B．C．D．1二、填空题1.数学竞赛后，小明、小乐和小强各获得一枚奖牌，其中一人得金牌，一人得银牌，一人得铜牌，老师猜测：“小明得金牌，小乐不得金牌，小强得的不是铜牌．”结果老师只猜对了一个，由此推断：得金牌、银牌、铜牌的依次是__________．2.省中医院5月1号至5月3号拟安排6位医生值班，要求每人值班1天，每天安排2人．若6位医生中的甲不能值2号，乙不能值3号，则不同的安排值班的方法共有__________种．3.已知函数，若对于任意的，存在，使得成立，则的取值范围为__________． 4.已知，则的取值范围为__________．5.已知是偶函数，时，(符号表示不超过的最大整数)，若关于的方程恰有三个不相等的实根，则实数的取值范围为__________．6.已知点为椭圆的右焦点，椭圆的离心率为，过点的直线交椭圆于两点(点在轴的上方)，且，则直线的斜率为__________．7.方程的正整数解为______________（写出所有可能的情况)．8.一个有限项的数列满足：任何3 个连续项之和都是负数，且任何4个连续项之和都是正数，则此数列项数的最大值为__________．三、解答题1.已知函数的图象恒过定点，且点又在函数的图象上．（Ⅰ）求实数的值； （Ⅱ）当方程有两个不等实根时，求的取值范围；（Ⅲ）设，，，求证，，．2.（12分）如图，椭圆（）的离心率，短轴的两个端点分别为B 1、B 2，焦点为F 1、F 2，四边形F 1 B 1F 2 B 2的内切圆半径为（1）求椭圆C 的方程；（2）过左焦点F 1的直线交椭圆于M 、N 两点，交直线于点P ，设，，试证为定值，并求出此定值．3.已知函数，直线为曲线的切线（为自然对数的底数）．（1）求实数的值； （2）用表示中的最小值，设函数，若函数为增函数，求实数的取值范围．浙江高三高中数学竞赛测试答案及解析一、选择题1.若集合，，，则集合（ ）A ．B ．C．D．【答案】D【解析】依题意，，．由，知；，知或．所以，或，即．故选D；2.若函数（，且）的值域为，则实数的取值范围为（）A．B．C．D．【答案】A【解析】当时，函数的值域为，当时，，即时，，且时恒成立．∴，的取值范围为．故选A；3.如图，在四面体中，已知两两互相垂直，且．则在该四面体表面上与点距离为的点形成的曲线段的总长度为（）A．B．C．D．【答案】B【解析】如图，设 (在上，在上，在上)．由，，知，，．∴在面内与点距离为的点形成的曲线段(图中弧) 长为．同理，在面内与点距离为的点形成的曲线段长为．同理，在面内与点距离为的点形成的曲线段长为．同理，在面内与点距离为的点形成的曲线段长为．所以，该四面体表面上与点距离为的点形成的曲线段的总长度为．故选B．点睛：想象出在每个截面上的弧线是一个个圆弧，找到相应的圆弧的圆心角，和半径，弧长就求出来了；4.在中，“”是“”的（）A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件【答案】C【解析】由正弦定理可得，在中，“”则，则，由倍角公式可得，可得，反之也成立，所以在中，“”是“”的充分必要条件，故选C.【考点】正弦定理与倍角公式.5.已知函数，则关于的不等式的解集为（）A．B．C．D．【答案】D【解析】令，则函数为奇函数且在实数上为增函教，不等式转化为故选D．6.记为三个数中的最小数，若二次函数有零点，则的最大值为（）A．2B．C．D．1【答案】B【解析】可以不妨设，因为，所以，故所以，，所以（当且仅当时取等号)故选B．二、填空题1.数学竞赛后，小明、小乐和小强各获得一枚奖牌，其中一人得金牌，一人得银牌，一人得铜牌，老师猜测：“小明得金牌，小乐不得金牌，小强得的不是铜牌．”结果老师只猜对了一个，由此推断：得金牌、银牌、铜牌的依次是__________．【答案】小乐，小强，小明．【解析】其一，若小明得金牌，则小乐一定不得金牌，不合题意；其二，小明得银牌时，再以小乐得奖情况分析，若小乐得金牌，小强得铜牌，不合提议，若小乐得铜牌小强得金牌，也不合题意；其三，若小明得铜牌，仍以小乐得奖情况分类，若小乐得金牌，小强得银牌，则老师才对一个合题意，若小乐得银牌，小强得金牌，则老师对了俩；不合题意，综上，小明得铜牌，小乐得金牌，小强得银牌．2.省中医院5月1号至5月3号拟安排6位医生值班，要求每人值班1天，每天安排2人．若6位医生中的甲不能值2号，乙不能值3号，则不同的安排值班的方法共有__________种．【答案】42;【解析】分两类(1) 甲、乙同一天值班，则只能排在1号，有种排法；(2) 甲、乙不在同一天值班，有种排法，故共有42 种方法．故结果为42．3.已知函数，若对于任意的，存在，使得成立，则的取值范围为__________．【答案】;【解析】函数视作为的函数问题等价于对于，由于，所以所以问题等价于，即，所以．故结果为．点睛：双变元问题，先看成函数视作为的函数，求出最值；再看成x的函数求最值．4.已知，则的取值范围为__________．【答案】;【解析】由及有，所故结果为．5.已知是偶函数，时， (符号表示不超过的最大整数)，若关于的方程恰有三个不相等的实根，则实数的取值范围为__________．【答案】;【解析】作出函数与的草图(如图所示)．易知直线恒过点，是方程的一个根．从图像可知，当，即时，两个函数的图像恰有三个不同的交点．∴的取值范围为．点睛：方程的根转化为函数的零点，图像的交点问题，且发现直线过定点；根据图像得到结果．6.已知点为椭圆的右焦点，椭圆的离心率为，过点的直线交椭圆于两点(点在轴的上方)，且，则直线的斜率为__________．【答案】;【解析】极点在右焦点的极坐标方程为，所以，，从而，可得，，所以直线的斜率为．7.方程的正整数解为______________（写出所有可能的情况)．【答案】;【解析】．∴，∴，．由，知，因此，．∴，若，则，，．将，代入题中方程，得．若，则，．由知，不存在．若，则．以，，又，因此，．经验证只有符合．将代入题中方程，得．∴符合条件的正整数解有或．8.一个有限项的数列满足：任何3 个连续项之和都是负数，且任何4个连续项之和都是正数，则此数列项数的最大值为__________．【答案】5;【解析】一方面可以构造5 项的数列：符合题设；另一方面，证明满足条件的数列不超过5项．否则取出前6 项，作出如下排列：由每行的和为负数，知这12 个数之和为负数；由每列的和为正数，知这12 个数之和为正数．矛盾．故结果为5．三、解答题1.已知函数的图象恒过定点，且点又在函数的图象上．（Ⅰ）求实数的值；（Ⅱ）当方程有两个不等实根时，求的取值范围；（Ⅲ）设，，，求证，，．【答案】(1)；(2)的取值范围为；（3）见解析．【解析】（1）点的坐标为；点在上，则（2）方程的根转化为图像的交点；（3）裂项求和．（Ⅰ）函数的图像恒过定点，点的坐标为又因为点在上，则即，∴（Ⅱ）即，∴由图像可知：，故的取值范围为．（Ⅲ），∴ ，．点睛：主要考查函数零点，方程的根，图像的交点可等价；再就是数列裂项求和问题．2.（12分）如图，椭圆（）的离心率，短轴的两个端点分别为B 1、B 2，焦点为F 1、F 2，四边形F 1 B 1F 2 B 2的内切圆半径为（1）求椭圆C 的方程；（2）过左焦点F 1的直线交椭圆于M 、N 两点，交直线于点P ，设，，试证为定值，并求出此定值． 【答案】（1）；（2）【解析】试题解析：（1）设四边形F 1B 1F 2B 2的内切圆与边B 1B 2的切点为G ，连接OG ，则|OG|=由S △OB2F2=|OB 2||OF 2|=|B 2F 2||OG|，|OB 2|=b ， |OF 2|=c ， |B 2F 2|=a ，得bc=a又∵e=解得a=2，b=故椭圆方程为：（2）设直线MN 的方程为y=k （x+1）代入椭圆方程，整理得 （3+4k 2）x 2+8k 2x+4（k 2-3）=0设M （x 1，y 1），N （x 2，y 2）， 则x 1+x 2= ，x 1x 2=又P （-4，-3k ），F 2（-1，0） 由 ， 得，∴∵∴为定值【考点】本题考查椭圆的几何性质 向量共线 点评：解决本题的关键是利用向量共线，求出即可3.已知函数，直线为曲线的切线（为自然对数的底数）．（1）求实数的值； （2）用表示中的最小值，设函数，若函数为增函数，求实数的取值范围． 【答案】（1）；（2）.【解析】（1）先求导，然后利用导数等于求出切点的横坐标，代入两个曲线的方程，解方程组，可求得；（2）设与交点的横坐标为，利用导数求得，从而，然后利用求得的取值范围为.试题解析：（1）对求导得．．．．．．．．．．．．．．．．．．．．．1分设直线与曲线切于点，则，解得，所以的值为1．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．3分（2）记函数，下面考察函数的符号，对函数求导得．．．．．．．．．．．．．．．．．．．．．．4分当时，恒成立．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．5分当时，，从而．．．．．．．．．．．．．．．．．．．．．7分∴在上恒成立，故在上单调递减．，∴，又曲线在上连续不间断，所以由函数的零点存在性定理及其单调性知唯一的，使．∴；，，∴，从而，∴，．．．．．．．．．．．．．．．．．．．．．．．．．．9分由函数为增函数，且曲线在上连续不断知在，上恒成立．①当时，在上恒成立，即在上恒成立，记，则，当变化时，变化情况列表如下：∴，故“在上恒成立”只需，即．②当时，，当时，在上恒成立，综合①②知，当时，函数为增函数．故实数的取值范围是．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分【考点】函数导数与不等式.【方法点晴】函数导数问题中，和切线有关的题目非常多，我们只要把握住关键点：一个是切点，一个是斜率，切点即在原来函数图象上，也在切线上；斜率就是导数的值.根据这两点，列方程组，就能解决.本题第二问我们采用分层推进的策略，先求得的表达式，然后再求得的表达式，我们就可以利用导数这个工具来求的取值范围了.。