高考大题分类5——分布列

2012-2021十年全国高考数学真题分类汇编 概率（精解精析）一，选择题1．(2021年高考全国甲卷理科)将4个1和2个0随机排成一行,则2个0不相邻地概率为( )A ．13B ．25C ．23D ．45【结果】C思路：将4个1和2个0随机排成一行,可利用插空法,4个1产生5个空,若2个0相邻,则有155C =种排法,若2个0不相邻,则有2510C =种排法,所以2个0不相邻地概率为1025103=+．故选：C ．2．(2021年高考全国乙卷理科)在区间(0,1)与(1,2)中各随机取1个数,则两数之和大于74地概率为( )A ．79B ．2332C ．932D ．29【结果】B思路：如图所示：设从区间()()0,1,1,2中随机取出地数分别为,x y ,则实验地所有结果构成区域为(){},01,12x y x y Ω=<<<<,其面积为111SΩ=⨯=．设事件A 表示两数之和大于74,则构成地区域为()7,01,12,4A x y x y x y ⎧⎫=<<<+⎨⎬⎩⎭,即图中地阴影部分,其面积为13323124432A S =-⨯⨯=,所以()2332A S P A S Ω==．故选：B ．【点睛】本题主要考查利用线性规划解决几何概型中地面积问题,解题关键是准确求出事件,A Ω对应地区域面积,即可顺利解出．3．(2020年高考数学课标Ⅲ卷理科)在一组样本数据中,1,2,3,4出现地频率分别为1234,,,p p p p ,且411i i p ==∑,则下面四种情形中,对应样本地标准差最大地一组是( )A ．14230.1,0.4p p p p ====B ．14230.4,0.1p p p p ====C ．14230.2,0.3p p p p ====D ．14230.3,0.2p p p p ====【结果】B思路：对于A 选项,该组数据地平均数为()()140.1230.4 2.5A x =+⨯++⨯=,方差为()()()()222221 2.50.12 2.50.43 2.50.44 2.50.10.65A s =-⨯+-⨯+-⨯+-⨯=。

专题一集合与常用逻辑用语1.（山东卷理T1）已知全集U=R, 集合M={x||x-1| 2},则（A ）{x|-1<x<3} (B){x|-1≤x ≤3} (C){x|x<-1或x>3} (D){x|x ≤-1或x ≥3} 2.（山东卷文T1）已知全集 , 集合 , 则 = A. B. C. D.3、（山东卷理T3）在空间, 下列命题对旳旳是 （A ）平行直线旳平行投影重叠 （B ）平行于同一直线旳两个平面平行 （C ）垂直于同一平面旳两个平面平行 （D ）垂直于同一平面旳两条直线平行 4.（山东卷文T1）已知全集 , 集合 , 则 （A ）{}22x x -<< （B ）{}22x x -≤≤（C ）{}22x x x <->或（D ） {}22x x x ≤-≥或5.（山东卷文T4）在空间, 下列命题对旳旳是 （A ）平行直线旳平行投影重叠（B ）平行于同一直线旳两个平面（C ）垂直于同一平面旳两个平面平行 （D ）垂直于同一平面旳两个平面平行6]、（山东卷文T7）设 是首项不小于零旳等比数列, 则“ ”是“数列 是递增数列”旳 （A ）充足而不必要条件 （B ）必要而不充足条件 （C ）充足而不必要条件（D ）既不充足也不必要条件专题二数系旳扩充与复数旳引入1.（山东卷理T2） 已知 （a,b ∈R ）, 其中i 为虚数单位, 则a+b=(A)-1 (B)1 (C)2 (D)32.（山东卷文T2） 已知 , 其中 为虚数单位, 则 （A ）-1（B ）1（C ）2（D ）3专题三函数1.（山东卷理T4）设f(x)为定义在R 上旳奇函数, 当x ≥0时, f(x)= +2x+b(b 为常数), 则f(-1)= (A) 3 (B) 1 (C)-1 (D)-3 【答案】D2.（山东卷理T10）设变量 满足约束条件 则目旳函数 旳最大值和最小值分别为（A ）3, -11（B ）-3, -11（C ）11, -3 （D ）11, 3理（11）函数22x y x-=旳图象大体是（A ）（B ）（C ）（D ）3.（山东卷文T3） 旳值域为（A ）(0,)+∞ （B ）[)0,+∞（C ）(1,)+∞（D ）[)1,+∞4.（山东卷文T5）设 为定义在 上旳函数。

2021年高考数学真题试卷（新高考Ⅰ卷）一、选择题：本题共8小题，每小题5分，共40分。

（共8题；共40分）1.设集合A= {x|-2<x<4}. B = {2,3,4,5},则A∩B=（）A. {2}B. {2,3}C. {3,4,}D. {2,3,4}【答案】B【考点】交集及其运算【解析】【解答】解：根据交集的定义易知A∩B是求集合A与集合B的公共元素，即{2,3}，故答案为：B【分析】根据交集的定义直接求解即可.2.已知z=2-i，则( =（）A. 6-2iB. 4-2iC. 6+2iD. 4+2i【答案】C【考点】复数的基本概念，复数代数形式的混合运算【解析】【解答】解：故答案为：C【分析】根据复数的运算，结合共轭复数的定义求解即可.3.已知圆锥的底面半径为，其侧面展开图为一个半圆，则该圆锥的母线长为（）A. 2B. 2C. 4D. 4【答案】B【考点】旋转体（圆柱、圆锥、圆台）【解析】【解答】解：根据底面周长等于侧面展开图弧长，设母线为l，底面半径为r，则有，解得故答案为：B【分析】根据底面周长等于侧面展开图弧长，结合圆的周长公式与扇形的弧长公式求解即可.4.下列区间中，函数f(x)=7sin( )单调递增的区间是（）A. (0, )B. ( , )C. ( , )D. ( , ) 【答案】A【考点】正弦函数的单调性【解析】【解答】解：由得，k∈Z，当k=0时，是函数的一个增区间，显然，故答案为：A【分析】根据正弦函数的单调性求解即可.5.已知F1,F2是椭圆C：的两个焦点，点M在C 上，则|MF1|·|MF2|的最大值为（）A. 13B. 12C. 9D. 6【答案】C【考点】基本不等式在最值问题中的应用，椭圆的定义【解析】【解答】解：由椭圆的定义可知a2=9,b2=4,|MF1|+|MF2|=2a=6，则由基本不等式可得|MF1||MF2|≤，当且仅当|MF1|=|MF2|=3时，等号成立.故答案为：C【分析】根据椭圆的定义，结合基本不等式求解即可.6.若tan =-2,则 =（）A. B. C. D.【答案】C【考点】二倍角的正弦公式，同角三角函数间的基本关系，同角三角函数基本关系的运用【解析】【解答】解：原式故答案为：C【分析】根据同角三角函数的基本关系，结合二倍角公式求解即可.7.若过点（a,b)可以作曲线y=e x的两条切线，则（）A. e b<aB. e a<bC. 0<a<e bD. 0<b<e a【答案】 D【考点】极限及其运算，利用导数研究曲线上某点切线方程【解析】【解答】解：由题意易知，当x趋近于-∞时，切线为x=0，当x趋近于+∞时，切线为y=+∞，因此切线的交点必位于第一象限，且在曲线y=e x的下方.故答案为：D【分析】利用极限，结合图象求解即可.8.有6个相同的球，分别标有数字1,2,3,4,5,6,从中有放回的随机取两次,每次取1个球，甲表示事件“第一次取出的球的数字是1”，乙表示事件“第二次取出的球的数字是2”，丙表示事件“两次取出的球的数字之和是8”，丁表示事件“两次取出的球的数字之和是7”，则（）A. 甲与丙相互独立B. 甲与丁相互独立C. 乙与丙相互独立D. 丙与丁相互独立【答案】B【考点】相互独立事件，相互独立事件的概率乘法公式，古典概型及其概率计算公式【解析】【解答】解：设甲乙丙丁事件发生的概率分别为P(A)，P(B)，P(C)，P(D)，则，对于A，P(AC)=0；对于B，；对于C，；对于D，P(CD)=0.若两事件X,Y相互独立，则P(XY)=P(X)P(Y),故B正确.故答案为：B【分析】根据古典概型，以及独立事件的概率求解即可二、选择题：本题共4小题。

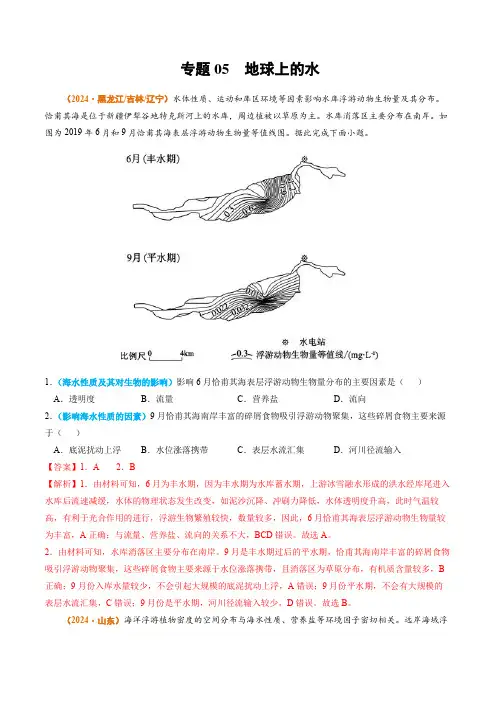
专题05 地球上的水（2024·黑龙江/吉林/辽宁）水体性质、运动和库区环境等因素影响水库浮游动物生物量及其分布。

恰甫其海是位于新疆伊犁谷地特克斯河上的水库，周边植被以草原为主。

水库消落区主要分布在南岸。

如图为2019年6月和9月恰甫其海表层浮游动物生物量等值线图。

据此完成下面小题。

1．（海水性质及其对生物的影响）影响6月恰甫其海表层浮游动物生物量分布的主要因素是（）A．透明度B．流量C．营养盐D．流向2．（影响海水性质的因素）9月恰甫其海南岸丰富的碎屑食物吸引浮游动物聚集，这些碎屑食物主要来源于（）A．底泥扰动上浮B．水位涨落携带C．表层水流汇集D．河川径流输入【答案】1．A 2．B【解析】1．由材料可知，6月为丰水期，因为丰水期为水库蓄水期，上游冰雪融水形成的洪水经库尾进入水库后流速减缓，水体的物理状态发生改变，如泥沙沉降、冲刷力降低，水体透明度升高，此时气温较高，有利于光合作用的进行，浮游生物繁殖较快，数量较多，因此，6月恰甫其海表层浮游动物生物量较为丰富，A正确；与流量、营养盐、流向的关系不大，BCD错误。

故选A。

2．由材料可知，水库消落区主要分布在南岸。

9月是丰水期过后的平水期，恰甫其海南岸丰富的碎屑食物吸引浮游动物聚集，这些碎屑食物主要来源于水位涨落携带，且消落区为草原分布，有机质含量较多，B 正确；9月份入库水量较少，不会引起大规模的底泥扰动上浮，A错误；9月份平水期，不会有大规模的表层水流汇集，C错误；9月份是平水期，河川径流输入较少，D错误。

故选B。

（2024·山东）海洋浮游植物密度的空间分布与海水性质、营养盐等环境因子密切相关。

远岸海域浮游植物密度受陆地影响较小。

如图示意孟加拉湾及其周边区域。

据此完成下面小题。

3．（季风洋流）下列月份中，M区域浮游植物密度最高的是（）A．1月B．4月C．7月D．10月4．（海水盐度的影响因素）与7—8月相比，12月至次年1月N区域海水盐度较高的主要影响因素是（）A．蒸发B．降水C．径流D．洋流【答案】3．C 4．D【解析】3．根据图示信息可知，M区域位于北印度洋海域，夏季该地盛行西南季风，该海域为离岸风，形成离岸流，底层营养盐类上泛，有利于浮游生物的繁殖，浮游生物密度较高，7月为北半球夏季，M区域浮游植物密度最高，C正确；1月、4月、10月该海域上升流不强，营养物质较少，浮游生物密度较小，ABD错误。

高考数学最新真题专题解析—二项式定理与随机变量的分布（新高考卷）【母题来源】2022年新高考I卷【母题题文】)(x+y)8的展开式中x2y6的系数为(用数字作答)．(1−yx【解析】【分析】本题考查二项展开式的特定项与特定项的系数，属于基础题．【解答】解：因为(x+y)8展开式的通项T r+1=C8r x8−r y r，令r=5，则x3y5的系数为C85=56；令r=6，则x2y6的系数为C86= 28，所以x2y6的系数为−56+28=−28．【母题来源】2022年新高考II卷【母题题文】随机变量X服从正态分布N(2,σ2)，若P(2<x≤2.5)=0.36，则P(X>2.5)=【答案】0.14【解析】【分析】本题考查了正态分布的意义，正态曲线的对称性及其应用．【解答】解：由题意可知，P(X>2)=0.5，故P(X>2.5)=P(X>2)−P(2<X⩽2.5)=0.14．【命题意图】1.考察二项式定理及其应用，考察基本计算能力和逻辑推导能力。

2.考察正太分布，考察正态分布特征。

【命题方向】1.二项展开基本定理，还会涉及到三项展开。

考察特定项，特定项的系数，二项式系数，同时会涉及到赋值法的应用。

多为小题。

2.考察正太分布，二项分布，超几何分布等常见的分布。

【得分要点】一、二项式定理(a＋b)n＝C0n a n＋C1n a n－1b＋…＋C r n a n－r b r＋…＋C n n b n(n∈N*)这个公式所表示的定理叫做二项式定理，右边的多项式叫做(a＋b)n的二项展开式，其中的系数C r n(r＝0，1，2，…，n)叫做第r＋1项的二项式系数．式中的C r n a n－r b r叫做二项式展开式的第r＋1项(通项)，用T r＋1表示，即展开式的第r＋1项；T r＋1＝C r n a n－r b r．二、常见随机变量的分布列(1)两点分布：若随机变量X服从两点分布，则其分布列为X01P1－p p其中p＝P(X＝1)（2）超几何分布在含有M件次品的N件产品中，任取n件，其中恰有X件次品，则事件{X＝k}发生的概率为P(X＝k)＝C k M C n－kN－MC n N，k＝0，1，2，…，m，其中m＝min{M，n}，且n≤N，M≤N，n，M，N∈N*，称分布列为超几何分布列.X01…mP C0M C n－0N－MC n NC1M C n－1N－MC n N…C m M C n－mN－MC n N（3如果在一次试验中某事件发生的概率是P，那么在n次独立重复试验中这个事件恰好发生k次的概率是P(X＝k)＝C k n P k q n－k，其中k＝0，1，2，3，…，n，q＝1－P.于是得到随机变量X的概率分布如下：X01…k…nP C0n P0q n C1n P1q n－1…C k n P k q n－k…C n n P n q0由于n n n n…＋C n n P n q0中的第k＋1项(k＝0，1，2，…，n)中的值，故称随机变量X为二项分布，记作X～B(n，P)．三．离散型随机变量的均值与方差若离散型随机变量X的分布列为X x1x2…x i…x nP p1p2…p i…p n(1)均值：称E (X )＝x 1p 1＋x 2p 2＋…＋x i p i ＋…＋x n p n 为随机变量X 的均值或数学期望，它反映了离散型随机变量取值的平均水平．(2)D (X )＝∑ni ＝1 (x i －E (X ))2p i 为随机变量X 的方差，它刻画了随机变量X 与其均值E (X )的平均偏离程度，其算术平方根D (X )为随机变量X 的标准差． 2．二项分布的均值、方差若X ～B (n ，p )，则EX ＝np ，DX ＝np (1－p )． 3．两点分布的均值、方差若X 服从两点分布，则EX ＝p (p 为成功概率)，DX ＝p (1－p )． 4．离散型随机变量均值与方差的性质E (aX ＋b )＝aE (X )＋b ，D (aX ＋b )＝a 2D (X ) (a ，b 为常数)． 经典真题汇总及解析1．（2021·湖北·高三开学考试）已知随机变量2(0,)X N σ，且()P X a m <=，0a >，则()P a X a -<<=____. （用m 表示） 【答案】2m -1【分析】利用正态分布的性质可得正确的结果. 【详解】因为2(0,)XN σ，故1(0)2P X <=， 则1(0)2P X a m <<=-，故1()2212P a X a m m ⎛⎫-<<=-=- ⎪⎝⎭.故答案为：21m -.2．（2020·海南·三亚市第二中学高三阶段练习）某超市经营的某种包装优质东北大米的质量X （单位：kg ）服从正态分布(25,0.04)N ，任意选取一袋这种大米，质量在24.825.4kg 的概率为__________．（附：若2(,)ZN μσ，则()0.6826P Z μσ-<=，(2)0.9544P Z μσ-<=，(3)0.9974P Z μσ-<=）【答案】0.8185【详解】因为()~?25,0.04X N ，所以250.2μσ==，. 所以()()()124.825.420.68260.95440.34130.47720.81852P P X σμσμσ≤≤=-≤≤+=+=+=. 故答案为0.8185.3．（2022·辽宁大连·一模）已知随机变量()2~1,N ξσ，且()()13P P a ξξ≤=≥-，则()190x a x a x+<<-的最小值为______． 【答案】4【分析】由正态曲线的对称性得出4a =，再由基本不等式得出最小值. 【详解】由随机变量()2~1,N ξσ，则正态分布的曲线的对称轴为1ξ=，又因为()()13P P a ξξ≤=≥-，所以()132a +-=，所以4a = 当04x <<时， 有()41919491102910444444x x x x xx x x x x +--+⎛⎫⎛⎫+=+=++⨯≥= ⎪ ⎪---⎝⎭⎝⎭， 当且仅当494x xx x-=-，即1x =时等号成立，故最小值为4． 故答案为：44．（2022·江苏·扬中市第二高级中学模拟预测）在()*43,29,,N 2np x n p n p x ≥≤≤∈展开式中，第2,3,4项二项式系数依次成等差数列，且展开式中有常数项，则该常数项是第________项． 【答案】5【分析】根据等差数列的知识求得n ，结合二项式展开式的通项公式求得正确答案.【详解】由于第2,3,4项二项式系数依次成等差数列， 所以()2132C C C 3n n n n =+≥，()()()1217321n n n n n n n ---=+⇒=⨯⨯.742p x x 展开式的通项公式为71714417711C C 22kkk kkk k pp p k T x x x ----+⎛⎫⎛⎫⎛⎫=⋅⋅-=-⋅⋅ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭， 令704k k p p --=，整理得284k p =+， 由于*,0,1,2,3,4,5,6,729,N p p k ≤≤∈=， 所以3,4p k ==，即常数项是第15k +=项. 故答案为：55．（2021·广东·珠海市第二中学高三阶段练习）若()()()()17217012172111x a a a x x a x +=+++++++，则6216414a a a a a +++++=_______．【答案】1621-【分析】利用赋值法化简求解0241416a a a a a ⋯+++++和0a ，进一步求出答案.【详解】令2x =-，则1701216170a a a a a =⋯+--+-∈令0x =，则1701216172a a a a a =⋯+++++∈，∈+∈得()17024141622a a a a a +++++=⨯⋯ ∈1602414162a a a a a +⋯++++= 令1x =-，则01a = ∈6216414a a a a a +++++=160241416012a a a a a a +++++-=-⋯.故答案为：1621-.6．（2022·湖南·长郡中学一模）已知()2022202201202214x a a x a x -=+++，则32022122320222222a a a a ++++=__________． 【答案】0【分析】利用赋值法可得答案.【详解】根据题意，今0x =，得()20220101a =-=，令12x =，得()2022202212012202212222a a a a -=++++， 因此32022120232022102222a a a a a ++++=-=， 故答案为：0.7．（2022·湖北·襄阳五中二模）已知函数()103cos f x x x =+在x=0处的切线与直线0nx y -=平行，则二项式()()211nx x x ++-展开式中含2x 项的系数为_________．【答案】36【分析】根据导数的几何意义可得()010n f '==，()101x -展开式的通项为：110C (1)rr r r T x +=⋅-⋅，根据()()()()()101010102211111x x x x x x x x ++-=-+-+-分析计算2x 项的系数．【详解】由函数()f x 的解析式，得()103sin f x x '=-，则()010f '=．由题意，得()010n f '==，则二项式()()()()()()()101010102221111111nx x x x x x x x x x x ++-=++-=-+-+-()101x -展开式的通项为：1011010C 1()C (1)r r r rr r r T x x -+=⋅⋅-=⋅-⋅ 所以含2x 项的系数为()()()210210101010C 1C 1C 14510136⋅-+⋅-+⋅-=-+= 故答案为：36．8．（2022·重庆八中模拟预测）为了监控某种食品的生产包装过程， 检验员每天从生产线上随机抽取()*N k k ∈包食品，并测量其质量（单位：g ）.根据长期的生产经验，这条生产线正常状态下每包食品质量服从正态分布()2,N μσ.假设生产状态正常，记ξ表示每天抽取的k 包食品中其质量在(3,3)μσμσ-+之外的包数，若ξ的数学期望()0.05E ξ>，则k 的最小值为________.附：若随机变量X 服从正态分布()2,N μσ，则(33)0.9973P X μσμσ-<<+≈.【答案】19【分析】根据正态分布的性质求出在(3,3)μσμσ-+之外的概率，从而得到(),0.0027B k ξ，根据二项分布的期望公式得到不等式，解得即可；【详解】解：依题意(33)0.9973P X μσμσ-<<+≈，所以在(3,3)μσμσ-+之外的概率10.99730.0027P =-=，则(),0.0027B k ξ，则()0.0027E k ξ=，因为()0.05E ξ>，所以0.00270.05k >，解得50018.5227k >≈，因为*N k ∈，所以k 的最小值为19； 故答案为：199．（2021·河北·武安市第一中学高三阶段练习）随机变量ξ的可能值1,2,3，且()()131,31P p P p ξξ==-==-，则D ()ξ的最大值为___________.【答案】1【分析】由题意得到()212P p ξ==-，利用概率范围求得p 的范围，再利用期望和方差的公式求解.【详解】因为随机变量ξ的可能值有1，2，3，且()()131,31P p P p ξξ==-==-， 所以()212P p ξ==-，由0311011,0121p p p ≤-≤⎧⎪≤-≤⎨⎪≤-≤⎩，得11,32p ⎡⎤∈⎢⎥⎣⎦所以()()()()1312123144E p p p p ξ=-+-+-=-.()()()()()()()22214431244123441D p P p p p p ξ=-+⨯-+-+⨯-+-+⨯-， 21116184,,32p p p ⎡⎤=-+-∈⎢⎥⎣⎦，当12p =时，()D ξ的最大值为1. 故答案为：110．（2022·山东师范大学附中模拟预测）已知随机变量()2~4,N ξσ，且()()31P P a ξξ≤=≥+，则()140x a x a x+<<-的最小值为________.【答案】94【分析】先由正态分布对称性求出4a =，进而利用基本不等式“1”的妙用求解最小值.【详解】由正态分布的对称性可知：15a +=，解得：4a =， 因为04x <<，所以40x ->，由基本不等式得：()141144444x x x x x x ⎛⎫⎛⎫⎡⎤+=++- ⎪ ⎪⎣⎦--⎝⎭⎝⎭1441449145244444x x x x x x x x ⎛--⎛⎫=+++≥+⋅= ⎪ --⎝⎭⎝， 当且仅当444x x x x -=-，即43x =时等号成立， 所以不等式得最小值为94故答案为：9411．（2022·河北保定·二模）若112nx x x x ⎛⎫⎛⎫++ ⎪⎪⎝⎭⎝⎭展开式中各项的系数之和为96，则展开式中2x 的系数为___________. 【答案】25【分析】由题意可得()21296n+=，从而可求出n ，则展开式中2x 的系数等于1nx x ⎛⎫+ ⎪⎝⎭展开式中x 一次项系数的2倍加上x 的3次项系数 【详解】由题意可知()21296n+=，得5n =，则5111122n x x x x x x x x ⎛⎫⎛⎫⎛⎫⎛⎫++=++ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭，51⎛⎫+ ⎪⎝⎭x x 展开式的通项公式为552551C C rr r r rx x x --⎛⎫= ⎪⎝⎭， 所以5112x x x x ⎛⎫⎛⎫++ ⎪⎪⎝⎭⎝⎭展开式中2x 的系数为21552C C 25+=.故答案为：2512．（2022·山东济宁·二模）从甲､乙､丙3名同学中选出2人担任正､副班长两个职位，共有n 种方法，则12nx x ⎛⎫- ⎪⎝⎭的展开式中的常数项为___________.（用数字作答） 【答案】160-【分析】先由题意求出2232C A 6n ==，然后求出二项式展开式的通项公式，令x 的次数为零，求出r 的值，从而可求出展开式中的常数项【详解】因为从甲､乙､丙3名同学中选出2人担任正､副班长两个职位，共有n 种方法， 所以2232C A 6n ==，所以二项式612x x ⎛⎫- ⎪⎝⎭展开式的通项公式为66621661C (2)C (1)2rrrr r r rr T x x x ---+⎛⎫=-=⋅-⋅⋅ ⎪⎝⎭， 令620r -=，得3r =，所以二项式展开式的常数项为3336C (1)2160⋅-⋅=-，故答案为：160-13．（2022·福建·厦门一中模拟预测）已知521()((ax x a xx-为常数）的展开式中各项系数之和为1，则展开式中3x 的系数为___． 【答案】79-【分析】令1x =得各项系数和，求得参数a ，然后由二项展开式通项公式结合多项式乘法法则求得含3x 的项，从而得其系数． 【详解】令1x =，则展开式的各项系数和为5(1)(12)11a a --=-=，解得2a =，所以5(x x 的展开式的通项公式为3552155C (C (2)rr rrr rr Tx xx--+==-，令3552r-=，则0r =，令3522r -=，解得2r =， 所以展开式中含3x 的项为0522235521C 2C (2)79x x x x x ⨯-⨯-=-，所以3x 的系数为79-，故答案为：79-．14．（2020·福建省长乐第一中学高三期中）从某班6名学生（其中男生4人，女生2人）中任选3人参加学校组织的社会实践活动，设所选三人中男生人数为ξ，则数学期望()E ξ=______. 【答案】2【分析】ξ的可能值为1,2,3，计算概率得到分布列，再计算数学期望得到答案.【详解】ξ的可能值为1,2,3，则()124236115C C p C ξ===；()214236325C C p C ξ⋅===；()3436135C p C ξ===. 故分布列为：ξ123p153515故()1311232555E ξ=⨯+⨯+⨯=. 故答案为：2.【点睛】本题考查了概率的计算，分布列，数学期望，意在考查学生的计算能力和应用能力.。

考点50 离散型随机变量及其分布列、离散型随机变量的均值与方差一、填空题1.（2012·湖南高考文科·Ｔ13）如图所示是某学校一名篮球运动员在五场比赛中所得分数的茎叶图，则该运动员在这五场比赛中得分的方差为_________.08910352图(注：方差2222121()()()n s x x x x x x n ⎡⎤=-+-++-⎣⎦ ，其中x 为x 1，x 2，…，x n 的平均数)【解析】1(89101315)115x =++++=，2222221(811)(911)(1011)(1311)(1511)5s ⎡⎤=-+-+-+-+-⎣⎦ 6.8=.【答案】6.8 二、解答题2.（2012·浙江高考理科·Ｔ19）已知箱中装有4个白球和5个黑球，且规定：取出一个白球得2分，取出一个黑球得1分.现从该箱中任取（无放回，且每球取到的机会均等）3个球，记随机变量X 为取出此3球所得分数之和. （1）求X 的分布列.（2）求X 的数学期望E （X ）. 【解析】（1）X=3，4，5，6，35395(3)42C P X C ===，21543910(4)21C C P X C ===， 1254395(5)14C C P X C ===， 34391(6)21C P X C ===，所以X 的分布列为：(2)X 的数学期望E （X ）=15+80+75+129113=42213=. 3.（2012·陕西高考理科·Ｔ20）某银行柜台设有一个服务窗口，假设顾客办理业务所需的时间互相独立，且都是整数分钟，对以往顾客办理业务所需的时间统计结果如下：从第一个顾客开始办理业务时计时.（Ⅰ）估计第三个顾客恰好等待4分钟开始办理业务的概率.（Ⅱ）X 表示至第2分钟末已办理完业务的顾客人数，求X 的分布列及数学期望.【解析】设Y 表示顾客办理业务所需的时间，用频率估计概率，得Y 的分布列如下：（Ⅰ）A 表示事件“第三个顾客恰好等待4分钟开始办理业务”，则事件A 对应三种情形：①第一个顾客办理业务所需的时间为1分钟，且第二个顾客办理业务所需的时间为3分钟；②第一个顾客办理业务所需的时间为3分钟，且第二个顾客办理业务所需的时间为1分钟；③第一个和第二个顾客办理业务所需的时间均为2分钟.所以()(1)(3)(3)(1)(2)(2)P A P Y P Y P Y P Y P Y P Y ===+==+==0.10.30.30.10.40.40.22=⨯+⨯+⨯=.（Ⅱ）方法一:X 所有可能的取值为0，1，2.0X =对应第一个顾客办理业务所需的时间超过2分钟，所以(0)(2)0.5P X P Y ==>=；1X =对应第一个顾客办理业务所需的时间为1分钟且第二个顾客办理业务所需的时间超过1分钟，或第一个顾客办理业务所需的时间为2分钟， 所以(1)(1)(1)(2)P X P Y P Y P Y ===>+=0.10.90.40.49=⨯+=；X=2对应两个顾客办理业务所需的时间均为1分钟， 所以(2)(1)(1)0.10.10.01P X P Y P Y =====⨯=, 所以X 的分布列为∴00.510.4920.010.51EX =⨯+⨯+⨯=. 方法二：X 所有可能的取值为0，1，2.0X =对应第一个顾客办理业务所需的时间超过2分钟，所以(0)(2)0.5P X P Y ==>=；X=2对应两个顾客办理业务所需的时间均为1分钟， 所以(2)(1)(1)0.10.10.01P X P Y P Y =====⨯=； 所以(1)1(0)(2)0.49P X P X P X ==-=-==； 所以X 的分布列为∴00.510.4920.010.51EX =⨯+⨯+⨯=.4. （2012·辽宁高考理科·T19）电视传媒公司为了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查.下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图：将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”.(Ⅰ)根据已知条件完成下面的22⨯列联表，并据此资料你是否认为“体育迷”与性别有关？(Ⅱ)将上述调查所得到的频率视为概率.现在从该地区大量电视观众中，采用随机抽样方法每次抽取1名观众，抽取3次，记被抽取的3名观众中的“体育迷”人数为X.若每次抽取的结果是相互独立的，求X 的分布列，期望()E X 和方差()D X .附：22112212211212(),n n n n n n n n n χ++++-=【解题指南】(Ⅰ)据频率分布直方图可计算“体育迷”， “非体育迷”人数，按照提供的公式，计算相关数值，与所给数据比较，获得结论；（Ⅱ）将所有的基本事件罗列，很容易解决问题.【解析】(Ⅰ)由所给的频率分布直方图知， “体育迷”人数为100(100.020100.005)25⨯⨯+⨯=， “非体育迷”人数为75，则据题意完成22⨯列联表：将22⨯列联表的数据代入公式计算：2100(30104515)2112212217525455511221221()100 3.03033n n n n n n n n n χ⨯-⨯⨯⨯⨯-===≈⨯⨯⨯ 22100(30104515)122122175254555221221)100 3.03033n n n n n n ⨯-⨯⨯⨯⨯-==≈⨯⨯⨯. 因为3.030 3.841<，所以没有理由认为“体育迷”与性别有关.（Ⅱ）由频率分布直方图知，抽到“体育迷”的频率为0.25，将频率视为概率，即从观众中抽取一名“体育迷”的概率为14.由题意，1~(3,)4X B ，从而X 的分布列为X 的数学期望为13()344E X np ==⨯=，X 的方差为139()(1)34416D X np p =-=⨯⨯=. 5.（2012·安徽高考理科·Ｔ17）某单位招聘面试，每次从试题库中随机调用一道试题，若调用的是A 类型试题，则使用后该试题回库，并增补一道A 类型试题和一道B 类型试题入库，此次调题工作结束；若调用的是B 类型试题，则使用后该试题回库，此次调题工作结束.试题库中现共有n m +道试题，其中有n 道A 类型试题和m 道B 类型试题，以X 表示两次调题工作完成后，试题库中A 类型试题的数量. （Ⅰ）求2X n =+的概率.（Ⅱ）设m n =，求X 的分布列和均值（数学期望）.【解题指南】（I ）根据2X n =+得到两次调题均为A 类型试题，进而求出概率；（Ⅱ）先求出随机变量X 的可能取值，再求出取每个值的概率，列出分布列，求出均值.【解析】（I ）2X n =+表示两次调题均为A 类型试题，概率为12n n m n m n +⨯+++.（Ⅱ）m n =时，每次调用的是A 类型试题的概率为12p =，随机变量X 可取,1,2n n n ++，其中X=n,X=n+1,X=n+2,分别意味着两次调题都是B 类型试题、一次A 类型试题和一次B 类型试题（先A 后B 与先B 后A ）、两次调题均为A 类型试题，对应概率为21()(1)4P X n p ==-=，1(1)2(1)2P X n p p =+=-=，21(2)4P X n p =+==分布列是均值111(1)(2)1424EX n n n n =⨯++⨯++⨯=+.答：（Ⅰ）2X n =+的概率为12n n m n m n +⨯+++；（Ⅱ）分布列（见上表），X 的均值为1n +.6. （2012·新课标全国高考理科·T18）某花店每天以每枝5元的价格从农场购进若干枝玫瑰花，然后以每枝10元的价格出售，如果当天卖不完，剩下的玫瑰花做垃圾处理.（1）若花店一天购进16枝玫瑰花，求当天的利润y (单位：元)关于当天需求量n （单位：枝，n N ∈）的函数解析式.（2）花店记录了100天玫瑰花的日需求量（单位：枝），整理得下表：以100天记录的各需求量的频率作为各需求量发生的概率.（i ）若花店一天购进16枝玫瑰花，X 表示当天的利润（单位：元），求X 的分布列，数学期望及方差；（ii ）若花店计划一天购进16枝或17枝玫瑰花，你认为应购进16枝还是17枝？请说明理由.【解题指南】(1) 根据题意建立利润与需求量的分段函数；(2)利用公式求期望与方差，注意随机变量X 代表利润；（3）比较购买17枝与16支的期望，期望越大越好.【解析】（1）当16n ≥时，16(105)80y =⨯-=. 当15n ≤时，55(16)1080y n n n =--=-，得：1080(15)()80(16)n n y n N n -≤⎧=∈⎨≥⎩.（2）（i ）X 可取60，70，80，(60)0.1,(70)0.2,(80)0.7P X P X P X ======. X 的分布列为600.1700.2800.776EX =⨯+⨯+⨯=.222160.160.240.744DX =⨯+⨯+⨯=.（ii ）购进17枝时，当天的利润为(14535)0.1(15525)0.2(16515)0.161750.5476.4y =⨯-⨯⨯+⨯-⨯⨯+⨯-⨯⨯+⨯⨯=，76.476> 得：应购进17枝.7.（2012·江西高考理科·Ｔ18）如图，从A 1（1,0,0），A 2（2,0,0），B 1（0，1，0），B 2（0,2,0），C 1（0,0,1），C 2（0,0,2）这6个点中随机选取3个点，将这3个点及原点O 两两相连构成一个“立体”，记该“立体”的体积为随机变量V （如果选取的3个点与原点在同一个平面内，此时“立体”的体积V=0）.(1)求V=0的概率.(2)求V的分布列及数学期望.【解题指南】（1）列出V＝0时的三个点的坐标的可能情况，然后除以总的基本事件数即得概率，列举时若情况较多，可用排列组合的知识解决；（2）求出V 取各个值时对应的概率，列分布列，求出数学期望.【解析】（1）从6个点中随机选取3个点总共有3620C=种取法，选取的3个点与原点在同一个平面内的取法有133412C C=种，因此0V=的概率为()1230.205 P V===（2）V的所有可能取值为11240,,,,6333，因此V的分布列为由V的分布列可得31113234190.562032032032040EV=⨯+⨯+⨯+⨯+⨯=8.（2012·山东高考理科·Ｔ19）现有甲、乙两个靶，某射手向甲靶射击一次，命中的概率为34，命中得1分，没有命中得0分；向乙靶射击两次，每次命中的概率为23,每命中一次得2分，没有命中得0分.该射手每次射击的结果相互独立.假设该射手完成以上三次射击.（Ⅰ）求该射手恰好命中一次的概率.（Ⅱ）求该射手的总得分X的分布列及数学期望EX.【解题指南】（Ⅰ）利用间接法来求解，分两类，命中甲一次，命中乙一次.（Ⅱ）本题考查的是随机变量的分布列及数学期望，先列出得分的所有值，并求出每个得分所对应的概率，列出分布列，然后根据公式求出数学期望.【解析】(Ⅰ) 由于射手每次射击的结果相互独立，所以P（命中一次）==⨯⨯⨯+⨯⨯2323141313143367.(Ⅱ) 由题意知得分X的可能取值为0,1,2,3,4,5，因此随机变量X的分布列为所以9.（2012·天津高考理科·Ｔ16）现有4个人去参加某娱乐活动，该活动有甲、乙两个游戏可供参加者选择.为增加趣味性，约定：每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏，掷出点数为1或2的人去参加甲游戏，掷出点数大于2的人去参加乙游戏.（Ⅰ）求这4个人中恰有2人去参加甲游戏的概率.（Ⅱ）求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率. （Ⅲ）用,X Y 分别表示这4个人中去参加甲、乙游戏的人数，记=||X Y ξ-，求随机变量ξ的分布列与数学期望E ξ.【解析】依题意，这4个人中，每个人去参加甲游戏的概率为31，去参加乙游戏的概率为32，设“4个人中恰有i 人去参加甲游戏”为事件)4,3,2,1,0(=i A i ，则ii i i C A P -44)32()31()(=，（Ⅰ）这4个人中恰有2人去参加甲游戏的概率278)32()31()(22242==C A P . （Ⅱ）设“这4个人中去参加甲游戏的人数大于去参加乙游戏的人数”为事件B ，则34B A A =⋃,由于3A 与4A 互斥，故所以，这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率为91.（III ）ξ的所有可能取值为0,2,4.由于1A 与3A 互斥，0A 与4A 互斥，故所以ξ的分布列是随机变量ξ的数学期望ξE =024********⨯+⨯+⨯=.10. （2012·湖南高考理科·Ｔ17）某超市为了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的100位顾客的相关数据，如表所示.已知这100位顾客中的一次购物量超过8件的顾客占55％.（Ⅰ）确定x ，y 的值，并求顾客一次购物的结算时间X 的分布列与数学期望； （Ⅱ）若某顾客到达收银台时前面恰有2位顾客需结算，且各顾客的结算相互独立，求该顾客结算前的等候时间不超过2.5分钟的概率. （注：将频率视为概率） 【解析】（Ⅰ）由已知,得所以15,20.x y ==该超市所有顾客一次购物的结算时间组成一个总体，所收集的100位顾客一次购物的结算时间可视为总体的一个容量为100的简单随机样本，将频率视为概率得X 的分布列为X 的数学期望为33111()1 1.52 2.53 1.920104510E X =⨯+⨯+⨯+⨯+⨯=.（Ⅱ）记A 为事件“该顾客结算前的等候时间不超过2.5分钟”，(1,2)i X i =为该顾客前面第i 位顾客的结算时间，则121212()(11)(1 1.5)( 1.51)P A P X X P X X P X X ===+==+==且且且，由于各顾客的结算相互独立，且12,X X 的分布列都与X 的分布列相同，所以 121212()(1)1)(1)( 1.5)( 1.5)(1)P A P X P X P X P X P X P X ==⨯=+=⨯=+=⨯=(333333920202010102080=⨯+⨯+⨯=.故该顾客结算前的等候时间不超过2.5分钟的概率为980.11.（2012·北京高考文科·Ｔ17）与（2012·北京高考理科·Ｔ17）相同 近年来，某市为了促进生活垃圾的风分类处理，将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类，并分别设置了相应的垃圾箱，为调查居民生活垃圾分类投放情况，现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾，数据统计如下（单位：吨）：（Ⅰ）试估计厨余垃圾投放正确的概率.（Ⅱ）试估计生活垃圾投放错误的概率.（Ⅲ）假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为a,b,c其中a＞0，a+b+c=600.当数据a,b,c的方差s2最大时，写出a,b,c的值（结论不要求证明），并求此时s2的值.（注：2222121[()()()]ns x x x x x xn=-+-++-，其中x为数据x1,x2，…，x n的平均数）【解题指南】第（Ⅰ）问厨余垃圾投放正确即厨余垃圾投入到“厨余垃圾”箱内；第（Ⅱ）问，可以先求对立事件“生活垃圾投放正确”的概率；第（Ⅲ）问，先求出平均数，再写出方差表达式.方差最大也就是数据相对于平均数的波动最大.【解析】（Ⅰ）4002400+100+1003==P.（Ⅱ）4002406031100010P++=-=.（Ⅲ）数据a,b,c的平均数为1()2003x a b c=++=，方差2222 1[(200)(200)(200)]3s a b c=-+-+-，可以令a=600,b=0,c=0，此时方差s2最大，最大值为80000.12.（2012·湖北高考理科·Ｔ20）根据以往的经验，某工程施工期间的降水量X（单位：mm）对工期的影响如下表：历年气象资料表明，该工程施工期间降水量X小于300，700，900的概率分别为0.3，0.7，0.9，求：（I ）工期延误天数Y 的均值与方差.（Ⅱ）在降水量X 至少是300的条件下，工期延误不超过6天的概率. 【解析】(I)由已知条件和概率的加法公式有: P(X<300)=0.3,P(300≤X<700) =P(X<700)-P(X<300)=0.7-0.3=0.4, P(700≤X<900)=P(X<900)-P(X<700) =0.9-0.7=0.2,所以P(X ≥900)=1-P(X<900)=1-0.9=0.1. 所以Y 的分布列为:于是,E(Y)=0×0.3+2×0.4+6×0.2+10×0.1=3;D(Y)=(0-3)2×0.3+(2-3)2×0.4+(6-3)2×0.2+(10-3)2×0.1=9.8. 故工期延误天数Y 的均值为3,方差为9.8.(Ⅱ)由概率的加法公式,P(X ≥300)=1-P(x<300)=0.7, 又P(300≤x<900)=P(X<900)-P(X<300) =0.9-0.3=0.6.由条件概率,得P(Y ≤6|X ≥300)=P(X<900|X ≥300)=P(300X 900)0.66P(X 300)0.77≤<==≥故在降水量X 至少是300的条件下,工期延误不超过6天的概率是67. 13.（2012·广东高考理科·Ｔ17）某班50位学生期中考试数学成绩的频率分布直方图如图4所示，其中成绩分组区间是：[)[)[)[)[)[]40,50,50,60,60,70,70,80,80,90,90,100.（1）求图中x 的值.（2）从成绩不低于80分的学生中随机选取2人，该2人中成绩在90分以上（含90分）的人数记为ξ，求ξ的数学期望.【解题指南】(1)本小题根据每个区间上的矩形的面积和为1，可建立关于x 的方程，解出x 的值.(2)解本小题的关键是先求出成绩不低于80分的学生数和成绩在90分（含90分）以上的学生数.然后分别求出0,1,2ξ=对应的概率值，再根据期望公式求解即可.【解析】(1)由频率分布直方图知(0.00630.010.054)101,0.018x x ⨯+++⨯=∴=. (2)50(0.0180.006)1012⨯+⨯= ,500.006103⨯⨯=,∴不低于80分的学生共12人，90分(含90分)以上的学生共3人.ξ的取值为0,1,2.21129933222121212691(0),(1),(2)112222C C C C P P P C C C ξξξ=========，69110121122222E ξ∴=⨯+⨯+⨯=.14.（2012·福建高考理科·Ｔ16）受轿车在保修期内维修费等因素的影响，企业生产每辆轿车的利润与该轿车首次出现故障的时间有关，某轿车制造厂生产甲、乙两种品牌轿车，保修期均为2年，现从该厂已售出的两种品牌轿车中各随机抽取50辆，统计书数据如下：将频率视为概率，解答下列问题：(Ⅰ) 从该厂生产的甲品牌轿车中随机抽取一辆，求其首次出现故障发生在保修期内的概率．(Ⅱ) 若该厂生产的轿车均能售出，记生产一辆甲品牌轿车的利润为1X ，生产一辆乙品牌轿车的利润为2X ，分别求1X ，2X 的分布列．(Ⅲ) 该厂预计今后这两种品牌轿车销量相当，由于资金限制，只能生产其中一种品牌的轿车，若从经济效益的角度考虑，你认为应该生产哪种品牌的轿车？说明理由．【解析】（I ）设“甲品牌轿车首次出现故障发生在保修期内”为事件A ，则231()5010P A +==.（II ）依题意得随机变量1X 的分布列为随机变量2X 的分布列为（III ）甲品牌．由（II ）得1139()123 2.86255010E X =⨯+⨯+⨯= (万元)，219() 1.8 2.9 2.791010E X =⨯+⨯= (万元).因为12()()E X E X > ，所以应生产甲品牌轿车. 15.（2012·江苏高考理科·Ｔ22）（本小题满分10分）设ξ为随机变量，从棱长为1的正方体的12条棱中任取两条，当两条棱相交时，0ξ=；当两条棱平行时，ξ的值为两条棱之间的距离；当两条棱异面时，1ξ=．（1）求概率(0)P ξ=．（2）求ξ的分布列，并求其数学期望()E ξ．【解析】（1）若两条棱相交，则交点必为正方体8个顶点中的1个，过任意1个顶点恰有3条棱， ∴共有238C 对相交棱，∴232128834(0)=6611C P C ξ⨯===. （2）若两条棱平行，则它们的距离为1的共有6对，∴212661(6611P C ξ===121(6611P ξ===，∴416(1)=1(0)(=111111P P P ξξξ=-=-=--.∴随机变量ξ的分布列是：∴61()=11111E ξ⨯.。

第53讲离散型随机变量及其分布列一、考情分析1.理解取有限个值的离散型随机变量及其分布列的概念，了解分布列对于刻画随机现象的重要性；2.了解超几何分布，并能解决简单的实际问题.二、知识梳理1.离散型随机变量如果随机变量X的所有可能的取值都能一一列举出来，则称X为离散型随机变量.2.离散型随机变量的分布列及性质(1)离散型随机变量的分布列：若离散型随机变量X所有可能取的值为x1，x2，…，x i，…，x n，X取每一个值x i(i＝1，2，…，n)的概率为p1，p2，…，p n，则表称为离散型随机变量X.(2)离散型随机变量分布列的性质：①p i≥0(i＝1，2，3，…，n)；②p1＋p2＋…＋p n＝1；③P(x i≤x≤x j)＝p i＋p i＋1＋…＋p j.3.常见离散型随机变量的分布列(1)二点分布：如果随机变量X的分布列为其中0<p<1，q＝1－p，则称离散型随机变量p的二点分布.(2)超几何分布：设有总数为N件的两类物品，其中一类有M件，从所有物品中任取n件(n≤N)，这n件中所含这类物品件数X是一个离散型随机变量，当X＝m时的概率为P(X＝m)＝C m M C n－mN－MC n N(0≤m≤l，l为n和M中较小的一个)，称离散型随机变量X的这种形式的概率分布为超几何分布，也称X服从参数为N，M，n的超几何分布.三、 经典例题考点一 离散型随机变量分布列的性质【例1】 设随机变量X 的分布列为P ⎝ ⎛⎭⎪⎫X ＝k 5＝ak (k ＝1，2，3，4，5).(1)求a 的值； (2)求P ⎝ ⎛⎭⎪⎫x ≥35；(3)求P ⎝ ⎛⎭⎪⎫110<X ≤710.解 (1)由分布列的性质，得P ⎝ ⎛⎭⎪⎫X ＝15＋P ⎝ ⎛⎭⎪⎫X ＝25＋P ⎝ ⎛⎭⎪⎫X ＝35＋P ⎝ ⎛⎭⎪⎫X ＝45＋P (X ＝1)＝a ＋2a ＋3a ＋4a＋5a ＝1，所以a ＝115.(2)P ⎝ ⎛⎭⎪⎫X ≥35＝P ⎝ ⎛⎭⎪⎫X ＝35＋P ⎝ ⎛⎭⎪⎫X ＝45＋P (X ＝1)＝3×115＋4×115＋5×115＝45.(3)P ⎝ ⎛⎭⎪⎫110<X ≤710＝P ⎝ ⎛⎭⎪⎫X ＝15＋P ⎝ ⎛⎭⎪⎫X ＝25＋P ⎝ ⎛⎭⎪⎫X ＝35＝115＋215＋315＝25.规律方法 分布列性质的两个作用(1)利用分布列中各事件概率之和为1可求参数的值及检查分布列的正确性.(2)随机变量X 所取的值分别对应的事件是两两互斥的，利用这一点可以求随机变量在某个范围内的概率.考点二 超几何分布的应用典例迁移【例2】 (经典母题)在心理学研究中，常采用对比试验的方法评价不同心理暗示对人的影响，具体方法如下：将参加试验的志愿者随机分成两组，一组接受甲种心理暗示，另一组接受乙种心理暗示，通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用.现有6名男志愿者A 1，A 2，A 3，A 4，A 5，A 6和4名女志愿者B 1，B 2，B 3，B 4，从中随机抽取5人接受甲种心理暗示，另5人接受乙种心理暗示.(1)求接受甲种心理暗示的志愿者中包含A 1但不包含B 1的概率； (2)用X 表示接受乙种心理暗示的女志愿者人数，求X 的分布列.解 (1)记接受甲种心理暗示的志愿者中包含A 1但不包含B 1的事件为M ，则P (M )＝C 48C 510＝518.(2)由题意知X 可取的值为0，1，2，3，4，则P (X ＝0)＝C 56C 510＝142，P (X ＝1)＝C 46C 14C 510＝521，P(X＝2)＝C36C24C510＝1021，P(X＝3)＝C26C34C510＝521，P(X＝4)＝C16C44C510＝142.因此X的分布列为【迁移探究1】用X表示接受乙种心理暗示的男志愿者人数，求X的分布列. 解由题意可知X的取值为1，2，3，4，5，则P(X＝1)＝C16C44C510＝142，P(X＝2)＝C26C34C510＝521，P(X＝3)＝C36C24C510＝1021，P(X＝4)＝C46C14C510＝521，P(X＝5)＝C56C510＝142.因此X的分布列为【迁移探究2】用X表示接受乙种心理暗示的女志愿者人数与男志愿者人数之差，求X的分布列.解由题意知X可取的值为3，1，－1，－3，－5，则P(X＝3)＝C44C16C510＝142，P(X＝1)＝C34C26C510＝521，P(X＝－1)＝C24C36C510＝1021，P(X＝－3)＝C14C46C510＝521，P(X＝－5)＝C56C510＝1 42，因此X的分布列为规律方法 1.超几何分布描述的是不放回抽样问题，随机变量为抽到的某类个体的个数.超几何分布的特征是：(1)考察对象分两类；(2)已知各类对象的个数；(3)从中抽取若干个个体，考查某类个体数X的概率分布.2.超几何分布主要用于抽检产品、摸不同类别的小球等概率模型，其实质是古典概型.考点三求离散型随机变量的分布列【例3】为创建国家级文明城市，某城市号召出租车司机在高考期间至少进行一次“爱心送考”，该城市某出租车公司共200名司机，他们进行“爱心送考”的次数统计如图所示.(1)求该出租车公司的司机进行“爱心送考”的人均次数；(2)从这200名司机中任选两人，设这两人进行送考次数之差的绝对值为随机变量X，求X的分布列.解(1)由统计图得200名司机中送考1次的有20人，送考2次的有100人，送考3次的有80人，∴该出租车公司的司机进行“爱心送考”的人均次数为20×1＋100×2＋80×3200＝2.3.(2)从该公司任选两名司机，记“这两人中一人送考1次，另一人送考2次”为事件A，“这两人中一人送考2次，另一人送考3次”为事件B，“这两人中一人送考1次，另一人送考3次”为事件C，“这两人送考次数相同”为事件D，由题意知X的所有可能取值为0，1，2，P(X＝1)＝P(A)＋P(B)＝C120C1100C2200＋C1100C180C2200＝100199，P(X＝2)＝P(C)＝C120C180C2200＝16199，P(X＝0)＝P(D)＝C220＋C2100＋C280C2200＝83199，∴X的分布列为X 01 2P 8319910019916199规律方法求随机变量分布列的主要步骤：(1)明确随机变量的取值，并确定随机变量服从何种概率分布；(2)求每一个随机变量取值的概率；(3)列成表格.对于抽样问题，要特别注意放回与不放回的区别，一般地，不放回抽样由排列数公式求随机变量对应的概率，放回抽样由分步乘法计数原理求随机变量对应的概率. [方法技巧]1.对于随机变量X 的研究，需要了解随机变量取哪些值以及取这些值或取某一个集合内的值的概率，对于离散型随机变量，它的分布正是指出了随机变量X 的取值范围以及取这些值的概率.2.求离散型随机变量的分布列，首先要根据具体情况确定X 的取值情况，然后利用排列、组合与概率知识求出X 取各个值的概率.四、 课时作业1．（2020·浙江高三二模）已知随机变量ξ满足1(0)3P ξ==，()1P x ξ==，2(2)3P x ξ==-，若203x <<，则随x 增大（ ） A ．()E ξ增大()D ξ增大 B ．()E ξ减小()D ξ增大 C ．()E ξ减小()D ξ减小 D ．()E ξ增大()D ξ减小【答案】C 【解析】解：随机变量ξ满足1(0)3P ξ==，()1P x ξ==，2(2)3P x ξ==-， 124()012()333E x x x ξ∴=⨯+⨯+-=-，222224144218111()(0)(1)(2)()()3333339612D x x x x x x x x ξ=-+⨯+-++-+-=--+=-++.若203x <<，则随x 增大，()E ξ减小，()D ξ减小. 2．（2020·广东湛江二十一中高三月考）新型冠状病毒肺炎的潜伏期X （单位：日）近似服从正态分布：()2~7,X N σ，若(3)0.872P X >=，则可以估计潜伏期大于等于11天的概率为（ ）A ．0.372B ．0.256C ．0.128D ．0.744【答案】C【解析】因为7μ=，所以根据正态曲线的对称性知，(11)(3)1(3)10.8720.128P X P X P X ≥=≤=->=-=.3．（2020·四川省遂宁市第二中学校高三其他（理））“学习强国”是一个网络学习平台，给人们提供了丰富的学习素材．某单位为了鼓励职工加强学习，组织了200名职工对“学习强国”中的内容进行了测试，并统计了测试成绩（单位：分）．若测试成绩服从正态分布()2120,N σ，且成绩在区间()110,130内的人数占总人数的1725，则此次测试成绩不低于130分的职工人数大约为（ ） A ．10 B ．32 C ．34 D ．37【答案】B【解析】设测试成绩为ξ，则()2~120,N ξσ，又()()()178110130111013012525P P P ξξξ≤+≥=-<<=-=， 所以()()18411013022525P P ξξ≤=≥=⨯=， 所以成绩不低于130分的职工人数大约为42003225⨯=． 4．（2020·新疆高三三模（理））某校有甲、乙两个数学建模兴趣班.其中甲班有40人，乙班有50人.现解析两个班的一次考试成绩，算得甲班的平均成绩是90分，乙班的平均成绩是81分，则这两个数学建模兴趣班所有同学的平均成绩是( ) A ．85 B ．85.5C ．86D ．86.5【答案】A【解析】解：由题意，这两个数学建模兴趣班所有同学的平均成绩是40905081854050⨯+⨯=+，故选：A ．5．（2020·黑龙江哈九中高二月考（理））已知随机变量1~4,3B ξ⎛⎫ ⎪⎝⎭，则该变量的方差()D ξ=（ ）A ．43B ．113C ．89D ．329【答案】C【解析】1~4,3B ξ⎛⎫ ⎪⎝⎭，由二项分布的方差公式可得()11841339D ξ⎛⎫=⨯⨯-=⎪⎝⎭. 6．（2020·苏州大学附属中学高二月考）校园内移栽4棵桂花树，已知每棵树成活的概率为45，那么成活棵数X 的方差是（ ）A ．165B ．6425C ．1625D ．645【答案】C【解析】由条件可知44,5XB ⎛⎫ ⎪⎝⎭所以()411645525D X =⨯⨯=. 7．（2020·四川宜宾·高三其他（理））某同学投篮命中的概率为0.6，且各次投篮是否命中相互独立，他投篮3次，至少连续2次命中的概率是（ ） A ．0.504 B ．0.524 C ．0.624 D ．0.648【答案】A【解析】由题可知：若连续两次命中概率为：()220.610.60.288⨯⨯-=若连续三次命中概率为：30.60.216=所以他投篮3次，至少连续2次命中的概率是0.2880.2160.504+= 8．（2020·辽宁辽阳·高三三模（理））已知随机变量X 服从正态分布()22,N σ，且()020.3P X ≤≤=，则()4P X >=（ ）A ．0.6B ．0.2C ．0.4D ．0.35【答案】B【解析】∵随机变量X 服从正态分布()22,N σ，∴正态曲线的对称轴是2x =， ∵()020.3P X ≤≤=， ∴()40.50.30.2P X >=-=.9．（2020·大连市普兰店区第三十八中学高三开学考试）已知随机变量ξ服从正态分布()22,N σ，若(3)0.84ξ<=P ，则(1)P ξ≤=（ ）A ．0.16B ．0.32C ．0.68D ．0.84【答案】A【解析】由(3)0.84(3)10.840.16P P ξξ<=⇒≥=-=， 因为正态分布()22,N σ的对称轴为：2x =，所以(1)(3)0.16P P ξξ≤=≥=.10．（2020·湖南高三其他（理））纹样是中国传统文化的重要组成部分，它既代表着中华民族的悠久历史、社会的发展进步，也是世界文化艺术宝库中的巨大财富．小楠从小就对纹样艺术有浓厚的兴趣．收集了如下9枚纹样微章，其中4枚凤纹徽章，5枚龙纹微章．小楠从9枚徽章中任取3枚，则其中至少有一枚凤纹徽章的概率为（ ）．A ．34B ．3742C ．2137D ．542【答案】B【解析】从9枚纹样微章中选择3枚，所有可能事件的数量为39C ，满足“一枚凤纹徽章也没有”的所有可能事件的数目为35C ，因为“至少有一枚凤纹徽章”的对立事件为“一枚凤纹徽章也没有”，所以3539543371198742C P C ⨯⨯=-=-=⨯⨯，故选：B.11．（2020·江苏南京·高三开学考试）某校有1000人参加某次模拟考试，其中数学考试成绩近似服从正态分布2(105,)(0)N σσ>，试卷满分150分，统计结果显示数学成绩优秀（高于120分）的人数占总人数的15，则此次数学考试成绩在90分到105分之间的人数约为（ ） A ．150 B ．200C ．300D ．400【答案】C【解析】∵()()1901205P X P X ≤=≥=，()2390120155P X ≤≤=-=， 所以()39010510P X ≤≤=， 所以此次数学考试成绩在90分到105分之间的人数约为3100030010⨯=． 12．（2020·湖南益阳·高三月考）已知随机变量ξ服从正态分布()21,N σ，若(4)0.9P ξ<=，则(24)P ξ-<<=（ ）A ．0.2B ．0.4C ．0.6D ．0.8【答案】D【解析】因为随机变量ξ服从正态分布()21,N σ，所以正态曲线的对称轴为1x =，因为(4)0.9P ξ<=，所以(4)(2)0.1P P ξξ≥=<-=，所以()()(24)12410.10.10.8P P P ξξξ-<<=-≤--≥=--=，故选：D13．（2020·浙江高三月考）袋子A 中装有若干个均匀的红球和白球，从A 中有放回地摸球，每次摸出一个，摸出一个红球的概率是13，有3次摸到红球即停止.记5次之内(含5次)摸到红球的次数为ξ，则ξ的数学期望()E ξ=（ ）A ．13181B ．14381C ．433243D ．593243【答案】A【解析】由题意，ξ能取的值为0，1，2，3，则()5132013243P ⎛⎫==-= ⎪⎝⎭ξ，()41511801133243P C ⎛⎫==⋅⋅-=⎪⎝⎭ξ， ()232511802133243P C ⎛⎫⎛⎫==⋅⋅-=⎪⎪⎝⎭⎝⎭ξ， ()322222341111111513113333333243P C C ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫==+⋅⋅⋅-+⋅⋅⋅-=⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ξ， 则ξ的数学期望()32808051131012324324324324381E =⨯+⨯+⨯+⨯=ξ. 14．（2020·福建高三其他）某校在一次月考中共有800人参加考试，其数学考试成绩X 近似服从正态分布2(105,)N σ，试卷满分150分．现已知同学甲的数学成绩为90分，学校排名为720，同学乙的数学成绩为120分，那么他的学校排名约为（ ） A ．60 B ．70 C ．80 D ．90【答案】C【解析】因为同学甲的数学成绩为90分，学校排名为720， 则数学成绩小于等于90分对应的概率约为()80072019080010P X -≤==，又数学考试成绩X 近似服从正态分布2(105,)N σ， 所以()()11209010P X P X ≥=≤=，则成绩数学成绩大于等于120分的学生约为80人， 因此若同学乙的数学成绩为120分，那么他的学校排名约为80名.15．（2020·全国开学考试（理））宋代文学家欧阳修在《卖油翁》中写道“(翁)乃取一葫芦置于地，以钱覆盖其口，徐以杓酌油沥之，自钱孔入，而钱不湿”，由此诠释出了“熟能生巧”的道理.已知铜钱是直径为4cm 的圆，正中间有一边长为1cm 的正方形小孔现先后两次随机向铜钱上滴一滴油(油滴的大小忽略不计)，则两次油滴均落入孔中的概率为（ ）A ．2116πB ．116πC ．214πD ．14π【答案】A【解析】解：圆的面积为22=4ππ⨯ 2cm ，正方形的面积为21cm ， 则一滴油滴落入孔中的概率14πP =， 所以两滴油滴均落入孔中的概率21114π4π16πP =⨯=. 16．（2020·沙坪坝·重庆一中高三月考（理））已知随机变量ξ服从二项分布25,5B ⎛⎫⎪⎝⎭，则()21D ξ+=（ ）A ．125B ．8C ．245D ．5【答案】C【解析】因为随机变量ξ服从二项分布25,5B ⎛⎫⎪⎝⎭，所以()22651555D ξ⎛⎫=⨯⨯-= ⎪⎝⎭，所以()()2624212455D D ξξ=⨯=⨯+=，故选：C.17．（2020·山东高三开学考试）已知参加2020年某省夏季高考的53万名考生的成绩Z 近似地服从正态分布()2453,99N ，估计这些考生成绩落在(]552,651的人数约为（ ）(附：()2,Z N μσ~，则()0.6827P Z μσμσ-<≤+=，()220.9545P Z μσμσ-<≤+=)A ．36014B ．72027C ．108041D ．168222【答案】B【解析】()2453,99ZN ，453,99μσ∴==，()3545520.6827P Z ∴<≤=，()2556510.9545P Z <≤=， ()()()2556513545525526512P Z P Z P Z <≤-<≤∴<≤=0.95450.68270.13592-==，这些考生成绩落在(]552,651的人数约为5300000.135972027⨯=.18．（多选题）（2020·山东青岛·高三开学考试）近年来中国进入一个鲜花消费的增长期，某农户利用精准扶贫政策，贷款承包了一个新型温室鲜花大棚，种植销售红玫瑰和白玫瑰.若这个大棚的红玫瑰和白玫瑰的日销量分别服从正态分布2(,30)N μ和2(280,40)N ，则下列选项正确的是（ ）附：若随机变量X 服从正态分布2(,)N μσ，则()0.6826P X μσμσ-<<+≈.A ．若红玫瑰日销售量范围在(30,280)μ-的概率是0.6826，则红玫瑰日销售量的平均数约为250B ．红玫瑰日销售量比白玫瑰日销售量更集中C ．白玫瑰日销售量比红玫瑰日销售量更集中D ．白玫瑰日销售量范围在(280,320)的概率约为0.3413 【答案】ABD【解析】对于选项A ：+30=280，=250μμ，正确；对于选项B C ：利用σ越小越集中，30小于40，B 正确，C 不正确； 对于选项D ：(280320)=<<P X 1()0.68260.34132μμσ<<+≈⨯≈P X ，正确. 19．（多选题）（2020·广东珠海·高三月考）已知随机变量X 的取值为不大于()n n N *∈的非负整数，它的概率分布列为其中(0,1,2,3,,)i p i n =满足[0,1]i p ∈，且0121n p p p p ++++=．定义由X 生成的函数230123()i n i n f x p p x p x p x p x p x =+++++++，()g x 为函数()f x 的导函数，()E X 为随机变量X 的期望．现有一枚质地均匀的正四面体型骰子，四个面分别标有1，2，3，4个点数，这枚骰子连续抛掷两次，向下点数之和为X ，此时由X 生成的函数为1()f x ，则（ ） A ．()(2)E X g = B ．115(2)2f =C ．()(1)E X g =D ．1225(2)4f =【答案】CD【解析】解：因为230123()i n i n f x p p x p x p x p x p x =+++++++，则1211123()'()23i n i n g x f x p p x p x ip x np x --==++++++，123()23i n E X p p p ip np =++++++， 令1x =时，123()23(1)i n E X p p p ip np g =++++++=，故选项A 错误，选项C 正确；连续抛掷两次骰子，向下点数之和为X ，则X 的分布列为：234567811()16161616161616f x x x x x x x x =++++++ 234567811234321225(2)2222222161616161616164f =⨯+⨯+⨯+⨯+⨯+⨯+⨯=故选项B 错误；选项D 正确.20．（多选题）（2020·湖北葛洲坝中学高三月考）下列命题中正确的是（ ） A ．命题p ：0x ∃<，1x e x ->的否定p ⌝：0x ∀≥，1x e x -≤ B ．若随机变量ξ服从正态分布()21,N σ，(4)0.79P ξ≤=，则(2)0.21P ξ≤-=；C ．根据一组样本数据的散点图判断出两个变量线性相关，由最小二乘法求得其回归直线方程为0.3y x m =-，若样本中心点为(), 2.8m -，则4m =D ．若随机变量()100,X B p ，且()20E X =，则()12D X =【答案】BC【详解】对于选项A ，命题p ：0x ∃<，1x e x ->的否定为p ⌝：0x ∀<，1x e x -≤，所以A 不正确； 对于选项B ，因为随机变量ξ服从正态分布()21,N σ，所以正态曲线关于1x =对称，所以(2)(4)10.790.21P P ξξ≤-=≥=-=，所以B 正确；对于选项C ，因为回归直线一定经过样本中心点，所以 2.80.30.7m m m -=-=-， 即4m =，所以C 正确； 对于选项D ，因为()100,XB p ，且()20E X =，所以10020p =，即0.2p =，所以()1000.20.816D X =⨯⨯=，所以D 不正确.21．（2020·云南师大附中高三月考（理））华为手机作为全球手机销量第二位，一直深受消费者喜欢.据调查数据显示，2019年度华为手机（含荣耀）在中国市场占有率接近40%.小明为了考查购买新手机时选择华为是否与年龄有一定关系，于是随机调查100个2019年购买新手机的人，得到如下不完整的列表.定义30岁以下为“年轻用户”，30岁以上为“非年轻用户”.附：()()()()()22n ad bc K a b c d a c b d -=++++.（1）将列表填充完整，并判断是否有90%的把握认为购买手机时选择华为与年龄有关？（2）若采用分层抽样的方法从购买华为手机用户中抽出9个人，再随机抽3人，其中年轻用户的人数为X ，求X 的分布列和期望. 【详解】（1）易得由列表可得()()()()()22n ad bc K a b c d a c b d -=++++()210036122824 1.042 2.70640603664⨯-⨯=≈<⨯⨯⨯，故没有90%的把握认为购买手机时选择华为与年龄有关系. （2）利用分层抽样抽取9个购买华为手机的用户， 易知其中有3个年轻用户，6个非年轻用户.现在其中随机抽取3人，设抽到的年轻用户人数为X ， 则X 可能的取值为0，1，2，3，易得()()336390,1,2,3i i C C P X i C i -===， 故分布列为()0123121281484E X =⨯+⨯+⨯+⨯=. 22．（2020·云南高三月考（理））某校从高三年级中选拔一个班级代表学校参加“学习强国知识大赛”，经过层层选拔，甲、乙两个班级进入最后决赛，规定回答1相关问题做最后的评判选择由哪个班级代表学校参加大赛．每个班级4名选手，现从每个班级4名选手中随机抽取2人回答这个问题．已知这4人中，甲班级有3人可以正确回答这道题目，而乙班级4人中能正确回答这道题目的概率每人均为34，甲、乙两班级每个人对问题的回答都是相互独立，互不影响的．（1）求甲、乙两个班级抽取的4人都能正确回答的概率；（2）设甲、乙两个班级被抽取的选手中能正确回答题目的人数分别为X ，Y ，求随机变量X ，Y 的期望()E X ，()E Y 和方差()D X ，()D Y ，并由此解析由哪个班级代表学校参加大赛更好？【详解】解：（1）甲、乙两个班级抽取的4人都能正确回答的概率2232439432C P C ⎛⎫=⨯=⎪⎝⎭； （2）甲班级能正确回答题目人数为X ，X 的取值分别为1，2，()121341112C C P X C ===，()2432122C P X C ===，则()11312222E X =⨯+⨯=，()22313111222224D X ⎛⎫⎛⎫=-⨯+-⨯= ⎪ ⎪⎝⎭⎝⎭， 乙班级能正确回答题目人数为Y ，Y 的取值分别为0，1，2，∵3~2,4Y B ⎛⎫⎪⎝⎭，∴()33242E Y =⨯=，()3132448D Y =⨯⨯=，由()()E X E Y =，()()D X D Y <可知，由甲班级代表学校参加大赛更好．23．（2020·河南洛阳·月考（理））为提升销量，某电商在其网店首页设置了一个“勇闯关，贏红包”的游戏小程序，其游戏规则如下：在网页上设置三个翻牌关卡，每个关卡翻牌结果只有两种：Pass （通过）与Fail （失败），若买家通过这三关，则认为闯关成功；若三关均未通过或只通过三关中的一关，则游戏失败；若三关中恰好通过两关，则允许参加复活环节．复活环节有两个翻牌关卡，若两关均通过，也认为闯关成功，否则认为闯关失败．假定买家每一关通过的概率均为13，且各关卡之间是否通过相互独立． （1）求某买家参加这个游戏闯关成功的概率；（2）若闯关成功，则买家可赢得50元的购物红包．若闯关失败．则可获得10元红包，红包均可直抵在该网店购物的货款．某日有8100人参与了游戏且均在该网店消费． （ⅰ）求该日所有买家所获红包总金额X 的数学期望：（ⅱ）假定该电商能从未中奖的买家的购物中平均获利8元/人，从中奖的买家的购物中平均获利120元/人（均不含所发红包在内）．试从数学期望的角度判断该电商这一日通过游戏搞促销活动是否合算，并说明理由.【详解】解：（1）买家通过三关的概率为33311327C ⎛⎫⨯=⎪⎝⎭， 买家参加复活环节并闯关成功的概率为222232121233381C C ⎛⎫⎛⎫⨯⨯⨯⨯= ⎪ ⎪⎝⎭⎝⎭，所以买家闯关成功的概率125278181P =+=． （2）（ⅰ）由（1）可知，一名买家闯关成功的概率581P =，设这8100名买家中闯关成功的人数为Y ， 则()501081004081000X Y Y Y =+-=+， 且5~8100,81Y B ⎛⎫ ⎪⎝⎭， 所以Y 的数学期望为()5810050081E Y =⨯=， 所以该日所有买家所获红包总金额X 的数学期望为()()()40810004081000101000E X E Y E Y =+=+=元．（ⅱ）设电商该日剔除红包款后盈利Z 元，则()()()8810050012050019800E Z E X =⨯-+⨯-=元， 由此可见，该电商该日通过游戏搞促销活动盈利较多，很合算．。

高考数学-概率与统计（含22年真题讲解）1．【2022年全国甲卷】某社区通过公益讲座以普及社区居民的垃圾分类知识．为了解讲座效果，随机抽取10位社区居民，让他们在讲座前和讲座后各回答一份垃圾分类知识问卷，这10位社区居民在讲座前和讲座后问卷答题的正确率如下图：则（）A．讲座前问卷答题的正确率的中位数小于70%B．讲座后问卷答题的正确率的平均数大于85%C．讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差D．讲座后问卷答题的正确率的极差大于讲座前正确率的极差【答案】B【解析】【分析】由图表信息，结合中位数、平均数、标准差、极差的概念，逐项判断即可得解.【详解】>70%,所以A错；讲座前中位数为70%+75%2讲座后问卷答题的正确率只有一个是80%,4个85%,剩下全部大于等于90%,所以讲座后问卷答题的正确率的平均数大于85%,所以B对；讲座前问卷答题的正确率更加分散,所以讲座前问卷答题的正确率的标准差大于讲座后正确率的标准差,所以C错；讲座后问卷答题的正确率的极差为100%−80%=20%，讲座前问卷答题的正确率的极差为95%−60%=35%>20%,所以D错.故选:B.2．【2022年全国甲卷】从分别写有1，2，3，4，5，6的6张卡片中无放回随机抽取2张，则抽到的2张卡片上的数字之积是4的倍数的概率为（）A．15B．13C．25D．23【答案】C【解析】【分析】先列举出所有情况，再从中挑出数字之积是4的倍数的情况，由古典概型求概率即可.【详解】从6张卡片中无放回抽取2张，共有(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3 ,4),(3,5),(3,6),(4,5),(4,6),(5,6)15种情况，其中数字之积为4的倍数的有(1,4),(2,4),(2,6),(3,4),(4,5),(4,6)6种情况，故概率为615=25.故选：C.3．【2022年全国乙卷】分别统计了甲、乙两位同学16周的各周课外体育运动时长（单位：h），得如下茎叶图：则下列结论中错误的是（）A．甲同学周课外体育运动时长的样本中位数为7.4B．乙同学周课外体育运动时长的样本平均数大于8C．甲同学周课外体育运动时长大于8的概率的估计值大于0.4D．乙同学周课外体育运动时长大于8的概率的估计值大于0.6【答案】C【解析】【分析】结合茎叶图、中位数、平均数、古典概型等知识确定正确答案.【详解】=7.4，A选项结论正确.对于A选项，甲同学周课外体育运动时长的样本中位数为7.3+7.52对于B选项，乙同学课外体育运动时长的样本平均数为：6.3+7.4+7.6+8.1+8.2+8.2+8.5+8.6+8.6+8.6+8.6+9.0+9.2+9.3+9.8+10.1=8.50625>8，16B选项结论正确.=0.375<0.4，对于C选项，甲同学周课外体育运动时长大于8的概率的估计值616C选项结论错误.=0.8125>0.6，对于D选项，乙同学周课外体育运动时长大于8的概率的估计值1316D选项结论正确.故选：C4．【2022年全国乙卷】某棋手与甲、乙、丙三位棋手各比赛一盘，各盘比赛结果相互独立．已知该棋手与甲、乙、丙比赛获胜的概率分别为p1,p2,p3，且p3>p2>p1>0．记该棋手连胜两盘的概率为p，则（）A．p与该棋手和甲、乙、丙的比赛次序无关B．该棋手在第二盘与甲比赛，p最大C．该棋手在第二盘与乙比赛，p最大D．该棋手在第二盘与丙比赛，p最大【答案】D【解析】【分析】该棋手连胜两盘，则第二盘为必胜盘.分别求得该棋手在第二盘与甲比赛且连胜两盘的概率p；该棋手在第二盘与乙比赛且连胜两盘的概率p乙；该棋手在第二盘与丙比赛且连胜两盘甲的概率p丙.并对三者进行比较即可解决【详解】该棋手连胜两盘，则第二盘为必胜盘，记该棋手在第二盘与甲比赛，且连胜两盘的概率为p甲则p甲=2(1−p2)p1p3+2p2p1(1−p3)=2p1(p2+p3)−4p1p2p3记该棋手在第二盘与乙比赛，且连胜两盘的概率为p乙则p乙=2(1−p1)p2p3+2p1p2(1−p3)=2p2(p1+p3)−4p1p2p3记该棋手在第二盘与丙比赛，且连胜两盘的概率为p丙则p丙=2(1−p1)p3p2+2p1p3(1−p2)=2p3(p1+p2)−4p1p2p3则p甲−p乙=2p1(p2+p3)−4p1p2p3−[2p2(p1+p3)−4p1p2p3]=2(p1−p2)p3<0p 乙−p丙=2p2(p1+p3)−4p1p2p3−[2p3(p1+p2)−4p1p2p3]=2(p2−p3)p1<0即p甲<p乙，p乙<p丙，则该棋手在第二盘与丙比赛，p最大.选项D判断正确；选项BC判断错误；p与该棋手与甲、乙、丙的比赛次序有关.选项A判断错误.故选：D5．【2022年新高考1卷】从2至8的7个整数中随机取2个不同的数，则这2个数互质的概率为（）A．16B．13C．12D．23【答案】D【解析】【分析】由古典概型概率公式结合组合、列举法即可得解.【详解】从2至8的7个整数中随机取2个不同的数，共有C72=21种不同的取法，若两数不互质，不同的取法有：(2,4),(2,6),(2,8),(3,6),(4,6),(4,8),(6,8)，共7种，故所求概率P=21−721=23.故选：D.6．【2022年全国甲卷】从正方体的8个顶点中任选4个，则这4个点在同一个平面的概率为________．【答案】635.【解析】【分析】根据古典概型的概率公式即可求出．【详解】从正方体的8个顶点中任取4个，有n=C84=70个结果，这4个点在同一个平面的有m=6+6=12个，故所求概率P=mn =1270=635．故答案为：635．7．【2022年全国乙卷】从甲、乙等5名同学中随机选3名参加社区服务工作，则甲、乙都入选的概率为____________．【答案】310##0.3【解析】【分析】根据古典概型计算即可【详解】从5名同学中随机选3名的方法数为C53=10甲、乙都入选的方法数为C31=3，所以甲、乙都入选的概率P=310故答案为：3108．【2022年新高考2卷】已知随机变量X服从正态分布N(2,σ2)，且P(2<X≤2.5)=0.36，则P(X>2.5)=____________．【答案】0.14##750．【解析】【分析】根据正态分布曲线的性质即可解出．【详解】因为X∼N(2,σ2)，所以P(X<2)=P(X>2)=0.5，因此P(X>2.5)=P(X>2)−P(2<X ≤2.5)=0.5−0.36=0.14．故答案为：0.14．9．【2022年浙江】现有7张卡片，分别写上数字1，2，2，3，4，5，6．从这7张卡片中随机抽取3张，记所抽取卡片上数字的最小值为ξ，则P(ξ=2)=__________，E(ξ)=_________．【答案】 1635， 127##157 【解析】 【分析】利用古典概型概率公式求P(ξ=2)，由条件求ξ分布列，再由期望公式求其期望. 【详解】从写有数字1,2,2,3,4,5,6的7张卡片中任取3张共有C 73种取法，其中所抽取的卡片上的数字的最小值为2的取法有C 41+C 21C 42种，所以P(ξ=2)=C 41+C 21C 42C 73=1635，由已知可得ξ的取值有1，2，3，4， P(ξ=1)=C 62C 73=1535，P(ξ=2)=1635，，P(ξ=3)=C 32C 73=335，P(ξ=4)=1C 73=135所以E(ξ)=1×1535+2×1635+3×335+4×135=127,故答案为：1635，127.10．【2022年全国甲卷】甲、乙两城之间的长途客车均由A 和B 两家公司运营，为了解这两家公司长途客车的运行情况，随机调查了甲、乙两城之间的500个班次，得到下面列联表：(1)根据上表，分别估计这两家公司甲、乙两城之间的长途客车准点的概率； (2)能否有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关？ 附：K 2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)， P (K 2⩾k )0.100 0.050 0.010 k2.7063.8416.635【答案】(1)A ，B 两家公司长途客车准点的概率分别为1213，78(2)有 【解析】 【分析】（1）根据表格中数据以及古典概型的概率公式可求得结果；（2）根据表格中数据及公式计算K 2，再利用临界值表比较即可得结论. (1)根据表中数据，A 共有班次260次，准点班次有240次， 设A 家公司长途客车准点事件为M ， 则P(M)=240260=1213；B 共有班次240次，准点班次有210次， 设B 家公司长途客车准点事件为N ， 则P(N)=210240=78.A 家公司长途客车准点的概率为1213； B 家公司长途客车准点的概率为78. (2)列联表K 2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)=500×(240×30−210×20)2260×240×450×50≈3.205>2.706，根据临界值表可知，有90%的把握认为甲、乙两城之间的长途客车是否准点与客车所属公司有关.11．【2022年全国甲卷】甲、乙两个学校进行体育比赛，比赛共设三个项目，每个项目胜方得10分，负方得0分，没有平局．三个项目比赛结束后，总得分高的学校获得冠军．已知甲学校在三个项目中获胜的概率分别为0.5，0.4，0.8，各项目的比赛结果相互独立． (1)求甲学校获得冠军的概率；(2)用X 表示乙学校的总得分，求X 的分布列与期望．【答案】(1)0.6；(2)分布列见解析，E(X)=13.【解析】【分析】（1）设甲在三个项目中获胜的事件依次记为A,B,C，再根据甲获得冠军则至少获胜两个项目，利用互斥事件的概率加法公式以及相互独立事件的乘法公式即可求出；（2）依题可知，X的可能取值为0,10,20,30，再分别计算出对应的概率，列出分布列，即可求出期望．(1)设甲在三个项目中获胜的事件依次记为A,B,C，所以甲学校获得冠军的概率为P=P(ABC)+P(A BC)+P(AB̅C)+P(ABC)=0.5×0.4×0.8+0.5×0.4×0.8+0.5×0.6×0.8+0.5×0.4×0.2=0.16+0.16+0.24+0.04=0.6．(2)依题可知，X的可能取值为0,10,20,30，所以，P(X=0)=0.5×0.4×0.8=0.16,P(X=10)=0.5×0.4×0.8+0.5×0.6×0.8+0.5×0.4×0.2=0.44，P(X=20)=0.5×0.6×0.8+0.5×0.4×0.2+0.5×0.6×0.2=0.34，P(X=30)=0.5×0.6×0.2=0.06.即X的分布列为期望E(X)=0×0.16+10×0.44+20×0.34+30×0.06=13.12．【2022年全国乙卷】某地经过多年的环境治理，已将荒山改造成了绿水青山．为估计一林区某种树木的总材积量，随机选取了10棵这种树木，测量每棵树的根部横截面积（单位：2）和材积量（单位：3），得到如下数据：并计算得∑x i 210i=1=0.038,∑y i 210i=1=1.6158,∑x i y i10i=1=0.2474． (1)估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量； (2)求该林区这种树木的根部横截面积与材积量的样本相关系数（精确到0.01）；(3)现测量了该林区所有这种树木的根部横截面积，并得到所有这种树木的根部横截面积总和为186m 2．已知树木的材积量与其根部横截面积近似成正比．利用以上数据给出该林区这种树木的总材积量的估计值． 附：相关系数r =∑(x i−x̅)n i=1(y i −y̅)√∑(x i −x̅)2ni=1∑(y i−y ̅)2ni=1√1.896≈1.377．【答案】(1)0.06m 2；0.39m 3 (2)0.97 (3)1209m 3 【解析】 【分析】（1）计算出样本的一棵根部横截面积的平均值及一棵材积量平均值，即可估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量；（2）代入题给相关系数公式去计算即可求得样本的相关系数值；（3）依据树木的材积量与其根部横截面积近似成正比，列方程即可求得该林区这种树木的总材积量的估计值． (1)样本中10棵这种树木的根部横截面积的平均值x̅=0.610=0.06样本中10棵这种树木的材积量的平均值y̅=3.910=0.39据此可估计该林区这种树木平均一棵的根部横截面积为0.06m 2， 平均一棵的材积量为0.39m 3 (2)r =∑(x i −x)10i=1(y i −y)√∑10i=1(x i −x)2∑10i=1(y i −y)2=∑10i=1i i 10xy√(∑10i=1x i 2−10x2)(∑10i=1y i 2−10y 2)=0.2474−10×0.06×0.39√(0.038−10×0.062)(1.6158−10×0.392)=0.0134√0.0001896≈0.01340.01377≈0.97则r ≈0.97 (3)设该林区这种树木的总材积量的估计值为Y m 3， 又已知树木的材积量与其根部横截面积近似成正比， 可得0.060.39=186Y，解之得Y =1209m 3． 则该林区这种树木的总材积量估计为1209m 313．【2022年新高考1卷】一医疗团队为研究某地的一种地方性疾病与当地居民的卫生习惯（卫生习惯分为良好和不够良好两类）的关系，在已患该疾病的病例中随机调查了100例（称为病例组），同时在未患该疾病的人群中随机调查了100人（称为对照组），得到如下数据：(1)能否有99%的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异？(2)从该地的人群中任选一人，A 表示事件“选到的人卫生习惯不够良好”，B 表示事件“选到的人患有该疾病”．P(B|A)P(B ̅|A)与P(B|A )P(B ̅|A )的比值是卫生习惯不够良好对患该疾病风险程度的一项度量指标，记该指标为R ．（ⅰ）证明：R =P(A|B)P(A |B)⋅P(A |B ̅)P(A|B ̅)；（ⅱ）利用该调查数据，给出P(A|B),P(A|B ̅)的估计值，并利用（ⅰ）的结果给出R 的估计值．附K 2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)，【答案】(1)答案见解析 (2)（i ）证明见解析；(ii)R =6； 【解析】【分析】(1)由所给数据结合公式求出K2的值，将其与临界值比较大小，由此确定是否有99%的把握认为患该疾病群体与未黄该疾病群体的卫生习惯有差异；(2)(i) 根据定义结合条件概率公式即可完成证明；(ii)根据（i）结合已知数据求R.(1)由已知K2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)=200(40×90−60×10)250×150×100×100=24，又P(K2≥6.635)=0.01，24>6.635，所以有99%的把握认为患该疾病群体与未患该疾病群体的卫生习惯有差异.(2)(i)因为R=P(B|A)P(B̅|A)⋅P(B̅|A)P(B|A)=P(AB)P(A)⋅P(A)P(AB̅)⋅P(A B̅)P(A)⋅P(A)P(A B)，所以R=P(AB)P(B)⋅P(B)P(A B)⋅P(A B̅)P(B̅)⋅P(B̅)P(AB̅)所以R=P(A|B)P(A|B)⋅P(A|B̅) P(A|B̅)，(ii)由已知P(A|B)=40100，P(A|B̅)=10100，又P(A|B)=60100，P(A|B̅)=90100，所以R=P(A|B)P(A|B)⋅P(A|B̅)P(A|B̅)=614．【2022年新高考2卷】在某地区进行流行病学调查，随机调查了100位某种疾病患者的年龄，得到如下的样本数据的频率分布直方图：(1)估计该地区这种疾病患者的平均年龄（同一组中的数据用该组区间的中点值为代表）；(2)估计该地区一位这种疾病患者的年龄位于区间[20,70)的概率；(3)已知该地区这种疾病的患病率为0.1%，该地区年龄位于区间[40,50)的人口占该地区总人口的16%.从该地区中任选一人，若此人的年龄位于区间[40,50)，求此人患这种疾病的概率．（以样本数据中患者的年龄位于各区间的频率作为患者的年龄位于该区间的概率，精确到0.0001）.【答案】(1)44.65岁；(2)0.89；(3)0.0014．【解析】【分析】（1）根据平均值等于各矩形的面积乘以对应区间的中点值的和即可求出；（2）设A={一人患这种疾病的年龄在区间[20,70)}，根据对立事件的概率公式P(A)=1−P (A)即可解出；（3）根据条件概率公式即可求出．(1)平均年龄x̅=(5×0.001+15×0.002+25×0.012+35×0.017+45×0.023 +55×0.020+65×0.012+75×0.006+85×0.002)×10=44.65（岁）．(2)设A={一人患这种疾病的年龄在区间[20,70)}，所以P(A)=1−P(A)=1−(0.001+0.002+0.006+0.002)×10=1−0.11=0.89．(3)设B={任选一人年龄位于区间[40,50)}，C={任选一人患这种疾病}，则由条件概率公式可得P(C|B)=P(BC)P(B)=0.1%×0.023×1016%=0.001×0.230.16=0.0014375≈0.0014．15．【2022年北京】在校运动会上，只有甲、乙、丙三名同学参加铅球比赛，比赛成绩达到9．50m以上（含9．50m）的同学将获得优秀奖．为预测获得优秀奖的人数及冠军得主，收集了甲、乙、丙以往的比赛成绩，并整理得到如下数据（单位：m）：甲：9.80，9.70，9.55，9.54，9.48，9.42，9.40，935，9.30，9.25；乙：9.78，9.56，9.51，9.36，9.32，9.23；丙：9.85，9.65，9.20，9.16．假设用频率估计概率，且甲、乙、丙的比赛成绩相互独立．(1)估计甲在校运动会铅球比赛中获得优秀奖的概率；(2)设X是甲、乙、丙在校运动会铅球比赛中获得优秀奖的总人数，估计X的数学期望E（X）；(3)在校运动会铅球比赛中，甲、乙、丙谁获得冠军的概率估计值最大？（结论不要求证明）【答案】(1)0.4(2)75(3)丙【解析】【分析】(1)由频率估计概率即可(2)求解得X的分布列，即可计算出X的数学期望.(3)计算出各自获得最高成绩的概率，再根据其各自的最高成绩可判断丙夺冠的概率估计值最大.(1)由频率估计概率可得甲获得优秀的概率为0.4，乙获得优秀的概率为0.5，丙获得优秀的概率为0.5，故答案为0.4(2)设甲获得优秀为事件A1,乙获得优秀为事件A2，丙获得优秀为事件A3P(X=0)=P(A1̅̅̅A2̅̅̅A3̅̅̅)=0.6×0.5×0.5=3，20P(X=1)=P(A1A2̅̅̅A3̅̅̅)+P(A1̅̅̅A2A3̅̅̅)+P(A1̅̅̅A2̅̅̅A3)=0.4×0.5×0.5+0.6×0.5×0.5+0.6×0.5×0.5=8，20P(X=2)=P(A1A2A3̅̅̅)+P(A1A2̅̅̅A3)+P(A1̅̅̅A2A3)=0.4×0.5×0.5+0.4×0.5×0.5+0.6×0.5×0.5=7，20P(X=3)=P(A1A2A3)=0.4×0.5×0.5=2.20∴X的分布列为∴E(X)=0×320+1×820+2×720+3×220=75 (3)丙夺冠概率估计值最大.因为铅球比赛无论比赛几次就取最高成绩.比赛一次，丙获得9.85的概率为14，甲获得9.80的概率为110，乙获得9.78的概率为16.并且丙的最高成绩是所有成绩中最高的，比赛次数越多，对丙越有利.1．（2022·河南省杞县高中模拟预测（理））某市有11名选手参加了田径男子100米赛的选拔比赛，前5名可以参加省举办的田径赛，如果各个选手的选拔赛成绩均不相同，选手小强已经知道了自己的成绩，为了判断自己能否参加省举办的田径赛，他还需要知道这11名选手成绩的（ ） A ．平均数 B ．中位数 C ．众数 D ．方差【答案】B 【解析】 【分析】中位数恰好是第6名，比中位数成绩高即可确认自己能否进入省田径赛． 【详解】因为11名选手成绩的中位数恰好是第6名，知道了第6名的成绩，小强就可以判断自己是否能参加省举办的田径赛了，其余数字特征不能反映名次． 故选：B ．2．（2022·黑龙江·大庆实验中学模拟预测（理））2021年5月30日清晨5时01分，天舟二号货运飞船在成功发射约8小时后，与中国空间站天和核心舱完成自主快速交接．如果下次执行空间站的任务由3名航天员承担，需要在3名女性航天员和3名男性航天员中选择，则选出的3名航天员中既有男性航天员又有女性航天员的概率为（ ） A ．67B ．910 C ．25D ．415【答案】B 【解析】 【分析】利用对立事件和古典概型的概率公式求解即可. 【详解】设“选出的3名航天员中既有男性航天员又有女性航天员”为事件M ，则()333336C C 91C 10P M ==+-.故选：B.3．（2022·全国·模拟预测（文））如图是一组实验数据的散点图，拟合方程()0by c x x=+>，令1t x=，则y 关于t 的回归直线过点()2,5，()12,25，则当()1.01,1.02y ∈时，x 的取值范围是（ ）A ．()0.01,0.02B ．()50,100C ．()0.02,0.04D ．()100,200【答案】D 【解析】 【分析】 先令1t x =可得()0y bt c t =+>，由y 关于t 的回归直线过点()2,5，()12,25可得522512b c b c=+⎧⎨=+⎩从而求得21y t =+，再由y 的范围求得t 的范围，进而求得x 的范围. 【详解】根据题意可得()0y bt c t =+>，由y 关于t 的回归直线过点()2,5，()12,25可得：522512b cb c =+⎧⎨=+⎩，所以2,1b c ==， 所以21y t =+，由()1.01,1.02y ∈可得1.0121 1.02t <+<， 所以0.0050.01t <<， 所以10.0050.01x<<，所以100200x <<， 故选：D4．（2022·辽宁实验中学模拟预测）某国计划采购疫苗，现在成熟的疫苗中，三种来自中国，一种来自美国，一种来自英国，一种由美国和德国共同研发，从这6种疫苗中随机采购三种，若采购每种疫苗都是等可能的，则买到中国疫苗的概率为（ ） A ．16B ．12C ．910D ．1920【答案】D 【解析】 【分析】由对立事件的概率公式计算． 【详解】没有买到中国疫苗的概率为13611C 20P ==， 所以买到中国疫苗的概率为119120P P =-=． 故选：D ．5．（2022·四川省泸县第二中学模拟预测（理））食物链亦称“营养链”，是指生态系统中各种生物为维持其本身的生命活动，必须以其他生物为食物的这种由食物联结起来的链锁关系．如图为某个生态环境中的食物链，若从鹰、麻雀、兔、田鼠以及蝗虫中任意选取两种，则这两种生物不能构成摄食关系的概率（ ）A ．35B ．25C ．23D ．13【解析】 【分析】用列举法写出构成的摄食关系，计数后可求得概率． 【详解】从鹰、麻雀、兔、田鼠以及蝗虫中任意选取两种，共有10种选法：鹰麻雀，鹰兔，鹰田鼠，鹰蝗虫，麻雀兔，麻雀田鼠，麻雀蝗虫，兔田鼠，兔蝗虫，田鼠蝗虫．其中田鼠鹰，兔鹰，麻雀鹰，蝗虫麻雀共四种可构成摄食关系，不能构成摄食关系的有6种，所以概率为63105P ==． 故选：A ．6．（2022·山东潍坊·模拟预测）Poisson 分布是统计学里常见的离散型概率分布，由法国数学家西莫恩·德尼·泊松首次提出，Poisson 分布的概率分布列为()()e 0,1,2,!kP X K k k λλ-===⋅⋅⋅，其中e 为自然对数的底数，λ是Poisson 分布的均值．当二项分布的n 很大()20n ≥而p 很小()0.05p ≤时，Poisson 分布可作为二项分布的近似．假设每个大肠杆菌基因组含有10000个核苷酸对，采用20.05/J m 紫外线照射大肠杆菌时，每个核苷酸对产生嘧啶二体的概率均为0.0003，已知该菌株基因组有一个嘧啶二体就致死，则致死率是（ ） A ．31e -- B ．3e - C ．313e -- D ．314e --【答案】A 【解析】 【分析】结合题意1000020n =≥，0.00030.05p =≤，此时Poisson 分布满足二项分布的近似条件，再计算二项分布的均值为Poisson 分布的均值λ，再代入公式先求不致死的概率，再用对立事件的概率和为1计算即可 【详解】由题， 1000020n =≥，0.00030.05p =≤，此时Poisson 分布满足二项分布的近似的条件，此时100000.00033λ=⨯=，故不致死的概率为()03330e e 0!P X --===，故致死的概率为()3101e P X --==-7．（2022·河南安阳·模拟预测（理））某房产销售公司有800名销售人员，为了了解销售人员上一个季度的房屋销量，公司随机选取了部分销售人员对其房屋销量进行了统计，得到上一季度销售人员的房屋销量(20,4)X N ，则全公司上一季度至少完成22套房屋销售的人员大概有（ ）附：若随机变量X 服从正态分布()2,N μσ，则()0.6827P X μσμσ-<≤+≈，(22)0.9545P X μσμσ-<≤+≈，(33)0.9973P X μσμσ-<≤+≈．A ．254人B ．127人C ．18人D ．36人【答案】B 【解析】 【分析】根据正态分布的性质求出()22P X ≥，从而估计出人数； 【详解】 解：因为(20,4)X N ，所以20μ=，2σ=，所以()1()10.6827220.1586522P X P X μσμσ--<≤+-≥===所以全公司上一季度至少完成22套房屋销售的人员大概有8000.15865127⨯≈（人）； 故选：B8．（2022·河南·模拟预测）某公司生产的一种产品按照质量由高到低分为A ，B ，C ，D 四级，为了增加产量、提高质量，该公司改进了一次生产工艺，使得生产总量增加了一倍．为了解新生产工艺的效果，对改进生产工艺前、后的四级产品的占比情况进行了统计，绘制了如下扇形图：根据以上信息：下列推断合理的是（ ） A ．改进生产工艺后，A 级产品的数量没有变化B．改进生产工艺后，D级产品的数量减少C．改进生产工艺后，C级产品的数量减少D．改进生产工艺后，B级产品的数量增加了不到一倍【答案】C【解析】【分析】由题可得改进生产工艺前后四个等级的生产量，逐项分析即得.【详解】设原生产总量为1，则改进生产工艺后生产总量为2，所以原A，B，C，D等级的生产量为0.3，0.37，0.28，0.05，改进生产工艺后四个等级的生产量为0.6，1.2，0.12，0.08，故改进生产工艺后，A级产品的数量增加，故A错误；改进生产工艺后，D级产品的数量增加，故B错误；改进生产工艺后，C级产品的数量减少，故C正确；改进生产工艺后，B级产品的数量增加超过2倍，故D错误.故选：C.9．（2022·河南安阳·模拟预测（文））为推动就业与培养有机联动、人才供需有效对接，促进高校毕业生更加充分更高质量就业，教育部今年首次实施供需对接就业育人项目．现安排甲、乙两所高校与3家用人单位开展项目对接，若每所高校至少对接两家用人单位，则两所高校的选择涉及到全部3家用人单位的概率为（）A．12B．23C．34D．1316【答案】D【解析】【分析】由古典概型与对立事件的概率公式求解即可【详解】因为每所高校至少对接两家用人单位，所以每所高校共有2333314C C+=+=种选择，所以甲、乙两所高校共有4416⨯=种选择，其中甲、乙两所高校的选择涉及两家用人单位的情况有233C =种，所以甲、乙两所高校的选择涉及到全部3家用人单位的概率为31311616P =-=， 故选：D10．（2022·江苏·南京师大附中模拟预测）某同学在课外阅读时了解到概率统计中的马尔可夫不等式，该不等式描述的是对非负的随机变量X 和任意的正数a ，都有()()(),P X a f E X a ≥≤，其中()(),f E X a 是关于数学期望()E X 和a 的表达式.由于记忆模糊，该同学只能确定()(),f E X a 的具体形式是下列四个选项中的某一种.请你根据自己的理解，确定该形式为（ ） A ．()aE X B ．()1aE XC ．()a E XD ．()E X a【答案】D 【解析】 【分析】根据期望的计算公式,以及m x a ≥即可求解. 【详解】设非负随机变量X 的所有可能取值按从小到大依次为0,i x i N *>∈,对应的概率分别为,0i i p p >设满足i x a ≥的有,,,m a a x k m n m N k N **≤≤∈∈,()ani i k P X a p =≥=∑,()111a ai nk i iii n i ii k i ax pE ax p x pX a -===+==∑∑∑,因为m x a ≥,所以1mx a≥()()()1111a a aaannniiiiiik k i k i k i k ii i i i x px px px p p P X a P X a E aa aaaX --=====⎛⎫+≥+=+≥≥≥ ⎪⎝⎭=∑∑∑∑∑故选：D11．（2022·吉林·三模（理））为了切实维护居民合法权益，提高居民识骗防骗能力，守好居民的“钱袋子”，某社区开展“全民反诈在行动——反诈骗知识竞赛”活动，现从参加该活动的居民中随机抽取了100名，统计出他们竞赛成绩分布如下：(1)求抽取的100名居民竞赛成绩的平均分x 和方差2s （同一组中数据用该组区间的中点值为代表）；(2)以频率估计概率，发现该社区参赛居民竞赛成绩X 近似地服从正态分布()2,N μσ，其中μ近似为样本成绩平均分x ，2σ近似为样本成缋方差2s ，若2μσμσ-<≤+X ，参赛居民可获得“参赛纪念证书”；若2μσ>+X ，参赛居民可获得“反诈先锋证书”，①若该社区有3000名居民参加本次竞赛活动，试估计获得“参赛纪念证书”的居民人数（结果保留整数）；②试判断竞赛成绩为96分的居民能否获得“反诈先锋证书”． 附：若()2,XN μσ，则()0.6827P X μσμσ-<≤+≈，(22)0.9545P X μσμσ-<≤+≈，(33)0.9973P X μσμσ-<≤+≈．【答案】(1)75x =，2100s = (2)①2456 ；②能 【解析】 【分析】（1）利用公式直接求出均值、方差即可；（2）①结合给的概率和正态分布的性质，确定获得“参赛纪念证书”，进而计算可得人数； ②利用正态分布的知识求出2μσ>+X ，即95>X ，进而可得结果. (1)100名居民本次竞赛成绩平均分24224028445556575859575100100100100100100=⨯+⨯+⨯+⨯+⨯+⨯=x ， 100名居民本次竞赛成绩方差22222422(4575)(5575)(6575)100100100=-⨯+-⨯+-⨯s 22240284(7575)(8575)(9575)100100100100+-⨯+-⨯+-⨯=， (2)①由于μ近似为样本成绩平均分x ，2σ近似为样本成绩方差2s ， 所以，275,100μσ==，可知，10σ=，由于竞赛成绩X 近似地服从正态分布()2,N μσ，因此竞赛居民可获得“参赛纪念证书”的概率 (2)P X μσμσ-<≤+11()(22)22μσμσμσμσ=-<≤++-<≤+P X P X 110.68270.95450.818622≈⨯+⨯= 30000.81862455.82456⨯=≈估计获得“参赛纪念证书”的居民人数为2456；②当2μσ>+X 时，即95>X 时，参赛居民可获得“反诈先锋证书”， 所以竞赛成绩为96分的居民能获得“反诈先峰证书”．12．（2022·贵州·贵阳一中模拟预测（文））“十四五”规划纲要提出，全面推动长江经济带发展，协同推动生态环境保护和经济发展长江水资源约占全国总量的36%，长江流域河湖､水库､湿地面积约占全国的20%，珍稀濒危植物占全国的39.7%，淡水鱼类占全国的33%.长江经济带在我国生态文明建设中占据重要位置.长江流域某地区经过治理，生态系统得到很大改善，水生动物数量有所增加.为调查该地区某种水生动物的数量，将其分成面积相近的100个水域，从这些水域中用简单随机抽样的方法抽取20个作为样区，调查得到样本数据()(),1,2,,20,i i x y i =其中i x 和i y 分别表示第i 个样区的水草覆盖面积（单位：公顷）和这种水生动物的数量，并计算得20160i i x ==∑，2011200i i y ==∑，2021-)120,i i x x ==∑（2021-)9000,i i y ==∑（y 201-)-)1000.i iix x y ==∑（（y (1)求该地区这种水生动物数量的估计值（这种水生动物数量的估计值等于样区这种水生动物数量的平均数乘以地块数）； (2)求样本()(),1,2,,20i i x y i =的相关系数（精确到0.01）；(3)根据现有统计资料，各地块间水草覆盖面积差异很大.为提高样本的代表性以获得该地区这种水生动物数量更准确的估计，请给出一种你认为更合理的抽样方法，并说明理由.附：相关系数-)-) 1.732.niix y x r =≈∑（（y【答案】(1)6000 (2)0.96(3)采用分层抽样的方法，理由见解析 【解析】 【分析】（1）根据该地区这种水生动物数量的估计值的计算方法求解即可； （2）根据相关系数的公式求解即可；（3）根据（2）中的结论各样区的这种水生动物的数量与水草覆盖面积有很强的正相关性考虑即可 (1)样区水生动物平均数为201111200602020i i y ==⨯=∑， 地块数为100，该地区这种水生动物的估计值为100606000⨯=. (2)样本()(),1,2,,20i i x y i =⋯的相关系数为()()20,0.96.iix x y y r -===≈∑ (3)由（2）知各样区的这种水生动物的数量与水草覆盖面积有很强的正相关性，由于各地块间水草覆盖面积差异很大，从而各地块间这种野生动物的数量差异很大，所以采用分层抽样的方法较好地保持了样本结构与总体结构得以执行，提高了样本的代表性，从而可以获得该地区这种水生动物数量更准确的估计.13．（2022·河南开封·模拟预测（理））大豆是我国重要的农作物，种植历史悠久．某种子实验基地培育出某大豆新品种，为检验其最佳播种日期，在A ，B 两块试验田上进行实验（两地块的土质等情况一致）.6月25日在A 试验田播种该品种大豆，7月10日在B 试验田播种该品种大豆．收获大豆时，从中各随机抽取20份（每份1千粒），并测量出每份的质量（单位：克），按照[)100,150，[)150,200，[]200,250进行分组，得到如下表格：。

专题05工业文明冲击下中国的转型（1840-1894）1．（2024·山东·高考真题）下表为1846—1905年英国建筑师在上海、汉口、天津、北京等四地的分布情况统计。

这体现了（）城市上海汉口天津北京人次年份1846—1860143001861—187********1876—189********1891—1905353206714A．晚清外交的不断退让B．英国势力范围的扩展C．列强侵略方式的转变D．中西文化交流的深入2．（2024·浙江1月卷·高考真题）有学者认为：“道光（皇帝）算是个幸运者，白莲教的事是他父亲嘉庆皇帝了结的；洪秀全的大动干戈则留给了他的儿子咸丰皇帝去担当。

但是，他躲开了这些，却躲不开另一种灾难，那就是相继困扰的边衅与外患。

”下列“边衅与外患”中，发生于道光时期的是（）A．噶尔丹叛乱B．鸦片战争C．大、小和卓叛乱D．中法战争3．（2024·江苏·高考真题）1850年，上海出现第一家专营进口棉布的商店，到1858年这类洋布店已有十五六家，以门市零售为主。

1860年以后，内地商人纷纷到上海采购，上海洋布店转向以批发为主，实力大增。

上海洋布店的发展反映出（）A．政府鼓励兴办实业B．外来经济因素逐渐渗入C．内地棉纺织业发达D．民族资本主义快速发展4．（2024·北京·高考真题）《万国公法》译成中文时，某法国外交官说：“那个打算让中国人领悟我们欧洲国际法的人是谁？……他会让我们陷于无尽的麻烦之中。

”另有英文报纸评论道：“我们为中国提供的武器在日后到底是会瞄准我们，还是只会转向新的征服者，现在还不好说。

”这说明（）A．引入《万国公法》破坏了中国司法主权B．中国社会对当时世界形势变化浑然不觉C．中国了解国际法将不利于列强对华侵略D．此时国际法的应用范围只限于欧洲国家5．（2024·甘肃·高考真题）19世纪70年代，英、日等国一方面以廉价棉纱倾销中国，另一方面从中国大量进口棉花，致使中国市场棉贵纱贱。