实验六因子分析分析解析

贡献率 特征值 a112+a212+a312
X3
a31
a32
ቤተ መጻሕፍቲ ባይዱa122+a222+a322
a312+a322
贡献率 (a112+a212+a312)/3 (a122+a222+a322)/3
数据要求
等比或等距数据，名义数据不能用于因子分 析，两点量表不能用于因素分析， 数据分布应近于正态分布， 相关应是线性的， 样本容量也有一定的要求，样本数应大小变 量数，变量与被试的比例最小为1：5，被试 样本总数不得小于100人。
因子分析
因子分析的概念
意义
因子分析是将多个实测变量转换为少数几个不相关 的综合指标的多元统计分析方法。即把多条信息浓缩为 较少的变量，归纳出来的变量之间是相对独立的，并且 应包含原有的大部分信息，只丢失较少的信息，因此也 是数据的压缩和概括。
(1)寻求基本结构。
(2)数据简化。
因子分析的概念

因子分析的主要步骤
确定数据结构是否适合做因子分析 提取因子
解释因子
计算因子值
确定数据结构是否适合做因子分析
(1) 所有变量的相关矩阵 (2) Bartlett test of sphereicity (3) KMO
a Corr elation Matr ix
Co rrelatio n
提取因子 (1) 主成分分析法 (2) 确定因子数目 ①因子特征值>1，即认为每个保留下来的因子至少 应该能解释一个变量的方差，否则达不到精简的目 的；②因子符合陡阶检验(碎石图)，即将每一因子 所能解释的变异量作成图，并连接成曲线，以曲线 呈台阶以后的那个因子为基准，决定抽取的因子数 目。③提取出的因子在旋转之前至少要求解释变异 的3%。④每个因素至少要包括3道题目。⑤考虑因 素的可解释性。

5色5变量
5色5主成分
一、案例引读
二、基本原理
三、历史渊源 四、分析步骤
五、案例详解
因素分析（Factor Analysis)就是将错综复杂的实测变量归结为 少数几个因子的多元统计分析方法。其目的是揭示变量之间的内在 关联性，简化数据维数，便于发现规律或本质。
因素分析的基本原理是根据相关性大小把变量分组，使得同组变 量之间的相关性较高，不同组变量之间相关性较低。每组变量代表 一个基本结构，这个结构用公共因子来进行解释。
一、案例引读
二、基本原理 三、历史渊源
四、分析步骤
五、案例详解
xi=aiF+ei
因子旋转
因子得分
因子负荷
F→F’ 主成分法 便于解释 样本的优劣
一、案例引读
二、基本原理 三、历史渊源
四、分析步骤
五、案例详解
因子负荷 主成分法
因子旋转
F→F’
利用主成分分 析把前几个主成分 作为未旋转的公共 因子。
案例 1
（3）设置对因素的抽取选项：单击图1-1对话框中的“Extraction…”按钮，弹出 “Factor Analyze:Extraction”（因素分析：萃取）对话框。 ① “Method”（方法）选项框：下拉式选项内 有其中抽取因素的方法： A “Principal components”法：主成份分析 未旋转因子解 共变异数矩阵 法抽取因素，此为SPSS默认方法。 陡坡图 相关矩阵 B “Unweighted least squares”法：未加权 特征值 最小平方法。 因子个数 C “Generalized least square”法：一般化最 小平方法。 图1-3 Factor Analyze：Extraction对话框 D “Maximum likelihood”法：最大概似法。 ② “Analyze”（分析）选项框 E “Principal-axis factoring”法：主轴法。 A “Correlation matrix”（相关矩阵） F “Alpha factoring”法：α因素抽取法。 ：以相关矩阵来抽取因素。 G “Image factoring”法：映像因素抽取法。 B “Covariance matrix”（共变异数矩 ④ “Extract”（抽取）选项框 阵）：以共变量矩阵来抽取因素。 A “Eigenvalues over”（特征值）：后面的空 ③ “Display”（显示）选项框 格默认为1，表示因素抽取时，只抽取特征值 大于1者，使用者可随意输入0至变量总数之间 A “Unrotated factor solution”（未 旋转因子解）：显示未转轴时因素负 的值。 荷量、特征值及共同性。 B “Number of factors”（因子个数）：选取 此项时，后面的空格内输入限定的因素个数。 B “Scree plot”（陡坡图）：陡坡图。

城管大气污染六项因子分析空气污染的六项指标为：二氧化氮、二氧化硫、一氧化碳、臭氧8小时浓度、可吸入颗粒物(PM10)、细颗粒物(PM2.5)。

1、细颗粒物细颗粒物（PM2.5）指环境空气中空气动力学当量直径小于等于2.5微米的颗粒物。

它能较长时间悬浮于空气中，其在空气中含量浓度越高，就代表空气污染越严重。

细颗粒物主要来源于扬尘、火山灰、花粉、真菌孢子，包括室内的二手烟、油烟等等。

细颗粒物粒径小，在大气中的停留时间更长、输送距离更远，因而对人体健康和大气环境质量的影响更大。

2、可吸入颗粒物可吸入颗粒物（PM10），通常是指粒径在10微米以下的颗粒物。

通常来自在未铺沥青、水泥的路面上行驶的机动车、材料破碎碾磨处理过程以及被风扬起的尘土。

可吸入颗粒物在环境空气中持续的时间很长，对人体健康和大气能见度的影响都很大。

3、二氧化硫二氧化硫（SO2）是最常见、最简单的硫氧化物。

火山爆发时会喷出该气体，在许多工业过程中也会产生二氧化硫。

由于煤和石油通常都含有硫元素，因此燃烧时会生成二氧化硫，也是二氧化硫的主要污染来源。

二氧化硫是大气中主要一次污染物，是衡量大气是否遭到污染的重要标志。

参与光化学反应过程的一次污染物和二次污染物的混合物所形成的烟雾污染现象称作光化学烟雾。

SO2、CO等一次污染物经过反应成为臭氧等二次污染物4、二氧化氮二氧化氮（化学式NO2)，高温下棕红色有毒气体。

在常温下(0～21.5℃)二氧化氮与四氧化二氮混合而共存。

二氧化氮的自然源主要是闪电和微生物生命活动，人为产生的二氧化氮主要来自高温燃烧过程的释放，工业生产和汽车尾气也会产生较多二氧化氮。

二氧化氮可以在大范围内引起多种环境问题，比如它是形成光化学烟雾的主要因素之一，也是酸雨的来源之一。

二氧化氮被人体吸入后，能够对肺组织产生强烈的刺激作用和腐蚀作用，从而引起肺水肿。

呼吸系统有疾患的人如哮喘病患者，较易受二氧化氮的影响。

对于儿童来说，二氧化氮可能会造成肺部发育障碍。

上式是假定了因子模型中特殊因子是不重要的，因而 从∑的分解中忽略掉特殊因子的方差 如果考虑了特殊因子以后，协差阵为：
当∑未知，可用样本协差阵S去代替，要经过标准化 处理，则S与相关阵R相同，仍然可作上面类似的表示。 一般设 则因子载荷阵的估计 即 为样本相关阵尺的特征根， 设 m < p， 相应的标准正交化特征向量为；
所以
也是公共因子，
ቤተ መጻሕፍቲ ባይዱ
也是因子载荷阵。
因子载荷这个不唯一性，从表面上看是不利的，但后面将 会看到当因子载荷阵A的结构不够简化时，可对A实行变 换以达到简化目的，使新的因子更具有鲜明的实际意义。 从因子分析的数学模型上看，它与多变量回归分析也有类 似之处，但本质的区别是因子分析模型作为“自变量”的 F是不可观测的。 2 因子模型中公共因子、因子载荷和变量共同度的 统计意义 为了便于对因子分析计算结果做解释，将因子分析数 学模型中各个量的统计意义加以说明是十分必要的， 假定因子模型中，各个变量以及公共因子、特殊因子 都已经是标准化(均值为0，方差为1)的变量。 (1)因子载荷的统计意义 已知模型：
为了说明它的统计意义，将下式两边求方差，即
由于
已标准化了，所以有
此式说明变量 的方差由两部分组成：第一部分为共 度 它刻划全部公共因子对变量 的总方差所作的贡 献， 越接近1，说明该变量的几乎全部原始信息都被 所选取的公共因子说明了，如 则说明 的 97%的信息被m个公共因子说明了，也就是说由原始变量 空间转为因子空间转化的性质越好， 保留原来信息量
A经过Tk j ，旋转(变换)后，矩阵A＝A T k j ，其元素为
其中旋转角度
仍按下面公式求得：
m个因子，每次取两个全部配对进行旋转，共需旋转

因子分析实验报告一、实验目的因子分析是一种多元统计分析方法，旨在将多个相关变量归结为少数几个综合因子，以简化数据结构和揭示潜在的变量关系。

本次实验的主要目的是通过因子分析方法，对给定的数据集进行分析，提取主要因子，并解释其含义和实际应用价值。

二、实验数据来源及描述本次实验所使用的数据来源于一项关于消费者购买行为的调查。

该数据集包含了 500 个样本，每个样本包含了 10 个变量，分别是：价格敏感度、品牌忠诚度、产品质量感知、售后服务满意度、促销活动参与度、购买频率、购买金额、购买渠道偏好、口碑传播意愿和推荐他人购买意愿。

这些变量反映了消费者在购买过程中的不同方面的态度和行为，通过对这些变量的分析，可以更好地了解消费者的购买模式和偏好，为企业的市场营销策略提供决策依据。

三、实验方法及步骤1、数据预处理首先，对数据进行了缺失值处理。

对于存在少量缺失值的变量，采用了均值插补的方法进行填充。

然后，对数据进行了标准化处理，以消除量纲的影响，使得不同变量之间具有可比性。

2、因子提取运用主成分分析法（PCA）进行因子提取。

通过计算相关矩阵的特征值和特征向量，确定因子的个数。

根据特征值大于 1 的原则，初步确定提取 3 个因子。

3、因子旋转为了使因子更具有可解释性，采用了方差最大正交旋转（Varimax rotation）方法对因子进行旋转。

4、因子解释对旋转后的因子载荷矩阵进行分析，解释每个因子所代表的含义。

四、实验结果及分析1、因子载荷矩阵经过旋转后的因子载荷矩阵如下：｜变量|因子 1|因子 2|因子 3|｜｜｜｜｜｜价格敏感度|075|－012|021|｜品牌忠诚度|018|072|－015|｜产品质量感知|025|068|028|｜售后服务满意度|022|065|031|｜促销活动参与度|032|－025|078|｜购买频率|015|028|072|｜购买金额|012|025|068|｜购买渠道偏好|028|－035|052|｜口碑传播意愿|018|032|058|｜推荐他人购买意愿|021|035|055|2、因子解释因子 1 主要反映了消费者对产品本身相关因素的关注，包括价格敏感度、产品质量感知、售后服务满意度等，可命名为“产品相关因子”。

因子分析实验报告因子分析实验报告引言：因子分析是一种常用的统计分析方法，用于探索变量之间的内在关系。

通过因子分析，我们可以找到隐藏在观测变量背后的潜在因素，从而更好地理解数据的结构和解释变量之间的关系。

本实验旨在通过因子分析方法，对某一特定数据集进行分析，以探索其内在因素和变量之间的关系。

实验设计：本实验选取了一个涉及消费者购买行为的数据集，包含了多个观测变量，如消费金额、购买频率、品牌忠诚度等。

我们希望通过因子分析，找出这些变量背后的潜在因素，以便更好地理解消费者购买行为的本质。

实验步骤：1. 数据准备：首先，我们收集了一份关于消费者购买行为的数据集，包含了1000个样本和10个观测变量。

这些变量包括消费金额、购买频率、品牌忠诚度等。

我们将这些变量进行了标准化处理，以消除量纲差异。

2. 因子提取：接下来，我们使用主成分分析方法进行因子提取。

主成分分析是一种常用的因子提取方法，通过线性变换将原始变量转化为一组互相无关的主成分。

我们计算了每个主成分的特征值和特征向量，并选取了特征值大于1的主成分作为因子。

3. 因子旋转：在因子提取后，我们进行了因子旋转，以使得因子更易于解释。

常用的因子旋转方法有方差最大旋转和极大似然旋转等。

在本实验中，我们选择了方差最大旋转方法，以最大化因子的方差。

4. 因子解释：最后，我们对提取出的因子进行解释。

通过观察每个因子所对应的变量载荷，我们可以确定每个因子的含义和影响因素。

同时，我们还计算了每个因子的方差贡献率，以评估其在解释总体方差中的贡献程度。

实验结果：经过因子分析，我们成功地提取出了3个主要因子，并对其进行了旋转和解释。

这些因子分别代表了消费者的购买能力、购买偏好和品牌忠诚度。

具体而言，第一个因子与消费金额和购买频率相关，代表了消费者的购买能力；第二个因子与购买偏好和购买意愿相关，代表了消费者的购买偏好；第三个因子与品牌忠诚度相关，代表了消费者对品牌的忠诚程度。

因子分析实验报告1. 引言因子分析是一种常用的数据分析方法，用于探索和解释观测变量背后的潜在因子结构。

它可以帮助我们发现变量之间的关联性，进而理解数据的本质和结构。

本实验报告旨在通过一个因子分析的具体案例，介绍因子分析的步骤和相关概念。

2. 实验设计2.1 数据收集首先，我们需要收集一组观测变量的数据。

在本实验中，我们选择了一个市场调查问卷作为数据源。

该问卷包含了多个问题，涉及不同的主题，如消费习惯、生活方式等。

我们将这些问题作为观测变量，以便进行因子分析。

2.2 变量选择在进行因子分析之前，我们需要对观测变量进行筛选和选择。

一般来说，我们会选择那些具有较高相关性的变量用于因子分析。

在本实验中，我们将根据变量之间的相关系数矩阵进行选择。

2.3 数据预处理在进行因子分析之前，我们还需要对数据进行一些预处理操作。

这可能包括缺失值处理、异常值处理、数据标准化等。

我们需要确保数据的可靠性和一致性，以获得准确的因子分析结果。

3. 因子分析步骤3.1 因子提取因子提取是因子分析的关键步骤。

它用于从观测变量中提取潜在因子。

常用的因子提取方法包括主成分分析法、最大方差法等。

在本实验中，我们将采用主成分分析法进行因子提取。

3.2 因子旋转因子旋转是为了使提取的因子更易解释和解读。

它通过改变因子载荷矩阵的结构，使得每个因子只与少数几个观测变量相关联。

常用的因子旋转方法包括方差最大旋转法、正交旋转法等。

在本实验中，我们将采用方差最大旋转法进行因子旋转。

3.3 因子解释因子解释是根据旋转后的因子载荷矩阵，对提取的因子进行解释和命名的过程。

我们需要分析每个因子与观测变量之间的关系，以确定每个因子所代表的概念或主题。

在本实验中，我们将尝试解释每个因子，并为其命名。

4. 实验结果经过因子分析的步骤，我们得到了旋转后的因子载荷矩阵。

根据这个矩阵，我们可以解释每个因子所代表的概念，并为其命名。

以下是我们得到的部分结果：•因子1：消费习惯因子，包括购买力、消费水平等变量。

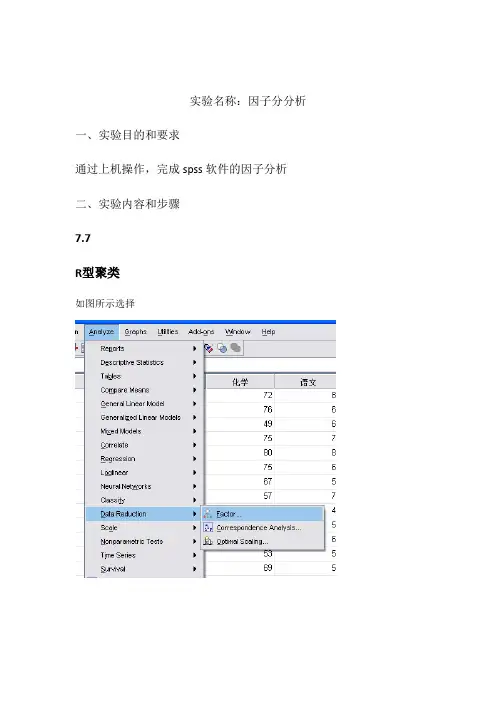
实验名称：因子分分析一、实验目的和要求通过上机操作，完成spss软件的因子分析二、实验内容和步骤7.7R型聚类如图所示选择将6个变量选入变量框中分别点击descriptive rotation选项，进行以下操作点击extraction点击options结果如下所示上表为相关矩阵，给出了6个变量之间的相关系数。

主对角线系数都为1，从表中我们可知，变量与变量之间有的会高度相关，有的相关性比较低，语文与历史，语文与英语，英语与历史都是高度相关的，其他的相关度较低。

KMO and Bartlett's TestKaiser-Meyer-Olkin Measure of Sampling Adequacy. .755Bartlett's Test of Sphericity Approx. Chi-Square 86.576df 15Sig. .000上表为KMO和Bartlett检验表，KMO检验是对变量是否适合做因子分析的检验，根据Kaiser常用度量标准，由于KMO=0.755，表明此时一般适合做因子分析。

CommunalitiesInitial Extraction数学 1.000 .812物理 1.000 .876化学 1.000 .670语文 1.000 .886历史 1.000 .876英语 1.000 .897Extraction Method: PrincipalComponent Analysis.上表为公因子方差，给出了该次分析中从每个原始变量中提取的信息，从表中可以看出除了化学外，主成分几乎都包含了其余各个变量至少80%的信息。

上表为特征根于方差贡献表，给出了个主成分解释原始变量总方差的情况，从表中可以看出，本例中保留了2个主成分，集中了原始变量总信息的75.260%上图为碎石土，分析碎石土看出因子1与因子2的特征值差值比较大，而其他特征值比较小，可以出保留2个因子能概括绝大部分信息。

因子分析实验报告范本一、实验目的本次因子分析实验旨在探究多个变量之间的潜在结构关系，通过降维的方法提取出主要的公共因子，以更简洁、有效地解释数据中的信息。

二、实验数据来源及描述实验数据来源于_____调查，共收集了_____个样本，涉及_____个变量。

这些变量包括但不限于：1、变量 1：＿____，用于衡量_____。

2、变量 2：＿____，反映了_____。

3、变量 3：＿____，其代表的含义是_____。

三、实验方法1、数据预处理对缺失值进行处理，采用_____方法进行填充。

对数据进行标准化处理，以消除量纲的影响。

2、因子提取方法选用主成分分析法提取公共因子。

根据特征根大于 1 的原则确定因子个数。

3、因子旋转方法采用方差最大化正交旋转，以使因子更具有可解释性。

四、实验步骤1、导入数据使用统计软件（如 SPSS）将数据文件导入。

2、数据预处理按照上述预处理方法进行操作。

3、因子分析在软件中选择因子分析模块，设置相应的参数进行分析。

4、结果解读观察公因子方差表，了解每个变量被公共因子解释的程度。

查看总方差解释表，确定提取的公共因子个数及解释的总方差比例。

分析旋转后的成分矩阵，解读公共因子的含义。

五、实验结果1、公因子方差变量 1 的公因子方差为_____，表明公共因子能够解释其_____%的方差。

变量 2 的公因子方差为_____，意味着公共因子对其的解释程度为_____%。

2、总方差解释提取了_____个公共因子，其特征根分别为_____、＿____、＿____。

这_____个公共因子累计解释了总方差的_____%。

3、旋转后的成分矩阵公共因子 1 在变量 1、变量 2 上有较高的载荷，分别为_____、＿____，可以将其解释为_____因素。

公共因子 2 在变量 3、变量 4 上的载荷较大，分别为_____、＿____，代表了_____方面。

六、结果讨论1、因子的可解释性提取的公共因子在实际意义上具有一定的合理性和可解释性，能够较好地概括原始变量所包含的信息。

精选全文完整版可编辑修改实验报告主成分分析（综合性实验）(Principal component analysis)实验原理：主成分分析利用指标之间的相关性，将多个指标转化为少数几个综合指标，从而达到降维和数据结构简化的目的。

这些综合指标反映了原始指标的绝大部分信息，通常表示为原始指标的某种线性组合，且综合指标间不相关。

利用矩阵代数的知识可求解主成分。

实验题目一：将彩色胶卷在显影液下处理后在不同情形下曝光，然后通过红、绿、蓝三种滤色片并在高、中、低三种密度下进行测量，每个胶卷有高红、高绿、高蓝、中红、…、低蓝等九个指标（分别记为X1－X9九个变量）。

试验了108个胶卷，由数据已算得如下协差阵：(S2a1)177 179 95 96 53 32 -7 -4 -3419 245 131 181 127 -2 1 4302 60 109 142 4 4 11158 102 42 4 3 2137 96 4 5 6128 2 2 834 31 3339 3948实验要求：（1）试从协差阵出发进行主成分分析；（2）计算方差累积贡献率；（3）作Scree图，并结合（2）的结果确定主成分的个数；（4）试对结果进行解释。

实验题目二：下表中给出了不同国家及地区的男子径赛记录：(t8a6)Country 100m(s) 200m(s)400m(s)800m(min)1500m(min)5000m(min)10,000m(min)Marathon(mins)Argentina 10.39 20.81 46.84 1.81 3.7 14.04 29.36 137.72 Australia 10.31 20.06 44.84 1.74 3.57 13.28 27.66 128.3 Austria 10.44 20.81 46.82 1.79 3.6 13.26 27.72 135.9 Belgium 10.34 20.68 45.04 1.73 3.6 13.22 27.45 129.95 Bermuda 10.28 20.58 45.91 1.8 3.75 14.68 30.55 146.62 Brazil 10.22 20.43 45.21 1.73 3.66 13.62 28.62 133.13 Burma 10.64 21.52 48.3 1.8 3.85 14.45 30.28 139.95 Canada 10.17 20.22 45.68 1.76 3.63 13.55 28.09 130.15 Chile 10.34 20.8 46.2 1.79 3.71 13.61 29.3 134.03 China 10.51 21.04 47.3 1.81 3.73 13.9 29.13 133.53 Columbia 10.43 21.05 46.1 1.82 3.74 13.49 27.88 131.35 Cook Islands 12.18 23.2 52.94 2.02 4.24 16.7 35.38 164.7 Costa Rica 10.94 21.9 48.66 1.87 3.84 14.03 28.81 136.58 Czechoslovakia 10.35 20.65 45.64 1.76 3.58 13.42 28.19 134.32 Denmark 10.56 20.52 45.89 1.78 3.61 13.5 28.11 130.78 Dominican Republic 10.14 20.65 46.8 1.82 3.82 14.91 31.45 154.12 Finland 10.43 20.69 45.49 1.74 3.61 13.27 27.52 130.87 France 10.11 20.38 45.28 1.73 3.57 13.34 27.97 132.3 German (D.R.) 10.12 20.33 44.87 1.73 3.56 13.17 27.42 129.92 German (F.R.) 10.16 20.37 44.5 1.73 3.53 13.21 27.61 132.23 Great Brit.& N. Ireland 10.11 20.21 44.93 1.7 3.51 13.01 27.51 129.13 Greece 10.22 20.71 46.56 1.78 3.64 14.59 28.45 134.6 Guatemala 10.98 21.82 48.4 1.89 3.8 14.16 30.11 139.33 Hungary 10.26 20.62 46.02 1.77 3.62 13.49 28.44 132.58 India 10.6 21.42 45.73 1.76 3.73 13.77 28.81 131.98Indonesia 10.59 21.49 47.8 1.84 3.92 14.73 30.79 148.83 Ireland 10.61 20.96 46.3 1.79 3.56 13.32 27.81 132.35 Israel 10.71 21 47.8 1.77 3.72 13.66 28.93 137.55 Italy 10.01 19.72 45.26 1.73 3.6 13.23 27.52 131.08 Japan 10.34 20.81 45.86 1.79 3.64 13.41 27.72 128.63 Kenya 10.46 20.66 44.92 1.73 3.55 13.1 27.38 129.75 Korea 10.34 20.89 46.9 1.79 3.77 13.96 29.23 136.25 D.P.R Korea 10.91 21.94 47.3 1.85 3.77 14.13 29.67 130.87 Luxembourg 10.35 20.77 47.4 1.82 3.67 13.64 29.08 141.27 Malaysia 10.4 20.92 46.3 1.82 3.8 14.64 31.01 154.1 Mauritius 11.19 22.45 47.7 1.88 3.83 15.06 31.77 152.23 Mexico 10.42 21.3 46.1 1.8 3.65 13.46 27.95 129.2 Netherlands 10.52 20.95 45.1 1.74 3.62 13.36 27.61 129.02 New Zealand 10.51 20.88 46.1 1.74 3.54 13.21 27.7 128.98 Norway 10.55 21.16 46.71 1.76 3.62 13.34 27.69 131.48 Papua New Guinea 10.96 21.78 47.9 1.9 4.01 14.72 31.36 148.22 Philippines 10.78 21.64 46.24 1.81 3.83 14.74 30.64 145.27 Poland 10.16 20.24 45.36 1.76 3.6 13.29 27.89 131.58 Portugal 10.53 21.17 46.7 1.79 3.62 13.13 27.38 128.65 Rumania 10.41 20.98 45.87 1.76 3.64 13.25 27.67 132.5 Singapore 10.38 21.28 47.4 1.88 3.89 15.11 31.32 157.77 Spain 10.42 20.77 45.98 1.76 3.55 13.31 27.73 131.57 Sweden 10.25 20.61 45.63 1.77 3.61 13.29 27.94 130.63 Switzerland 10.37 20.46 45.78 1.78 3.55 13.22 27.91 131.2 Taipei 10.59 21.29 46.8 1.79 3.77 14.07 30.07 139.27 Thailand 10.39 21.09 47.91 1.83 3.84 15.23 32.56 149.9 Turkey 10.71 21.43 47.6 1.79 3.67 13.56 28.58 131.5 USA 9.93 19.75 43.86 1.73 3.53 13.2 27.43 128.22 USSR 10.07 20 44.6 1.75 3.59 13.2 27.53 130.55Western Samoa 10.82 21.86 49 2.02 4.24 16.28 34.71 161.83 （数据来源：1984年洛杉机奥运会IAAF/AFT径赛与田赛统计手册）实验要求：（1）试求主成分，并对结果进行解释；（2）试用方差累积贡献率和Scree图确定主成分的个数；（3）计算各国第一主成分的得分并排名。

例如，在企业形象或品牌形象的研究中，消费者可
以通过一个有 24 个指标构成的评价体系，评价百货商 场的24个方面的优劣。 但消费者主要关心的是三个方面，即商店的环境、商 店的服务和商品的价格。因子分析方法可以通过24个 变量，找出反映商店环境、商店服务水平和商品价格 的三个潜在的因子，对商店进行综合评价。而这三个 公共因子可以表示为：
2 Var (ε) diag ( 12 , 2 , 2 , p )
E ( F1 p ) E ( F2 p ) 0 E ( Fp p )
7
二、因子分析模型的性质
1、原始变量X的协方差矩阵的分解 X - μ = AF + ε
Var ( X - μ) = AVar (F) A + Var (ε)
F* F
9
E (F* ) 0 E (ε ) 0
*
Var (F* ) I
2 Var (ε* ) diag ( 12 , 2 , 2 , p )
cov(F , ε ) E (F ε ) 0
* * * *
10
设T为一个p×p的正交矩阵，令A*=AT，
3、因子载荷不是惟一的
11
降维与不等于单纯的减少指标 19头牛，老大1/2，老二1/4，老三1/5 如何分？ 牛皮公路与数据简化
例
假定某地固定资产投资率 x1 ，通货膨胀率 x2 ，失
业率 x3 ，相关系数矩阵为
1/ 5 1/ 5 1 1/ 5 1 2 / 5 1 1/ 5 2 / 5
1 0.24 1 0.34 0.24 1 0.02 0.17 0.02 181
因子载荷矩阵可以看出，除第一因子在所有的变量在公共因子 上有较大的正载荷，可以称为一般运动因子。其他的3个因子不太 容易解释。似乎是跑和投掷的能力对比，似乎是长跑耐力和短跑速 19 度的对比。于是考虑旋转因子，得下表

因子分析一．因子分析原理因子分析是根据相关性大小把原始变量进行分组，使得同组内的变量之间相关性高，而不同组的变量之间的相关性低。

每组变量代表一个基本结构（即公共因子），并用一个不可观测的综合变量来表示。

对于所研究的某一具体问题，原始变量分解为两部分之和。

一部分是少数几个不可观测的公共因子的线性函数，另一部分是与公共因子无关的特殊因子。

从全部计算过程来看作R 型因子分析与作Q 型因子分析都是一样的，只不过出发点不同，R 型从相关系数矩阵出发，Q 型从相似系数阵出发都是对同一批观测数据，可以根据其所要求的目的决定用哪一类型的因子分析因子模型的性质：模型不受变量量纲的影响；因子载荷不是唯一的。

二．因子分析的数学模型设有p 个指标，则因子分析数学模型为：11111221221122221122p p p pp p p pp p X r Y r Y r Y X r Y r Y r Y X r Y r Y r Y=+++⎧⎪=+++⎪⎨⎪⎪=+++⎩ 其中，12,,,p X X X 是已标准化的可观测的评价指标。

12,,,k F F F 出现在每个指标i X 的表达式中，称为公共因子，公共因子是不可观测的，其含义要根据具体问题来解释。

i ε是各个对应指标i X 所特有的因子，故称为特殊因子，它与公共因子之间彼此独立。

ij r 是指标i X 在公共因子j F 上的系数，称为因子载荷，因子载荷ij r 的统计含义是指标i X 在公共因子j F 上的相关系数，表示i X 与j F 线性相关程度。

用矩阵形式表示为：X AF ε=+其中12(,,,)p X X X X '=，12(,,,)k F F F F '=，12(,,,)p εεεε'=，111212122212m m p p pm r r r r r r A rr r ⎛⎫⎪⎪= ⎪ ⎪ ⎪⎝⎭，A 称为因子载荷矩阵。

其统计含义是：A 中的第i 行元素12,,,i i im r r r 说明了指标i X 依赖于各个公共因子的程度。

因子分析实验1：分析评价全国35个中心城市的综合发展水平，无论是对城市自身的发展，还是对周边地区的进步，都具有十分重要的意义。

应用因子分析模型，选取反应城市综合发展水平的12各指标作为原始变量，对全国35各中心城市的综合发展水平作分析评价。

（变量的含义见书215页例6-3中的解释。

）第一步：分析——降维——因子分析将12个变量选入变量窗口中。

第二步：提取—— 碎石图点击OK即可。

按照特征根大于1的原则，选入3个公因子，累计方差贡献率为87.1%。

此时得到的未旋转的公共因子的实际意义不好解释，因此对公共因子进行方差最大化正交旋转。

第三步：旋转——方差最大化正交旋转上表结果为：旋转成份矩阵a成份123x1.929-.183.039x2.806.309.344x3.870-.147.253x4.791.091-.437x5.934.194.155x6.970.174-.053x7.947.030-.191x8.952.199-.155x9.010.205.840x10.034.914.175x11.068.921.259x12.092.809-.106提取方法 :主成份。

旋转法 :具有 Kaiser 标准化的正交旋转法。

a. 旋转在 4 次迭代后收敛。

由上表结果，原变量x1可由各因子表示为：X1=0.929*F1-0.183*F2+0.039*F3.其余依次类推。

最后计算因子得分，以各因子的方差贡献率占三个因子总方差贡献率的比重作为权重进行加权汇总，得出各城市的综合得分F，即：F=（54.381*F1+22.077*F2+10.647*F3）/87.105.第四步：得分——保存变量得到运行结果并计算综合得分。

因子得分值会在数据表中显示。

以F1因子得分为x轴，F2因子得分为y轴，画出各城市的因子得分图。

步骤：选择 “图形——旧对话框——三点、点状——简单分布”将F1因子得分放入x轴，F2因子得分放入y轴。

因子分析是一种常用的数据分析方法，用于发现变量之间的潜在关系和结构。

在因子分析中，因子结构验证是一个至关重要的步骤，它可以帮助研究者确认所得因子结构的合理性和有效性。

本文将介绍因子分析中常用的因子结构验证方法，以帮助读者更好地理解和运用因子分析技术。

第一部分：因子分析的基本原理因子分析是一种用于分析多个变量之间关系的统计方法，它可以帮助研究者发现这些变量之间的潜在结构和模式。

在因子分析中，通过对变量之间的协方差矩阵进行特征值分解，得到一组新的变量，称为因子，来代表原始变量的共性部分。

因子分析可以帮助研究者减少变量的数量，发现变量之间的潜在关系，并简化数据分析过程。

第二部分：因子结构验证的意义和方法在进行因子分析后，研究者需要对所得的因子结构进行验证，以确认其有效性和合理性。

因子结构验证方法包括验证因子的旋转、因子负荷量的检验、因子相关性的检验等。

其中，因子旋转是最常用的方法之一，它可以帮助研究者更好地解释因子之间的关系和含义。

此外，因子负荷量的检验可以帮助确认每个变量对因子的贡献程度，从而进一步验证因子结构的合理性。

第三部分：因子结构验证方法的应用在实际应用中，因子结构验证方法可以帮助研究者更好地理解数据，发现变量之间的潜在结构和模式。

例如，在心理学研究中，研究者可以利用因子分析来分析调查问卷数据，发现不同问题之间的潜在关系和结构。

通过对因子结构的验证，研究者可以确认问卷的有效性和信度，进而提出更有效的研究结论。

第四部分：因子结构验证方法的局限性和发展方向尽管因子结构验证方法在数据分析中具有重要意义，但也存在一些局限性。

例如，在因子旋转过程中，存在不同的旋转方法和标准，研究者需要根据具体情况选择合适的方法。

此外，在因子负荷量的检验过程中，也需要考虑样本量、变量相关性等因素的影响。

因此，未来的发展方向可以包括进一步完善因子结构验证方法，提出更科学的验证标准和流程，以应对不同领域和研究对象的需求。

结论因子分析是一种重要的数据分析方法，通过发现变量之间的潜在结构和模式，可以帮助研究者更好地理解数据和提出有效的结论。

因子分析实验报告引言概述：因子分析是一种多变量统计分析方法，用于确定一组观测变量中的潜在因子结构。

通过因子分析，我们可以分析一个大量的观测变量，将其归纳为较少数量的相互关联的因子，从而简化复杂的数据结构。

本实验旨在通过实际应用因子分析方法，对潜在因子结构进行探索和解释。

正文内容：1.因子分析的基本原理1.1数据预处理1.1.1数据清洗1.1.2数据标准化1.2因子提取方法1.2.1主成分分析法1.2.2最大似然法1.2.3主轴法1.3因子旋转方法1.3.1方差最大旋转法（Varimax）1.3.2极简旋转法（Simplimax）1.3.3最大似然旋转法（Promax）1.4因子解释和命名1.4.1因子载荷1.4.2解释方差1.4.3因子命名2.实验设计和数据收集2.1实验目的和假设2.2实验设计2.3数据收集方法2.4样本选择和数量3.数据分析和结果解释3.1因子提取3.1.1因素的选择3.1.2因子提取方法的比较3.1.3因子间关系3.2因子旋转3.2.1旋转前的因子载荷3.2.2旋转后的因子载荷3.2.3旋转后的因子解释3.3因子的可解释变异3.3.1总方差解释比例3.3.2单个因子的方差解释比例3.3.3组合因子的方差解释比例4.结果分析和讨论4.1因子结构和因子载荷4.2因子的解释和命名4.3因子的解释力度和相关性4.4结果的稳定性和可靠性4.5结果与假设的一致性5.实验总结和建议5.1实验结果总结5.2实验中的问题和限制5.3进一步研究方向和建议5.4实验应用和意义文末总结：通过本次因子分析实验，我们成功地应用了因子分析方法对观测变量进行了潜在因子结构的探索和解释。

通过数据分析和结果解释，我们得到了一组有意义和可解释的因子结构，并对其进行了详细的分析和讨论。

我们还总结了本次实验的结果、问题和限制，并提出了进一步研究方向和建议。

本实验对研究者在实际应用因子分析方法时提供了宝贵的经验和指导。

因子分析实验报告因子分析实验报告引言：因子分析是一种常用的统计方法，用于研究变量之间的关系和潜在结构。

通过因子分析，可以将一组观测变量转化为较少的潜在因子，从而减少数据的复杂性，提取出变量背后的共同因素。

本实验旨在探究因子分析在数据分析中的应用，并通过实例分析来展示其效果。

实验设计：本实验选取了一个由20个观测变量组成的数据集，包括心理测试中的各项指标。

首先，我们对数据进行了描述性统计分析，包括计算均值、方差等指标，以了解数据的基本情况。

接下来，我们使用因子分析方法对数据进行了降维处理，提取出主要的潜在因子。

最后，我们对提取出的因子进行了解释，并分析了各个因子与观测变量之间的关系。

实验结果：在描述性统计分析中，我们发现数据集中的观测变量具有一定的相关性，但并不完全一致。

这表明存在一些共同的潜在因子，可以通过因子分析来提取。

在进行因子分析时，我们采用了主成分分析法，通过计算特征值和特征向量，确定了最重要的潜在因子。

根据特征值-特征向量的结果，我们提取了3个主要因子，这些因子解释了总方差的70%以上。

接下来，我们对提取出的因子进行了命名和解释。

第一个因子被命名为“情绪状态”，它包括了焦虑、抑郁和情绪波动等观测变量。

第二个因子被命名为“自信与社交能力”，它包括了自尊、社交能力和自信等观测变量。

第三个因子被命名为“认知能力”，它包括了记忆力、注意力和思维敏捷等观测变量。

进一步分析发现，这些因子与观测变量之间存在一定的相关性。

例如，情绪状态因子与焦虑、抑郁等观测变量呈正相关，而与自尊、社交能力等观测变量呈负相关。

这些结果表明，通过因子分析可以揭示出变量之间的内在关系，为后续的数据分析和研究提供了重要线索。

讨论与结论：本实验通过因子分析方法，成功地将一个包含20个观测变量的数据集转化为3个潜在因子。

这些因子能够解释数据集中70%以上的总方差，具有较好的降维效果。

通过对提取出的因子进行解释和分析，我们发现了变量之间的内在关系，并为进一步的研究提供了重要线索。