2013年高考数学总复习-3-1导数的概念及运算课件-新人教B版

2013年高考数学总复习-3-1-导数的概念及运算-新人教B版Dsin x 1＋cos x，x ∈(0，π)，当y ′＝2时，x 等于( ) A.π3 B.2π3C.π4D.π6[答案] B[解析] y ′＝cos x ·1＋cos x －sin x ·－sin x 1＋cos x2 ＝11＋cos x＝2，∴cos x ＝－12， ∵x ∈(0，π)，∴x ＝2π3. 5．(2011·山东淄博一中期末)曲线y ＝13x 3＋x 在点⎝⎛⎭⎪⎪⎫1，43处的切线与坐标轴围成的三角形面积为( )A ．1B .19C.13D.23[答案] B[解析] ∵y ′＝x 2＋1，∴k ＝2，切线方程y －43＝2(x －1)，即6x －3y －2＝0，令x ＝0得y ＝－23，令y ＝0得x ＝13，∴S ＝12×13×23＝19. 6．(文)已知f (x )＝log a x (a >1)的导函数是f ′(x )，记A ＝f ′(a )，B ＝f (a ＋1)－f (a )，C ＝f ′(a ＋1)，则( )A ．A >B >C B ．A >C >BC ．B >A >CD ．C >B >A[答案] A[解析] 记M (a ，f (a ))，N (a ＋1，f (a ＋1))，则由于B ＝f (a ＋1)－f (a )＝f a ＋1－f a a ＋1－a，表示直线MN 的斜率，A ＝f ′(a )表示函数f (x )＝log a x 在点M 处的切线斜率；C ＝f ′(a ＋1)表示函数f (x )＝log a x 在点N 处的切线斜率．所以，A >B >C .(理)设函数f (x )＝sin ⎝⎛⎭⎪⎪⎫ωx ＋π6－1(ω>0)的导函数f ′(x )的最大值为3，则f (x )图象的一条对称轴方程是( )A ．x ＝π9B ．x ＝π6C ．x ＝π3D ．x ＝π2[答案] A[解析] f ′(x )＝ωcos ⎝⎛⎭⎪⎪⎫ωx ＋π6的最大值为3， 即ω＝3，∴f (x )＝sin ⎝⎛⎭⎪⎪⎫3x ＋π6－1. 由3x ＋π6＝π2＋k π得，x ＝π9＋k π3(k ∈Z)． 故A 正确．7．如图，函数y ＝f (x )的图象在点P (5，f (5))处的切线方程是y ＝－x ＋8，则f (5)＋f ′(5)＝________.[答案] 2[解析]由条件知f′(5)＝－1，又在点P处切线方程为y－f(5)＝－(x－5)，∴y＝－x＋5＋f(5)，即y＝－x＋8，∴5＋f(5)＝8，∴f(5)＝3，∴f(5)＋f′(5)＝2.8．(文)(2011·北京模拟)已知函数f(x)＝3x3＋2x2－1在区间(m,0)上总有f′(x)≤0成立，则m 的取值范围为________．[答案][－49，0)[解析]∵f′(x)＝9x2＋4x≤0在(m,0)上恒成立，且f′(x)＝0的两根为x1＝0，x2＝－49，∴－4≤m<0.9(理)设a∈R，函数f(x)＝x3＋ax2＋(a－3)x 的导函数是f′(x)，若f′(x)是偶函数，则曲线y ＝f(x)在原点处的切线方程为________．[答案]y＝－3x[解析]f′(x)＝3x2＋2ax＋(a－3)，又f′(－x)＝f′(x)，即3x2－2ax＋(a－3)＝3x2＋2ax＋(a－3)对任意x∈R都成立，所以a＝0，f′(x)＝3x2－3，f′(0)＝－3，曲线y＝f(x)在原点处的切线方程为y＝－3x.9．(2011·济南模拟)设曲线y＝x n＋1(n∈N*)在点(1,1)处的切线与x轴的交点的横坐标为x n，令a n＝lg x n，则a1＋a2＋…＋a99的值为________．[答案]－2[解析]点(1,1)在曲线y＝x n＋1(n∈N*)上，点(1,1)为切点，y ′＝(n ＋1)x n ，故切线的斜率为k ＝n ＋1，曲线在点(1,1)处的切线方程y －1＝(n ＋1)(x －1)，令y ＝0得切点的横坐标为x n ＝n n ＋1，故a 1＋a 2＋…＋a 99＝lg(x 1x 2…x 99)＝lg(12×23×…×99100)＝lg 1100＝－2.10．(文)设函数y ＝ax 3＋bx 2＋cx ＋d 的图象与y 轴交点为P ，且曲线在P 点处的切线方程为12x －y －4＝0. 若函数在x ＝2处取得极值0，试确定函数的解析式.[解析] ∵y ＝ax 3＋bx 2＋cx ＋d 的图象与y 轴的交点为P (0，d )，又曲线在点P 处的切线方程为y ＝12x －4，P 点坐标适合方程，从而d ＝－4；又切线斜率k ＝12，故在x ＝0处的导数y ′|x＝0＝12而y ′|x ＝0＝c ，从而c ＝12； 又函数在x ＝2处取得极值0，所以⎩⎨⎧ y ′|x ＝2＝0f 2＝0即⎩⎨⎧12a ＋4b ＋12＝08a ＋4b ＋20＝0解得a ＝2，b ＝－9所以所求函数解析式为y ＝2x 3－9x 2＋12x －4.(理)(2010·北京东城区)已知函数f (x )＝ax 2＋b ln x 在x ＝1处有极值12.(1)求a ，b 的值；(2)判断函数y ＝f (x )的单调性并求出单调区间．[解析] (1)因为函数f (x )＝ax 2＋b ln x ， 所以f ′(x )＝2ax ＋bx .又函数f (x )在x ＝1处有极值12，所以⎩⎨⎧ f ′1＝0f 1＝12，即⎩⎨⎧2a ＋b ＝0a ＝12，可得a ＝12，b ＝－ 1.(2)由(1)可知f (x )＝12x 2－ln x ，其定义域是(0，＋∞)，且f ′(x )＝x －1x ＝x ＋1x －1x .当x 变化时，f ′(x )，f (x )的变化情况如下表：x (0,1) 1 (1，＋∞) f ′(x ) － 0 ＋f (x )↘极小值↗所以函数y ＝f (x )的单调减区间是(0,1)，单调增区间是(1，＋∞).11.(文)(2011·聊城模拟)曲线y ＝e x 在点(2，e 2)处的切线与坐标轴所围成的三角形的面积为( )A.94e 2B ．2e 2C ．e 2 D.e22[答案] D[解析] y ′|x ＝2＝e 2，∴切线方程为y －e 2＝e 2(x －2)，令x ＝0得y ＝－e 2，令y ＝0得x ＝1， ∴所求面积S ＝e 22.(理)(2011·湖南文，7)曲线y ＝sin x sin x ＋cos x －12在点M (π4，0)处的切线的斜率为( )A ．－ 12 B.12C ．－ 22 D.22[答案] B[解析] ∵y ′＝cos x sin x ＋cos x －sin x cos x －sin xsin x ＋cos x2＝1sin x ＋cos x2，∴y ′|x ＝π4＝12. 12．(文)(2011·江西理，4)若f (x )＝x 2－2x －4ln x ，则f ′(x )＞0的解集为( )A ．(0，＋∞)B ．(－1,0)∪(2，＋∞)C ．(2，＋∞)D ．(－1,0) [答案] C[解析] 因为f (x )＝x 2－2x －4ln x ， ∴f ′(x )＝2x －2－4x ＝2x 2－x －2x>0， 即⎩⎨⎧x >0x 2－x －2>0，解得x >2，故选C.(理)(2011·广东省汕头市四校联考)已知函数f (x )(x ∈R)满足f (1)＝1，且f (x )的导函数f ′(x )<12，则f (x )<x 2＋12的解集为( )A ．{x |－1<x <1}B ．{x |x <－1}C ．{x |x <－1或x >1}D ．{x |x >1} [答案] D[解析] 令φ(x )＝f (x )－x 2－12，则φ′(x )＝f ′(x )－12<0，∴φ(x )在R 上是减函数，φ(1)＝f (1)－12－12＝1－1＝0，∴φ(x )＝f (x )－x 2－12<0的解集为{x |x >1}，选D.13．(文)二次函数y ＝f (x )的图象过原点，且它的导函数y ＝f ′(x )的图象是过第一、二、三象限的一条直线，则函数y ＝f (x )的图象的顶点在( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限 [答案] C[解析] 由题意可设f (x )＝ax 2＋bx ，f ′(x )＝2ax ＋b ，由于f ′(x )图象是过第一、二、三象限的一条直线，故2a >0，b >0，则f (x )＝a (x ＋b 2a )2－b 24a ，顶点(－b 2a ，－b 24a)在第三象限，故选C. (理)函数f (x )＝x cos x 的导函数f ′(x )在区间[－π，π]上的图象大致为( )[答案] A[解析] ∵f (x )＝x cos x ， ∴f ′(x )＝cos x －x sin x ，∴f ′(－x )＝f ′(x )，∴f ′(x )为偶函数，排除C ； ∵f ′(0)＝1，排除D ；由f ′⎝⎛⎭⎪⎪⎫π2＝－π2<0，f ′(2π)＝1>0，排除B ，故选A.14．(文)(2011·山东省济南市调研)已知函数f(x)的图象在点M(1，f(1))处的切线方程是2x－3y＋1＝0，则f(1)＋f′(1)＝________.[答案]5 3[解析]由题意知点M在f(x)的图象上，也在直线2x－3y＋1＝0上，∴2×1－3f(1)＋1＝0，∴f(1)＝1，又f′(1)＝23，∴f(1)＋f′(1)＝53.(理)(2011·朝阳区统考)若曲线f(x)＝ax3＋ln x存在垂直于y轴的切线，则实数a的取值范围是________．[答案](－∞，0)[解析]由题意，可知f′(x)＝3ax2＋1x，又因为存在垂直于y轴的切线，所以3ax2＋1x＝0⇒a＝－13x3(x >0)⇒a ∈(－∞，0)．15．(文)(2010·北京市延庆县模考)已知函数f (x )＝x 3－(a ＋b )x 2＋abx ，(0<a <b )．(1)若函数f (x )在点(1,0)处的切线的倾斜角为3π4，求a ，b 的值； (2)在(1)的条件下，求f (x )在区间[0,3]上的最值；(3)设f (x )在x ＝s 与x ＝t 处取得极值，其中s <t ，求证：0<s <a <t <b .[解析] (1)f ′(x )＝3x 2－2(a ＋b )x ＋ab ，tan 3π4＝－1.由条件得⎩⎨⎧f 1＝0f ′1＝－1，即⎩⎨⎧1－a ＋b ＋ab ＝03－2a ＋b ＋ab ＝－1，解得a＝1，b＝2或a＝2，b＝1，因为a<b，所以a＝1，b＝2.(2)由(1)知f(x)＝x3－3x2＋2x，f′(x)＝3x2－6x＋2，令f′(x)＝3x2－6x＋2＝0，解得x1＝1－3 3，x2＝1＋3 3.在区间[0,3]上，x，f′(x)，f(x)的变化情况如下表：x 0(0，x1)x1(x1，x2)x2(x2,3) 3 f′(x)＋0－0＋f(x)0递增239递减－239递增 6所以f(x)max＝6；f(x)min＝－23.(3)证明：f′(x)＝3x2－2(a＋b)x＋ab，依据题意知s，t为二次方程f′(x)＝0的两根．∵f′(0)＝ab>0，f′(a)＝a2－ab＝a(a－b)<0，f′(b)＝b2－ab＝b(b－a)>0，∴f′(x)＝0在区间(0，a)与(a，b)内分别有一个根．∵s<t，∴0<s<a<t<b.(理)已知定义在正实数集上的函数f(x)＝1 2x2＋2ax，g(x)＝3a2ln x＋b，其中a>0.设两曲线y ＝f(x)，y＝g(x)有公共点，且在该点处的切线相同．(1)用a表示b，并求b的最大值；(2)求证：f(x)≥g(x)(x>0)．[解析](1)设y＝f(x)与y＝g(x)(x>0)的公共点为(x0，y0)，∴x0>0.∵f′(x)＝x＋2a，g′(x)＝3a2 x，由题意f(x0)＝g(x0)，且f′(x0)＝g′(x0)．∴⎩⎪⎨⎪⎧ 12x 20＋2ax 0＝3a 2ln x 0＋b x 0＋2a ＝3a 2x 0，由x 0＋2a ＝3a 2x 0得x 0＝a 或x 0＝－3a (舍去)． 则有b ＝12a 2＋2a 2－3a 2ln a ＝52a 2－3a 2ln a . 令h (a )＝52a 2－3a 2ln a (a >0)， 则h ′(a )＝2a (1－3ln a )．由h ′(a )>0得，0<a <e 13 ，由h ′(a )<0得，a >e 13 .故h (a )在(0，e 13)为增函数，在(e 13，＋∞)上为减函数，∴h (a )在a ＝e 13时取最大值h (e 13)＝32e 23 .即b 的最大值为32e 2 3.(2)设F(x)＝f(x)－g(x)＝12x2＋2ax－3a2ln x－b(x>0)，则F′(x)＝x＋2a－3a2x＝x－a x＋3ax(x>0)．故F(x)在(0，a)为减函数，在(a，＋∞)为增函数，于是函数F(x)在(0，＋∞)上的最小值是F(a)＝F(x0)＝f(x0)－g(x0)＝0.故当x>0时，有f(x)－g(x)≥0，即当x>0时，f(x)≥g(x)．1．(2011·安徽省“江南十校”高三联考)已知函数f(x)的导函数为f′(x)，且满足f(x)＝2xf′(1)＋x2，则f′(1)＝()A．－1 B．－2C．1 D．2[答案] B[解析]f′(x)＝2f′(1)＋2x，令x＝1得f′(1)＝2f′(1)＋2，∴f′(1)＝－2，故选B.2．(2011·茂名一模)设函数f(x)＝g(x)＋x2，曲线y＝g(x)在点(1，g(1))处的切线方程为y＝2x ＋1，则曲线y＝f(x)在点(1，f(1))处切线的斜率为()A．4 B．－1 4C．2 D．－1 2[答案] A[解析]∵f(x)＝g(x)＋x2，∴f′(x)＝g′(x)＋2x，∴f′(1)＝g′(1)＋2，由条件知，g′(1)＝2，∴f′(1)＝4，故选A.3．(2010·360题库网高考)曲线y＝xx＋2在点(－1，－1)处的切线方程为()A．y＝2x＋1 B．y＝2x－1C．y＝－2x－3 D．y＝－2x－2[答案] A[解析]∵y′＝x′x＋2－x x＋2′x＋22＝2x＋22，∴k＝y′|x＝－1＝2－1＋22＝2，∴切线方程为：y＋1＝2(x＋1)，即y＝2x＋1.4．(2011·湖南湘西联考)下列图象中有一个是函数f(x)＝13x3＋ax2＋(a2－1)x＋1(a∈R，a≠0)的导函数f′(x)的图象，则f(－1)＝()A.13 B ．－13C.53 D ．－53[答案] B[解析] f ′(x )＝x 2＋2ax ＋(a 2－1)，∵a ≠0， ∴其图象为最右侧的一个．由f ′(0)＝a 2－1＝0，得a ＝±1.由导函数f ′(x )的图象可知，a <0，故a ＝－1，f (－1)＝－13－1＋1＝－13. 5．(2011·广东省佛山市测试)设f (x )、g (x )是R 上的可导函数，f ′(x )、g ′(x )分别为f (x )、g (x )的导函数，且满足f ′(x )g (x )＋f (x )g ′(x )<0，则当a <x <b 时，有( )A ．f (x )g (b )>f (b )g (x )B ．f (x )g (a )>f (a )g (x )C ．f (x )g (x )>f (b )g (b )D ．f (x )g (x )>f (a )g (a )[答案] C[解析] 因为f ′(x )g (x )＋f (x )g ′(x )＝[f (x )g (x )]′，所以[f (x )g (x )]′<0，所以函数y ＝f (x )g (x )在给定区间上是减函数，故选C.6．若函数f (x )＝e x sin x ，则此函数图象在点(4，f (4))处的切线的倾斜角为( )A.π2B ．0C ．钝角D ．锐角[答案] C[解析] y ′|x ＝4＝(e x sin x ＋e x cos x )|x ＝4＝e 4(sin4＋cos4)＝2e 4sin(4＋π4)<0，故倾斜角为钝角，选C.7．(2010·东北师大附中模拟)定义方程f (x )＝f ′(x )的实数根x 0叫做函数f (x )的“新驻点”，若函数g (x )＝x ，h (x )＝ln(x ＋1)，φ(x )＝x 3－1的“新驻点”分别为α，β，γ，则α，β，γ的大小关系为()A．α>β>γB．β>α>γC．γ>α>βD．β>γ>α[答案] C[解析]由g(x)＝g′(x)得，x＝1，∴α＝1，由h(x)＝h′(x)得，ln(x＋1)＝1x＋1，故知1<x＋1<2，∴0<x<1，即0<β<1，由φ(x)＝φ′(x)得，x3－1＝3x2，∴x2(x－3)＝1，∴x>3，故γ>3，∴γ>α>β.[点评]对于ln(x＋1)＝1x＋1，假如0<x＋1<1，则ln(x＋1)<0，1x＋1>1矛盾；假如x＋1≥2，则1x＋1≤12，即ln(x＋1)≤12，∴x＋1≤e，∴x≤e－1与x≥1矛盾．8．等比数列{a n}中，a1＝2，a8＝4，函数f(x)＝x(x－a1)(x－a2)…(x－a8)，则f′(0)＝() A．26B．29C．212 D．215[答案] C[解析]f′(x)＝x′·[(x－a1)(x－a2)…(x－a8)]＋[(x－a1)(x－a2)…(x－a8)]′·x＝(x－a1)(x－a2)…(x－a8)＋[(x－a1)(x－a2)…(x－a8)]′·x，所以f′(0)＝(0－a1)(0－a2)...(0－a8)＋[(0－a1)(0－a2)...(0－a8)]′.0＝a1a2 (8)因为数列{a n}为等比数列，所以a2a7＝a3a6＝a4a5＝a1a8＝8，所以f′(0)＝84＝212.。

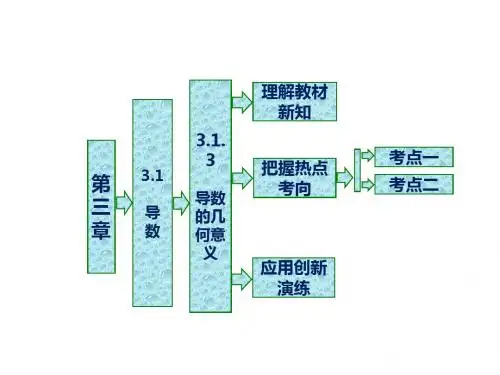
新高考数学新题型一轮复习课件第三章§3.1　导数的概念及其意义、导数的运算考试要求1.了解导数的概念、掌握基本初等函数的导数.2.通过函数图象，理解导数的几何意义3.能够用导数公式和导数的运算法则求简单函数的导数，能求简单的复合函数(形如 f(ax＋b))的导数.落实主干知识探究核心题型内容索引课时精练L U O S H I Z H U G A N Z H I S H I 落实主干知识知识梳理1.导数的概念(1)函数y ＝f (x )在x＝x0处的导数记作 或 .0'|x x y f ′(x 0)(2)函数y ＝f (x )的导函数2.导数的几何意义函数y ＝f (x )在x ＝x 0处的导数的几何意义就是曲线y ＝f (x )在点P (x 0，f (x 0))处的切线的，相应的切线方程为 .y －f (x 0)＝f ′(x 0)(x －x 0)斜率3.基本初等函数的导数公式基本初等函数导函数f (x )＝c (c 为常数)f ′(x )＝___f (x )＝x α(α∈Q ，且α≠0)f ′(x )＝______f (x )＝sin xf ′(x )＝______f (x )＝cos xf ′(x )＝_______f (x )＝a x (a >0，且a ≠1)f ′(x )＝_______0αx α－1cos x －sin x a x ln ae xf(x)＝e x f′(x)＝____ f(x)＝log a x(a>0，且a≠1)f′(x)＝______ f(x)＝ln x f′(x)＝___4.导数的运算法则若f ′(x )，g ′(x )存在，则有[f (x )±g (x )]′＝ ；[f (x )g (x )]′＝ ；f ′(x )±g ′(x )f ′(x )g (x )＋f (x )g ′(x)[cf (x )]′＝ .cf ′(x )5.复合函数的定义及其导数复合函数y＝f(g(x))的导数和函数y＝f(u)，u＝g(x)的导数间的关系为y′x y′u·u′x＝，即y对x的导数等于y对u的导数与u对x的导数的乘积.1.区分在点处的切线与过点处的切线(1)在点处的切线，该点一定是切点，切线有且仅有一条.(2)过点处的切线，该点不一定是切点，切线至少有一条.判断下列结论是否正确(请在括号中打“√”或“×”)(1)f ′(x 0)是函数y ＝f (x )在x ＝x 0附近的平均变化率.( )(2)与曲线只有一个公共点的直线一定是曲线的切线.( )(3)f ′(x 0)＝[f (x 0)]′.( )(4)若f (x )＝sin (－x )，则f ′(x )＝cos (－x ).( )××××教材改编题∴f ′(1)＝e －1，又f (1)＝e ＋1，∴切点为(1，e ＋1)，切线斜率k ＝f ′(1)＝e －1，即切线方程为y －(e ＋1)＝(e －1)(x －1)，即y ＝(e －1)x ＋2.1.函数f (x )＝e x ＋ 在x ＝1处的切线方程为______________.y ＝(e －1)x ＋22.已知函数f(x)＝x ln x＋ax2＋2，若f′(e)＝0，则a＝______. f′(x)＝1＋ln x＋2ax，3.若f(x)＝ln(1－x)＋e1－x，则f′(x)＝____________.T A N J I U H E X I N T I X I N G 探究核心题型题型一导数的运算例1　(1)(多选)(2022·济南质检)下列求导运算正确的是√√(x2e x)′＝(x2＋2x)e x，故B错误；教师备选1.函数y＝sin 2x－cos 2x的导数y′等于√y′＝2cos 2x＋2sin 2x2.(2022·济南模拟)已知函数f′(x)＝e x sin x＋e x cos x，则f(2 021)－f(0)等于√A.e2 021cos 2 021B.e2 021sin 2 021C. D.e因为f′(x)＝e x sin x＋e x cos x，所以f(x)＝e x sin x＋k(k为常数)，所以f(2 021)－f(0)＝e2 021sin 2 021.(1)求函数的导数要准确地把函数拆分成基本初等函数的和、差、积、商，再利用运算法则求导.(2)抽象函数求导，恰当赋值是关键，然后活用方程思想求解.(3)复合函数求导，应由外到内逐层求导，必要时要进行换元.跟踪训练1　(1)若函数f(x)，g(x)满足f(x)＋xg(x)＝x2－1，且f(1)＝1，则f′(1)＋g′(1)等于√A.1B.2C.3D.4当x＝1时，f(1)＋g(1)＝0，∵f(1)＝1，得g(1)＝－1，原式两边求导，得f′(x)＋g(x)＋xg′(x)＝2x，当x＝1时，f′(1)＋g(1)＋g′(1)＝2，得f′(1)＋g′(1)＝2－g(1)＝2－(－1)＝3.e2 (2)已知函数f(x)＝ln(2x－3)＋ax e－x，若f′(2)＝1，则a＝___.∴f′(2)＝2＋a e－2－2a e－2＝2－a e－2＝1，则a＝e2.命题点1　求切线方程题型二导数的几何意义例2　(1)(2021·全国甲卷)曲线y ＝ 在点(－1，－3)处的切线方程为_____________.5x －y ＋2＝0所以切线方程为y ＋3＝5(x ＋1)，即5x －y ＋2＝0.(2)已知函数f(x)＝x ln x，若直线l过点(0，－1)，并且与曲线y＝f(x)相切，x－y－1＝0则直线l的方程为_____________.∵点(0，－1)不在曲线f(x)＝x ln x上，∴设切点为(x0，y0).又f′(x)＝1＋ln x，∴直线l的方程为y＋1＝(1＋ln x0)x.∴直线l的方程为y＝x－1，即x－y－1＝0.命题点2　求参数的值(范围)例3　(1)(2022·青岛模拟)直线y＝kx＋1与曲线f(x)＝a ln x＋b相切于点P(1,2)，则2a＋b等于√A.4B.3C.2D.1∵直线y＝kx＋1与曲线f(x)＝a ln x＋b相切于点P(1,2)，将P(1,2)代入y＝kx＋1，可得k＋1＝2，解得k＝1，解得a＝1，可得f(x)＝ln x＋b，∵P(1,2)在曲线f(x)＝ln x＋b上，∴f(1)＝ln 1＋b＝2，解得b＝2，故2a＋b＝2＋2＝4.(2)(2022·广州模拟)过定点P(1，e)作曲线y＝a e x(a>0)的切线，恰有2条，(1，＋∞)则实数a的取值范围是__________.由y ′＝a e x ，若切点为(x0，　)，则切线方程的斜率k ＝ ＝ >0，∴切线方程为y ＝ (x －x 0＋1)，又P (1，e)在切线上，∴　(2－x 0)＝e ，0'|x x y 0e x a 0e x 0e x a 0e x a 0e x a 令φ(x )＝e x (2－x )，∴φ′(x )＝(1－x )e x ，当x ∈(－∞，1)时，φ′(x )>0；当x∈(1，＋∞)时，φ′(x)<0，∴φ(x)在(－∞，1)上单调递增，在(1，＋∞)上单调递减，∴φ(x)max＝φ(1)＝e，又x→－∞时，φ(x)→0；x→＋∞时，φ(x)→－∞，解得a>1，即实数a的取值范围是(1，＋∞).1.已知曲线f (x )＝x 3－x ＋3在点P 处的切线与直线x ＋2y －1＝0垂直，则P 点的坐标为A.(1,3)B.(－1,3)C.(1,3)或(－1,3)D.(1，－3)√教师备选设切点P(x0，y0)，f′(x)＝3x2－1，又切点P(x0，y0)在y＝f(x)上，∴当x0＝1时，y0＝3；当x0＝－1时，y0＝3.∴切点P为(1,3)或(－1,3).2.(2022·哈尔滨模拟)已知M是曲线y＝ln x＋x2＋(1－a)x上的任一点，若曲线在M点处的切线的倾斜角均是不小于的锐角，则实数a的取值范围是A.[2，＋∞) B.[4，＋∞)√C.(－∞，2]D.(－∞，4]故a≤2，所以a的取值范围是(－∞，2].(1)处理与切线有关的参数问题，关键是根据曲线、切线、切点的三个关系列出参数的方程：①切点处的导数是切线的斜率；②切点在切线上；③切点在曲线上.(2)注意区分“在点P处的切线”与“过点P处的切线”.跟踪训练2　(1)(2022·南平模拟)若直线y＝x＋m与曲线y＝e x－2n相切，则√设直线y ＝x ＋m 与曲线y ＝e x －2n 切于点(x0， )，因为y ′＝e x －2n ，所以　 ＝1，所以x 0＝2n ，所以切点为(2n ,1)，代入直线方程得1＝2n ＋m ，02e x n -02e x n -(2)若函数f(x)＝ln x＋2x2－ax的图象上存在与直线2x－y＝0平行的切线，[2，＋∞)则实数a的取值范围是__________.直线2x－y＝0的斜率k＝2，又曲线f(x)上存在与直线2x－y＝0平行的切线，∴a≥4－2＝2.∴a的取值范围是[2，＋∞).例4　(1)(2022·邯郸模拟)已知函数f (x )＝x ln x ，g (x )＝x 2＋ax (a ∈R )，直线l 与f (x )的图象相切于点A (1,0)，若直线l 与g (x )的图象也相切，则a 等于A.0B.－1C.3D.－1或3√题型三两曲线的公切线由f(x)＝x ln x求导得f′(x)＝1＋ln x，则f′(1)＝1＋ln 1＝1，于是得函数f(x)在点A(1,0)处的切线l的方程为y ＝x－1，因为直线l与g(x)的图象也相切，即关于x的一元二次方程x2＋(a－1)x＋1＝0有两个相等的实数根，因此Δ＝(a－1)2－4＝0，解得a＝－1或a＝3，所以a＝－1或a＝3.(2)(2022·韶关模拟)若曲线C1：y＝ax2(a>0)与曲线C2：y＝e x存在公共切线，则a的取值范围为__________.由y ＝ax 2(a >0)，得y ′＝2ax ，由y ＝e x ，得y ′＝e x ，曲线C 1：y ＝ax 2(a >0)与曲线C 2：y ＝e x 存在公共切线，与曲线C 2切于点(x 2，　)，2e x 222121e e ,x x ax x x -=-则2ax 1＝可得2x 2＝x 1＋2，1121e 2x x +∴a ＝ ，12e 2x x+记f (x )＝ ，122e (2)4x x x +-则f ′(x )＝ ，当x ∈(0,2)时，f ′(x )<0，f (x )单调递减；当x ∈(2，＋∞)时，f ′(x )>0，f (x )单调递增.延伸探究　在本例(2)中，把“存在公共切线”改为“存在两条公共切线”，则a的取值范围为___________.由本例(2)知，∵两曲线C 1与C 2存在两条公共切线，∴a ＝ 有两个不同的解.1121e 2x x +12e 2x x +∵函数f (x )＝ 在(0,2)上单调递减，又x →0时，f (x )→＋∞，x →＋∞时，f (x )→＋∞，1.若f (x )＝ln x 与g (x )＝x 2＋ax 两个函数的图象有一条与直线y ＝x 平行的公共切线，则a 等于A.1B.2C.3D.3或－1教师备选√解得x＝1，故切点为(1,0)，可求出切线方程为y＝x－1，此切线和g(x)＝x2＋ax也相切，故x2＋ax＝x－1，化简得到x2＋(a－1)x＋1＝0，只需要满足Δ＝(a－1)2－4＝0，解得a＝－1或a＝3.。