冶金传输原理 吴铿编习题参考答案 (1)
- 格式:doc
- 大小:749.50 KB
- 文档页数:18

理想流体的有旋及无旋流动1.流体微团____ 。
(A) 具有规则的几何形状(B) 质量大小不受限制(C) 线尺度是小量2.流体微团的变形速度包括____ 。
(A) 线变形速度(B) 角变形速度(C) 旋转角速度(D) 前三者之和3.旋转角速度是____ 。
(A) 标量(B) 矢量(C) 既不是标量也不是矢量4.流体微团的旋转角速度____ 。
(A)于刚体转动的情况相同(B) 随时随地都可以改变(C) 收到变形速度的影响5.涡量和旋转角速度的关系是____ 。
(A) 相等(B) 涡量等于旋转角速度的两倍(C) 没有一定关系6.流体作有旋运动的特征是____ 。
(A)流体质点的运动轨迹是曲线(B) 速度的旋度非零(C) 涡量的三个分量都不等于零7.速度势只存在于____ 。
(A)不可压缩流体的流动中(B) 可压缩流体的定常流动(C) 无旋流动中(D) 二维流动中8.速度势函数____ 。
(A)梯度为速度(B) 满足拉普拉斯方程(B)在不可压缩流动中满足拉普拉斯方程(D) 在定常流动中满足拉普拉斯方程9.流函数存在于____ 。
(A)不可压缩流体的流动中(B) 可压缩流体的平面流动中(C) 不可压缩流体的轴对称流动中(D) 任意二维流动中10.平面流动的流函数____ 。
(A)在无旋条件下满足拉普拉斯方程(B)在流场中两点的差值与过两点间的曲线的流量相等(C)在流场中两点的差值与过两点间的曲线的环量相等11.不可压缩流体的平面无旋流动____ 。
(A)同时存在速度势函数和流函数(B) 等势线与流线正交(C) 不一定存在速度势函数和流函数(D) 速度势函数和流函数均为调和函数12.两个不可压缩的平面无旋流动的速度场叠加,则其____ 。
(A)速度势函数也叠加(B) 流函数也叠加(C) 速度势函数大喝流函数不满足叠加关系13.偶极子可以看成是____叠加的极限过程的产物。
(A)点源与点涡(B) 点汇与点涡(C) 等强度点源与点汇(D) 不等强度点源与点汇14.均匀流绕圆柱体无环量流动是由____和____叠加而成的。

冶金传输原理考试题一、选择题(每题2分,共30分)请在每道题的括号内选择出正确答案,并将其序号填写在答题卡上。
1. 冶金传输原理主要研究的是()。
A. 金属的冶炼过程B. 金属的物理性质C. 金属的化学性质D. 金属的机械性质2. 冶金传输原理课程的教学目标是培养学生掌握()。
A. 冶金工艺设计的基本原理B. 金属材料的性能分析方法C. 输送过程中温度、压力、流动速度等参数的计算能力D. 冶金设备的选择与配置能力3. 冶金传输原理的基本假设之一是()。
A. 金属在输送过程中不会发生相变B. 输送过程中不考虑能量损失C. 流体处于非稳定状态D. 输送过程中不考虑阻力4. 输送系统中由于管道摩擦而产生的能量损失称为()。
A. 动能损失B. 摩擦损失C. 管道耗散D. 流体摩擦阻力5. 管道输送中的瞬时损失主要是指()。
A. 弯头和管径突变带来的局部阻力B. 管道与周围环境的传热损失C. 由于管道内液体流动产生的压力波动造成的损失D. 输送过程中发生的事故导致的能量损失二、判断题(每题2分,共20分)请在每道题的括号内选择出正确答案,并将其序号填写在答题卡上。
1. 对于非牛顿流体,其粘滞系数与应变速率呈正相关。
()A. 正确B. 错误2. 液体在沿管道流动时,由于摩擦阻力将产生管道壁面附近的速度剖面,即流速剖面会变平整。
()A. 正确B. 错误3. 定常流体运动的主要特点是流量、速度和流态都随时间的变化而变化。
()A. 正确B. 错误4. 弯头对流体流动的阻力主要是由于流体在弯头处的对流和扰动效应引起的。
()A. 正确B. 错误5. 管道摩阻系数是和管道长度成正比的。
()A. 正确B. 错误三、简答题(每题10分,共30分)请简要回答下列问题,并将答案写在答题卡上。
1. 请简述流体的黏度和流变特性对管道输送过程的影响。
答案:黏度是流体流动的基本性质之一,对管道输送过程中的摩擦阻力、能量损失和泵功耗等起到重要影响。

冶金传输原理习题答案冶金传输原理习题答案冶金传输原理是冶金学中的一个重要分支,研究金属和合金在加热、冷却和变形过程中的传输规律和机制。
在学习和研究冶金传输原理时,习题是不可或缺的一部分,通过解答习题可以加深对该学科的理解和掌握。
下面将给出一些常见的冶金传输原理习题及其答案。
1. 请简述热传导的基本原理。
热传导是指物质内部由于温度差异而传递热量的过程。
其基本原理是热量从高温区传递到低温区,传递过程中热量通过物质内部的分子或电子的碰撞和传递完成。
热传导的速率与温度差、物质的导热性质和传热距离有关。
2. 什么是对流传热?请举例说明。
对流传热是指通过流体(气体或液体)的传热方式。
当物体表面与流体接触时,流体会受热膨胀,形成对流循环,将热量从高温区传递到低温区。
例如,热水器中的水受热后上升,冷水下降,形成对流循环,使整个水体均匀受热。
3. 请解释辐射传热的特点。
辐射传热是指通过电磁波的传热方式。
辐射传热不需要介质,可以在真空中传递热量。
辐射传热的特点是传热速率与温度差的四次方成正比,与物体表面特性和距离的平方成反比。
例如,太阳辐射的热量可以通过真空传递到地球上。
4. 请简述固体变形的原理。
固体变形是指固体在外力作用下发生形状和尺寸的改变。
固体变形的原理是固体内部的晶格结构发生变化,从而使整个固体发生形变。
固体变形可以分为弹性变形和塑性变形两种。
弹性变形是指在外力作用下,固体发生形变后能够恢复原状;塑性变形是指在外力作用下,固体发生形变后不能恢复原状。
5. 请解释扩散的基本原理。
扩散是指物质在非均匀温度和浓度条件下的自发性传递过程。
扩散的基本原理是物质分子或原子的热运动引起的碰撞和交换。
扩散的速率与温度、浓度差、物质的扩散系数和距离有关。
扩散在冶金过程中起着重要的作用,如金属中的杂质扩散、合金的相变等都与扩散有关。
通过以上习题的解答,我们可以更加深入地理解和掌握冶金传输原理。
在实际应用中,冶金传输原理的理论和方法可以帮助我们解决金属加工和冶炼过程中的问题,提高生产效率和产品质量。


冶金传输原理课后习题答案【篇一:冶金传输原理课后答案(朱光俊版,第一章)】/m3 10001?273prtprtprt1-16 , r=(1) (2)1-21 dvxdy65010.5?0.0012dvx dy=vd1-23,,o=vx=hdy0.181.3?0.001=0.1385?1000 1/sdvx dy=1.011?1030.1385?107.2 pa.s【篇二:《冶金传输原理》吴铿编质量传输习题参考答案】s=txt>1. 解:(1)?ch4?ych4mch4ych4mch4?yc2h6mc2h6?yc3h8mc3h8?yco2mco2?90.27%(2)?ych4mch4?yc2h6mc2h6?yc3h8mc3h8?yco2mco2?16.82 (3)pch4?ych4p?9.62?104pa2. 解:dab?1/3b1/3pva?v?1.56?10?5m2/s3. 解:ch4的扩散体积24.42,h2的扩散体积7.07dab?1/3b1/3pva?v?3.19?10-5m2/s4. 解:(1)v??co2vco2??o2vo2??h2ovh2o??n2vn2?3.91m/s (2)vm?yco2vco2?yo2vo2?yh2ovh2o?yn2vn2?4.07m/s (3)jco2??co2?co2?????mco2pco2rtpco2rt??co2????0.212kg/?m2?s? ?(4)jco2?cco2?co2??m?????co2??m??5.33mol/?m2?s? ?5. 解:(1)21% (2)21%pvm?15.46kg (3)m?nm?rtm(4)?o2??0.117kg/m3vm(5)?n2??0.378kg/m3vm(6)?空气??0.515kg/m3v(7)c空气??空气m?17.4mol/m3(8)29.6g/mol(9)pn2?yn2p?7.9?104pa6. 证明:?a?manamaxama??mnama?nbmbxama?xbmb得证。
![冶金传输原理1-8[1].2.](https://uimg.taocdn.com/8dea92db900ef12d2af90242a8956bec0975a5df.webp)
冶金传输原理1-8[1].2.冶金传输原理(Principles of Transfer in Metallurgy)绪论1、冶金的分类:钢铁冶金、有色冶金共同特点(1)发生物态变化固?液态(2)物理化学变化原料与产品的性质、化学成分截然不同钢铁冶金:原料是矿石产品是钢铁钢铁工艺流程:(1)长流程:高炉、转炉、轧机(2)短流程:直接还原或熔融还原、电炉、轧机(1)高炉炼铁:烧结矿或球团矿(铁矿石造块)、焦炭(煤炼焦)、熔剂铁水(2)非高炉炼铁:天然块矿、粉矿或造块、块煤或气体还原剂、熔剂海绵铁(3)转炉炼钢:铁水、废钢、铁合金、氧气、造渣剂钢水(4)电炉炼钢:废钢(海绵铁)、铁水、铁合金、造渣剂钢水2.有色冶金:原料是矿石产品是有色金属(1)重金属:铜(造锍熔炼)、铅(还原熔炼)、锌(湿法冶炼)、锡(火法精炼)(2)轻金属:铝冶金、镁冶金(3)稀贵金属:锂冶炼、铍冶炼、钙锶钡制取、金银提炼3、课程概况一、课程性质专业基础课,是基础课和专业课之间的桥梁。
二、课程内容传输原理(动量、热量、质量传输)简称“三传”传输是指流体的(输送、转移、传递)动力过程、传热过程、物质传递过程的统称热量、动量、质量的传递与输送,热量传输、质量传输、动量传输(类似统一性)传输原理类似性:基本概念、运动规律、解析方法类似。
冶炼过程:高温、多相条件下进行的复杂物理化学过程。
传输过程:?冶炼过程中的物理过程,不涉及化学反应。
动量、热量、质量传递的过程。
(TransportPhenomena)举例:高炉炼铁的气固两相流动。
高炉强化冶炼,目的就是改善传输条件。
转炉炼钢的气液两相流动。
转炉底吹,目的也是改善传输条件。
冶金传输原理已成为现代冶金过程理论的基础!研究对象:动量、热量、质量传输(传递)过程的速率。
研究方法:理论研究(简单问题)、实验研究、数值计算(复杂问题)习题与思考题:如何加深对所学传输理论的理解和应用。
三、课程特点物理概念抽象,数学推导繁琐,计算公式多,计算过程复杂。

精编【冶⾦⾏业】材料加⼯冶⾦传输原理习题答案修改过版【冶⾦⾏业】材料加⼯冶⾦传输原理习题答案修改过版xxxx年xx⽉xx⽇xxxxxxxx集团企业有限公司Please enter your company's name and contentv第⼀章流体的主要物理性质(吉泽升版)1-1何谓流体,流体具有哪些物理性质?答:流体是指没有固定的形状、易于流动的物质。
它包括液体和⽓体。
流体的主要物理性质有:密度、重度、⽐体积压缩性和膨胀性。
1-2某种液体的密度ρ=900 Kg/m3,试求教重度y和质量体积v。
解:由液体密度、重度和质量体积的关系知:∴质量体积为1.4某种可压缩液体在圆柱形容器中,当压强为2MN/m2时体积为995cm3,当压强为1MN/m2时体积为1000 cm3,问它的等温压缩率k T为多少?解:等温压缩率K T公式(2-1):ΔV=995-1000=-5*10-6m3注意:ΔP=2-1=1MN/m2=1*106Pa将V=1000cm3代⼊即可得到K T=5*10-9Pa-1。
注意:式中V是指液体变化前的体积1.6 如图1.5所⽰,在相距h=0.06m的两个固定平⾏乎板中间放置另⼀块薄板,在薄板的上下分别放有不同粘度的油,并且⼀种油的粘度是另⼀种油的粘度的2倍。
当薄板以匀速v=0.3m/s被拖动时,每平⽅⽶受合⼒F=29N,求两种油的粘度各是多少?解:流体匀速稳定流动时流体对板⾯产⽣的粘性阻⼒⼒为平板受到上下油⾯的阻⼒之和与施加的⼒平衡,即代⼊数据得η=0.967Pa.s第⼆章流体静⼒学(吉泽升版)2-1作⽤在流体上的⼒有哪两类,各有什么特点?解:作⽤在流体上的⼒分为质量⼒和表⾯⼒两种。
质量⼒是作⽤在流体内部任何质点上的⼒,⼤⼩与质量成正⽐,由加速度产⽣,与质点外的流体⽆关。
⽽表⾯⼒是指作⽤在流体表⾯上的⼒,⼤⼩与⾯积成正⽐,由与流体接触的相邻流体或固体的作⽤⽽产⽣。
2-2什么是流体的静压强,静⽌流体中压强的分布规律如何?解:流体静压强指单位⾯积上流体的静压⼒。
第一章 流體的主要物理性質1-1何謂流體,流體具有哪些物理性質?答:流體是指沒有固定的形狀、易於流動的物質。
它包括液體和氣體。
流體的主要物理性質有:密度、重度、比體積壓縮性和膨脹性。
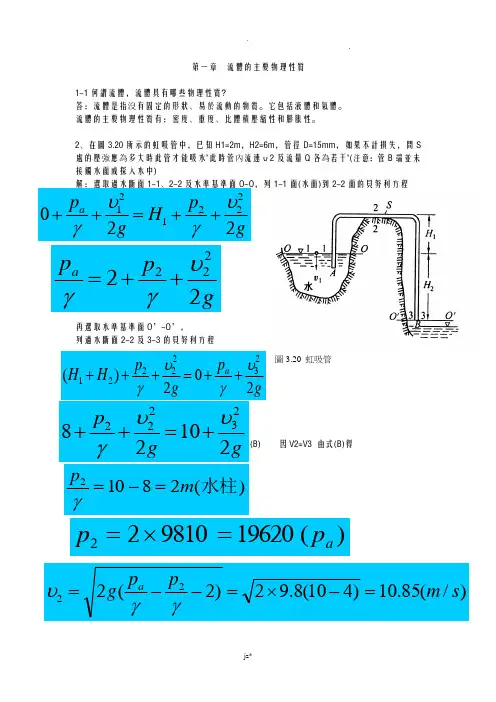
2、在圖3.20所示的虹吸管中,已知H1=2m ,H2=6m ,管徑D=15mm ,如果不計損失,問S 處的壓強應為多大時此管才能吸水"此時管內流速υ2及流量Q 各為若干"(注意:管B 端並未接觸水面或探入水中)解:選取過水斷面1-1、2-2及水準基準面O-O ,列1-1面(水面)到2-2面的貝努利方程再選取水準基準面O ’-O ’,列過水斷面2-2及3-3的貝努利方程(B) 因V2=V3 由式(B)得圖3.20 虹吸管 gpH gpa 220222121υγυγ++=++gppa 22222υγγ++=gp g p H H a 202)(2322221υγυγ++=+++ggp2102823222υυγ+=++)(28102水柱m p=-=γ)(19620981022a p p =⨯=)/(85.10)410(8.92)2(222s m ppg a =-⨯=--=γγυ)/(9.1)/(0019.085.104)015.0(3222s L s m A Q ==⨯⨯==πυ5、有一文特利管(如下圖),已知d 1 =15cm ,d 2=10cm ,水銀差壓計液面高差∆h =20cm 。
若不計阻力損失,求常溫(20℃)下,通過文氏管的水的流量。
解:在喉部入口前的直管截面1和喉部截面2處測量靜壓力差p 1和p 2,則由式const v p =+22ρ可建立有關此截面的伯努利方程: ρρ22212122p v p v +=+根據連續性方程,截面1和2上的截面積A 1和A 2與流體流速v 1和v 2的關係式為2211v A v A =所以 ])(1[)(2212212A A p p v --=ρ 通過管子的流體流量為 ])(1[)(2212212A A p p A Q --=ρ )(21p p -用U 形管中液柱表示,所以074.0))15.01.0(1(10)1011055.13(2.081.92)1.0(4])(1[)(22223332212'2=-⨯⨯-⨯⨯⨯⨯=--∆=πρρρA A h g A Q (m 3/s)式中 ρ、'ρ——被測流體和U 形管中流體的密度。

(题目改成单位质量力的国际单位) (不能承受拉力) (d 为表现形式)13. 解:由体积压缩系数的定义,可得:()()69669951000101d 15101/Pa d 1000102110p V V p β----⨯=-=-⨯=⨯⨯-⨯ 14. 解:由牛顿内摩擦定律可知, d d x v F A y μ= 式中A dl π= 由此得d 8.57d xv vF A dl N y μμπδ==≈5. 解:112a a p p gh gh gh p ρρρ=++=+汞油水12220.4Fgh gh d h m g ρρπρ++⎛⎫ ⎪⎝⎭==油水(测压计中汞柱上方为标准大气压,若为真空结果为1.16m )6.解:(测压管中上方都为标准大气压)(1)()()13121a a p p g h h g h h p ρρ=+-=-+油水ρ=833kg/m 3(2)()()13121a a p p g h h g h h p ρρ=+-=-+油水h 3=1.8m.220.1256m 2D S π== 31=Sh 0.12560.50.0628V m =⨯=水()331=S 0.1256 1.30.16328V h h m -=⨯=油7.解:设水的液面下降速度为为v ,dz v dt=- 单位时间内由液面下降引起的质量减少量为:24d v πρ 则有等式:224d v v πρ=,代入各式得:20.50.2744dz d z dt πρ-=整理得: 120.5200.2740.2744t d zdz dt t πρ--==⎰⎰解得:(212115180.2744d t s πρ⎛⎫=-= ⎪⎝⎭8. 解:10p p gh ρ=+a20s p p gh ρ=+()12a 248.7Pa s p p p gh ρρ∆=-=-=第三章习题参考答案(仅限参考)5.答:拉格朗日法即流体质点法必须首先找出函数关系x(a,b,c,t),y(a,b,c,t),z(a,b,c,t),ρ(a,b,c,t)等。

冶⾦传输原理课后答案1、什么是连续介质,在流体⼒学中为什么要建⽴连续介质这⼀理论模型?答:(1)连续介质是指质点毫⽆空隙的聚集在⼀起,完全充满所占空间的介质。
(2)引⼊连续介质模型的必要性:把流体视为连续介质后,流体运动中的物理量均可以看为空间和时间的连续函数,就可以利⽤数学中的连续函数分析⽅法来研究流体运动,实践表明采⽤流体的连续介质模型,解决⼀般⼯程中的流体⼒学问题是可以满⾜要求的。
1-9 ⼀只某液体的密度为800kg/,求它的重度及⽐重。
解: 重度:γ=ρg=800*9.8=7840kg/(˙)⽐重:ρ/=800/1000=0.8注:⽐重即相对密度。
液体的相对密度指该液体的密度与⼀个⼤⽓压下4℃⽔的密度(1000kg/)之⽐---------------------------------------------课本p4。
1-11 设烟⽓在标准状态下的密度为1.3kg/m3,试计算当压⼒不变温度分别为1000℃和1200℃时的密度和重度解:已知:t=0℃时,0=1.3kg/m3,且=则根据公式当t=1000℃时,烟⽓的密度为kg/m3=0.28kg/m3烟⽓的重度为kg/m3=2.274kg/m3当t=1200℃时,烟⽓的密度为kg/m3=0.24kg/m3烟⽓的重度为kg/m3=2.36kg/m31—6答:绝对压强:以绝对真空为起点计算的压⼒,是流体的实际,真实压⼒,不随⼤⽓压的变化⽽变化。
表压⼒:当被测流体的绝对压⼒⼤于外界⼤⽓压⼒时,⽤压⼒表进⾏测量。
压⼒表上的读数(指⽰值)反映被测流体的绝对压⼒⽐⼤⽓压⼒⾼出的数值,称为表压⼒。
既:表压⼒=绝对压⼒-⼤⽓压⼒真空度:当被测流体的绝对压⼒⼩于外界⼤⽓压⼒时,采⽤真空表测量。
真空表上的读数反映被测流体的绝对压⼒低于⼤⽓压⼒的差值,称为真空度。
既:真空度=︱绝对压⼒-⼤⽓压⼒︱=⼤⽓压⼒-绝对压⼒1-81 物理⼤⽓压(atm)= 760 mmHg = 10332 mm H2O1 物理⼤⽓压(atm) = 1.033 kgf/cm2 = 101325 Pa1mmH20 = 9.81 Pa1-21 已知某⽓体管道内的绝对压⼒为117kPa,若表压为70kPa,那么该处的绝对压⼒是多少(已经当地⼤⽓压为98kPa),若绝对压⼒为68.5kPa 时其真空度⼜为多少?解:P 绝=P 表+P ⼤⽓=70kPa+98kPa=168kPaP 真=-(P 绝-P ⼤⽓)=-(68.5kPa-98kPa)=29.5kPa1、⽓体在什么条件下可作为不可压缩流体?答:对于⽓体,在压⼒变化不太⼤(压⼒变化⼩于10千帕)或流速不太⾼(V<70⽶/秒)条件下(如流速较低的通风道),⽓体压缩程度很⼩,可忽略⽓体密度变化⽽作为不可压缩流体来处理。

第一章 动量传输基本概念作业1.什么是粘性?流体的粘性与流体的宏观运动是否有关?2.请判断拉格朗日法适合于描述下述哪一类流动:A.研究一污染物粒子在水中运动的轨道;B.研究无数质点组成的质点群的运动;C.研究一流动空间的速度分布。
3.什么是连续性介质,在流体力学中为何要建立连续介质模型?4.粘性系数如何随温度变化?5.请写出压强梯度、速度散度、速度旋度的直角坐标系下的表达式,并叙述其物理意义。
6.某人坐在匀速运动的飞机上测量和记录周围各点空气的速度和压强,请问它采用的研究方法是:A.拉格朗日法;B.欧拉法;C.两者均不是。
7.请判断下列说法是否正确:过流场中的一点可以有多条迹线。
A.根本不可能;B.在定常流中是正确的;C.在不定常流中是正确的。
8.比较拉格朗日法与欧拉法的区别。
9.比较流线与迹线。
10.设速度场为上式中k 为常数。
试求流线方程,并画出流线图。
11.设非稳态速度场为t = 0时刻流体质点A 位于原点。
试求(1)质点A 的迹线方程;(2)t = 0时刻过原点的流线方程;(3)t = 1时刻质点A 的运动方向。
12.已知:速度场:求:①加速度场;②原点和(1,1,1)点的加速度。
13.两平行平板之间充满粘度为μ0的液体,在对称面上有一面积为A 的薄板,薄板以等速度v 作平移运动,如图a 所示。
现以另一种液体充满上述平板之间,但其粘度μ未知,若其中薄板置于底板以上h ′处,也以等速v 作平移运动,如图b 所示,且已知拖动力与两种情况相同,试由μ0、h ′确定μ。
⎪⎩⎪⎨⎧==+=xz w tyv tx u ⎩⎨⎧=+=11v t u ⎩⎨⎧-==ky v kxu。
第六章 可压缩气体的流动例6-1 空气缸中的绝对压强40,/700020==t m kN p ℃,通过一喉部直径mm d 25=的拉瓦喷管向大气中喷射,大气压强22/1.98m kN P =,求: (1) 质量流量G ;(2) 喷管出口断面直径d 2; (3) 喷管出口的马赫数M 2。
解:由于02528.0P P <,喷管喉部可达到音速,由已知喉部条件,决定质量流量。
(1)33000/793.731328710700m kg RT p =⨯⨯==ρ由公式(6-19)()0012112ρKp K A G K K C -+⎪⎭⎫ ⎝⎛+=792.7107004.14.22105.243342⨯⨯⨯⎪⎭⎫⎝⎛⨯⨯=-πs kg /785.0=(2)由公式(6-19)计算喷管出口断面直径:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫⎝⎛-=-KK Kp P p P p K Kd G 10220200221124ρπ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=-KK K p P p P p K KGd 10220200221124ρπ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫⎝⎛-⎪⎭⎫⎝⎛⨯⨯⨯⨯⨯=286.043.137001.9817001.98792.7107007785.04π3100037.1-⨯=mm m d 7.310317.02==(3)37143.010202/914.17001.98792.7m kg p P K=⎪⎭⎫⎝⎛⨯=⎪⎪⎭⎫⎝⎛=ρρs m p K a /268914.1101.984.13222=⨯⨯==ρs m A G V /5201017.3914.1785.0442222=⨯⨯⨯⨯==-πρ 914.1268520222===a V M 例6-2 空气(K=1.4,R=287J/kg ·k )在400K 条件下以声速流动,试确定:(1)气流速度;(2)对应的滞止音速;(3)对应的最大可能速度;(4)滞止焓;(5)克罗克数max V V C r =。
第十六章习题参考答案(仅限参考)1. 解:(1)44444262638382290.27%CH CH CH CH CH C H C H C H C H CO CO y M y M y M y M y M ω==+++(2)44262638382216.82CH CH C H C H C H C H CO CO M y M y M y M y M =+++= (3)4449.6210CH CH p y p Pa ==⨯2. 解:52AB 1/31/3A B1.5610/D m s p V V -==⨯+3. 解:CH 4的扩散体积24.42,H2的扩散体积7.072AB 1/31/3A B 3.1910/D m s p V V ==⨯+-54. 解:(1)22222222 3.91/CO CO O O H O H O N N v v v v v m s ωωωω=+++= (2)22222222 4.07/m CO CO O O H O H O N N v y v y v y v y v m s =+++= (3)()()()22222220.212/CO CO CO CO CO CO M p kg m s RT ρ=-=-=-⋅j υυυυ (4)()()()2222225.33/CO CO CO CO m CO m p c mol m s RT=-=-=-⋅J υυυυ5. 解:(1)21% (2)21%(3)15.46pVm nM M kg RT === (4)230.117/O mkg m V ρ==(5)230.378/N mkg m V ρ==(6)30.515/mkg m Vρ==空气(7)317.4/c mol m Mρ==空气空气(8)29.6g/mol(9)2247.910N N p y p Pa ==⨯6. 证明:A A A A AA A AB B A A B Bm n M x M m n M n M x M x M ω===++ 得证。
冶金传输原理试题11.牛顿黏性定律的物理意义说明流体所产生的黏性力的大小与流体的()和()成正比,并与流体的黏性有关。
2.()以流场中某一空间点作研究对象,分析该点以及该点与其他点之间物理量随()的变化过程来研究流体运动情况的。
3.按照流体流速、压力、密度等有关参数是否随时间而变化,可以将流体分为()和()。
4.流体密度的倒数称为流体的();气体重度γ与密度ρ的关系为()。
5.流体包括液体和气体,流体具有流动性、()和()。
6.超出大气压力的那部分压力称之为相对压力,一般测压仪表都是测定相对压力的,则又称为(),当相对压力为负值时称为负压,其差值的绝对值称为(),而()是以绝对真空作零压而计算的。
7.实际流体的动量平衡微分方程,又称纳维尔-斯托克斯方程,是()定律,即动量守恒定律在流体流动现象中的应用,当=0时,可简化为理想流体的动量平衡方程,亦称()方程;理想流体微小流束单位质量流体的伯努利方程可写成()=常数;质量守恒定律在流体力学中的具体表现形式为()方程。
8.水平圆管层流条件下,截面平均流速为管中心流速的()。
9.()以流场中某一空间点作研究对象,分析该点以及该点与其他点之间物理量随()的变化过程来研究流体运动情况的。
10.雷诺准数的定义式或表达式Re=()或(),其物理意义反映了流体流动过程中()的相对大小。
11.流态化现象中,随流体流速由小到大的变化,床层出现三个不同阶段,即()阶段、()阶段和()阶段。
12.流体流动时,由于外部条件不同,其流动阻力与能量损失可分为局部阻力损失和沿程阻力损失两种形式,沿程阻力损失也称作()损失。
13.压缩性气体流动能量转换关系具有显著特点,当流速增大,流体()减少时,会引起温度相应地降低。
14.作用在流体上的力可分为两大类:()、质量力或体积力。
15.准数是指几个有内在联系的物理量按无量纲条件组合起来的数群,它既反映所含物理量之间的内在联系,又能说明某一现象或过程的()。
(题目改成单位质量力的国际单位) (不能承受拉力) (d 为表现形式)13. 解:由体积压缩系数的定义,可得:()()69669951000101d 15101/Pa d 1000102110p V V p β----⨯=-=-⨯=⨯⨯-⨯ 14. 解:由牛顿内摩擦定律可知, d d x v F A y μ= 式中A dl π= 由此得d 8.57d xv vF A dl N y μμπδ==≈5. 解:112a a p p gh gh gh p ρρρ=++=+汞油水12220.4Fgh gh d h m g ρρπρ++⎛⎫ ⎪⎝⎭==油水(测压计中汞柱上方为标准大气压,若为真空结果为1.16m )6.解:(测压管中上方都为标准大气压)(1)()()13121a a p p g h h g h h p ρρ=+-=-+油水ρ=833kg/m 3(2)()()13121a a p p g h h g h h p ρρ=+-=-+油水h 3=1.8m.220.1256m 2D S π== 31=Sh 0.12560.50.0628V m =⨯=水()331=S 0.1256 1.30.16328V h h m -=⨯=油7.解:设水的液面下降速度为为v ,dz v dt=- 单位时间内由液面下降引起的质量减少量为:24d v πρ 则有等式:224d v v πρ=,代入各式得:20.50.2744dz d z dt πρ-=整理得: 120.5200.2740.2744t d zdz dt t πρ--==⎰⎰解得:(212115180.2744d t s πρ⎛⎫=-= ⎪⎝⎭8. 解:10p p gh ρ=+a20s p p gh ρ=+()12a 248.7Pa s p p p gh ρρ∆=-=-=第三章习题参考答案(仅限参考)5.答:拉格朗日法即流体质点法必须首先找出函数关系x(a,b,c,t),y(a,b,c,t),z(a,b,c,t),ρ(a,b,c,t)等。
实际上就是要跟踪每一个流体质点,可见这个方法在方程的建立和数学处理上将是十分困难的。
因而除研究波浪运动等个别情况外很少采用。
实际上,在大多数的工程实际问题中,通常并不需要知道每个流体质点至始至终的运动过程,而只需要知道流体质点在通过空间任意固定点时运动要素随时间变化状况,以及某一时刻流场中各空间固定点上流体质点的运动要素,然后就可以用数学方法对整个流场进行求解计算。
6.答:流体在运动过程中,若每一空间点的物理量(运动参数)不随时间改变,则称为恒定流动(又称定常流动),否则称为非恒定流动(又称非定常流动) 流体质点的运动轨迹称为迹线。
流线是速度场的矢量线,是某瞬时在流场中所作的一条空间曲线。
7.解:(1) 356120010=2102300110m e v d R v --⨯⨯==⨯>⨯,湍流 (2) 350.215010=107.123002810m e v d R v --⨯⨯==<⨯,层流8.答:v=Q/A ,断面平均流速是一种假想的流速,即过断面上每一点的平均流速都相同。
断面平均流速的概念十分重要,它将使我们的研究和计算大为简化。
9.答:不正确。
均匀流是相对于空间分布而言,恒定流是相对于时间而言。
均匀流的不同时刻的速度可以不同,也可以相同。
恒定流的不同空间点上的速度可以不同,也可以相同。
当流量不变时,通过一变直径管道,显然是恒定流,但不是均匀流。
10. 解:根据欧拉法中速度的定义:()()(),,,,,,,y,z,x y z x V x y z t t y V x y z t t z V x t t ∂⎧=⎪∂⎪∂⎪=⎨∂⎪∂⎪=⎪∂⎩ 得: 112dx k y dt dy k x dt dz k dt ⎧-=⎪⎪⎪=⎨⎪⎪=⎪⎩右边第一个式子,两边对t 求导,联合第二个式子可得:22120d x k x dt+=,解这个常微分方程得: 1121cos()sin()x c k t c k t =+将x 带入原方程得:1121sin()cos()y c k t c k t =-,23z k t c =+再根据初始条件,得:123c a c b c c ==-=,,于是得到拉格朗日法表示为:11cos()sin()x a k t b k t =-11sin()cos()y a k t b k t =+2z k t c =+11. 解:根据随体导数定义:x x x x x x y z y y y y y x y z z z z z z x y z v v v v a v v v t x y z v v v v a v v v t x y z v v v v a v v v t x y z ∂∂∂∂⎧=+++⎪∂∂∂∂⎪∂∂∂∂⎪=+++⎨∂∂∂∂⎪⎪∂∂∂∂=+++⎪∂∂∂∂⎩将速度代入随体导数中,得:()()()22322023023x a x y xy y x x y x y =++-+=-()()033009y a y y =+--++=3300088z a z z =+++=代入点(1,2,3)得:218216x y z a a a ⎧=⎪=⎨⎪=⎩第四章习题参考答案(仅限参考)1. 错、错、错4.解:根据平面不可压缩流体连续性的性质:(1)0x z V V x z∂∂+=∂∂;连续 (2)101x z V V x z∂∂+=+=∂∂;不连续 (3)21x z V V x x z∂∂+=+∂∂;当x=时连续,其他情况不连续5. 解:同题4,(1)cos()cos()x y V Ay xy x V Ax xy y∂⎧=⎪∂⎪⎨∂⎪=-⎪∂⎩;当x=y 时,连续;其他情况不连续 (2)x y V A x y V Ayy ∂⎧=-⎪∂⎪⎨∂⎪=⎪∂⎩;连续6. 解:应用伯努利方程:'2+0+0+02p v p g g gρρ+= 解得20.98/v m s == 流量2331 3.14 2.3710/4Q d v m s -=⨯=⨯7. 解:根据流体静力学知识得到以下关系式:122p gh p gh g h ρρρ+=++∆水根据左右两管水的体积相等,有:22244d D h h ⨯=∆⨯得:222d h h D ∆=,代入可解得: 12220.12p p h m d g g g D ρρρ-==-+水8. 解:选取圆柱坐标系,假设流动是沿z 轴方向进行,且为充分发展的层流流动。
根据已知条件可知,流动是轴对称,θ方向可不考虑,仅z 方向有流动。
由连续性方程、稳定流动,忽略质量力,则有:2222222111z z z z z z z z r z z P F t r r z z r r r r z θυυυυυυυυυμυυθρρθ⎛⎫∂∂∂∂∂∂∂∂∂+++=-++++ ⎪∂∂∂∂∂∂∂∂∂⎝⎭0r θυυ==;0z z z υυθ∂∂==∂∂;22220z z z υυθ∂∂==∂∂;0t ∂=∂; 化简得:11()z P r r r r z υμ∂∂∂=∂∂∂;11()z P r r r r zυμ∂∂∂=∂∂∂=常数 进行第一次积分,并将边界条件r=0处,代入,算得积分常数C1;再进行第二次积分,并将r=R 处,υz=0代入,算得出C2。
最后得到:22221()[1()]44z dP R dP r R r dz dz Rυμμ=--=-- 式中r 为管截面上速度为υz 处到管中心的距离,R 为圆管半径。
显然其速度分布呈抛物线形。
下面很容易推导出υz 与υzmax 的关系为:2max [1()]z z r Rυυ=-9.解:列1-2处的伯努力方程:(以2处为0基点),用相对压强计算:2212200022v v gh ++=++ 由于水槽的直径比虹吸管的直径大很多,那么就可以近似设v 1等于0。
代入可得28.86/v m s ==流量2233222 3.14 3.14 6.2610/44d d Q v m s -=⨯=⨯=⨯ 同理列2-3处的伯努利方程(p 2为什么为0):(以2处为0基点)2233212()0022p v v g h h ρ+++=++根据质量守恒:3处和2处的速度满足:22322144v v d d =,得23 2.215/4v v m s == 代入得:2221312()22024.32v v p h h g Pa g ρ⎡⎤⎛⎫-=-+=-⎢⎥ ⎪⎝⎭⎣⎦负号表示C 处的压强低于一个大气压,处于真空状态。
正是由于这一真空,才可将水箱中的水吸起。
用绝对压强表示:.3= Pa.第五章习题参考答案(仅限参考)6.解: 22m v L p d ρλ∆=假设雷诺数小于2300,有6464Re m λv d ν==,代入上式得:2226464222m m m m v v L v L L p d v d d dρρνρνλ∆=== 则2264220.150.96510 1.84/64644109201000m d p v m s L νρ-∆⨯⨯⨯===⨯⨯⨯⨯ 41.840.15Re 6902300410m v dν-⨯===<⨯,符合假设 ()2233.140.15 1.840.03m s 44m m d Q Av v π⨯⨯==== 另一种简单计算方法:假设雷诺数小于2300,有 226240.150.96510 1.84/832324109201000m p d p v R m s L L μνρ-∆∆⨯⨯====⨯⨯⨯⨯ 41.840.15Re 6902300410m v dν-⨯===<⨯,符合假设 ()2233.140.15 1.840.03m s 44m m d Q Av v π⨯⨯====7.解: ()22440.030.425m 3.140.3m Q v d π⨯===⨯ 40.4250.3Re 106323001.210m v d ν-⨯===<⨯ 640.06Reλ==22300.4250.060.0620.329.81m f v L h m d g λ∆==⨯⨯=⨯8.解: ()22440.05 1.02m s 3.140.25m Q v d π⨯===⨯ 5561.020.25Re 2.510101.00710m v dν-⨯===⨯>⨯ 0.00130.00520.25d ε==;查莫迪图得0.031λ= 22100 1.020.0310.6620.2529.81m f v L h m d g λ∆==⨯⨯=⨯9.解: ()220.32944260 1.4m s 3.140.05m Q v d π⨯⨯===⨯ 22m v p L h g d gζλρ∆⎛⎫∆==+ ⎪⎝⎭ 22226168.6100.03 6.2960.291000 1.40.05m p L v d ζλρ∆⨯=-=-⨯=-=⨯ 10.解:22700 1.132.930.02 6.6420.1529.81m i i v L h m d g ζλ⎛⎫⎛⎫∆=+=⨯+⨯⨯= ⎪ ⎪⨯⎝⎭⎝⎭∑11.解:550.250.305 1.23Re 5269101.7810m m v dv d ρνμ-⨯⨯====<⨯ 025031640.037.e .λR ==2233234()11248()32110.3960.3050.037 1.230.25 5.5880.390.0012m d p L v d Pa πελρεπ-∆=-=⨯⨯⨯⨯⨯⨯=12.解:()2212000044606025m 3.14m Q v d d π⨯⨯===⨯ 解得d=1.3m65525 1.3Re 2.0710101.5710m v dν-⨯===⨯>⨯ 0.00050.0003851.3d ε==;查莫迪图得0.0155λ= 22120252.5110.0155921.572 1.329.81m i i v L h m d g ζλ⎛⎫⎛⎫∆=+=⨯+⨯⨯= ⎪ ⎪⨯⎝⎭⎝⎭∑ 1.239.81921.5711120p g h Pa ρ∆=∆=⨯⨯=()551.569 1.013250.1110 2.47110i M a p p p p Pa =+-∆=+-⨯=⨯13.解:()221750044606011.9m s 3.140.72m Q v d π⨯⨯===⨯ 5411.90.72Re 5.46100.15710m v dν-⨯===⨯⨯ (1)0.20.000278720d ε==;查莫迪图得0.0147λ= 2228.611.90.0147 4.2120.7229.81m f v L h m d g λ∆==⨯⨯=⨯ (2)20.00278720d ε==;查莫迪图得0.0265λ= 2228.611.90.03657.6020.7229.81m f v L h m d g λ∆==⨯⨯=⨯第六章习题参考答案(仅限参考)1.解:66173 3.4101510x x Re υν∞-⨯=⨯⨯==x δ=38.1310m δ-===⨯2.解:5630.172101510x x x Re υν∞-=⨯⨯== 0.1x m =3.解:66500.93101510cr cr x x Re υν∞-⨯=⨯⨯== 76503 1.0101510L L Re υν∞-⨯=⨯⨯==30.4110L f C -==⨯ 30.20.074 2.9510T f L C Re -==⨯ ()*7620cr T L f f x A C C Re =-=(若查表,则A *=8700)22*0.20.0749.8622f f LL A F C bl bl N Re Re ρυρυ∞∞⎛⎫==-= ⎪⎝⎭ (查附录1,对应的ρ=1.205kg/m 3)4.解:379.6L L Re ρυμ∞==δ=max 0.128mδ==0.068L fC==22 1.702Lf fF C bl Nρυ∞==第七章习题参考答案(仅限参考)1.解:由于00.50.528p p =<,所以应为超声速流动,但收缩喷管出口喷速最大只能达到声速,即Ma =1。