2019届九年级中考数学复习《动点构成的相似问题》专题精练解析卷
- 格式:pdf
- 大小:225.49 KB
- 文档页数:3

中考数学《相似的综合》专项训练及答案解析一、相似1.如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线于点M.(1)求该抛物线所表示的二次函数的表达式;(2)已知点F(0,),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?(3)点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.【答案】(1)解:由抛物线过点A(-1,0)、B(4,0)可设解析式为y=a(x+1)(x-4),将点C(0,2)代入,得:-4a=2,解得:a=- ,则抛物线解析式为y=- (x+1)(x-4)=- x2+ x+2(2)解:由题意知点D坐标为(0,-2),设直线BD解析式为y=kx+b,将B(4,0)、D(0,-2)代入,得:,解得:,∴直线BD解析式为y= x-2,∵QM⊥x轴,P(m,0),∴Q(m,- m2+ m+2)、M(m, m-2),则QM=- m2+ m+2-( m-2)=- m2+m+4,∵F(0,)、D(0,-2),∴DF= ,∵QM∥DF,∴当- m2+m+4= 时,四边形DMQF是平行四边形,解得:m=-1或m=3,即m=-1或3时,四边形DMQF是平行四边形。
(3)解:如图所示:∵QM∥DF,∴∠ODB=∠QMB,分以下两种情况:①当∠DOB=∠MBQ=90°时,△DOB∽△MBQ,则,∵∠MBQ=90°,∴∠MBP+∠PBQ=90°,∵∠MPB=∠BPQ=90°,∴∠MBP+∠BMP=90°,∴∠BMP=∠PBQ,∴△MBQ∽△BPQ,∴,即,解得:m1=3、m2=4,当m=4时,点P、Q、M均与点B重合,不能构成三角形,舍去,∴m=3,点Q的坐标为(3,2);②当∠BQM=90°时,此时点Q与点A重合,△BOD∽△BQM′,此时m=-1,点Q的坐标为(-1,0);综上,点Q的坐标为(3,2)或(-1,0)时,以点B、Q、M为顶点的三角形与△BOD相似.【解析】【分析】(1)A(-1,0)、B(4,0)是抛物线与x轴的交点,则可由抛物线的两点式,设解析为y=a(x+1)(x-4),代入C(0,2)即可求得a的值;(2)由QM∥DF且四边形DMQF是平行四边形知QM=DF,由D,F的坐标可求得DF的长度;由P(m,0)可得Q(m,-m2+m+2),而M在直线BD上,由B,D的坐标用待定系数法求出直线BD的解析式,并当=m时,表示出点M的坐标,可用m表示出QM的长度。

1. (2019年四川内江市)如图,将△ ABC 沿着过BC 的中点D 的直线折叠,使点 B 落在AC 边上的B i 处,称为第一次操作,折痕DE 到AC 的距离为h 仁还原纸片后,再将△ BDE沿着过BD 的中点D i 的直线折叠,使点 B 落在DE 边上的B 2处, 痕D i E i 到AC 的距离记为h 2;按上述方法不断操作下去……经过第 D n -i E n -i ,到AC 的距离记为h n .若h i = i ,则h n 的值为(h 4、h 5、……h n ,再对h n 进行计算变形即可.【解答】解:••• D 是BC 的中点,折痕 DE 到AC 的距离为 •••点B 到DE 的距离=h i = i ,•••D i 是BD 的中点,折痕 D i E i 到AC 的距离记为h 2, •••点 B 到 D i E i 的距离=h 2= i^h i = i+ ,22同理:h 3= h 2+—h i=i+ 1 + 丄,42 4h 4=h 3+ h i = i+-!-+—+—:: ::-:;.i+l +l +l + + 1 2 1 hn = i+_ —+ +__+••• + ------- = 2 — --------2 4 8211-1 2n_1故选:C .【点评】考查图形变化规律的问题,首先根据变化求出第一个、第二个、第三个……发 现规律得出一般性的结论.2. (20i9 年四川内江市)如图,在△ ABC 中,DE // BC , AD = 9, DB = 3, CE = 2,贝U AC 的 长为()A . 6B . 7C . 8D . 9【分析】利用平行线分线段成比例定理得到二=「,利用比例性质求出AE ,然后计算 AE+EC 即可.【解答】解:• DE // BC ,称为第二次操作,折 n 次操作后得到折痕A . i+— 2n_1B . 1 + 2nC . 2 - 尹1【分析】根据相似三角形的性质,对应高的比对于相似比,得出 D . 2 -2nh 2 = -L ,依次得出h 3、 ::hiAD = AE 即9 = AEDB 丽’3~••• AE= 6,•. AC= AE+ EC= 6+2 = 8.故选:C.【点评】本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.3. (2019年广西玉林市)如图,AB // EF // DC , AD // BC, EF与AC交于点G,则是相似三角形共有()A . 3对B . 5对C. 6对 D . 8对【分析】图中三角形有:△ AEG ,△ ADC , CFG , △ CBA,因为AB // EF // DC , AD // BC,所以△ AEGADC s CFGCBA,有 6 种组合【解答】解:图中三角形有:△ AEG,^ ADC , CFG , △ CBA ,T AB// EF // DC , AD // BC• △AEG s^ ADC s CFGCBA共有 6 个组合分别为:AEGADC , △ AEG s CFG , △ AEGCBA, △ ADC s CFG , △ ADC CBA , CFG CBA故选:C.【点评】本题主要考查相似三角形的判定.4. (2019年内蒙古赤峰市)如图,D、E分别是△ ABC边AB , AC上的点,/ ADE = /ACB , 若AD = 2 , AB= 6 , AC= 4,贝U AE 的长是()A . 1B . 2 C. 3 D. 4【分析】证明△ ADE ACB,根据相似三角形的性质列出比例式,计算即可.【解答】解:•••/ ADE = / ACB ,Z A=Z A,• △ ADEACB ,.AD AE 0n2 AE-- = ,即__= ,AC AB 4 6解得,AE = 3,故选:C.【点评】本题考查的是相似三角形的判定和性质,掌握相似三角形的判定定理和性质定理是解题的关键.5. (2019年海南省)如图,在Rt△ ABC中,/ C= 90°, AB= 5, BC = 4.点P是边AC上一动点,过点P作PQ // AB交BC于点Q, D为线段PQ的中点,当BD平分/ ABC时,PQ // AB ,• / ABD = Z BDQ ,又/ ABD = Z QBD , • / QBD = Z BDQ , -QB = QD , • QP =2QB , PQ / AB ,• △ CPQ s^ CAB ,CP^Q = PQ:=7T =7T 解得,CP ==,13AP = CA - CP = ,13故选:B .【点评】本题考查的是相似三角形的判定和性质,掌握相似三角形的判定定理和性质定 理是解题的关键.6. (2019年黑龙江省哈尔滨市)如图,在?ABCD 中,点E 在对角线AB 于点M , EN // AB ,交AD 于点N ,则下列式子一定正确的是(D【分析】根据平行四边形的性质以及相似三角形的性质. 【解答】解:•••在?ABCD 中,EM // AD.易证四边形AMEN 为平行四边形15 13AC ,根据角平分线的定义、平行线的性质得到/C .13【分析】根据勾股定理求出BDQ ,得到QB = QD ,根据相似三角形的性质列出比例式,计算即可. 【解答】解:•••/ C = 90°, AB = 5, BC = 4,D .二13QBD = Z2QBBD 上,EM // AD ,交)Alt NE A ------- = ----- .-'i rir. Alt ANB =B .「’ MBC BEC . - r.riD .「厂BE EM)•••易证△ BEM s\ BAD S \ END、' =亠=-,A 项错误BM BN BE=—,B 项错误AD=丄_=二_, C 项错误ME BE=二_=上_, D 项正确ME ME故选:D .【点评】此题主要考查相似三角形的性质及平行四边形的性质,本题关键是要懂得找相 似三角形,利用相似三角形的性质求解.7. (2019年黑龙江省鸡西市)如图,在平行四边形ABCD 中,/ BAC = 90°, AB = AC ,过点A 作边BC 的垂线AF 交DC 的延长线于点 E ,点F 是垂足,连接 BE 、DF , DF 交AC 于点O .则下列结论: ①四边形ABEC 是正方形;②CO : BE = 1: 3;③DE =「BC ; ④S 四边形OCEF = Ss OD ,正确的个数是()A . 1B . 2C . 3D . 4【分析】①先证明厶ABF ◎△ ECF ,得AB = EC ,再得四边形ABEC 为平行四边形,进而 由/BAC = 90。

2019年中考数学真题汇编----图形的相似与位似一.选择题1. (2019•浙江杭州•3分)如图,在△ABC中,点D,E分别在AB和AC上,DE∥BC,M为BC边上一点(不与点B,C重合),连接AM交DE于点N,则( )A.=B.=C.=D.=【分析】先证明△ADN∽△ABM得到=,再证明△ANE∽△AMC得到=,则=,从而可对各选项进行判断.【解答】解:∵DN∥BM,∴△ADN∽△ABM,∴=,∵NE∥MC,∴△ANE∽△AMC,∴=,∴=.故选:C.【点评】本题考查了相似三角形的判定与性质:三在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;灵活运用相似三角形的性质表示线段之间的关系.2. (2019•广西贺州•3分)如图,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,若AD=2,AB=3,DE=4,则BC等于( )A.5B.6C.7D.8【分析】由平行线得出△ADE∽△ABC,得出对应边成比例=,即可得出结果.【解答】解:∵DE∥BC,∴△ADE∽△ABC,∴=,即=,解得:BC=6,故选:B.【点评】本题考查了相似三角形的判定与性质;证明三角形相似得出对应边成比例是解题的关键.3. (2019•甘肃省庆阳市•3分)如图,将图形用放大镜放大,应该属于( )A.平移变换B.相似变换C.旋转变换D.对称变换【分析】根据放大镜成像的特点,结合各变换的特点即可得出答案.【解答】解:根据相似图形的定义知,用放大镜将图形放大,属于图形的形状相同,大小不相同,所以属于相似变换.故选:B.【点评】本题考查的是相似形的识别,关键要联系图形,根据相似图形的定义得出.二.填空题1. (2019•江苏无锡•2分)如图,在△ABC中,AC:BC:AB=5:12:13,⊙O在△ABC内自由移动,若⊙O的半径为1,且圆心O在△ABC内所能到达的区域的面积为,则△ABC的周长为 25 .【分析】如图,由题意点O所能到达的区域是△EFG,连接AE,延长AE交BC于H,作HM⊥AB于M,EK⊥AC于K,作FJ⊥AC于J.利用相似三角形的性质以及三角形的面积公式求出EF,再证明△HAC≌△HAM(AAS),推出AM=AC=5m,CH=HM,BM=8m,设CH=HM=x,在Rt△BHM中,则有x2+(8m)2=(12m图x)2,推出x=m,由EK∥CH,推出=,推出=,可得AK=,求出AC即可解决问题.【解答】解:如图,由题意点O所能到达的区域是△EFG,连接AE,延长AE交BC于H,作HM⊥AB于M,EK⊥AC于K,作FJ⊥AC于J.∵EG∥AB,EF∥AC,FG∥BC,∴∠EGF=∠ABC,∠FEG=∠CAB,∴△EFG∽△ACB,∴EF:FG:EG=AC:BC:AB=5:12:13,设EF=5k,FG=12k,∵×5k×12k=,∴k=或图(舍弃),∴EF=,∵四边形EKJF是矩形,∴KJ=EF=,设AC=5m,BC=12m,AB=13m,∵∠ACH=∠AMH=90°,∠HAC=∠HAM,AH=AH,∴△HAC≌△HAM(AAS),∴AM=AC=5m,CH=HM,BM=8m,设CH=HM=x,在Rt△BHM中,则有x2+(8m)2=(12m图x)2,∴x=m,∵EK∥CH,∴=,∴=,∴AK=,∴AC=AK+KJ+CJ=++1=,∴BC=××12=10,AB=××13=,∴△ABC的周长=AC+BC+AB=+10+=25,故答案为25.【点评】本题考查动点问题,轨迹,相似三角形的判定和性质,全等三角形的判定和性质,解直角三角形等知识,解题的关键是理解题意,学会添加常用辅助线,构造相似三角形解决问题,属于中考填空题中的压轴题.2. (2019•江苏无锡•2分)如图,在△ABC中,AB=AC=5,BC=4,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为 8 .【分析】过点C作CG⊥BA于点G,作EH⊥AB于点H,作AM⊥BC于点M.由AB=AC=5,BC=4,得到BM=CM=2,易证△AMB∽△CGB,求得GB=8,设BD =x,则DG=8图x,易证△EDH≌△DCG,EH=DG=8图x,所以S△BDE===,当x=4时,△BDE面积的最大值为8.【解答】解:过点C作CG⊥BA于点G,作EH⊥AB于点H,作AM⊥BC于点M.∵AB=AC=5,BC=4,∴BM=CM=2,易证△AMB∽△CGB,∴,即∴GB=8,设BD=x,则DG=8图x,易证△EDH≌△DCG(AAS),∴EH=DG=8图x,∴S△BDE===,当x=4时,△BDE面积的最大值为8.故答案为8.【点评】本题考查了正方形,熟练运用正方形的性质与相似三角形的判定与性质以及全等三角形的判定与性质是解题的关键.3. (2019•江苏扬州•3分)如图,在△ABC 中,AB =5,AC =4,若进行一下操作,在边BC 上从左到右一次取点D 1、D 2、D 3、D 4…;过点D 1作AB 、AC 的平行线分别交于AC 、AB 与点E 1、F 1;过点D 2作AB 、AC 的平行线分别交于AC 、AB 于点E 2、F 2;过点D 3作AB 、AC 的平行线分别交于AC 、AB 于点E 3、F 3…,则4(D 1E 1+D 2E 2+…+D 2019E 2019)+5(D 1F 1+D 2F 2+…+D 2019F 2019)= 40380 .【考点】:相似三角形,比例性质【解析】:∵D 1E 1∥AB D 1F 1∥AC ∴CB CD AB E D 111=BCBD AC F D 11=∵AB =5 AC =4∴CB CD E D 1115=BCBD F D 114=∴14511111==+=+BCBCBC BD CB CD F D E D ∴4D 1E +5D 1F =20有2019组,即2019×20=40380【答案】:403804. (2019•江西•3分)在平面直角坐标系中,A ,B ,C 三点的坐标分别为(4,0), (4,4),(0,4),点P 在x 轴上,点D 在直线AB 上,DA =1, CP ⊥DP 于点P ,则点P 的坐标为P (2,0), P (,0), P (,0) .x图2图1解析:设P (m ,0)如图1,∠CPD=90°,△OCP∽△PAD∴即:∴m=2 ∴P(2,0)如图2,∠CPD=90°,△OCP∽△APD ∴即:∴m=∴P(,0)P(,0)综上分析可知:P(2,0),P(,0),P(,0)5. (2019•浙江杭州•4分)如图,把某矩形纸片ABCD沿EF,GH折叠(点E,H在AD边上,点F,G在BC边上),使点B和点C落在AD边上同一点P处,A点的对称点为A′点,D点的对称点为D′点,若∠FPG=90°,△A′EP的面积为4,△D′PH的面积为1,则矩形ABCD的面积等于 2(5+3) .【分析】设AB=CD=x,由翻折可知:PA′=AB=x,PD′=CD=x,因为△A′EP的面积为4,△D′PH的面积为1,推出A′E=4D′H,设D′H=a,则A′E=4a,由△A′EP∽△D′PH,推出=,推出=,可得x=2a,再利用三角形的面积公式求出a即可解决问题.【解答】解:∵四边形ABC是矩形,∴AB=CD,AD=BC,设AB=CD=x,由翻折可知:PA′=AB=x,PD′=CD=x,∵△A′EP的面积为4,△D′PH的面积为1,∴A′E=4D′H,设D′H=a,则A′E=4a,∵△A′EP∽△D′PH,∴=,∴x2=4a2,∴x=2a或图2a(舍弃),∴PA′=PD′=2a,∵•a•2a=1,∴a=1,∴x=2,∴AB=CD=2,PE==2,PH==,∴AD=4+2++1=5+3,∴矩形ABCD的面积=2(5+3).故答案为2(5+3)【点评】本题考查翻折变换,矩形的性质,勾股定理,相似三角形的判定和性质等知识,解题的关键是学会利用参数解决问题,属于中考填空题中的压轴题.6.(2019•四川自贡•4分)如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,CD∥AB,∠ABC的平分线BD交AC于点E,DE= .【分析】由CD∥AB,∠D=∠ABE,∠D=∠CBE,所以CD=BC=6,再证明△AEB∽△CED,根据相似比求出DE的长.【解答】解:∵∠ACB=90°,AB=10,BC=6,∴AC=8,∵BD平分∠ABC,∴∠ABE=∠CDE,∵CD∥AB,∴∠D =∠CBE ,∴CD =BC =6,∴△AEB ∽△CED ,∴,∴CE =AC =×8=3,BE =,DE =BE =×=,故答案为.【点评】本题考查了相似三角形,熟练掌握相似三角形的判定与性质以及勾股定理是解题的关键.7.(2019•天津•3分)如图,正方形纸片ABCD 的边长为12,E 是边CD 上一点,连接AE ,折叠该纸片,使点A 落在AE 上的G 点,并使折痕经过点B ,得到折痕BF ,点F 在AD 上,若DE =5,则GE 的长为.【答案】1349【解析】因为四边形ABCD 是正方形,易得△AFB ≌△DEA ,∴AF =DE =5,则BF =13.又易知△AFH ∽△BFA ,所以,即AH =,∴AH =2AH =,∴由勾股定理BF AF BA AH136013120得AE =13,∴GE =AE -AG =13498.(2019•河南•3分)如图,在矩形ABCD 中,AB =1,BC =a ,点E 在边BC 上,且BE =a.连接AE,将△ABE沿AE折叠,若点B的对应点B′落在矩形ABCD的边上,则a 的值为 或 .【分析】分两种情况:①点B′落在AD边上,根据矩形与折叠的性质易得AB=BE,即可求出a的值;②点B′落在CD边上,证明△ADB′∽△B′CE,根据相似三角形对应边成比例即可求出a的值.【解答】解:分两种情况:①当点B′落在AD边上时,如图1.∵四边形ABCD是矩形,∴∠BAD=∠B=90°,∵将△ABE沿AE折叠,点B的对应点B′落在AD边上,∴∠BAE=∠B′AE=∠BAD=45°,∴AB=BE,∴a=1,∴a=;②当点B′落在CD边上时,如图2.∵四边形ABCD是矩形,∴∠BAD=∠B=∠C=∠D=90°,AD=BC=a.∵将△ABE沿AE折叠,点B的对应点B′落在CD边上,∴∠B=∠AB′E=90°,AB=AB′=1,EB=EB′=a,∴DB′==,EC=BC图BE=a图a=a.在△ADB′与△B′CE中,,∴△ADB′∽△B′CE,∴=,即=,解得a1=,a2=0(舍去).综上,所求a的值为或.故答案为或.【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质,勾股定理,相似三角形的判定与性质.进行分类讨论与数形结合是解题的关键.9.10.三.解答题1. (2019•江苏宿迁•12分)如图①,在钝角△ABC中,∠ABC=30°,AC=4,点D为边AB中点,点E为边BC中点,将△BDE绕点B逆时针方向旋转α度(0≤α≤180).(1)如图②,当0<α<180时,连接AD、CE.求证:△BDA∽△BEC;(2)如图③,直线CE、AD交于点G.在旋转过程中,∠AGC的大小是否发生变化?如变化,请说明理由;如不变,请求出这个角的度数;(3)将△BDE从图①位置绕点B逆时针方向旋转180°,求点G的运动路程.【分析】(1)如图①利用三角形的中位线定理,推出DE∥AC,可得=,在图②中,利用两边成比例夹角相等证明三角形细相似即可.(2)利用相似三角形的性质证明即可.(3)点G的运动路程,是图③图1中的的长的两倍,求出圆心角,半径,利用弧长公式计算即可.【解答】解:(1)如图②中,由图①,∵点D为边AB中点,点E为边BC中点,∴DE∥AC,∴=,∴=,∵∠DBE=∠ABC,∴∠DBA=∠EBC,∴△DBA∽△EBC.(2)∠AGC的大小不发生变化,∠AGC=30°.理由:如图③中,设AB交CG于点O.∵△DBA∽△EBC,∴∠DAB=∠ECB,∵∠DAB+∠AOG+∠G=180°,∠ECB+∠COB+∠ABC=180°,∠AOG=∠COB,∴∠G=∠ABC=30°.(3)如图③图1中.设AB的中点为K,连接DK,以AC为边向右作等边△ACO,连接OG,OB.以O为圆心,OA为半径作⊙O,∵∠AGC=30°,∠AOC=60°,∴∠AGC=∠AOC,∴点G在⊙O上运动,以B为圆心,BD为半径作⊙B,当直线与⊙B相切时,BD⊥AD,∴∠ADB=90°,∵BK=AK,∴DK=BK=AK,∵BD=BK,∴BD=DK=BK,∴△BDK是等边三角形,∴∠DBK=60°,∴∠DAB=30°,∴∠DOG=2∠DAB=60°,∴的长==,观察图象可知,点G的运动路程是的长的两倍=.【点评】本题属于相似形综合题,考查了相似三角形的判定和性质,弧长公式,等边三角形的判定和性质,圆周角定理等知识,解题的关键是正确寻找相似三角形解决问题,学会正确寻找点的运动轨迹,属于中考压轴题.2. (2019•江西•9分)数学活动课上,张老师引导同学进行如下研究:如图1,将长为12cm的铅笔AB斜靠在垂直于水平桌面AE的直尺FO的边沿上,一端A 固定在桌面上,图2是示意图活动一如图3,将铅笔AB绕端点A顺时针旋转,AB与OF交于点D,当旋转至水平位置时铅笔AB的中点C与点O重合。
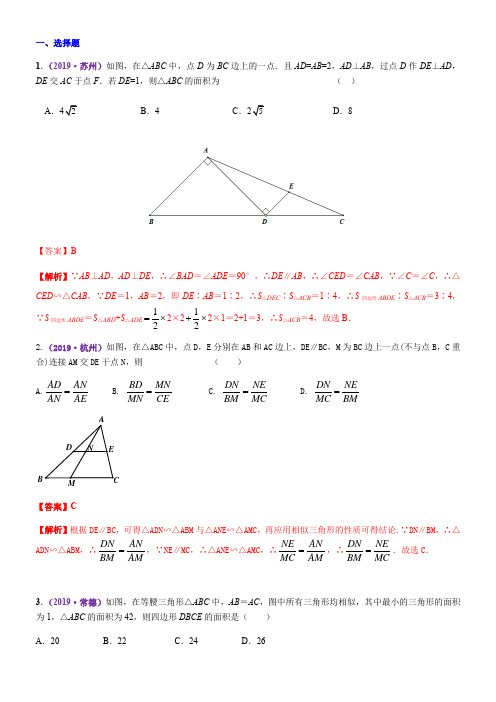
一、选择题1.(2019·苏州)如图,在△ABC 中,点D 为BC 边上的一点.且AD =AB =2,AD ⊥AB ,过点D 作DE ⊥AD ,DE 交AC 于点F .若DE =1,则△ABC 的面积为( ) A .B .4C .D .8【答案】B【解析】∵AB ⊥AD ,AD ⊥DE ,∴∠BAD =∠ADE =90°,∴DE ∥AB ,∴∠CED =∠CAB ,∵∠C =∠C ,∴△CED ∽△CAB ,∵DE =1,AB =2,即DE ∶AB =1∶2,∴S △DEC ∶S △ACB =1∶4,∴S 四边形ABDE∶S △ACB =3∶4,∵S 四边形ABDE =S △ABD +S △ADE 12=⨯2×212+⨯2×1=2+1=3,∴S △ACB =4,故选B . 2.(2019·杭州)如图,在△ABC 中,点D ,E 分别在AB 和AC 边上,DE ∥BC ,M 为BC 边上一点(不与点B ,C 重合)连接AM 交DE 干点N ,则( )A.AD AN AN AE = B. BD MN MN CE = C. DN NE BM MC = D. DN NEMC BM=【答案】C【解析】根据DE ∥BC ,可得△ADN ∽△ABM 与△ANE ∽△AMC ,再应用相似三角形的性质可得结论.∵DN ∥BM ,∴△ADN ∽△ABM ,∴DN AN BM AM =,∵NE ∥MC ,∴△ANE ∽△AMC ,∴NE AN MC AM =,∴DN NEBM MC=.故选C .3.(2019·常德)如图,在等腰三角形△ABC 中,AB =AC ,图中所有三角形均相似,其中最小的三角形的面积为1,△ABC 的面积为42,则四边形DBCE 的面积是( ) A .20 B .22 C .24 D .26B【答案】D【解析】∵图中所有三角形均相似,其中最小的三角形的面积为1,△ABC 的面积为42,∴最小的三角形与△ABC∵△ADE ∽△ABC ,∴ADE ABC S S V V =2DE BC ⎛⎫⎪⎝⎭,∵DE BC =4∴ADE ABC S S V V =1642=821, ∴S △ADE =821×42=16,∴四边形DBCE 的面积=S △ABC -S △ADE =26,故选项D 正确. 4.(2019·陇南)如图,将图形用放大镜放大,应该属于( )A .平移变换B .相似变换C .旋转变换D .对称变换【答案】B【解析】由图可知,放大前与放大后图形是相似的,故选:B .5. (2019·枣庄)如图,将△ABC 沿BC 边上的中线AD 平移到△A'B'C'的位置,已知△ABC 的面积为16,阴影部分三角形的面积为9,若AA'=1,则A'D 等于 A.2B.3C.4D.32【答案】B【解析】由平移可得,△ABC ∽△A'MN,设相似比为,∵S △ABC =16,S △A'MN =9,∴2=169,∴=43,因为AD 和A'D分别为两个三角形的中线,∴ADA'D ==43,∵AD =AA'+A'D,∴AA'A'D =13,∵AA'=1,则A'D =3,故选B.6.(2019·淄博)如图,在△ABC 中,AC =2,BC =4,D 为BC 边上的一点,且∠CAD =∠B. 若△ADC 的面积为a ,则△ABD 的面积为()A .2aB .52a C .3a D .72a 【答案】C .【解析】在△BAC 和△ADC 中,∵∠C 是公共角,∠CAD =∠B.,∴△BAC ∽△ADC ,∴2BCAC=, ∴2AB DA =()4C C S BC S AC=V V ,又∵△ADC 的面积为a ,∴△ABC 的面积为4a ,∴△ABD 的面积为3a . 7. (2019· 巴中)如图,Y ABCD,F 为BC 中点,延长AD 至E,使DEAD =13,连接EF 交DC 于点G,则S△DEGS △CFG=( ) A.23B.32C.94D.49【答案】D【解析】因为DEAD =13,F 为BC 中点,所以DECF =23,Y ABCD 中,DE ∥CF,所以△DEG ∽△CFG,相似比为23,B所以S △DEG S △CFG =49.故选D.8.(2019·乐山)把边长分别为1和2的两个正方形按如图的方式放置.则图中阴影部分的面积为( )A.61 B .31 C .51 D .41【答案】A第8题答图【解析】∵四边形ABCD 与四边形CEFG 都是正方形,∴AD =DC =1,CE =2,AD ∥CE ,∴△ADH ∽△ECF ,∴AD DH CE CH =,∴121DH DH =-,解得DH =13,∴阴影部分面积为12×13×1=16,故选A. 9.(2019·乐山)如图,在边长为3的菱形ABCD 中,︒=∠30B ,过点A 作BC AE ⊥于点E ,现将△ABE 沿直线AE 翻折至△AFE 的位置,AF 与CD 交于点G .则CG 等于( )A .13-B .1C .21D .23第9题图【答案】A【解析】∵BC AE ⊥,∴∠AEB=90°,菱形ABCD 的边长为3,︒=∠30B ,∴AE=12AB=123,GD12第8题图BE=CF=,BF=3,CF=BF -BC=3-,∵AD ∥CF ,∴△AGD ∽△FGC ,∴DG ADCG CF=,∴=CG 1,故选A. 10.(2019·凉山)如图,在△ABC 中,D 在AC 边上,AD ∶DC = 1∶2,O 是BD 的中点,连接A 0并延长交BC 于 E ,则BE ∶EC =( ▲ ) A. 1∶2 B . 1∶3 C . 1∶4 D . 2∶3 【答案】B【解析】过点D 作DF ∥AE ,则1==OD BO EF BE ,21==CD AD FC EF ,∴BE ∶EF ∶FC =1∶1∶2,∴BE ∶EC =1∶3.故选B .11.(2019·眉山)如图,在菱形ABCD 中已知AB =4,∠ABC =60°,∠EAF =60°,点E 在CB 的延长线上,点F 在DC 的延长线上,有下列结论:①BE =CF ,②∠EAB =∠CEF ;③△ABE ∽△EFC ,④若∠BAE =15°,则点F 到BC 的距离为2,则其中正确结论的个数是A .1个B . 2个C .3个D . 4个【答案】B【解析】连接AC ,在菱形ABCD 中,AB=BC ,∠ABC=60°,∴△ABC 是等边三角形,∴AB=AC ,∠BAC=60°,∵∠EAF=60°,∴∠EAB+∠BAF=∠CAF+∠BAF=60°,即∠EAB=∠CAF ,∵∠ABE=∠ACF=120°,∴△ABE ≌△ACF ,∴BE=CF ,故①正确;由△ABE ≌△ACF ,可得AE=AF ,∵∠EAF=60°,∴△AEF 是等边三角形,∴∠AEF=60°,∴∠AEB+∠CEF=60°,∵∠AEB+∠EAB=60°,∴∠CEF=∠EAB ,故②正确;在△ABE 中,∠AEB <60°,∠ECF=60°,∴③错误;过点A 作AG ⊥BC 于点G ,过点F 作FH ⊥EC 于点H ,∵∠EAB=15°,∠ABC=60°,∴∠AEB=45°,在Rt △AGB 中,∵∠ABC=60°,AB=4,∴BG=12AB=2,Rt △AEG 中,∵∠AEG=∠EAG=45°,∴AG=GE=∴EB=EG -BG=-2,∵∠BAC=∠EAF=60°,∴∠BAE=∠CAF ,∵∠ABC=∠ACD=60°,∴∠ABE=∠ACF=120°在△AEB 和△AFC 中,⎧⎪⎨⎪⎩∠∠∠∠︒EAB FAC AB AC ABE ACF 120====,∴△AEB ≌△AFC ,∴AE=AF ,EB=CF=2,在Rt △CHF 中,∵∠HCF=180°-∠BCD=60°,CF=2,∴FH=CF •sin60°=(2=3 ∴点F 到BC的距离为3故④错误.故选B.12.(2019·重庆B 卷)下列命题是真命题的是( )A.如果两个三角形相似,相似比为49,那么这两个三角形的周长比为23B.如果两个三角形相似,相似比为49,那么这两个三角形的周长比为49C.如果两个三角形相似,相似比为49,那么这两个全角形的面积比为23D.如果两个三角形相似,相似比为49,那么这两个三角形的面积比为49 【答案】B【解析】如果两个三角形相似,那么这两个三角形的周长比等于相似比,面积比是相似比的平方.即如果两个三角形相似,相似比为49,那么这两个三角形的周长比为49;面积比是相似比的平方,即1681.故选B. 二、填空题13.(2019·滨州)在平面直角坐标系中,△ABO 三个顶点的坐标分别为A (-2,4),B (-4,0),O (0,0).以原点O 为位似中心,把这个三角形缩小为原的12,得到△CDO ,则点A 的对应点C 的坐标是________________________.【答案】(-1,2)或(1,-2)【解析】点A的对应点C的坐标是(-2×12,4×12)或(-2×(-12),4×(-12)),即(-1,2)或(1,-2).14.(2019·滨州)如图,▱ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:①EO⊥AC;②S△AOD=4S△OCF;③AC:BD=:7;④FB2=OF•DF.其中正确的结论有____________.(填写所有正确结论的序号)【答案】①③④【解析】在Y ABCD中,AB∥DC,∠ABC=60°,∴∠BCD=120°.∵CE平分∠BCD,∴∠BCE=60°,∴△BCE是等边三角形,∴BE=BC=CE,∠BEC=60°.∵AB=2BC,∴AE=BE=CE,∴∠EAC=∠ACE=30°,∴∠ACB=90°.在Y ABCD 中,AO=CO,BO=DO,∴OE是△ACB的中位线,∴OE∥BC,∴OE⊥AC,故①正确;∵OE是△ACB的中位线,∴OE=12BC,∵OE∥BC,∴△OEF∽△BCF,∴OF:BF=OE:BC=1:2,∴S△AOD=S△BOC=3S△OCF,故②错误;在Rt△ABC中,∵AB=2BC,∴,∴OC=2BC.在Rt△BCO中,OB=2BC,BC,∴AC:BC:7,故③正确;∵OF:BF=1:2,∴BF=2OF,OB=3OF,∵OD=OB,∴DF=4OF,∴BF2=(2OF)2=4OF2,OF·DF=OF·4OF=4OF2,∴BF2=OF·DF,故④正确.15.(2019·凉山)在□ABCD中,E是AD上一点,且点E将AD分为2∶3的两部分,连接BE、AC相交于F,则S△AEF∶S△CBF是▲.【答案】4:25或9∶25【解析】在□ABCD中,∵AD∥BC,∴△AEF∽△CBF.如答图1,当AE∶DE=2∶3时,AE∶AD=2∶5,∵AD=BC,∴AE∶BC=2∶5,∴S△AEF∶S△CBF=4∶25;如答图2,当AE∶DE=3∶2时,AE∶AD=3∶5,∵AD=BC,∴AE∶BC=3∶5,∴S△AEF∶S△CBF=9∶25.故答案为4∶25或9∶25.(第16题图答图1) (第16题图答图2)16.(2019·衢州)如图,由两个长为2,宽为1的长方形组成“7”字图形。

2019届中考数学专题复习相似模型(讲义及答案)D DEO CBO相似模型(⼀)(讲义)课前预习1. 请证明以下结论:①如图 1,在△ABC 中,DE ∥BC ,求证:△ADE ∽△ABC .②如图 2,在△ABC 中,∠B =∠AED ,求证:△AED ∽△ABC .③如图 3,在△ABC 中,∠B =∠ACD ,求证:△ACD ∽△ABC .④如图 4,直线 AB ,CD 相交于点 O ,连接 AC ,BD ,且 AC ∥BD ,求证:△AOC ∽△BOD .⑤如图 5,直线 AB ,CD 相交于点 O ,连接 AC ,BD ,∠B = ∠C ,求证:△AOC ∽△DOB .⑥如图 6,在 Rt △ABC 中,∠BAC =90°,AD ⊥BC 于点 D ,求证:△ADB ∽△CDA ,△ADB ∽△CAB .A ABC BC图 1图 2图 3D BAADD 图 4图 5图 6DD知识点睛1. 六种相似基本模型:AA AEBCB C B C DE ∥BC ∠B =∠AED∠B =∠ACD A 型 D B CAB O O AC A DBD CAC ∥BD∠B =∠CAD 是 Rt △ABC 斜边上的⾼X 型母⼦型2. 相似、⾓相等、⽐例线段间的关系:⾓相等⽐例线段相似性质⾓相等⽐例线段列⽅程(或表达边)⽐的传递转移相似往往与等信息组合搭配起来使⽤.多个相似之间⼀般会通过来转移条件.⼀般碰到不熟悉的线段间关系时,常需要还原成来观察和分析. 3. 影⼦上墙:、、是影⼦上墙时的三种常见处理⽅式,它们的实质是构造三⾓形相似.DAGE FBD HHGGE F H E F EF △DEH ∽△ABC △DHG ∽△ABC △HEF ∽△ABC当两个三⾓形相似且有公共边时,借助对应边成⽐例往往可以得到a 2=bc 形式的关系.例如:“母⼦型”中△ABD ∽△CBA →AB 2=BC ·BD △ACD ∽△BCA →△ADB ∽△CDA →E D FDEG精讲精练1. 如图,在△ABC 中,EF ∥DC ,∠AFE =∠B ,AE =6,ED =3,AF =8,则 AC =A, CD = . BC第1 题图第2 题图 2. 如图,AB ∥CD ,线段 BC ,AD 相交于点 F ,点 E 是线段 AF 上⼀点且满⾜∠BEF =∠C ,其中 AF =6,DF =3,CF =2,则AE = .3. 如图,在 Rt △ABC 中,∠ACB =90°,CD ⊥AB 于点 D ,BD =2,AD =8,则 CD = ,AC = ,BC = .ACBC D4. 如图,在同⼀平⾯内,将两个全等的等腰直⾓三⾓形 ABC 和AFG 摆放在⼀起,A 为公共顶点,∠BAC =∠AGF =90°,它们的斜边长为 2,若△ABC 固定不动,△AFG 绕点 A 旋转,AF , AG 与边 BC 的交点分别为 D ,E (点 D 不与点 B 重合,点 E 不与点 C 重合).①请写出图中所有的相似三⾓形;②若 BD = 1,则 CE = .2FGCD4 5 55. 如图,M 为线段 AB 上⼀点,AE 与 BD 交于点 C ,∠DME =∠A =∠B =α,且 DM 交 AE 于点 F ,ME 交 BD 于点 G .(1)写出图中的三对相似三⾓形;(2)连接 FG ,当 AM =MB 时,求证:△MFG ∽△BMG .AMBE6. 如图,在矩形 ABCD 中,对⾓线 AC ,BD 相交于点 O ,E 为AD 的中点,连接 BE 交 AC 于点 F ,连接 FD .若∠BFA =90°,给出以下三对三⾓形:①△BEA与△ACD ;②△FED 与△DEB ;③△CFD 与△ABO .其中相似的有(填写序号).A E DFOBC7. 如图,在△ABC 中,∠ACB =90°,CE ⊥AB 于点 E ,D 在 AB的延长线上,且∠DCB =∠A ,BD :CD =1:2, AE ,则△BCD 的⾯积是()A .1 3B .D . 2 5 3 CA EB DEAN MAE8.如图,在Rt△ABD 中,过点D 作CD⊥BD,垂⾜为D,连接BC 交AD于点E,过点E 作EF⊥BD于点F,若AB=15,CD=10,则BF:FD= .AC DB F D B E C第8 题图第9 题图9.如图,在□ABCD 中,E 为BC 的中点,连接AE,AC,分别交BD 于M,N,则BM:DN= .10. 如图,直线l1∥l2,若AF:FB=2:3,BC:CD=2:1,则CE:AE= .2第10 题图第11 题图11.如图,在□ABCD 中,E是BA 延长线上⼀点,CE 分别与AD,BD 交于点G,F.则下列结论:①EG=AG;②EFGC GD③FC=BF;④CF 2 =GF ?EF .其中正确的是GF FDFC FD.12.如图所⽰,AB∥CD,AD,BC 交于点E,过E 作EF∥AB 交BD 于点F.则下列结论:①△EFD∽△ABD;②EF=BF;③EF+EF=FD+BFCD BD= 1 ;④1+1=1.其中正确的AB CD BD BD有.AB CD EFCB F D13.如图,在△ABC 中,CD⊥AB 于点D,正⽅形EFGH 的四个1=1.AB CD EFCA H D G B14.数学兴趣⼩组想测量⼀棵树的⾼度.在阳光下,⼀名同学测得⼀根长为1 ⽶的⽵竿的影长为0.8 ⽶,同时另⼀名同学测量⼀棵树的⾼度时,发现树的影⼦不全落在地⾯上,有⼀部分影⼦落在教学楼的墙壁上(如图),这部分影长为1.2 ⽶,落在地⾯上的影长为2.4 ⽶,则树⾼为.ADB C第14 题图第15 题图15.⼩阳发现电线杆AB 的影⼦落在⼟坡的坡⾯CD 和地⾯BC 上,量得CD=8 ⽶,BC=20 ⽶,CD 与地⾯成30°⾓,且此时测得1 ⽶杆的影长为2 ⽶,则电线杆的⾼度为()A.9 ⽶B.28 ⽶C.(7 + 3) ⽶D.(14 + 2 3) ⽶E F16.如图,在斜坡的顶部有⼀铁塔AB,B 是CD 的中点,CD 是⽔平的,在阳光的照射下,塔影DE 留在坡⾯上.若铁塔底座宽CD=12 m,塔影长DE=18 m,⼩明和⼩华的⾝⾼都是1.6 m,同⼀时刻⼩明站在点E 处,影⼦在坡⾯上,⼩华站在平地上,影⼦也在平地上,两⼈的影长分别为2 m 和1 m,则塔⾼AB 为()A.24 m B.22 m C.20 m D.18 mAC B DE【参考答案】课前预习1.证明略;知识点睛2.⾓相等、⽐例线段,⽐例的传递与整合,⽐例形式框1:AC 2 =BC ?CD ;AD2 =CD ?DB .精讲精练1. 12,342. 10 33. 4,4 5 ,24.①△ABE∽△DA E;△D AC∽△D EA;△ABE∽△DC A;△ABC≌△GAF.②2 .35.(1)△AMF∽△BGM;△AME∽△MFE;△BMD∽△MGD;(2)证明略.6. ①②③7. A8. 3:29. 2:310. 1:211. ①②③④12. ①②③④13. 证明略14. 4.2 ⽶15.D16.A5EFB相似模型(⼀)(习题)例题⽰范例 1:如图,某⼀时刻,旗杆 AB 的影⼦⼀部分在地⾯上,另⼀部分在建筑物的墙⾯上.⼩明测得旗杆 AB 在地⾯上的影长 BC 为 9.6 m ,在墙⾯上的影长 CD 为 2 m .同⼀时刻,⼩明⼜测得矩形.A 由题意,BC =9.6,CD =2,∴BC =DE =9.6,CD =BE =2 由题意,AE ED 1 1.2∴AE =8∴AB =AE +EB =8+2=10 ∴旗杆的⾼度为 10 m .巩固练习2. 如图,在锐⾓三⾓形 ABC 中,⾼ CD ,BE 相交于点 H ,则图中与△CEH 相似(除△CEH ⾃⾝外)的三⾓形有() A .1 个 B .2 个 C .3 个 D .4 个AAD DE HCC第1 题图第2 题图3.如图,E是□ABCD 的边CD 上⼀点,连接AC,BE 交于点F.若DE:EC=1:2,则BF:EF= .EM N FA FGD4.如图,⼩明在A 时刻测得某树B时A时的影长为2 m,B 时刻⼜测得该树的影长为8 m,若两次⽇照的光线互相垂直,则树的⾼度为.5.如图,在Rt△ABC 中,∠BAC=90°,AD⊥BC 于点D,若BD:CD=3:2,则AC:AB=()A.3223AC.62D.63B第4 题图第5 题图6.如图,已知□ABCD,过点B 的直线依次与AC,AD 及CD 的延长线相交于点E,F,G.若BE=5,EF=2,则FG 的长为.7.如图,梯形ABCD 的中位线EF 分别交对⾓线BD,AC 于点M,N,AD=1,BC=3,则EF= ,MN= .A DB E B C第6 题图第7 题图8.如图,D 是AB 的中点,AF∥CE,若CG:GA=3:1,BC=8,则AF= .9.如图,P 是□ABCD 的对⾓线BD 上⼀点,⼀直线过点P 分别交BA,BC 的延长线于点Q,S,交AD,CD 于点R,T.有下列结论:①△RQA∽△RTD;②PS ?PD =PR ?PB ;③PQ=PB;④PQ ?PR =PS ?PT .其中正确的是. PT PDGAFDECGADC9.如图,在△ABC 中,D 为AC 边的中点,AE∥BC,ED 交AB 于点G,交BC 的延长线于点F.若BG:GA=3:1,BC=10,则AE= .B10.11.如图,在△ABC 中,∠BAC=90°,AD⊥BC,垂⾜为D,E 是AC 上的点,若AF⊥BE,垂⾜为F.求证:∠BFD=∠C.AEFB D C12.如图,⼀同学在某时刻测得1 m 长的标杆竖直放置时影⼦长为1.6 m,同⼀时刻测量旗杆的影⼦长时,因旗杆靠近⼀栋楼房,影⼦不全落在地⾯上,有⼀部分落在墙上,他测得落在地⾯上的影⼦长为11.2 m,留在墙上的影⼦⾼为1 m,则旗杆的⾼度是.ADB C第11 题图第12 题图13.如图,⼩明想测量电线杆AB 的⾼度,发现电线杆的影⼦恰好落在⼟坡的坡⾯CD 和地⾯BC 上,量得CD=4 m,BC=10 m,CD 与地⾯成30°⾓,且此时测得1 m 杆的影⼦长为2 m,则电线杆的⾼度为.14.如图,在斜坡的顶部有⼀竖直铁塔AB,B 是CD 的中点,且CD 是⽔平的.在阳光的照射下,塔影DE 留在坡⾯上,已知铁塔底座宽CD=14 m,塔影长DE=36 m,⼩明和⼩华的⾝⾼都是1.6 m,⼩明站在点E 处,影⼦也在斜坡⾯上,⼩华站在沿DE ⽅向的坡脚下,影⼦在平地上,两⼈的影长分别为4 m,2 m,那么塔⾼AB=.AC B DE第13 题图第14 题图15.某兴趣⼩组的同学要测量树的⾼度.在阳光下,⼀名同学测得⼀根长为1 m 的⽵竿的影长为0.4 m,同时另⼀名同学测量树的⾼度时,发现树的影⼦不全落在地⾯上,有⼀部分落在教学楼的第⼀级台阶上,测得此影⼦长为0.2 m,⼀级台阶⾼为0.3 m,如图所⽰,若此时落在地⾯上的影长为4.4 m,则树⾼为.思考⼩结4.相似基本模型除了图形本⾝往往有公共⾓、对顶⾓相等之外,还需要满⾜⼀些其他特征,这些特征能够帮助我们快速验证模型.①平⾏线,往往配合对顶⾓相等(X 型)、有公共⾓(A 型)②⼀组⾓对应相等,往往配合对顶⾓相等(X 型)、有公共⾓(A 型)③多直⾓结构,往往利⽤互余关系得到⾓相等后,配合有公共⾓(母⼦型)5.影⼦上墙问题的常见处理⽅法:推墙法、砍树法、抬⾼地⾯法,这三种⽅法的实质都是构造三⾓形相似,在构造的时候,我们主要是想办法构造出来太阳光线与地⾯的夹⾓.【参考答案】?巩固练习1. C2. 3:210.4 m11.D5. 21 26. 2,17. 48. ①②③④9.510.证明略11.证明略12.8 m13. (714. 20 m3) m15. 11.8 m。

中考数学压轴题专题复习——相似的综合附答案解析一、相似1.如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).(1)直接用含t的代数式分别表示:QB=________,PD=________.(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q 的速度;(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.【答案】(1)8-2t;(2)解:不存在在Rt△ABC中,∠C=90°,AC=6,BC=8,∴AB=10∵PD∥BC,∴△APD∽△ACB,∴,即,∴AD= ,∴BD=AB-AD=10- ,∵BQ∥DP,∴当BQ=DP时,四边形PDBQ是平行四边形,即8-2t= ,解得:t= .当t= 时,PD= ,BD=10- ,∴DP≠BD,∴▱PDBQ不能为菱形.设点Q的速度为每秒v个单位长度,则BQ=8-vt,PD= ,BD=10- ,要使四边形PDBQ为菱形,则PD=BD=BQ,当PD=BD时,即 =10- ,解得:t=当PD=BQ,t= 时,即,解得:v=当点Q的速度为每秒个单位长度时,经过秒,四边形PDBQ是菱形.(3)解:如图2,以C为原点,以AC所在的直线为x轴,建立平面直角坐标系.依题意,可知0≤t≤4,当t=0时,点M1的坐标为(3,0),当t=4时点M2的坐标为(1,4).设直线M1M2的解析式为y=kx+b,∴,解得,∴直线M1M2的解析式为y=-2x+6.∵点Q(0,2t),P(6-t,0)∴在运动过程中,线段PQ中点M3的坐标(,t).把x= 代入y=-2x+6得y=-2× +6=t,∴点M3在直线M1M2上.过点M2作M2N⊥x轴于点N,则M2N=4,M1N=2.∴M1M2=2∴线段PQ中点M所经过的路径长为2 单位长度.【解析】【解答】(1)根据题意得:CQ=2t,PA=t,∴QB=8-2t,∵在Rt△ABC中,∠C=90°,AC=6,BC=8,PD∥BC,∴∠APD=90°,∴tanA= ,∴PD= .【分析】CQ=2t,PA=t,可得QB=8﹣2t,根据tanA=,可以表示PD;易得△APD∽△ACB,即可求得AD与BD的长,由BQ∥DP,可得当BQ=DP时,四边形PDBQ是平行四边形;求得此时DP与BD的长,由DP≠BD,可判定▱PDBQ不能为菱形;然后设点Q 的速度为每秒v个单位长度,由要使四边形PDBQ为菱形,则PD=BD PD=BQ,列方程即可求得答案.以C为原点,以AC所在的直线为x轴,建立平面直角坐标系,求出直线M1M2解析式,证明M3在直线M1M2上,利用勾股定理求出M1M2.2.如图,点A、B、C、D是直径为AB的⊙O上的四个点,CD=BC,AC与BD交于点E。
一、相似真题与模拟题分类汇编(难题易错题)1.在△ABC中,∠ABC=90°.(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为M、N,求证:△ABM∽△BCN;(2)如图2,P是边BC上一点,∠BAP=∠C,tan∠PAC= ,求tanC的值;(3)如图3,D是边CA延长线上一点,AE=AB,∠DEB=90°,sin∠BAC= ,,直接写出tan∠CEB的值.【答案】(1)解:∵AM⊥MN,CN⊥MN,∴∠AMB=∠BNC=90°,∴∠BAM+∠ABM=90°,∵∠ABC=90°,∴∠ABM+∠CBN=90°,∴∠BAM=∠CBN,∵∠AMB=∠NBC,∴△ABM∽△BCN(2)解:如图2,过点P作PM⊥AP交AC于M,PN⊥AM于N.∵∠BAP+∠1=∠CPM+∠1=90°,∴∠BAP=∠CPM=∠C,∴MP=MC∵tan∠PAC=,设MN=2m,PN=m,根据勾股定理得,PM=,∴tanC=(3)解:在Rt△ABC中,sin∠BAC= = ,过点A作AG⊥BE于G,过点C作CH⊥BE交EB的延长线于H,∵∠DEB=90°,∴CH∥AG∥DE,∴ =同(1)的方法得,△ABG∽△BCH∴,设BG=4m,CH=3m,AG=4n,BH=3n,∵AB=AE,AG⊥BE,∴EG=BG=4m,∴GH=BG+BH=4m+3n,∴,∴n=2m,∴EH=EG+GH=4m+4m+3n=8m+3n=8m+6m=14m,在Rt△CEH中,tan∠BEC= =【解析】【分析】(1)根据垂直的定义得出∠AMB=∠BNC=90°,根据同角的余角相等得出∠BAM=∠CBN,利用两个角对应相等的两个三角形相似得出:△ABM∽△BCN;(2)过点P作PF⊥AP交AC于F,在Rt△AFP中根据正切函数的定义,由tan∠PAC=,同(1)的方法得,△ABP∽△PQF,故,设AB= a,PQ=2a,BP= b,FQ=2b(a>0,b>0),然后判断出△ABP∽△CQF,得从而表示出CQ,进根据线段的和差表示出BC,再判断出△ABP∽△CBA,得出再得出BC,从而列出方程,表示出BC,AB,在Rt△ABC中,根据正切函数的定义得出tanC的值;(3)在Rt△ABC中,利用正弦函数的定义得出:sin∠BAC=,过点A作AG⊥BE于G,过点C作CH⊥BE交EB的延长线于H,根据平行线分线段成比例定理得出,同(1)的方法得,△ABG∽△BCH ,故,设BG=4m,CH=3m,AG=4n,BH=3n,根据等腰三角形的三线合一得出EG=BG=4m,故GH=BG+BH=4m+3n,根据比例式列出方程,求解得出n与m的关系,进而得出EH=EG+GH=4m+4m+3n=8m+3n=8m+6m=14m,在Rt△CEH中根据正切函数的定义得出tan∠BEC的值。
2019 初三数学中考复习图形的相像专题练习题1.以下说法正确的选项是 ( )A .全部的等腰三角形都相像B.四个角都是直角的两个四边形必然相像C.全部的正方形都相像D.四条边对应成比率的两个四边形相像2. 以下各组条件中,不可以判断△ABC 与△ A′B′相C′似的是 ()A.∠A=∠ A′,∠ B=∠ B′B.∠ C=∠ C′=90°,∠ A=12°,∠B′=78°C.∠ A=∠ B,∠B′=∠ A′D.∠A+∠ B=∠ A′+∠ B′,∠A-∠ B=∠ A′-∠ B′3.如图,在? ABCD 中,点 E 是边 AD 的中点,EC 交对角线 BD 于点 F,则 EF∶EC 等于()A .3∶2B.3∶1C.1∶1D.1∶34.如图,△ ABC 中,∠ C=90°,四边形DEFC 是正方形, AC=4cm,BC =3cm,则正方形的面积为 ()12cm2B.3 cm2C.4 cm2144cm2A. 7 D. 495.如图,身高为 1.6 m 的吴格婷想丈量学校旗杆的高度,当她站在 C 处时,她头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2.0 m,BC=8.0 m,则旗杆的高度是 ()第1页/共6页6.如图,点 A ,B ,C ,D 的坐标分别是 (1,7),(1,1),(4,1),(6,1),以点C ,D ,E 为极点的三角形与 △ABC 相像,则点 E 的坐标不可以能是 ( )A .(6,0)B .(6,3)C .(6,5)D .(4,2)7.如图,以点 O 为位似中心,将△ABC 放大获得 △DEF.若 AD = OA ,则△ABC与△ DEF 的面积之比为 ()A .1∶2B .1∶4C .1∶5D .1∶68.如图,△ OAB 与△ OCD 是以点 O 为位似中心的位似图形,相像比为 1∶2,∠OCD =90°, CO =CD.若 B(1,0),则点 C 的坐标为 ()A .(1,2)B .(1,1)C .( 2, 2)D .(2,1)9.将边长分别为 2,3,5 的三个正方形按如图方式摆列,则图中暗影部分的面积为()21157A. 4B. 4C.2 D .310.如图,矩形 ABCD 的边长 AD =3,AB =2,E 为 AB 的中点,点 F 在边 BC 上,且 BF =2FC ,AF 分别与 DE ,DB 订交于点 M ,N ,则 MN 的长为 ()2 2 9 23 24 2A. 5B. 20C. 4D. 511. 如图,△ ABC 中,∠A =78°,AB =4,AC =6.将△ ABC 沿图示中的虚线剪开,剪下的暗影三角形与原三角形不相像的是 ()12. 小强身高 1.7 m ,测得他站立在阳光下的影子长为0.85 m ,紧接着他把手臂竖直举起,此时影子长为 1.1 m ,那么小强举起的手臂超出头顶 () A .0.4 mB .0.5 mC .0.8 mD .1 m.假如 x =y =z ≠0,那么 x +2y +3z的值是 ______.13 2 3 43x +2y -2z14.两个相像三角形的面积比为9∶25,此中一个三角形的周长为36,则另一个三角形的周长为 ________.15.如图,D,E 是 AB 的三均分点, DF∥EG∥BC,则图中三部分面积S1∶S2∶S3=________.16.如图,一束光芒从点A(3, 3)出发,经过 y 轴上的 C 点反射后经过点B(1,0),则光芒从 A 点到 B 点经过的路线长是 _________.17.如图,正方形 ABCD 和正方形 OEFG 中,点 A 和点 F 的坐标分别为 (3,2),(- 1,- 1),则两个正方形的位似中心的坐标是 ________.18.如图,在△ABC 中,BC=6,E,F 分别是 AB ,AC 的中点,动点 P 在射线1EF 上, BP 交 CE 于点 D,∠ CBP 的均分线交 CE 于点 Q,当 CQ=3CE 时, EP +B P=________.19.如图,△ ABC 与△A′B′是C′位似图形,点 A,B,A′,B′,O 共线,点 O 为位似中心.(1)AC 与 A′C平′行吗?为何?(2)若 AB =2A′B,′OC′= 5,求 CC′的长.20.如图,在矩形 ABCD 中, CD=2 3,CF⊥BD 分别交 BD,AD 于点 E,F,连结 BF.(1)求证:△DEC∽△ FDC;(2)当 F 为 AD 的中点时,求BC 的长度.21.如图,M ,N 为山双侧的两个乡村,为了两村交通方便,依据国家的惠民政策,政府决定打向来线涵洞.工程人员为了计算工程量,必然计算M,N 两点之间的直线距离,选择丈量点A,B,C,点 B,C 分别在 AM ,AN 上,现测得AM =1 千米, AN =1.8 千米, AB =54 米, BC=45 米, AC=30 米,求 M,N 两点之间的直线距离.22.如图,在矩形ABCD 中, AB =12 cm, BC=8 cm,点 E,F,G 分别从 A ,B,C 三点同时出发,沿矩形的边按逆时针方向挪动,点E,G 的速度为 2 cm/s,点 F 的速度为 4 cm/s,当点 F 追上点 G(即点 F 与点 G 重合 )时,三个点随之停止挪动.设挪动开始后第 t s 时,△ EFG 的面积为 S(cm2).(1)当 t=1 s 时, S 的值是多少?(2)若点 F 在矩形的边 BC 上挪动,当 t 为何值时,以点E,B,F 为极点的三角形与以点 F, C,G 为极点的三角形相像?请说明原因.23.如图,为了丈量山的高度,在山前的平川上先竖一根已知长度的木棒 O′B,′比较木棒的影长 A′ B与′山的影长 AB ,即可近似求出山的高度 OB.假如 O′ B=′1 m,A′B=′2 m,AB =270 m,求山的高度.参照答案1---12CCDDC BBBBB CB13. 510814.5或6015.1∶3∶516. 517.(1,0)或(-5,-2)18.1219.(1)AC∥ A′C,′原因以下:∵△ ABC 与△A′B′是C′位似图形,∴△ ABC ∽△ A′B′C′.∴∠ A=∠C′A′∴B′AC.∥A′ C′.(2)∵△ABC ∽ △A ′B ′C′,∴AB=AC.∵AB =2A′B,′∴AC=2.又A′ B′A′ C′A′ C′1∵△ ABC 与△A′B′是C′位似图形,∴OC=AC=2.∵OC′=5,∴OC=10,CC′O′ C′A′ C′1=O C-OC′=10-5=5.20.(1)∵∠ DEC=∠FDC=90°,∠ DCE=∠FCD,∴△ DEC∽△ FDC.(2)∵F 为 AD 的中点, AD ∥BC,∴FE∶EC=FD∶BC=1∶2,∴FE∶ FC=1∶,设EF =,则FC=3x,∵△DEC∽△FDC,∴CE=CD,可得 6x2=12,解3x CD FC得 x= 2,则 CF=3 2,在 Rt△CFD 中, DF= FC2-CD2= 6,∴ BC=2DF=2 6.AC 30 5 AM 21.连结 MN ,图略.在△ ABC 与△ANM 中,∠ A=∠A,AB=54=9,AN=1=5,∴△ ABC ∽△ ANM ,∴AC=AM,即30=1,解得 MN =1.5.故 M ,1.8 9BC MN45MNN 两点之间的直线距离是 1.5 千米.111×4×2 22. (1)当 t=1 s时,S=S梯形EBCG-S△EBF-S△FCG=×(10+2) ×8-×10×4-222=24(cm2).(2)当点 F 在边 BC 上挪动时, F 与 B,E 能组成三角形且 F 与 C,G 能组成三角形,则 0<t<2,有 AE=CG=2t,EB=12-2t,BF=4t,FC=8-4t.在△EBF 和△中,∠=∠ =°,①若EB=BF,即12-2tFCG B=4t,解得 t=2,又 t=2C90FC CG8-4t2t33知足 0<t<2,因此当 t=2时,△ EBF∽△ FCG;②若EB=BF,即12-2t4t,2t=3GC CF8-4t333解得 t=2,又 t=2知足 0<t<2,因此当 t=2时,△ EBF∽△ GCF.综上所述,当t23=3或 t=2时,以点 E, B,F 为极点的三角形与以点 F,C,G 为极点的三角形相像.23.解:∵太阳光芒是平行线,∴∠ OAB =∠O′A′,B∵′OB⊥AB ,O′B⊥′A′B,′∴∠ ABO =∠A′B′=O′90°,∴△ OAB ∽△ O′A′,B′∴OB=AB,当 O′B=′1 m, O′ B′A′ B′OB 270A′ B=′2 m,AB =270 m 时,1=2,OB=135 m,∴山的高度为 135 m.。
2019年中考数学试卷20 年月日A4打印/ 可编辑2019年中考数学试卷1、如图,在Rt△ABC中,△C=90°,AB=10cm,AC:BC=4:3,点P从点A出发沿AB方向向点B 运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.(1)求AC、BC的长;(2)设点P的运动时间为x(秒),△PBQ的面积为y(cm2),当△PBQ存在时,求y与x的函数关系式,并写出自变量x的取值范围;(3)当点Q在CA上运动,使PQ△AB时,以点B、P、Q为定点的三角形与△ABC是否相似,请说明理由;(4)当x=5秒时,在直线PQ上是否存在一点M,使△BCM得周长最小,若存在,求出最小周长,若不存在,请说明理由.解:(1)设AC=4x,BC=3x,在Rt△ABC中,AC2+BC2=AB2,即:(4x)2+(3x)2=102,解得:x=2,∴AC=8cm,BC=6cm;(2)①当点Q在边BC上运动时,过点Q作QH⊥AB于H,∵AP=x,∴BP=10﹣x,BQ=2x,∵△QHB∽△ACB,∴,∴QH=x,y=BP•QH=(10﹣x)•x=﹣x2+8x(0<x≤3),②当点Q在边CA上运动时,过点Q作QH′⊥AB于H′,∵AP=x,∴BP=10﹣x,AQ=14﹣2x,∵△AQH′∽△ABC,∴,即:,解得:QH′=(14﹣x),∴y=PB•QH′=(10﹣x)•(14﹣x)=x2﹣x+42(3<x<7);∴y与x的函数关系式为:y=;(3)∵AP=x,AQ=14﹣x,∵PQ⊥AB,∴△APQ∽△ACB,∴,即:,解得:x=,PQ=,∴PB=10﹣x=,∴,∴当点Q在CA上运动,使PQ⊥AB时,以点B、P、Q为定点的三角形与△ABC不相似;(4)存在.理由:∵AQ=14﹣2x=14﹣10=4,AP=x=5,∵AC=8,AB=10,∴PQ是△ABC的中位线,∴PQ∥AB,∴PQ⊥AC,∴PQ是AC的垂直平分线,∴PC=AP=5,∴当点M与P重合时,△BCM的周长最小,∴△BCM的周长为:MB+BC+MC=PB+BC+PC=5+6+5=16.∴△BCM的周长最小值为16.2、(12分)如图,矩形ABCD中,点P在边CD上,且与点C、D不重合,过点A作AP的垂线与CB的延长线相交于点Q,连接PQ,PQ的中点为M.(1)求证:△ADP∽△ABQ;(2)若AD=10,AB=20,点P在边CD上运动,设DP=x, BM 2=y,求y与x的函数关系式,并求线段BM长的最小值;(3)若AD=10, AB=a,DP=8,随着a的大小的变化,点M的位置也在变化,当点M落在矩形ABCD 外部时,求a的取值范围。