Energy- Angular Correlation of Medium Energy Particles Produced in Heavy Ion Collisions

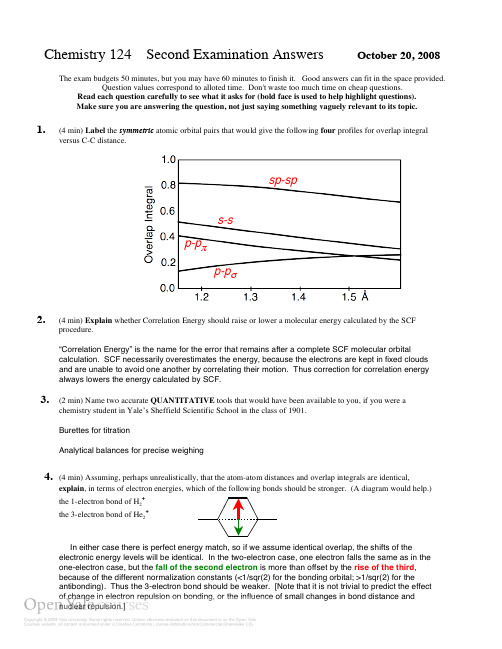
Chemistry 124 Second Examination Answers October 20, 2008The exam budgets 50 minutes, but you may have 60 minutes to finish it. Good answers can fit in the space provided.Question values correspond to alloted time. Don't waste too much time on cheap questions.Read each question carefully to see what it asks for (bold face is used to help highlight questions). Make sure you are answering the question, not just saying something vaguely relevant to its topic.1.(4 min) Label the symmetric atomic orbital pairs that would give the following four profiles for overlap integral versus C-C distance.2.(4 min) Explain whether Correlation Energy should raise or lower a molecular energy calculated by the SCF procedure.“Correlation Energy” is the name for the error that remains after a complete SCF molecular orbitalcalculation. SCF necessarily overestimates the energy, because the electrons are kept in fixed clouds and are unable to avoid one another by correlating their motion. Thus correction for correlation energy always lowers the energy calculated by SCF.3.(2 min) Name two accurate QUANTITATIVE tools that would have been available to you, if you were a chemistry student in Yale’s Sheffield Scientific School in the class of 1901.Burettes for titrationAnalytical balances for precise weighing4. (4 min) Assuming, perhaps unrealistically, that the atom-atom distances and overlap integrals are identical,explainthe 1-electron bond of H 2+ the 3-electron bond of He 2+In either case there is perfect energy match, so if we assume identical overlap, the shifts of theelectronic energy levels will be identical. In the two-electron case, one electron falls the same as in the one-electron case, but the fall of the second electron is more than offset by the rise of the third , because of the different normalization constants (<1/sqr(2) for the bonding orbital; >1/sqr(2) for theantibonding). Thus the 3-electron bond should be weaker. [Note that it is not trivial to predict the effect sp-sps-s p-p σp-p π5.(4 min) Use the idea of plum-pudding orbitals to rank these three one-node MOs of the water molecule (A,B,C) by their relative energy (low, medium, high ). Each orbital is shown in both top and side view, as is the molecular skeleton in the first row. Explain your reasoning in a very few words. (You need not give names or signs)6.(6 min) Use hybridization theory to explain whether the F-C-F angles of the •CF 3 radical should be larger or smaller than the H-C-H angles of the •CH 3 radical. Describe the experiment that justifies your prediction.This problem is discussed in detail in frames 15 and 16 of Lecture 14 and at the end of the XH 3 webpage. The idea is that because the electrons in the C-F bond spend more time on F than on C (because the F AO is lower in energy), the C finds it more profitable to use more than average low-energy s -character for the odd, unshared electron, which it has all to itself. Thus the bonding hybrids on C have less s -character, more p -character, and form sharper angles with one another. Thus the bond angles are smaller in •CF 3 than in •CH 3.The experimental evidence was from ESR, which measured a large splitting due to magnetic interaction between the 13C nucleus and an unpaired electron on the nucleus in an orbital with substantial s -character.[NOTE: Doubling of the IR “umbrella” frequency doesn ’t work here to demonstrate non-planarity, because F is so muchheavier than H that wave functions in the double minimum potential for umbrella distortion are much narrower than for NH 3 and do not overlap significantly, so tunnel splitting is negligible.Low Medium High ?BC ATop View Side ViewLowHighMediumFrom the “plum-pudding” perspective these are all 2p orbitals with a single nodal“plane”, and they would have the same energy except for differences in the location of the proton “plums” relative to the lobes of high electron density.They all have the C nucleus very near their node, but orbital C has the H nuclei very near the maximum electron density. It is thus the lowest in electronic energy. Orbital B is highest because all nuclei are on its nodal plane.7.(5 min) How was the Bürgi-Dunitz angle for attack of N on C=O established experimentally?This problem is discussed in detail in frame 13 of Lecture 17 and at the end of theC=O be attacked?” web page. They compared the locations of the N, C, “Where should R2O atoms, and of the R atoms directly attached to C in a large number of crystalstructures. In those structures in which the N was unusually close to the C, as if it were in the process of attacking the C=O LUMO, the N-C-O angle was about 110°.[A number of answers were faulty because they did not mention that theexperiments involved x-ray diffraction studies on many different crystals, in each ofwhich the “reaction” was arrested at a different stage because of other groups in themolecules running into one another.]8. (6 min) Use proper curved arrows to draw the 3 steps in a mechanistic scheme for conversion of NH3 to NH2NH3Cl by Cl2.This problem is discussed in detail in frame 5 of Lecture 17. It is important that curved arrows begin at the location of the relevant electron pair in the starting material and end where the pair is to be located in the product (on a lone pair, or between atoms to bebonded). Note that all the processes are “make & break”.9.(6 min) According to “resonance” the properties of an amide are different from those expected for a molecule withsimple carbonyl and amine groups. Briefly explain three different ways in which resonance influences theproperties of protein polymers that contain multiple amide groups.This problem is discussed in detail in frames 4 to 6 of Lecture 18 and on the Intramolecular HOMO/LUMO mixing and "Resonance" web page. The three importantare:results of internal mixing of the unshared pair of N with the pi*C=Oa) Special stability and lack of reactivity (raised LUMO, lowered HOMO). This makesproteins chemically stable.b) Enforced planarity and inhibition of rotation about the N-C(=O) bond. This reducesflexibility in the protein chain and helps to stabilize structures like the α-helix of Pauling(your chemical great-grandfather).c) N+ O polarity in a direction that caused favorable electrostatic interaction amongneighbors in the α-helix, making it more stable. This is often explained by saying thatthere is O•••H-N Hydrogen-bonding.10.(9 min) Using all of the following four moleculesaccount for significant reactivity, and EXPLAINUnusually high σC-Lienergy – low nuclear charge)Li-CH3Unusually low unmixed 2pfor an AO, but unshifted, thus lower that σ*C-H)Unusually low π*C=Nfrom 2p C AO because of poor p overlap andmismatch with lower-energy 2p N AO) R2C=N-HUnusually high unmixed sppair on N (lowish in energy for an AO, butunshifted, thus higher that σC-H)[Note that σ*N-Hpoorish energy match. The pKaof NH3strong acid]Unusually low σ*O-O2spOcharge)R-O-O-R[Note that σ*O-Hpoorish energy match. The pKaof H2very strong acid, but better than NH3.Poor overlap of 2sp Csmall shift of σC--CHOMO and σ*2H2H2。

流体力学中英文术语Index 翻译（Fluid Mechanics）Absolute pressure,绝对压力（压强）Absolute temperature scales, 绝对温标Absolute viscosity, 绝对粘度Acceleration加速度centripetal, 向心的convective, 对流的Coriolis, 科氏的field of a fluid, 流场force and，作用力与……local, 局部的Uniform linear, 均一线性的Acceleration field加速度场Ackeret theory, 阿克莱特定理Active flow control, 主动流动控制Actuator disk, 促动盘Added mass, 附加质量Adiabatic flow绝热流with friction,考虑摩擦的isentropic,等熵的air, 气体with area changes, 伴有空间转换Bemoullii’s equation and, 伯努利方程Mach number relations,马赫数关系式，pressure and density relations, 压力-速度关系式sonic point，critical values, 音速点，临界值，stagnation enthalpy, 滞止焓Adiabatic processes, 绝热过程Adiabatic relations, 绝热关系Adverse pressure gradient, 逆压力梯度Aerodynamic forces, on road vehicles, 交通工具,空气动力Aerodynamics, 空气动力学Aeronautics, new trends in, 航空学，新趋势Air空气testing/modeling in, 对……实验/建模useful numbers for, 关于……的有用数字Airbus Industrie, 空中客车产业Aircraft航行器airfoils机翼new designs, 新型设计Airfoils, 翼型aspect ratio (AR), 展弦比cambered, 弧形的drag coefficient of , 阻力系数early, 早期的Kline-Fogleman, 克莱恩-佛莱曼lift coefficient, 升力系数NACA,(美国) 国家航空咨询委员会separation bubble, 分离泡stalls and, 失速stall speed, 失速速度starting vortex, 起动涡stopping vortex, 终止涡Airfoil theory, 翼型理论flat-plate vortex sheet theory, 平板面涡理论Kutta condition, 库塔条件Kutta-Joukowski theorem, 库塔-儒科夫斯基定理1thick cambered airfoils, 厚弧面翼型thin-airfoils, 薄翼型wings of finite span, 有限展宽的翼型A-380 jumbo jet, 大型喷气式客机Alternate states, 交替状态American multiblade farm HA WT, 美式农庄多叶水平轴风机Angle of attack, 攻角Angle valve, 角阀Angular momentum角动量differential equation of , 关于…的微分方程relation/theorem, 联系/理论Annular strips, 环形带Applied forces, linear momentum, 外加力，线性冲力Apron,of a dam, 大坝的护坦Arbitrarily moving/deformable control volume, 任意运动/可变形控制体Arbitrary fixed control volume, 任意固定控制体Arbitrary viscous motion, 随机粘性运动Archimedes, 阿基米德Area changes, isentropic flow. 域变换，等熵流Aspect ratio (AR), 展弦比Automobiles, aerodynamic forces on, 汽车，气动力A verage velocity, 平均速度Axial-flow pumps. 轴流泵Axisymmetric flow, stream function 轴对称流，流函数Axisymmetric Potential flow, 轴对称有势流hydrodynamic mass, 水力学质量Point doublet, 点偶极子point source or sink, 点源与点汇spherical Polar coordinates and, 球极坐标uniform stream in the x direction, x方向的均匀流uniform stream plus a point doublet, 均匀流附加点偶极子uniform stream plus a point source, 均匀流附加点源BBackward-curved impeller blades, 后向曲叶轮片,Backwater curves, 回水曲线Basic equations, non dimensional, 基本方程，无量纲的Bernoulli obstruction theory, 伯努利障碍理论Bernoulli's equation, 伯努利方程with adiabatic and isentropic steady flow, as绝热、等熵稳态流frictionless flow, 无摩擦流assumptions/restrictions for, 假想/约束HGLs and EGLs, 水力坡度线和能量梯度线steady flow energy and, 定常流动能量in rotating coordinates. 在旋转坐标下，Best efficiency point (BEP), pumps, 最佳效率点，Betz number, 贝兹数Bingham plastic idealization, 宾汉塑性理想化，Biological drag reduction, 生物学阻力衰减Blade angle effects, on pump head, 叶片安装角效率，泵头处Blasius equation, 布拉修斯方程Body drag, at high Mach numbers, 机体阻力，在高马赫数下Body forces, 体力Boeing Corp., 波音公司Boundaries, of systems, 边界，系统Boundary conditions. 边界条件，differential relations for fluid flow, 流体的微分关系nondimensionalizalion and, 无量纲化Boundary element method (BEM), 边界元方法2Boundary layer (BL) analysis, 边界层分析boundary layer flows, 边界层流动boundary layer separation on a half body, 边界层半体分离displacement thickness, 位移厚度drag force and, 阻力equations, 方程flat-plate. 平板，Karman's analysis, 卡门分析momentum integral estimates, 动量积分估计momentum integral relation. 动量积分关系momentum integral theory, 动量积分理论pressure gradient 压力梯度separation on a half body, 半模分离skin friction coefficient, 表面摩擦系数two-dimensional flow derivation, 二维流推导Boundary layers with Pressure gradient, 边界层压力梯度adverse gradient, 反梯度favorable gradient, 正梯度laminar integral theory, 层流积分理论，nozzle-diffuser example,喷口扩散算例Bourdon tube, 波登管Bow shock wave, 弓形激波Brake horsepower,制动马力Broad-crested weirs, 宽顶堰Buckingham Pi Theorem, 白金汉定理Bulb Protrusion, 球形突出物（船头）Bulk modulus. 体积模量Buoyancy, 浮力Buoyant particles, local velocity and, 悬浮颗粒，局部速度Buoyant rising light spheres, 浮力作用下自由上升的球体Butterfly valve, 蝶形阀CCambered airfoils, 弓型翼Cauchy-Riemann equations, 柯西-黎曼方程Cavitation/Cavitation number, 气穴/气蚀数Celsius temperature scales, 摄氏温标Center of buoyancy, 浮心Center of Pressure (CP),压力中心，压强中心Centrifugal pumps, 离心泵backward-curved impeller blades, 后曲叶轮片blade angle effects on pump head, 泵头处叶片安装角效率brake horsepower, 制动马力circulation losses, 环量损失closed blades, 闭叶片efficiency of, 效率的elementary pump theory. 基泵理论Euler turbomachine equations, 欧拉涡轮机方程eye of the casing, 泵体通风口friction losses, 摩擦损失hydraulic efficiency, 水力[液压]效率mechanical efficiency.机械效率open blades, 开放式叶片output parameters, 输出参数power, delivered, 功率，传递pump surge, 泵涌，scroll section of casing, 卷形截面，泵体，shock losses, 激波损失vaneless, 无叶片的3volumetric efficiency, 容积效率[系数]water horsepower, 水马力Centripetal acceleration, 向心加速度Channel control Point, 传送控制点Characteristic area. external flows, 特征区域，外流Chezy coefficient, 薛齐系数Chezy formula, 薛齐公式Chezy coefficient,薛齐系数flow in a Partly full circular pipe, 流体非充满的圆管流Manning roughness correlation. 曼宁粗糙度关系，normal depth estimates, 法向深度估计Choking, 壅塞；堵塞of compressors, 压缩机的due to friction, compressible duct and, 由于摩擦，可压缩管的isentropic flow with area changes, 变横截面积等熵流simple heating and, 单纯加热Circular cylinder, flow with circulation. 圆柱体，Circulation环量and flow past circular cylinder, 流体经过圆柱体losses, in centrifugal pumps, 损失，离心泵potential flow and, 有势流Circumferential pumps, 环型泵Classical venturi, 标准文氏管Closed blades, centrifugal pumps. 闭叶片，离心泵Closed-body shapes, 闭体外形，circular cylinder, with circulation, 圆柱体，环量Kelvin oval, 开尔文椭圆，Kutta-Joukowski lift theorem,库塔－儒科夫斯基升力定理，Potential flow analogs, 有势流模拟Rankine oval, 兰金椭圆rotating cylinders. lift and drag, 旋转柱体，升力与阻力Coanda effect, 柯恩达效应( 沿物体表面的高速气流在Cobra P-530 supersonic interceptor, 眼镜蛇超音速拦截机Coefficient matrix. 系数矩阵Coefficient of surface tension, 表面张力系数Coefficient of viscosity, 粘滞系数Commercial CFD codes, viscous flow, 商业的计算流体力学代码，粘流Commercial ducts, roughness values for, 商业管道Composite-flow, open channels, 合成流，开槽道Compressibility, non dimensional. 压缩性，无量纲Compressibility effects, 压缩效果Compressible duct flow with friction, 伴有摩擦的可压缩管流adiabatic, 绝热的, 隔热的choking and, 壅塞；堵塞isothermal flow in long pipelines, 管线中的等温流动，long pipelines, isothermal flow in, 管线，等温流动，mass flow for a given pressure drop, 给定压降下质量流动minor losses in, 最小损失subsonic inlet, choking due to friction, 亚音速进口，摩擦引发阻塞，supersonic inlet, choking due to friction, 超音速进口，摩擦引发阻塞，Compressible flow, 可压缩流flow with friction摩擦流choking and, 壅塞；堵塞converging-diverging nozzles, 拉瓦尔喷管converging nozzles, 收缩喷嘴Fanno flow, 法诺流动，gas flow correction factor, 气流校正参数hypersonic flow, 高超音速气流4incompressible flow, 不可压缩流isentropic.等熵的isentropic Process, 等熵过程，Mach number, 马赫数normal shock wave. 正激波the perfect gas, 理想气体Prandtl-Meyer waves. 普朗特－麦耶膨胀波shock waves. 激波specific-heat ratio, 比热比speed of sound and,声速subsonic, 亚音速的supersonic,超音速的transonic, 跨音速的two-dimensional supersonic, 二维超音速的Compressible gas flow correction factor, 可压缩气流校正因数Compressors, 压缩机Computational fluid dynamics (CFD), 计算流体力学pump simulations, 泵模拟viscous flow. 粘流Concentric annulus, viscous flows in, 同心环Cone flows, 锥体绕流Conformal mapping, 保角映射[变换] Conservation of energy, 能量守恒定律Conservation of mass. 质量守恒定律Consistent units, 相容单元Constants, 常量dimensional, 空间的pure, 纯粹的Constant velocity, fluid flow at, 常速度, 等速度Constructs, 结构Contact angle, 交会角Continuity, 连续性，equation of ,方程nondimensionalization and, 无量纲的Continuum, fluid as, 连续流体Contraction flow, 收缩流动Control Point, channel, 控制点，管道Control volume analysis,控制体分析angular momentum theorem. 角动量定理，arbitrarily moving/deformable CV,任意运动/可变形控制体arbitrarily fixed control volume, 任意固定控制体conservation of mass, 质量守恒定律control volume moving at constant velocity, 控制体以等速运动control volume of constant shape but variable velocity作变速运动的刚性控制体energy equation. 能量方程introductory definitions, 介绍性定义linear momentum equation. 线性动量方程，one-dimensional fixed control volume, 一维固定控制体，one-dimensional flux term approximations, 一维通量项近似Physical laws. 物理定律。

a rXiv:n ucl-t h /961127v114Nov1996Medium effects in high energy heavy-ion collisions C.M.Ko and G.Q.Li Cyclotron Institute and Physics Department Texas A&M University,College Station,Texas 77843,USA The change of hadron properties in dense matter based on various theoretical approaches are reviewed.Incorporating these medium effects in the relativistic transport model,which treats consistently the change of hadron masses and energies in dense matter via the scalar and vector fields,heavy-ion collisions at energies available from SIS/GSI,AGS/BNL,and SPS/CERN are studied.This model is seen to provide satisfactory explanations for the observed enhancement of kaon,antikaon,and antiproton yields as well as soft pions in the transverse direction from the SIS experiments.In the AGS heavy-ion experiments,it can account for the enhanced K +/π+ratio,the difference in the slope parameters of the K +and K −transverse kinetic energy spectra,and the lower apparent temperature of antiprotons than that of protons.This model also provides possible explanations for the observed enhancement of low-mass dileptons,phi mesons,and antilambdas in heavy-ion collisions at SPS energies.Furthermore,the change of hadron properties in hot dense matter leads to new signatures of the quark-gluon plasma to hadronic matter transition in future ultrarelativistic heavy-ion collisions at RHIC/BNL.I.INTRODUCTIONAn important feature of quantum chromodynamics(QCD)is its approximate SU(3)L×SU(3)R chiral symmetry as a result of small quark masses[1].This symmetry is,however,spontaneously broken,leading to afinite quark condensate in vacuum, ¯q q 0≈ ¯u u 0≈ ¯dd 0,as given by the Gell−Mann-Oaks-Renner relation,m2πf2π=−2m q ¯q q 0.(1) In the above,mπ≈138MeV and fπ≈aµ93MeV are the pion mass and decay constant,respectively;and m q= (m u+m d)/2≈5.5MeV is the average up and down quark masses.The quark condensate in vacuum thus has a value ¯q q 0≈−(245MeV)3.As the density and/or temperature of a hadronic system increase,this spontaneously broken symmetry is expected to be partially restored,so the quark condensate would decrease with increasing density and/or temperature.At zero baryon chemical potential,the decrease of quark condensate with increasing temperature has been observed in lattice QCD simulations[2]as well as in calculations based on the chiral perturbation theory[3]and the interacting pion gas model[4].Atfinite baryon density,model-independent studies using the Feynman-Hellmann theorem[5,6]have shown that the ratio of the quark condensate in medium to its value in vacuum is given by¯q q ρρN,(2)f2πm2πwhereρN is the nuclear density andΣπN≈45MeV is theπN sigma term.At normal nuclear matter densityρ0≈0.16 fm−3,the condensate is seen to decrease already by≈1/3.Higher-order contributions to the quark condensate in nuclear matter due to nucleon-nucleon(NN)interactions have been studied using various models[6–11].It is found that at normal nuclear matter density they change the leading-order result by only about5%[9,11].The decrease of quark condensate in medium may lead to reduced hadron masses as shown in QCD sum-rule studies[12,13].The study of chiral symmetry breaking and partial restoration in hot dense matter is a topic of great current interest in nuclear physics[14–16].In high energy heavy-ion collisions,theoretical simulations based on transport models have shown that a hot dense hadronic matter is formed in the initial stage of the collisions.This provides thus the possibility of studying the partial restoration of chiral symmetry through the changes of hadron properties in medium[17–19].Unfortunately, the dynamics of heavy-ion collisions is very complex,involving a violent initial compression,which is then followed by a relatively slow expansion andfinally reaches the freeze out when particle interactions become unimportant.The entire reaction typically lasts for about a few tens fm/c.The interesting physics of hadron in-medium properties and chiral symmetry restoration can only be studied for a few fm/c during the early part of the expansion stage when both the density and temperature of the hadronic matter are high.This stage of the collision can in principle be probed by detecting the emitted electromagnetic radiation such as the real and virtual(dilepton)photons.However,both are not easy to measure due to their small rates.Furthermore,they can also be produced from initial hard collisions andfinal hadron decays,and this makes it difficult to extract the signals from the hot dense matter.What are usually measured in heavy-ion experiments are instead the momentum distributions of hadrons,such as the nucleon, nuclear clusters,pion,kaon,etc.,which are mostly ejected from the colliding system at freeze out.To infer what have happened in the initial hot dense matter from thefinal hadron phase space distributions requires thus a model thatcan describe the whole collision process.Indeed,various transport models have been developed during the past ten years for this purpose.We shall review briefly the history of the development of transport models.We note that a number of good review articles are available on both relativistic and nonrelativistic transport models for heavy-ion collisions at various energies[20–27].Since the reduced hadron masses in medium can be consistently included in the relativistic transport model[28–30] we shall concentrate mostly on the results obtained from this model.In the relativistic transport model,which is derived from the Walecka model[31,32],the effective hadron mass is connected to the scalarfield while its energy is shifted by the vector potential.Because of dropping hadron masses due to the attractive scalarfield,particle production is enhanced as a result of reduced threshold and increased phase space.Furthermore,the dense nuclear matter also provides a strong mean-field vector potential,which then affects the momentum distributions of hadrons. The relation of the Walecka model to the chiral effectivefield theory has recently been explored in Refs.[33–35]. The attractive scalar and repulsive vector potentials for a nucleon in nuclear matter have also been obtained in the Dirac-Brueckner-Hartree-Fock(DBHF)approach[36–41]as well as the QCD sum-rule studies[12,42–44].For heavy-ion collisions at energies available from the SIS at GSI,the relativistic transport model gives a satisfactory explanation for the observed enhancement of kaon[45–48],antikaon[49,50],and antiproton yields[51,52]as well as low energy pions in the transverse direction[53–55].Experiments on kaonflow have also provided important information on the kaon potential in dense matter[56,57].Furthermore,the study of dilepton production from these collisions is expected to allow us to probe directly the in-medium properties of vector mesons in dense matter[58,59].The relativistic transport model has also been used to describe the expansion stage of heavy-ion collisions at energies available from the AGS at BNL.It can account for the enhanced K+/π+ratio[60],the difference between the slope parameters of the K+and K−transverse mass spectra[61],and the lower apparent temperature of antiprotons than that of protons[62]as observed in experiments[63,64].For the expansion stage of heavy-ion collisions at energies available from the SPS at CERN,it has been found that the relativistic transport model can explain quantitatively the observed enhancement of low-mass dileptons if one includes the decrease of vector meson masses in hot dense matter[65–69].In a simplified hydrochemical model, medium effects also lead to enhanced production of phi mesons[70,71]and antilambdas[72,73]in these collisions. The success of theoretical studies including the medium effects in explaining a large body of experimental data from high energy heavy-ion collisions thus provides the possible evidence for the partial restoration of chiral sym-metry in hot dense matter formed in high energy heavy-ion collisions.The purpose of this article is to review the theoretical predictions for hadron properties in dense matter,the consistent incorporation of these medium effects in the relativistic transport model,and the observable consequences in heavy-ion collisions from SIS to SPS energies. In Section II,hadron properties in dense matter are discussed using various theoretical approaches,such as the Walecka model,the DBHF approach,the QCD sum-rule approach,and the effective hadronic model.The relativistic transport model based on the nonlinearσ-ωmodel is then described in Section III,together with a brief review of the development of transport models.In Section IV,the results obtained from the relativistic transport model for particle production andflow in heavy-ion collisions at SIS energies,the strangeness enhancement in heavy-ion collisions at AGS and SPS energies,and dilepton production in heavy-ion collisions are then presented and compared with the experimental data.The relevance of these experimental observables as the probes of hadron properties in dense matter is emphasized.A summary and outlook is then given in Section V.II.HADRONS IN DENSE MATTERTheoretically,lattice QCD simulations should provide us with the most reliable information about the temperature and/or density dependence of hadron properties.Currently,these simulations can be carried out only forfinite temperature systems with zero baryon chemical potential.Furthermore,the quenched approximation is usually introduced for quarks,so their dynamical role is only crudely included.From the hadronic correlation functions at large spatial separations the hadron screening masses have been obtained in the lattice QCD[74–76].In a recent paper,Boyd et al[76]have shown that,up to about0.92T c,where T c is the critical temperature for the quark-gluon to hadronic matter phase transition,there is no significant change of the rho-meson screening mass.They have also found that the quark condensate does not change very much until one is extremely close to the critical temperature. This is in contrast with the result from chiral perturbation theory which shows a more appreciable decrease of the quark condensate with temperature[3].Therefore,the study of hadron properties in dense nuclear matter at present time has to rely on theoretical models.In this section,we shall review some of these approaches.In particular,the properties of baryons(mainly nucleon),pseudoscalar mesons(mainly pion and kaon),and vector mesons(mainly rho, omega,and phi mesons)will be discussed.A.baryonsA simple model for nuclear matter at high density is the Walecka model,also known as the quantum hadrodynamics (QHD-I)or linearσ-ωmodel,in which nucleons interact with each other through the exchange of a scalar sigma and a vector omega meson[31,32].The sigma meson gives rise to an intermediate-range attraction while the omega exchange leads to a short-range repulsion,both are the essential properties of nuclear force.In this phenomenological model, the nucleon mass is reduced by the attractive scalar interaction,while its energy is shifted by the repulsive vector interaction.The parameters in this model are adjusted tofit the nuclear matter properties at saturation density using the mean-field approximation.This model gives,however,too small a nucleon effective mass and too large a compression modulus at saturation density compared to what are known empirically.To correct for these deficiencies,self interactions of cubic and quartic forms have been introduced for the scalarfield[77,78].The Lagrangian for this nonlinearσ-ωmodel is given byL=¯N[γµ(i∂µ−gωωµ)−(m N−gσN)]N+13bσ3−1(∂µων−∂νωµ)(∂µων−∂νωµ)+14matter.The equation of motion for a nucleon with momentum p in a nuclear matter of densityρN is then given by the Dirac equation(α·p+βm∗N)N=ǫ∗(p)N,(4)where the nucleon effective mass is related to the scalar potentialΣS=−gσ σ ,i.e.,m∗N=m N+ΣS,(5)and its energy is shifted by the vector potentialΣ0V=g2ωmσCω=gωm Ng3σm NC=cA(MeV)m∗Nsoft13.958.4980.0199-0.00296-15.960.83200.0 stiff15.9412.928.0×10−42.26×10−3-15.960.68380.0rapidly at high temperature.A similar temperature dependence of the constituent quark mass has been found in studies based on the Nambu−Jona-Lasinio model[83].Fig.1Left panel:The nucleon effective mass in medium.Solid and dashed curves are from the nonlinearσ-ωmodel and DBHF theory,respectively.Right panel:Nuclear equation of state.Dotted curves are from the Skyrme interaction.A more microscopic approach to nucleon properties in nuclear matter is provided by the DBHF calculation[37–41] using,e.g.,the Bonn one-boson-exchange potential[36,37].As in conventional Brueckner approach,the basic quantity in DBHF approach is the G-matrix which satisfies the in-medium Thompson equation[37,40,41],G(q′,q;P)=V(q′,q)+ d3k E∗2P/2+k Q(k,P)A =1E∗i+1E∗i E∗j ij|G|ij−ji −m N,(9)where the nucleon bare mass has been subtracted out.The G-matrix also allows one to determine the nucleon scalar and vector potentials in nuclear matter,i.e.,m∗NE∗i E∗j ij|G|ij−ji .(10) The nuclear equation of state and the nucleon effective mass obtained from the DBHF calculation with the Bonn A potential are shown in Figs.1by dashed curves.Nucleon properties in dense matter have also been studied in approaches based on the QCD.In the QCD sum-rule approach[5,12,42–44,84,85],hadron properties are related to a number of condensates,which are the vacuum expectation values of quark and gluonfields and describe the nonperturbative aspects of the QCD vacuum.The QCD sum rules have been quite successful in describing the hadron properties in free space,e.g,the nucleon mass is quantitatively reproduced in this approach[86–89].The extension of QCD sum rules to hadrons in nuclear matter is achieved by using in-medium condensates.For a nucleon,it has been shown that the change of scalar quark condensate in medium leads to an attractive scalar potential which reduces its mass,while the change of vector quark condensate leads to a repulsive vector potential which shifts its energy[12,42–44].The nucleon scalar and vector self-energies in this study are given,respectively,byΣπNΣS≈−8π2M2Bq+q ρ=32π23M2Bvarious attempts to generalize the Walecka-type model from SU(2)to SU(3)to include the hyperon degrees of freedom [103–106].In the naive SU(3)quark model,the hyperon potential is about2/3of the nucleon potential,as there are only two light quarks in a hyperon instead of three light quarks in a nucleon.Recently,hyperon properties in nuclear matter have also been studied using the QCD sum-rule approach.It has been found that both lambda scalar and vector potentials are significantly weaker than the prediction from the naive quark model[107],while those of the sigma hyperon are somewhat stronger and are close to the ones for the nucleon[108].The accuracy of these findings are,however,limited by uncertainties in the nucleon strangeness content and certain in-medium four-quark condensates.B.pseudoscalar mesonsPseudoscalar mesons play a special role in nuclear physics.On the one hand,they are the Goldstone bosons of spontaneously broken chiral symmetry and are thus closely related to chiral symmetry restoration in nuclear medium. Furthermore,their small masses make the chiral perturbation theory applicable for low energy phenomena[109–112]. On the other hand,in heavy-ion collisions,pions are the most copiously produced particles;e.g.,at SPS energies, the pion/nucleon ratio approaches10in midrapidity region.Knowledge on the properties of pseudoscalar mesons in medium is thus very important for understanding both chiral symmetry restoration and the dynamics of high energy heavy-ion collisions.1.pionPion properties in dense matter have been a subject of extensive studies over many years[113].The strong p-wave pion-nucleon interaction through the delta resonance is known to modify appreciably the pion dispersion relation at finite density[113–115].In the delta-hole model,the pion dispersion relation in nuclear medium can be written asω(k,ρB)=m2π+k2+Π(ω,k),(12) where the pion self-energy is given byk2χ(ω,k)Π(ω,k)=9 fπN∆ω2−ω2R exp −2k2/b2 ρN,(14) where fπN∆≈2is the pion-nucleon-delta coupling constant,b≈7mπis the range of the form factor,andωR≈k2Pion properties in dense matter have also been studied using the chiral perturbation theory[121,122].In effective chiral Lagrangians a pion has a negligible vector interaction with a nucleon.The s-waveπN scalar interaction, proportional to theπN sigma termΣπN,would lead to a reduction of the pion mass[121].This effect is,however, almost completely canceled by the range term from the energy dependence of theπN scattering amplitude,so the net mean-field effects are quite small[123],and the pion mass is found to increase only slightly with increasing density. This is consistent with the results determined from the pionic atom data[113].The Nambu−Jona-Lasinio model has also been used to study pion(or in general Goldstone boson)properties at bothfinite density and temperature[124,125].In this model,pseudoscalar mesons are treated as quark-antiquark collective modes.Because of thefinite scalar mean squared radius of a constituent quark,the s-waveπN attraction is found to be screened,leading to a slow increase of the pion mass with increasing density and/or temperature[125]. On the other hand,the pion mass is found to decrease slightly with temperature in an effective Lagrangian that includes its interactions in a pion gas via the rho and a1mesons[126].Fig.2The pion dispersion relation from the delta-hole model.(From Ref.[115])2.kaonThe study of kaon properties in dense matter has recently attracted a lot of attention as it is relevant for un-derstanding not only the strangeness enhancement in heavy-ion collisions,which has been suggested as a possible signature of quark-gluon plasma formation in these reactions[127],but also the kaon condensation in neutron stars [128]and the possible formation of mini-black holes in galaxies[129].The properties of kaon in dense matter werefirst studied in chiral Lagrangian by Kaplan and Nelson[130],and further pursued by many others[110–112,131–138].The SU(3)L×SU(3)R nonlinear chiral Lagrangian used by Kaplanand Nelson is written as[130,134,136]L=12f2Λ[Tr M q(Σ−1)+h.c.]+Tr¯B(iγµ∂µ−m B)B+i Tr¯Bγµ[Vµ,B]+D Tr¯Bγµγ5{Aµ,B}+F Tr¯Bγµγ5[Aµ,B]+a1Tr¯B(ξM qξ+h.c.)B+a2Tr¯BB(ξM qξ+h.c.)+a3[Tr M qΣ+h.c.]Tr¯BB.(15) In the above,B is the baryon octet with a degenerate mass m B,andΣ=exp(2iπ/f),andξ=√2(ξ+∂µξ+ξ∂µξ+)and Aµ=i8f2¯Nγ0N¯K↔∂tK+···,(20)whereN= p n and¯N=(¯p¯n),(21) and the ellipsis denotes terms involving other baryons and mesons.The last three terms in Eq.(15)can be similarly worked out,and the results areTr¯B(ξM qξ+h.c.)B=2m q¯NN−¯NNf2(m q+m s)¯KK+···,[Tr M qΣ+h.c.]Tr¯BB=2(2m q+m s)¯N N−2¯NNCombining above expressions,one arrives at the following Lagrangian,L=¯N(iγµ∂µ−m B)N+∂µ¯K∂µK−Λ(m q+m s)¯KK−3i2f2(m q+m s)(a1+2a2+4a3)+ (23)From this equation,one can identify the kaon mass bym2K=Λ(m q+m s)(24) and the nucleon mass bym N=m B−2[a1m q+a2m s+a3(2m q+m s)].(25) Also,the KN sigma term can be expressed asΣKN≡12(m q+m s) 1∂m q+∂m N2(m q+m s)(a1+2a2+4a3).(26) The second line in the above follows from explicit chiral symmetry breaking in the QCD Lagrangian,and the last step is obtained using Eq.(25).Then Eq.(23)can be rewritten asL=¯N(iγµ∂µ−m N)N+∂µ¯K∂µK−(m2K−ΣKN8f2¯Nγ0N¯K↔∂tK+ (27)The above Lagrangian does not describe properly the nuclear matter properties.In Ref.[134],an attempt has been made to combine this SU(3)L×SU(3)R chiral Lagrangian with the Walecka model[31,32]by allowing the nucleon toalso couple with the phenomenological scalar(σ)and vector(ω)fields so that the saturation properties of nuclear matter can be obtained in mean-field level.Possible justifications of this approach have been further studied in Ref. [139]based on the chiral perturbation theory.Following this approach,one modifies Eq.(27)toL=¯N(iγµ∂µ−m N+gσσ)N−gω¯NγµNωµ+L0(σ,ωµ)+∂µ¯K∂µK−(m2K−ΣKN8f2¯Nγ0N¯K↔∂t K+ (28)In the above,L0contains the kinetic and mass terms of theσandωfields as well as possible cubic and quarticσself-interaction terms.From the Euler-Lagrange equation and using the mean-field approximation for the nucleonfield,i.e.,replacing ¯Nγ0N by the nuclear densityρN and ¯NN by the scalar densityρS,one obtains the following Klein-Gordon equation for a kaon in nuclear medium,∂µ∂µ+3i f2ρS K=0.(29)The kaon dispersion relation in nuclear matter is then given byω2(k ,ρB )=m 2K +k 2−ΣKN4ωf 2ρS + 3f 2 2 1/2+3f 2.(31)Using the KFSR relation (m ρ=2√f 2m 2K ρS 1/2,(32)for both kaon and antikaon.In Ref.[136],the quadratic vector term, 3f 22,in Eq.(31)was discarded based on the expectation that it would be cancelled by higher order terms not included in the calculation.Then,the kaon “effective”mass should involve only the scalar field,while the vector mean field shifts the kaon chemical potential or energy,as in Walecka mean-field theory.From Eq.(31)one can define the kaon potential as the difference between its energies in the medium and in free space[56,143].In the mean-field approximation this potential at normal nuclear matter density is about10MeV for a kaon at rest.This is smaller than what is expected from the impulse approximation using the kaon-nucleon(KN) scattering length in free space which gives about30MeV.The inclusion of higher-order terms[110–112]and possible scaling of the pion decay constant f in medium[34,144,145]would bring the chiral perturbation results in agreement with that obtained from the KN scattering length.Fig.3Kaon and antikaon in-medium masses as functions of density from the mean-field approximation to the chiral Lagrangian.Antikaon properties in nuclear matter deserve some further discussions.The possibility of K−condensation in neutron stars has been the focus of many recent studies[110,146–149].The isospin averaged K−N scattering length is negative in free space[150],implying a repulsive K−optical potential in the simple impulse approximation.However, a systematic analysis of the kaonic atom data shows that the K−optical potential is deeply attractive,with a value of about200±20MeV at normal nuclear matter density[151].Unlike the kaon which interacts with nucleons relatively weakly so that the impulse approximation is reasonable,the antikaon interacts strongly with nucleons so we do not expect the impulse approximation to be reliable.The antikaon-nucleon(¯KN)interaction at low-energy is strongly affected by theΛ(1405)which is a quasi bound state of an antikaon and a nucleon in the isospin I=0channel and can decay intoΣπchannel[152,153].Thus,in principle one needs to carry out a coupled-channel calculation for ¯KN,ΛπandΣπincluding the effects ofΛ(1405)in both free space and in nuclear medium[152–157].Because of Pauli blocking effects on the intermediate states,the possibility of forming a bound¯KN state(Λ(1405))decreases with increasing density,leading to a dissociation ofΛ(1405)in nuclear medium.This induces a transition of the K−potential from repulsion at very low densities to attraction at higher densities[153,156].It was shown in Ref.[157], that,because of the diminishing role ofΛ(1405)in dense matter,the prediction for the kaon condensation threshold is relatively robust with respect to different treatments ofΛ(1405).Also,the strong attraction found in kaonic atoms can be understood in chiral perturbation theory if the possible scaling of the pion decay constant f in nuclear mediumis included[34,144,145].C.vector mesonsBased on the restoration of scale invariance of QCD,Brown and Rho have argued that masses of nonstrange vector mesons would be reduced in dense matter[158,159].This is supported by studies based on the QCD sum-rule approach [13],the effective hadronic model including¯NN vacuum polarization[160–162],and the quark-meson coupling model [163].In the QCD sum-rule study of vector meson masses in nuclear medium,one considers the correlation function of a vector current,Πµν(q)=i e iqx T Jµ(x)Jν(0) ρd4x,(33) In nuclear medium,it can be written asΠ00=q2ΠL,Πij= δij−q i q j q2ΠL,(34) whereΠT andΠL denote the transverse and longitudinal parts of the polarization tensor,respectively.At zero momentum,q=0,there is no distinction between the transverse and longitudinal directions,andΠL is thus related toΠT,i.e.,ΠT=(ω2−q2)ΠL,ΠL=−12.(36)For large Euclidean four momenta,Q2(=−q2=−s)→∞,ΠL(Q2)can be evaluated perturbatively by the operator product expansion(OPE)[88].Including operators up to dimension6,one hasΠL(Q2)=−1π log Q2Q4 ¯q q ρ+αsQ6 (¯qγµγ5λa q)(¯qγµγ5λa q) ρ−2παsπ θ(s−s0),(38)where F is a constant.The theoretical side (Q 2>0)and the phenomenological side (s >0)are related through the dispersion relation,ReΠL (Q 2)=Ps +Q 2+subtractions .(39)From the above equation,the rho meson mass m ∗ρand the continuum threshold s 0can then be determined.To suppress contributions from the higher order operators,one usually introduces the Borel transform defined byL M B =lim Q 2,n →∞;Q 2/n =M 2B1dQ 2 n ,(40)where M B is the Borel mass in Eq.(11).TheBorel transform also removes the need for subtractions in the dispersion relation.Carrying out the Borel transform of both sides of eq.(39)and taking the ratio of the resulting equation to itsderivative with respect to −1/M 2B ,one obtainsm ∗ρπ)[1−(1+s 0M 4B ¯q q ρ−αs π81M 6B ¯q q 2ρπ)(1−e −s 0/M 2B )+8π2m q 3M 4B G µνG µν ρ−448π3αs 9 ¯q q 2ρ,(¯q γµλa q )(¯q ′γµλa q ′) ρ≈−16πG µνG µν 0=(330MeV)4),quark mass (m q =5.5MeV),and QCD coupling constant (αs =0.3),the empirical rhomeson mass (776MeV)can be reproduced with s 0≈1.77GeV 2in the range of Borel masses 0.55≤M 2B ≤0.75GeV 2.In nuclear medium,vector meson masses depend on in-medium condensates.Because of small light quark masses,terms in Eq.(41)linear in quark condensates can be neglected.The results for ρand ωmesons in nuclear medium thus depend on the density dependence of four-quark condensates.For phi meson, ¯s s ρdominates due to the relatively large strange quark mass m s ≈100∼200MeV,its in-medium mass thus depends on the nucleon strangeness content as ¯s s ρ≈ ¯s s 0+ N |¯s s |N ρN ,where ¯s s ≈−0.8 ¯q q 0is the strange quark condensate in vacuum.Based on the factorization assumption for the four-quark condensate,i.e.,Eq.(42),and using a simple delta-function plus continuum ansatz for the vector meson spectral function as shown in Eq.(38),Hatsuda and Lee have obtained thefollowing results for the in-medium vector meson masses [13],m ∗ρ,ωm φ≈1−0.15y (ρN /ρ0).(44)The density dependence of rho(omega)and phi meson masses is shown in Fig.4,where the nucleon strangeness content is taken to be y=0.17.It is seen that the rho(omega)meson mass decreases significantly with density due to a strong density dependence of the light quark condensate.Since the strange quark condensate does not change much in nuclear medium as a result of the small nucleon strangeness content,the phi meson mass thus shows a weaker density dependence.However,the phi meson mass would decrease substantially if the temperature is high so that many strange particles are present and reduce thus the strange quark condensate[164].The temperature dependence of phi meson mass is shown in Fig.5and is seen to decrease significantly at high temperatures.We note that recent studies on phi meson mass atfinite temperature using the hidden gauge theory[165,166]show a much smaller reduction than that from the QCD sum rules.This may be due to the incomplete treatment of vacuum effects in the latter approach as it is carried out only at the one-loop level.Fig.4Rho and phi meson masses as functions of density from QCD sum rules.(from Ref.[13])A similar QCD sum-rule calculation of in-medium rho-meson mass has been carried out by Asakawa and Ko[167] using in the RHS of Eq.(39)a more realistic spectral function that is obtained by coupling the rho meson to pions via the vector dominance model and using the pion in-medium dispersion relation determined from the delta-hole model as discussed in Section II.B.1[168,169].A decrease of rho meson mass with increasing density as that of Ref.[13]has also been obtained.This is due to the stronger effect from reduced quark condensate in the presence of nucleons than that from the matter polarization.Vector meson masses have also been studied using effective hadronic models[160–162].Taking into account the change of¯NN vacuum polarization in medium as a result of reduced nucleon mass,the rho and omega meson masses have been found to decrease with density and temperature as in QCD sum-rule approach.If one includes only the matter effect,i.e.,the polarization of the Fermi sea,the rho meson mass is seen to increase at high density.The inclusion of the vacuum effect,i.e.,the polarization of the Dirac sea,however,brings the rho meson mass down in medium.The modification of the vacuum polarization in effective hadronic models is thus related to the change of quark condensate in medium in the QCD sum-rule approach.Since the nucleon is a composite particle,the large。

AIM – (Atoms In Molecule) An analysis method based upon the shape of the total electron density; used to define bonds, atoms, etc. Atomic charges computed using this theory are probably the most justifiable theoretically, but are often quite different from those from older analyses, such as Mulliken populations.AO – (Atomic Orbital) An orbital described by wavefunction for a single electron centered on a single atom.AOM – (Angular Overlap Model)AM1 – (Austin Model 1) Dewar's NDDO semiempirical parameterization.ASE – (Aromatic Stabilization Energy)BAC-MP4 –(Bond Additive Corrections to energies from Møller-Plesset 4th order perturbation theory) empirical corrections to calculated energy based (exponentially) on bond lengths.Bader's analysis – see AIMBasis Set –finite set of functions used to approximately express the Molecular Orbital wavefunction(s) of system, normally atom centered, consisting of AOs differing in local angular momentum for each atom.BCUT – (Burden CAS University of Texas) topological molecular similarity index of Burden. BDE – (Bond Dissociation Energy)BSSE – (Basis Set Superposition Error) error introduced when the energy of two molecules modeled together is lower than the sum of the energies when modeled separately, because more basis sets are available for each fragment (more degrees of freedom) during the calculation. Minimal basis sets can have less BSSE because only diffuse functions can span a to b. A particular problem for binding energies of weakly bonded molecular complexes, less with more complete basis sets.BLYP – (Becke-Lee-Yang-Parr)bohr - One atomic unit of distance, equal to 0.5292 Å.CADPAC – (Cambridge Analytical Derivatives PACkage)CAS – (Complete Active Space)CASPT – (Complete Active Space Perturbation Theory)CASSCF –(Complete Active Space Self-Consistent Field) popular variant of the MCSCF method, using a specific choice of configurations. One selects a set of active orbitals and active electrons, then forms all of the configurations possible by placing the active electrons in the active orbitals, consistent with the proper spin and space symmetry requirements. Essentially equivalent to the FORS method.CBS-QCI –(Complete Basis Set Quadratic Configuration Interaction) alternative extrapolation algorithm to complete basis set.CC –(Coupled Cluster) A perturbation theory of electron correlation with an excited configuration that is "coupled" to the reference configuration. Complete to infinite order, but only for a subset of possible excitations (doubles, for CCD). Newer than CI.CCD – (Coupled Cluster, Doubles only.) Complete to infinite order for doubles excitations. CCSD – (Coupled Cluster, Singles and Doubles only.) Complete to � order for singles & doubles excitations.CCSD(T) – (Coupled Cluster, Singles and Doubles with Triples treated approximately.) Size consistent. ΔHdiss ± 1.0 kcal/molCCSDT – (Coupled Cluster, Singles, Doubles and Triples)CCSS –(Correlated Capped Small Systems) Special case of IMOMO. See Truhlar's and Hass's work.CEPA – (Coupled Electron Pair Approximation)CFF – (Consistent Force Field) Class II force field based on ab initio data developed by Biosym Consortium/MSI.CFMM – (Continuous Fast Multipole Method) linear scaling method for matrix formation for DFT.CFSE – (Crystal Field Stabilization Energy)CHA – (Chemical Hamiltonian Approach) excludes BSSE effects from wavefunction w/ BSSE free Hamiltonian.CHF – (Coupled Hartree-Fock method)CHELP – (CHarges from Electrostatic Potential) an attempt to obtain atomic charges by fitting the electrostatic potential to a set of atomic point charges. The key component to theCHELP method is that it is non-iterative, rather using a Lagrangian multiplier method.chemical shift tensor –representation of the chemical shift. 3x3 matrix field felt in a direction induced by current due to applied field in b direction.CI – (Configuration Interaction) The simplest variational approach to incorporate dynamic electron correlation. Combination of the Hartree-Fock configuration (Slater determinant) and a large set of other configurations is used as a many e- basis set. The expansion coefficients are determined (in principal) by diagonalizing the Hamiltonian matrix and variationally minimizing the total energy of the CI wavefunction. Not size consistent.CID – (Configuration Interaction, Doubles substitution only) post-Hartree-Fock method that involves configuration interaction where the included configurations are the Hartree-Fock configuration and all configurations derived from doubles substitution.CIDEP – (Chemically Induced Dynamic Electron Polarization)CIDNP – (Chemically Induced Dynamic Nuclear Polarization)CIS – (Configuration Interaction with Singles excitations) simplest method for calculating electronically excited states; limited to singly-excited states. Contains no e- correlation and has no effect on the ground state (Hartree-Fock) energy.CISD –(Configuration Interaction, Singles and Doubles substitution only) post-Hartree-Fock method that involves configuration interaction where the included configurations are the Hartree-Fock configuration and all configuration derived from singles and doubles substitution. Comparable to MP2.CKFF – (Cotton-Kraihanzel Force Field)CNDO –(Complete Neglect of Differential Overlap) The simplest of the semi-empirical methods. The principle feature is the total neglect of overlap between different orbitals. In other words, the overlap matrix S is the unit matrix. The only two-electron integrals kept are those where electron 1 is in just one orbital and electron 2 is in just one orbital. Like all semiempirical methods the integrals are evaluated empirically.Combinatorial Chemistry – testing a large number of related compounds (as a mixture?) to find a compound that is active.CoMFA – (Comparative Molecular Field Analysis) technique used to establish 3-D similarity of molecular structure in relation to a target property.COMPASS –(Condensed-phase Optimized Molecular Potentials for Atomistic Simulation Studies) Molecular Mechanics force field derived from Class II force field, but optimized forcondensed phase properties.contraction – the particular choice of scheme for generating the linear combinations of Gaussian functions that constitute a contracted basis set. A "generally-contracted" basis set is one in which each primitive is used in many basis functions. A "segmented" basis set, in contrast, is one in which each primitive is used in only one (or maybe two) contracted function.COOP – (Crystal Overlap pOPulation)Correspondence Principle –classical mechanics becomes a special case of quantum mechanics at larger masses/scale.COSMO – (Conductor-Like Screening Model) implicit solvation model of Andreas Klamt. Considers macroscopic dielectric continuum around solvent accessible surface of solute. Less sensitive to outlying charges then PCM.COSMO-RS – (COSMO for Realistic Solvents) describes solute and solvent on the same footing. Allows for realistic calculations of fluid thermodynamics: partition coefficients, solubilities, activity coefficients, vapor pressures, & phase diagrams.Coulomb integral –1-center, 2 electron integral in Hamiltonian. Represents localized contribution of e- pair (in A+B- or A-B+) to bonding.CP –(Counter Poise) correction method for BSSE based on assumption of additivity of effects caused by BSSE on intermolecular interactions. The BSSE is approximated as the energy difference between (1) an isolated fragment and (2) t fragment accompanied by the basis functions, but not the atoms, of its companion fragment(s).CPHF – (Coupled Perturbed Hartree-Fock )CVFF – (Consistent Valence Force Field)Density Matrix –DFT – (Density Functional Theory) ab initio electronic method from solid state physics. Tries to find best approximate functional to calculate energy from e- density. Scales as 2nd power times a large number. Static correlation built in. Not variational. Believed to be size consistent.diffuse –refers to basis functions that are typically of low angular momentum (unlike polarization functions) but with much smaller exponents, so that they spread more thinly over space. Usually essential for calculations involving negative ions or Rydberg states.DIIS – (Direct Inversion in the Iterative Space) Pulay's extremely efficient, extrapolation procedure, to accelerate the convergence of the SCF in Hartree-Fock calculations. DISCO –DOS – (Density Of States)dynamic correlation – All the correlation energy or correlation effect that is not considered "nondynamic" or "static." Essential for dispersion interactions.DZ – (Double-Zeta) A basis set for which there are twice as many basis functions as are minimally necessary. "Zeta" (Greek letter z) is the usual name for the exponent that characterizes a Gaussian function.DZP – (Double-Zeta with Polarization functions added) A polarization set generally has an angular momentum one unit higher than the highest valence function. So a polarization set on carbon is a set of d-functions.ECP = pseudopotential – (Effective Core Potential) The core electrons have been replaced by an effective potential. Saves computational expense. May sacrifice some accuracy, but can include some relativistic effects for heavy elements.EFFF – (Energy Factored Force Field)EHT – (Extended Hückel Theory)electron correlation – explicitly considering the effect of the interactions of specific e- pairs, rather than the effect each e- feels from the average of all the other e-. High correlation effects for e- rich systems, transition states, "unusual" coordination numbers, no unique Lewis structure, condensed multiple bonds, radicals, & biradicals.Embedded Cluster –Sauer's (and Teunissen's and others) approach to modeling large/extended systems, using a high accuracy (QM) method for the important site, and a less accurate (MM) method for the environment. Subtract out duplicated overlap term, in case of extended system. See also IMOMM, and CCSS.ESFF – (Extensible & Systematic Force Field) Rule based force field designed for generality rather than accuracy by Biosym/MSI.ESP – (ElectroStatic Potential) The electrical potential due to the nuclei and electrons in the molecule, as experienced by a test charge.exchange energy – Also called "exchange correlation energy." The energy associated with the correlation among the positions of electrons of like spin. This is included in Hartree-Fockcalculations.Exchange integral – integral in Hamiltonian centered on 2 atoms. Corresponds to covalent bond term.FMO – (Frontier Molecular Orbital Theory) reaction controlled by interaction and overlap (energy, symmetry, accessibility) of frontier MO. Fukui calculation of weighted contributions, but dominated by HOMO for electrophilic, LUMO for nucleophilic susceptibility, closest energy for free radical superdelocalizability.Fock Matrix – 1 particle/e- Hamiltonian; matrix of 1 e-, 2 e- Coulomb, & 2 e- Exchange integrals in total energyFock Operator – replaces the Hamiltonian Operator in the Schrödinger equation for a spin orbital/single electron in a mean field of the other electronsFORS – (Fully Optimized Reaction Space) The FORS method, first proposed by Ruedenberg and coworkers, is essentially equivalent to the CASSCF method, except for the implementation of the MCSCF.G1, G2 –(Gaussian 1 theory, Gaussian 2 theory) empirical algorithm to extrapolate to complete basis set and full correlation (beyond MP2/6-31G**) from combination of lower level calculations: HF/6-31G(d) frequencies; MP2/6-311G(dp) geometries; single point energies of MP4SDTQ w/ 6-311G**, 6-311+G** & 6-311G**(2df) and QCISD(T)/6-311G**. Practical up to ~7 heavy atoms. Cons: Cl, F BDE's. ΔHf ± 1.93 kcal/molG3 – (Gaussian 3 "slightly empirical" theory) extension of G2, add systematic correction for each paired e- (3.3 mHa) & each unpaired e- (3.1 mH a). ΔHf ± 1.45 kcal/molGaussians – functions frequently used as primitive functions to expand total wave function. Typically defined with Cartesian coordinates w/ respect to a point in space.GAPT – (Generalized Atomic Polar Tensor) A method for determining atomic charge on the basis of dipole moment derivatives.GGA –(Generalized Gradient Approximation) Corrects local density approximation by including a functional of the density gradient (i.e., f[grad rho]) in addition to the local functional. Favors greater densities and inhomogeneity, overcomes LDA tendency to overbind. Uses scale factors from density & 1st derivative of density. Adds ~20% to compute time.ghost function – A basis function that is not accompanied by an atomic nucleus, usually for counterpoise corrections for BSSE.GIAO –(Gauge Independent Atomic Orbitals) Ditchfield's method for canceling out the arbitrariness of the choice of origin & form (gauge) of the vector potential used to introduce the magnetic field in the Hamiltonian when calculating chemical shielding and chemical shift tensor. An exponential term containing the vector potential is included with each atomic orbital. Originally developed based on Hartree-Fock, improved by Pulay w/ DFT to be faster, also used w/MP2 & CCSD. Pros: less basis set dependence than IGAIMGreen's Function – inverse of the Hessian Matrix.GTO –(Gaussian-Type Orbital) Basis function consisting of a Gaussian function, i.e., exp(-r2), multiplied by an angular function. If the angular function is "Cartesian", there are six d-functions, ten f-functions, etc. (6d, 10f). If the angular function is spherical, there will the usual number of functions (5d, 7f).GUGA – (Graphical Unitary Group Approximation)GVB –(Generalized Valence Bond) Bill Goddard's "laid back Southern California wavefunctions." Equivalent to MCSCF correlation treatment: 2 configurations used to represent each e- pair and solved for 2 associated orthogonal functions. Excitations are taken within an electron pair but not between orbitals in different pairs Dissociation-consistent. If restricted to doubles, is called "perfect pairing" (GVB-PP). If includes both singles and doubles, is called "restricted configuration interaction" (GVB-RCI).Hamiltonian –Matrix of bare nucleus, 0 e- Fock Matrix. Matrix that operates on wavefunction to calculate the energy in Schrödingers equation.hartree – One atomic unit of energy, equal to 2625.5 kJ/mol, 627.5 kcal/mol, 27.211 eV, and 219474.6 cm-1.Hessian – Matrix of mass normalized 2nd derivatives of energy with respect to nuclear displacement in Cartesian coordinates. Diagonalized to determine normal modes & calculate vibrational frequencies.HF – (Hartree-Fock) Named after the developers of the most widely practiced method for solving the Schrödinger Equation for multi-electronic systems. The Hartree-Fock approximation (sometimes called the Self-Consistent Field Approximation) assumes a single (Slater) determinant wavefunction, or in other terms, the standard molecular orbital model. Approximates the molecular, all e- wavefunction as product of single e- wavefunctions, and approximate molecular wavefunctions as LCAO. Orbitals that contain e- are occupied, those that are vacant are called "virtual." The orbital for each electron is determined in the average field of the other electrons, and iterated until self-consistency is achieved. Uses exact form of the (electronic) Hamiltonian Operator in Schrödinger’s equation, and tries to find the best approximate wavefunction. Scales as n^3-4.HMO – (Hückel Molecular Orbital theory)HOMO – (Highest Occupied Molecular Orbital) The occupied molecular orbital having the greatest energy. In Frontier Molecular Orbital theory the HOMO plays a significant role in determining the course and barrier to reactions. The energy of this orbital approximates the ionization energy of the molecule by Koopman's Theorem.HONDO –IEHT – (Iterative Extended Hückel Theory)IEPA –(Independent Electron Pair Approximation) An alternative method to the CI approach for obtaining electron correlation. Assumes the correlation energy is pair-wise additive: the correlation energy for each pair of electrons is obtained independently of all other electrons and then summed up. The method was developed by Sinanoglu (who called it Many-Electron Theory or MET) and Nesbet (who called it Bethe-Goldstone Theory).IGLO –(Individual Gauge for Localized Orbitals) Kutzelnigg & Schiendler's method for canceling out the arbitrariness of the choice of origin & form (gauge) of the vector potential used to introduce the magnetic field in the Hamiltonian when calculating chemical shielding & chemical shift tensors at nuclei. An exponential term containing the vector potential premultiplies MOs that have been localized in real space. Faster than HF based GIAOIMOMM – (Integrated Molecular Orbital & Molecular Mechanics) Morokuma's method to extrapolate to high level calculation on large systems by integrating addition of ΔE between large system and small model systems calculated at low level (MM), to the energy of the small model calculated at a high level (MO).IMOMO – (Integrated Molecular Orbital & Molecular Orbital) same as IMOMM with high (ab initio) and low level (semiempirical) MO calculations.INDO –(Intermediate Neglect of Differential Overlap) A semiempirical method closely related to the CNDO method, where all terms of the Fock matrix used in CNDO are included, but the restriction that the monocentric two-electron integrals all be equal is lifted. internal coordinates –Bond lengths, bond angles, and dihedral (torsional) angles; sometimes called "natural coordinates."IRC – (Intrinsic Reaction Coordinate) An optimized reaction path that is followed downhill, starting from a transition state, to approximate the course (mechanism) of an elementary reaction step. (Ignores tunneling, contribution of vibrationally excited modes/partition function, etc.)isodesmic –a chemical reaction that conserves types of chemical bond. Due to bettercancellation of systematic errors, energy changes computed using such reactions are expected to be more accurate than those computed using reactions that do not conserve bond types.isogyric –a chemical reaction that conserves net spin. Due to better cancellation of systematic errors, energy changes computed using such reactions are expected to be more accurate than those computed using reactions that do not conserve spin.Koopman's Theorem – the ionization potential can be approximated by the energy of the HOMO. Errors from neglect of e- correlation & e- relaxation tend to cancel for IP, but compound for trying to approximate EA from LUMO energy.LCAO – (Linear Combination of Atomic Orbitals) Molecular orbitals are usually constructed as a linear combination of atomic orbitals. The coefficients in this expansion are determined by solving the Schrödinger equation, typically in the Hartree-Fock approximation.LDA = LSDA – (Local Density/Spin-Density Approximation) A DFT method involving only local functionals: those that depend only upon the value of the density, f[rho]: no dependence upon the gradient of the electron density.level shifting – method to avoid oscillations during SCF convergence by artificially raising the energies of the virtual orbitals to separate the different states.LFER – (Linear Free Energy Relationship)LNDO – (Local Neglect of Differential Overlap)LORG – (Localized Orbitals, Local Origin) Hansen & Bouman Gauge invariant method for calculating chemical shielding & chemical shift tensors: expanding angular momentum terms relative to local origin for each orbital so no reference to gauge origin. Similar to IGLO.LST – (Linear Synchronous Transit) An interpolative method to provide an initial guess for a transition state. Assumes each atom position in the transition state is in a direct line between its position in the reactants and its position in the products.LUMO – (Lowest Unoccupied Molecular Orbital) The unoccupied molecular orbital having the lowest energy. In Frontier Molecular Orbital theory the LUMO plays a significant role in determining the course and barrier to reactions. The energy of the LUMO is a poor approximation of the EA.Madelung Potential – a set of point charges used to represent a solid continuum.MBPT = Møller-Plesset Perturbation Theory – (Many Body Perturbation Theory)MC – (Monte Carlo) method of sampling based on generating random numbers.MCCM – (Multi Coefficient Correction Method) Truhlar's method to scale each component of the correlation energy to extrapolate to full correlation: HF, MP2, and MP4 terms. MCPF – (Modified Couple Pair Functional)MCSCF – (MultiConfiguration Self-Consistent Field) A limited type of CI. A simple extension of the SCF approach to include non-dynamic electron correlation, with the added feature of orbital optimization. A number of configurations are chosen in some manner, then both the expansion coefficients and the orbital coefficients are optimized.MD – (Molecular Dynamics) method of sampling geometries based on Newtonian laws of motion.MEP – (Molecular Electrostatic Potential)MERP – (Minimum Energy Reaction Path)MINDO –(Modified Intermediate Neglect of Differential Overlap) Refers to the parametrization set (and computer code) developed by the Dewar group for performing INDO calculations. The most useful of the MINDO series is MINDO/3.Minimal Basis Set – The smallest # of functions needed to hold all electrons and still be spherical. Commonly refers to STO-3G.MM – (Molecular Mechanics) classical description of molecules as atoms held together by spring-like bonds. Chemical "Hamiltonian" based on force constants.MM2 –(Molecular Mechanics, Allinger Force Field version 2) one of the earliest, and probably the best known and tested Molecular Mechanics force field for organic molecules. MMFF – (Merck Molecular Force Field)MMP2 –(Molecular Mechanics, Allinger Force Field version 2 with Pi electrons handled quantum mechanically). Pi bond stretch calculated on the fly based on simple SCF bond order.MM3 – (Molecular Mechanics, Allinger Force Field version 3)MNDO –(Modified Neglect of Diatomic Overlap) Dewar’s first parametrization of the NDDO semiempirical method. First incorporated into the MOPAC program.MNDOC –(Modified Neglect of Diatomic Overlap Correlated) Thiel’s version of MNDO whichincludes limited configuration interaction.MNDO/d – (MNDO with d-orbitals) Thiel's version of MNDO with extra set of orbitals for second row transition and main group elements.MO – (Molecular Orbital) An orbital described by the wavefunction for a single electron in a molecule, usually delocalized across the entire molecule. Usually, molecular orbitals are constructed as combinations of atomic orbitals.MP2 –(Møller-Plesset theory, 2nd order) Møller-Plesset developed the perturbative approximation to include electron correlation, using the Hartree-Fock wavefunction as the zeroth order wavefunction. MP2 refers to the second order energy correction. Comparable to CISD.MP3 –(Møller-Plesset Theory, 3rd order) A perturbative approximation for including electron correlation, using the Hartree-Fock wavefunction as the zeroth order wavefunction. MP3 refers to the third-order energy correction.MP4 –(Møller-Plesset Theory, 4th order) A perturbative approximation for including electron correlation, using the Hartree-Fock wavefunction as the zeroth order wavefunction. MP4 refers to the fourth order energy correction. MP4 as implemented in GAUSSIAN can be calculated using various configurations. For example, MP4SDQ means that all terms involving singles, doubles and quadruples configurations are included through fourth order.MPA – ( Mulliken Population Analysis)MR – (Multi-Reference)MRCI –(Multi-Reference Configuration Interaction) CI using more that one reference determinant, instead of the usual single Hartree-Fock reference (ie. the ground state wavefunction). Among multi-reference theories, MR-CISD (singles and doubles CI) is popular and high-level (but not dissociation consistent).Mulliken Charges – Charges are assigned to each atom from an electronic calculation, by arbitrarily attributing the e- density of the diagonal terms (single atom terms) to each atom, plus half of the e- density of each off-diagonal term for that atom. Very sensitive (<100%) to basis set.NAO – (Natural Atomic Orbital)natural orbital – those orbitals for which the first-order density matrix is diagonal; each will contain some non-integer number of electrons between 0 and 2. Usually discussed in the context of a correlated calculation. RHF calculations give molecular orbitals that are also natural orbitals. The NOs are the orbitals for which the CI expansion converges fastest.Particularly valuable in modeling organometallic complexes.NEMD – (Non Equilibrium Molecular Dynamics) MD w/ applied forces, such as shear. NBO –NDDO – (Neglect of Differential Diatomic Overlap) This semiempirical method that keeps all terms of the Fock matrix except those involving diatomic differential overlap: the only two-electron terms, are those where e- 1 is in one orbital on atom A and e- 2 is in one orbital on atom B.NPA – (Natural Population Analysis) A method for determining atomic charge distributions in a molecule. Based on creating atomic natural orbitals from the molecular orbitals, by finding eigenfunctions of atomic sub-blocks of the molecular density matrix, based on chemical concepts of bonds, lone pairs, etc. Fairly independent of basis set.OPLS – (Optimized Potentials for Liquid Simulations) force field for condensed (aqueous) simulations. Electrostatic only for H-bond, "Disappearing L-J" H-bond.ONIOM – (Our own N-layered Integrated molecular Orbital molecular Mechanics method) Morokuma's generalized method for modeling large/condensed systems. Model critical part of chemical system with a high accurate/level method, intermediate region with a less expensive method, outer region approximately.orbital – the wavefunction describing where an e- is in an atom or molecules. Usually an eigenfunction of a one-electron Hamiltonian, e.g., from Hartree-Fock theory. A spin orbital has an explicit spin and a spatial orbital does not. Orbitals are probably the most useful concept from quantum chemistry: one can think of an atom or molecule as having a set of orbitals that are filled with electrons (occupied) or vacant (unoccupied or "virtual".Pauling point – calculation that gives a good result because systematic, but opposed errors cancel out.PCI –(Parameterized Configuration Interaction) empirical scaling of contribution of dynamic correlation to bond strengths. See Siegbahn, Blomberg, et. al.PCM – (Polar Continuum Model) implicit solvation model of Tomasi.PES –(Potential Energy Surface) The 3N-6 (or 3N-5, for linear molecules) dimensional function that indicates how the molecule's energy depends upon its geometry. Perturbation Theory – approximation to include electron correlation, based on T aylor Series expansion of the Hartree-Fock wavefunction (1 e- Hamiltonian) as the 0th orderwavefunction, for E in Schrödinger equation, truncated after n terms.PM3 – (Parametric Method number 3) A re-parameterized version of AM1 by Stewart. PMO – (Perturbation Molecular Orbital theory)PNDO – (Partial Neglect of Differential Overlap)polarized – basis set that includes functions that are of higher angular momentum than is minimally required. (Combination of p-orbitals added to the valence s-orbitals, or d-orbitals in addition to valence p-orbitals on carbon, for instance.) The added functions are often called "polarization functions." Polarization functions help to account for the fact that atoms within molecules are not spherical.PPP – (Pariser-Parr-Pople)PRDDO – (Partial Retention of Diatomic Differential Overlap)primitive – individual Gaussian functions used singly to produce a contracted basis function: a set of p-functions is three basis functions, but may be many primitives (3n, where there are n primitives in the cGTO).PRISM – (Polymer Reference Interaction Site Model) Adaptation of RISM theory for liquid polymers by Schweizer & Curro. Based on single chain conformational statistics and interaction potentials.PUHF – (spin-Projected UHF) An approximation to provide the energy that would result from a UHF calculation, if it did not suffer spin-contamination. The PUHF energy is usually lower than the UHF energy because the contributions of higher-multiplicity states, which usually have high energies, have been (approximately) subtracted.QCI –(Quadratic Configuration Interaction) CI method with terms added to confer size-consistency. An approximation to coupled-cluster theory.QCISD(T) – (Quadratic Configuration Interaction with all Single and Double excitations and perturbative inclusion of Triple excitations) post Hartree-Fock method. Similar results to QCISDT, used in G2. Scales as n^7.QCPE –(Quantum Chemistry Program Exchange) The Quantum Chemistry Program Exchange is a warehouse of chemistry computer codes. They have operated since 1962, providing a depository of what is now well over 600 different programs. QCPE can be contacted at QCPE Creative Arts Building 181 Indiana University Bloomington, IN 47405 USA telephone: (812)855-4784 fax: (812)855-5539 E-mail: ****************.edu anonymous ftp access: 。

部分造纸英文缩写AAA = atomic absorption原子吸收ABS = acrylonitrile－buladrene styrene丙烯腈—丁；烯—苯乙烯ACAR = angular correlation of annihilation radiation消除辐射的角相关性AM = acrylamide丙烯酰胺AOX = adsorbable organic halides可吸附的有机卤化物AP = plkali pulp碱法纸浆APAM = anionic polyacrylamide阴离子型聚丙烯酰胺ASB = aerotion stabilization basin稳定曝气池AST = activated sludge treatment活性污泥处理BBCT = best convential pollutant cotrol technology最常用污染物控制技术BDMT = bone dry metric tons绝干公吨BME = bipolar membrane electro dialysis两极膜电透析BMP = best management practices最优管理实践BOD = biochemical oxygen demand生化耗氧量BP = boiling point沸点BPK = bleached papergrade kraft and soda(生产)白纸用硫酸盐和荷性纳法浆BPT = best practicable control technology最佳实用控制技术BTU = british thermal unit英热单位BW = basis weight定量CCAD = computer aided design计算机辅助设计CBLI = chemistry－based leak indicator化学(法)示漏器CC = consistency controller浓度调节器CFD = computational fluid dynamics计算流体动力学CI = colour index比色指数= cofidence interval置信区间CL = colored ledger彩色底板CLSM = confocal laser scanning microscopy共焦激光扫描显微镜CMC = carboxy methylated cellulose羧甲基纤维素COMS = compliance optimization modeling system寻优模型系统CP = chemical pulp化学浆= chemical pure化学纯CPPC = coordinated phosphate/pH chemistry controller配位磷酸盐/pH调节器CR = consistency regulator浓度调节器CRP = chloride removal process氯化物排出法CSD = condensate steam distillation column冷凝汽馏塔CTMP = chemical treatment in terms of sulphonation硫化期间的化学处理= chemithermomechanical pulp化学热磨机械浆CTU = centigrade thermal unit公制热量单位CV = coefficient variation偏离系数= crystal violet结晶紫DD = dioxide二氧化物DAF = dissolved air floatation(溶)气浮DCS = dissolved and colloidal substances溶解与胶态物 = distributed control system集散控制系统DELS = Doppler electrophoretic light scattering多普勒电泳光扫描DIP = deinked pulp脱墨纸浆DKP = deinked kraft pulp脱墨牛皮纸浆DLK = double－line clippings双线限位DMS = dynamic mechanical spectroscopy动力谱学DMSO = dimethyl sulfoxide二甲亚砜DMT = dimethyl terephthalate对邻苯二甲酸二甲酯DO = dissolved oxygen溶解氧DP = degree of polymerization聚合度DSC = differential scanning calorimetry微分扫描量热法DVC = digital valve controller数字伐控制器EEC = embedded costs插入成本ECF = elemental chlorine free无元素氯(漂白)EDTA = ethylene eiamine tetraacetic acid乙二胺四乙酸EPC = experimental prismatic calcite实验棱镜方解石ERV = estimated replacement value预计取代值ESP = electrostatic precipitator静电滤尘器= emergency shutdown procedure事故停机程序EV A = ethylene vinyl acetate乙烯乙酸乙烯酯ESPRA = empire state paper research associates国立造纸研究会EVOH = ethylene－vinyl alcohol乙烯－乙烯醇FFAS = formamidine sulfinic acid甲脒亚磺酸FBB = folding box board折叠箱纸板FBK = fully bleached kraft全漂牛皮纸FC = flow controller流量控制器FID = free induction decays自由感应衰减FP = freezing point冰点；凝固点GGDP = gross domestic product本国生产总值GEMS = general energy and materials balance system通用能量和物料平衡系统GLC = gas－liquid chromatography气液色谱GPC = gel permeation chromatographic analysis凝胶渗透色谱分析GPM = gallons per minute加仑/分钟HHC = high consistency高浓HCR = high consistency refiner高浓磨浆机HD = high density高密度HPR = high production rate高生产率HPSEC = high－performance size－exclusion chromatography高性能粒度筛析色谱法HRT = hydraulic retention time水力停留时间HTH = high test hypochlorite高级漂粉HV = high voltage高压HW = hardwood硬木IIMPM = interactive multiplanar model相互作用的多面模型IPST = institute of paper science and technology造纸科技研究院IWC = international water consultants国际水质顾问团JJIT = just－in－time正好；准时KKP = kraft pulp牛皮浆；硫酸盐浆LLC = level controller液面控制器LCC = lignin－carbohydrate complexes木素－碳水化合物复合体LCL = lower control limits控制下限LCR = level cotroller and recorder液面控制记录仪LDPE = low density poly ethylene低密度聚乙烯LDV = laser Doppler velocimetry激光多普勒测速法LIVG = low inlet velocity gasification process低入口速度气化工艺LPR = low production rate低生产率LRD = long rang dependence广范围相关LVDT = linear position transducer线性位移变送器LWC = lightweight coated低定量涂布的MMACT = maximum achievable control technology最大可达控制技术MAP = modified atmosphere packaging改良常压包装法MC = marginal cost边际成本= medium consistency中浓(度)MDI = methylendiphenyl diisocyanate亚甲苯二苯二异氰酸酯MeB = methylene blue亚甲基兰，四甲基兰MEK = methyl ethyl ketone甲(基)乙(基)酮MF = machine finished机械整饰的MG = machine glazed机械上光的= malachte green孔雀绿MISS = mixed liquor suspended solids (有机物与活性污泥)混合液中悬浮固体MOW = mixed office waste混合办公废纸MRP = matal removal process金属(离子)脱除过程MSW = municipal solid waste城市固体废物MVP = moisture vapor permeability水蒸汽渗透性MWL = milled wood lignin磨木木素NNC = nitrocellulose 硝化纤维素NF = nanofiltration超滤(毫微过滤)NMR = nuclear magnetic resonance核磁共振NSPS = new source performance standards新的资源性能标准NSSC = neutral sulfite semi－chemical pulp中性亚硫酸半化学浆OOCC = old corrugated container旧瓦楞纸箱OD = over dry绝干；烘干OEE = overall equipment efficiency总设备效率OIT = oxidative induction temperature氧化起始温度O＆M = operating and maintenance 使用与维护ONP = old newspaper旧新闻纸OPP = oriented polypropylene取向聚丙烯OPR = oil penetration rates渗油率OWL = oxidized white liquor氧化白液PPAL = positron annihilation life time正电子湮没寿命PC = pressure controller压力调节器PCA = principal components analysis主成分分析PCC = precipitated calcium carbonate沉淀碳酸钙PCR = pressure controller and recorder压力调节记录仪PDSC = pressure differential scanning colorimetry压差扫描量热术PEMS = predictive emissions modeling system预测排放模型系统PEO = poly ethylene oxide聚氧化乙烯PGS = papergrade sulfite造纸用硫磺PGW = pressurized groundwood压力磨木浆PM = paper machine 造纸机；抄纸机PM/ECCM = preventive maintenance and essential care and condition monitoring预防维修／基本维修及状态监测PP = polypropylene聚丙烯PSES = pretreatment standards for existing sources现存资源预测标准PSM = process safety management(生产)过程安全管理PTFE = polytetrafluoroethylene聚四氟乙烯PTR = photothermal radiometry光热辐射分析法PVC = polyvinylchloride聚氯乙烯PVDC = polyvinyl dichloride聚二氯乙烯PVSK = polyvinylsulfate聚乙烯硫酸酯RRDH = rapid displacement heating快速置换加热法RH = relative humidity相对湿度RMP = refiner mechanical pulp木片磨木浆；盘磨机械浆RN = regular number纸板标准号RT = radiographic testing射线照相试验，X射线检验SSBK = solid bleached kraft(同质)漂白牛皮纸SBR = sequencing batch reactors程序化间歇反应器SC = super calendered超级压光的SDI = silt density index淤泥浓度指数SE = supplemental energy补充能量；辅助能SEC = size exclusion chromatographic粒度筛析色谱法SEM = scanning electron microscope扫描电子显微镜SEM－EDS = scanning electron microscope－energy dispersive spectrometry扫描电子显微镜—能量分散能谱测定法SGW = stone ground wood磨石磨木浆SIF = stress intensity factor应力强度系数；应力强化因子SOPs = standard operating procedures标准作业程序SP = sulphite pulp亚硫酸盐纸浆SPC = satislical process control过程控制SRT = solids retention time粒子留着时间SUB = solid unbleached board(同质)本色浆纸板SW = softwood软木；针叶树SWL = sulphite waste liguor亚硫酸盐废液TTAC = totally applied chlorine总用氯量TC = temperature controller温度调节器TCDF = tetrachlorodibenzofuran四氯二苯并呋喃TCF = totally chlorine－free全无氯(漂白)TCR = temperature controller and recorder温度调节记录仪TGA = thermal gravimetric analysis热重分析TLA = thin layer activation薄层活性化TMP = thermo mechanical pulp热磨机械浆TP = thermo－plastic热塑性的TQ = threshold quantity临界量(值)TRS = total reduced sulfur总还原硫TS = tensile strength抗张强度TSS = total suspended solids总悬浮固体量UUBB = unbeached board本色(浆)纸板UBK = unbeached kraft本色牛皮纸UCL = upper control limits控制上限UT = ultrasonic testing超声试验UV = ultraviolet紫外光VVOC = volatile organic compound挥发性有机化合物WW AS = waste－activated sludge废活性污泥WFMT = wet fluorescent magnetic particle test湿荧光磁粉试验WL = white ledger白色帐簿纸WLC = white－lined chipboard白浆衬里的粗纸板WP = wood pulp木浆WVTR = water vapor transmission rate水蒸汽传递速度YYI = yellow index返黄值；返黄指数YP = yield point屈服(软化)点。