离散元 ppt课件

格式：ppt
大小：2.64 MB
文档页数：103

下载文档原格式

离散数学ppt课件

02
集合论基础
集合的基本概念
总结词
集合是离散数学中的基本概念，是研究离散对象的重要工具。
详细描述
集合是由一组确定的、互不相同的、可区分的对象组成的整体。这些对象称为集合的元素。例如，自然数集、平面上的点集等。
集合的运算和性质
总结词
集合的运算和性质是离散数学中的重要内容，包括集合的交、并、差、补等基本运算，以及集合的确定性、互异性、无序性等性质。
生，1表示事件一定会发生。
离散概率论的运算和性质
概率的加法性质
如果两个事件A和B是互斥的，那么P(A或B)等于P(A)加上 P(B)。
概率的乘法性质
如果事件A和B是独立的，那么P(A和B)等于P(A)乘以P(B) 。
全概率公式
对于任意的事件A，存在一个完备事件组{E1, E2, ..., En}，使得P(Ai)>0 (i=1,2,...,n)，且E1∪E2∪...∪En=S，那么 P(A)=∑[i=1 to n] P(Ai)P(A|Ei)。
工程学科
离散数学在工程学科中也有着重要的应用，如计算机通信网络、控制系统、电子工程等领域。
离散数学的重要性
基础性
离散数学是数学的一个重要分支，是学习其他数学课程的基础。
应用性
离散数学在各个领域都有着广泛的应用，掌握离散数学的知识和方法对于解决实际问题具有重要的意义。
培养逻辑思维
学习离散数学可以培养人的逻辑思维能力和问题解决能力，对于个人的思维发展和职业发展都有很大的帮助。
详细描述
邻接矩阵是一种常用的表示图的方法，它是一个二维矩阵，其中行和列对应于图中的节点，如果两个节点之间存在一条边，则矩阵中相应的元素为1，否则为0。邻接表是一种更有效的表示图的方法，它使用链表来存储与每个节点相邻的节点。

离散元课件(三)

Ci : Ci dA dB ni / 2
否则，把参考点移动到两个最邻近顶点的中间位置
Ci
v v Amax i
Bmin
i
/2
式中，vi Amax
v 与 Bmin i
分别为块体
A 、B 上最接近公共面的顶点。
二基本原理-多面体单元离散元法
公共面法
确定公共面位置的算法：
3、公共面的转动
公共面经历过平动后，如果两个块体存在接触，那么该面上的参考
二基本原理-多面体单元离散元法
公共面法
确定公共面位置的算法：
3、公共面的转动
过公共面上的参考点 Ci 在当前公共面内构造两个方向任意但互相
垂直的矢量作为转轴，然后，令公共面的法向量绕两轴发生微小转动，转动角正负各一次，迭代的每一步令公共面的法向矢量转
动四次。如果 pi 与 qi 为所构造的两个互相正交的向量，则四次转
二基本原理-多面体单元离散元法
公共面法
基本思路：
•进一步对金属盘与两个块体间的相对位置进行分析，当两个块体逐步靠近但还没有接触时，金属盘在块体的推力作用下发生移动和扭转，这时，金属盘总是位于两个块体中间的某个位置，这样就可以很容易地通过把两个块体到金属盘的距离相加而求得两个块体间的空隙尺寸。
块体质心力更新
接触力更新
相对接触速度更新
块体位置更新
计算循环
二基本原理-多面体单元离散元法
接触力的计算（本构关系）相对速度
把在接触点处块体B相对于块体A的速度定义为接触速度，可由下式计算
Vi
xiB
eijk
B j
Ck
Bk
xiA
eijk
A j

离散完整ppt课件5.2-3共23页文档

代数系统定义与实例
定义非空集合 S 和 S 上 k 个一元或二元运算 f1, f2, … , fk 组成的系统称为一个代数系统, 简称代数，记做 V=<S, f1, f2, … , fk>.
S 称为代数系统的载体， S 和运算叫做代数系统的成分. 有的代数系统定义指定了S中的特殊元素，称为代数常数, 例如二元运算的单位元. 有时也将代数常数作为系统的成分.
6
积代数
定义设 V1=<S1,o>和 V2=<S2,>是代数系统，其中 o 和是二元运算. V1 与 V2 的积代数是V=<S1S2,∙>,
<x1,y1>, <x2,y2>S1S2 , <x1,y1> ∙ <x2,y2>=<x1ox2, y1y2>
例3 V1=<Z,+>, V2=<M2(R), ∙ >, 积代数< ZM2(R),o> <z1,M1>, <z2,M2>ZM2(R) , <z1,M1> o <z2,M2> = <z1+z2, M1∙M2>
单同态、满同态、同构自同态
同态映射的性质
9
同态映射的定义
定义设 V1=<S1,∘>和 V2=<S2,>是代数系统，其中 ∘ 和是二元运算. f: S1S2, 且x,yS1, f (x∘y) = f(x) f( y), 则称 f 为V1到 V2 的同态映射，简称同态.
10
更广泛的同态映射定义
f (x∘y)=f(x)f(y), f (x∙y)=f(x)◊f(y), f (∆ x)=∇f(x) 则称 f 为V1到 V2 的同态映射，简称同态.

离散完整ppt课件3.1-3共41页

证明 X=Y
命题演算法等式代入法反证法运算法
以上的 X, Y 代表集合公式
18
命题演算法证 XY
任取 x ， xX … xY
例3 证明AB P(A)P(B) 任取x xP(A) xA xB xP(B) 任取x xA {x}A {x}P(A) {x}P(B) {x}B xB
13
例1
F:一年级大学生的集合
S：二年级大学生的集合
R：计算机系学生的集合
M：数学系学生的集合
T：选修离散数学的学生的集合
L：爱好文学学生的集合
P：爱好体育运动学生的集合
所有计算机系二年级学生都选修离散数学
数学系一年级的学生都没有选修离散数学
数学系学生或爱好文学或爱好体育运动只有一、二年级的学生才爱好体育运动除去数学和计算机系二年级学生外都不选修离散数学3.2 集合的基本运算
集合基本运算的定义
文氏图（John Venn）例题集合运算的算律集合包含或恒等式的证明
10
集合基本运算的定义
并交相对补对称差
绝对补
AB = { x | xA xB } AB = { x | xA xB } AB = { x | xA xB } AB = (AB)(BA)
由已知包含式通过运算产生新的包含式 XY XZYZ, XZYZ
= (AB)(AB) A = EA
11
文氏图表示
12
关于运算的说明
运算顺序：和幂集优先，其他由括号确定并和交运算可以推广到有穷个集合上，即
A1A2…An= {x | xA1xA2…xAn} A1A2…An= {x | xA1xA2…xAn} 某些重要结果 ABA AB AB=（后面证明） AB= AB=A

离散数学教程PPT课件

A＝B C或A＝B C或A＝B C，则公式A是n＋1层公式， n max( i, j)。
例（1）p q r (2)r q p q p
第23页/共292页
1.2 命题公式及其赋值
( p q) r
p：2是素数，q：3是偶数，r：2是有理数 p：2是素数，q：3是偶数，r：2是无理数
例2.等值等价式p q p q q p
等值演算的应用： 1.验证等值式 ( p q) ( p r) p (q r) 2.判定公式的类型 ( p q) p q,( p ( p q)) r, p ((( p q) p) q) 3.解决工作生活中的判断问题
甲、已、丙3人根据口音对王教授是哪人进行了判断：甲说：王教授不是苏州人，是上海人已说：王教授不是上海人，是苏州人丙说：王教授既不是上海人，也不是杭州人
例：1.如果3＋3＝6，那么雪是白的。 2.除非我能工作完成了，我才去看电影。 3.只要天下雨，我就回家。 4.我回家仅当天下雨。 p→q的逻辑关系为q是p的必要条件或p是q的充分条件。
第15页/共292页
1.1 命题和命题联结词
5).等价词由命题p、q和组成的复合命题记作p q,读作“p当且仅当q”。是自然语言中的“充要条件”，“当且仅当”的逻辑抽象。
1.3 命题公式的等值式
定义1.设A和B是两个命题公式，若A B为重言式，则称公式A, B是等值的公式，记作A B。
例1.证明（p q) (q p); p p p.
注意：和的区别是公式间的关系符号，如：p q 是命题联结词.p q
第28页/共292页
1.3 命题公式的等值式
1.1 命题和命题联结词
例：1）海洋的面积比陆地的面积大。例 q2:）： 22p6:6海 9洋 9。。的面积比陆地的面积大。 r3:）火火星星上上有有生生命命。。 s4:）三三角角形形的的内内角角和和等等于于118800。。 55））你你喜喜欢欢数学吗吗？？ 66））我我们们要要努努力力学学习习。。 77））啊啊，，我我的的天天哪哪！！ 88））我我正正在在说说谎谎。。

PFC(经典)解析PPT课件

1、模型介质的宏观基本物理力学特征不可能通过直接赋值的形式实现； 2、介质的初始条件如地应力场条件会影响介质的结构特征； 3、介质的力学特性取决于介质内部粒子的结构和接触特征； 4、构建PFC模型和进行相应的运算准备工作必须使用PFC的二次开发功
能。
.
15
PFC中几何特征、物理特性和解题条件的说明不如 FLAC和UDEC程序那样直截了当。（微观参数选取）
整颗粒单元直径，可以调节孔隙率，通过jset 命令可以模拟岩体中节理
等软弱面。颗粒间接触相对位移的计算，不需要增量位移而直接通过坐
标来计算。
举例
①允许粒子发生有限位移和转动，粒子间可以完全脱离
②在计算过程中能够自动辩识新的. 接触
9
PFC 优点：
1、它有潜在的高效率。因为圆形物体间的接触探测比角状物体间的更简单。 2、对可以模拟的位移大小实质上没有限制。
当要求满足有实验室实际测试的模拟物体的力学特性时，出现了更大的困难。在某种程度上，这是一个反复试验的过程，因为目前还没有完善的理论可以根据微观特性来预见宏观特性。
（try-exam-determine）举例
然而，给出一些准则应该有助于模型与原型的匹配，如
哪些因素对力学行为的某些方面产生影响，哪些将不产生影响。应该意识到，由于受现有知识的限制，这样的模拟很难。然而，用PFC进行试验，对固体力学，特别是对断裂力学和损伤力学，可以获得一些基本认识。
用户定义的接触本构模型
可以用C++语言来编写，并编译成动态链接库文件，一旦需要就可以加载。
并行处理技术
允许将一个PFC2D模型分成几个部分，每个部分可以在单独的处理器上平行运行。与一个PFC2D模型在一个处理器上运行相比，平行处理在内存容量和计算速度方面得到大大提高。

离散元课件

运动描述
转动方程：
转动方程可以表示为
dωi Ii Ti dt j 1
式中，I i 与ωi 分别为颗粒 i 的转动惯量与角速度，对于球形颗粒 I i为
ki
2 I i mi Ri2 5
二基本原理-球形颗粒元离散元法
接触模型
综述：
关于接触力的计算模型已有大量的研究成果，目前仍旧是一个活跃的研究领域，特别是对于切向力的计算方法。
二基本原理
离散化模型
图1 颗粒元与块体元示意图
二基本原理-球形颗粒元离散元法
俞缙
bugyu0717@
华侨大学岩土工程研究所
二基本原理
根据离散化模型中所采用的单元种类分别介绍离散元法的基本原理：
颗粒元
• 二维圆盘单元 • 三维圆球单元
块体元
• 多边形单元 • 多面体单元
对于理想散体颗粒（无粘连）：采用 Hertz 理论描述法向作用，而采用Mindlin与Deresiewicz理论描述切向作用；对于存在粘连的散体颗粒：法向接触力根据在 Hertz 理论基础上考虑粘连力的JKR（Johnson-Kendall-Roberts）理论确定，切向接触力增量则根据把 Savkoor 和 Briggs 理论与 Mindlin 和 Deresiewicz理论相结合形成的理论确定。
1988 年 Cundall 所在的 ITASCA 咨询公司推出针对三维块体元的 3DEC程序。至此，离散元的理论体系基本形成。
一历史由来及研究现状
早期的离散单元法
Cundall称之为“Distinct Element Method”，随着该方法的推广，有的学者称其为“ Discrete Element Method” ，缩写形式均为 DEM。最初，离散元的研究对象主要是岩石等非连续介质的力学行为，它的基本思想是把不连续体分离为刚性元素的集合，使各个刚性元素满足运动方程，用时步迭代的方法求解各刚性元素的运动方程，继而求得不连续体的整体运动形态。离散元法允许单元间的相对运动，不一定要满足位移连续和变形谐调条件，计算速度快，所需存储空间小，尤其适合求解大位移和非线性问题。

离散完整ppt课件2.1-2共25页

2.1 一阶逻辑基本概念
▪ 个体词 ▪ 谓词 ▪ 量词 ▪ 一阶逻辑中命题符号化
1
基本概念——个体词、谓词、量词
个体词（个体）: 所研究对象中可以独立存在的具体或抽象的客体
个体常项：具体的事物，用a, b, c表示个体变项：抽象的事物，用x, y, z表示个体域: 个体变项的取值范围
有限个体域，如{a, b, c}, {1, 2} 无限个体域，如N, Z, R, … 全总个体域: 宇宙间一切事物组成
12
原子公式
定义设R(x1, x2, …, xn)是任意的n元谓词，t1,t2,…, tn 是任意的n个项，则称R(t1, t2, …, tn)是原子公式. 原子公式是由项组成的n元谓词. 例如，F(x,y), F(f(x1,x2),g(x3,x4))等均为原子公式
13
合式公式
定义合式公式（简称公式）定义如下： (1) 原子公式是合式公式. (2) 若A是合式公式，则 (A)也是合式公式 (3) 若A, B是合式公式，则(AB), (AB), (AB), (AB)也是合式公式 (4) 若A是合式公式，则xA, xA也是合式公式 (5) 只有有限次地应用(1)~(4)形成的符号串是合式公式.
15
公式的解释与分类
给定公式 A=x(F(x)G(x)) 成真解释: 个体域N, F(x): x>2, G(x): x>1
代入得A=x(x>2x>1) 真命题成假解释: 个体域N, F(x): x>1, G(x): x>2
(2) x (F(x)G(x))
这是两个基本公式, 注意这两个基本公式的使用.
7
一阶逻辑中命题符号化(续)
例3 在一阶逻辑中将下面命题符号化

离散数学的ppt课件

科学中的许多问题。
03
例如，利用图论中的最短路径算法和最小生成树算法
等，可以优化网络通信和数据存储等问题。
运筹学中的应用
01
运筹学是一门应用数学学科，主要研究如何在有限资源下做出最优决策，离散数学在运筹学中有着广泛的应用。
02
利用离散数学中的线性规划、整数规划和非线性规划等理论，可以解决运筹学中的许多问题。
并集是将两个集合中的所有元素合并在一起，形成一个新的集合。
详细描述
例如，{1, 2, 3}和{2, 3, 4}的并集是 {1, 2, 3, 4}。
总结词
补集是取一个集合中除了某个子集以外的所有元素组成的集合。
详细描述
例如，对于集合{1, 2, 3}，{1, 2}的补集是{3}。
集合的基数
总结词
）的数学分支。
离散数学的学科特点
03
离散数学主要研究对象的结构、性质和关系，强调推
理和证明的方法。
离散数学的应用领域
计算机科学
01
离散数学是计重要的工具和方法。
通信工程
02
离散数学在通信工程中广泛应用于编码理论、密码学、信道容
量估计等领域。
集合的基数是指集合中元素的数量。
详细描述
例如，集合{1, 2, 3}的基数是3，即它包含三个元素。
03 图论
图的基本概念
顶点
图中的点称为顶点或节点。
边
连接两个顶点的线段称为边。
无向图
边没有方向，即连接两个顶点的线段可以是双向的。
有向图
边有方向，即连接两个顶点的线段只能是从一个顶点指向另一个顶点。
研究模态算子（如necessity、possibility）的语义和语法。

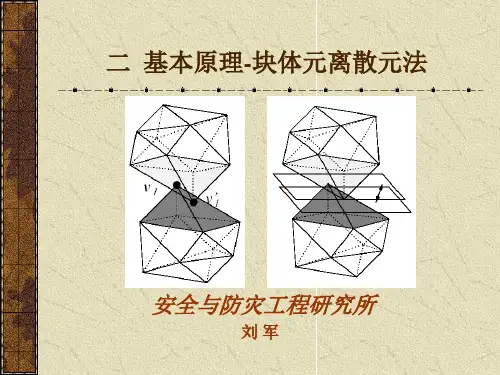
离散元课件(三)..

二基本原理-多面体单元离散元法
公共面法
基本思路：
•构造一个公共面，通过公共面把两个块体所占据的空间分为两部分； •分别检验每个块体与公共面的接触情况。公共面的构造方法可以用一个悬在两个未接触块体间的金属盘来说明，当两个块体未接触时，金属盘与任何一个块体都不接触，但是，随着两个块体逐步靠近直至接触时，金属盘在两个块体的作用下发生扭转直至完全被两个块体夹紧。无论这两个块体的形状和位向如何，金属盘被夹紧后，总会在一个特定位置达到稳定，而金属盘达到稳定的位置恰恰就是处于接触中的两个块体的接触面。
况，检测次数为
n v A vB
•
•对于两个立方体的情况，公共面法的检测次数为 16 ，而直接法为 240。
二基本原理-多面体单元离散元法
公共面法
优点：
•对于点- 面接触类型，没有必要检测该接触是否位于面的周边以内，因为公共面的位置在不断变化（见后面叙述），如果两个块体都与公共面接触，那么这两个块体必然接触，如果两个块体没有接触，则肯定与公共面不接触； •公共面的法向矢量就是接触的法向矢量，不需要额外进行计算； •既然公共面的法向是唯一的，那么就可以排除接触法向矢量的不连续变化。公共面的法向矢量可能化发生迅速变化（如点-点接触），但是不会因为接触类型的改变而发生跳跃式变化。 •可以很容易地确定两个未接触块体间的最大空隙：只需要把两个块体距公共面的距离相加即可。 •
分析：
•接触检验的次数直接取决于所要判别块体的边、顶点与面的平均数量； •模拟中不仅要确定块体间是否接触，还要确定接触时的详细信息，如：侵入深度、接触面的法向向量以及接触点等；
•对某些类型的接触检测是很困难的，例如，在点-面接触检测中，

离散数学第章课件PPT高等教育出版社屈婉玲耿素云张立昂主编(共43张PPT)

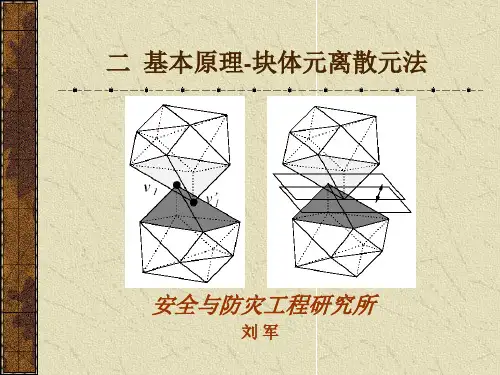
定义14.16 G=<V,E>, E E E 是边割集——p(G E )>p(G)且有极小性 e是割边〔桥〕——{e}为边割集
23
点割集与割点
例3 {v1,v4}，{v6}是点割集，v6是割点. {v2,v5} 是点割集吗？ {e1,e2}，{e1,e3,e5,e6}， {e8}等是边割集，e8是桥，{e7,e9,e5,e6} 是边割集吗？
8
握手定理
定理14.1 设G=<V,E>为任意无向图，V={v1,v2,…,vn}, |E|=m, 那
n
d(vi ) 2m
i1
证 G中每条边 (包括环) 均有两个端点，所以在计算G中各顶点度数之和时，每条边均提供2度，m 条边共提供 2m 度.
定理14.2 设D=<V,E>为任意有向图，V={v1,v2,…,vn}, |E|=m, 那么
简单图化的，而(2, 2, 3, 4, 5)，(3, 3, 3, 4) 都不是可简单图化的，特别是后者也不是可图化的
12
n 阶完全图与竞赛图
定义14.6 (1) n (n1) 阶无向完全图——每个顶点与其余顶点均相邻的
无向简单图，记作 Kn.
简单性质：边数 mn(n1),n1
2
(2) n (n1)阶有向完全图——每对顶点之间均有两条方向相反的有向边的有向简单图.
D的度数列：d(v1), d(v2), …, d(vn) D的入度列：d+(v1), d+(v2), …, d+(vn) D的出度列：d(v1), d(v2), …, d(vn) 3. 非负整数列d=(d1, d2, …, dn)在什么条件下是可图化的，是可简单图化的？定理14.4 p277 易知：(2, 4, 6, 8, 10)，(1, 3, 3, 3, 4) 是可图化的，后者又是可

EDEM校园培训PPT

EDEM
颗粒夹带
EDEM
颗粒夹带
EDEM
气流喷射
EDEM
流化床
EDEM
气力输送
EDEM
气力输送
EDEM
气力输送
EDEM
气力输送
EDEM
砂石抽吸
EDEM
抽吸区域颗粒层表面呈现“W”型与实验结果的吻合度很高
砂石抽吸
EDEM
铁矿石软化熔融区域通透性降低改变气体流量分布受矿石性质与操作工况影响发生复杂的多相化学反应
溜槽结构外移
物料输运
减小物料飞溅
调整溜槽倾角稳定皮带料线
运行工况明显改善
EDEM
球磨机内衬板磨损
磨损严重影响提升性能
物料破碎
预测磨损率与性能下降的关系设计合适的衬板更换周期
EDEM
改进卡车车斗结构提高装卸料效率
卸料时间大大缩短车斗重量减轻20%以上燃料消耗减少11%
卡车车斗装卸料
每辆卡车每年节约成本5.5万美元
EDEM
挖掘机铲斗挖料过程铲斗受力变化
挖掘机铲斗
EDEM
挖掘机铲斗挖料过程铲斗受力变化
初始受力较小随着挖料增加受力增大最终受力为物料重量摩擦及铲斗方向变化使得受力有一高峰值模拟与实验结果一致
挖掘机铲斗
cn
YA, local
Fnormal
EDEM
模拟工艺或过程中的颗粒行为
DEM Solutions
第一款基于离散元方法的通用CAE软件与Fluent耦合模拟颗粒-流体系统（DEM+CFD）与Ansys耦合模拟设备的应力-应变状况（DEM+FEM）

离散数学完整版课件全套ppt教学教程最全整套电子讲义幻灯片(最新)

逻辑运算符“析取”，与汉语中“或”含义相当，但有细微的区别
1.1 命题及联结词
运算符“析取” 与汉语的“或”几乎一致但有区别：哪些老师讲离散数学？有人回答如下：
(16)“讲离散数学的老师是杨老师或吴老师”，分解为
“讲离散数学的老师是杨老师”或 “讲离散数学的老师是吴老师”，这两个原子命题有可能都是对的，这种“或”称为“可同时为真的或”，或简称为“可兼或”。这种“或”表示可表示为“析取”
1.1 命题及联结词
定义1.4条件:当p是1 ,q是0时,pq为0,即10 为0,其他情况为1。
逻辑运算符“如果…那么”，如老妈说：“如果期终考了年级前10 名，那么奖励1000元”。 p:期终考了年级前10名 q:奖励1000元则上面的语句表示为pq。先考虑值为0即假的情况：当p为1即“期终考了年级前10”，且q为0即“没有奖励1000元” 这时老妈的话是假话空话，
这个例题有点不正点！ “郎才当且仅当女貌”，
可以表示为“郎才女貌”
1.2命题公式
对错明确的陈述语句称为命题，其真值t/f 0/1 C运算：加+、减-、乘x、除/、余数%，命题逻辑：合、析、否定、条件、双条件(版) C语言中用变量x表示某些数，如x*x+x+10是表达式，
命题逻辑中用变量p,q,r表示任意命题，由命题常元与此类变量所构成表达式，称为“命题公式”。
无论p/q取何值，这两个公式的值，与前面各例不同，此表是将运算结果写在联结词的下方！
1.3 等值式
定义1.3.1等值：对于合法的命题公式A、B，若无论其中的命题变元取何值，A 、B值总相等，称为两个公式等值，记为AB (边播边板)
目的:
1．掌握离散数学五大核心内容（集合论、数理逻辑、代数结构、图论、组合数学）的基本概念、基本理论、基本方法，训练提高学生的概括抽象能力、逻辑思维能力、归纳构造能力，培养学生严谨、完整、规范的科学态度和学习思维习惯。

离散元ppt课件

一历史由来及研究现状
离散单元法的研究现状
离散元理论研究的发展
近30年来，离散元法的应用领域在不断扩大，它自身的内涵也发生了变化，以致于目前很难对离散元法给出一个严格的定义。下面，我们从离散元法的离散模型特点及便于甄别与其它数值计算方法的关系的角度给予离散元法一个比较宽松的定义。
一历史由来及研究现状
一历史由来及研究现状
产生背景
散粒岩土材料在自然界中普遍存在
从本质上讲，岩土材料都是由离散的、尺寸不一、形状各异的颗粒或块体组成的，例如，土就是松散颗粒的堆积物，同样，天然岩体也是由被结构面切割而成的大小不一、形态各异的岩石块体所组成。散粒岩土材料的力学特性有着重要的工程应用，如泥砂的沉淀，土堤、土（岩）坡、铁路道渣等的稳定性研究，散粒岩土材料的力学特性研究是岩土力学中最基本的、也是最重要的问题之一。
离散单元法的研究现状
离散元理论研究的发展
• 数值方法通常将实际具有无限自由度的介质近似为具有有限自由度的离散体(或网络)的计算模型(有限离散模型)进行计算。有限离散模型具有三个要素：单元(或网络)、节点和节点间的关联。
一历史由来及研究现状
离散单元法的研究现状
离散元理论研究的发展
• 离散元单元的形状有形形色色，但它只有一个基本节点(取单元的形心点)，是一种物理元(physicalelement)．这种单元与有限元法、边界元法等数值方法采用的由一组基本节点联成的单元(一般称为网络元，mesh element)相比有明显的不同。
一历史由来及研究现状
早期的离散单元法
Cundall称之为“Distinct Element Method”，随着该方法的推广，有的学者称其为“Discrete Element Method”，缩写形式均为 DEM。最初，离散元的研究对象主要是岩石等非连续介质的力学行为，它的基本思想是把不连续体分离为刚性元素的集合，使各个刚性元素满足运动方程，用时步迭代的方法求解各刚性元素的运动方程，继而求得不连续体的整体运动形态。离散元法允许单元间的相对运动，不一定要满足位移连续和变形谐调条件，计算速度快，所需存储空间小，尤其适合求解大位移和非线性问题。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一历史由来及研究现状
早期的离散单元法
主要思路：用Newton定律描述颗粒运动，通过颗粒间及颗粒与边界间的相互作用传递载荷，求解方法是解藕的。理论难点：接触力模型（Contact Force Model)与接触发现算法 (Contact Detection Algorithm)。
一历史由来及研究现状
离散单元法的基本理论及应用
应用
理想散体岩土介质中的应用
• 堆积问题 • 磨矿 • 铁路道砟
离散单元法的基本理论及应用
应用
在连续岩土介质中的应用
• 岩石力学性质分析 • 颗粒破碎模拟 • 边坡稳定性分析 • 洞室围岩稳定性分析 • 桩与土介质相互作用模拟 • 分层岩土介质中侵彻与爆炸模拟
一历史由来及研究现状
历史由来及研究现状
产生背景发展现状存在的问题
离散单元法的基本理论及应用
基本原理
Cundall二维圆盘单元离散元法三维球体单元(颗粒元)离散元法多边形单元离散元法多面体单元离散元法接触发现算法
• Cundall公共面法 • 其他方法
离散单元法的基本理论及应用
程序设计及商业软件介绍
程序设计方法 UDEC 3DEC PFEC2D与PFC3D
一历史由来及研究现状
早期的离散单元法
离散元法的思想源于较早的分子动力学（Molecular Dynamics）。 1971年Cundall提出适于岩石力学的离散元法； 1979年Cundall和Strack又提出适于土力学的离散元法，并推出二维圆盘（Disc）程序BALL和三维圆球程序TRUBAL（后来发展为商业软件PFC-2D/3D），形成较系统的模型与方法，被称为软颗粒模型。 1988 年 Cundall 所在的 ITASCA 咨询公司推出针对三维块体元的 3DEC程序。至此，离散元的理论体系基本形成。
产生背景
散粒岩土材料在自然界中普遍存在
从本质上讲，岩土材料都是由离散的、尺寸不一、形状各异的颗粒或块体组成的，例如，土就是松散颗粒的堆积物，同样，天然岩体也是由被结构面切割而成的大小不一、形态各异的岩石块体所组成。散粒岩土材料的力学特性有着重要的工程应用，如泥砂的沉淀，土堤、土（岩）坡、铁路道渣等的稳定性研究，散粒岩土材料的力学特性研究是岩土力学中最基本的、也是最重要的问题之一。
离散单元法的研究现状
离散元法自问世以来，在岩土工程和粉体(颗粒散体)工程这两大传统的应用领域中发挥了其它数值算法不可替代的作用。
一历史由来及研究现状
离散单元法的研究现状
岩土工程中的应用
由于离散元单元具有更真实地表达节理岩体的几何特点能力，便于处理以所有非线性变形和破坏都集中在节理面上为特征的岩体破坏问题，被广泛地应用于模拟边坡、滑坡和节理岩体下地下水渗流等力学过程的分析和计算中；离散元法还可以在颗粒体模型基础上通过随机生成算法建立具有复杂几何结构模型，通过单元间多种连接方式来体现土壤等多相介质间的不同物理关系，从而更有效地模拟土壤的开裂、分离等非连续现象，成为分析和处理岩土工程问题的不可缺少的方法。
量散体组成的岩土材料则相当困难。
一历史由来及研究现状
分子动力学方法的引入
分子动力学模拟是一种用来计算一个经典多体体系的平衡河传递性质的方法。所谓的经典意味着颗粒体系的运动遵守经典力学定律。该方法最初是用来描述分子运动的（当处理一些较轻的原子或分子时，才需要考虑量子效应）。分子动力学方法模拟分子的运动时，邻近分子间存在吸引或排斥力。该方法可以模拟大量分子的运动。去除分子间作用力，把分子动力学中的小尺度粒子作为散体岩土材料中的颗粒，并入颗粒间及颗粒与边界间的相互作用描述，即是Cundall离散元法的最初思路。
第6章离散单元法
The Theory of DEM (Discrete Element Method) and Its Applications
俞缙
bugyu0717@
华侨大学岩土工程研究所
离散单元法的基本理论及应用
历史由来及研究现状基本原理程序设计及商业软件介绍应用
离散单元法的基本理论及应用
用多体动力学描述散粒体的力学行为的困难
（1）对于被研究的多粒子系统而言，已经存在的接触不断地分开，而新的接触频繁的形成，在多体动力学中，接触的分开与形成都需要改变控制方程；（2）即使接触网络保持相同，在每一个接触中，也可能发生在依附与滑动间的过渡，而这种过渡也会导致系统运动方程的改变。
因而：多体动力学方法只能描述少数散体体系的力学行为，对于大
一历史由来及研究现状
离散单元法的研究现状
粉体工程中的应用
其次，在粉体工程(过程)方面，颗粒离散元被广泛地应用于粉体在复杂物理场作用下的复杂动力学行为的研究和多相混合材料介质或具有复杂结构的材料其力学特性的研究中．它涉及到粉末加工、研磨术、混合搅拌等工业加工和粮食等颗粒离散体的仓储和运输等生产实践领域中。
一历史由来及研究现状
早期的离散单元法
Cundall称之为“Distinct Element Method”，随着该方法的推广，有的学者称其为“Discrete Element Method”，缩写形式均为 DEM。最初，离散元的研究对象主要是岩石等非连续介质的力学行为，它的基本思想是把不连续体分离为刚性元素的集合，使各个刚性元素满足运动方程，用时步迭代的方法求解各刚性元素的运动方程，继而求得不连续体的整体运动形态。离散元法允许单元间的相对运动，不一定要满足位移连续和变形谐调条件，计算速度快，所需存储空间小，尤其适合求解大位移和非线性问题。
一历史由来及研究现状
离散单元法的研究现状
一历史由来及研究现状
产生背景
用连续介质力学研究散粒岩土材料力学特性的不足
连续介质力学把散粒体作为一个整体来考虑，研究的重点放在建立粒子集合的本构关系，从粒子集合整体的角度研究散粒体介质的力学行为。不足：不能体现颗粒间的复杂相互作用及高度非线性行为；不能真实刻画散体材料的流动变形特征。
一历史由来及研究现状