期末考试试卷及参考答案

苏教版三年级语文上册期末考试 (试卷一)班级姓名成绩第一部分日积月累（12分）⑴诗文储蓄。

（2分）1、独在异乡为异客，。

2、停车坐爱枫林晚，。

3、，任尔东西南北风。

4、书到用时方恨少，。

⑵常识擂台。

（10分）1、杭州素有“”的美称；拉萨是有名的“”；生活在北大荒的人喜欢用“”来赞美遍地金黄的九月；郑燮号，是“”之一；香港是我国通向世界的，是一颗无比璀璨的。

哈尔滨及济南有、的别称。

西湖的白堤及苏堤及唐朝诗人和有关。

2、本册书中我最喜欢（人物），因为。

3、人们也称苏州为，通过本册古诗的学习，你认识了苏州的和两处名胜。

4、说脸谱。

关羽是脸，包公是脸，秦桧是脸。

第二部分基础知识（46分）一、生词聚会。

（12分）yán í cōnɡìǎn pánɡ yōu yánɡ qīnɡ róu lún útòu ànɡ qīn lüèǎn bùǎn yào méi tàn āé二、生字变脸。

（10分）倍（倍数）佳（）钱（）彼（）维（）（陪同）（）（）（）（）险（）佛（）讯（）股（）珍（）三、我会模仿。

（6分）酸溜溜（）（）（）银灰（）（）（）层层叠叠（）（）（）和风细雨（）（）（）四、精挑细选。

（7分）1、发人深省（ěnɡ xǐnɡ）丢三落（làò）四参差（cān à cēn cī）2、（漂飘）荡挺（拔拨）（映印）照拜（访防）随（即既）精（彩采）（维唯）一（状壮）丽五、精彩回放。

（11分）1、这学期我们学习了好几首古诗。

你能把你喜欢的一首介绍给我们吗？请把它写下来。

这首诗的作者是（），你喜欢它的原因是（）。

2、课余，你还能背诵的诗有《》、《》、《》。

3、小露珠像钻石则。

像水晶则，像珍珠则。

3、它们有的，有的，有的，有的，游客不时被逗得。

学年－ 学年第 学期期末考试 《老年社会工作》试卷 答卷说明：1、本试卷共7页，6个大题，满分100分，100分钟完卷。

2、开卷考试。

评阅人:_____________ 总分人：______________ 一、单项选择题（下列选项中只有一个是正确的，请将正确的答案序号填写在括号内。

本大题共16题，每小题1分，共计16分） 1．下列哪一项不属于老年社会工作的基本技巧。

（ ） A.生命回顾 B.善于发现老年人的潜能 C.怀旧 D.给予老年人物质帮助 2．“去机构化”是20世纪60年代早期在（ ）产生的、对照顾方式谋求改革的运动。

A.中国 B.德国 C.英国 D.美国 3．1987年民政部第一次提出了( )的概念来代替“社区福利服务网络”。

A.社区照顾 B.社区管理 C.社区服务 D.社区福利 4．老年人格类型理论认为，（ ）是人格调适良好的类型。

①成熟型 ②摇椅型 ③防卫型 ④愤怒型 ⑤自怨自艾型 A.① B.①② C.①②③ D.①②③④ 5.社会脱离理论属于（ ）的观点，是1961年由卡明和亨利提出的，也是在老年社会工作中引起争论最多的理论。

__________________系__________专业___________班级姓名_______________学号_______________………………………………（密）………………………………（封）………………………………（线）………………………………A.功能派B.互动派C.批判派D.冲突派6.1999年的世界卫生日，世界卫生组织提出了（）A. 实现建立一个“不分年龄，人人共享社会”的目标B.“积极健康的老年生活”的口号C.“应当教育普通大众消除对于老龄化的消极看法、各种不正确的说法和陈旧观念”的观点D.“保障老年人合法权益”的草案7.老年小组工作在针对相对健康且具有活动能力的社区中的老年人时，主要是以开展（）为主要内容的团体辅导活动。

《学前儿童游戏》期末考试卷及答案班级姓名成绩一、单项选择题。

1．现代意义上的积木来源于( B )。

A．希尔地面积木 B．福禄贝尔的“恩物”C. 以原木制成的“单元积木”D. 蒙氏教具中的积木2．在游戏中，幼儿总能通过不断尝试，找到适合自己能力与兴趣的游戏内容和方式方法，获得满足感和自信心。

在这个过程中，游戏让幼儿获得了( C )内部心理体验。

A. 兴趣性体验 B．自主性体验C. 胜任感体验 D．幽默感体验3．幼儿利用积木、积塑、橡皮泥、竹木制品或者金属配件材料等进行游戏，或者用沙、泥、雪等材料进行的游戏，这类游戏称为( D )。

A．表演游戏 B．角色游戏C. 智力游戏 D．结构游戏4．在角色游戏中，幼儿会以物代物，一根小小的冰糕棍，幼儿可以想象成吃饭的筷子、喝汤的勺子、炒菜的铲子等，这体验了角色游戏的( A )特点。

A．假想性 B．主动性 C．创造性 D. 模仿性5.从幼儿的立场上考虑，幼儿园游戏实施时应遵循（ C ）原则。

A.教育性B.发展性C.主体性D.创造性6.亲子游戏的早期阶段和启蒙阶段是（ C ）。

A.1岁前B.6岁前C.婴儿时期D.幼儿时期7.由于0～2岁的婴儿处于感知运动阶段，因而婴儿游戏以（ B ）为主。

A．象征性游戏 B.练习性游戏C．结构游戏 D.角色游戏8.学前儿童游戏现场指导中教师的双重身份是( A )。

A.既是教育指导者又是游戏伙伴B.既是权威者又是游戏伙伴C.既是游戏支持者又是游戏观察者D.既是游戏观察者又是游戏的评价者9.大家一起玩雪花片，插一个小公园，甲插小桥，乙插小花、丙插树??大家组合一起就成为一个小公园。

这属于（ C ）。

Ａ、平行的游戏Ｂ、联合游戏Ｃ、合作游戏Ｄ、单独的游戏10.实践证明，游戏由于能大量提供体育运动、技能训练，动手操作的机会，因此对发展( B )非常有利。

A.大脑左半球B.整个大脑 C大脑右半球 D.小脑二、简答题。

1.简述结构游戏的教育作用。

五年级数学期末考试试卷及答案五年级数学期末考试试卷及答案试卷是纸张答题，在纸张有考试组织者检测考试者学习情况而设定在规定时间内完成的试题。

以下是店铺为大家收集的五年级数学期末考试试卷及答案，仅供参考，欢迎大家阅读。

五年级数学期末考试试卷及答案篇1一、填空（每小题2分，共20分）1．小明买了4块橡皮，每块a元，需要（）元。

当a=1.5时，需要（）元。

2．在○里填上“＞”、“＜”或“=”。

3.78÷0.99○3.78 2.6×1.01○2.6 7.2×1.3○7.2÷1.3 9.7÷1.2○9.7—1.23．在（）里填上合适的数。

2.05吨=（）吨（）千克 3升50毫升=（）升4．一个两位小数保留一位小数是2.3，这个两位小数是（），最小是（）。

5.一个数的小数点先向左移动两位，再向右移动三位后是0.123，这个数是（）。

6.一个平行四边形的底是2.6厘米，高是4厘米，面积是（），一个三角形的底是2.5厘米，面积是10平方厘米，高是（）。

7.一条裤子n元，一件上衣的价格是一条裤子的6倍，则一件上衣需要（）元，买一套服装共需（）元。

8. 501班进行1分钟跳绳测试，六位学生的成绩分别是：137个、142个、136个、150个、138个、149个，这组数据的平均数是（），中位数是（）。

9.正方体的六个面分别写着1、2、3、4、5、6，每次掷出“3”的可能性是（），每次掷出双数的可能性是（）。

10.一辆汽车开100公里需要8升汽油，开1公里需要（）升汽油，1升汽油可以开（）公里。

二、判断（每小题1分，共5分）1．被除数不变，除数扩大100倍，商也扩大100倍。

（）2．a的平方就是a×2. … （）3．大于0.2而小于0.4的数只有0.3一个。

（）4．两个等底等高的三角形一定可以拼成一个平行四边形。

（）5．一组数据的中位数和平均数可能相等。

（）三、选择（每小题1分，共5分）1．2.695保留两位小数是（）。

2023北京东城初二（上）期末英语2023.1学校__________ 班级__________ 姓名__________教育ID号__________考生须知1.本试卷共10页, 共两部分, 共39道小题, 满分60分, 考试时间90分钟。

2.在试卷和答题卡上准确填写学校、班级﹑姓名和教育ID号.3.试题答案一律填涂或书写在答题卡上, 在试卷上作答无效。

4.在答题卡上, 选择题用2B铅笔作答, 其他试题用黑色字迹签字笔作答。

5.考试结束后, 请将答题卡交回。

本部分共33题,共40分。

在每题列出的四个选项中,选出最符合题目要求的一项。

一、单项填空(每题0.5分, 共6分)从下面各题所给的A、B、C、D四个选项中,选择可以填入空白处的最佳选项。

1. Peter’s mother went to Lao She Teahouse yesterday. ________ took Peter with her.A. SheB. HeC. TheyD. We2. Qian Xuesen, a famous Chinese scientist, was born ________ December 11,1911.A. inB. onC. atD. to3. — Be careful when you walk across this old bridge. It________ be very safe.— I will.A. must notB. need notC. might notD. should not4. In my hometown, the streets are ________ than two years ago.A. cleanB. cleanerC. cleanestD. the cleanest5. —________ did you go to the Beijing Museum of Natural History yesterday?— By bus.A. HowB. How oftenC. whyD. When6. My uncle had an accident last year. Now, he drives ________ than before.A. carefulB. more carefulC. carefullyD. more carefully7. I wanted to help Lisa with her study, ________ she said she could do it herself.A. butB. orC. forD.so8. Paul enjoys reading famous stories. He ________ one now.A. readsB.is readingC. readD. will read9. I ________ a painting when my mother came back home.A. drawB. drewC. was drawingD. will draw10. Emma ________ up early this morning and went for a morning run with her father.A. getsB. will getC. was gettingD. got11. I can’t meet you next Sunday. A friend of mine ________ to see me.A. comesB. cameC. was comingD. will come12. My grandmother has two dogs. She ________ them in the park every morning.A. walksB. was walkingC. will walkD. walked二、完形填空(每题1分, 共8分)阅读下面的短文, 掌握其大意, 然后从短文后各题所给的A、B、C、D 四个选项中,选择最佳选项。

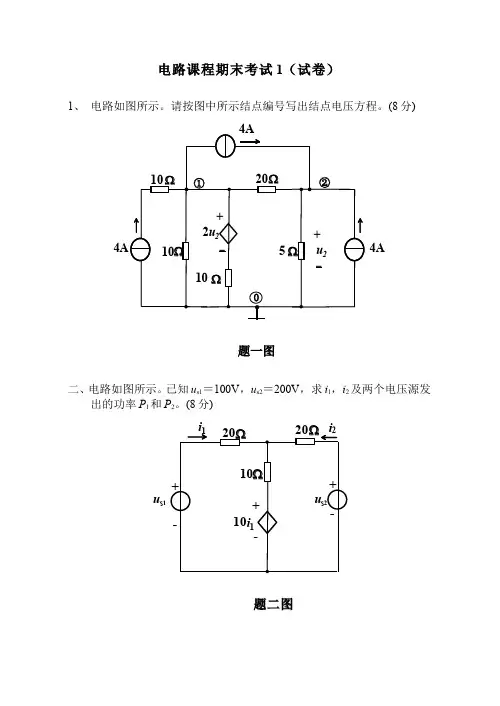
电路课程期末考试1（试卷）1、电路如图所示。

请按图中所示结点编号写出结点电压方程。

(8分)10Ω2u 2+题一图4A4A10Ω5Ω20Ωu 2+-4A10Ω①②-0二、电路如图所示。

已知u s1＝100V ，u s2＝200V ，求i 1，i 2及两个电压源发出的功率P 1和P 2。

(8分)Ωu s 1+20Ωi 110Ω10i 1u s 2++20Ωi 2题二图---三、电路如图所示。

(1) 求从a 、b 端看进去的戴维宁等效电路；(2) 求R L 为何值时，R L 能获得最大功率，并求此最大功率P max 。

(10分)10Ω20V +-题三图4A5Ωu +0.2u10Ω10ΩabR L-四、电路如图所示。

请应用叠加定理求电压u 3。

(8分)40题四图5A4Ω4Ω+－10i 1i 1u 3+10V+2Ω－－Ω五、含理想运放的电路如图所示。

求u 0和u x 。

(8分)+u o_+∞++∞+u x 6V+_+_ΩΩ1K ΩΩΩΩ题五图__1231K 1K 1K 1K 1Kk Ωk Ωk Ωk Ωk Ωk Ω题五图六、一阶动态电路如图所示。

电路原来处于稳定状态，t=0时，开关S 从1合向2，求t>0时的u c (t )和i c (t )。

(10分)u c0.2F题六图2A10Ω5ΩS(t =0)2.5Ω10V++i c--12七、正弦稳态电路如图所示。

已知M =0.4H ，L 1=L 2=0.6H ，L 3=1.4H ，C 1=10-4F ，C 2=0.5×10-4F ，电源角频率ω=100rad/s ，(1) 求1I ，2I ；(2) 求两个电压源发出的复功率1S 、2S 。

(10分)12j C ω11j C ω八、正弦稳态电路如图所示。

已知u s1=2100cos100t V , i s1=22cos100t A,求，i 1、u 。

(10分)100Ω1H－＋100Ω100Ω10-4F 10-4F－＋1H u 题八图i 1i s2u s1九、对称三相电路如图所示。

深圳中学2023-2024学年度第一学期期末考试试题年级：高一 科目：数学参考：以10为底的对数叫常用对数，把10log N 记为lg N ；以()e e 2.718281828=⋯为底的对数叫自然对数，把e log N 记为ln N ．一､选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 为了解某地区居民使用手机扫码支付的情况，拟从该地区的居民中抽取部分人员进行调查，事先已了解到该地区老、中、青三个年龄段的人员使用手机扫码支付的情况有较大差异，而男、女使用手机扫码支付的情况差异不大.在下面的抽样方法中，最合理的是（ ）A. 抽签法B. 按性别分层随机抽样C. 按年龄段分层随机抽样D. 随机数法2. 下列与7π4的终边相同的角的表达式中，正确的是（ ）A. ()2π315Z k k +∈B. ()36045Z k k ⋅-∈C ()7π360Z 4k k ⋅+∈D. ()5π2πZ 4k k +∈3. 角α的终边与单位圆O 相交于点P ，且点P 的横坐标为35的值为（ ）A.35B. 35-C.45 D. 45-4. 已知角()0,πα∈，且1cos 23α=，则sin α的值为（ ）A.B.C.D. 5. 健康成年人的收缩压和舒张压一般为90~139mmhg 和60~89mmhg ，心脏跳动时，血压在增加或减小，血压的最大值、最小值分别为收缩压和舒张压，血压计上的读数就是收缩压和舒张压，读数为120/80mmhg 为标准值．设某人的血压满足函数式()11525sin(160π)P t t =+，其中()P t 为血压（mmhg ），t 为时间（min ）．给出以下结论：①此人血压在血压计上的读数为140/90mmhg ②此人的血压在健康范围内③此人的血压已超过标准值④此人的心跳为80次/分.的其中正确结论的个数为（ ）A. 1B. 2C. 3D. 46. 孩子在成长期间最需要父母的关爱与陪伴，下表为2023年中国父母周末陪孩子日均时长统计图．根据该图，下列说法错误的是（ ）A. 2023年母亲周末陪伴孩子日均时长超过8小时的占比大于13B. 2023年父亲周末陪伴孩子日均时长超过6小时占比大于12C. 2023年母亲周末陪伴孩子日均时长的5个时段占比的极差为28.8%D. 2023父母周末陪伴孩子日均时长10个时段占比的中位数为20.2%7. 将函数()2sin f x x =图象上所有点横坐标缩小为原来的12，再向右平移π6个单位长度，得到函数()g x 的图象，若()0g x a -=在π0,2⎡⎤⎢⎥⎣⎦上有两个不同的零点1x ，2x ，则()12tan x x +=（ ）A.B.C.D. 8. 如果对于任意整数πππ,sin,cos ,tan n n n n k k k都是有理数，我们称正整数k 是“好整数”，下面的整数中哪个是最大的“好整数”（ ）A. 1B. 2C. 3D. 4二､多选题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项是符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．的的的9. 下列说法中正确的是（ ）A. 度与弧度是度量角的两种不同的度量单位B. 1度的角是周角的1360，1弧度的角是周角的12πC. 根据弧度的定义，180︒一定等于π弧度D. 不论是用角度制还是用弧度制度量角，角的大小均与圆的半径长短有关10. 下列各式中，值是12的是（ ）A. ππc s cos sin os n 3i 3x x x x ⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭ B. tan10tan 35tan10tan 35︒+︒+︒︒C.2tan 22.51tan 22.5︒-︒D.22cos 203sin 50-︒-︒11. 2023年是共建“一带一路”倡议提出十周年．某校组织了“一带一路”知识竞赛，将学生的成绩（单位：分，满分：120分）整理成如图的频率分布直方图（同一组中的数据用该组区间的中点值为代表），则（ ）A. 该校竞赛成绩的极差为70分B. a 的值为0.005C. 该校竞赛成绩的平均分的估计值为90.7分D. 这组数据的第30百分位数为8112. 在平面直角坐标系中，已知角α的顶点与坐标原点重合，始边与x 轴的非负半轴重合，终边经过点ππsin ,cos 33⎛⎫- ⎪⎝⎭，()cos sin 2sin cos 2f x x x αα=-则下列结论正确的是（ ）A. 11cos 22α-=B. 2π3x =是()y f x =的图象的一条对称轴C. 将函数()y f x =图象上的所有点向左平移5π6个单位长度，所得到的函数解析式为sin 2y x=D. ()y f x =在4π0,3⎛⎫⎪⎝⎭内恰有3个零点三､填空题：本题共4小题，每小题5分，共20分．13. 某班级有50名同学，一次数学测试平均成绩是92分，如果30名男生的平均成绩为90分，那么20名女生的平均成绩为____分.14. 已知1cos 7α=，()sin αβ+=，π02α<<，π02β<<，则cos β=________.15. 已知函数()()πsin 0,02f x x ωϕωϕ⎛⎫=+>≤≤⎪⎝⎭是R 上的奇函数，其图象关于点3,04A π⎛⎫⎪⎝⎭对称，且在区间0,4⎡⎤⎢⎥⎣⎦π上是单调函数，则ω的值为______.16. cos()cos cos 1y αβαβ=++--的取值范围是_________．四､解答题：本题共6小题，共70分．解答应写出文字说明､证明过程或演算步骤．17. 已知()()()()3πsin πcos 2πcos 2.πcos sin π2f αααααα⎛⎫--- ⎪⎝⎭=⎛⎫--- ⎪⎝⎭（1）化简()f α；（2）若α是第三象限角，且()1sin π5α-=，求()f α的值.18. 据调查，某市政府为了鼓励居民节约用水，减少水资源的浪费，计划在本市试行居民生活用水定额管理，即确定一个合理的居民用水量标准x （单位：吨），月用水量不超过x 的部分按平价收费，超出x 的部分按议价收费．为了了解全市居民用水量分布情况，通过抽样，获得了n 户居民某年的月均用水量（单位：吨），其中月均用水量在(]9,12内的居民人数为39人，并将数据制成了如图所示的频率分布直方图．（1）求a 和n 的值；（2）若该市政府希望使80%的居民月用水量不超过标准x 吨，试估计x 的值；（3）在（2）的条件下，若实施阶梯水价，月用水量不超过x 吨时，按3元/吨计算，超出x 吨的部分，按5元/吨计算．现市政府考核指标要求所有居民的月用水费均不超过70元，则该市居民月用水量最多为多少吨？19. 已知函数()()2πcos 2cos f x x x x =-+．（1）若ππ,63x ⎡⎤∈-⎢⎥⎣⎦，求函数()f x 的值域；（2）若函数()()1g x f x =-在区间π,6m ⎡⎤-⎢⎥⎣⎦上有且仅有两个零点，求m 的取值范围．20. 某生物研究者于元旦在湖中放入一些凤眼莲（其覆盖面积为k ），这些凤眼莲在湖中的蔓延速度越来越快，二月底测得凤眼莲的覆盖面积为224m ，三月底测得凤眼莲的覆盖面积为236m ，凤眼莲的覆盖面积y （单位：2m ）与月份x （单位：月）的关系有两个函数模型()0,1xy ka k a =>>与()120,0y px k p k =+>>可供选择．（1）试判断哪个函数模型更合适并求出该模型的解析式；（2）求凤眼莲的覆盖面积是元旦放入凤眼莲面积10倍以上的最小月份．（参考数据：lg 20.3010,lg 30.4711≈≈）．21. 已知函数()()sin (0,0π)f x x ωϕωϕ=+><<的最小正周期为π，且直线π2x =-是其图象的一条对称轴．（1）求函数()f x 的解析式；（2）将函数()y f x =的图象向右平移π4个单位，再将所得的图象上每一点的纵坐标不变，横坐标伸长为原来的2倍后所得到的图象对应的函数记作()y g x =，已知常数*,n λ∈∈R N ，且函数()()()F x f x g x λ=+在()0,πn 内恰有2023个零点，求常数λ与n 的值．22. 已知二次函数()f x 满足：()()224132,log 231x f x x x g x ⎛⎫+=++=+⎪-⎝⎭（1）求()f x 的解析式；（2）求()g x 的单调性与值域（不必证明）；（3）设()ππ2cos cos2,22h x x m x x ⎛⎫⎡⎤=+∈-⎪⎢⎥⎣⎦⎝⎭，若()()f h x g h x ⎡⎤⎡⎤≥⎣⎦⎣⎦，求实数m 的值．深圳中学2023-2024学年度第一学期期末考试试题年级：高一 科目：数学参考：以10为底的对数叫常用对数，把10log N 记为lg N ；以()e e 2.718281828=⋯为底的对数叫自然对数，把e log N 记为ln N ．一､选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 为了解某地区居民使用手机扫码支付的情况，拟从该地区的居民中抽取部分人员进行调查，事先已了解到该地区老、中、青三个年龄段的人员使用手机扫码支付的情况有较大差异，而男、女使用手机扫码支付的情况差异不大.在下面的抽样方法中，最合理的是（ ）A 抽签法B. 按性别分层随机抽样C. 按年龄段分层随机抽样D. 随机数法【答案】C 【解析】【分析】根据抽样方法确定正确答案.【详解】依题意，“居民人数多”， “男、女使用手机扫码支付的情况差异不大”，“老、中、青三个年龄段的人员使用手机扫码支付的情况有较大差异”，所以最合理的是按年龄段分层随机抽样.故选：C 2. 下列与7π4的终边相同的角的表达式中，正确的是（ ）A. ()2π315Z k k +∈B. ()36045Z k k ⋅-∈C. ()7π360Z 4k k ⋅+∈D. ()5π2πZ 4k k +∈【答案】B 【解析】【分析】AC 项角度与弧度混用，排除AC ；D 项终边在第三象限，排除D.【详解】因为7πrad 3154= ，终边落在第四象限，且与45- 角终边相同，故与7π4终边相同的角的集合.的{}{}31536045360S k k αααα==+⋅==-+⋅即选项B 正确；选项AC 书写不规范，选项D 表示角终边在第三象限.故选：B.3. 角α的终边与单位圆O 相交于点P ，且点P 的横坐标为35的值为（ ）A.35B. 35-C.45 D. 45-【答案】A 【解析】【分析】利用三角函数定义以及同角三角函数之间的平方关系即可得出结果.【详解】根据三角函数定义可知3cos 5α=，又22sin cos 1αα+=53cos α===.故选：A4. 已知角()0,πα∈，且1cos 23α=，则sin α的值为（ ）A.B.C. D. 【答案】B 【解析】【分析】根据余弦的二倍角公式即可求解.【详解】因为21cos 212sin3αα=-=，所以sin α=，因为()0,πα∈，所以sin α=.故选：B .5. 健康成年人的收缩压和舒张压一般为90~139mmhg 和60~89mmhg ，心脏跳动时，血压在增加或减小，血压的最大值、最小值分别为收缩压和舒张压，血压计上的读数就是收缩压和舒张压，读数为120/80mmhg为标准值．设某人的血压满足函数式()11525sin(160π)P t t =+，其中()P t 为血压（mmhg ），t 为时间（min ）．给出以下结论：①此人的血压在血压计上的读数为140/90mmhg ②此人的血压在健康范围内③此人的血压已超过标准值 ④此人的心跳为80次/分其中正确结论的个数为（ ）A. 1 B. 2 C. 3 D. 4【答案】C 【解析】【分析】根据所给函数解析式及正弦函数的性质求出()P t 的取值范围，即可得到此人的血压在血压计上的读数，从而判断①②③，再计算出最小正周期，即可判断④.【详解】因为某人的血压满足函数式()11525sin(160π)P t t =+，又因为1sin(160π)1t -≤≤，所以11525()11525P t -≤≤+，即90()140P t ≤≤，即此人的血压在血压计上的读数为140/90mmhg ，故①正确；因为收缩压为140mmhg ，舒张压为90mmhg ，均超过健康范围，即此人的血压不在健康范围内，故②错误，③正确；对于函数()11525sin(160π)P t t =+，其最小正周期2π1160π80T ==（min ），则此人的心跳为180T=次/分，故④正确；故选：C6. 孩子在成长期间最需要父母的关爱与陪伴，下表为2023年中国父母周末陪孩子日均时长统计图．根据该图，下列说法错误的是（ ）A. 2023年母亲周末陪伴孩子日均时长超过8小时的占比大于13B. 2023年父亲周末陪伴孩子日均时长超过6小时的占比大于12C. 2023年母亲周末陪伴孩子日均时长的5个时段占比的极差为28.8%D. 2023父母周末陪伴孩子日均时长的10个时段占比的中位数为20.2%【答案】C 【解析】【分析】根据题意结合统计相关知识逐项分析判断.【详解】由题图可知：2023年母亲周末陪伴孩子日均时长超过8小时的占比为138.7%3>，A 说法正确；2023年父母周末陪伴孩子日均时长超过6小时的占比为131.5%24.2%55.7%2+=>，B 说法正确；2023年母亲周末陪伴孩子日均时长的5个时段占比的极差为38.7% 2.5%36.2%-=，C 说法错误；2023年父母周末陪伴孩子日均时长的10个时段占比的中位数为21.4%19.0%20.2%2+=，D 说法正确．故选：C ．7. 将函数()2sin f x x =图象上所有点的横坐标缩小为原来的12，再向右平移π6个单位长度，得到函数()g x 的图象，若()0g x a -=在π0,2⎡⎤⎢⎥⎣⎦上有两个不同的零点1x ，2x ，则()12tan x x +=（ ）A.B. C.D. 【答案】B 【解析】【分析】根据函数图象的变换可得()π2sin 23g x x ⎛⎫=-⎪⎝⎭，即可结合正弦函数的对称性得12πt t +=，进而125π6x x +=，即可求解.【详解】将函数()2sin f x x =图象上所有点的横坐标缩小为原来的12，得到2sin 2y x =的图象，再向右平移π6个单位长度，得到()ππ2sin 22sin 263g x x x ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭的图象．当π0,2x ⎡⎤∈⎢⎥⎣⎦时，ππ2π2,333x ⎡⎤-∈-⎢⎥⎣⎦，令π23x t -=，π2π,33t ⎡⎤∈-⎢⎥⎣⎦，则关于t 的方程2sin t a =在π2π,33-⎡⎤⎢⎥⎣⎦上有两个不等的实数根1t ，2t ，所以12πt t +=，即12ππ22π33x x -+-=，则125π6x x +=，所以()125πtan tan 6x x +==．故选：B8. 如果对于任意整数πππ,sin,cos ,tan n n n n k k k都是有理数，我们称正整数k 是“好整数”，下面的整数中哪个是最大的“好整数”（ ）A. 1 B. 2C. 3D. 4【答案】A 【解析】【分析】利用三角函数定义域代入选项逐个验证即可得出结论.【详解】考虑三角函数的定义域，对于选项A ，当1k =时，sin π,cos π,tan πn n n 对于任意整数n ，都是整数，满足题意；对于B ，当2k =时，2ππtantan n n k =对于整数1，没有意义，不满足题意；同理可得对于C 和D ，当3ππtantan n n k =或4ππtan tan n n k =时，代入验证可知不满足题意；所以可知最大“好整数”为1故选：A二､多选题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项是符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9. 下列说法中正确的是（ ）A. 度与弧度是度量角的两种不同的度量单位B. 1度的角是周角的1360，1弧度的角是周角的12πC. 根据弧度的定义，180︒一定等于π弧度D. 不论是用角度制还是用弧度制度量角，角的大小均与圆的半径长短有关【答案】ABC 【解析】【分析】根据角度制与弧度制的定义，以及角度制和弧度制的换算公式，以及角的定义，逐项判定，即可求解.【详解】根据角度制和弧度制的定义可知，度与弧度是度量角的两种不同的度量单位，所以A 正确；由圆周角的定义知，1度的角是周角的1360，1弧度的角是周角的12π，所以B 正确；根据弧度的定义知，180︒一定等于π弧度，所以C 正确；无论是用角度制还是用弧度制度量角，角的大小均与圆的半径长短无关，只与弧长与半径的比值有关，故D 不正确.故选：ABC.10. 下列各式中，值是12的是（ ）A. ππc s cos sin os n 3i 3x x x x ⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭ B. tan10tan 35tan10tan 35︒+︒+︒︒C.2tan 22.51tan 22.5︒-︒D.22cos 203sin 50-︒-︒【答案】ACD 【解析】【分析】利用两角差的余弦公式，诱导公式，二倍角公式即可逐个选项判断.【详解】ππc s cos sin os n 3i 3x x x x ⎛⎫⎛⎫+++ ⎪ ⎪⎝⎭⎝⎭ππ1cos cos 332x x ⎛⎫=--== ⎪⎝⎭，A 正确；tan10tan 35tan10tan 35︒+︒+︒︒()()tan 10351tan10tan 35tan10tan 35=︒+︒-︒︒+︒︒tan 451=︒=，B 不对；22tan 22.512tan 22.511tan 451tan 22.521tan 22.522︒︒==︒=-︒-︒，C 正确；()2311cos 403sin502cos 2012223sin 503sin503sin502-︒-︒-︒===-︒-︒-︒，D 正确.故选：ACD11. 2023年是共建“一带一路”倡议提出十周年．某校组织了“一带一路”知识竞赛，将学生的成绩（单位：分，满分：120分）整理成如图的频率分布直方图（同一组中的数据用该组区间的中点值为代表），则（ ）A. 该校竞赛成绩的极差为70分B. a 的值为0.005C. 该校竞赛成绩的平均分的估计值为90.7分D. 这组数据的第30百分位数为81【答案】BC【解析】【分析】利用频率分布直方图，用样本估计总体，样本的极差、平均值、百分位数相关知识计算即可.【详解】因为由频率分布直方图无法得出这组数据的最大值与最小值，所以这组数据的极差可能为70，也可能为小于70的值，所以A 错误；因为(0.00820.0120.01540.030)10700.651a a a a ++++++⨯=+=，解得0.005a =，所以B 正确；该校竞赛成绩的平均分的估计值550.00510650.00810x =⨯⨯+⨯⨯+750.01210850.01510950.03010⨯⨯+⨯⨯+⨯⨯10540.0051011520.0051090.7+⨯⨯⨯+⨯⨯⨯=分，所以C 正确．设这组数据的第30百分位数为m ，则(0.0050.0080.012)10(80)0.015100.3m ++⨯+-⨯⨯=，解得2413m =，所以D 错误．故选：BC ．12. 在平面直角坐标系中，已知角α的顶点与坐标原点重合，始边与x 轴的非负半轴重合，终边经过点ππsin ,cos 33⎛⎫- ⎪⎝⎭，()cos sin 2sin cos 2f x x x αα=-则下列结论正确的是（ ）A. 11cos 22α-=B. 2π3x =是()y f x =的图象的一条对称轴C. 将函数()y f x =图象上的所有点向左平移5π6个单位长度，所得到的函数解析式为sin 2y x=D. ()y f x =在4π0,3⎛⎫⎪⎝⎭内恰有3个零点【答案】AB 【解析】【分析】利用三角函数的定义求得α，从而得到()f x 的解析式，进而利用三角函数的性质与平移的结论，逐一分析各选项即可得解.【详解】因为ππ1sin ,cos 332⎛⎫⎛⎫-= ⎪ ⎪ ⎪⎝⎭⎝⎭，所以由三角函数的定义得1sin 2α=，cos α=，所以5π2π,6k k α∈=+Z ，则()()cos sin 2sin cos 2sin 2f x x x x ααα=-=-5π5πsin 22πsin 2,66x k x k ∈⎛⎫⎛⎫=--=- ⎪ ⎪⎝⎭⎝⎭Z ，A : 22111cos 22sin 222αα⎛⎫-==⨯= ⎪⎝⎭，故A 正确；B ：因为5π62π4ππsin sin 1332f ⎛⎫⎛⎫=-==⎪ ⎪⎝⎭⎝⎭，所以2π3x =是()y f x =的图象的一条对称轴，故B 正确；C ：将函数()y f x =图象上的所有点向左平移5π6个单位长度，所得到的函数解析式为5π5πsin 2sin 2665π6y x x ⎡⎤⎛⎫⎛⎫=+-=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，故C 错误；D ：令()0f x =，得5πsin 206x ⎛⎫-= ⎪⎝⎭，解得5π5ππ2π,,6122k x k k x k ∈∈-=⇒=+Z Z ，仅0k =，1，即5π11π,1212x =符合题意，即()y f x =在4π0,3⎛⎫⎪⎝⎭内恰有两个零点，故D 错误.故选：AB三､填空题：本题共4小题，每小题5分，共20分．13. 某班级有50名同学，一次数学测试平均成绩是92分，如果30名男生的平均成绩为90分，那么20名女生的平均成绩为____分.【答案】95【解析】【分析】利用平均数的求法计算即可.【详解】设所求平均成绩为x ，由题意得5092309020x ⨯=⨯+⨯，∴95x =.故答案为：9514. 已知1cos 7α=，()sin αβ+=，π02α<<，π02β<<，则cos β=________.【答案】12##0.5【解析】【分析】根据题意，分别求得()sin ,cos ααβ+，再由余弦的差角公式，代入计算，即可得到结果.【详解】因为π02α<<且11cos c 2πos 73α=<=，则ππ32α<<，又02βπ<<，所以π3παβ<+<，且()sin αβ+=<，所以π2π3αβ<+<，则()11cos 14αβ+==-，sin α==，所以()()()cos cos cos cos sin sin βαβααβααβα=+-=+++⎡⎤⎣⎦11111472=-⨯+=.故答案为：1215. 已知函数()()πsin 0,02f x x ωϕωϕ⎛⎫=+>≤≤⎪⎝⎭是R 上的奇函数，其图象关于点3,04A π⎛⎫⎪⎝⎭对称，且在区间0,4⎡⎤⎢⎥⎣⎦π上是单调函数，则ω的值为______.【答案】43【解析】【分析】由函数为奇函数，得0ϕ=，再根据函数图像关于点3,04A π⎛⎫⎪⎝⎭对称，可知43kω=，根据函数的单调性可得04ω<≤，进而得解.【详解】因为函数()()sin 0,02f x x πωϕωϕ⎛⎫=+>≤≤ ⎪⎝⎭是R 上的奇函数，则()()f x f x -=-，即sin cos cos sin x x ϕωωϕ=-，又因为0ω>，所以sin 0ϕ=，因为π02ϕ≤≤，所以0ϕ=；故()sin f x x ω=；又因为图象关于点3π,04A ⎛⎫⎪⎝⎭对称，则3ππ4k ω=，Z k ∈，所以43k ω=，Z k ∈，因为函数在区间π0,4⎡⎤⎢⎥⎣⎦上是单调函数，则12ππ24ω⨯≥，得04ω<≤；所以43ω=，故答案为：43.16. cos()cos cos 1y αβαβ=++--取值范围是_________．【答案】1[4,]2-【解析】【分析】由和角的余弦公式变形给定函数，再利用辅助角公式变形，结合正弦函数的性质用含cos β的关系式表示y ，再借助二次函数最值求解即得.【详解】cos cos sin sin cos cos 1y αβαβαβ=-+--(cos 1)cos (sin )sin (cos 1)βαβαβ=+--+)(cos 1)αϕβ=+-+)(cos 1)αϕβ=+-+由sin()[1,1]αϕ+∈-，得(cos 1)(cos 1)y ββ-+≤≤+，令t =，则t ∈，则22t y t ≤≤--，所以221(42y t t ≥-=-+≥-，当且仅当t =，即cos 1β=时取等号，且2211(22y t t ≤-=-+≤，当且仅当t =，即1cos 2β=-时取等号，的所以y 的取值范围为1[4,]2-.故答案为：1[4,]2-四､解答题：本题共6小题，共70分．解答应写出文字说明､证明过程或演算步骤．17. 已知()()()()3πsin πcos 2πcos 2.πcos sin π2f αααααα⎛⎫--- ⎪⎝⎭=⎛⎫--- ⎪⎝⎭（1）化简()f α；（2）若α是第三象限角，且()1sin π5α-=，求()f α的值.【答案】（1）()cos f αα=-（2【解析】【分析】（1）利用诱导公式化简即可；（2）利用诱导公式及同角三角函数的关系计算即可.【小问1详解】因为()()()()3πsin πcos 2πcos 2πcos sin π2f αααααα⎛⎫--- ⎪⎝⎭=⎛⎫--- ⎪⎝⎭()sin cos sin cos sin sin αααααα⋅⋅-==-⋅，所以()cos fαα=-.【小问2详解】由诱导公式可知()1sin πsin 5αα-=-=，即1sin 5α=-，又α是第三象限角，所以cos α===所以()cos fαα=-=.18. 据调查，某市政府为了鼓励居民节约用水，减少水资源的浪费，计划在本市试行居民生活用水定额管理，即确定一个合理的居民用水量标准x （单位：吨），月用水量不超过x 的部分按平价收费，超出x 的部分按议价收费．为了了解全市居民用水量分布情况，通过抽样，获得了n 户居民某年的月均用水量（单位：吨），其中月均用水量在(]9,12内的居民人数为39人，并将数据制成了如图所示的频率分布直方图．（1）求a 和n 的值；（2）若该市政府希望使80%的居民月用水量不超过标准x 吨，试估计x 的值；（3）在（2）的条件下，若实施阶梯水价，月用水量不超过x 吨时，按3元/吨计算，超出x 吨的部分，按5元/吨计算．现市政府考核指标要求所有居民的月用水费均不超过70元，则该市居民月用水量最多为多少吨？【答案】（1）1300a =，200n = （2）16.6吨 （3）20.64吨【解析】【分析】（1）频率分布直方图总面积为1，由此即可求解.（2）先判断所求值所在的区间，再按比例即可求解.（3）按题意列不等式即可求解.【小问1详解】()0.0150.0250.0500.0650.0850.0500.0200.0150.00531a +++++++++⨯= ，1.300a ∴=用水量在(]9,12频率为0.06530.195⨯=，392000.195n ∴==（户）【小问2详解】()0.0150.0250.0500.0650.08530.720.8++++⨯=< ，()0.0150.0250.0500.0650.0850.05030.870.8+++++⨯=>，0.800.7215316.60.870.72-∴+⨯=-（吨）【小问3详解】设该市居民月用水量最多为m 吨，因为16.6349.870⨯=<，所以m 16.6>，则()16.6316.6570w m =⨯+-⨯≤，解得20.64m ≤，答：该市居民月用水量最多为20.64吨．19. 已知函数()()2πcos 2cos f x x x x =-+．（1）若ππ,63x ⎡⎤∈-⎢⎥⎣⎦，求函数()f x 的值域；（2）若函数()()1g x f x =-在区间π,6m ⎡⎤-⎢⎥⎣⎦上有且仅有两个零点，求m 的取值范围．【答案】（1）[]0,3（2）5π11π,1212⎡⎫⎪⎢⎣⎭【解析】【分析】（1）利用诱导公式以及二倍角公式化简可得()f x 的表达式，结合ππ,63x ⎡⎤∈-⎢⎥⎣⎦，确定π26x +的范围，即可求得答案；（2）由π,6x m ⎡⎤∈-⎢⎥⎣⎦，确定πππ2[,2666x m +∈-+，根据()g x 在区间π,6m ⎡⎤-⎢⎥⎣⎦上有且仅有两个零点，结合正弦函数的零点，列出相应不等式，即求得答案.【小问1详解】由题意得()()2πcos 2cos f x x x x=-+的πcos 212sin 216x x x ⎛⎫=++=++ ⎪⎝⎭，当ππ,63x ⎡⎤∈-⎢⎥⎣⎦，则ππ5π2[,666x +∈-，则1πsin 2126x ⎛⎫-≤+≤ ⎪⎝⎭，则π02sin 2136x ⎛⎫≤++≤ ⎪⎝⎭，即函数()f x 的值域为[]0,3；【小问2详解】由题可得π6m >-，当π,6x m ⎡⎤∈-⎢⎥⎣⎦时，πππ2[,2666x m +∈-+，()()π2sin 216g x x f x ⎛⎫+ ⎪⎝=-⎭=，且()g x 在区间π,6m ⎡⎤-⎢⎥⎣⎦上有且仅有两个零点，而sin y x =在π[,2π)6-有且仅有2个零点，分别为0,π，故π5π11ππ22π,61212m m ≤+<∴≤<，即5π11π,1212m ⎡⎫∈⎪⎢⎣⎭.20. 某生物研究者于元旦在湖中放入一些凤眼莲（其覆盖面积为k ），这些凤眼莲在湖中的蔓延速度越来越快，二月底测得凤眼莲的覆盖面积为224m ，三月底测得凤眼莲的覆盖面积为236m ，凤眼莲的覆盖面积y （单位：2m ）与月份x （单位：月）的关系有两个函数模型()0,1x y ka k a =>>与()120,0y px k p k =+>>可供选择．（1）试判断哪个函数模型更合适并求出该模型的解析式；（2）求凤眼莲的覆盖面积是元旦放入凤眼莲面积10倍以上的最小月份．（参考数据：lg 20.3010,lg 30.4711≈≈）．【答案】（1）选择模型()0,1x y ka k a =>>符合要求，*32323N 2,11,xy x x ⎛⎫=⋅ ⎪⎝≤≤∈⎭ （2）六月份【解析】【分析】（1）根据指数函数与幂函数的增长速度即可选得哪一个模型，再利用待定系数法即可求出该模型的解析式；（2）由（1）结合已知可得3233210323x ⎛⎫⋅>⨯ ⎪⎝⎭，再结合已知数据即可得出答案.【小问1详解】函数()0,1x y ka k a =>>与()120,0y pxk p k =+>>在()0,∞+上都是增函数，随着x 的增加，函数()0,1x y kak a =>>的值增加的越来越快，而函数()120,0y px k p k =+>>的值增加的越来越慢，由于凤眼莲在湖中的蔓延速度越来越快，因此选择模型()0,1x y kak a =>>符合要求，根据题意可知2x =时，24y =；3x =时，36y =，所以232436ka ka ⎧=⎨=⎩，解得32323a k ⎧=⎪⎪⎨⎪=⎪⎩，故该函数模型的解析式为*32323N 2,11,x y x x ⎛⎫=⋅ ⎪⎝≤≤∈⎭；【小问2详解】当0x =时，323y =，元旦放入凤眼莲的覆盖面积是232m 3，由3233210323x ⎛⎫⋅>⨯ ⎪⎝⎭，得3102x ⎛⎫> ⎪⎝⎭，所以32lg1011log 10 5.93lg 3lg 20.47110.3010lg 2x >==≈≈--，又*N x ∈，所以6x ≥，即凤眼莲的覆盖面积是元旦放入凤眼莲面积10倍以上的最小月份是六月份．21. 已知函数()()sin (0,0π)f x x ωϕωϕ=+><<的最小正周期为π，且直线π2x =-是其图象的一条对称轴．（1）求函数()f x 的解析式；（2）将函数()y f x =的图象向右平移π4个单位，再将所得的图象上每一点的纵坐标不变，横坐标伸长为原来的2倍后所得到的图象对应的函数记作()y g x =，已知常数*,n λ∈∈R N ，且函数()()()F x f x g x λ=+在()0,πn 内恰有2023个零点，求常数λ与n 的值．【答案】（1）()cos2f x x =（2）1,1349n λ==【解析】【分析】（1）由周期求得ω，再由对称性求得ϕ得解析式；（2）由图象变换求得()g x ，然后可得()F x 的表达式，令[]sin 1,1t x =∈-，()0F x =化为22210,Δ80t t λλ--==+>，则关于t 的二次方程2210t t λ--=必有两不等实根12t t ､，则1212t t =-，则12t t ､异号，然后分类讨论()0F x =在(0,π)n 上解的个数后得出结论．【小问1详解】由三角函数的周期公式可得()()2π2,sin 2πf x x ωϕ==∴=+，令()π2π2x k k Z ϕ+=+∈，得()ππ422k x k Z ϕ=-+∈，由于直线π2x =-为函数()y f x =的一条对称轴，所以，()πππZ 2422k k ϕ-=-+∈，得()3ππZ 2k k ϕ=+∈，由于0π,1k ϕ<<∴=-，则π2ϕ=，因此，()πsin 2cos22f x x x ⎛⎫=+= ⎪⎝⎭；小问2详解】将函数()y f x =的图象向右平移π4个单位，得到函数ππcos 2cos 2sin242y x x x ⎡⎤⎛⎫⎛⎫=-=-= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，再将所得的图象上每一点的纵坐标不变，横坐标伸长为原来的2倍后所得到的图象对应的函数为()sin g x x =，()()()2cos2sin 2sin sin 1F x f x g x x x x x λλλ=+=+=-++ ，令()0F x =，可得22sin sin 10x x λ--=，令[]sin 1,1t x =∈-，得22210,Δ80t t λλ--==+>，【则关于t 的二次方程2210t t λ--=必有两不等实根12t t ､，则1212t t =-，则12t t ､异号，（i ）当101t <<且201t <<时，则方程1sin x t =和2sin x t =在区间()()*0,πNn n ∈均有偶数个根，从而方程22sin sin 10x x λ--=在()()*0,πNn n ∈也有偶数个根，不合乎题意；（ii ）当11t =-时，则212t =，当()0,2πx ∈时，1sin x t =只有一根，2sin x t =有两根，所以，关于x 的方程22sin sin 10x x λ--=在()0,2π上有三个根，由于202336741=⨯+，则方程22sin sin 10x x λ--=在()0,1348π上有36742022⨯=个根，由于方程1sin x t =在区间()1348π,1349π上无实数根，方程2sin x t =在区间()1348π,1349π上有两个实数解，因此，关于x 的方程22sin sin 10x x λ--=在区间()0,1349π上有2024个根，不合乎题意，（iii ）当11t =，则212t =-，当()0,2πx ∈时，1sin x t =只有一根，2sin x t =有两根，所以，关于x 的方程22sin sin 10x x λ--=在()0,2π上有三个根，由于202336741=⨯+，则方程22sin sin 10x x λ--=在()0,1348π上有36742022⨯=个根，由于方程1sin x t =在区间()1348π,1349π上只有一个根，方程2sin x t =在区间()1348π,1349π上无实数解，因此，关于x 的方程22sin sin 10x x λ--=在区间()0,1349π上有2023个根，合乎题意；此时，1122λ-+=，1λ=，综上所述：1,1349n λ==．22. 已知二次函数()f x 满足：()()224132,log 231x f x x x g x ⎛⎫+=++=+ ⎪-⎝⎭（1）求()f x 的解析式；（2）求()g x 的单调性与值域（不必证明）；（3）设()ππ2cos cos2,22h x x m x x ⎛⎫⎡⎤=+∈- ⎪⎢⎥⎣⎦⎝⎭，若()()f h x g h x ⎡⎤⎡⎤≥⎣⎦⎣⎦，求实数m 的值．【答案】（1）()2f x x x =+ （2）在()0,∞+上单调递减，值域是()1,+∞．（3）1-【解析】【分析】（1）利用换元法，令1t x =+，代入化简即可求出函数的解析式；（2）可设4231x u =+-，利用复合函数的单调性，即可判定函数的单调性，进而求得值域；（3）由（2）知，()12g =，()12f =，结合()(),f x g x 的单调性可知当1x ≥时，()()2,01f x g x x ≥≥<<时，()()2f x g x <<，由()()f h x g h x ⎡⎤⎡⎤≥⎣⎦⎣⎦恒成立，即为()1h x ≥恒成立，设[]cos 0,1x t =∈，只需不等式()22210mt t m +-+≥在[]0,1t ∈上恒成立，讨论m 的取值范围即可求解.【小问1详解】由题意()2132f x x x +=++，令1t x =+，则1x t =-，有()()22(1)312f t t t t t =-+-+=+，故()2f x x x =+【小问2详解】函数()24log 231x g x ⎛⎫=+⎪-⎝⎭，由420031x x +>⇒>-，即定义域为()0,∞+，且4231x u =+-在()0,∞+上单调递减及2log y u =单调递增所以()24log 231x g x ⎛⎫=+ ⎪-⎝⎭在()0,∞+上单调递减．因为()0,x ∞∈+，42231x u =+>-，所以()g x 的值域是()1,∞+【小问3详解】结合（2）结论知()24log 231x g x ⎛⎫=+⎪-⎝⎭在()0,∞+上单调递减且()12g =，又()2f x x x =+在()0,∞+上单调递增且()12f =故当1x ≥时，()()2,01f xg x x ≥≥<<时，()()2f x g x <<，由()()()1f h x g h x h x ⎡⎤⎡⎤≥⇒≥⎣⎦⎣⎦恒成立，即()22cos 2cos 11x m x +-≥在ππ,22x ⎡⎤∈-⎢⎥⎣⎦上恒成立，设[]cos 0,1x t =∈，则不等式()22210mt t m +-+≥在[]0,1t ∈上恒成立，①当0m =时，不等式化为210t -≥，显然不满足恒成立；②当0m >时，将0=t 代入得()10m -+≥，与0m >矛盾；③当0m <时，只需()()10,1,12210,1,m m m m m m ⎧-+≥≤-⎧⎪⇒⇒=-⎨⎨+-+≥≥-⎪⎩⎩，综上，实数m 的值为-1．【点睛】关键点点睛：本题考查了换元法求函数的解析式，函数的单调性，解题的关键是根据函数的单调性得出()1h x ≥，转化为二次不等式恒成立，考查了分类讨论的思想.。

北京市西城区2023—2024学年度第一学期期末试卷高三化学 2024.1本试卷共10页，100分。

考试时长90分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

可能用到的相对原子质量：H 1 N 14 O 16 Mg 24 Cl 35.5第一部分本部分共14题，每题3分，共42分。

在每题列出的四个选项中，选出最符合题目要求的一项。

1．中国科研团队开发出柔性单晶硅太阳能电池。

单晶硅的晶体结构与金刚石类似，下列说法不．正确．．的是 A ．C 和Si 均位于元素周期表中第ⅣA 族 B ．单晶硅和金刚石均属于共价晶体 C ．单晶硅和金刚石中的键角均相同 D ．单晶硅的熔点高于金刚石的熔点 2．下列化学用语或图示表达不．正确．．的是 A ．NaClB ．基态Cr 原子的价层电子排布式：3d 44s 2C ．乙醇的分子式：C 2H 6OD ．乙炔的分子结构模型：3．下列物质的应用不涉及．．．氧化还原反应的是 A ．次氯酸钠作纸张的漂白剂 B ．铁粉作食品保鲜的吸氧剂 C ．过氧化钠作呼吸面具的供氧剂D ．硫化钠作工业废水中Cu 2+、Hg 2+的沉淀剂 4．下列事实不能．．用平衡移动原理解释的是 A ．密闭烧瓶内的NO 2和N 2O 4的混合气体，受热后颜色加深 B ．Na 2CO 3溶液将水垢中的CaSO 4转化为CaCO 3 C ．pH ＝1的醋酸溶液稀释10倍，溶液的pH ＜2 D ．H 2O 2溶液中滴加FeCl 3溶液，促进H 2O 2分解 5．下列方程式与所给事实不相符．．．的是 A ．电镀铜时阴极析出铜：Cu 2+ + 2e − === CuB ．钠在空气中加热生成淡黄色固体：4Na + O 2 === 2Na 2OC ．电解饱和食盐水制氯气：2Cl －+ 2H 2O ===== 2OH －+ H 2↑+ Cl 2↑ D ．氨催化氧化生成一氧化氮：4NH 3 + 5O 2 ====== 4NO + 6H 2O 6．下列事实不能．．用氢键解释的是 催化剂 △电解A ．密度：H 2O(l)＞H 2O(s)B ．沸点：H 2O ＞H 2SC ．稳定性：HF ＞H 2OD ．溶解性（水中）：NH 3＞CH 4 7．阿斯巴甜是一种合成甜味剂，其结构简式如下。

2024北京朝阳初一（上）期末数 学（选用）（考试时间90分钟 满分100分）考生须知1．本试卷共6页．在试卷和答题卡上准确填写学校名称、班级、姓名和考号． 2．试题答案一律填涂或书写在答题卡上，在试卷上作答无效．3．在答题卡上，选择题用2B 铅笔作答，其他试题用黑色字迹签字笔作答． 4．考试结束，将本试卷、答题卡和草稿纸一并交回． 一、选择题（共24分，每题3分）下面1-8题均有四个选项，其中符合题意的选项只有一个． 1．2−的绝对值为（ ）A ．2−B ．2−−C ．12− D ．22．2023年我国规模以上内容创作生产营业收人累计值前三个季度分别约为6500亿元13000亿元，20000亿元，合计约39500亿元．将39500用科学记数法表示应为（ ） A ．239510⨯ B ．43.9510⨯ C ．33.9510⨯ D ．50.39510⨯ 3．若34x y −与a x y 是同类项，则a 的值为（ ） A ．2− B ．2 C ．3 D ．44．下列图形中可以作为一个正方体的展开图的是（ ）A B CD5．如果a b =，那么下列等式一定成立的是（ ） A ．33a b +=− B ．0a b += C ．44a b= D ．1ab = 6．已知α∠与β∠互为补角，并且α∠的2倍比β∠大30︒，则,αβ∠∠分别为（ ）A ．70︒，110︒B ．40︒，50︒C ．75︒，115︒D ．50︒，130︒7．,a b 是有理数，它们在数轴上的对应点的位置如图所示．下列各式正确的是（ ）A ．b a a b −<−<<B ．a b a b −<−<<C ．b a a b <−<<−D ．b b a a <−<−<8．对幻方的研究体现了中国古人的智慧．如图1是一个幻方的图案，其中9个格中的点数分别为1，2，3，4，5，6，7，8，9．每一横行、每一竖列、每一斜对角线上的点数的和都是15．如图2是一个没有填完整的幻方，如果它处于同一横行、同一竖列、同一斜对角线上的3个数的和都相等，那么正中间的方格中的数字为（ ）A ．5B ．1C ．0D ．1−二、填空题（共24分，每题3分）9．如果60m 表示向东走60m ，那么80m −表示______．10．请写出一个次数为3，系数是负数的单项式：______． 11．计算：2(2)43−÷⨯=______． 12．计算：48296021''︒+︒=______．13．北京冬季某一天的温差是10℃，若这天的最高气温是t ℃，则最低气温是______℃．（用含t 的式子表示）14．举例说明“若,a b 是有理数，则a b a +>”是错误的，请写出一个b 的值：b =______．15．如图，一艘快艇S 从灯塔O 南偏东60︒的方向上的某点出发，绕着灯塔O 逆时针方向以每个时间单位3︒的转速旋转1周，当14AOS BOS ∠=∠时，快艇S 旋转了______个时间单位．16．某社区为增强居民体质，体现以人民为中心的理念，准备到一家健身器材专卖店购置一批健身器材供居民健身使用．该专卖店推出两种优惠活动，并规定只能选择其中一种． 活动一：所购商品按原价打八折；活动二：所购商品按原价每满．．400元减100元．（如：所购商品原价为400元，可减100元，需付款300元；所购商品原价为900元，可减200元，需付款700元）（1）若购买一件原价为550元的健身器材，更合算的选择方式为活动______；（2）若购买一件原价为(01200)a a <<元的健身器材，选择活动二比选择活动一更合算，则a 的取值范围是______．三、解答题（共52分，第17-24题，每题5分，第25-26题，每题6分） 17．如图，已知线段AB 和点,C D 是线段AB 的中点．（1）根据要求画图： ①画直线DC ； ②画射线BC ；③连接AC 并延长到点E ，使CE AC =；④连接BE ．（2）（1）中线段,DC BE 之间的等量关系是______． 18．计算：()()81021−+++−．19．计算：()12112236⎛⎫−−⨯−⎪⎝⎭． 20．当x 取何值时，式子37x +与式子322x −的值相等？21．解方程：21224x x+−=． 22．先化简，再求值：()()2222545x x x x −−−−+，其中2x =−．23．小明家经营一家文化创意产品商店，他在课余时间关注了文化创意背包和文化创意摆件两种商品的销售情况，如下表：元，那么售出文化创意背包和文化创意摆件各多少件？24．如图，长方形的一组邻边长分别为10，(1015)m m <<，在长方形的内部放置4个完全相同的小长方形纸片（图中阴影所示），这样得到长方形ABCD 和长方形EFGH ．（1）线段,FG EF 之间的等量关系是______；（2）记长方形ABCD 的周长为1C ，长方形EFGH 的周长为2C ，对于任意的m 值，12C C +的值是否为一个确定的值？若是一个确定的值，请写出这个值，并说明理由；若不是一个确定的值，请举出反例． 25．已知AOB ∠与COD ∠共顶点,,O AOB COD αβ∠=∠=．（1）如图1，点,,A O C 在一条直线上，若60,30,OM αβ=︒=︒为AOD ∠的平分线，ON 为COB ∠的平分线，求MON ∠的度数；（2）若2,,AOB COD αβ=∠∠绕点O 运动到如图2所示的位置，OE 为BOD ∠的平分线，用等式表示AOD ∠与COE ∠之间的数量关系，并说明理由．26．对于数轴上的两条线段，给出如下定义：若其中一条线段的中点恰好是另一条线段的一个三等分点，则称这两条线段互为友好线段．（1）在数轴上，点A 表示的数为-4，点B 表示的数为2，点1C 表示的数为52−，点2C 表示的数为2−，点3C 表示的数为4，在线段123,,BC BC BC 中，与线段AB 互为友好线段的是______； （2）在数轴上，点,,,A B C D 表示的数分别为39,2,,22x xx x −−−−，且,A B 不重合．若线段,AB CD 互为友好线段，直接写出x 的值．参考答案一、选择题（共24分，每题3分）9．向西走80m 10．答案不唯一，如3x − 11．3 12．10850'︒ 13．10t − 14．答案不唯一，如1b =− 15．34或50 16．（1）一 （2）400500a ≤<或8001000a ≤<三、解答题（共52分，第17-24题，每题5分，第25-26题，每题6分）17，解：（1）根据要求所画的图形如图所示：（2）12DC BE =． 18．解：原式()()102811293=++−+−=−=．19．解：()121126824236⎛⎫−−⨯−=−++=⎪⎝⎭． 20．解：根据题意，得37322x x +=−． 32327x x +=−． 525x =． 5x =．所以当5x =时，式子37x +与式子322x −的值相等．21．解：21224x x+=． ()2218x x +−=．428x x +−=． 36x =． 2x =．22．解：原式2222454591x r x x x x =−−+++=++． 当2x =−时，原式13=−．23．解：根据题意可得每件文化创意背包单价260元，每件文化创意摆件单价80元． 设小明家的文化创意产品商店售出文化创意背包x 件． 根据题意，得()26080153000x x +−=． 解得10x =． 所以155x −=．答：小明家的文化创意产品商店售出文化创意背包10件，文化创意摆件5件． 24．解：（1）2EF FC =；（2）1240C C +=． 说明：设FG a =． 根据题意可知2EF a =． 所以()226C FG EF a =+=．因为长方形的一组邻边长分别为10，m ， 所以102,2,10BC a AB m a m a =−=−−=． 所以()122028C AB BC m a =+=+−． 所以1220286C C m a a +=+−+2022m a =+−()202m a =+− 40=．25．解：（1）因为点,,A O C 在一条直线上，所以180AOC ∠=︒． 因为60,30αβ=︒=︒，所以150,120AOD COB ∠=︒∠=︒． 因为OM 为AOD ∠的平分线，ON 为COB ∠的平分线，所以1175,6022DOM AOD CON COB ∠=∠=︒∠=∠=︒． 所以30DON CON COD ∠=∠−∠=︒． 所以45MON DOM DON ∠=∠−∠=︒． （2）2AOD COE ∠=∠．说明：如图，因为OE 为BOD ∠的平分线，所以12DOE BOD ∠=∠． 因为COE DOE COD ∠=∠−∠，所以12COE BOD COD ∠=∠−∠．因为2αβ=，所以1122COE BOD α∠=∠−． 因为AOD DOB AOB DOB α∠=∠−∠=∠−， 所以2AOD COE ∠=∠． 26．解：（1）12,BC BC ．（2）225，7，9，26．。

选择题下列词语中加点字注音完全正确的一项是( )A. 勾勒（lè）憧憬（tóng）遮掩（yǎn）瞻仰（zhān）B. 妩媚（wǔ）参差（cī）摇曳（zhuài）山坳（ào）C. 沉着（zhuó）围歼（jiān）渲染（xuān ）瞬间（shùn）D. 斗室（dǒu）笨拙（zhuō）叱咤（zhà）迥然（jiǒng）【答案】D【解析】D加点字注音完全正确。

A憧憬（chōng）。

B摇曳（yè）。

C渲染（xuàn）。

选择题下列词语书写没有错别字的一项是( )A. 疾弛诞生俨然嘎然而止B. 肃穆摘要倚靠井然有序C. 陶醉放肆娇健不加思索D. 菜畦干躁风靡别出新裁【答案】B【解析】B词语书写没有错别字。

A疾驰，戛然而止。

C矫健，不假思索。

D 干燥，别出心裁。

选择题下列加点的词在句中的含义不正确的一项是（）（A. 我婆娑起舞，芳草为我鼓掌。

（婆娑：盘旋舞动的样子。

）B. 五位壮士屹立在狼牙山顶峰。

（屹立：像山峰一样高耸而稳固地立着，形容坚定而不可动摇）。

C. 后来才知道，在这千钧一发的时刻，是郝副营长划着了火柴，点燃了那本书。

（千钧一发：千钧的重量系在一根头发上，形容重量很重。

）D. 银河系又是宇宙的沧海一粟。

（沧海一粟：大海里的一颗谷粒，形容非常渺小。

）【答案】C【解析】C加点的词在句中的含义不正确。

千钧一发：形容事态极其危险。

选择题将下列短语依次填入文中括号里恰当的是（）爱心是（），使饥寒的人感到人间的温暖；爱心是（），使濒临绝境的人重新看到生活的希望；爱心是（），使孤苦无依的人获得心灵的慰藉；爱心是（），使心灵枯萎的人感受到情感的滋润。

①一首飘荡在夜空里的歌谣②沙漠中的一片绿洲③一场洒落在久旱的土地上的甘霖④一片冬日的阳光A. ③②①④B. ④③②①C. ②①④③D. ④②①③【答案】D【解析】我们先看有争议的第二个与第四个，第二个，濒临绝境的人看到生活的希望，在毫无希望的情况下，就如在干涸的旱地中，总似乎想找寻找清澈的水源，而“沙漠中的一片绿洲”这个比喻，就如我们在旱地中绝望而又无助的时候，只有一场甘霖才能让我们重拾信心。

北京市西城区2023—2024学年度第一学期期末试卷高二数学 2024.1本试卷共5页，共150分.考试时长120分钟.考生务必将答案写在答题卡上，在试卷上作答无效.第一部分（选择题共40分）一､选择题共10小题，每小题4分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.1.直线3410x y -+=不经过（ ）A.第一象限B.第二象限C.第三象限D.第四象限2.抛物线26x y =的焦点到其准线的距离等于（ ） A.32B.3C.6D.8 3.在空间直角坐标系O xyz -中，点()4,2,8A -到平面xOz 的距离与其到平面yOz 的距离的比值等于（ ） A.14 B.12C.2D.4 4.在312x x ⎛⎫+ ⎪⎝⎭的展开式中，x 的系数为（ ） A.3 B.6 C.9 D.125.在正四面体ABCD 中，棱AB 与底面BCD 所成角的正弦值为（ ）C.136.已知直线,a b 和平面α，且b α⊂，则“直线a ∥直线b ”是“直线a ∥平面α”的（ ） A.充分而不必要条件 B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件7.设,A B 为双曲线2222:1(0,0)x y E a b a b-=>>的左､右顶点，M 为双曲线E 上一点，且AMB 为等腰三角形，顶角为120，则双曲线E 的一条渐近线方程是（ ）A.y x =B.2y x =C.y =D.y =8.在正方体的8个顶点中任选3个，则这3个顶点恰好不在同一个表面正方形中的选法有（ ）A.12种B.24种C.32种D.36种9.如图，在长方体1111ABCD A B C D -中，13,4,AB BC CC E ===为棱11B C 的中点，P 为四边形11BCC B 内（含边界）的一个动点.且DP BE ⊥，则动点P 的轨迹长度为（ ）A.5B.C.10.在直角坐标系xOy 内，圆22:(2)(2)1C x y -+-=，若直线:0l x y m ++=绕原点O 顺时针旋转90后与圆C 存在公共点，则实数m 的取值范围是（ ）A.⎡⎣B.44⎡--⎣C.22⎡--+⎣D.2⎡-+⎣第二部分（非选择题共110分）二､填空题共5小题，每小题5分，共25分.11.过点()2,3A -且与直线30x y ++=平行的直线方程为__________.12.在4(21)x +的展开式中，所有项的系数和等于__________.（用数字作答）13.两个顶点朝下竖直放置的圆锥形容器盛有体积相同的同种液体（示意图如图所示），液体表面圆的半径分别为3，6，则窄口容器与宽口容器的液体高度的比值等于__________.14.若方程22124x y m m+=+-m 的取值范围是__________；若此方程表示的曲线为椭圆，则实数m 的取值范围是__________.15.如图，在正方体1111ABCD A B C D -中，2,AB E =为棱1BB 的中点，F 为棱1CC （含端点）上的一个动点.给出下列四个结论：①存在符合条件的点F ，使得1B F ∥平面1A ED ；①不存在符合条件的点F ，使得BF DE ⊥；①异面直线1A D 与1EC 所成角的余弦值为5； ①三棱锥1F A DE -的体积的取值范围是2,23⎡⎤⎢⎥⎣⎦. 其中所有正确结论的序号是__________.三､解答题共6小题，共85分.解答应写出文字说明，演算步骤或证明过程.从6男4女共10名志愿者中，选出3人参加社会实践活动.（1）共有多少种不同的选择方法？（2）若要求选出的3名志愿者中有2男1女，且他们分别从事经济､文化和民生方面的问卷调查工作，求共有多少种不同的选派方法？17.（本小题15分）如图，在直三棱柱111ABC A B C -中，1,3,4BA BC BC AB AA ⊥===.（1）证明：直线1AB ⊥平面1A BC ；（2）求二面角1B CA A --的余弦值.18.（本小题15分）已知C 经过点()1,3A 和()5,1B ，且圆心C 在直线10x y -+=上.（1）求C 的方程；（2）设动直线l 与C 相切于点M ，点()8,0N .若点P 在直线l 上，且PM PN =，求动点P的轨迹方程.19.（本小题15分）已知椭圆2222:1(0)x y C a b a b+=>>的一个焦点为)，四个顶点构成的四边形面积等于12.设圆22(1)25x y -+=的圆心为,M P 为此圆上一点.（1）求椭圆C 的离心率；（2）记线段MP 与椭圆C 的交点为Q ，求PQ 的取值范围.20.（本小题15分）如图，在四棱锥P ABCD -中，AD ⊥平面,PAB AB ∥,DC E 为棱PB 的中点，平面DCE 与棱PA 相交于点F ，且22PA AB AD CD ====，再从下列两个条件中选择一个作为已知. 条件①：PB BD =；条件①：PA BC ⊥.（1）求证：AB ∥EF ；（2）求点P 到平面DCEF 的距离；（3）已知点M 在棱PC 上，直线BM 与平面DCEF 所成角的正弦值为23，求PM PC的值.设椭圆2222:1(0)x y C a b a b+=>>左､右焦点分别为12,F F ，过1F 的直线与椭圆C 相交于,A B 两点.已知椭圆C 的离心率为21,2ABF 的周长为8. （1）求椭圆C 的方程；（2）判断x 轴上是否存在一点M ，对于任一条与两坐标轴都不垂直的弦AB ，使得1MF 为AMB 的一条内角平分线？若存在，求点M 的坐标；若不存在，说明理由.北京市西城区2023—2024学年度第一学期期末试卷高二数学参考答案 2024.1一､选择题：本大题共10小题，每小题4分，共40分1.D2.B3.B4.D5.B6.D7.A8.C9.B 10.A二､填空题：本大题共5小题，每小题5分，共25分11.10x y ++= 12.81 13.414.()(),24,∞∞−−⋃+；()()2,11,4−⋃ 15.①②④注：第14题第一问3分，第二问2分；第15题全部选对得5分，有两个选对且无错选得3分，有一个选对且无错选得2分，其他得0分.三､解答题：本大题共6小题，共85分.其他正确解答过程，请参照评分标准给分. 16.（本小题10分）解：（1）从6男4女共10名志愿者中，选出3人参加社会实践活动，选择方法数为310C 120=种.（2）从10名志愿者中选2男1女，选择方法数共有2164C C 60=种，故从10名志愿者中选2男1女，且分别从事经济､文化和民生方面的问卷调查工作的选派方法数为213643C C A 360=种.17.（本小题15分）解：（1）在直三棱柱111ABC A B C −中，因为1AA ⊥.平面,ABC BC ⊂平面ABC ，所以1AA BC ⊥.又因为1,BA BC BA AA A ⊥⋂=，所以BC ⊥平面11AA B B ，所以1BC AB ⊥.由14AB AA ==，得四边形11AA B B 为正方形.所以11AB A B ⊥.又因为1BC A B B ⋂=，所以1AB ⊥平面1A BC .（2）因为1BB ⊥平面,ABC BA BC ⊥，所以1,,BA BC BB 两两互相垂直，故以B 为原点，1,,BA BC BB 的方向分别为x 轴､y .轴､z 轴正方向，建立如图所示的空间直角坐标系.则()()()()114,0,0,0,3,0,4,0,4,0,0,4A C A B .所以()()14,3,0,0,0,4AC AA =−=.设平面1A AC 的法向量为(),,m x y z =，则10,0,m AC m AA ⎧⋅=⎪⎨⋅=⎪⎩即430,40.x y z −+=⎧⎨=⎩ 令3x =，则4,0y z ==.于是()3,4,0m =.由（1）可知：()14,0,4AB =−是平面1A BC 的一个法向量.因为11112cos ,1042||AB mAB m AB m ⋅−===−⨯， 由图可知二面角1B CA A −−的平面角为锐角，所以二面角1B CA A −−的余弦值为10. 18.（本小题15分）解：（1）由题意，设C 的圆心(),1C a a +，半径为r ， 则222222(1)(31),(5)(11).a a r a a r ⎧−+−−=⎨−+−−=⎩ 解得：5,5.a r =⎧⎨=⎩所以C 的方程为22(5)(6)25x y −+−=.（2）由平面几何，知PMC 为直角三角形，且PM MC ⊥，所以222||||||PM MC PC +=.由PM PN =，得222||||||PN MC PC +=.设(),P x y ，则2222(8)25(5)(6)x y x y −++=−+−.即36140x y −−=，经检验符合题意.所以动点P 的轨迹方程为36140x y −−=.19.（本小题15分）解：（1）由题意，得222212,c ab a b c ===+，所以3,2a b ==，所以椭圆C 的离心率c e a ==. （2）由题意，得5PQ MP MQ MQ =−=−.设()11,Q x y ，则2211194x y +=.所以MQ ===. 因为[]13,3x ∈−，所以当195x =时，min ||MQ =；当13x =−时，max ||4MQ =.所以PQ 的取值范围为1,5⎡−⎢⎣⎦. 20.（本小题15分）解：选择条件①：（1）因为AB ∥,DC AB ⊄平面,DCEF DC ⊂平面DCEF ，所以AB ∥平面DCEF .又因为AB ⊂平面PAB ，平面PAB ⋂平面DCEF EF =，所以AB ∥EF .（2）因为AD ⊥平面PAB ，所以,AD PA AD AB ⊥⊥.又因为,22PB BD PA AB AD CD ====，所以PAB DAB ≅.因此90PAB DAB ∠∠==，即,,AB AD AP 两两垂直.如图，以A 为原点，,,AB AD AP 的方向分别为x 轴，y 轴，z 轴正方向，建立空间直角坐标系，所以()()()()0,2,0,1,2,0,0,0,2,2,0,0D C P B .由（1），得AB ∥EF ，且E 为棱PB 的中点，所以点F 为棱PA 的中点.()()1,0,1,0,0,1E F ，故()()()0,0,1,0,2,1,1,0,0FP DF CD ==−=−.设平面DCEF 的一个法向量为(),,n x y z =，则20,0,DF n y z CD n x ⎧⋅=−+=⎪⎨⋅=−=⎪⎩ 取1y =，则0,2x z ==，即()0,1,2n =.所以点P 到平面DCEF 的距离255FP n d n ⋅==. （3）设[],0,1PM PCλλ=∈， 则()()1,2,2,2,2PM PC λλλλλ==−=−.所以()2,2,22BM BP PM λλλ=+=−−.设直线BM 与平面DCEF 所成角为θ，所以||sin |cos ,|||||BM n BMn BM n θ⋅=<>== 23=. 化简，得29610λλ−+=，解得13λ=， 即13PM PC =. 选择条件②：（1）与上述解法相同，略.（2）因为AD ⊥平面PAB ，所以,AD PA AD AB ⊥⊥，又因为,PA BC BC ⊥与AD 相交，所以PA ⊥平面ABCD . 所以PA AB ⊥.即,,AB AD AP 两两垂直.以下与上述解法相同，略.21.（本小题15分）解：（1）由题意，得22248,1,2,a c a abc =⎧⎪⎪=⎨⎪=+⎪⎩ 解得2,1.a b c =⎧⎪=⎨⎪=⎩所以椭圆C 的方程为22143x y +=. （2）假设x 轴上存在一点()0,0M x 符合题意.由题意，设直线()()()()1122:10,,,,AB y k x k A x y B x y =+≠.联立方程()221,1,43y k x x y ⎧=+⎪⎨+=⎪⎩消去y ， 得()22223484120k x k x k +++−=. 所以221212228412,3434k k x x x x k k−+=−=++. 由题意，知直线AM 的斜率存在，且为()11101010AM k x y k x x x x +−==−−， 同理，直线BM 的斜率为()22202010BM k x y k x x x x +−==−−. 所以()()12102011AM BM k x k x k k x x x x +++=+−− ()()()()12120120102022k x x x x x x x x x x x x ⎡⎤++−+−⎣⎦=−−. 因为1MF 为AMB 的一条内角平分线，所以0AM BM k k +=.所以()()1212010220k x x x x x x x x ⎡⎤++−+−=⎣⎦.因为上式要对任意非零的实数k 都成立， 所以2220022241288220343434k k k x x k k k−⨯−+⨯−=+++， 解得04x =−.故x 轴上存在一点()4,0M −，对于任一条与两坐标轴都不垂直的弦AB ，使得1MF 为AMB 的一条内角平分线.。

2023年八年级语文下册期末试卷（及参考答案)满分：120分考试时间：120分钟一、语言的积累与运用。

（35分）1、下列各组词语中加点字的书写或注音有误的一组是（）A．颁．发诘．责（jié）不逊．（xùn）摧枯拉朽．B．娴．熟翘．首（qiào）屏．息（bǐng）眼花瞭．乱C．浩瀚．教诲．（huì）锃．亮（zèng）殚．精竭虑D．篡．改炽．热（chì）窒．息（zhì）惨绝人寰．3、下列句子中加点成语使用不正确的一项是（）A．回首这部画册的完成过程，我们可以说是殚精竭虑．．．．了。

B．经过两个小时惊心动魄．．．．的斗智斗勇，人质安全获救了。

C．昨日重庆一市民收到中奖短信，喜冲冲跑去银行汇钱，却见银行前一道防诈骗横幅后如梦初醒．．．．。

D．年龄大了，又遇上感冒，这两天，他总有一种眼花缭乱．．．．的感觉。

4、下列句子中没有语病的一项是（）A．有关部门最近发出通知，要求各地在中考期间严防安全不出问题。

B．我反对将儿子送到贵族幼儿园去，希望儿子不毁在优裕的生活环境里，让他从小就具有刚毅、诚实、吃苦耐劳。

C．保障儿童权利是设置儿童节的初衷，这一要义在今天丝毫没有过时，所以仍需要成人时时反思。

D．虽然人生的幕布徐徐拉开，但在少年的眼里，世界和未来都是崭新的充满吸引力的。

5、下列句子没有运用比喻修辞手法的一项是( )A．一些薄云掠过月亮时,就像丽江古城中,一个银匠,正在擦拭一只硕大的银盘。

B．活动时只能以极轻极慢动作进行,犹如霹雳舞的“太空步”。

C．洁白轻薄的云朵,微光闪烁,仿佛身披霓裳羽衣的纯洁天使。

D．当河水正这般畅畅快快地驰骋着时,突然脚下出现一条四十多米宽的深沟,它们还来不及想一下,便一齐跌了进去,更闹,更挤,更急。

6、请选出下列句子排序最确切的一项（）①这时只有细细的雨声，打着船篷，打着江面，打着岸边的草和树。

②从桂林到阳朔，有人比喻为一幅天然的画卷。

合肥一中2022—2023学年第二学期高一年级期末考试语文试卷参考答案一、现代文阅读(35分)1.(3分)【参考答案】A【解析】A项“由于梁启超的推动”错误，“一些较早接触域外文学文化的知识分子”“梁启超首倡”“小说的译印和创作风起云涌”等内容都表现出这种推动是由先进知识分子群体推动的。

2.(3分)【参考答案】B【解析】B项“这一观点终结了有关《红楼梦》作者之谜的争论”错误，原文陈述的是胡适的观点，并未提及争论被终结。

3.(3分)【参考答案】C【解析】A项“索隐派即以此种方法探寻作品背后的真相”分析不当，“谐音”只是索引的一种方法。

B项“最重要的原因莫过于此”错误，蔡胡论战最后以胡适胜利告终，固然与胡适的不同批评策略有关，但“蔡元培的身份背景”“亚东版《红楼梦》的大行于世”“对著者和本子的考证”等都是重要原因，文中信息不足以支撑“莫过于此”的表述。

D项“如果没有……胡适的考证成果就很难被公众认可”不恰当。

其一，《新青年》杂志刊发的是《论短篇小说》的演讲，非考证成果；其二，亚东版《红楼梦》的大行于世促进了胡适考证学说的影响力，但不等于没有小说的出版就不会被公众认可。

4.(4分)【答案示例】示例1：①传统史学讲究微言大义，以曲折、精微的文笔隐寓褒贬、寄托深意。

如“夜缒”可反映出国势之危急，并暗含对统治者昏庸短视的批评，对烛之武深明大义爱国精神的赞美。

示例2：①文学作品中常常运用比喻和象征等手段，蕴含深刻的意蕴。

比如《赤壁赋》中以“桂、兰”象征美好的德行，以“美人”象征美政。

示例3：①文学作品中有时似贬实褒，字里行间隐含深意。

比如草莽、傻、狂等词语，看似批评宝玉性格乖张、不学无术，实则写出宝玉之重情脱俗。

【解析】“史学和文学”与“孔子的春秋笔法、屈原的香草美人”间的呼应关系，表明史学和文学作品通常有着微言大义、含蓄蕴藉的特点；而“隐秀”，与“比兴”“夸饰”等并举，“文外之重旨”等内容，则暗示“隐”通常借助约定俗成的比喻、象征等手法，来表达字面以外的意思。

考试试题 共 5 页 ，第 1 页财经学院期末考试试卷及答案 课程名称 高等数学 教师 学时 学分 教学方式 讲授 考核日期 20xx 年 xx 月 x 日 成绩 一、填空题（3′×5 = 15′） 1.设由方程确定是的函数，则 2.设，则 3. =___________. 4.若级数收敛，则 5.差分方程的通解为__________ 二、选择题（3′×5 = 15′） 1.下列命题中，正确的是（） A.若是函数的驻点，则必在取得极值 B.若函数在取得极值，则必是的驻点 C.若函数在处可微，则必是连续点 D.若函数在处偏导数存在，则在处必连续 2.设D 由围成，则二重积分( ) 学号姓名学院……………………密……………封……………线……………以……………内……………答……………题……………无……………效……………………3.若收敛，则（）A.绝对收敛B.条件收敛C.发散D.敛散性不定4.方程可化为形如（）的微分方程5.差分方程的特解可设为（）三、计算题（6′×8 = 48′）1.设，求2.交换积分次序，求3.求，其中.考试试题共5 页，第2 页4.判定级数的敛散性.5.求微分方程满足的特解.6.设，其中具有二阶连续偏导数，求7.求级数的收敛域及和函数.考试试题共5 页，第3 页8.求微分方程的通解.四、应用题（8′×2 = 16′）1.假设某产品的销售量是时间的可导函数，如果商品的销售量对时间的增长速率与销售量及销售量接近于饱和水平的程度之积成正比（N为饱和水平，比例常数），当时，.求销售量.2.设生产某种产品需用原料A和B，它们的单位价格分别是10元和15元，用单位原料A 和单位原料B 可生产单位的该产品，现要以最低成本产生112单位的该产品，问需要多少原料A和B？五、证明题（6′）设，证明：若收敛，则收敛.考试试题共5 页，第4 页参考答案一、1.二、1.C2.A3.A 4.D5.C三、；4.收敛；5.8.四、1. 2.A4单位，B2单位五、提示：用比较判别法证明.考试试题共5 页，第5 页。

java期末考试试卷及答案Java期末考试试卷及答案一、选择题（每题2分，共20分）1. Java中，哪个关键字用于声明一个类？A. classB. interfaceC. structD. enum答案：A2. 在Java中，下列哪个不是合法的变量名？A. $nameB. name$C. _nameD. 2name答案：D3. 下列哪个选项是Java中的一个基本数据类型？A. StringB. intC. ArrayListD. HashMap答案：B4. Java中，哪个方法用于获取数组的长度？A. length()B. size()C. lengthD. size答案：A5. 下列哪个是Java中的一个控制流语句？A. tryB. catchC. finallyD. all of the above答案：D6. 在Java中，哪个关键字用于抛出异常？A. throwB. throwsC. catchD. try答案：A7. Java中，哪个关键字用于定义一个接口？A. classB. interfaceC. abstractD. final答案：B8. 在Java中，下列哪个是正确的继承关系？A. A extends BB. A implements BC. A implements AD. A extends A答案：A9. Java中，哪个关键字用于定义一个抽象方法？A. abstractB. finalC. staticD. synchronized答案：A10. 在Java中，哪个关键字用于定义一个静态方法？A. staticB. finalC. abstractD. synchronized答案：A二、填空题（每题2分，共20分）1. Java中，用于声明一个字符串常量的关键字是________。

答案：String2. Java中，用于声明一个整型变量的关键字是________。

2024北京朝阳初三（上）期末道德与法治 (选用)2024.1(考试时间70分钟满分70分)学校姓名班级考号第一部分本部分共15题，每题2分，共30 分。

在每题列出的四个选项中，选出最符合题目要求的一项。

1.2023年9月 17日，第45届世界遗产大会上，我国“ ”获准列入《世界遗产名录》，这是全球首个茶主题世界文化遗产，实现了对文化和生物多样性的保护以及自然资源的可持续利用。

A. 普洱景迈山古茶林文化景观B. 云南三江并流保护区C. 杭州西湖文化景观D. 红河哈尼梯田文化景观2.某校开展“庆祝改革开放45 周年”成就展，展览包括“综合国力增强”“人民生活幸福”“国际地位提升”三个板块。

下列内容能在“人民生活幸福”板块看到的有①我国国内生产总值显著增长，进入高速发展阶段②我国人均预期寿命达78岁，较 1981 年增长10岁③各地博物馆数量增长，不断满足群众精神文化需求④举办第六届进博会，让中国大市场成为世界大机遇A.①②B.①④C.②③D.③④3. 小东解数学题喜欢挑战权威，尝试不同的方法；经常把不用的饮料瓶制作成漂亮的装饰品；写作文的角度总能别出心裁，令人交口称赞。

这说明①生活处处有创新，创新是一种生活方式②科学技术日新月异，时代发展呼唤创新③创新让我们获得成就感，使生命充满活力④中学生是创新创造的主力军，要勇于实践A.①③B.①④C.②③D.②④4.中央政治局第五次集体学习，聚焦建设教育强国，总结了我国建设教育强国的进展和成就，分析了面临的形势和需要解决的问题，探究了我国建设什么样的教育强国、怎样建设教育强国这一重大课题。

党和国家高度重视教育强国建设是因为①教育成就显著，是当代中国最鲜明的特色②教育已经成为综合国力竞争的决定性因素③教育事关建设创新型国家，事关民族振兴伟业④教育是提高国民素质、培养创新型人才的根本途径A.①②B.①③C.②④D.③④5. 北京某街道推行“社区治理合伙人机制”，构建以社区党组织为“主心骨”、居委会为“组织者”、业主为“当家人”、物业公司为“大管家”、政府职能部门为“后援团”、辖区单位为“共建者”的工作格局，围绕居民反馈的问题进行六方会谈，及时解决。

深圳大学期末考试试卷参考解答及评分标准基本题6小题，每小题5分，满分30分。

在每小题给出的四个选项中，只有一（每道选择题选对满分，选0分）事件表达式A B 的意思是 ( ) 事件A 与事件B 同时发生 (B) 事件A 发生但事件B 不发生 事件B 发生但事件A 不发生 (D) 事件A 与事件B 至少有一件发生 D ，根据A B 的定义可知。

假设事件A 与事件B 互为对立，则事件A B ( ) 是不可能事件 (B) 是可能事件 发生的概率为1 (D) 是必然事件 A ，这是因为对立事件的积事件是不可能事件。

已知随机变量X ,Y 相互独立，且都服从标准正态分布，则X 2＋Y 2服从 ( ) 自由度为1的χ2分布 (B) 自由度为2的χ2分布 自由度为1的F 分布 (D) 自由度为2的F 分布选B ，因为n 个相互独立的服从标准正态分布的随机变量的平方和服从自由度为n 的2分布。

已知随机变量X ,Y 相互独立，X ~N (2,4),Y ~N (-2,1), 则( ) X +Y ~P (4) (B) X +Y ~U (2,4) (C) X +Y ~N (0,5) (D) X +Y ~N (0,3) 选C ，因为相互独立的正态变量相加仍然服从正态分布，而E (X +Y )=E (X )+E (Y )=2-2=0, (X +Y )=D (X )+D (Y )=4+1=5, 所以有X +Y ~N (0,5)。

样本(X 1,X 2,X 3)取自总体X ，E (X )=μ, D (X )=σ2, 则有( ) X 1+X 2+X 3是μ的无偏估计(B)1233X X X ++是μ的无偏估计22X 是σ2的无偏估计(D)21233X X X ++⎛⎫ ⎪⎝⎭是σ2的无偏估计B ，因为样本均值是总体期望的无偏估计，其它三项都不成立。

随机变量X 服从在区间(2,5)上的均匀分布，则X 的数学期望E (X )的值为( ) (B) 3 (C) 3.5 (D) 4 C ，因为在(a ,b )区间上的均匀分布的数学期望为(a +b )/2。