当前位置：文档之家 › 第四章 数学规划问题(中文)

第四章 数学规划问题(中文)

  • 格式：ppt
  • 大小：593.50 KB
  • 文档页数：48

下载文档原格式

  / 48

合集下载

运筹学——.整数规划与分配问题

运筹学——.整数规划与分配问题


2.4 匈牙利法实例(2)
第二步：找出矩阵每列的最小元素，再分别从各列中减去。
必定满足：bij = aij–ui–vj
0 11 2 0 0
8 0 3 11 0
7 5 0 11 10 4 2 5 0 9 5 0 5 0
8 2 5 0 5 4 3 0 0 11 4 5
二、分配问题与匈牙利法
2.3 匈牙利法
分配问题可以用单纯形法或运输表求解。 库恩(W.W.Kuhn)于1955年提出了指派问题的解 法，他引用了匈牙利数学家康尼格(D.Kö nig)一 个关于矩阵中零元素的定理：系数矩阵中独立0 元素的最多个数等于能覆盖所有0元素的最少直 线数。这个解法称为匈牙利法。
二、分配问题与匈牙利法
2.2 分配问题实例(1)
例：有一份中文说明书，需要译成英、日、德、 俄四种文字。现有甲、乙、丙、丁四人，他们 将中文说明书译成不同语种的说明书所需时间 如下，问应指派何人去完成工作，使所需总时 间最少? 人员
任务 译成英文 译成日文 译成德文 译成俄文 甲 乙 丙 丁 7 8 11 9 2 15 13 4 10 4 14 15 9 14 16 13
一、整数规划的特点及作用
1.2 0-1整数规划
某公司拟在市东、西、南三区建立门市部。拟 议中有7个位置（点）Ai供选择。规定
在东区，由A1，A2，A3三个点中至多选两个； 在西区，由A4，A5两个点中至少选一个； 在南区，由A6，A7两个点中至少选一个。
如选用Ai点，设备投资估计为bi元，每年可获利 润估计为ci元，但投资总额不能超过B元。 问：应如何选址，可使年利润为最大？
第一步：找出每 行的最小元素， 每行对应减去这 个元素。
第4章 整数规划

第4章 整数规划

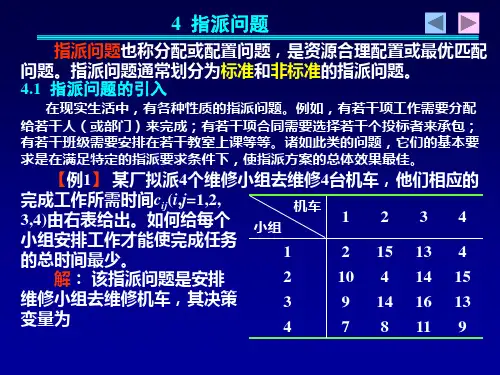
第4章 整数规划判断:用分枝定界法求解一个极大化的整数规划问题，任何一个可行解的目标函数值是该问题目标函数值的下界；指派问题数学模型的形式同运输问题十分相似，故也可以用表上作用法求解；效率矩阵的任一行（或列）减去（或加上）任一常数，指派问题最优解不会受到影响； 匈牙利法只能用于平衡分配问题；对于极大化问题，匈牙利法不能直接求解。

整数规划问题解的目标函数值优于其相应的线性规划问题的解的目标函数。

用割平面法求解整数规划问题，构造的割平面有可能切去一些不属于最优解的整数解。

用分枝定界法求解一个极大化的整数规划问题时，当得到多于一个可行解时，通常可任取其中一个作为下界值，在进行比较剪枝。

分配问题的每个元素都加上同一个常数k ，并不会影响最优分配方案。

分配问题的每个元素都乘上同一个常数k ，并不会影响最优分配方案。

分配问题域运输问题的数学模型结构形式十分相似，故也可以用表上作业法求解。

隐枚举法也可以用来求解分配问题简答试述分枝定界法求解问题的主要思想。

试述隐枚举法的步骤。

试讲述割平面方法的基本原理. 试例举三种应该剪枝的情况。

计算题分枝定界法用分枝定界法求解下列整数规划问题12max Z x x =+1212129511414123,x x x x x x +≤-+≤≥0且为整数用分枝定界法求解下列整数规划问题12max 32Z x x =+121212231429,x x x x x x +≤+≤≥0且为整数用分枝定界法求解下列整数规划问题12max 2010Z x x =+1232312312324434323,,x x x x x x x x x x x ++≤≤+≤≥－--0且为整数用分枝定界法求解下列整数规划问题12max 79Z x x =+121212136735,x x x x x x x +≤+≤≥－0，且为整数用分枝定界法求解下列整数规划问题123max 33Z x x x =++123231231231324432323,,,x x x x x x x x x x x x x ++≤≤+≤≥－--0，且为整数用分枝定界法解下列整数规划问题：1212121212232478188..3219,0MaxZ x x x x x x s t x x x x =+-+≤⎧⎪+≤⎪⎨+≤⎪⎪≥⎩且为整数用分枝定界法解下列整数规划问题1212121212250..6221,0MaxZ x x x x x x s t x x x x =++≤⎧⎪-+≤⎪⎨+≤⎪⎪≥⎩且为整数用分枝定界法解下列整数规划问题12312121225231050..7228,0,MaxZ x x x x x s t x x x x x =-+-+≤⎧⎪-≤⎨⎪≥⎩为整数用分枝定界法解下列整数规划问题12312341234345272222..0,1,2,3,4,5,j MaxZ x x x x x x x x x x x s t x j x x =-+-⎧-+-+=⎪⎪⎪-++=⎨⎪≥=⎪⎪⎩为整数用分枝定界法求解下列整数规划模型12max 23z x x =+121257354936x x x x +≤+≤12,0x x ≥且为整数有如下整数规划问题12max z x x =+12129511414123x x x x +≤-+≤12,0x x ≥且为整数试用分枝定界法求其最优解。

数学规划问题

数学规划问题

首先将问题转化为matlab要求的格式;即求出 fun,A,b,aeq,beq,X0,Lb,Ub 解:首先建立一个m文件fun3.m
x1
function y=fun3(x)
y=-exp(x(1))*x(2)^2*(3-exp(x(1))-x(2)^2); 存储为fun3.m
因题目中有非线性约束条件，所以建立非线性约束m-文件。 然后建立一个 m文件 fun4.m function [c,cep]=fun4(x) c=[]; % c为非线性不等式,且为c<=0 cep=exp(x(1))+x(2)^2-3; % cep为非线性等式 然后存储为fun4.m 最后在命令窗口中输入：
同时返回fval=-2
对应到原来的线性规划中即知目标函数的最大值为2，此时 x1=4,x2=1,x3=9。
第二节 无约束规划计算方法
一、实验目的
1、了解无约束规划问题的求解原理与方法 ；
2、会用Matlab软件求解无约束规划问题。
二、实验原理和方法
无约束规划问题的解法一般按目标函数的形式分为两大类： 一类是一元函数的一维搜索法，如黄金分割法、插值法等； 另一类是求解多元函数的下降迭代法。
在命令窗口输入： x0=[0;0]; x=fminunc(‘fun2’,x0) 结果显示： f =5.2979e-011 x =1.0673 0.1392 则非线性方程组的解为x1=1.0673,x2=0.1392。
第三节 约束非线性规划计算方法 一、实验目的
1、了解约束非线性规划问题的求解原理与方法； 2、会用Matlab软件求解约束非线性规划问题。
三、实验内容与步骤
在Matlab软件中，求解无约束规划的常用命令是：
x=fminunc(‘fun’,x0) 其中，fun函数应预先定义到M文件中，并设置初始 解向量为x0。
运筹学--第四章 整数规划与分配问题

运筹学--第四章 整数规划与分配问题


一、整数线性规划问题的提出
引例：生产组织计划问题与选址问题 例4-1（生产组织计划问题）某工厂在一个计划期 内拟生产甲、乙两种大型设备。除了A、B两种部件 需要外部供应且供应受到严格限制之外，该厂有充 分的能力来加工制造这两种设备所需的其余零件， 并且所需原材料和能源也可满足供应。每种设备所 用部件数量和部件的供应限额以及设备的利润由表 3-1-1给出。问该厂在本计划期内如何安排甲、乙 设备的生产数量，才能获取最大利润？
例4-3某人有一背包可以装10公斤重、0.025m3的物
品。他准备用来装甲、乙两种物品，每件物品的重 量、体积和价值如表4-3-1所示。问两种物品各装 多少件，所装物品的总价值最大？
表4-3-1 物品 甲 乙 重量 （公斤/每件） 1.2 0.8 体积 （m3/每件） 0.002 0.0025 价值 (元/每件) 4 3
应寻找仅检查可行的整数组合的一部分，就能定出 分支定界法可用于解纯整数或混合整数线性规划问
最优的整数解的方法。分支定界解法就是其中之一。
题。
–20世纪60年代初由Land Doig和Dakin等提出，是 解整数线性规划的重要方法之一。
–由于这方法灵活且便于用计算机求解，所以现在
它已是解整数规划的重要方法。
了。 但这常常是不行的，因为化整后不见得是可行解； 或虽是可行解，但不一定是最优解。 因此，对求最优整数解的问题，有必要另行研究。
例4-4 说明整数规划问题的求解不能直接在单纯形
法最优解的基础上四舍五入 求下述整数规划问题的最优解（P105）
max z 3x1 2 x2 2 x1 3x2 14 s.t. x1 0.5 x2 4.5 x , x 0, 且均取整数值 1 2
第4章 整数规划

第4章 整数规划

第四章
整数规划
整数规划问题的提出
整数规划模型与一般的线性规划模型 的区别仅在于： 的区别仅在于：整数规划的变量要求 部分的或全部的为整数。例如： 部分的或全部的为整数。例如：
m Z = x + x2 ax 1 14 1 x +9x2 ≤ 51 −6x +3x2 ≤1 1 x , x ≥ 0且 整 为 数 1 2
(纯整数规划问题) 纯整数规划问题)
解：设xi为第i天开始上班的人数： 为第i天开始上班的人数： Min： Min：z=x1+x2+x3+x4+x5+x6+x7 s.t. x1 +x4+x5+x6+x7≥17 +x5+x6+x7≥13 x1+x2 x1+x2+x3 +x6+x7≥15 x1+x2+x3+x4+ +x7≥19 x1+x2+x3+x4+x5 ≥14 x2+x3+x4+x5+x6 ≥16 x3+x4+x5+x6+x7≥11 xi≥0 （ i=1,2,…,7） i=1,2,…,7）
例：某市6 例：某市6个区，希望设 置最少消防站以便节省 费用。条件：
必须保证在城区任何地方发 生火警时，消防车能在15 生火警时，消防车能在15分 15分 钟之内赶到现场。各区之间 消防车行驶的时间见右表。
请确定设站方案。
布点问题的数学模型： 0－1规划 布点问题的数学模型：
设0−1为决策变量，当表示i地区设站，表示i 为决策变量，当表示i地区设站，表示i 地区不设站。这样根据消防车15分钟赶到现 地区不设站。这样根据消防车15分钟赶到现 场的限制，可得到如下模型
运筹学基础及应用第4章-整数规划与分配问题

运筹学基础及应用第4章-整数规划与分配问题


整数规划的特点及应用
解：对每个投资项目都有被选择和不被选择两种可能，因此 分别用0和1表示，令xj表示第j个项目的决策选择，记为：
j投 资 1 对 项 目 xj ( j 1,2,..., n) j不 投 资 0 对 项 目
投资问题可以表示为：
max z
c
j 1
n
j
xj
n a j x j B j 1 x2 x1 s .t x 3 x4 1 x5 x6 x7 2 ） x j 0或者1 （j 1, 2, L n
B1 B2 B3 B4 年生产能力
A1
A2 A3 A4 年需求量
2
8 7 4 350
9
3 6 5 400
3
5 1 2 300
4
7 2 5 150
400
600 200 200
工厂A3或A4开工后，每年的生产费用估计分别为1200万或1500万元。 现要决定应该建设工厂A3还是A4，才能使今后每年的总费用最少。
0-1型整数线性规划：决策变量只能取值0或1的整数线性 规划。
整数规划的特点及应用
整数规划的典型例子
例4.1 工厂A1和A2生产某种物资。由于该种物资供不应求，故需要 再建一家工厂。相应的建厂方案有A3和A4两个。这种物资的需求地 有B1,B2,B3,B4四个。各工厂年生产能力、各地年需求量、各厂至各 需求地的单位物资运费cij，见下表：
例4.3 设整数规划问题如下
max Z x1 x 2 14x1 9 x 2 51 6 x1 3 x 2 1 x , x 0且 为 整 数 1 2
首先不考虑整数约束，得到线性规划问题（一般称为松弛问 题）。
第四章规划问题

第四章规划问题


m ax z = 4x1 + 3x2 + 2x3 2x 1 - 5x 2 + 3x 3 <= 4 4x1 + x2 + 3x3 >= 3 x2 + x3 >= 1 4x + 3x + 2x >= 2 1 2 3 x 1, x 2 , x 3 = 0或 1 (1 ) (2 ) (3 ) (4 )
(1) (2)
• 工序 3只能从两种加工方式中选择一种，那么约束条件 工序B 只能从两种加工方式中选择一种， （1）和（2）就成为相互排斥的约束条件。为了统一在一 ） ）就成为相互排斥的约束条件。 个问题中，引入0-1变量 个问题中，引入 变量
1, yi = 0,
则数学模型为
B3采用B3i加工方式 B3不采用B3i加工方式
n
(i = 1,2,⋯ ,m) (j = 1,2,⋯ ,n)
二、0－1整数规划求解
– 0－1整数规划的求解方法有穷举法、隐枚举法和分枝 － 整数规划的求解方法有穷举法 整数规划的求解方法有穷举法、 定界法. 定界法 – 隐枚举法求解举例
m axz = 4x1 + 3x2 + 2x3 2x 1 - 5x 2 + 3x 3 <= 4 4x + x + 3x >= 3 1 2 3 s .t x2 + x3 >= 1 x 1, x 2 , x 3 = 0或 1
一、0－1整数规划模型
– 0－1整数规划在实际中应用较多。因为实际问题中经 － 整数规划在实际中应用较多 整数规划在实际中应用较多。 常碰到大量的决策问题，要求回答“ 常碰到大量的决策问题，要求回答“是－否”或“有 问题，这类问题可以借助整数规划中的0－ 整 －无”问题，这类问题可以借助整数规划中的 －1整 数变量，使许多复杂的、困难的问题相对变得简单。 数变量，使许多复杂的、困难的问题相对变得简单。 – 0－1变量一般可表示为： － 变量一般可表示为 变量一般可表示为：
第4章整数规划——指派问题

第4章整数规划——指派问题



13 11 2 0 10 11 57 4 4 2 13 7 0 0 6 9 5 32 0 0
0 0 X 1 0
0 0 1 1 0 0 0 0 0 0 1 0

故可得到指派问题的最优解X，这样 安排能使总的维修时间最少，维修时间为 z=4＋4＋9＋11=28（小时）。
X (2)
都是指派问题的最优解。
4 指派问题
4.3 指派问题的求解 指派问题既是一类特殊的整数规划问题，又是特殊的运输问 题，因此可以用多种相应的解法来求解，然而这些解法都没有充 分利用指派问题的特殊性质，有效地减少计算量，直到1955年库 恩（W. W. Kuhn）提出的匈牙利法才有效地解决了指派问题。 匈牙利法的理论基础 定义2 独立零元素组 在效率矩阵中，有一组在不同行不同 列的零元素，称为独立零元素组，其每个元素称为独立零元素。 5 0 2 0 2 3 0 0 C 【例4】 已知效率矩阵 0 5 6 7 4 8 0 0 求其独立零元素组。
4 指派问题
0 , 不 指 派 第 i小 组 维 修 第 j台 机 床 x ij ( i , j 1, 2 ,3, 4 ) 1, 指 派 第 i 小 组 维 修 第 j 台 机 床 机车 该问题的数学模型为： 1 2 3 4 4 小组 min z cij xij i 1 j 1 1 x11 x12 x13 2 x11 15 x12 2 x21 x22 x23 任务约束 4 x 1, j 1, 2 , 3 , 4 3 x31 x32 x33 ij i 1 4 x41 x42 x43 人员约束 4 x ij 1, i 1, 2 , 3, 4 j 1 x ij 0 或 1 i , j 1 , 2 , 3 , 4
运筹学第四章--整数规划和分配问题(新)aPPT课件

运筹学第四章--整数规划和分配问题(新)aPPT课件


-
1
整数线性规划的一般形式: n max(或min)z cj xj j 1
n
aij xj ( 或 ）bi (i 1,2,...m)
j 1
xj 0( j 1,2,...n),且部分或全部取整数
例1.求下述整数规划问题的最优解
max z 3x1 2x2
2x1 3x2 14 x1 0.5x2 4.5
先不考虑整数解的限制，用单纯形法求 解其松弛问题，如果求得的解恰好是整数解， 则得整数规划最优解，停止计算。否则，将 松弛问题分解为两个子问题（也称后继问 题），每个子问题都是在原松弛问题的基础 上增加一个变量取整数的约束条件，这样就 缩小了原来的可行域，然后用单纯形法求解， 直至得到最终结果。
-
21
-
23
例.用分枝定界法求下述数整规划问题的最优
maxz 3x1 2x2
2x1 3x2 14 x1 0.5x2 4.5 x1, x2 0,且均取整数值
-
24
-
25
-
26
-
27
-
28
-
29
第四节 割平面法 一、割平面法的基本思想
先不考虑整数条件，用单纯形法求解其 松弛问题，若得整数解，即得整数规划最优 解。否则，增加线性约束条件（称为割平面 方程），将原问题的可行域切割掉一部分， 被切割掉的都是非整数解，再用单纯形法求 解新的线性规划问题，依次进行下去，直到 使问题的最优解恰好在可行域的某个具有整 数坐标的顶点上得到。
0.5 + 0.4 x4 + 0.4 x5≥ 1
-
35
2. 借助单纯形表法
对求解整数规划问题的松弛问题（LP问题）得到
最优单纯形表，设xi=bi 是最优解中取分数值（分数 部分最大）的基变量，则有
数学规划模型 2

数学规划模型 2

与送水方案无关！ 与送水方案无关！ 450×160=72,000(元)与送水方案无关！ 与送水方案无关！ 与送水方案无关
引水管理费+ 引水管理费+其他费用
其他费用: 元 千吨 其他费用:450元/千吨
确定送水方案使利润最大 确定送水方案使利润最大
使引水管理费最小ห้องสมุดไป่ตู้
模型建立
决策变量
确定3个水库向 个小区的供水量 确定 个水库向4个小区的供水量 个水库向 水库i 水库 向j 区的日供水量为 xij（x34=0） ）
求解
A(100) 100 30 B(120) 40 30 50 C(100) 50 甲(30;50) 乙(70;70) 丙(10;20) 丁(10;40)
Global optimal solution found. Objective value: Total solver iterations: Variable X11 X12 X13 X14 X21 X22 X23 X24 X31 X32 X33 Value 0.000000 100.0000 0.000000 0.000000 30.00000 40.00000 0.000000 50.00000 50.00000 0.000000 30.00000
货机装运
模型建立
x11 + x21 + x31 + x41 10 x12 + x22 + x32 + x42 = 16 x13 + x23 + x33 + x43 = 8
xij--第i 种货物装入第 个货舱的重量 --第 种货物装入第j 平衡 要求 约束 条件 货物 供应
10； ； 6800 16； ； 8700 8； ； 5300
第4章--数学规划模型-姜启源

第4章--数学规划模型-姜启源

第4章 数学规划模型在上一章中我们看到，建立优化模型要确定优化的目标和寻求的决策。

用x 表示决策变量，)(x f 表示目标函数。

实际问题一般对决策变量x 的取值范围有限制，不妨记作x ∈Ω，Ω称为可行域。

优化问题的数学模型可表示为∈x x f Max Min ),()(或Ω在第3章x 通常是1维或2维变量，Ω通常是1维或2维的非负域。

实际中的优化问题通常有多个决策变量，用n 维向量T n x x x x ),,,(21 =表示，目标函数)(x f 是多元函数，可行域Ω比较复杂，常用一组不等式（也可以有等式）)(x g i ≤0 (i =1,2, …,m )来界定，称为约束条件。

一般地，这类模型可表述成如下形式=z Min x)(x f s.t.)(x g i ≤m i ,,2,1,0 =这里的s. t. (subject to)是“受约束于”的意思。

显然，上述模型属于多元函数的条件极值问题的范围，然而许多实际问题归结出的这种形式的优化模型，其决策变量个数n 和约束条件个数m 一般较大，并且最优解往往在可行域的边界上取得，这样就不能简单地用微分法求解，数学规划是解决这类问题的有效方法。

需要指出的是，本章无意涉及数学规划（或运筹学）的具体计算方法，仍然着重于从数学建模的角度，介绍如何建立若干实际优化问题的模型，并且在用现成的数学软件求解后，对结果作一些分析。

4．1 奶制品的生产和销售企业内部的生产计划有各种不同的情况。

从空间层次来看，在工厂级要根据外部需求和内部设备、人力、原料等条件，以最大利润为目标制订产品的生产计划，在车间级则要根据产品生产计划、工艺流程、资源约束及费用参数等，以最小成本为目标制订生产批量计划。

从时间层次看，若在短时间内认为外部需求和内部资源等不随时间变化，可制订单阶段生产计划，否则就要制订多阶段生产计划。

本节选择几个单阶段生产计划的实例，说明如何建立这类问题的数学规划模型，并利用软件求解的输出对结果作一些分析。

第4章数学规划模型


NO. ITERATIONS= 2
2.000000 0.000000
时间增加1单位, 利润增长2 加工能力增长不影响利润
• 35元可再买到1桶牛奶，要买吗？ 35 <48, 应该买！
• 聘用临时工人付出的工资最多每小时几元？ 2元！
DO RANGE(SENSITIVITY) ANALYSIS? Yes 最优解不变时目标函
利润 = 收入(900) –其它费用(450) –引水管理费
利润(元/千吨)
甲
乙
丙
丁
A
290
320
230
280
B
310
320
260
300
C
260
250
220
/
目标 函数
供应 限制
MZ a 2 xx 9 1 1 3 0x 2 1 2 2 0x 3 1 3 2 0x 8 140
3x 1 2 1 3 0x 2 2 2 2 0x 6 2 3 3 0x 0 2 4 2 0x 6 3 1 2 0x 5 3 2 2 0x 2 3
模型分析与假设
线性规划模型
假设加工A1,A2的牛奶桶数分别是x1 ,
x比
例2
xi对目标函数的“贡 A1,A2每公斤的获利是与各 献”与xi取值成正比 自产量无关的常数
性 xi对约束条件的“贡 每桶牛奶加工出A1,A2的数量
献”与xi取值成正比
和时间是与各自产量无关的常 数
可 加
x1对目标函数的“贡 A1,A2每公斤的获利是与相 献”与x2取值无关 互产量无关的常数
OBJECTIVE FUNCTION VALUE
1) 88700.00
VARIABLE VALUE REDUCED COST

第四章 数学规划问题(中文)


x1 + x 2 + L + x n = S
④假设在一个生长期内树木至多只能生长一个高度级。 假设在一个生长期内树木至多只能生长一个高度级。 n-1)是生长参数 即第i级的数目进入第i+1 是生长参数， 设gi (i=1, 2, …, n-1)是生长参数，即第i级的数目进入第i+1 级的比例数。 级的比例数。 （２）建模及计算 设向量Ｚ表示经过一个生长期后， 设向量Ｚ表示经过一个生长期后，森林中树木高度的 分布。 分布。则有
M = P2 g 1 x1 + ( P3 − P2 ) g 2 x 2 + L + ( Pn − Pn −1 ) g n −1 x n −1
max M = P2 g1 x1 + ( P3 − P2 ) g 2 x2 + L + ( Pn − Pn −1 ) g n −1 xn −1 s.t. x1 + x2 + L + xn = S g1 x1 ≥ g 2 x2 ≥ L ≥ g n −1 xn −1 ≥ 0 x ≥ 0 i = 1,2,L, n i
min W= 2πρDh(b 2 + h 2 )
1 2
1 2
π 2 E(D 2 + h 2 ) P (b 2 + H 2 ) ≤ πDhH 8(b 2 + H 2 ) 1 P (b 2 + H 2 ) 2 s.t. ≤σy πDhH D1 ≤ D ≤ D2 , H 1 ≤ H ≤ H 2
-
+ 6
+ 3
+ 4
+ 5
2
∑ ∑ ∑ ∑ ∑ ∑
§6 .2 动态规划模型

应用高等数学第4章4.4 线性规划-精品文档


满约束条件的一组变量的值称为该线性规划问题的 可行解.所有可行解构成的集合称为可行域，使目标函数取 得最大（或最小）值的可行解，称为最优解.
10
4.4.2 线性规划问题的图解法
若线性规划问题只含有两个决策变量，则可考虑用 几何作图法求解.下面通过例题说明图解法的一般步骤. 例1 对引例4.5给出的线性规划问题的数学模型
9
一般的线性规划问题的数学模型可记为： 目标函数
m a x (m 或 i n ) S c x c x c x 1 1 2 2 n n
a11 x1 a12 x2 a1n xn (, )b1 a x a x a x (, )b 21 1 22 2 2n n 2 约束条件(s . t . ) a x a x a x (, )b mn n m m1 1 m 2 2 x1 , x2 , , xn 0
目标函数 S3 可以看成是以S为参数， 为斜率 x 4 x 1 2 4 3
的一族平行直线：
3 S x2 x1 4 4
位于同一条直线上的点，具有同样的目标函数值.
12
直线
3 S x2 x1 4 4
沿着法线的方向向右上角移动时，
的值由小到大.当移动到B点时，S的值最大.即目标函数值
x x2 8 1 2
x1
5
x ,x 1 0 2 0
5
综上所述，本问题的数学模型为
m a x S 3 x 4 x 1 2
x1 x 2 6 x 2x 8 1 2 5 x1 x1 0 , x 2 0
满足
max S ”表示函数 其中，记号“ 的最大值，函数 S S 称为目标函数，不等式组称为约束条件.

运筹学-第4章--整数规划习题

第四章 整数规划４.1 某工厂生产甲、乙两种设备,已知生产这两种设备需要消耗材料A 、材料B,有关数据如下,问这两种设备各生产多少使工厂利润最大？(只建模不求解）解:设生产甲、乙这两种设备的数量分别为x １、x 2,由于是设备台数,则其变量都要求为整数,建立模型如下:2123max x x z +=⎪⎪⎩⎪⎪⎨⎧≥≤+≤+为整数21212121,0,5.45.01432x x x x x x x x４．2 2197max x x z +=⎪⎩⎪⎨⎧≥≤+≤+-且为整数0,35763.212121x x x x x x t s 割平面法求解。

(下表为最优表）线性规划的最优解为：63max ,0,2/7,2/94321=====z x x x x由最终表中得:27221227432=++x x x ﻩ④ 将系数和常数项分解成整数和非负真分式之和，上式化为；2132********+=++x x x移项后得:①②③④①②③即：21221227212212274343-≤--→≥+x x x x 只要把增加的约束条件加到B 问题的最优单纯形表中。

表4-4由ｘ1行得:7327171541=-+x x x 将系数和常数项分解成整数和非负真分数之和:74476715541+=+-+x x x x得到新的约束条件： 74767154-≤--x x747671654-=+--x x x 在的最优单纯形表中加上此约束，用对偶单纯形法求解：则最优解为3,421==x x ，最优目标函数值为z *=55。

4．3 m ａx z =４ｘ1+３x 2+2x ３⎪⎪⎩⎪⎪⎨⎧=≥+≥++≤+-10,,13344352.32132321321或x x x x x x x x x x x t s 隐枚举法解：(１）先用试探的方法找出一个初始可行解,如x 1=ｘ２＝０,x 3＝1。

满足约束条件，选其作为初始可行解，目标函数z 0=2。

运筹学：第4章 整数规划与分配问题


2021/4/18
17
资源 金属板（吨） 劳动力（人月） 机器设备（台月）
小号容器 2 2 1
中号容器 4 3 2
大号容器 8 4 3
解：设 x1, x2, x3 分别为小号容器、中号容器和大号容 器的生产数量。
0， 不生产j型号容器 y j 1， 生产j型号容器
建立如下的数学模型：
2021/4/18
为：
C
j
(x
j
)
K 0,
j
c
j
x
j
,
xj 0 xj 0
其中 K j 是与产量无关 的生产准备费用
n
目标函数： min z C j (x j )
j 1
定义
0 y j 1
则原问题可表示为
xj 0
xj 0
n
min z (c j x j K j y j ) j 1
s.t
0 x j Myj
y
j
0或1
2021/4/18
10
§2.2 应用举例
例1 东方大学计算机实验室聘用4名大学生（代号
1,2,3,4）和2名研究生（代号5,6）值班。已知各学生从 周一至周五每天可安排的值班时间及每人每小时报酬见下 表所示。
学生 代号
1 2 3 4 5 6
酬金 (元/h) 10.0 10.0
9.9 9.8 10.8 11.3
2021/4/18
29
（0） 8
2
5
11 （0） 5
4
2
3 （0） 0
0
11
4
5
根据上图，k=2，
周一 6 0 4 5 3 0
每天可安排的值班时间(h) 周二 周三 周四
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

②假设树木经过一个生长期后被砍伐，再就地补种幼 苗，其状态和初始状态相同。 ③设树木总和为Ｓ。设X=(x1, x2, …, xn)T为初始树木向 量，因此有
x1 x2 xn S
④假设在一个生长期内树木至多只能生长一个高度级。 设gi (i=1, 2, …, n-1)是生长参数，即第i级的数目进入第i+1 级的比例数。
假设 ①因为出售的树木，价值与树木的高度有关，所以 我们把树木生长情况用高度区间来表示，即高度用h1, h2, …, hn, …表示。这样就可用下表表示各确定高度区间 与价格之间的关系。
级别 1(幼苗) 2 3 … n 价格 P1=0 P2 P3 … Pn 高度区间 [0, h1) [h1, h2) [h2, h3) … [hn-1, ∞)
max
M P2 g1 x1 ( P3 P2 ) g 2 x2 ( Pn Pn 1 ) g n 1 xn 1 x1 x2 xn S g1 x1 g 2 x2 g n 1 xn 1 0 x 0 i 1,2,, n i
经济效益为 C ij 元，问应如何购置和安装这些设备，才有使总经济效益最高。
yi 设 x ij 表示设备 Ai 安在B j 处的台数，
置 Ai 的台数，Z 表示总的经济效益。
表示购
max
Z C ij x ij
i 1 j 1
m
n
xij ≤ yi + ai ∑
s.t .
n
xij ≤ b j ∑ Pi yi ≤ M ∑
s.t.
线性规划问题：若干个等式或不等式约束下的优化问题。 求解：单纯形法
§2. 非线性规划
实例一
元件是在 A 点铰支的钢管。在 A 点，结构受到垂直
ቤተ መጻሕፍቲ ባይዱ
负荷载 2P。设已选定管壁厚度为 h，跨度为 2b。试选择钢管 的平均直径 D 与架高度 H，使杆件既不屈服又不失平稳，而 且架的总重量最轻。
2 2 min W= 2Dh (b h )
4．整数规划模型
Ai 的单价为 Pi 实例四 某工厂需要 m 种设备A1 ，A2 ，…， Am ，其中
元，该厂
ai 台（i=1，2，…，m） 已有第 i 种设备 。今有资金 M 元可用于购置这些设备，
该厂有 n 处可安装这些设备，B j 处最多可安装 b j
B j 处， 台， 一台设备 Ai 安在
第四章 数学规划
线性规划模型
实例一 合理伐木
森林中的每年都要有一批被砍伐出售，为了使这片森 林不被耗尽而且年年都能有收获，每砍伐一棵时，应该就 地补种一棵幼苗，使森林树木的总数保持不变。被出售的 树木，其价值取决于树木的高度，我们希望能够找到一个 方案，在维持收获的前提下，如何砍伐树木，才能获得最 大的经济价值？
（２）建模及计算 设向量Ｚ表示经过一个生长期后，森林中树木高度的 分布。则有
Z (( 1 g1 )x1 , g1x1 ( 1 g 2 )x2 , g 2 x2 ( 1 g3 )x3 , , g n2 xn2 ( 1 g n1 )xn1 , g n1xn1 xn )T
设x1 , x2 ,x3 分别为购买香蕉、 苹果、 葡萄三种水果 的重量。用于买水果的总钱数为 y1 ,所买的水果的总量
y y y 2 1 为 ，自然，我们希望 取最小值， 2 取最大值。
约束条件为
s.t.

1 2
P(b 2 H 2 ) 2 E(D 2 h 2 ) DhH 8(b 2 H 2 ) 1 P(b 2 H 2 ) 2 y s.t. DhH D1 D D2 , H 1 H H 2
1 2
• 非线性规划问题求解比较复杂： •① 用线性规划、二次规划来逐步逼近 非线性规划的方法；②随机试验法等； • ③ 可行方向法、凸单纯形法等； • ④ SUMT外点法、SUMT内点法、乘子法等。
２．多目标规划模型
•
在许多客观实际问题中，要达到的目标往往 不止一个。例如，设计导弹时既要使其射程最远 有要燃料最省，还要精度最高。这类含有多个目 标的优化问题称为多目标规划问题。
实例 设市场上有香蕉、苹果、葡萄三种水果， 其单价分别为 4.2 元/千克，2.4 元/千克，2.2 元/千 克。现在某单位要筹办一次节日茶话会，要求买水 果的重量不少于 10 千克，香蕉、苹果的总和不少 于 6 千克，现共有 30 元钱，问如何确定最好的购 买方案。
因为yi≥0，i=1, 2, …, n。可推出
g1x1 g 2 x2 g n1xn1 0
设收获的总价值为Ｍ，则有
M P2 y2 P 3 y3 P n yn
利用前面的方程组及上式，我们得到
M P 2 g1x1 ( P 3 P 2 ) g2 x2 ( P n P n1 ) gn1xn1
i=1 m
j=1 m
i = 1,2,, m j = 1,2,, n
i=1 xij , yi ≥ 0,且xij , yi : 整数
i = 1,2,, m; j = 1,2,, n
所有的变量都是整数的规划， 称整数规划问题为纯 整数规划问题。 解此类问题的方法有： ①分枝定界算法； ②割平面法；③分解方法；④松弛方法；⑤群论方法； ⑥动态规划法等。
Ｙ=(y1, y2, …, yn)T为收获向量。故 y１+y２+…+yn 就是收获的总数，从而补种向量为 Ｒ＝（y１+y２+…+yn, 0, …, 0)T
依据维持每年收获的原则，有 生长期未状态－收获＋新的幼苗替换＝生长期状态 即 Ｚ－Ｙ＋Ｒ＝Ｘ
y2 y3 yn g1x1 y g x g x 1 1 2 2 2 y3 g 2 x2 g3 x3 yn1 g n2 xn 2 g n1xn 1 yn g n1xn 1