高邮市20112012学年度九年级数学期中考试试

2011－2012学年上学期期中考试九年级数学试题（考试时间120分钟，满分120分）一．细心选一选（每题只有一个正确选项．每小题3分，8小题，共24分）1．若二次根式x－1 有意义，则x的取值范围是（）A．x≠1 B．x≥1 C．x＜1 D．x≥02．方程x2－3x+6=0的根的情况是（）A．有两个不相等的实数根B．有两个相等的实数根C．没有实数根D．无法确定是否有实数根3．下列图形中，既是中心对称图形又是轴对称图形的是（）A．B．C．D．4．用配方法解方程x2－2x－5=0时，原方程应变形为（）A．(x+1)2=6 B．(x－1)2=6 C．(x+2)2=9 D．(x－2)2=95．如图，在4×4的正方形网格中，△MNP绕某点旋转90°，得到△M1N1P1，则其旋转中心可以是（）A．点E B．点F C．点G D．点H第5小题图第6小题图6．如图，点A、B、C在⊙O上，BC为直径，∠AOC＝70°，则∠ABC的度数为（）A．10°B．20°C．35°D．55°7．某次球赛共有x个队参加，每两个队之间打一场比赛，共打了176场，则根据题意可列出的方程是（）A．x(x+1)=176 B．x(x－1)=176C．2x(x+1)=176 D．x(x－1)=2×1768．在⊙O中，⊙O的半径为6厘米，弦AB的长为6厘米，则弦AB所对的圆周角是（）A．30°B．30°或150°C．60°D．60°或120°二．认真填一填（每小题3分，8小题，共24分）9．写出一个能与12合并的最简二次根式：_______________________．10．方程x2－2x－3=0的根是：_______________________．11．某药品原价每盒25元，为了响应国家解决老百姓看病贵的号召，经过连续两次降价，现在售价每盒16元，则该药品平均每次降价的百分率是．12．如图是“靠右侧通道行驶”的交通标志，若将图案绕其中心顺时针旋转90°，则得到的图案是“___________________”交通标志(不画图案，只填含义)．13．如图，⊙O的半径OA=10cm，弦AB=16cm，P为AB上一动点，则点P到圆心O的最短距离为．14．如图，AB是⊙O的直径，点C，D在⊙O上，∠BAC=30°，则∠ADC=_________．第12小题图第13小题图第14小题图第16小题图15．在平面直角坐标系中，半径为5的⊙O与x轴交于x(－2，0)、B(4，0)，则圆心点M坐标为_________．16．如图：AB 是⊙O的直径，AB=AC，BC交⊙O与D点，AC交⊙O于E，∠BAC=45°，下面五个结论①∠EBC=22.5°；②BD=DC；③AE=2EC；④劣弧AE是劣弧DE的2倍；⑤AE=BC；其中正确结论的序号是___________________．三．（本大题共3小题，每小题6分，共18分）17．化简：22－ 3－(π－3)0+(12)－1－|－12 |OP BA学校：班级：姓名：座号：18．已知关于x 的方程x 2－2(m+1)x+m 2=0． （1）当m 取什么值时，原方程没有实数根．（2）对m 选取一个合适的非零整数，使原方程有两个实数根，并求这两个实数根．19．认真观察下列4个图中阴影部分构成的图案，回答下列问题：（1）请写出这四个图案都具有的两个共同特征．特征1：_________________________________________________； 特征2：_________________________________________________．（2）请在右图网格中设计出你心中最美丽的图案，使它也具备你所写出的上述特征． 四．（本大题共2个小题，每小题8分，共16分）20．已知：如图，AD 、BC 是⊙O 的两条弦，且AD=BC ，求证：AB=CD ．21．某小区要修建一块矩形绿地，计划用18米的建筑材料来修建绿地边框．（1）根据小区的规划要求，所修建的矩形绿地面积必须是18平方米，矩形长、宽各多少米？ （2）有人建议把矩形绿地面积改为21平方米，此人建议是否合理？说明理由．五．（本大题共2小题，每小题9分，共18分）22．如图，AB 是⊙O 的直径，BC 是弦，OD ⊥BC 于E ，交⌒BC 于D ． （1）请写出四个不同类型的正确结论；① ；② ； ③ ；④ ．（2）连结CD 、BD ，设∠CDB=α，∠ABC=β．试找出α与β之间的一种．．关系式，并说明理由．23．如图，Rt △ABC 中，∠C=90°，∠A=30°，AB=2．（1）用尺规作图，作出△ABC 绕点A 逆时针旋转60°后得到的△AB 1C 1（不写画法，保留画图痕迹）；（2）在（1）的条件下，连接B 1C ，求B 1C 的长．六．（本大题共2小题，每小题10分，共20分）24．如图，已知A、B、C、D为矩形的四个顶点，AB=16㎝，AD=6㎝，动点P、Q分别从点A、C同时出发，点P以3㎝/s的速度向点B移动，一直到点B为止，点Q以2㎝/s的速度向点D移动．问：（1）P、Q两点从出发开始几秒时，点P点Q间的距离是10厘米．（2）P、Q两点间距离何时最小．25．如图，以直角梯形OBDC的下底OB所在的直线为x轴，以垂直于底边的腰OC所在的直线为y轴，O为坐标原点，建立平面直角坐标系，CD和OB是方程x2－5x+4=0的两个根．（1）试求S△OCD∶S△ODB的值；（2）若OD2=CD·OB，试求直线DB的解析式；（3）在(2)的条件下，线段OD上是否存在一点P，过P作PM//x轴交y轴于M，交DB于N，过N作NQ//y轴交x轴于Q，使四边形MNQO的面积等于梯形OBDC面积的一半，请说明理由．D C。

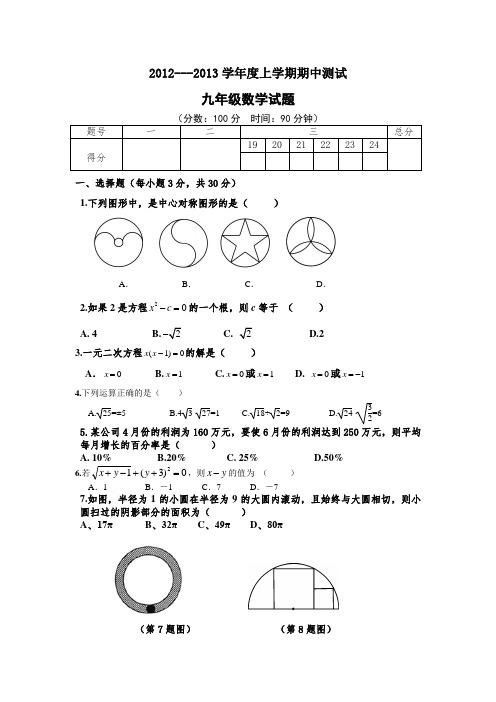
2012---2013学年度上学期期中测试九年级数学试题一、选择题（每小题3分，共30分）1.下列图形中，是中心对称图形的是（）A．B．C．D．2.如果2是方程20x c-=的一个根，则c等于（）A. 4B.C.D.23.一元二次方程0)1(=-xx的解是（）A．0=x B.1=x C.0=x或1=x D. 0=x或1-=x4.下列运算正确的是（）A.25=±5B.43-27=1C.18÷2=9D.24·32=65.某公司4月份的利润为160万元，要使6月份的利润达到250万元，则平均每月增长的百分率是（）A. 10%B.20%C. 25%D.50%6.若0)3(12=++-+yyx，则yx-的值为（）A．1 B．－1 C．7 D．－77.如图，半径为1的小圆在半径为9的大圆内滚动，且始终与大圆相切，则小圆扫过的阴影部分的面积为（）A、17πB、32πC、49πD、80π（第7题图）（第8题图）8．如图，两正方形彼此相邻且内接于半圆，若小正方形的面积为16cm2，则该半圆的半径为（）cm.A. (4+cmB. 9 cmC. D.cm9. 如图所示，已知在三角形纸片ABC中，BC=3，AB=6，∠BCA=90°，在AC上取一点E，以BE为折痕，使AB的一部分与BC重合，A与BC延长线上的点D重合，则DE的长度为（）A．6 B．3 C．D．10．如图，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN＝30°，B为 A N 的中点，P是直径MN上一动点，则PA＋PB的最小值为( )A．2B C．1 D．2（第10题图）NAC二、填空题（每空2分，共18分）11.有意义的条件是 .12.已知n n 的最小值为 .13.如图，正方形ABCD 绕点A 逆时针旋转50 ，得到正方形AEFG ， 则B A G ∠=.（第13题图） （第17题图）14.已知扇形的面积为12π，半径等于6，则它的圆心角等于 度． 15.用一根长26m 的细绳围成面积为422m 的长方形，则长和宽分别为 m 和 m .16.关于x 的一元二次方程2(2)10x m x m +-++=有两个相等的实数根，则m 的值是 ．17.如图，在平面直角坐标系中，正方形ABCO 的顶点A 、C 分别在y 轴、x 轴上，以AB 为弦的⊙M 与x 轴相切．若点A 的坐标为（0，8），则圆心M 的坐标为 .18.母线长为2，底面圆的半径为1的圆锥的侧面积为．三、解答题(本大题共52分)19.（本题满分620.（每小题4分，本题满分8分）计算：（1）(÷（2）⎛⎛⎝⎝21．（每小题5分，本题满分10分）解下列方程：（1）2560+-=（2）4(3)(3)(1)0 x x+-++=x x x x22.（本题满分8分）将两块大小完全相同的含30°角的直角三角板（∠BAC＝∠B′A′C＝30°）按图①方式放置，固定三角板A′B′C，然后将三角板ABC绕直角顶点C顺时针方向旋转（旋转角小于90°）至图②所示的位置，AB与A′C交于点E，AC与A′B′交于点F，AB与A′B′相交于点O．（1）求证：△BCE≌△B′CF；（2）当旋转角等于30°时，AB与A′B′垂直吗？请说明理由．（第22题图）为落实国务院房地产调控政策，使“居者有其屋”，某市加快了廉租房的建设力度．2011年市政府共投资2亿元人民币建设了廉租房8万平方米，预计到2013年底三年将共累计投资9.5亿元人民币建设廉租房，若在这两年内每年投资的增长率相同．(1)求每年市政府投资的增长率；(2)若这两年内的建设成本不变，求到2013年底将共建设多少万平方米廉租房．(第24题图)2012---2013学年度上学期期中测试九年级数学试题参考答案一、选择题二、填空题 11. 32x ≥ 12. 2 13. 140° 14. 120 15. 7,6 16. 0或8 17. （-4,5） 18.2π 三、解答题19.每种方法3分（本题方法多种，现给出三种方法，其它方法参考赋分）方法1：原式12==；方法2：原式12=；方法3：原式2142===.20. 解：（1）原式=62736482-=29382-………………2分=2233222⨯-⨯=22122924-=-………………4分（2）原式=3352561223⨯+--………………2分=33521733+- (3)分=2173314-………………4分（其它方法参考赋分）21.（1）16x =-，21x =；（2）13x =-，213x =.（每小题5分，解法不限）22. （1）因∠B ＝∠B /，BC ＝B /C ，∠BCE ＝∠B /CF ， 所以△BCE ≌△B ′CF ；…………………… 4分 （2）AB 与A ′B ′垂直，…………………… 5分 理由：旋转角等于30°，即∠ECF ＝30°， 所以∠FCB /＝60°，…………………… 6分 又∠B ＝∠B /＝60°，根据四边形的内角和可知∠BOB /=360°－60°－60°－150°＝90°，…………………… 7分 所以AB ⊥A ′B ′. …………………… 8分23．解：（1）设每年市政府投资的增长率为x ，…………………… 1分 根据题意，得：222(1)2(1)9.5x x ++++=整理，得：23 1.750x x +-=………………………3分解之，得：32x -±=，∴10.5x =，2 3.5x =-（舍去），…………………5分答：每年市政府投资的增长率为50%；……………………6分 （2）到2013年底将共建廉租房面积为：29.5388÷=（万平方米）． (9)分24.解：（1）∵AD ∥BC ，∠BAD =120°．∴∠ABC =60°． 又∵BD 平分∠ABC ， ∴∠ABD =∠DBC =∠ADB =30°∴AB AD DC ==，∠BCD =60° ∴AB =AD =DC ，∠DBC =90°．………………………3分 又在直角△BDC 中，BC 是圆的直径，BC =2DC ．∴32B C B C+=15………………………5分∴BC =6∴此圆的半径为3．………………………6分（2）设BC 的中点为O ，由（1）可知O 即为圆心． 连接OA ，OD ，过O 作OE ⊥AD 于E ．……………………7分 在直角△AOE 中，∠AOE =30° ∴1322A E O A ==,∴2O E ==，∴S △AOD =13224⨯⨯=．………………………9分∴S 阴影=S 扇形AOD -S △AOD =260333604244ππ⨯-=-=．………………………11分。

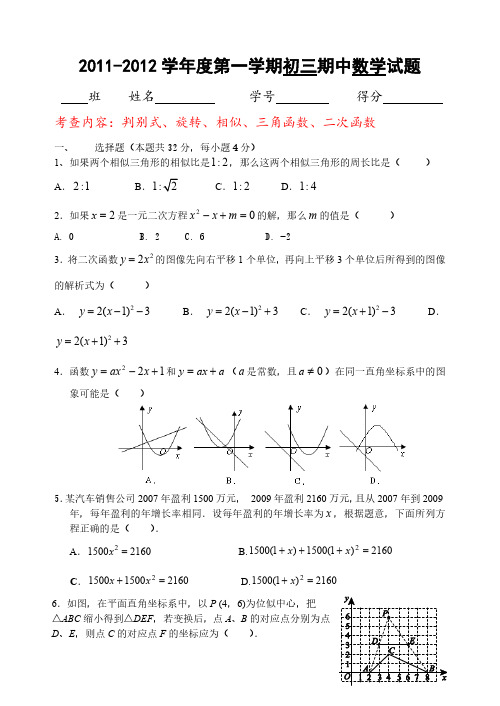
2011—2012学年第一学期 九年级数学期中测试题班级_______ 座号_______ 姓名________ 得分_______一、选择题（每小题3分，共30分）1、在△ABC 和△DEF 中，已知AB=DE ，∠B=∠E ，增加下列条件后，不能判定△ABC ≌△DEF 的是（ ）A. BC=EFB. AC=DFC. ∠A=∠DD. ∠C=∠F2、如图，在△ABC 中，点E 、F 分别为AB 、AC 的中点． 若△ABC 的周长为6，则△AEF 的周长为（ ） A ．12 B ．3 C ．4 D ．不能确定3、正方形具有而菱形不一定具有的性质是（ ） A 、对角线互相平分 B 、对角线相等 C 、对角线平分一组对角D 、对角线互相垂直4、方程 032=-x x 的解是（ ） A ．x=3 B ．x 1=0，x 2=3 C ．x 1=0，x 2=-3 D ．x 1=1，x 2=35、关于x 的一元二次方程01)1(22=-++-a x x a 有一个根为0，则a 的值是（ ）A ．±1 B.－1 C.1 D.06、用配方法解方程2x 2 + 3 = 7x 时，方程可变形为（ ） A ．（x – 72 ）2 = 374B ．（x – 72 ）2 = 434C ．（x – 74 ）2 = 116D ．（x – 74 ）2 = 25167、不能判定四边形ABCD 是平行四边形的条件是（ ）A 、∠A=∠C ∠B=∠DB 、AB ∥CD AD=BC C 、AB ∥CD ∠A=∠C D 、AB ∥CD AB=CD8、直角三角形中，两条直角边长分别为6cm 和8cm ，则连接这两条直角边中点的线段的长是（ ）A 、3cmB 、4 cmC 、5cmD 、12cmAB CE F第2题图D 9、某超市一月份的营业额为30万元，三月份的营业额为56万元。

设每月的平均增长率为x ，则可列方程为（ ）A 、56(1＋x)2 =30B 、56(1－x)2 =30C 、30(1＋x)2 =56D 、30(1＋x)3 =5610、如图1-3，△ABC 中，AB=AC ，∠BAC=120︒，D 是BC 的中 点，DE ⊥AB 于E ，若AE=4cm ，则AD 的长为( ) A ．4cm B ．6cm C ．8cm D ．12cm二、 填空题（每小题3分，共24分）11、一元二次方程2)2)(1(=++x x 的一般形式是____________,它的二次项系数是______；它的常数项是______.12、关于x 的一元二次方程0122=++x kx 有两个不相等的实数根, 则k 的取值范围是_______。

高邮市2011—2012学年度九年级数学期中考试试卷一、选择题（每题3分，共24分）1、在实数2-、、0中，最小的是（ ） A 、2-B、C 、0D2、如图，在矩形ABCD 中，对角线AC 、BD 相交于点O ，已知060,16AOB AC ∠==，则图中长度为8的线段条数有（ ） A 、2B 、4C 、5D 、63、一元二次方程(2)0x x -=根的情况是（ ） A 、有两个不相等的实数根 B 、有两个相等的实数根 C 、只有一个实数根D 、没有实数根4、2011年我国西南地区发生了严重的干旱，高邮市政府号召居民节约用水，为了解居民用水情况，在某小区随机抽查了10户家族的用水量，结果如下表：则关于这10户家族的用水量，下列说法错误的是（ ） A 、众数B 、极差是2 C、平均数是6 D 、方差是45、与方程3916x -=的根最接近的是（ ） A 、2B 、3C 、4D 、56、矩形ABCD 中，AB=8， BC=，点P 在边AB 上，且BP=3AP ，如果P e 是以点P 为圆心，PD 为半径的圆，那么下列判断正确的是（ ） A 、点B 、C 均在P e 外B 、点B 在P e 外、点C 在P e 内 C 、点B 在P e 内、点C 在P e 外D 、点B 、C 均在P e 内7、如图1，平行四边形纸片ABCD 的面积为120，AD=20，AB=18,沿两条对角线将四边形ABCD 剪成甲、乙、丙、丁四个三角形纸片，将甲、丙拼成如图2所示的轴对称图形戊，则图形戊的两条对角线长度之和为（ ）B ）（CB图1 图2 A 、26B 、29C 、2243D 、12538、如图，梯形ABCD 中，AB CD P ，点E 、F 、G 分别是BD 、AC 、DC 的中点，已知两底差是6，两腰和是12，则EFG ∆的周长是（ ） A 、 8 B 、9 C 、10D 、12二、填空题（每题3分，共30分）9a 的取值范围是10、如果关于x 的方程220x x m -+=（m 为常数）有两个相等实数根，那么m=。

2011-2012学年度第一学期九年级期末数学试卷一、单项选择题：1．如果a a 2-1)1-22=（，则 A ．21<a B ．21≤a C ．21>a D ．21≥a2．已知x =1是方程x 2+b x -2=0的一个根，则方程的另一个根是 A ．1 B ．2 C ．-2 D ．-l3．如图是一个旋转对称图形，要使它旋转后能与自身重合，至少应将它绕中心点旋转A ．30°B ．60°C ．120°D ．180°4．下列说法中，正确的是 A ．到圆心的距离大于半径的点在圆内 B ．圆的半径垂直于圆的切线C ．圆周角等于圆心角的一半D ．等弧所对的圆心角相等5．在平面直角坐标系xoy 中，以点（-3，4）为圆心，4为半径的圆 A ．与x 轴相交，与y 轴相切 B ．与x 轴相离，与y 轴相交C ．与x 轴相切，与y 轴相交D ．与x 轴相切，与y 轴相离6．已知相交两圆的半径分别为4和7，则它们的圆心距可能是 A ．2 B ．3 C ．6 D ．11 7．下列事件中属于随机事件的是 A ．抛出的篮球会落下B ．从装有黑球、白球的袋里摸出红球C ．367人中有2人是同月同日出生D ．买l 张彩票，中500万大奖8．在一个不透明的布袋中装有红色，白色玻璃球共40个，除颜色外其他完全相同，小明通过多次摸球试验后发现，其中摸到红色球的频率稳定在15％左右，则口袋中红色球可能有A ．4个 B ．6个 C ．34个 D ．36个9．下列函数关系中，可以看做二次函数c bx ax y ++=2（a ≠0）模型的是A ．在一定的距离内汽车的行驶速度与行驶时间的关系B ．我国人口年自然增长率l ％，这样我国人口总数随年份的关系C ．竖直向上发射的信号弹，从发射到落回地面，信号弹的高度与时间的关系（不计空气阻力）D ．圆的周长与圆的半径之间的关系10．二次函数3-2-2x x y =的图象如下图所示．当y <0时，自变量x 的取值范围是A ．-l<x <3B ．x <-1C ．x >3D ．x <-1或x >311．已知：如下图，在∆ABC 中，∠AED=∠B ，则下列等式成立的是 A ．DEAD BCDE =B ．BDAD BCAE =C ．ABAE CEDE =D ．ACAE ABAD =12．由二次函数1)3-(22+=x y 可知 A ．其图象的开口向下 B ．其图象的对称轴为直线x =-3C ．其最小值为lD ．当x <3时，y 随x 的增大而增大13．如下图，小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC 相似的是14．如下图，在矩形ABCD 中，AB=3，BC=4，点P 在BC 边上运动，连接DP ，过点A 作AE ⊥DP ，垂足为E ，设DP=x ，AE=y ，则能反映y 与x 之间函数关系的大致图象是二、填空题 15．1-)21(24-8+=_________________16．∆ABC 的3个顶点都在5×5的网格（每个小正方形的边长均为1个单位长度）的格点上，将∆ABC 绕点B 顺时针旋转到△A′B′C′的位置，且点A′、C′仍落在格点上，则线段AB 扫过的图形面积是__________平方单位（结果保留π）17．如下图，有三个同心圆，由里向外的半径依次是2cm ，4cm ，6cm 将圆盘分为三部分，飞镖可以落在任何一部分内，那么飞镖落在阴影圆环内的概率是_______________18．点A （2，1y ）、B （3，2y ）是二次函数=y 12-2+x x 的图象上两点，则1y 与2y 的大小关系为1y __________2y （填“>”“<”“=”）19．已知圆锥底面半径为5cm ，母线长为15cm ，那么它的侧面积为_________（结果保留π）20．如下图，在正方形网格中，点A 、B 、C 、D 都是格点，点E 是线段AC 上任意一点．如果AD=1。

2012-2013学年江苏省扬州市高邮市菱塘初中九年级（上）期中数学模拟试卷一、选择题（每题3分，共24分）1．(★★★★★)化简的结果是（）A．3B．-3C．±3D．92．(★★★★)已知0和-1都是某个方程的根，则此方程是（）A．x2-1=0B．x（x+1）=0C．x2-x=0D．x2+2x+1=03．(★★★)用配方法解方程：x 2-2x-3=0时，原方程变形为（）A．（x+1）2=4B．（x-1）2=4C．（x+2）2=2D．（x-2）2=34．(★★★★)下列命题中，真命题是（）A．两条对角线垂直的四边形是菱形B．对角线垂直且相等的四边形是正方形C．两条对角线相等的四边形是矩形D．两条对角线相等的平行四边形是矩形5．(★★★★)样本方差的计算式S 2= （x 1-40）2+（x 2-40）2+…+（x n-40）2中，数字20和40分别表示样本中的（）A．样本中数据的个数、平均数B．方差、标准差C．众数、中位数D．样本中数据的个数、中位数6．(★★)如图△ABC是等腰直角三角形，BC是斜边，将△ABP绕点A逆时针旋转后，能与△ACP′重合，已知AP=3，则PP′的长度是（）A．3B．C．D．47．(★★★★)如图，⊙O的弦AB=8，M是AB的中点，且OM=3，则⊙O的半径等于（）A．8B．4C．10D．58．(★★★)如图，点C是线段AB上的一个动点，△ADC和△CEB是在AB同侧的两个等边三角形，DM，EN分别是△ADC和△CEB的高，点C在线段AB上沿着从点A向点B的方向移动（不与点A，B重合），连接DE，若AB=1，则四边形DMNE面积为（）A．B．C．D．二、填空题（每题3分，共30分）9．(★★★★)计算：+ = ．10．(★★★★)使代数式有意义的x的取值范围是 x≤3且x≠-2 ．11．(★★★★)若关于x的方程x 2-5x+k=0的一个根是0，则另一个根是 5 ．12．(★★★★)一组数据2，-1，0，x，1的极差是5，则x的值是 -3或4 ．13．(★★)等腰△ABC两边的长分别是一元二次方程x 2-5x+6=0的两个解，则这个等腰三角形的周长是 7或8 ．14．(★★★★)关于x的方程kx 2-2x+3=0有两个不相等的实数根，则k的取值范围是k＜且k≠0 ．15．(★★★)已知等腰梯形ABCD的中位线EF的长为5，腰AD的长为3，则这个等腰梯形的周长为 16 ．16．(★★★)如图，已知P是正方形ABCD对角线BD上一点，且BP=BC，则∠ACP度数是 22.5 度．17．(★★★★)如图，点A、B、C在⊙O上，∠AOC=60o，则∠ABC的度数是 150o ．18．(★★)如图，矩形纸片ABCD中，AB=5cm，BC=10cm，CD上有一点E，EC=2cm，AD上有一点P，PA=6cm，过点P作PF⊥AD交BC于点F，将纸片折叠，使P与E重合，折痕交PF于Q，则线段PQ的长是 cm．三、解答题（共96分）19．(★★★★)计算：（1）（2）．20．(★★★★)解方程：（1）（x+1）2-9=0（2）x 2-12x-4=0（3）3（x-2）2=x（x-2）21．(★★★)如图，在平行四边形ABCD中，对角线AC、BD相交于点O，AF⊥BD，CE⊥BD，垂足分别为E、F；（1）连接AE、CF，得四边形AFCE，试判断四边形AFCE是下列图形中的哪一种？①平行四边形；②菱形；③矩形；（2）请证明你的结论．22．(★★★)王华、张伟两位同学九年级10次数学单元自我检测的成绩（成绩均为整数，且个位数为0）分别如下图所示：（1）根据上图中提供的数据填写下表：（2）如果将90分以上（含90分）的成绩视为优秀，则优秀率高的同学是张伟．（3）如果要从这两个同学选一位去参加数学竞赛，你可以给老师一些建议吗？23．(★★★)如图，在梯形ABCD中，AB∥DC，DB平分∠ADC，过点A作AE∥BD，交CD的延长线于点E，且∠C=2∠E．（1）求证：梯形ABCD是等腰梯形；（2）若∠BDC=30o，AD=5，求CD的长．24．(★★★★)已知关于x的方程x 2-（2k+1）x+4（k- ）=0（1）判断方程根的情况；（2）k为何值时，方程有两个相等的实数根，并求出此时方程的根．25．(★★)某商店经销一种销售成本为每千克40元的水产品，据市场分析，若每千克50元销售，一个月能售出500kg，销售单价每涨1元，月销售量就减少10kg，针对这种水产品情况，请解答以下问题：（1）当销售单价定为每千克55元时，计算销售量和月销售利润；（2）设销售单价为每千克x元，月销售利润为y元，求y与x的关系式；（3）商品想在月销售成本不超过10000元的情况下，使得月销售利润达到8000元，销售单价应为多少？26．(★★)如图①，将边长为4cm的正方形纸片ABCD沿EF折叠（点E、F分别在边AB、CD 上），使点B落在AD边上的点M处，点C落在点N处，MN与CD交于点P，连接EP．（1）如图②，若M为AD边的中点，①△AEM的周长= 6 cm；②求证：EP=AE+DP；（2）随着落点M在AD边上取遍所有的位置（点M不与A、D重合），△PDM的周长是否发生变化？请说明理由．。

高邮市2011—2012学年度九年级数学期中考试试卷一、选择题（每题3分，共24分）1、在实数2-、、0） A 、2-B、C 、0D2、如图，在矩形ABCD 中，对角线AC 、BD 相交于点O ，已知60,16AOB AC ∠==，则图中长度为8的线段条数有（ ）A 、2B 、4C 、5D 、63、一元二次方程(2)0x x -=根的情况是（ ）A 、有两个不相等的实数根B 、有两个相等的实数根C 、只有一个实数根D 、没有实数根4、2011年我国西南地区发生了严重的干旱，高邮市政府号召居民节约用水，为了解居民用则关于这10户家族的用水量，下列说法错误的是（ ） A 、众数 B 、极差是2C 、平均数是6D 、方差是45、与方程3916x -=的根最接近的是（ ） A 、2B 、 3C 、4D 、56、矩形ABCD 中，AB=8， BC=，点P 在边AB 上，且BP=3AP ，如果P 是以点P为圆心，PD 为半径的圆，那么下列判断正确的是（ ） A 、点B 、C 均在P 外 B 、点B 在P 外、点C 在P 内C 、点B 在P 内、点C 在P 外D 、点B 、C 均在P 内7、如图1，平行四边形纸片ABCD 的面积为120，AD=20，AB=18,沿两条对角线将四边形ABCD 剪成甲、乙、丙、丁四个三角形纸片，将甲、丙拼成如图2所示的轴对称图形戊，则图形戊的两条对角线长度之和为（ ）图1 图2 （第8题） A 、26B 、29C 、2243D 、12538、如图，梯形ABCD 中，AB CD ，点E 、F 、G 分别是BD 、AC 、DC 的中点，已知两底差是6，两腰和是12，则EFG ∆的周长是（）B （CA 、 8B 、9C 、10D 、12二、填空题（每题3分，共30分）9，则a 的取值范围是10、如果关于x 的方程220x x m -+=（m 为常数）有两个相等实数根，那么m= 。

11、已知3y =，则2xy 的值为 。

2011---2012学年度第一学期九年级数学期中试卷答案一、选择题（16分）1. D2. B3. A4. C5. B6. B7.__C___8.___B_二、填空题（20分）9. 4 ，2 ； 10. 5； 11.矩形； 12. 2+ 3 ; 13. 2:1(或2）14. 直角； 15. 4，-1； 16. （-3,0）或（5，0）或（-5,4）全对给分.三、化简与计算（16分）17. （1）（4分） 52直接写答案，不分步给分。

（2）（4分） 206 -10去括号2分，化简2分。

或先化简2分，去括号，合并2分。

18. （4分）22 化简成 1x-1 得2分，结果22得2分。

19. （4分） 0-a-1+b+1+a-b 每个去绝对号各得1分，合并得1分。

四、解方程（每题4分，共16分）20. （每题4分，共16分）（1）解：x+1=±2.............2分 （2）解：x 2-52x=-1 ∴x 1=2-1................1分 x 2-52 x+（54 ）2=-1+（54）2.。

1分x 2=-2-1...............1分 (x-54 )2=916x-54 = ± 34..........................1分 ∴x 1=2................1分x 2=12............1分 （3）解：△= ......= 0....................2分x 1=x 2=3...............2分（4）解：(x+3)(1-x)=0.......2分∴x 1=-3............1分x 2=1..............1分五、解答题（7分）21.（1）△= .....=（2k-3)2≥0. ∴...........3分（2）①若a=1是腰，则1是方程的解，∴1-2k-1+4k-2=0k=1∴ 原方程为x 2-3x+2=0∴x 1=1, x 2=2以1,1,2为边的三角形不存在...........2分② 若a=1为底，则b=c∴△=........=0k=32∴ 原方程为x 2-4x+4=0∴x 1= x 2=2∴三角形周长为5............2分六、阅读理解（22题8分，23题8分，共16分）22.解：x 1+x 2=32..................1分 x 1x 2=-12...................1 分① x 1+x 1x 2+x 2=32 -12=1.....................2分②1x 1 +1x 2=2121x x x x + =-3.........................2分③3x 12-3x 1+x 22=2x 12-3x 1+x 12+x 22=1+（x 1+x 2）2-2x 1x 2=174.....................2分23.（1）4×154=1544+.....................................2分（2）n 12-n n =12-+n n n ...........................2分 验证：n 12-n n =123-n n =1)122-+-n n n n （=12-+n n n .................4分 七、图形与证明（24题9分、25题8分、26题12分24.每个图3分，全等只按一个得分。

1学校 班级 考号 姓名_________________装订线内不要答题◆◆◆◆◆◆◆◆◆◆◆◆◆装◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆订◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆◆线◆◆◆◆◆◆◆◆◆◆◆◆◆双湾中学2011～2012学年度第一学期期中考试试卷九年级数学亲爱的同学：这份试卷将再次记录你的自信、沉着、智慧和收获，我们一直投给你信任的目光。

请认真审题，看清要求，仔细答题，祝你成功！一、相信你，都能选择对！在四个选项中只有一个是正确的.（每题3分，共30分） 1．下列二次根式中，最简二次根式是 （ ）A ．8aB ．5aC ．3aD ．b a a 22+2.下列图形中，既是轴对称图形又是中心对称图形的是 （ ）3. 要使1213-+-x x 有意义，则x 应满足 （ ）A ．21≤x ≤3B ．x ≤3且x ≠21C ．21＜x ＜3D ．21＜x ≤34．下列二次根式4、12、50、21其中与2是同类二次根式的个数为 （ ） A ．1个B ．2个C ．3个D ．4个5．三角形两边长分别为3和6,第三边是方程x 2-6x+8=0的解，则这个三角形的周 长是 （ ） A ．11 B ．13 C ．11或13 D ．11和13 6. 用配方法解方程2x 2 + 3 = 7x 时，方程可变形为 （ ）A.（x – 72 ）2 = 374B.（x – 72 ）2 = 434C.（x – 74 ）2 = 116D.（x – 74 ）2= 25167.S 型电视机经过连续两次降价，每台售价由原来的1500元降到了980元．设平均每次降价的百分率为x ，则下列方程中正确的是 （ ）A ．980)1(15002=+xB ．1500)1(9802=+xC ．980)1(15002=-xD ．1500)1(9802=-x 8．关于x 的方程（a -5）x 2-4x -1=0有实数根，则a 满足 （ ）A ． a ≥ 1B ．a ＞1且a ≠ 5C ．a ≥1且a ≠ 5D ．a ≠5 9. 以3和-1为两根的一元二次方程是 （ ）A.0322=-+x xB.0322=++x xC.0322=--x xD.0322=+-x x10．十年后，我班学生聚会，见面时相互间均握了一次手，好事者统计：一共握了780次。