螺旋桨片条理论简介
- 格式:doc
- 大小:37.50 KB
- 文档页数:3

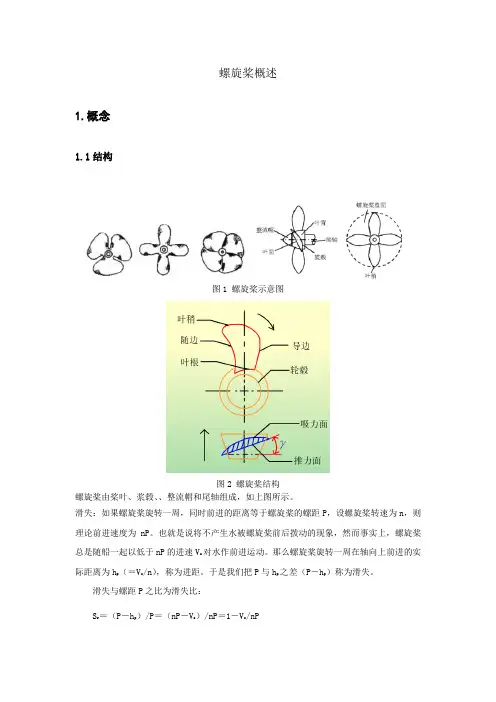
螺旋桨概述1.概念1.1结构图1 螺旋桨示意图图2 螺旋桨结构螺旋桨由桨叶、浆毂、、整流帽和尾轴组成,如上图所示。
滑失:如果螺旋桨旋转一周,同时前进的距离等于螺旋桨的螺距P,设螺旋桨转速为n,则理论前进速度为nP。
也就是说将不产生水被螺旋桨前后拨动的现象,然而事实上,螺旋桨总是随船一起以低于nP的进速V s对水作前进运动。
那么螺旋桨旋转一周在轴向上前进的实际距离为h p(=V s/n),称为进距。
于是我们把P与h p之差(P-h p)称为滑失。
滑失与螺距P之比为滑失比:S r=(P-h p)/P=(nP-V s)/nP=1-V s/nP式中V s/nP称为进距比。
从式中可以得出,当V s=nP时,S r=0。
即P=h,也就是螺旋桨将不产生对水前后拨动的现象,螺旋桨给水的推力为零。
因此我们可以得出结论:滑失越大,滑失比越高,则螺旋桨推水的速度也就越高,所得到的推力就越大。
1.2工作原理船用螺旋桨工作原理可以从两种不同的观点来解释,一种是动量的变化,另一种则是压力的变化。
在动量变化的观点上,简单地说,就是螺旋桨通过加速通过的水,造成水动量增加,产生反作用力而推动船舶。
由于动量是质量与速度的乘积,因此不同的质量配合上不同的速度变化,可以造成不同程度的动量变化。
另一方面,由压力变化的观点可以更清楚地说明螺旋桨作动的原理。
螺旋桨是由一群翼面构建而成,因此它的作动原理与机翼相似。
机翼是靠翼面的几何变化与入流的攻角,使流经翼面上下的流体有不同的速度,且由伯努利定律可知速度的不同会造成翼面上下表面压力的不同,因而产生升力。
而构成螺旋桨叶片的翼面,它的运动是由螺旋桨的前进与旋转所合成的。
若不考虑流体与表面间摩擦力的影响,翼面的升力在前进方向的分量就是螺旋桨的推力,而在旋转方向的分量就是船舶主机须克服的转矩力。
1.3推力和阻力以一片桨叶的截面为例:当船艇静止时,螺旋桨开始工作,把螺旋桨看成不动,则水流以攻角α流向桨叶,其速度为2πnr(n为转速;r为该截面半径)。

关于螺旋桨的一些知识螺旋桨是船舶和飞机等交通工具的重要部件,具有推动物体前进的功能。
在本文中,我们将介绍螺旋桨的工作原理、结构构造、选材等相关知识。
一、螺旋桨的工作原理螺旋桨依靠空气或水流动的原理产生推力,从而推动船舶或飞机前进。
其工作原理可简单归纳为以下几个方面:1. 流体动力学理论:根据流体动力学理论,螺旋桨叶片受到流体的作用会形成载荷,通过迎角改变和旋转速度调节,将动力转化为推进力。
2. 套氏定理:套氏定理指出,在涉及固定的螺旋桨时,液体或气体在进入螺旋桨以前,质量流率保持不变,但速度和压力会发生变化。
这种速度和压力的变化使得螺旋桨产生了推力。
二、螺旋桨的结构构造螺旋桨的结构构造通常由叶片、轴、轴套等组成。
1. 叶片:螺旋桨叶片是螺旋桨的最重要部分,其形状和数量会直接影响推力的大小和效率的高低。
通常,螺旋桨叶片会根据具体设计要求进行定制,以达到最佳的推进效果。
2. 轴和轴套:螺旋桨的轴起到支撑和固定作用,通常由高强度合金钢或碳纤维材料制成,以确保其在高速旋转时的安全可靠性。
轴套则用于固定轴与螺旋桨叶片的连接。
三、螺旋桨的选材螺旋桨的选材对于其使用寿命和推进效果有着重要影响。
常见的螺旋桨选材有以下几种:1. 铝合金:铝合金螺旋桨具有重量轻、制造成本低的优点,适用于速度较低的船舶和小型飞机。
2. 不锈钢:不锈钢螺旋桨在耐蚀性、强度和硬度方面表现出众,适用于海洋环境和高速航行的船舶和飞机。
3. 青铜:青铜螺旋桨具有较好的耐腐蚀性和抗磨损性能,适用于大型船舶和高负荷工况下的飞机。
四、螺旋桨的维护保养为了确保螺旋桨的正常运行和延长其使用寿命,维护保养工作至关重要。
以下是一些建议:1. 定期清洗:螺旋桨表面容易附着赘物,定期清洗可以减少其阻力,提高推进效率。
2. 检查叶片状态:定期检查螺旋桨叶片的变形、裂纹和磨损情况,及时修复或更换叶片,以确保其正常工作。
3. 螺母紧固:定期检查螺旋桨的连接螺母是否紧固,防止因螺母松动而导致螺旋桨脱落或异常运转。





螺旋桨片条理论简介螺旋桨片条理论(Standard Strip Analysis)又称为涡流理论是在儒可夫斯基螺旋桨涡流理论基础上,将普朗特(Prandtl)有限翼展理论应用于螺旋桨涡流模型中提出的螺旋桨特性计算理论。
根据有限翼展理论,一个产生升力的有限翼展机翼,当前方来流绕过机翼时将改变方向,引起气流下洗(Airflow downwash),下洗角取决于机翼升力大小、机翼截面尾迹沿(Trailing Edge)的切线方向和机翼展长。
在无限翼展情况下,机翼扰流无下洗角,机翼扰流仅取决于叶型剖面形状。
下洗角的产生会使螺旋桨叶素相对气流攻角减小,在后面的螺旋桨特性计算中此下洗角称为干涉角。
叶素分析法就是在某半径处剖开螺旋桨桨叶,取出径向一段微元段,利用翼型升阻特性数据对此微元(即叶素)进行受力分析。
由于在航空涡桨发动机控制系统仿真实验过程中,需要建立实时计算的航空螺旋桨模型,一般使用的计算流体力学CFD方法是无法完成计算的,但是又无法避免螺旋桨建模,所以就会使用螺旋桨片条理论进行实时模型的建立,简化螺旋桨模型计算过程,提高实时仿真效率,并通过实验数据进行仿真验证。
片条叶素的示意图如右图所示。
图中叶素段被单独示出,c标示叶素厚度,b标示叶素弦长,叶素的本质是一段机翼翼型。
叶素具有翼型的升力系数、阻力系数,通过对翼型的升力和阻力的计算,可以得到叶素的整体受力,最后积分整个螺旋桨的受力情况。
[编辑本段]详细内容螺旋桨片条理论的关键是将螺旋桨叶片半径剖开(即所谓叶素,构成叶片的片段形状要素)后对叶片的气动特性进行分析,得到截面的力学量变化,如右图所示。
图中β角就是气流下洗干涉角度,图中标示的螺旋桨运行状态时最常用的螺旋桨前进状态,其他的螺旋桨共作状态有:静拉力状态,零拉力状态,制动状态,自转状态,风车状态,全部的工作状态一共六种。
图中V0 ——螺旋桨来流空速α——叶片实际攻角β——叶片的下洗角(Airflow downwash)dLp ——叶片叶素的升力(通过升力系数得到)dDp ——叶片叶素的阻力(通过阻力系数得到)dFp ——叶素的扭矩方向力分量dT' ——叶素的前进推力方向力分量dRp ——叶素受力的合力φ——干涉角β和空气角度φ0角度和φ0——actg(V0/2nπr)2nπr——螺旋桨转速旋转分量v ——干涉角度的气流速度和向量va ——干涉角度的气流速度轴向分量vt ——干涉角度的气流速度周向分量θ——螺旋桨桨叶角度螺旋桨片条理论计算的最关键步骤是计算干涉角度β,计算的根本是求解一个非线性方程f(β)=0,由于百度百科无法提供公式编辑,所以请参阅《空气螺旋桨理论及其应用》(刘沛清编著,北航社)[编辑本段]理论发展螺旋桨理论经历了如下的发展历程:来源于《空气螺旋桨理论及其应用》1- 基于力学原得出的螺旋桨起动理论(19世纪及以前)仅仅实现了功率和拉力与螺旋桨在气流中所起速度建立的联系,而不能把桨叶尺寸和几何关系与其在空气中所激起的速度联系起来,所以这些理论没有设计上的意义。


轮船螺旋桨工作原理
轮船螺旋桨是一种用于推动船只前进的装置,它的工作原理可以简述如下:
1. 螺旋桨的结构:轮船螺旋桨通常由数片叶片组成,这些叶片呈弯曲的形状,安装在轴上形成一个圆盘。
2. 水流动力学:当桨叶转动时,叶片与周围水域发生作用。
根据牛顿第三定律,水流对螺旋桨叶片的作用力与叶片对水流的作用力大小相等,方向相反。
3. 推进原理:当螺旋桨转动时,叶片与水流作用,将叶片前方的水流推动向后。
由于叶片的形状,叶片背面的水流速度较大,而叶片面前的水流速度较小。
4. 牛顿第二定律:根据牛顿第二定律,对于一个物体,当施加的力超过阻力时,物体将加速。
螺旋桨在水中形成的水流差异产生一个反作用力,这个反作用力即为推力,推动船只向前移动。
5. 调节推力:轮船螺旋桨的推力大小可以通过调整螺旋桨转速和叶片的角度来控制。
更高的转速和较大的叶片角度可以产生更大的推力,从而加快船只的速度。
总结起来,轮船螺旋桨利用螺旋桨叶片与水流的作用力来产生推力,从而推动船只前进。
推力的大小可以通过调整转速和叶片角度进行控制。
涡轮螺旋桨动力飞机桨发匹配性能仿真研究史永运;钟易成;邓君湘;田野;徐伟祖【摘要】基于螺旋桨片条理论和航空发动机热力循环原理分别建立了螺旋桨性能和涡桨发动机性能仿真模型.在此基础上,基于飞行器需用推力建立了螺旋桨巡航阶段桨发匹配优化模型,提出了一种计算某一匹配推力系数下螺旋桨效率和进距比关系曲线的方法,并设计了桨发匹配优化方案.针对某型涡桨动力飞机,开展了巡航剖面桨发匹配优化.结果表明:相比于原来的巡航剖面,优化后的巡航剖面飞机巡航航程提高了13%,显著地提升了巡航性能.【期刊名称】《机械制造与自动化》【年(卷),期】2019(000)004【总页数】5页(P116-120)【关键词】涡桨发动机;螺旋桨;桨发匹配;螺旋桨飞机【作者】史永运;钟易成;邓君湘;田野;徐伟祖【作者单位】南京航空航天大学江苏省航空动力系统重点实验室,江苏南京210016;南京航空航天大学江苏省航空动力系统重点实验室,江苏南京210016;沈阳特种设备检测研究研究,辽宁沈阳110000;沈阳特种设备检测研究研究,辽宁沈阳110000;南京普国科技有限公司,江苏南京210000【正文语种】中文【中图分类】V23;TP391.90 引言随着燃油费用的上涨,具有低油耗优点的螺旋桨飞机在军民用飞机市场有着越来越广泛的应用前景[1]。
螺旋桨飞机不同于常规的喷气式动力飞机,其推力/拉力由发动机轴带动旋转的螺旋桨产生,整个动力系统的性能涉及到螺旋桨和发动机两部分的性能,其桨发匹配性能对飞行器推进系统数学模型的准确性及飞行器整体性能影响极大。
因此,亟需开展桨发匹配性能建模研究,便于飞机设计阶段和后期使用阶段的桨发匹配设计,以提高螺旋桨推进系统的性能。
传统的螺旋桨多是定距螺旋桨,只能保证在设计点具有较高的推进效率,很难保证整个飞行包线的飞行性能。
变距螺旋桨的研制解决了这一问题,并由此推动了桨发匹配设计理论的发展。
美国早在1943年就开展了恒速桨的全尺寸风洞试验[2],针对几种典型的标准螺旋桨与机身/短舱组合方式,研究了不同风速下螺旋桨推进效率与旋进比对应的关系,同时形成了一套根据螺旋桨气动数据和发动机特性进行桨发匹配设计的方法[3],用于活塞动力螺旋桨战斗机的方案设计及动力系统选型。
当前位置:首页> 网络课堂> 第八章> 螺旋桨的工作原理螺旋桨的几何特征鱼雷螺旋桨位于鱼雷的尾部,由发动机带动以产生推力,利用该推力克服鱼雷运动时的阻力,使鱼雷以既定的速度航行。
不难理解,为了经商鱼雷的速度,不仅要求鱼雷具有阻力最小的雷体外形,还须要配置效率较高的螺旋桨,才能获得较好的推进效果。
螺旋桨通过推进轴直接由发动机驱动,当螺旋桨旋转时,将水流推向鱼雷后方。
根据作用与反作用原理,水便对螺旋桨产生反作用力,该反作用力即称为螺旋桨的推力。
我们研究螺旋桨的几何特征时,首先要对螺旋面有所了解。
设有一水平线AB(图8-1),匀速地绕线EE旋转,同时又以均匀速度向上移动,则线AB上每一个点就形成一条螺旋线,由这些螺旋线所组成的面叫做螺旋面。
线段AB称为螺旋面的母线,它可以是直线或曲线。
展开了的螺旋线与圆柱体底线间的角度称为螺旋角,以表示,其值可按下式求得(8-1)式中H为螺距。
图8-1 螺旋面的形成(螺旋面的形成演示动画)当母线的圆周运动和直线运动均为匀速运动时,所得到的螺旋面称为等螺距螺旋面。
其螺旋线的展开图形如图8-1所示,不同半径处具有相同的螺距。
图8-2a 径向变螺距螺旋面螺旋线的展开图螺旋面也可以由不同螺距的螺旋线组成。
例如母线AB以均匀的速度绕EE轴线旋转。
也以均匀速度直线上升,只是在不同的半径上具有不同的上升速度,则得到径向变螺距螺旋面,不同的半径处螺距是不同的,其螺旋线的展开图如图8-2(a)所示。
假若母线的旋转运动和前进运动不是均匀的.或者其中任一种运动不是均匀的,则得到轴向变螺距螺旋面,其螺旋线的展开图如图8-2(b)所示。
图8-2b 轴向变螺距螺旋面螺旋线的展开图图8-3 螺旋桨的结构参数(螺旋桨的结构参数演示动画)螺旋桨的结构参数如图8-3所示。
螺旋桨与推进轴联接的部分称为桨毂以一定的角度联按于轮毅上。
鱼雷的桨叶一般为2-7片。
叶片数主要决定于螺旋桨推力的大小。
螺旋桨片条理论简介
螺旋桨片条理论(Standard Strip Analysis)又称为涡流理论是在儒可夫斯基螺旋桨涡流理论基础上,将普朗特(Prandtl)有限翼展理论应用于螺旋桨涡流模型中提出的螺旋桨特性计算理论。
根据有限翼展理论,一个产生升力的有限翼展机翼,当前方来流绕过机翼时将改变方向,引起气流下洗(Airflow downwash),下洗角取决于机翼升力大小、机翼截面尾迹沿(Trailing Edge)的切线方向和机翼展长。
在无限翼展情况下,机翼扰流无下洗角,机翼扰流仅取决于叶型剖面形状。
下洗角的产生会使螺旋桨叶素相对气流攻角减小,在后面的螺旋桨特性计算中此下洗角称为干涉角。
叶素分析法就是在某半径处剖开螺旋桨桨叶,取出径向一段微元段,利用翼型升阻特性数据对此微元(即叶素)进行受力分析。
由于在航空涡桨发动机控制系统仿真实验过程中,需要建立实时计
算的航空螺旋桨模型,一般使用的计算流体力学CFD方法是无法完成计算的,但是又无法避免螺旋桨建模,所以就会使用螺旋桨片条理论进行实时模型的建立,简化螺旋桨模型计算过程,提高实时仿真效率,并通过实验数据进行仿真验证。
片条叶素的示意图如右图所示。
图中叶素段被单独示出,c标示叶素厚度,b标示叶素弦长,叶素的本质是一段机翼翼型。
叶素具有翼型的升力系数、阻力系数,通过对翼型的升力和阻力的计算,可以得到叶素的整体受力,最后积分整个螺旋桨的受力情况。
[编辑本段]
详细内容
螺旋桨片条理论的关键是将螺旋桨叶片半径剖开(即所谓叶素,构成叶片的片段形状要素)后对叶片的气动特性进行分析,得到截面的力学量变化,如右图所示。
图中β角就是气流下洗干涉角度,图中标示的螺旋桨运行状态时最常用的螺旋桨前进状态,其他的螺旋桨共作状态有:静拉力状态,零拉力状态,制动状态,自转状态,风车状态,全部的工作状态一共六种。
图中
V0 ——螺旋桨来流空速
α——叶片实际攻角
β——叶片的下洗角(Airflow downwash)
dLp ——叶片叶素的升力(通过升力系数得到)
dDp ——叶片叶素的阻力(通过阻力系数得到)
dFp ——叶素的扭矩方向力分量
dT' ——叶素的前进推力方向力分量
dRp ——叶素受力的合力
φ——干涉角β和空气角度φ0角度和
φ0——actg(V0/2nπr)
2nπr——螺旋桨转速旋转分量
v ——干涉角度的气流速度和向量
va ——干涉角度的气流速度轴向分量
vt ——干涉角度的气流速度周向分量
θ——螺旋桨桨叶角度
螺旋桨片条理论计算的最关键步骤是计算干涉角度β,计算的根本是求解一个非线性方程f(β)=0,由于百度百科无法提供公式编辑,所以请参阅《空气螺旋桨理论及其应用》(刘沛清编著,北航社)
[编辑本段]
理论发展
螺旋桨理论经历了如下的发展历程:来源于《空气螺旋桨理论及其应用》
1- 基于力学原得出的螺旋桨起动理论(19世纪及以前)
仅仅实现了功率和拉力与螺旋桨在气流中所起速度建立的联系,而不能把桨叶尺寸和几何关系与其在空气中所激起的速度联系起来,所以这些理论没有设计上的意义。
2- 螺旋桨叶素理论(1878年,W.Froud)
把螺旋桨桨叶当做螺旋桨的机翼建立的理论,这种理论也成为孤立桨叶理论(螺旋桨叶素理论)。
同样的这种理论也不能用来设计螺旋桨,仅仅给出某些联系。
3- 动量和叶素理论的联合理论(19世纪)
这样的理论可以对螺旋桨的几何尺寸进行指导性的修正,从而可以指导螺旋桨叶片的设计工作。
4- 螺旋桨涡流理论(20世纪)
茹科夫斯基涡流理论和普朗特的有限翼展理论综合理论,也就是现在的片条理论,更进一步得到了几何特性和气动特性之间的关系,在螺旋桨气动设计中得到了广泛应用。
可以应用于数值模拟。
5- 螺旋桨数值模拟设计阶段(20世纪末)
纳维斯托克斯方程(N-S方程)数值计算,优点是结果精确可信,缺点是不可实时计算。
[编辑本段]
应用实例
可以通过如下步骤使用螺旋桨片条理论计算螺旋桨力学参数。
1-查找资料得到需要建立数学模型螺旋桨的叶型,叶型的全部数据可以百度一下"Airfoil Investigation Database"里面有上千种叶片的升力系数阻力系数的吹风数据,通过这些数据得到螺旋桨的风洞曲线。
2-通过这些曲线,带入到f(β)=0(上一环节提到过)中,求解得到干涉气流角。
3-根据干涉气流角度会进而通过公式演算得到全部的螺旋桨计算数据。
计算时间不会长于0.01s。
(Windows平台,32位core2酷睿二处理器2G内存,Matlab建模验证)。