运筹学资料报告材料护士值班

线性规划方法在护士值班安排中的应用研究【摘要】本文依据线性规划模型理论，阐述了线性规划模型的标准形式及模型建立的基本步骤；在此基础上，以护士值班安排为案例，建立了一周护士需求最少的线性规划模型，确定了其边界约束条件。

计算表明，线性规划最优化方法是解决护士人力资源分配的科学可行的方法。

【Abstract】Objective Based on related theory, standard form and basic steps of the Linear Programming(LP)Model were expatiated in this paper. The linear programming model of arrangement of nurses on duty was built and the boundary condition was confirmed. It is proved that LP approach is a practical and scientific tool for allocating manpower of nurses.【Key words】linear programming；nurse；mathematics models最优化方法是数学模型与应用科学技术结合的产物。

最优化问题主要包括线性规划方法、约束条件下的优化、无约束条件下的优化、线性约束下的二次规划、离散规划优化、整数规划优化、多目标规划优化等内容。

最优化方法中，目前应用最广泛和最成熟的是线性规划方法，它为实际应用提供了很好的基础平台和技术方法［1 2］。

科学合理地配置人员，目的是最大限度地发挥人力资源的作用，实现各类成本最低、工作效率最高。

宋焕虎［3］针对生产管理中出现的问题，利用线性规划理论合理优化配置了劳动力资源，优化了生产工艺衔接，实现了人员、设备、材料、时间的优化配置，提高了劳动生产率和经济效益。

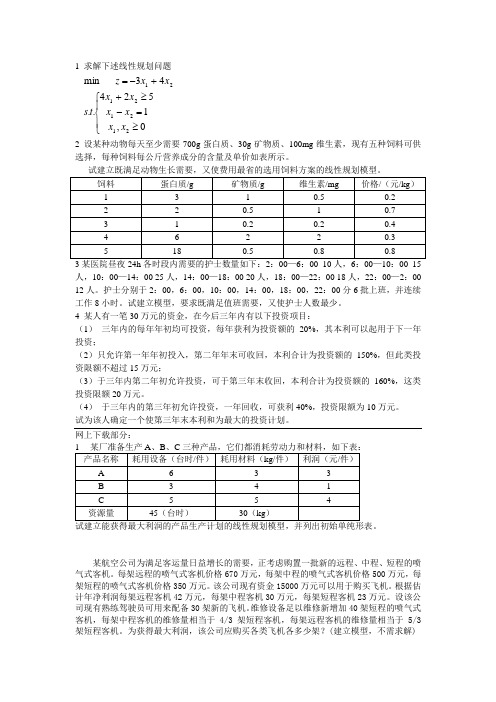
1 求解下述线性规划问题⎪⎩⎪⎨⎧≥=-≥++-=0,1524..43min21212121x x x x x x t s x x z2 设某种动物每天至少需要700g 蛋白质、30g 矿物质、100mg 维生素，现有五种饲料可供选择，每种饲料每公斤营养成分的含量及单价如表所示。

3某医院昼夜24h 各时段内需要的护士数量如下：2：00—6：00 10人，6：00—10：00 15人，10：00—14：00 25人，14：00—18：00 20人，18：00—22：00 18人，22：00—2：00 12人。

护士分别于2：00，6：00，10：00，14：00，18：00，22：00分6批上班，并连续工作8小时。

试建立模型，要求既满足值班需要，又使护士人数最少。

4 某人有一笔30万元的资金，在今后三年内有以下投资项目：（1） 三年内的每年年初均可投资，每年获利为投资额的20%，其本利可以起用于下一年投资；（2）只允许第一年年初投入，第二年年末可收回，本利合计为投资额的150%，但此类投资限额不超过15万元；（3）于三年内第二年初允许投资，可于第三年末收回，本利合计为投资额的160%，这类投资限额20万元。

（4） 于三年内的第三年初允许投资，一年回收，可获利40%，投资限额为10万元。

试为该人确定一个使第三年末本利和为最大的投资计划。

网上下载部分：某航空公司为满足客运量日益增长的需要，正考虑购置一批新的远程、中程、短程的喷气式客机。

每架远程的喷气式客机价格670万元，每架中程的喷气式客机价格500万元，每架短程的喷气式客机价格350万元。

该公司现有资金15000万元可以用于购买飞机。

根据估计年净利润每架远程客机42万元，每架中程客机30万元，每架短程客机23万元。

设该公司现有熟练驾驶员可用来配备30架新的飞机。

维修设备足以维修新增加40架短程的喷气式客机，每架中程客机的维修量相当于4/3架短程客机，每架远程客机的维修量相当于5/3架短程客机。

西安电子科技大学硕士研究生入学考试2007 年运筹学试题参考解答考试时间：3 小时一、（25 分）某医院在每天各时段内需护士人数如下表所示时段6:00-8:00 8:00-14:00 14:00-16:00 16:00-22:00 22:00-6:00(次日) 需护士数25 35 32 28 22该医院安排4 个护士上班班次：早班6:00-14:00，白班8:00-16:00，晚班14:00:22:00，夜班22:00-6:00(次日)。

每名护士每天值一个班次。

（1）该医院每天至少需要多少名护士才能满足值班需要？（2）有人提议为简化管理，只设早、晚、夜三个班，取消白班，这种情况下又需要多少名护士能满足值班需要。

对（1）（2）两种情况分别建立数学模型，需要求解。

但需作出直观判断，哪一种情况需要护士数多一些，为什么？二、（25 分）已知线形规划问题用单纯形法求解时，其最终单纯形表如下：x1 X2 X3 X4 X5X1 5/3 1 -1/3 0 1/3 -1/3X3 3 0 1 1 -1/5 2/5cj-xj 0 -2 0 -1/5 -3/5（1）写出上述线形规划的对偶问题及其最优解；（2）若问题中x2 列的系数由(1,3,4)T 变为(3,2,3)T，求新的最优解；（3）若问题中约束（b）的右端项变为30，求解的最优解。

三、（25 分）某公司承担4 条航线的运输任务，已知：（1）各条航线的起点城市和终点城市及每天的航班数（见本题表1）；（2）各城市间的航行时间（见本题表2）；（3）所有航线都使用同一种船只，每次装船和卸船时间均为1 天，问该公司至少应配备多少条船才能满足所有航线运输的需要？表1表2（航行时间：天）A B C D E FA 0 1 2 14 7 7B 1 0 3 13 8 8C 2 3 0 15 5 5D 14 13 15 0 17 20E 7 8 5 17 0 3F 7 8 5 20 3 0四、（25 分）公司决定使用1000 万元新产品基金开发A、B、C 三种新产品。

护士排班与值班制度引言概述：护士排班与值班制度是医疗机构中重要的管理环节，它直接关系到患者的医疗安全和医疗质量。

合理的排班和值班制度能够保障医院各科室的正常运转，提高医护人员的工作效率和满意度。

本文将从五个方面详细阐述护士排班与值班制度的重要性和实施方法。

一、人力资源管理1.1 护士人员需求分析：根据科室的工作量和患者的需求，进行科学合理的人员需求分析，确保每个科室有足够的护士人员。

1.2 护士编制与配备：根据科室的特点和工作强度，合理制定护士编制和配备标准，确保每个科室的护士人员数量和质量。

1.3 护士岗位职责与要求：明确护士的岗位职责和工作要求，确保护士人员能够胜任各种工作任务。

二、排班制度设计2.1 排班周期：根据科室的工作特点和人员数量，制定合理的排班周期，一般可以按照一周或一个月为周期进行排班。

2.2 排班模式：根据科室的工作强度和护士的休息需求，选择合适的排班模式，如固定班次、轮班制等。

2.3 排班规则：制定科学合理的排班规则，包括工作时间、休息时间、加班制度等，确保护士的工作时间和休息时间合理安排。

三、值班制度管理3.1 值班表的制定：根据科室的工作特点和护士的排班情况，制定科学合理的值班表，确保每个时间段都有足够的护士在岗。

3.2 值班交接：在每个班次的交接时，进行详细的值班交接，包括患者的病情、医嘱的执行情况等，确保患者的医疗安全。

3.3 值班考核：建立完善的值班考核机制，对护士的值班情况进行评估和考核，及时发现问题并进行整改。

四、应急值班管理4.1 应急值班准备：制定应急值班预案，明确各类突发事件的应对措施和值班人员的职责，确保在突发情况下能够及时有效地应对。

4.2 应急值班培训：组织护士进行应急值班培训，提高其应对突发事件的能力和水平，确保患者的安全和医疗质量。

4.3 应急值班评估：定期对应急值班情况进行评估和总结，发现问题并进行改进，提高应对突发事件的能力。

五、信息化管理系统支持5.1 排班管理系统：引入信息化排班管理系统，实现排班的自动化和规范化，提高排班效率和准确性。

护士值班报告范本一、基本信息1、值班日期：具体年月日2、值班护士姓名：姓名3、接班时间：具体时间4、交班时间：具体时间二、病人概况1、总病人数：数字新入院病人：数字，分别为：病人 1：姓名，性别，年龄，诊断，入院时间，主要症状和体征。

病人 2：……出院病人：数字，分别为：病人 1：姓名，性别，年龄，诊断，出院时间，出院情况。

病人 2：……病重病人：数字，分别为：病人 1：姓名，性别，年龄，诊断，目前病情和治疗措施。

病人 2：……病危病人：数字，分别为：病人 1：姓名，性别，年龄，诊断，目前病情和紧急处理情况。

病人 2：……2、手术病人：数字术前病人：数字，分别为：病人1：姓名，性别，年龄，手术名称，手术时间，术前准备情况。

病人 2：……术后病人：数字，分别为：病人 1：姓名，性别，年龄，手术名称，手术时间，术后恢复情况和护理要点。

病人 2：……三、病情变化及处理1、病人 1：姓名病情变化：详细描述病情的变化，如症状加重、生命体征异常等处理措施：描述采取的护理措施和治疗手段，如调整药物、吸氧、进行某项检查等处理结果：说明病情变化经过处理后的情况，是否稳定、好转或仍需进一步观察2、病人 2：……四、特殊情况记录1、病人投诉或纠纷：如有，详细记录事件的经过、原因和处理结果2、医疗设备故障：记录故障设备的名称、故障发生时间和处理情况3、突发事件：如病人摔倒、突然停电等，记录事件的经过和处理措施五、护理操作执行情况1、输液：总人次，其中包括具体药物和输液量，有无输液反应。

2、注射：总人次，包括肌肉注射、皮下注射等的次数和药物，有无不良反应。

3、伤口护理：人次，分别描述伤口的情况和护理方法。

4、导尿：人次，说明导尿的原因和过程，以及尿液的情况。

5、其他护理操作：如鼻饲、吸痰等，分别记录操作的人次和具体情况六、医嘱执行情况1、已执行的长期医嘱：列出医嘱的内容和执行时间2、临时医嘱：详细记录临时医嘱的内容、执行时间和执行护士3、未执行医嘱及原因：如有，说明未执行医嘱的名称和原因七、护理文书记录情况1、护理记录单：是否按时、准确记录，有无遗漏或错误2、体温单：绘制是否规范，数据是否准确3、其他护理文书：如评估单、交接单等，记录其完成情况八、物品交接情况1、药品：列出重点药品的名称、数量和有效期，有无短缺或过期2、医疗器械：如血糖仪、血压计等，检查其性能和数量是否正常3、一次性物品：如注射器、输液器等，统计剩余数量和使用情况九、问题与建议1、工作中遇到的问题：如护理人员不足、物资配备不全等2、对科室管理和护理工作的建议：提出改进的意见和措施十、签名值班护士签名：姓名需要注意的是，护士值班报告的内容应真实、客观、准确、及时，不得虚构或隐瞒任何信息。

护士值班、交接班制度标题：护士值班、交接班制度引言概述：护士值班和交接班制度是医疗机构中非常重要的环节，对于患者的安全和护理质量起着至关重要的作用。

本文将从五个大点来阐述护士值班、交接班制度的重要性和具体内容。

正文内容：1. 护士值班制度1.1 值班制度的意义- 值班制度保证了医疗机构全天候的护理服务。

- 通过合理安排护士的工作时间，确保护士队伍的稳定性和连续性。

1.2 值班制度的组织- 值班表的制定：根据科室需求、护士人数和工作强度，制定合理的值班表。

- 值班人员的轮班：采取轮班制度，确保每位护士都能参与值班工作，减轻个别护士的工作压力。

1.3 值班期间的职责- 护士在值班期间需负责患者的护理、监测和记录，及时处理突发状况。

- 值班期间需与医生、其他科室和患者家属保持有效的沟通，协调各方的工作。

2. 护士交接班制度2.1 交接班制度的意义- 交接班制度确保了患者的连续护理，避免信息的遗漏和错误。

- 通过交接班，护士可以及时了解患者的病情和治疗计划，提供更加个性化的护理。

2.2 交接班的流程- 交接班前的准备：整理患者的病历资料、医嘱和检查结果，准备好交接班表格。

- 交接班的内容：包括患者的基本信息、病情变化、治疗计划、特殊注意事项等。

- 交接班的形式：可以是面对面的交流、书面记录或电子化系统，确保信息的准确传递。

2.3 交接班的注意事项- 交接班时需保持专注，避免分心和疏漏。

- 交接班时需注意保护患者的隐私和机密信息。

- 交接班时需及时反馈和沟通，确保信息的准确性和完整性。

总结：护士值班、交接班制度对于医疗机构的正常运作和患者的安全至关重要。

值班制度的合理组织和职责分工保证了全天候的护理服务；交接班制度的规范和信息传递确保了患者护理的连续性和个性化。

在实际操作中，护士需要严格遵守制度要求，保持专业和高效的工作态度，以提供优质的护理服务。

医院护士值班工作汇报尊敬的领导：您好！本人是某医院的护士，现就值班工作情况向您汇报。

一、工作概况本周，我所在的8个科室共有35名护士轮流值班，每个班次为12小时，上午7:00-19:00或晚上19:00-7:00。

在这段时间里，我们主要负责病人的生活护理、监护、病情观察等工作，并及时进行病情反馈，以便医生能够采取及时有效的治疗。

二、重点工作1. 生命体征监测作为护士，我们要时刻关注病人的生命体征变化，定时测量体温、血压、心率、呼吸等指标，并及时记录在病历中，保证医生能够及时了解病人身体状况。

2. 安全防范在门禁、巡查、消毒、隔离、污染物处置等方面，我们采取了各种必要措施，确保医院内部环境无菌、安全，保障医护人员和病人的身体健康。

3. 睡眠监测医院里有不少病人需要持续观察，有些病人需要24小时照顾。

我们要尽可能地控制噪音，避免打扰到病人，同时保证我们护士值班期间能够保持清醒。

三、开展情况在本周的值班过程中，我们精心组织协调，务求让病人得到最好的护理。

通过我们的努力，病人对我们的工作给予了高度评价，医院领导和同事也给予了充分的认可和支持。

四、存在问题在日常护理过程中，我们经常会出现人手不足的情况，有时候需要同时照顾多位病人，并进行各种护理操作。

因此，在值班期间，我们需要更加努力、更加细心，以保证病人得到最精细的照顾。

五、总结作为医院中重要的一份力量，我们的护士队伍将继续保持全情投入，以优质的服务、高效的工作效率为病患提供更好的医疗体验。

同时，我们也会不断总结工作中的经验和教训，优化工作流程，提高工作效率，为医院的发展做出更大的贡献。

医院护士值班工作汇报完毕，谢谢领导的关注与支持！此致敬礼！XXX医院护士XXXX年XX月XX日。

运筹学实验报告一、实验目的：通过实验熟悉单纯形法的原理，掌握matlab循环语句的应用，提高编程的能力和技巧，体会matlab在进行数学求解方面的方便快捷。

二、实验环境：Matlab2012b,计算机三、实验内容（包含参数取值情况）：构造单纯形算法解决线性规划问题Min z=cxs.t. Ax=bxj>=0,j=1,…,n函数功能如下：function[S,val]=danchun(A1,C,N)其中，S为最优值，Val为最优解，A1为标准形式LP问题的约束矩阵及最后一列为资源向量（注：资源向量要大于零），A1=[A+b]；C是目标函数的系数向量，C=c；N为初始基的下标（注：请按照顺序输入，若没有初始基则定义N=[]）。

先输入A1,C,N三个必要参数，然后调用danchun（A1,C,N）进行求解。

在此函数中，首先判断N的长度是否为空，若为空，则flag=1，进入初始解问题的迭代求值，添加辅助问题，构建单纯形表，求g所对应的RHS值，若其>0,则返回该问题无解，若其=0，则返回A1,C,N三个参数，继续构造单纯形表求解。

A1为经过变换后的系数及资源向量，C为单纯形表的第一行，N为经过辅助问题求解之后的基的下标。

否则，直接构建单纯形表，对该问题进行求解，此时flag=2,多次迭代后找到解。

另外，若在大于零的检验数所对应的系数均小于零时，会显示“此问题无界”。

若找到最优解和最优值时，会输出“val”和“S=”以及具体数值。

四、源程序（在matlab中输入edit后回车，写在.M文件中，并保存为danchun.M）function[S,val]=danchun(A1,C,N)if(length(N)==0)gN=zeros(1,length(A1(:,1)));gC=[-C,gN,0];%原文题的检验数的矩阵G=[zeros(1,length(C)),-ones(1,length(gN)),0];val=zeros(1,length(C));%val为最优解；for i=(length(C)+1):length(C)+length(A1(:,1))%生成基变量gN(i-length(C))=i;endNn=gN;%%%%%%%ll=zeros(1,length(N));%比值最小原则%生成除了最上端两行的表的矩阵gb=A1(:,length(C)+1);A1(:,length(C)+1)=[];l=zeros(length(gN),length(gN));gA=[A1,l,gb];for i=1:length(gb)gA(i,gN(i))=1;endfor i=1:length(gN)%J为基本可行基所对应的检验数J(i)=G(gN(i));endfor i=1:length(gN)%找到基本可行基的检验数，将其赋值为0 if(J(i)~=0)G=G-(J(i)/gA(i,gN(i)))*gA(i,:);endendflag=1;elseflag=2;A=A1;Z=[-C,0];%单纯形表的第一行val=zeros(1,length(C));%val为最优解；ll=zeros(1,length(N));%比值最小原则end%%初始解问题while flag==1for i=1:length(gN)%J为基本可行基所对应的G的检验数J(i)=G(gN(i));JZ(i)=Z(gN(i));%JZ为基本可行基所对应的Z的检验数endfor i=1:length(gN)%找到基本可行基的检验数，将其赋值为0 if(J(i)~=0)G=G-(J(i)/gA(i,gN(i)))*gA(i,:);Z=Z-(JZ(i)/gA(i,gN(i)))*gA(i,:);endG1=G;%G1为检验数G1(:,length(G1))=[];D=max(G1);%找到检验数的最大值if(D<=0)%检验数都小于0if(G(length(G))>=1)disp('此情况无解');flag=0;elseif(G(length(G))>=0)for i=1:length(gN)if(max(gN)<=length(A1(1,:)));flag=2;for j=1:length(Nn)a=Nn(1);gA(:,a)=[];Z(a)=[];endA=gA;N=gN;break;endendendendelse%检验数大于0for i=1:length(G)if(G(i)==D)%找到最大的那个检验数所对应的元素for j=1:length(gN)if(gA(j,i)>0)ll(j)=gA(j,length(G))/gA(j,i);%求比值elsell(j)=10000;endendd=min(ll);for k=1:length(ll)%找到进基和离基if(ll(k)==d)gN(k)=i;gA(k,:)=gA(k,:)/gA(k,i);for m=1:k-1gA(m,:)=-(gA(m,i)/gA(k,i))*gA(k,:)+gA(m,:);endfor n=k+1:length(ll)gA(n,:)=-(gA(n,i)/gA(k,i))*gA(k,:)+gA(n,:);endbreak;endendendendendendwhile(flag==2)for i=1:length(N)%J为基本可行基所对应的检验数J(i)=Z(N(i));endfor i=1:length(N)%找到基本可行基的检验数，将其赋值为0if(J(i)~=0)Z=Z-(J(i)/A(i,N(i)))*A(i,:);endendZ1=Z;%Z1为检验数Z1(:,length(Z1))=[];D=max(Z1);%找到检验数的最大值if(D<=0)%检验数都小于0disp('已找到最优解和最优值')for i=1:length(N)val(N(i))=A(i,length(Z));endS=Z(length(Z));disp('val');disp(val);flag=0;else%检验数大于0for i=1:length(Z)if(Z(i)==D)%找到最大的那个检验数所对应的元素for j=1:length(N)if(A(j,i)>0)ll(j)=A(j,length(Z))/A(j,i);%求比值elsell(j)=10000;endendd=min(ll);if(d==10000)disp('此问题无界')flag=0;break;endfor k=1:length(ll)%找到进基和离基if(ll(k)==d)N(k)=i;A(k,:)=A(k,:)/A(k,i);for m=1:k-1A(m,:)=-(A(m,i)/A(k,i))*A(k,:)+A(m,:);endfor n=k+1:length(ll)A(n,:)=-(A(n,i)/A(k,i))*A(k,:)+A(n,:);endbreakendendendendendend五、运行结果与数据测试参考例题：例1：Min z=3x1+x2+x3+x4s.t. -2x1+2x2+x3=43x1+2x+x4=6Xj>=0,j=1,2,3,4在workspace中写入，形式如下：>> A=[-2 2 1 0 43 1 0 1 6]A =-2 2 1 0 43 1 0 1 6>> C=[3 1 1 1]C =3 1 1 1>> N=[3 4]N =3 4>> danchun(A,C,N)已找到最优解和最优值val0 2 0 4ans =6例2：初始解问题Min z=5x1+21x3s.t. x1-x2+6x3-x4=2x1+x2+2x3-x5=1xj>=0,j=1,…,5在workspace中写入，形式如下：>> A=[1 -1 6 -1 0 21 12 0 -1 1]A =1 -1 6 -1 0 21 12 0 -1 1 >> C=[5 0 21 0 0]C =5 0 21 0 0>> N=[]N =[]>> danchun(A,C,N)已找到最优解和最优值val0.5000 0 0.2500 0 0ans =7.7500六、求解实际问题（即解决附件中的实验题目）实验题目列出下列问题的数学模型，并用你自己的单纯形算法程序进行计算，最后给出计算结果。